Theoretical Study of a Novel Power Cycle for Enhanced Geothermal Systems
Abstract
:1. Introduction
- (1)
- The critical point of each CO2-based mixture working fluid investigated in this study is higher than that of the pure CO2; hence, a condensing process with phase change could be realized. As a result, a conventional condenser could be used, without being restricted to the use of costly large-area coolers, as in a Brayton cycle. Thus, it was thermodynamically possible to realize a transcritical power cycle with a higher thermal efficiency.
- (2)
- An increasing-pressure endothermic process (instead of an isobarically endothermic process) could be realized in a few-hundred-meters-long downhole heat exchanger (DHE) by making use of gravitational potential energy [17]. This resulted in an increase of the cycle’s heat gain. In addition, the CO2-based mixture working fluid used in this proposed power cycle had a obvious buoyancy-driven thermosiphon effect; hence, the working-fluid’s DHE outlet pressure (i.e., the working-fluid’s turbine inlet pressure) could be increased. As a result, the cycle’s power output was increased.
- (3)
- In the downhole heat exchanger (DHE), the working fluid absorbed heat from the geofluid with a higher temperature at depth; thus, a higher working-fluid’s DHE outlet temperature (i.e., a higher working-fluid’s turbine inlet temperature) could be obtained, which would also benefit the cycle’s power generation.
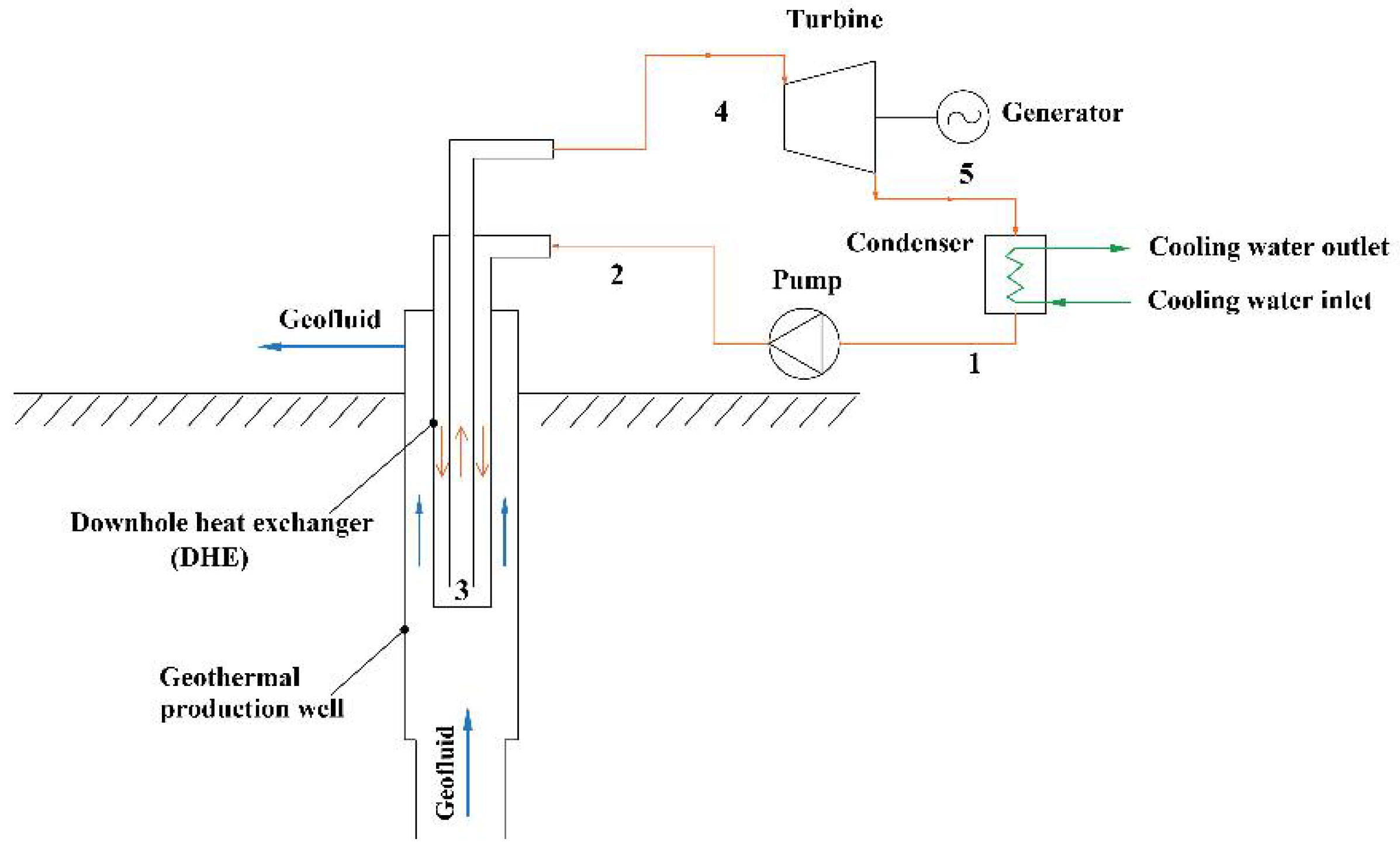
2. System Description
3. Model Development
3.1. Assumptions and Boundary Conditions
- (1)
- The entire system is analyzed under steady-state conditions.
- (2)
- Friction losses and heat losses in pipes (except in the downhole heat exchanger) and in the condenser are ignored.
- (3)
- The working fluid is in a saturated liquid state at the condenser outlet
- (4)
- The working fluid is pressurized to a pressure higher than the working fluid’s critical pressure before it is injected into the downhole heat exchanger.
- (5)
- The geofluid temperature is defined to be that at the bottom of the downhole heat exchanger; both the geofluid temperature and the pressure at the wellhead are set as the boundary conditions.
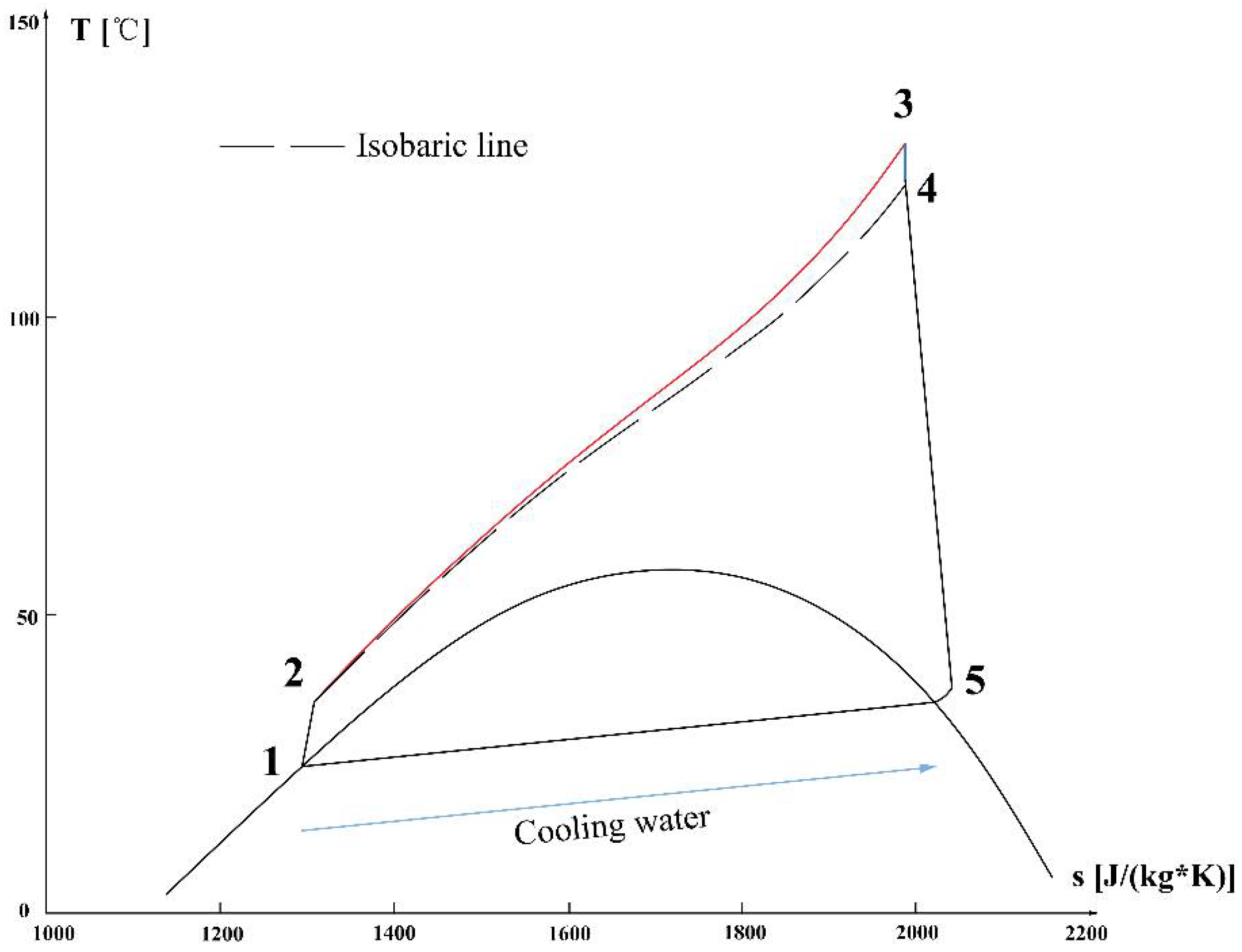
3.2. Power Cycle Model
3.2.1. Turbine
3.2.2. Condenser
3.2.3. Injection Pump
3.2.4. Coaxial Double-Pipe Downhole Heat Exchanger
3.2.5. Cycle’s Net and Specific Power Output
4. Results and Discussion
4.1. Comparison of Using Different CO2-Based Binary Working Fluids
4.2. Effect of Mixture Mass Fractions
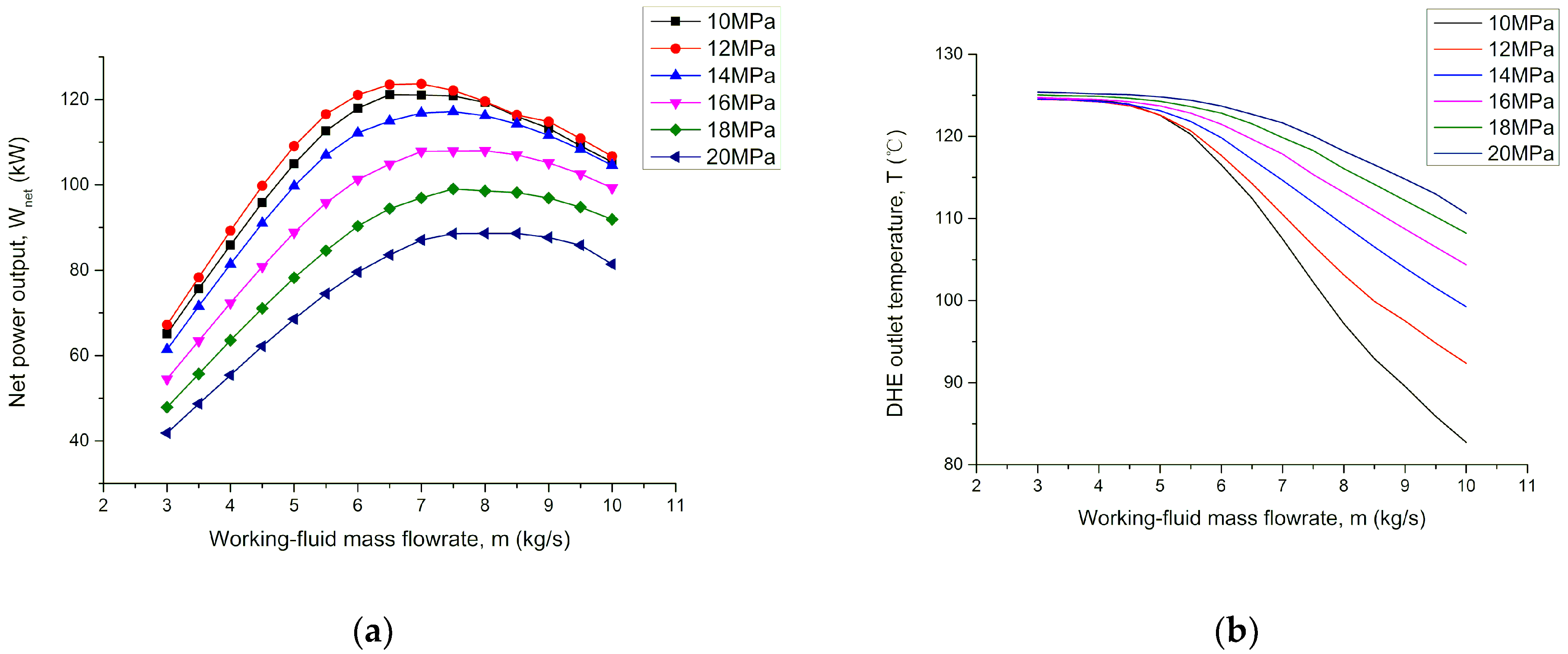
4.3. Effect of Working-Fluid’s DHE Inlet Pressure
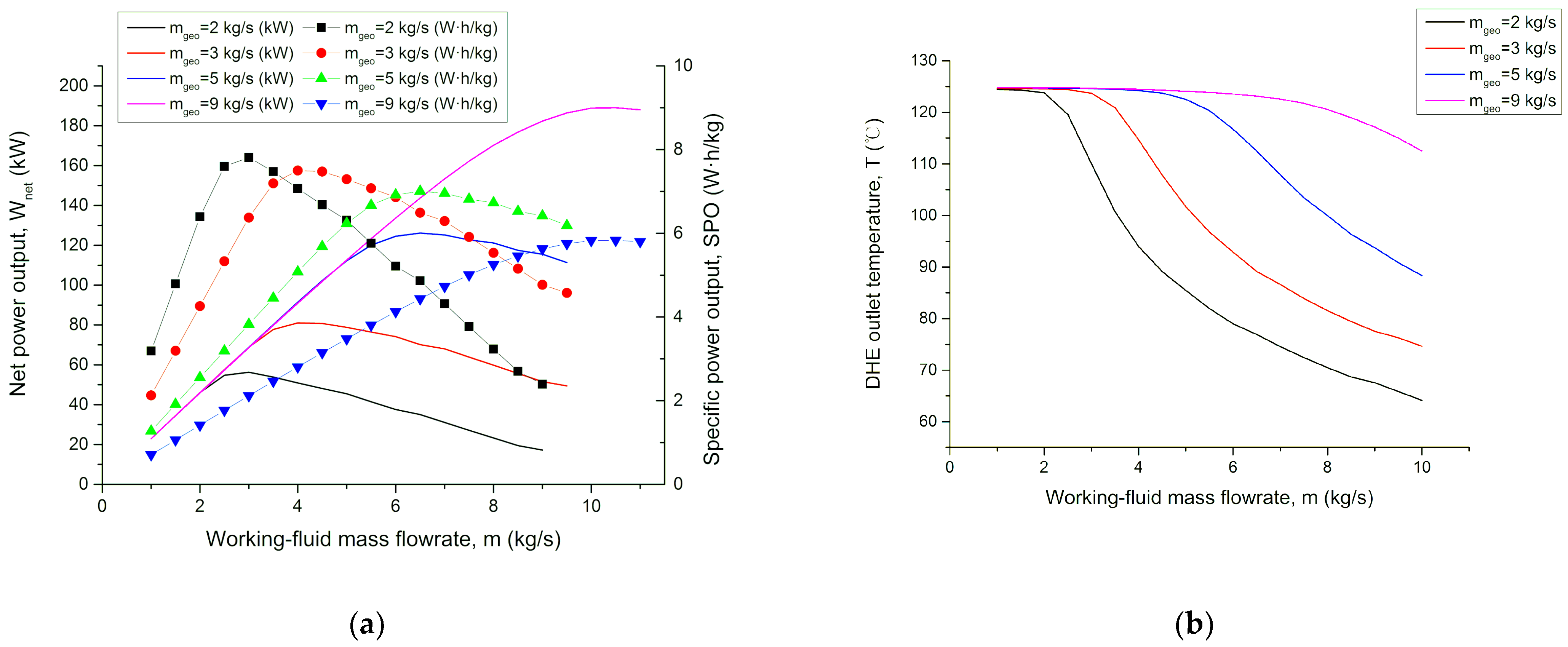
4.4. Effect of Geofluid Mass Flowrate
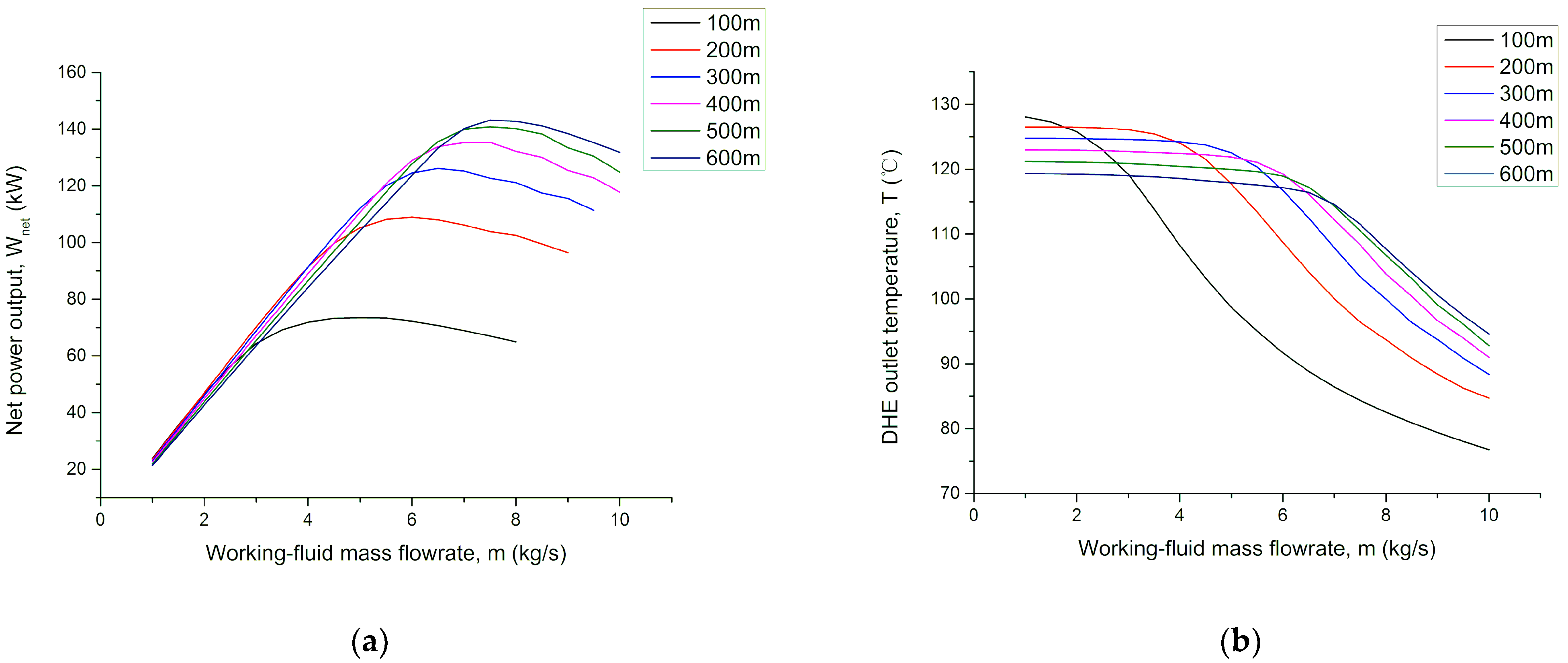
4.5. Effect of the Downhole Heat Exchanger (DHE) Length
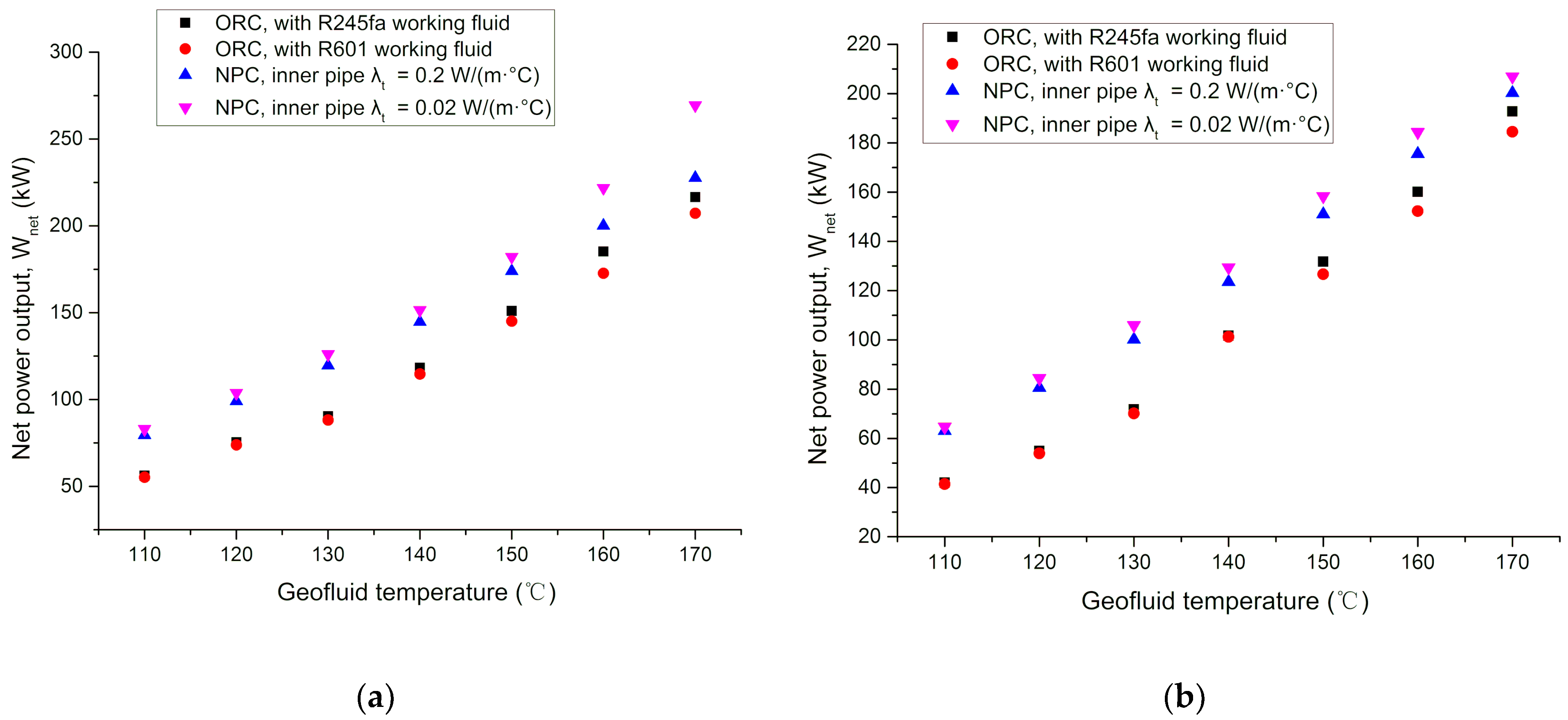
4.6. Performance Comparison between the Developed NPC and Conventional ORC
5. Conclusions
- (1)
- A transcritical power cycle with a higher net power output was developed using a suitable CO2-based mixture working fluid. Since the critical point of each used CO2-based mixture working fluid is higher than that of the pure CO2, a condensing process with a phase change can be realized. As a result, conventional condenser can be used, without being restricted to the use of costly large-area coolers, as in a CO2 Brayton cycle.
- (2)
- In the developed novel power cycle, an increasing-pressure endothermic process (instead of an isobarically endothermic process) was realized in a few-hundred-meters-long downhole heat exchanger (DHE) by making use of gravitational potential energy, which increases the cycle’s heat gain, as well as the working fluid’s pressure at the turbine inlet and, hence, increases the cycle’s power output.
- (3)
- In the downhole heat exchanger, the working fluid absorbs heat from the geofluid with a higher temperature at depth; thus, a higher outlet temperature of working fluid can be obtained, resulting in an increase of the working fluid’s temperature at the turbine inlet, contributing to a higher power output.
- (4)
- The increasing-pressure endothermic process in the DHE has a better match with the temperature change of the heat source (geofluid), as does the exothermic process in the condenser with the temperature change of the sink (cooling water), which reduces the heat transfer irreversibility and improves the power cycle efficiency.
- (5)
- For a given geofluid mass flowrate, the working-fluid’s flowrate and its DHE inlet pressure should be optimized simultaneously to get the maximum net power output. Higher geofluid mass flowrate usually corresponds to a higher optimum working-fluid flowrate.
- (6)
- From the thermophysical point of view, the longer the DHE, the greater the corresponding (optimum) working-fluid flowrate, the higher the net power output. In practice, however, the optimum length of the DHE should be determined based on engineering economics, considering the costs of both the DHE and the mixture working fluid.
- (7)
- In terms of the net power output, the developed NPC has a better thermodynamic performance than the conventional ORC for the geofluid temperature ranging from 110 °C to 170 °C. The lower the geofluid temperature, the more advantage of using the developed NPC.
- (8)
- Future research regarding an experimental study on the condensing process of the CO2-based mixture working fluid has been planned and will be carried out later.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| H | Specific enthalpy, kJ/kg |
| j | Joule-Thomson coefficient |
| m | Working fluid mass flowrate, kg/s |
| Nu | Nusselt number, dimensionless |
| Pr | Prandtl number, dimensionless |
| Q | Heat transfer rate, kW |
| Raw | The thermal resistance between the geothermal water and the annulus, kW/(m2·°C) |
| Re | Reynolds number, dimensionless |
| Rta | The thermal resistance between the inner tube and the annulus, kW/(m2·°C) |
| Rw | The thermal resistance between the geothermal water and the formation, kW/(m2·°C) |
| t | Injection time, s |
| tD | Dimensionless injection time |
| W | The power output, kW |
| Wnet | Net power output, kW |
| α | Formation heat diffusivity(α = λe/(ce ρe)), m2/s |
| Subscripts | |
| 1,2,3… | State points |
| C | Condenser |
| cw | Cooling water |
| geo | Geofluid |
| h | Downhole heat exchanger |
| in | Inlet working fluid state |
| p | Pump |
| pinch | Pinch point |
| T | Turbine |
| Acronym | |
| CPG | CO2 Plume Geothermal |
| DHE | Downhole heat exchanger |
| EGS | Enhanced geothermal system |
| HDR | Hot Dry Rock |
| LEL | lower explosive limit |
| OEL | occupational exposure limit |
| ORC | Organic Rankine cycle |
| TRC | Transcritical Rankine cycle |
Appendix A
Appendix A.1. Flow Pressure Model of Downhole Heat Exchanger
Appendix A.2. DHE Temperature Field Model
Appendix A.3. DHE Heat Transfer Model
- (a)
- Heat transfer between the inner pipe and annulus


- (b)
- Heat transfer between the annulus and geofluid
- (c)
- Heat transfer between the geofluid and formation
Appendix A.4. DHE Model Solution Procedure

References
- Yamankaradeniz, N.; Bademlioglu, A.H.; Kaynakli, O. Performance Assessments of Organic Rankine Cycle With Internal Heat Exchanger Based on Exergetic Approach. J. Energy Resour. Technol. 2018, 140, 102001. [Google Scholar] [CrossRef]
- Chen, H.; Goswami, D.Y.; Stefanakos, E.K. A review of thermodynamic cycles and working fluids for the conversion of low-grade heat. Renew. Sustain. Energy Rev. 2010, 14, 3059–3067. [Google Scholar] [CrossRef]
- El Haj Assad, M.; Aryanfar, Y.; Javaherian, A.; Khosravi, A.; Aghaei, K.; Hosseinzadeh, S.; Pabon, J.; Mahmoudi, S.M.S. Energy, exergy, economic and exergoenvironmental analyses of transcritical CO2 cycle powered by single flash geothermal power plant. Int. J. Low-Carbon Technol. 2021, 16, 1504–1518. [Google Scholar] [CrossRef]
- Khosravi, A.; Syri, S.; Zhao, X.; Assad, M.E.H. An artificial intelligence approach for thermodynamic modeling of geothermal based-organic Rankine cycle equipped with solar system. Geothermics 2019, 80, 138–154. [Google Scholar] [CrossRef]
- Pasinato, H.D. Working Fluid Dependence on Source Temperature for Organic Rankine Cycles. J. Energy Resour. Technol. 2019, 142, 012103. [Google Scholar] [CrossRef]
- Karellas, S.; Schuster, A. Supercritical Fluid Parameters in Organic Rankine Cycle Applications. Int. J. Thermodyn. 2008, 11, 101–108. [Google Scholar]
- Zhang, X.R.; Yamaguchi, H.; Fujima, K.; Enomoto, M.; Sawada, N. Study of solar energy powered transcritical cycle using supercritical carbon dioxide. Int. J. Energy Res. 2006, 30, 1117–1129. [Google Scholar] [CrossRef]
- Zhang, X.; Yamaguchi, H.; Fujima, K.; Enomoto, M.; Sawada, N. Theoretical analysis of a thermodynamic cycle for power and heat production using supercritical carbon dioxide. Energy 2007, 32, 591–599. [Google Scholar] [CrossRef]
- Chen, Y.; Lundqvist, P.; Johansson, A.; Platell, P. A comparative study of the carbon dioxide transcritical power cycle compared with an organic rankine cycle with R123 as working fluid in waste heat recovery. Appl. Therm. Eng. 2006, 26, 2142–2147. [Google Scholar] [CrossRef]
- Adams, B.M.; Kuehn, T.H.; Bielicki, J.M.; Randolph, J.B.; Saar, M.O. On the importance of the thermosiphon effect in CPG (CO2 plume geothermal) power systems. Energy 2014, 69, 409–418. [Google Scholar] [CrossRef]
- Sun, X.; Liao, Y.; Wang, Z.; Sun, B. Geothermal exploitation by circulating supercritical CO2 in a closed horizontal wellbore. Fuel 2019, 254, 115566. [Google Scholar] [CrossRef]
- Adams, B.; Kuehn, T.H.; Bielicki, J.; Randolph, J.B.; Saar, M.O. A comparison of electric power output of CO2 Plume Geothermal (CPG) and brine geothermal systems for varying reservoir conditions. Appl. Energy 2015, 140, 365–377. [Google Scholar] [CrossRef]
- Amaya, A.; Scherer, J.; Muir, J.; Patel, M.; Higgins, B. GreenFire Energy Closed-Loop Geothermal Demonstration using Supercritical Carbon Dioxide as Working Fluid. In Proceedings of the 45th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 10–12 February 2020; Available online: https://pangea.stanford.edu/ERE/db/GeoConf/papers/SGW/2020/Higgins.pdf (accessed on 22 December 2020).
- Xia, J.; Wang, J.; Zhang, G.; Lou, J.; Zhao, P.; Dai, Y. Thermo-economic analysis and comparative study of transcritical power cycles using CO2-based mixtures as working fluids. Appl. Therm. Eng. 2018, 144, 31–44. [Google Scholar] [CrossRef]
- Dai, B.; Li, M.; Ma, Y. Thermodynamic analysis of carbon dioxide blends with low GWP (global warming potential) working fluids-based transcritical Rankine cycles for low-grade heat energy recovery. Energy 2014, 64, 942–952. [Google Scholar] [CrossRef]
- Wu, C.; Wang, S.-S.; Jiang, X.; Li, J. Thermodynamic analysis and performance optimization of transcritical power cycles using CO2-based binary zeotropic mixtures as working fluids for geothermal power plants. Appl. Therm. Eng. 2017, 115, 292–304. [Google Scholar] [CrossRef]
- Matthews, H.B. Gravity Head Geothermal Energy Conversion System. U.S. Patent No. 4,077,220, 7 March 1978. [Google Scholar]
- Hogarth, R.A.; Daniel, B. Flow performance of the Habanero EGS closed loop. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 16–24 April 2015. [Google Scholar]
- Hogarth, R.; Holl, H.G. Lessons learned from the Habanero EGS Project. Trans. Geotherm. Resour. Counc. 2017, 41, 865–877. [Google Scholar]
- Calm, J.M.; Hourahan, G.C. Physical, safety, and environmental data for current and alternative refrigerants. In Proceedings of the 23rd international congress of refrigeration (ICR2011), Prague, Czech Republic, 21–26 August 2011; pp. 4120–4141. [Google Scholar]
- Heberle, F.; Preißinger, M.; Brüggemann, D. Zeotropic mixtures as working fluids in Organic Rankine Cycles for low-enthalpy geothermal resources. Renew. Energy 2012, 37, 364–370. [Google Scholar] [CrossRef]
- Bell, I.H.; Lemmon, E.W. Automatic Fitting of Binary Interaction Parameters for Multi-fluid Helm-holtz-Energy-Explicit Mixture Models. J. Chem. Eng. Data 2016, 61, 3752–3760. [Google Scholar] [CrossRef]
- Chys, M.; Van Den Broek, M.; Vanslambrouck, B.; De Paepe, M. Potential of zeotropic mixtures as working fluids in organic Rankine cycles. Energy 2012, 44, 623–632. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Yin, H.; Sabau, A.; Conklin, J.C.; McFarlane, J.; Qualls, A.L. 2013. Mixtures of SF6–CO2 as working fluids for geothermal power plants. Appl. Energy 2013, 106, 243–253. [Google Scholar] [CrossRef]
- Larjola, J. Electricity from industrial waste heat using high-speed organic Rankine cycle (ORC). Int. J. Prod. Econ. 1995, 41, 227–235. [Google Scholar] [CrossRef]
- Mondal, S.; De, S. 2015 CO2 based power cycle with multi-stage compression and intercooling for low temperature waste heat recovery. Energy 2015, 90, 1132–1143. [Google Scholar] [CrossRef]
- Wang, J.; Guo, Y.; Zhou, K.; Xia, J.; Li, Y.; Zhao, P.; Dai, Y. Design and performance analysis of compressor and turbine in supercritical CO2 power cycle based on system-component coupled optimization. Energy Convers. Manag. 2020, 221, 113179. [Google Scholar] [CrossRef]
- Liu, Z.; Luo, W.; Zhao, Q.; Zhao, W.; Xu, J. Preliminary Design and Model Assessment of a Supercritical CO2 Compressor. Appl. Sci. 2018, 8, 595. [Google Scholar] [CrossRef] [Green Version]
- Dyreby, J.; Klein, S.; Nellis, G.; Reindl, D. Design Considerations for Supercritical Carbon Dioxide Brayton Cycles with Recompression. J. Eng. Gas Turbines Power 2014, 136, 101701. [Google Scholar] [CrossRef]
- Lu, X.; Zhao, Y.; Zhu, J.; Zhang, W. Optimization and applicability of compound power cycles for enhanced geothermal systems. Appl. Energy 2018, 229, 128–141. [Google Scholar] [CrossRef]
- He, C.; Liu, C.; Gao, H.; Xie, H.; Li, Y.; Wu, S.; Xu, J. The optimal evaporation temperature and working fluids for subcritical organic Rankine cycle. Energy 2012, 38, 136–143. [Google Scholar] [CrossRef]
- Hung, T.; Wang, S.; Kuo, C.; Pei, B.; Tsai, K. A study of organic working fluids on system efficiency of an ORC using low-grade energy sources. Energy 2010, 35, 1403–1411. [Google Scholar] [CrossRef]
- Mago, P.J.; Chamra, L.M.; Somayaji, C. Performance analysis of different working fluids for use in organic Rankine cycles. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 255–263. [Google Scholar] [CrossRef]
- Guo, T.; Wang, H.; Zhang, S. Comparative analysis of CO 2-based transcritical Rankine cycle and HFC245fa-based subcritical organic Rankine cycle using low-temperature geothermal source. Sci. China Technol. Sci. 2010, 53, 1638–1646. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S.; Sarica, C. Fluid Flow and Heat Transfer in Wellbores; Society of Petroleum Engineers Richardson: Richardson, TX, USA, 2002. [Google Scholar]
- Wang, Z.; Sun, B.; Wang, J.; Hou, L. Experimental study on the friction coefficient of supercritical carbon dioxide in pipes. Int. J. Greenh. Gas Control. 2014, 25, 151–161. [Google Scholar] [CrossRef]
- Hasan, A.; Kabir, C. A mechanistic model for computing fluid temperature profiles in gas-lift wells. SPE Prod. Facil. 1996, 11, 179–185. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Wang, H.; Tian, S.; Song, X.; Lu, P.; Wang, M. A unified model for wellbore flow and heat transfer in pure CO2 injection for geological sequestration, EOR and fracturing operations. Int. J. Greenh. Gas Control. 2017, 57, 102–115. [Google Scholar] [CrossRef]
- Hasan, A.; Kabir, S. Wellbore heat-transfer modeling and applications. J. Pet. Sci. Eng. 2012, 86-87, 127–136. [Google Scholar] [CrossRef]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transf. 1985, 12, 3–22. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Heat transfer during two-Phase flow in Wellbores; Part I—Formation temperature. In SPE Annual Technical Conference and Exhibition; OnePetro: Richardson, TX, USA, 1991. [Google Scholar]
- Cheng, W.-L.; Huang, Y.-H.; Lu, D.; Yin, H.-R. A novel analytical transient heat-conduction time function for heat transfer in steam injection wells considering the wellbore heat capacity. Energy 2011, 36, 4080–4088. [Google Scholar] [CrossRef]
- Cheng, W.; Nian, Y. High precision approximate solution of transient heat-conduction time function of wellbore heat transfer. Huagong Xuebao/CIESC J. 2013, 64, 1561–1565. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST reference fluid thermodynamic and transport properties–REFPROP. NIST Stand. Ref. Database 2002, 23, v7. [Google Scholar]
| Substance | Molecular Mass (g/mol) | Tb (°C) | Tc (°C) | Pc (MPa) | OEL (PPMv) | LEL (%) | ASHRAE 34 Safety Group | Atmospheric Life (yr) | ODP | GWP |
|---|---|---|---|---|---|---|---|---|---|---|
| R32 | 52.02 | 51.7 | 78.1 | 5.78 | 1000 | 14.1 | A2 | 4.9 | 0 | 675 |
| R1270 | 42.08 | 47.7 | 92.4 | 4.66 | 660 | 2.0 | A3 | 0.001 | 0 | ~20 |
| R161 | 48.06 | 37.6 | 102.2 | 5.09 | - | 3.8 | - | 0.21 | 0 | 12 |
| R1234yf | 114.04 | 29.5 | 94.7 | 3.38 | 500 | 6.2 | A2L | 0.029 | 0 | <4.4 |
| R134a | 102.03 | 26.1 | 101.1 | 4.06 | 1000 | None | A1 | 14.0 | 0 | 1370 |
| R152a | 66.05 | 24.0 | 113.3 | 4.52 | 1000 | 4.8 | A2 | 1.4 | 0 | 124 |
| R1234ze | 114.04 | 19.0 | 109.4 | 3.64 | 1000 | 7.6 | e | 0.045 | 0 | 6 |
| Parameters | Value |
|---|---|
| Turbine isentropic efficiency, ηT | 0.75 |
| Pump isentropic efficiency, ηP | 0.80 |
| Condenser pinch temperature difference (°C) | 4 |
| Cooling water inlet temperature, TCW,in (°C) | 18 |
| Inner diameter of the wellbore (m), dwi | 0.215 |
| Outer diameter of the wellbore (m), dwo | 0.380 |
| Inner diameter of inner pipe of the DHE, dti (m) | 0.073 |
| Outer diameter of inner pipe of the DHE, dto (m) | 0.089 |
| Inner diameter of annulus of the DHE, dai (m) | 0.120 |
| Outer diameter of annulus of the DHE, dao (m) | 0.138 |
| Density of formation rock, ce (kg/m3) | 2650 |
| Heat capacity of formation rock, ρe [J/(kg·°C)] | 837 |
| Thermal conductivity of casing, λca [W/(m·°C)] | 30 |
| Thermal conductivity of formation rock, λe [W/(m·°C)] | 2.5 |
| Thermal conductivity of insulated tube, λt [W/(m·°C)] | 0.02 |
| Thermal conductivity of cement, λce [W/(m·°C)] | 0.72 |
| Working Fluids | Optimal Mixing Ratio | Optimal Inlet Pressure (MPa) | Optimal Flowrate (kg/s) | Maximum Net Power Output |
|---|---|---|---|---|
| R161/CO2 | 0.094/0.906 | 13.9 | 8.0 | 141.3 |
| R32/CO2 | 0.7/0.3 | 12 | 7.5 | 151.5 |
| R134a/CO2 | 0.042/0.958 | 15.7 | 8.3 | 138.4 |
| R1270/CO2 | 0.084/0.916 | 15.1 | 7.9 | 140.2 |
| R152a/CO2 | 0.045/0.955 | 15.5 | 8.1 | 139.5 |
| R1234yf/CO2 | 0.01/0.99 | 15.2 | 8.3 | 137.2 |
| R1234ze/CO2 | 0.01/0.99 | 15.1 | 8.3 | 137.3 |
| Geofluid Temperature (°C) | Optimal R32/CO2 Mass Fraction | Optimal DHE Inlet Pressure (MPa) | Optimal Working Fluid Mass Flowrate (kg/s) | Maximum Net Power Output (kW) |
|---|---|---|---|---|
| 100 | 0.2 | 11 | 6 | 63.8 |
| 110 | 0.3 | 11 | 6.5 | 83.0 |
| 115 | 0.3 | 11 | 6.5 | 91.6 |
| 120 | 0.4 | 11 | 6.5 | 103.8 |
| 125 | 0.4 | 11 | 6.5 | 114.1 |
| 130 | 0.5 | 11 | 6.5 | 126.1 |
| 135 | 0.6 | 11 | 6.5 | 139.6 |
| 140 | 0.7 | 12 | 7.5 | 151.5 |
| 145 | 0.7 | 12 | 7.5 | 165.3 |
| 150 | 0.8 | 12 | 7.5 | 182.1 |
| 155 | 0.8 | 12 | 7.5 | 199.3 |
| 160 | 0.9 | 12 | 7.5 | 221.8 |
| 165 | 0.9 | 12 | 7.5 | 238.4 |
| 170 | 1 | 12 | 8 | 269.4 |
| Simulation Parameters | Value |
|---|---|
| Turbine isentropic efficiency | 0.75 |
| Pump isentropic efficiency | 0.80 |
| Condenser pinch temperature difference (°C) | 4 |
| Evaporator pinch point temperature difference (°C) | 7 |
| Cooling Water Temperature °C | Geofluid Temperature °C | Cooling Water Flowrate kg/s | R245fa Condensing Temperature °C | R601 Condensing Temperature °C |
|---|---|---|---|---|
| 18 | 110 | 22.53 | 30 | 30 |
| 120 | 26.45 | 30 | 30 | |
| 130 | 22.89 | 33 | 33 | |
| 140 | 29.58 | 32 | 32 | |
| 150 | 35.03 | 31 | 31 | |
| 160 | 36.24 | 32 | 32 | |
| 170 | 38.91 | 33 | 32 | |
| 25 | 110 | 16.55 | 38 | 38 |
| 120 | 16.18 | 40 | 40 | |
| 130 | 17.05 | 41 | 41 | |
| 140 | 30.95 | 38 | 37 | |
| 150 | 36.54 | 37 | 37 | |
| 160 | 37.59 | 38 | 38 | |
| 170 | 39.01 | 39 | 38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, C.; Lu, X.; Yu, H.; Zhang, W.; Zhang, J.; Wang, J. Theoretical Study of a Novel Power Cycle for Enhanced Geothermal Systems. Processes 2022, 10, 516. https://doi.org/10.3390/pr10030516
Geng C, Lu X, Yu H, Zhang W, Zhang J, Wang J. Theoretical Study of a Novel Power Cycle for Enhanced Geothermal Systems. Processes. 2022; 10(3):516. https://doi.org/10.3390/pr10030516
Chicago/Turabian StyleGeng, Changyou, Xinli Lu, Hao Yu, Wei Zhang, Jiaqi Zhang, and Jiansheng Wang. 2022. "Theoretical Study of a Novel Power Cycle for Enhanced Geothermal Systems" Processes 10, no. 3: 516. https://doi.org/10.3390/pr10030516
APA StyleGeng, C., Lu, X., Yu, H., Zhang, W., Zhang, J., & Wang, J. (2022). Theoretical Study of a Novel Power Cycle for Enhanced Geothermal Systems. Processes, 10(3), 516. https://doi.org/10.3390/pr10030516





