Quantitative Measurement of Solids Holdup for Group A and B Particles Using Images and Its Application in Fluidized Bed Reactors
Abstract
:1. Introduction
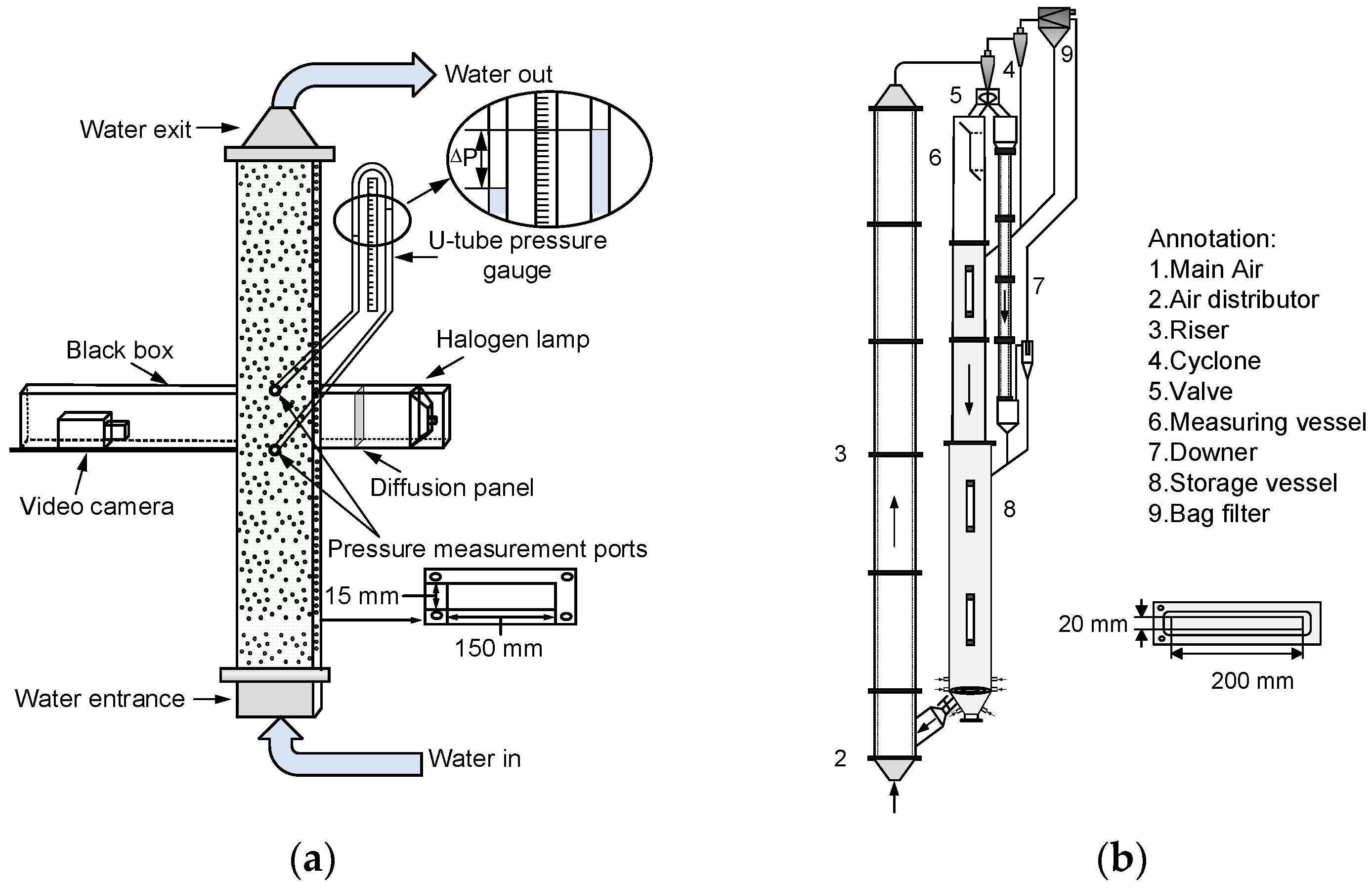
2. Experimental Apparatus
3. Results and Discussion
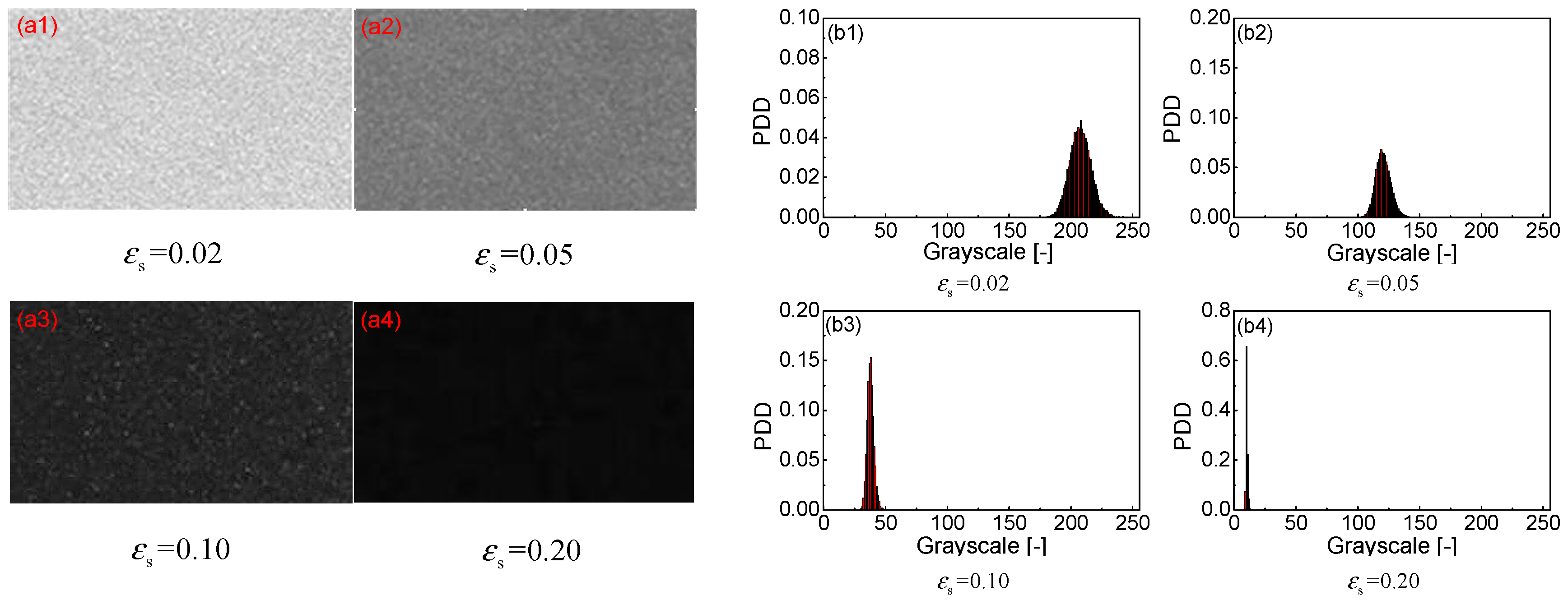
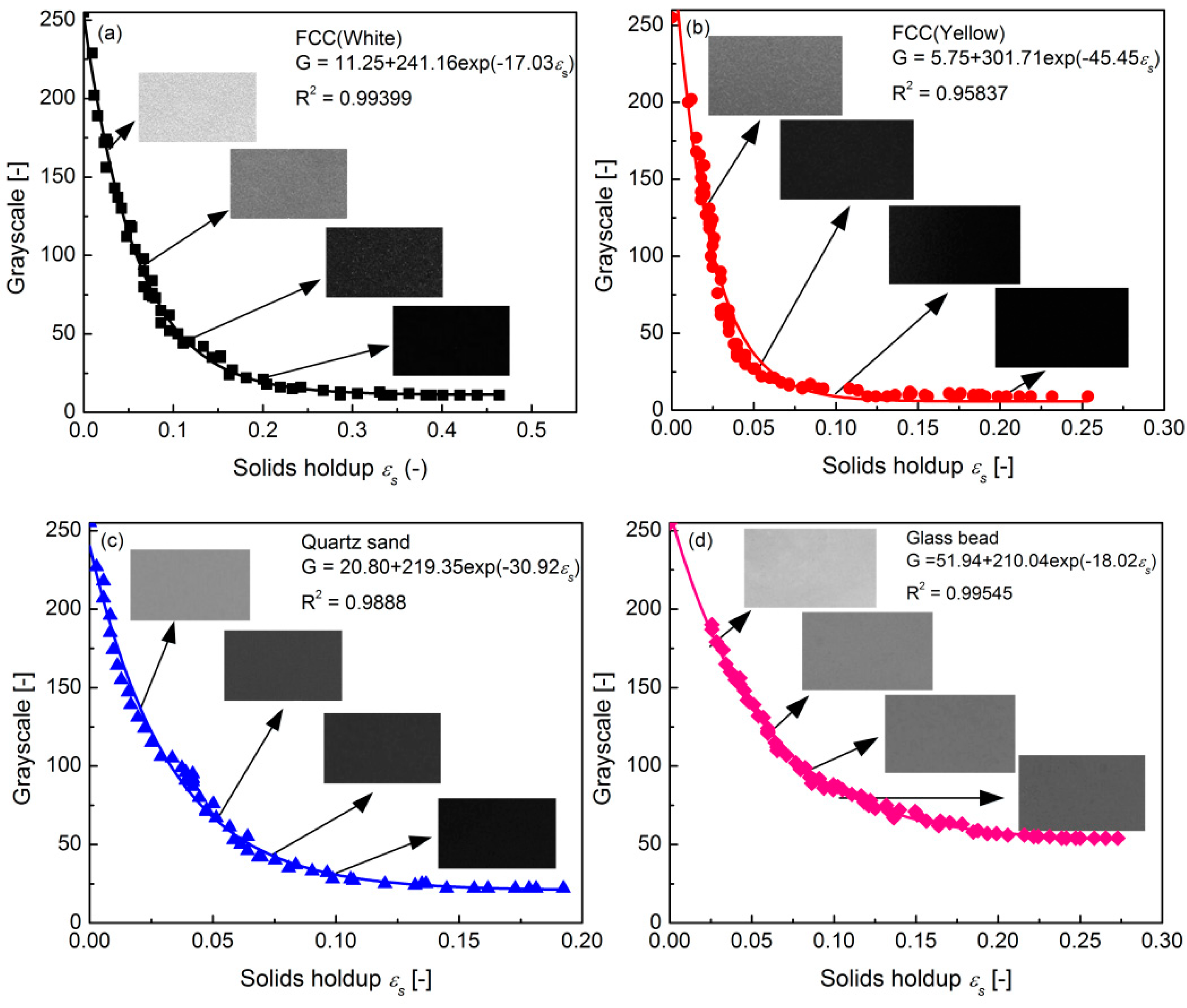
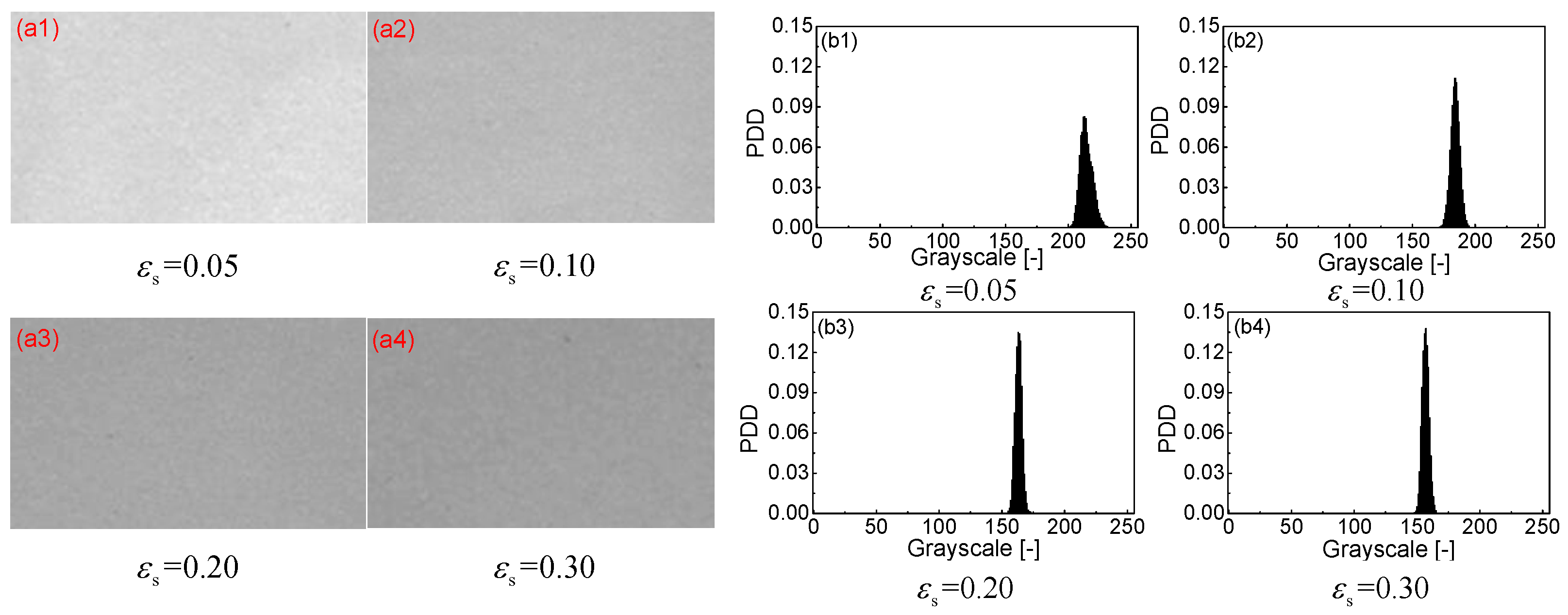
3.1. Calibration Curve for Group A FCC Particles
3.2. Calibration Curve for Group A Quartz Sand
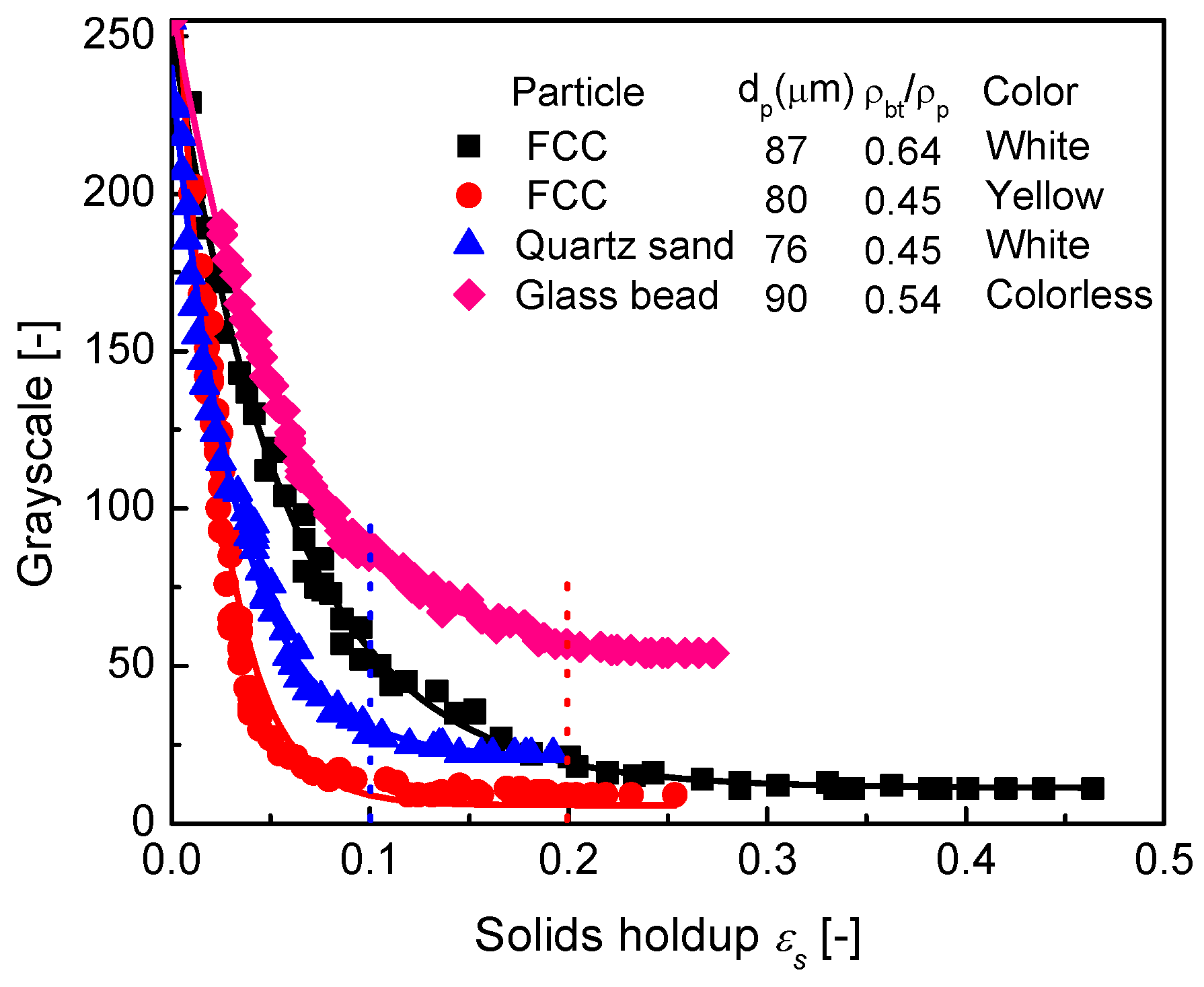
3.3. Comparison of Calibration Curves of Different Group A Particles
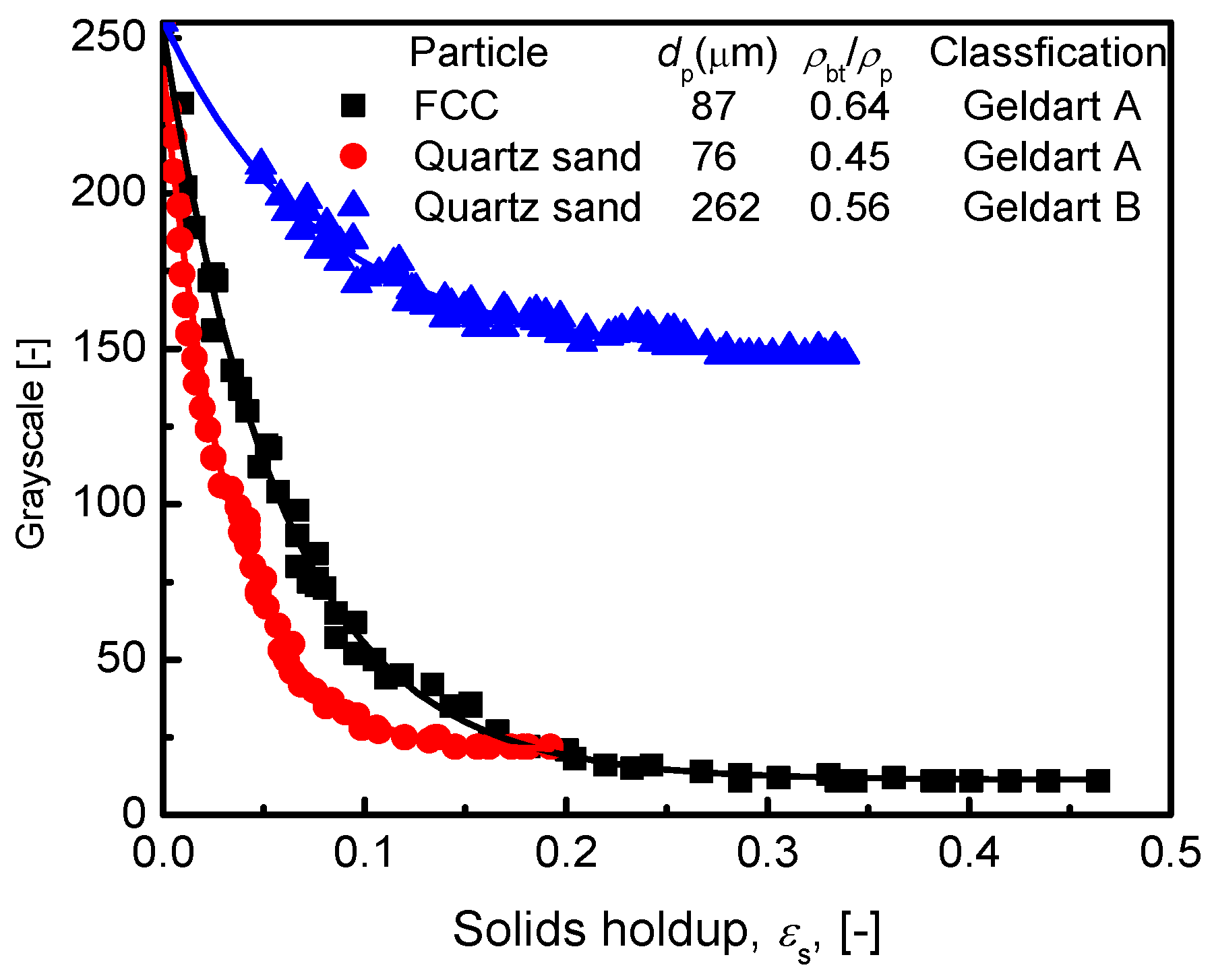
3.4. Calibration Curve for Group B Particles

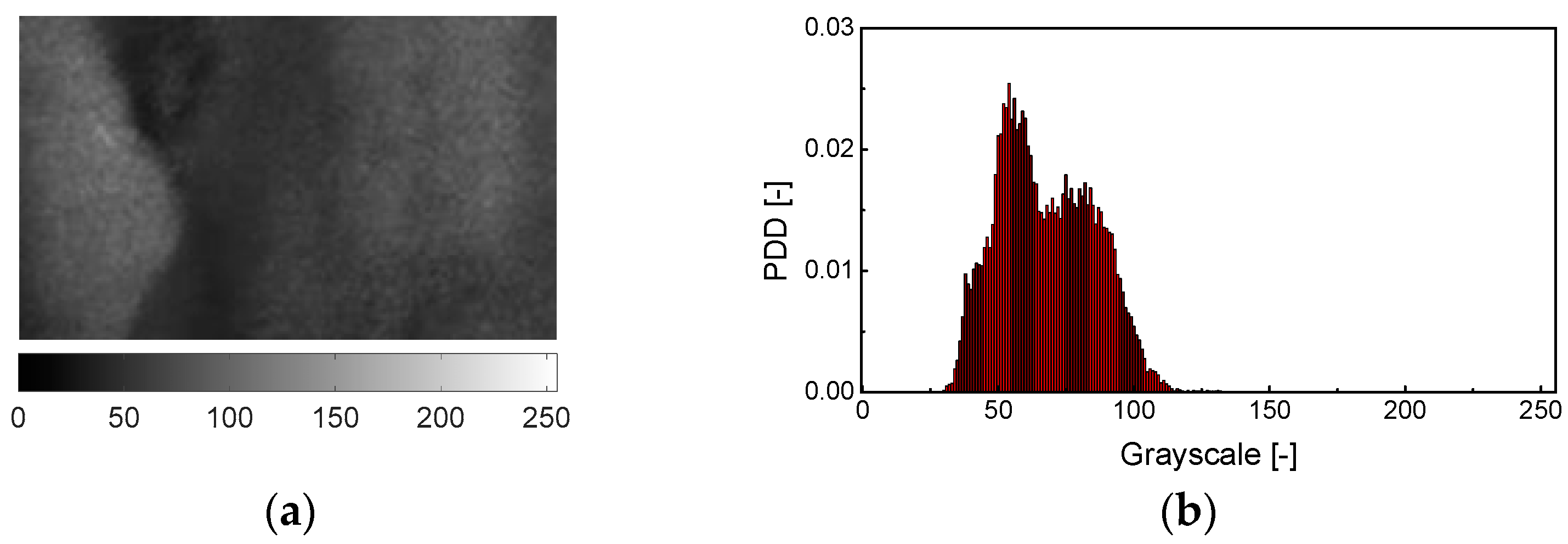
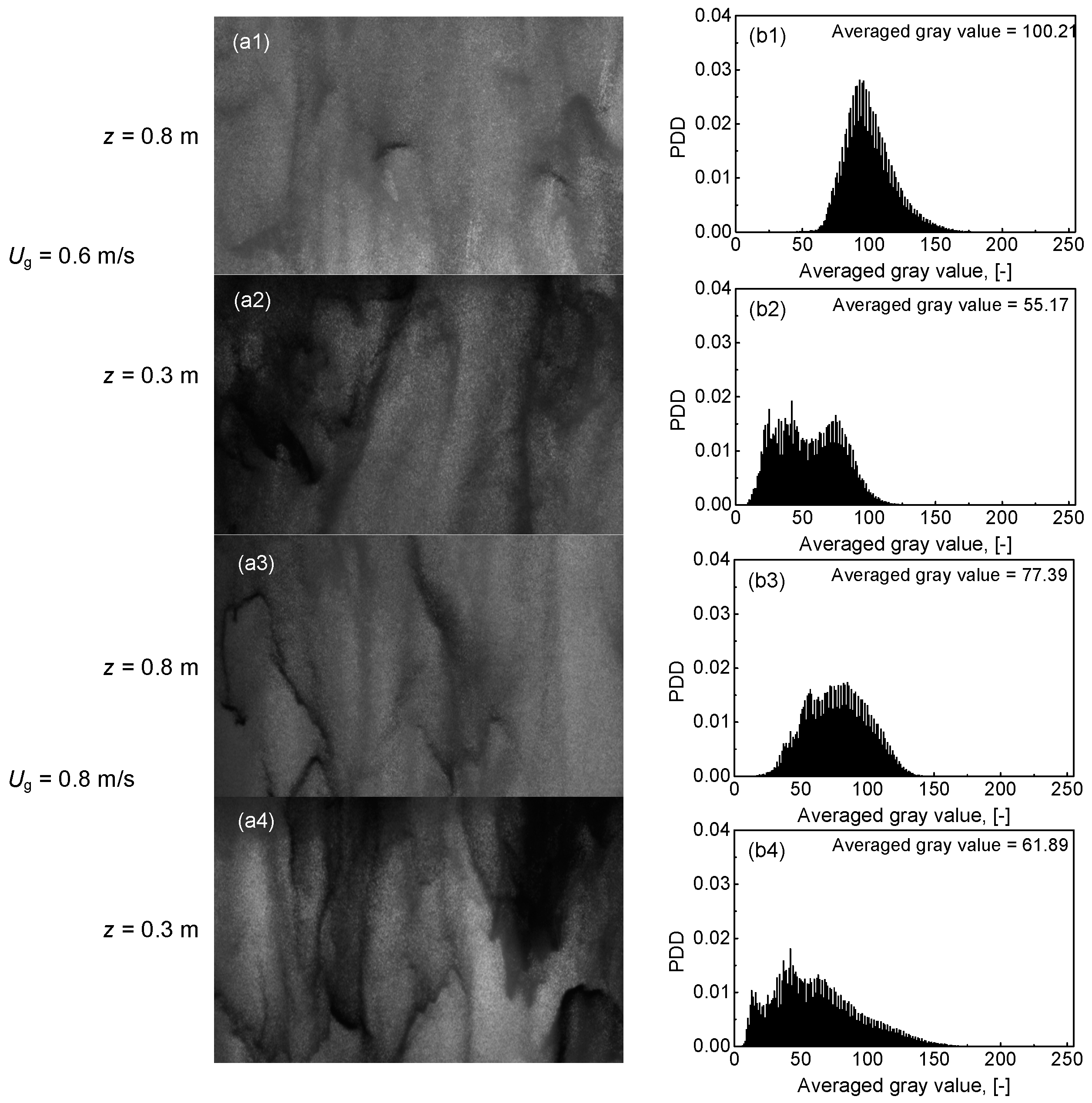
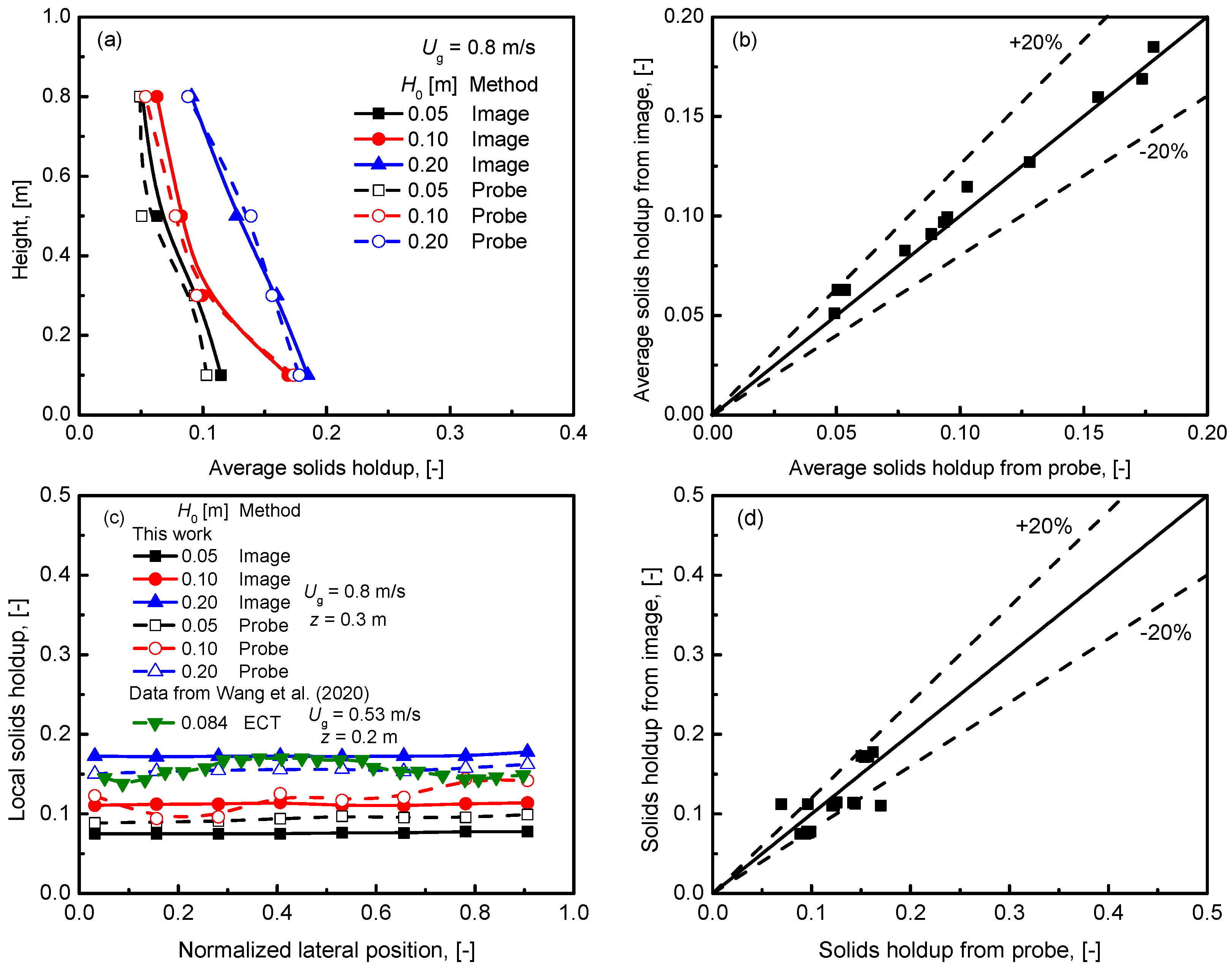
3.5. Method Application in Fluidized Bed System with Group A Particles of FCC
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| dp | particle size (μm) |
| G | grayscale |
| Gi | grayscale for each pixel of the image |
| g | gravitational acceleration (m/s2) |
| h | height (m) |
| Ug | superficial gas velocity (m/s) |
| P | pressure drop (Pa) |
| z | axial coordinate (m) |
| Greek letters | |
| εs | solids holdup |
| εsi | solids holdup for each pixel of the image |
| ρb | bulk density of the particles (kg/m3) |
| ρp | particle density of solids (kg/m3) |
| ρwater | density of water (kg/m3) |
| Subscripts | |
| b | bulk |
| g | gas |
| p | particle |
| s | solids |
References
- Li, Y.; Li, T.; Zhang, H.; Sun, Q.; Ying, W. LDV measurements of particle velocity distribution and annular film thickness in a turbulent fluidized bed. Powder Technol. 2017, 305, 578–590. [Google Scholar] [CrossRef]
- Bi, H.T.; Ellis, N.; Abba, I.A.; Grace, J.R. A state-of-the-art review of gas–solid turbulent fluidization. Chem. Eng. Sci. 2000, 55, 4789–4825. [Google Scholar] [CrossRef]
- Grace, J.R. Reflections on turbulent fluidization and dense suspension upflow. Powder Technol. 2000, 113, 242–248. [Google Scholar] [CrossRef]
- Du, B.; Warsito, W.; Fan, L.-S. Bed nonhomogeneity in turbulent gas-solid fluidization. AlChE J. 2003, 49, 1109–1126. [Google Scholar] [CrossRef]
- Gidaspow, D.; Jung, J.; Singh, R.K. Hydrodynamics of fluidization using kinetic theory: An emerging paradigm: 2002 Flour-Daniel lecture. Powder Technol. 2004, 148, 123–141. [Google Scholar] [CrossRef]
- Andreux, R.; Gauthier, T.; Chaouki, J.; Simonin, O. New description of fluidization regimes. AlChE J. 2005, 51, 1125–1130. [Google Scholar] [CrossRef]
- Yan, D.; Li, H.; Zou, Z.; Zhu, Q. Simulation with a structure-based mass-transfer model for turbulent fluidized beds. Particuology 2018, 39, 40–47. [Google Scholar] [CrossRef]
- Chew, J.W.; Cocco, R.A. Fast versus turbulent fluidization of Geldart Group B particles. AlChE J. 2021, 67, e17216. [Google Scholar] [CrossRef]
- Edwards, M.; Avidan, A. Conversion model aids scale-up of mobil’s fluid-bed MTG process. Chem. Eng. Sci. 1986, 41, 829–835. [Google Scholar] [CrossRef]
- Zhang, C.; Lu, B.; Yuan, X.; Li, H.; Ye, M.; Wang, W. Reactive simulation of industrial methanol-to-olefins fluidized bed reactors and parameter analysis. Powder Technol. 2021, 393, 681–691. [Google Scholar] [CrossRef]
- Horio, M.; Clift, R. A note on terminology: ‘Clusters and agglomerates. Powder Technol. 1992, 70, 196. [Google Scholar] [CrossRef]
- Manyele, S.V.; Pärssinen, J.H.; Zhu, J.X. Characterizing particle aggregates in a high-density and high-flux cfb riser. Chem. Eng. J. 2002, 88, 151–161. [Google Scholar] [CrossRef]
- Wiesendorf, V.; Werther, J. Capacitance probes for solids volume concentration and velocity measurements in industrial fluidized bed reactors. Powder Technol. 2000, 110, 143–157. [Google Scholar] [CrossRef]
- Magnusson, A.; Rundqvist, R.; Almstedt, A.E.; Johnsson, F. Dual fibre optical probe measurements of solids volume fraction in a circulating fluidized bed. Powder Technol. 2005, 151, 19–26. [Google Scholar] [CrossRef]
- Rhodes, M.J.; Laussmann, P. A simple non-isokinetic sampling probe for dense suspensions. Powder Technol. 1992, 70, 141–151. [Google Scholar] [CrossRef]
- Issangya, A.S.; Bai, D.R.; Bi, H.T.; Lim, K.S.; Grace, J.R. Suspension densities in a high-density circulating fluidized bed riser. Chem. Eng. Sci. 1999, 54, 5451–5460. [Google Scholar] [CrossRef]
- Wu, C.; Gao, Y.; Cheng, Y.; Wang, L.; Li, X. Solid concentration and velocity distributions in an annulus turbulent fluidized bed. Chin. J. Chem. Eng. 2015, 23, 1077–1084. [Google Scholar] [CrossRef]
- Wei, X.; Zhu, J. Capturing the instantaneous flow structure in gas-solid circulating fluidized bed using high-speed imaging and fiber optic sensing. Chem. Eng. Sci. 2019, 207, 713–724. [Google Scholar] [CrossRef]
- Ma, Z.; Ma, H.; Qian, W.; Li, Y.; Zhang, H.; Sun, Q.; Ying, W. Flow development and prediction of solids concentration in a large gas-solids turbulent fluidized bed. Can. J. Chem. Eng. 2020, 99, S809–S819. [Google Scholar] [CrossRef]
- Yu, S.; Yang, X.; Xiang, J.; Zhou, H.; Li, Q.; Zhang, Y. Effects of bed size on the voidage in gas-solid bubbling fluidized beds. Powder Technol. 2021, 387, 197–204. [Google Scholar] [CrossRef]
- Rhodes, M.; Mineo, H.; Hirama, T. Particle motion at the wall of a circulating fluidized bed. Powder Technol. 1992, 70, 207–214. [Google Scholar] [CrossRef]
- Xu, Y.; Li, T.; Lu, L.; Gao, X.; Tebianian, S.; Grace, J.R.; Chaouki, J.; Leadbeater, T.W.; Jafari, R.; Parker, D.J.; et al. Development and confirmation of a simple procedure to measure solids distribution in fluidized beds using tracer particles. Chem. Eng. Sci. 2020, 217, 115501. [Google Scholar] [CrossRef]
- Yianneskis, M. Velocity, particle sizing concentration measurement techniques for multi-phase flow. Powder Technol. 1987, 49, 261–269. [Google Scholar] [CrossRef]
- Kim, S.W. Effect of Particle Size on Carbon Nanotube Aggregates Behavior in Dilute Phase of a Fluidized Bed. Processes 2018, 6, 121. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Sun, X.; Xu, C.; Bao, J.; Peng, C.; Tang, Z. Investigation of a circulating turbulent fluidized bed with a fractal gas distributor by electrostatic-immune electrical capacitance tomography. Powder Technol. 2020, 361, 562–570. [Google Scholar] [CrossRef]
- Maestri, M.; Salierno, G.; Piovano, S.; Cassanello, M.; Cardona, M.A.; Hojman, D.; Somacal, H. CFD-DEM modeling of solid motion in a water-calcium alginate fluidized column and its comparison with results from radioactive particle tracking. Chem. Eng. J. 2019, 377, 120339. [Google Scholar] [CrossRef]
- Casleton, D.K.; Shadle, L.J.; Ross, A.A. Measuring the voidage of a CFB through image analysis. Powder Technol. 2010, 203, 12–22. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, J. A novel method based on image processing to visualize clusters in a rectangular circulating fluidized bed riser. Powder Technol. 2014, 254, 407–415. [Google Scholar] [CrossRef]
- Yin, S.; Zhong, W.; Song, T.; Lu, P.; Chen, Y. Clusters identification and meso-scale structures in a circulating fluidized bed based on image processing. Adv. Powder Technol. 2019, 30, 3010–3020. [Google Scholar] [CrossRef]
- Zhang, H.; Johnston, P.M.; Zhu, J.X.; de Lasa, H.I.; Bergougnou, M.A. A novel calibration procedure for a fiber optic solids concentration probe. Powder Technol. 1998, 100, 260–272. [Google Scholar] [CrossRef]
- Chen, R.C.; Fan, L.S. Particle image velocimetry for characterizing the flow structure in three-dimensional gas-liquid-solid fluidized beds. Chem. Eng. Sci. 1992, 47, 3615–3622. [Google Scholar] [CrossRef]
- Lackermeier, U.; Rudnick, C.; Werther, J.; Bredebusch, A.; Burkhardt, H. Visualization of flow structures inside a circulating fluidized bed by means of laser sheet and image processing. Powder Technol. 2001, 114, 71–83. [Google Scholar] [CrossRef]
- Cocco, R.; Shaffer, F.; Hays, R.; Reddy Karri, S.B.; Knowlton, T. Particle clusters in and above fluidized beds. Powder Technol. 2010, 203, 3–11. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, J. A New Method for the Determination of Cluster Velocity and Size in a Circulating Fluidized Bed. Ind. Eng. Chem. Res. 2012, 51, 2143–2151. [Google Scholar] [CrossRef]
- McMillan, J.; Shaffer, F.; Gopalan, B.; Chew, J.W.; Hrenya, C.; Hays, R.; Karri, S.B.R.; Cocco, R. Particle cluster dynamics during fluidization. Chem. Eng. Sci. 2013, 100, 39–51. [Google Scholar] [CrossRef]
- Chew, J.W.; Parker, D.M.; Cocco, R.A.; Hrenya, C.M. Cluster characteristics of continuous size distributions and binary mixtures of Group B particles in dilute riser flow. Chem. Eng. J. 2011, 178, 348–358. [Google Scholar] [CrossRef]
- Xu, J.; Zhu, J.X. Visualization of particle aggregation and effects of particle properties on cluster characteristics in a CFB riser. Chem. Eng. J. 2011, 168, 376–389. [Google Scholar] [CrossRef]
- Yang, J.S.; Zhu, J. Cluster identification using image processing. Particuology 2015, 23, 16–24. [Google Scholar] [CrossRef]
- Mondal, D.N.; Kallio, S.; Saxén, H. Length scales of solid clusters in a two-dimensional circulating fluidized bed of Geldart B particles. Powder Technol. 2015, 269, 207–218. [Google Scholar] [CrossRef]
- Wei, X.; Zhu, J. Tracking the flow dynamics in circulating fluidized bed through high-speed photography. Ind. Eng. Chem. Res. 2019, 58, 17540–17548. [Google Scholar] [CrossRef]
- Shaffer, F.; Gopalan, B.; Breault, R.W.; Cocco, R.; Karri, S.B.R.; Hays, R.; Knowlton, T. High speed imaging of particle flow fields in CFB risers. Powder Technol. 2013, 242, 86–99. [Google Scholar] [CrossRef]
- Gao, X.; Wu, C.; Cheng, Y.-w.; Wang, L.-j.; Li, X. Experimental and numerical investigation of solid behavior in a gas–solid turbulent fluidized bed. Powder Technol. 2012, 228, 1–13. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, J.; Li, G.; Li, F. Detailed measurements of flow structure inside a dense gas–solids fluidized bed. Powder Technol. 2008, 180, 339–349. [Google Scholar] [CrossRef]
- Qiang, G.; Zhu, X.; Liu, Y.; Liu, Y.; Li, C.; You, X. Gas–solid flow behavior and contact efficiency in a circulating-turbulent fluidized bed. Powder Technol. 2013, 245, 134–145. [Google Scholar]
- Zhu, H.; Zhu, J. Comparative study of flow structures in a circulating-turbulent fluidized bed. Chem. Eng. Sci. 2008, 63, 2920–2927. [Google Scholar] [CrossRef]
- Cui, H.; Mostoufi, N.; Chaouki, J. Gas and solids between dynamic bubble and emulsion in gas-fluidized beds. Powder Technol. 2001, 120, 12–20. [Google Scholar] [CrossRef]
- Wang, C.; Yang, X.; Wang, M.; Zhang, J.; Lan, X.; Gao, J.; Ye, M.; Zhu, J. Particle Velocity Distribution and Its Prediction in a 14 m Two-Dimensional Circulating Fluidized Bed Riser. Ind. Eng. Chem. Res. 2021, 60, 1901–1911. [Google Scholar] [CrossRef]
- Su, X.; Wang, C.; Lan, X.; Pei, H.; Mao, X.; Gao, J. Flow of high solids density suspensions in an 18 m high circulating fluidized bed. Ind. Eng. Chem. Res. 2020, 59, 1336–1349. [Google Scholar] [CrossRef]
- Su, X.; Wang, C.; Pei, H.; Li, J.; Lan, X.; Gao, J. Experimental study of solids motion in an 18 m gas–solids circulating fluidized bed with high solids flux. Ind. Eng. Chem. Res. 2019, 58, 23468–23480. [Google Scholar] [CrossRef]





| Particle | dp (μm) | ρp (kg/m3) | ρb (kg/m3) | ρb/ρp | Particle Color | Geldart Classification |
|---|---|---|---|---|---|---|
| FCC | 87 | 1519 | 960 | 0.64 | White/Yellow | Geldart A |
| Quartz sand | 76 | 2785 | 1251 | 0.45 | White | Geldart A-B |
| Quartz sand | 262 | 2530 | 1415 | 0.56 | White | Geldart B |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Li, Z.; Wei, J.; Lan, X.; Ye, M.; Gao, J. Quantitative Measurement of Solids Holdup for Group A and B Particles Using Images and Its Application in Fluidized Bed Reactors. Processes 2022, 10, 610. https://doi.org/10.3390/pr10030610
Wang C, Li Z, Wei J, Lan X, Ye M, Gao J. Quantitative Measurement of Solids Holdup for Group A and B Particles Using Images and Its Application in Fluidized Bed Reactors. Processes. 2022; 10(3):610. https://doi.org/10.3390/pr10030610
Chicago/Turabian StyleWang, Chengxiu, Zhihui Li, Jianjin Wei, Xingying Lan, Mao Ye, and Jinsen Gao. 2022. "Quantitative Measurement of Solids Holdup for Group A and B Particles Using Images and Its Application in Fluidized Bed Reactors" Processes 10, no. 3: 610. https://doi.org/10.3390/pr10030610
APA StyleWang, C., Li, Z., Wei, J., Lan, X., Ye, M., & Gao, J. (2022). Quantitative Measurement of Solids Holdup for Group A and B Particles Using Images and Its Application in Fluidized Bed Reactors. Processes, 10(3), 610. https://doi.org/10.3390/pr10030610







