Study of the Fluid Passing through the Screen in the Three Products Hydrocyclone Screen (TPHS): A Theoretical Analysis and Numerical Simulation
Abstract
:1. Introduction
2. Methodology
2.1. Geometric Models
2.2. Numerical Models
3. Results and Discussion
3.1. Dynamic Analysis of Screen Underflow
3.1.1. Analysis of Ideal Fluid Permeability Sieve
- (1)
- the fluid was ideal with the kinematic viscosity υ of 0 m2/s;
- (2)
- the fluid-permeable screen can be considered as the fluid passing through the inner surface of the screen (namely the small end of the cone frustum in Figure 2b);
- (3)
- the process of permeating the screen was the result of the fluid migration in the radial and tangential directions; thus, the axial flow can be ignored.
3.1.2. Analysis of Viscous Fluid Permeability Sieve
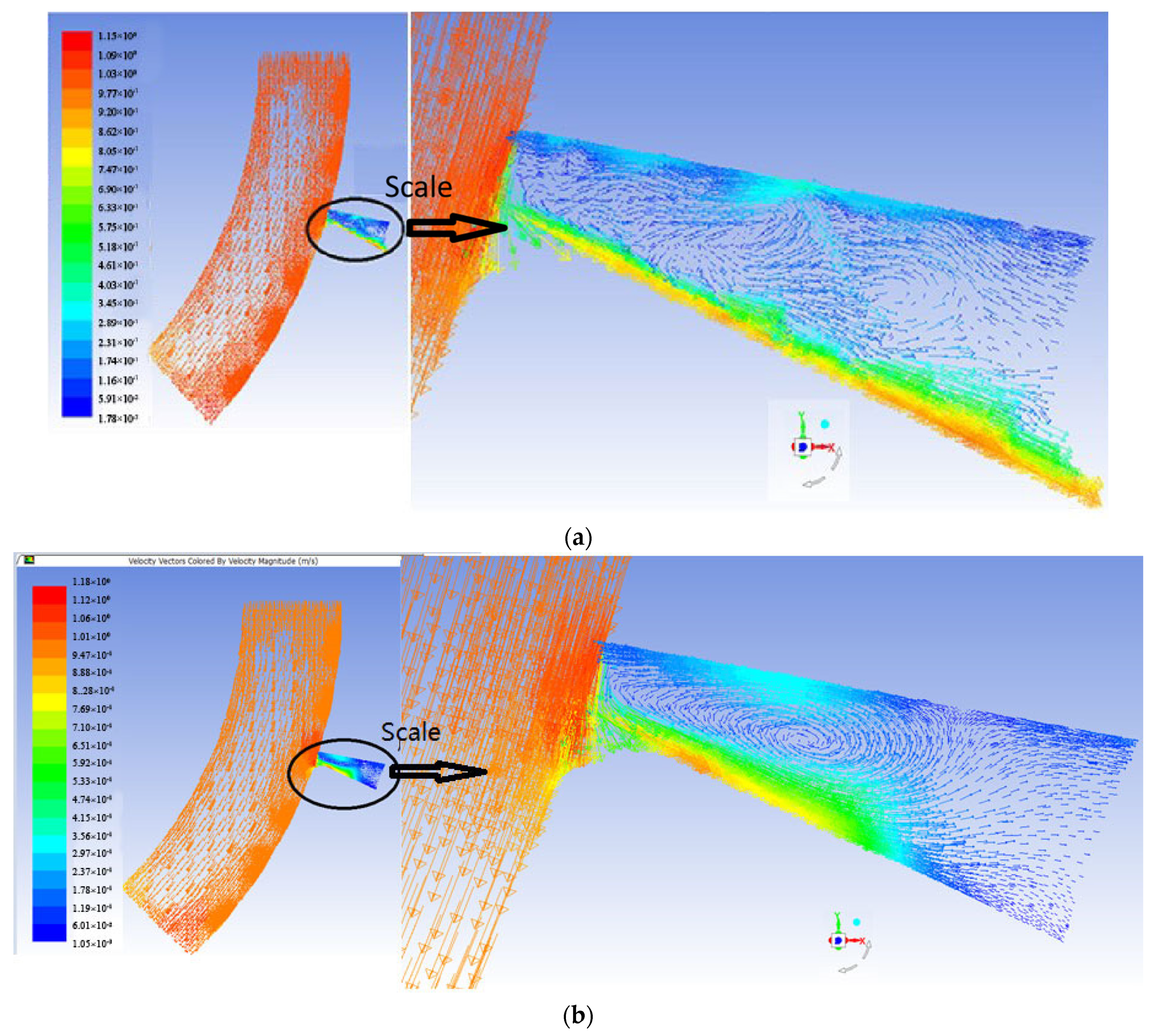
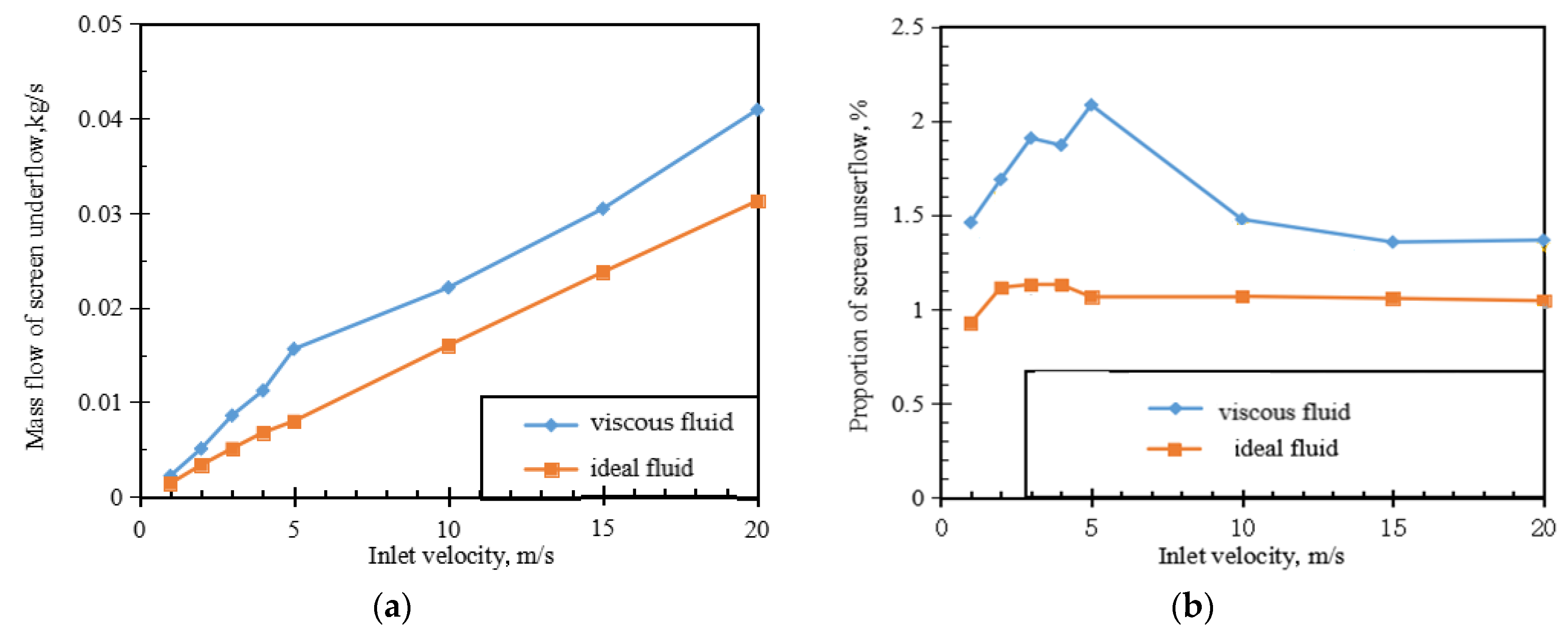
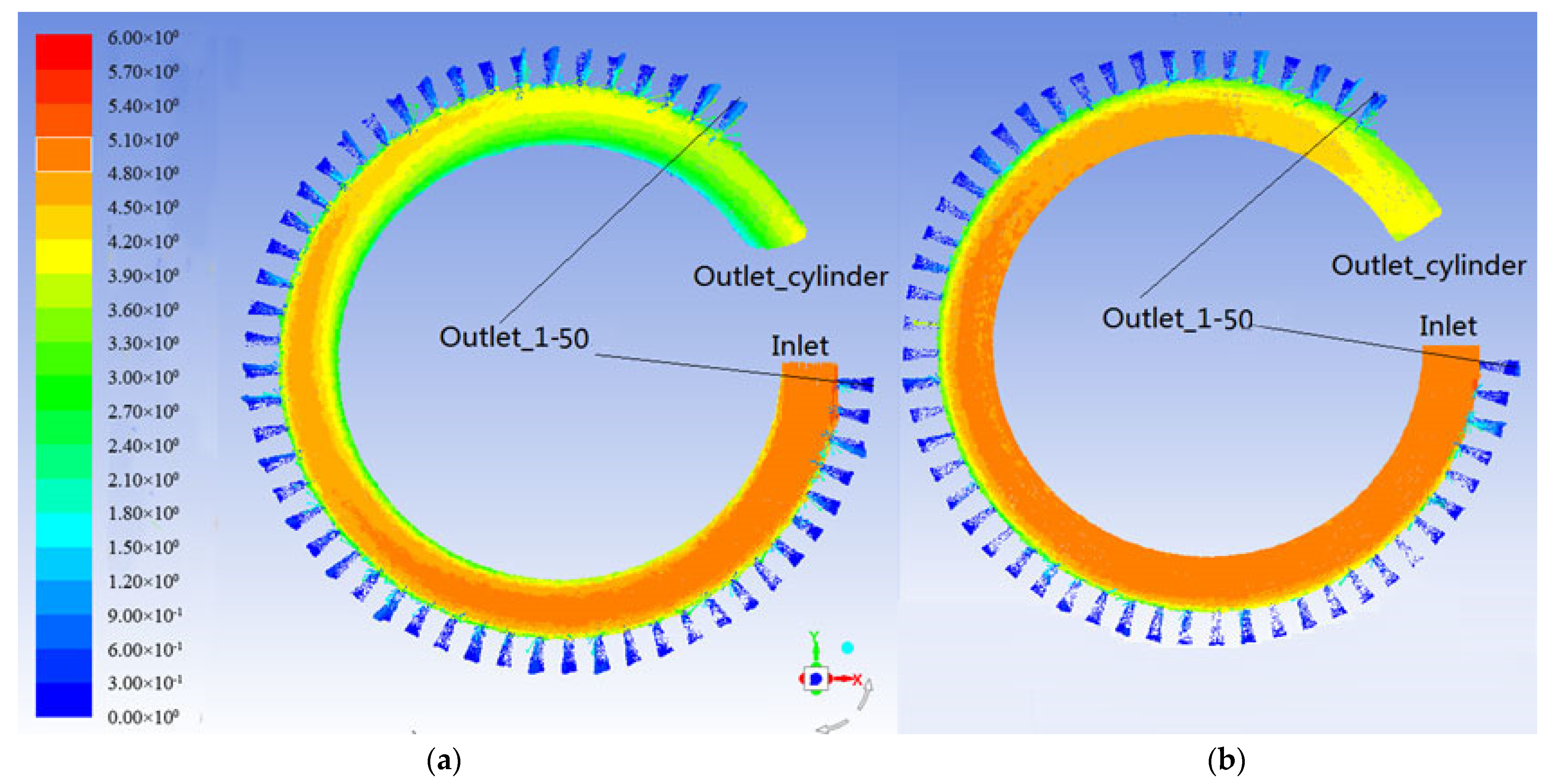
3.2. Verification by Simulation
3.3. Flow Equation of Screen Underflow
4. Conclusions
- (1)
- The fluid passing through the screen in the TPHS can be abstracted into a simple fan model. The flow rate and the driving force models of the permeating fluid were built using this model (see Equations (26) and (28) in Section 3.1). Furthermore, for the ideal fluid, the pressure difference near the screen aperture was the root cause of the penetration, which generated a higher radial velocity. The penetration process of the viscous fluid was affected not only by the pressure difference but also by the viscous force to produce a larger velocity gradient with a vortex. Under the same conditions, the sieving volume of the viscous fluid was greater than that of the ideal fluid.
- (2)
- Under the same inlet velocity, the viscous fluid exhibited a higher flow rate than the ideal fluid during the permeating process. This demonstrates that the viscosity promoted the permeation. Furthermore, while the increased inlet velocity (0~20 m/s) increased the flow rate of the fluid passing through the screen, the proportion of the screen underflow first increased to a peak, then dropped, and then finally remained stable.
- (3)
- The CFD simulation results of the fluid permeation under the multiple screen aperture conditions were consistent with those of a single mesh. When there are multiple screen apertures in the direction of the fluid movement, the fluid permeability behaviour can be abstracted as the sum of the fluid permeability behaviour in each screen aperture. The fluid velocity gradually decreased along the flow direction at the same velocity inlet, and the viscous fluid decelerated faster than the ideal fluid. When compared to the ideal fluid, the viscous fluid had greater sieve penetration at the different screen apertures along the rotation direction.
- (4)
- The flow equation of the screen underflow for the TPHS was developed (see Equation (36) in Section 3.3), and it was related to the structure and the process parameters such as the rotation radius, length of the cylindrical screen, aperture size, open-area percentage, dynamic viscosity of the fluid, and pressure difference between the feed inlet and the screen outlet.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| , , | The unit mass force component in the r, θ, and z direction |
| , , | The compressive stress perpendicular to the r plane, θ arc surface, and z plane |
| , , | Position (m) |
| , , | The radius, rotation angle, and axial in the cylindrical coordinate system |
| , , | The unit vector on the axes |
| , | The radial and tangential velocity of the fluid microelement |
| , | The radial velocity distribution, tangential velocity distribution |
| () | The mass transfer from phase () to phase () |
| , | The relationship coefficients between the initial velocity term, the shear stress term, and the compressive stress term |
| , | The phase of the fluid |
| The velocity vector (m/s) | |
| Hamiltonian | |
| The fluctuation velocity component (m/s) | |
| The displacement along the radial direction | |
| The mean velocity component (m/s) | |
| The kinematic viscosity | |
| The qth fluid’s volume fraction in the cell | |
| The turbulence kinetic energy at the wall-adjacent cell centroid, P | |
| Density (kg/m3) | |
| The fluctuation velocity component (m/s) | |
| The Kronecker symbol | |
| The distance from the fluid microelement to the wall | |
| The wall shear stress | |
| The flow rate in the 2D plane flow | |
| The flow rate in the 3D spatial flow | |
| The distance from the centroid of the wall-adjacent cell to the wall, P | |
| The mean velocity of the fluid at the wall-adjacent cell centroid, P | |
| The fluid kinematic viscosity | |
| The open-area percentage of the cylindrical screen | |
| The dynamic viscosity | |
| A | The through-screen fluid flow area |
| A, B, C, D, C′ | Position |
| t | Time (s) |
| c | A parameter related to the fluid permeability |
| n | The pressure index |
| k | The screen aperture permeability |
| The rotation radius | |
| R | The radius of the cylindrical screen |
| D | The width of the screen aperture |
| H | The height of the column-section inlet |
| l | The length of the screen aperture |
| P | The hydrodynamic pressure |
| The pressure difference between the feed inlet and the screen outlet | |
| The flow rate of the ideal fluid passing through the screen | |
| The flow rate of the viscous fluid passing through the screen |
References
- Wills, B.A.; Finch, J.A. (Eds.) Wills’ mineral processing technology: An introduction to the practical aspects of ore treatment and mineral recovery. In Wills’ Mineral Processing Technology, 8th ed.; Butterworth-Heinemann: Boston, MA, USA, 2016; pp. 1–27. [Google Scholar]
- Eckert, K.; Schach, E.; Gerbeth, G.; Rudolph, M. Carrier Flotation: State of the Art and its Potential for the Separation of Fine and Ultrafine Mineral Particles. Mater. Sci. Forum 2019, 959, 125–133. [Google Scholar] [CrossRef]
- Li, Z.; Fu, Y.; Yang, C.; Yu, W.; Liu, L.; Qu, J.; Zhao, W. Mineral liberation analysis on coal components separated using typical comminution methods. Miner. Eng. 2018, 126, 74–81. [Google Scholar] [CrossRef]
- Obeng, D.P.; Morrell, S. The JK three-product cyclone—Performance and potential applications. Int. J. Miner. Process. 2003, 69, 129–142. [Google Scholar] [CrossRef]
- Randjic, D. Proposition of new indices and parameters for grain size classification efficiency estimation. J. Min. Metall. A Min. 2008, 44, 17–23. [Google Scholar]
- Honaker, R.Q.; Boaten, F.; Luttrell, G.H. Ultrafine coal classification using 150 mm gMax cyclone circuits. Miner. Eng. 2007, 20, 1218–1226. [Google Scholar] [CrossRef]
- Wang, C.; Chen, J.; Shen, L.; Hoque, M.M.; Ge, L.; Evans, G.M. Inclusion of screening to remove fish-hook effect in the three products hydro-cyclone screen (TPHS). Miner. Eng. 2018, 122, 156–164. [Google Scholar] [CrossRef]
- Chen, J.; Shen, L.; Wang, C.; Zhang, Y. Desliming performance of the three-product cyclone classification screen. Eng. Village 2016, 45, 813. [Google Scholar]
- Wang, C.; Sun, X.; Shen, L.; Wang, G. Analysis and Prediction of Influencing Parameters on the Coal Classification Performance of a Novel Three Products Hydrocyclone Screen (TPHS) Based on Grey System Theory. Processes 2020, 8, 974. [Google Scholar] [CrossRef]
- Yu, A.; Wang, C.; Liu, H.; Khan, M.S. Computational Modeling of Flow Characteristics in Three Products Hydrocyclone Screen. Processes 2021, 9, 1295. [Google Scholar] [CrossRef]
- Davailles, A.; Climent, E.; Bourgeois, F. Fundamental understanding of swirling flow pattern in hydrocyclones. Sep. Purif. Technol. 2012, 92, 152–160. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Chen, J.; Shen, L.; Ge, L. Study of flow behaviour in a three products hydrocyclone screen: Numerical simulation and experimental validation. Physicochem. Probl. Miner. Process. 2019, 55, 879–895. [Google Scholar] [CrossRef]
- Banerjee, C.; Chaudhury, K.; Majumder, A.K.; Chakraborty, S. Swirling Flow Hydrodynamics in Hydrocyclone. Ind. Eng. Chem. Res. 2015, 54, 522–528. [Google Scholar] [CrossRef]
- Wang, C.; Yu, A.; Zhu, Z.; Liu, H.; Khan, M.S. Mechanism of the Absent Air Column in Three Products Hydrocyclone Screen (TPHS): Experiment and Simulation. Processes 2021, 9, 431. [Google Scholar] [CrossRef]
- Xi-zeng, Z.; Chang-hong, H.; Zhao-chen, S. Numerical Simulation of Extreme Wave Generation Using VOF Method. J. Hydrodyn. 2010, 22, 466–477. [Google Scholar] [CrossRef]
- Yuekan, Z.; Peikun, L.; Jiangbo, G.; Xinghua, Y.; Meng, Y.; Lanyue, J. Simulation analysis on the separation performance of spiral inlet hydrocyclone. Int. J. Coal Prep. Util. 2021, 41, 474–490. [Google Scholar]
- Gibson, M.M.; Launder, B.E. Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech. 1978, 86, 491–511. [Google Scholar] [CrossRef]
- Leschziner, M.A.; Hogg, S. Computation of highly swirling confined flow with a Reynolds stress turbulence model. AIAA J. 1989, 27, 57–63. [Google Scholar] [CrossRef]
- Yang, Z.; Cheng, X.; Zheng, X.; Chen, H. Reynolds-Averaged Navier-Stokes Equations Describing Turbulent Flow and Heat Transfer Behavior for Supercritical Fluid. J. Therm. Sci. 2021, 30, 191–200. [Google Scholar] [CrossRef]
- StephenWhitaker. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Media 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Souza, F.J.; Vieira, L.G.M.; Damasceno, J.J.R. Analysis of the influence of the filtering medium on the behaviour of the filtering hydrocyclone. Powder Technol. 2000, 107, 259–267. [Google Scholar] [CrossRef]
- Vieira, L.G.M.; Barbosa, E.A.; Damasceno, J.J.R.; Barrozo, M.A.S. Performance analysis and design of filtering hydrocyclones. Br. J. Chem. Eng. 2005, 22, 143–152. [Google Scholar] [CrossRef]
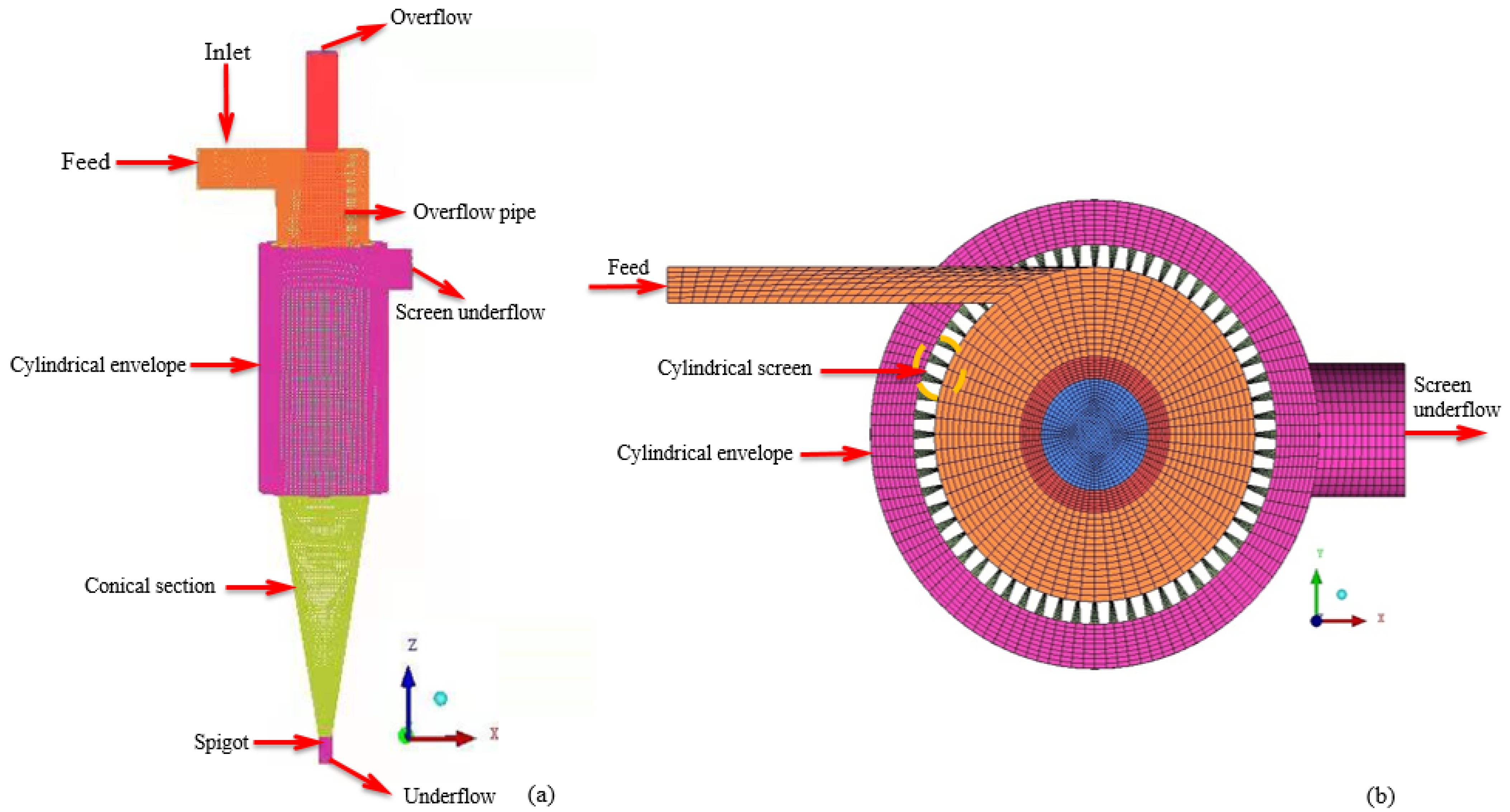
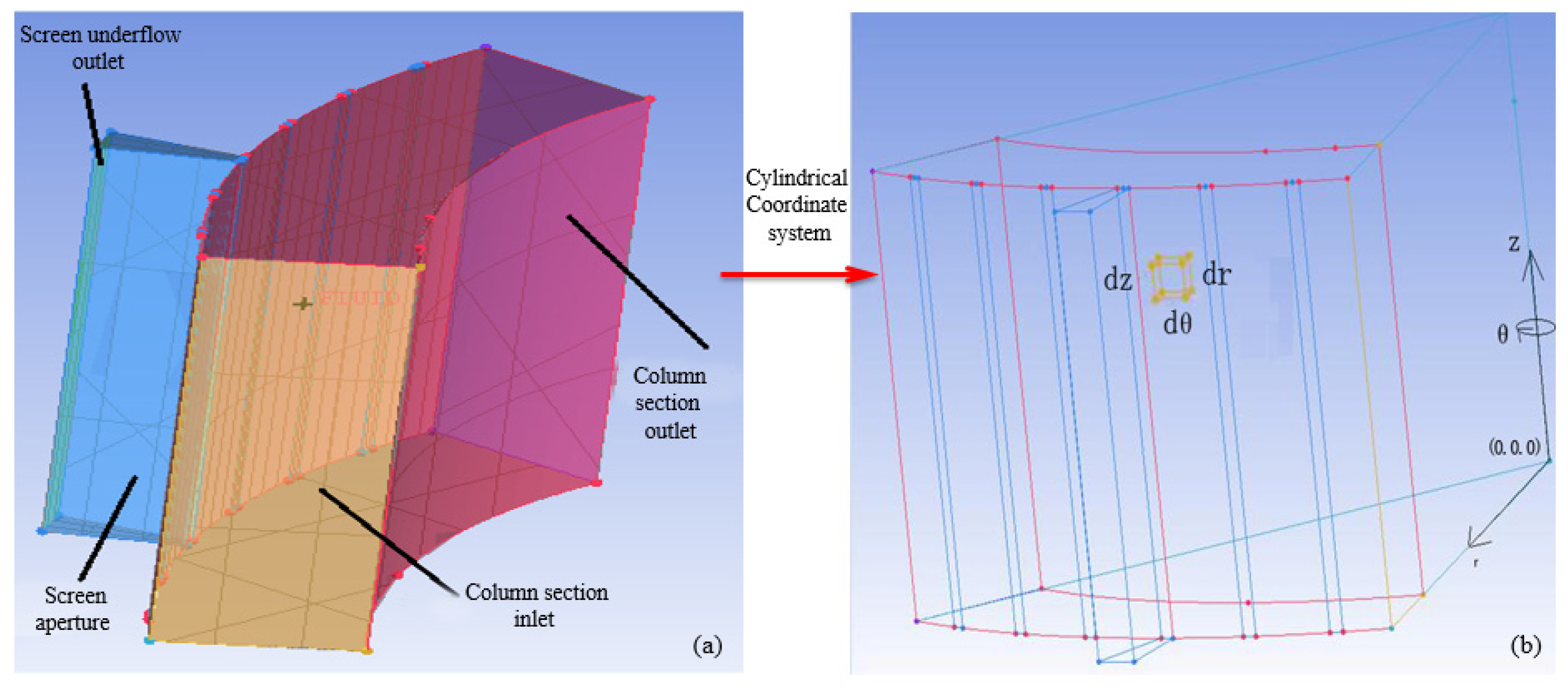
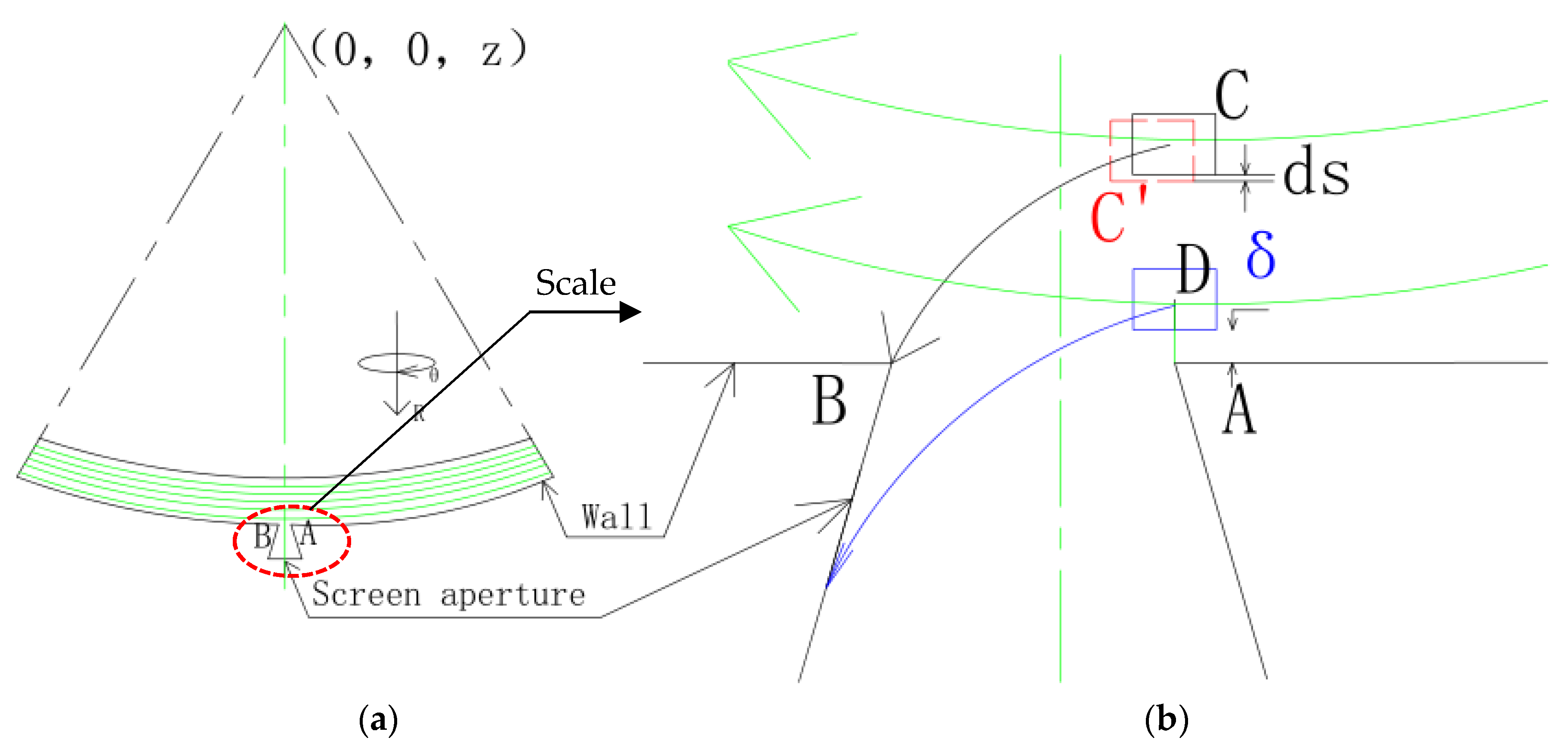

| Items | Abstract Fan Model |
|---|---|
| Radius of gyration | 37.5 mm |
| Screen aperture size | 0.7 mm |
| Thickness of screen bar | 5 mm |
| Width of screen bar | 3.25 mm |
| Length × Width of column-section inlet | 29 mm × 8 mm |
| Length × Width of column-section outlet | 29 mm × 8 mm |
| Items | Models | |
|---|---|---|
| Multiphase flow model | ||
| VOF equation: | (1) | |
| (2) | ||
| Turbulence model | ||
| Velocity: | (3) | |
| Continuity equation: | (4) | |
| Motion equation: | (5) | |
| Linear RSMs: | (6) | |
| Standard wall function: | (7) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yu, A.; Lv, J.; Wang, C.; Zhu, Z.; Khan, M.S. Study of the Fluid Passing through the Screen in the Three Products Hydrocyclone Screen (TPHS): A Theoretical Analysis and Numerical Simulation. Processes 2022, 10, 628. https://doi.org/10.3390/pr10040628
Liu H, Yu A, Lv J, Wang C, Zhu Z, Khan MS. Study of the Fluid Passing through the Screen in the Three Products Hydrocyclone Screen (TPHS): A Theoretical Analysis and Numerical Simulation. Processes. 2022; 10(4):628. https://doi.org/10.3390/pr10040628
Chicago/Turabian StyleLiu, Haizeng, Anghong Yu, Jintao Lv, Chuanzhen Wang, Zaisheng Zhu, and Md. Shakhaoath Khan. 2022. "Study of the Fluid Passing through the Screen in the Three Products Hydrocyclone Screen (TPHS): A Theoretical Analysis and Numerical Simulation" Processes 10, no. 4: 628. https://doi.org/10.3390/pr10040628
APA StyleLiu, H., Yu, A., Lv, J., Wang, C., Zhu, Z., & Khan, M. S. (2022). Study of the Fluid Passing through the Screen in the Three Products Hydrocyclone Screen (TPHS): A Theoretical Analysis and Numerical Simulation. Processes, 10(4), 628. https://doi.org/10.3390/pr10040628









