Diffusion of Ethanol in Supercritical Carbon Dioxide—Investigation of scCO2-Cosolvent Mixtures Used in Pharmaceutical Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Equipment and Procedure
3. Results and Discussion
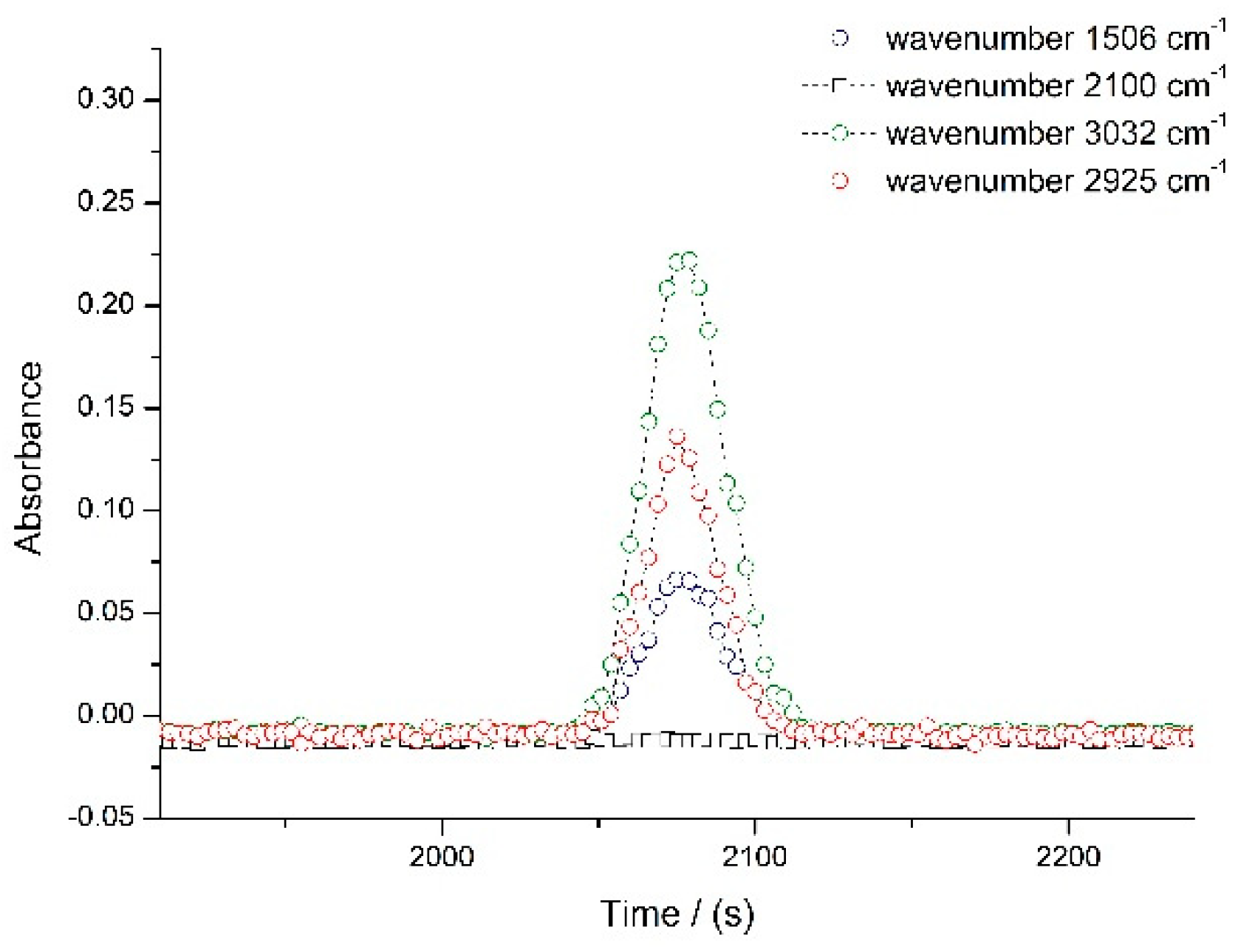
3.1. Optimization of Experimental Parameters
- (i)
- Laminar regime of the solvent flow, with Reynolds number, Re ranging from 55 to 144 for supercritical CO2 , where a0 is the radius of the tube, is the average velocity of the flow, ρ is the density, and η is the viscosity of the solvent);
- (ii)
- (iii)
- Secondary flow effects associated to coiled columns were negligible with De2Sc < 14, where De and Sc are the Dean and Schmidt numbers, respectively (, and , where Rc is the radius of dispersion coil).
3.2. Diffusion Coefficients for Ethanol in Supercritical CO2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brunner, G. Applications of Supercritical Fluids. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 321–342. [Google Scholar] [CrossRef] [PubMed]
- Davies, O.R.; Lewis, A.L.; Whitaker, M.J.; Tai, H.; Shakesheff, K.; Howdle, S.M. Applications of Supercritical CO2 in the Fabrication of Polymer Systems for Drug Delivery and Tissue Engineering. Adv. Drug Deliv. Rev. 2008, 60, 373–387. [Google Scholar] [CrossRef] [PubMed]
- Yasuji, T.; Takeuchi, H.; Kawashima, Y. Particle Design of Poorly Water-Soluble Drug Substances Using Supercritical Fluid Technologies. Adv. Drug Deliv. Rev. 2008, 60, 388–398. [Google Scholar] [CrossRef]
- Djerafi, R.; Masmoudi, Y.; Crampon, C.; Meniai, A.; Badens, E. Supercritical Anti-Solvent Precipitation of Ethyl Cellulose. J. Supercrit. Fluids 2015, 105, 92–98. [Google Scholar] [CrossRef]
- Yeo, S.-D.; Lim, G.-B.; Debendetti, P.G.; Bernstein, H. Formation of Microparticulate Protein Powder Using a Supercritical Fluid Antisolvent. Biotechnol. Bioeng. 1993, 41, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, P.; Gupta, R.B. Production of Griseofulvin Nanoparticles Using Supercritical CO2 Antisolvent with Enhanced Mass Transfer. Int. J. Pharm. 2001, 228, 19–31. [Google Scholar] [CrossRef]
- Reverchon, E. Supercritical Antisolvent Precipitation of Micro- and Nano-Particles. J. Supercrit. Fluids 1999, 15, 1–21. [Google Scholar] [CrossRef]
- Thiering, R.; Dehghani, F.; Dillow, A.; Foster, N.R. Solvent Effects on the Controlled Dense Gas Precipitation of Model Proteins. J. Chem. Technol. Biotechnol. 2000, 75, 42–53. [Google Scholar] [CrossRef]
- Türk, M.; Hils, P.; Helfgen, B.; Schaber, K.; Martin, H.-J.; Wahl, M. Micronization of Pharmaceutical Substances by the Rapid Expansion of Supercritical Solutions (RESS): A Promising Method to Improve Bioavailability of Poorly Soluble Pharmaceutical Agents. J. Supercrit. Fluids 2002, 22, 75–84. [Google Scholar] [CrossRef]
- Phillips, E.M.; Stella, V.J. Rapid Expansion from Supercritical Solutions: Application to Pharmaceutical Processes. Int. J. Pharm. 1993, 94, 1–10. [Google Scholar] [CrossRef]
- Dixon, D.J.; Johnston, K.P.; Bodmeier, R.A. Polymeric Materials Formed by Precipitation with a Compressed Fluid Antisolvent. AIChE J. 1993, 39, 127–139. [Google Scholar] [CrossRef]
- Benedetti, L.; Bertucco, A.; Pallado, P. Production of Micronic Particles of Biocompatible Polymer Using Supercritical Carbon Dioxide. Biotechnol. Bioeng. 1997, 53, 232–237. [Google Scholar] [CrossRef]
- Young, T.J.; Johnston, K.P.; Mishima, K.; Tanaka, H. Encapsulation of Lysozyme in a Biodegradable Polymer by Precipitation with a Vapor-over-Liquid Antisolvent. J. Pharm. Sci. 1999, 88, 640–650. [Google Scholar] [CrossRef] [PubMed]
- Badens, E.; Magnan, C.; Charbit, G. Microparticles of Soy Lecithin Formed by Supercritical Processes. Biotechnol. Bioeng. 2000, 72, 194–204. [Google Scholar] [CrossRef]
- Gref, R.; Minamitake, Y.; Peracchia, M.T.; Trubetskoy, V.; Torchilin, V.; Langer, R. Biodegradable Long-Circulating Polymeric Nanospheres. Science 1994, 263, 1600–1603. [Google Scholar] [CrossRef] [Green Version]
- Subra, P.; Jestin, P. Powders Elaboration in Supercritical Media: Comparison with Conventional Routes. Powder Technol. 1999, 103, 2–9. [Google Scholar] [CrossRef]
- Ventosa, N.; Sala, A.S.; Veciana, J.; Torres, J.; Llibre, J. Depressurization of an Expanded Liquid Organic Solution (DELOS): A New Procedure for Obtaining Submicron- or Micron-Sized Crystalline Particles. Cryst. Growth Des. 2001, 1, 299–303. [Google Scholar] [CrossRef]
- Behnejad, H.; Sengers, J.V.; Anisimov, M.A. Chapter 10: Thermodynanic Behaviour of Fluids near Critical Points. In Applied Thermodynamics of Fluids; RSC Publishing: Cambridge, UK, 2010; Volume 8, pp. 321–367. ISBN 9781849730983. [Google Scholar]
- Bush, J.R.; Akgerman, A.; Hall, K.R. Synthesis of Controlled Release Device with Supercritical CO2 and Co-Solvent. J. Supercrit. Fluids 2007, 41, 311–316. [Google Scholar] [CrossRef]
- Al-Hamimi, S.; Mayoral, A.A.; Cunico, L.P.; Turner, C. Carbon Dioxide Expanded Ethanol Extraction: Solubility and Extraction Kinetics of α-Pinene and cis-Verbenol. Anal. Chem. 2016, 88, 4336–4345. [Google Scholar] [CrossRef] [Green Version]
- Araus, K.A.; Casado, V.; del Valle, J.M.; Robert, P.S.; de la Fuente, J.C. Cosolvent Effect of Ethanol on the Solubility of Lutein in Supercritical Carbon Dioxide. J. Supercrit. Fluids 2018, 143, 205–210. [Google Scholar] [CrossRef]
- Suehiro, Y.; Nakajima, M.; Yamada, K.; Uematsu, M. Critical Parameters of {xCO2+ (1−x) CHF3} forx= (1.0000, 0.7496, 0.5013, and 0.2522). J. Chem. Thermodyn. 1996, 28, 1153–1164. [Google Scholar] [CrossRef]
- Tyrell, H.J.V.; Harris, K.R. Diffusion in Liquids, A Theoretical and Experimental Study; Butterworths-Heinemann: Oxford, UK, 1985. [Google Scholar]
- Callendar, R.; Leaist, D.G. Diffusion Coefficients for Binary, Ternary, and Polydisperse Solutions from Peak-Width Analysis of Taylor Dispersion Profiles. J. Solut. Chem. 2006, 35, 353–379. [Google Scholar] [CrossRef]
- Leaist, D.G. Ternary Diffusion Coefficients of 18-Crown-6 Ether–KCl–Water by Direct Least-Squares Analysis of Taylor Dispersion Measurements. J. Chem. Soc. Faraday Trans. 1991, 87, 597–601. [Google Scholar] [CrossRef]
- Santos, C.; Ribeiro, A.C.F.; Esteso, M.A. Drug Delivery Systems: Study of Inclusion Complex Formation between Methylxanthines and Cyclodextrins and Their Thermodynamic and Transport Properties. Biomolecules 2019, 9, 196. [Google Scholar] [CrossRef] [Green Version]
- Santos, C.I.; Esteso, M.A.; Lobo, V.M.; Cabral, A.M.; Ribeiro, A.C. Taylor Dispersion Technique as a Tool for Measuring Multicomponent Diffusion in Drug Delivery Systems at Physiological Temperature. J. Chem. Thermodyn. 2015, 84, 76–80. [Google Scholar] [CrossRef]
- Santos, C.I.; Ramos, M.L.; Justino, L.L.; Burrows, H.D.; Valente, A.J.; Esteso, M.A.; Leaist, D.G.; Ribeiro, A.C. Effect of pH in the Structure and Mass Transport by Diffusion of Theophylline. J. Chem. Thermodyn. 2017, 110, 162–170. [Google Scholar] [CrossRef]
- Secuianu, C.; Maitland, G.C.; Trusler, J.P.M.; Wakeham, W.A. Mutual Diffusion Coefficients of Aqueous KCl at High Pressures Measured by the Taylor Dispersion Method. J. Chem. Eng. Data 2011, 56, 4840–4848. [Google Scholar] [CrossRef]
- Cadogan, S.P.; Maitland, G.; Trusler, J.P.M. Diffusion Coefficients of CO2 and N2 in Water at Temperatures between 298.15 K and 423.15 K at Pressures up to 45 MPa. J. Chem. Eng. Data 2014, 59, 519–525. [Google Scholar] [CrossRef] [Green Version]
- Morin, P.; Caude, M.; Richard, H.; Rosset, R. Carbon Dioxide Supercritical Fluid Chromatography-Fourier Transform Infrared Spectrometry. Chromatographia 1986, 21, 523–530. [Google Scholar] [CrossRef]
- Lee, C.H.; Holder, G.D. Use of Supercritical Fluid Chromatography for Obtaining Mass Transfer Coefficients in Fluid-Solid Systems at Supercritical Conditions. Ind. Eng. Chem. Res. 1995, 34, 906–914. [Google Scholar] [CrossRef]
- Suárez, J.J.; Medina, I.; Bueno, J.L. Diffusion Coefficients in Supercritical Fluids: Available Data and Graphical Correlations. Fluid Phase Equilibria 1998, 153, 167–212. [Google Scholar] [CrossRef]
- Lai, C.-C.; Tan, C.-S. Measurement of Molecular Diffusion Coefficients in Supercritical Carbon Dioxide Using a Coated Capillary Column. Ind. Eng. Chem. Res. 1995, 34, 674–680. [Google Scholar] [CrossRef]
- Bruno, T. A Supercritical Fluid Chromatograph for Physicochemical Studies. J. Res. Natl. Bur. Stand. 1989, 94, 105–112. [Google Scholar] [CrossRef]
- Sengers, J.M.H.L.; Deiters, U.; Klask, U.; Swidersky, P.; Schneider, G.M. Application of the Taylor Dispersion Method in Supercritical Fluids. Int. J. Thermophys. 1993, 14, 893–922. [Google Scholar] [CrossRef]
- Santos, C.I.A.V.; Barros, M.C.F.; Faro, M.P.R.T.; Ribeiro, A.C.F. FTIR as Powerful Tool for Measurements of Diffusion in Supercritical Carbon Dioxide Using Taylor Dispersion Method. Microgravity Sci. Technol. 2022; to be submitted. [Google Scholar]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical Properties of Fluid Systems. In NIST Chemistry Webbook; NIST Standard Reference Database: Gaitherburg, MD, USA, 2017; No. 69. [Google Scholar]
- Bueno, J.L.; Suarez, J.J.; Dizy, J.; Medina, I. Infinite Dilution Diffusion Coefficients: Benzene Derivatives as Solutes in Supercritical Carbon Dioxide. J. Chem. Eng. Data 1993, 38, 344–349. [Google Scholar] [CrossRef]
- Alizadeh, A.; De Castro, C.A.N.; Wakeham, W.A. The Theory of the Taylor Dispersion Technique for Liquid Diffusivity Measurements. Int. J. Thermophys. 1980, 1, 243–284. [Google Scholar] [CrossRef]
- Levenspiel, O.; Smith, W. Notes on the Diffusion-Type Model for the Longitudinal Mixing of Fluids in Flow. Chem. Eng. Sci. 1995, 50, 3891–3896. [Google Scholar] [CrossRef]
- Gaponenko, Y.; Gousselnikov, V.; Santos, C.; Shevtsova, V. Near-Critical Behavior of Fick Diffusion Coefficient in Taylor Dispersion Experiments. Microgravity Sci. Technol. 2019, 31, 475–486. [Google Scholar] [CrossRef]
- Hertz, H.G. T. Erdey-Grúz: Transport Phenomena in Aqueous Solutions; 512 Seiten, Berichte der Bunsengesellschaft für physikalische Chemie; Adam Hilger Ltd.: London, UK, 1975; Volume 79, p. 841. [Google Scholar] [CrossRef]
- Wilke, C.R.; Chang, P. Correlation of Diffusion Coefficients in Dilute Solutions. AIChE J. 1955, 1, 264–270. [Google Scholar] [CrossRef]
- Scheibel, E.G. Correspondence. Liquid Diffusivities. Viscosity of Gases. Ind. Eng. Chem. 1954, 46, 2007–2008. [Google Scholar] [CrossRef]
- Lusis, M.A.; Ratcliff, C.A. Diffusion in Binary Liquid Mixtures at Infinite Dilution. Can. J. Chem. Eng. 1968, 46, 385–387. [Google Scholar] [CrossRef]
- Vaz, R.V.; Magalhães, A.L.; Silva, C.M. Improved Stokes–Einstein Based Models for Diffusivities in Supercritical CO2. J. Taiwan Inst. Chem. Eng. 2014, 45, 1280–1284. [Google Scholar] [CrossRef]
- Tyn, M.T.; Calus, W.F. Temperature and Concentration Dependence of Mutual Diffusion Coefficients of Some Binary Liquid Systems. J. Chem. Eng. Data 1975, 20, 310–316. [Google Scholar] [CrossRef]





| T/K | ρ/kg/m3 | η/(10−5 cP) | (D ± SD) a/(10−8 m2 s−1) |
|---|---|---|---|
| 306.15 | 752.30 | 6.37 | 1.49 ± 0.01 |
| 311.15 | 690.79 | 5.51 | 1.69 ± 0.04 |
| 316.15 | 604.79 | 4.52 | 1.98 ± 0.05 |
| 321.15 | 489.18 | 3.49 | 2.10± 0.08 |
| 326.15 | 393.92 | 2.85 | 2.57 ± 0.09 |
| 331.15 | 338.03 | 2.57 | 2.98 ± 0.15 |
| Model | AAD % | |
|---|---|---|
| Original | Modified | |
| Wilke–Chang (Equation (2)) | 13.2 a | 5.8 e |
| Scheibel (Equation (3)) | 16.4 b | 12.7 e |
| Lusis–Ratcliff (Equation (4)) | 15.8 c | 7.4 e |
| Lai-Tan (Equation (5)) | 6.8 d | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, C.I.A.V.; Barros, M.C.F.; Ribeiro, A.C.F. Diffusion of Ethanol in Supercritical Carbon Dioxide—Investigation of scCO2-Cosolvent Mixtures Used in Pharmaceutical Applications. Processes 2022, 10, 660. https://doi.org/10.3390/pr10040660
Santos CIAV, Barros MCF, Ribeiro ACF. Diffusion of Ethanol in Supercritical Carbon Dioxide—Investigation of scCO2-Cosolvent Mixtures Used in Pharmaceutical Applications. Processes. 2022; 10(4):660. https://doi.org/10.3390/pr10040660
Chicago/Turabian StyleSantos, Cecília I. A. V., Marisa C. F. Barros, and Ana C. F. Ribeiro. 2022. "Diffusion of Ethanol in Supercritical Carbon Dioxide—Investigation of scCO2-Cosolvent Mixtures Used in Pharmaceutical Applications" Processes 10, no. 4: 660. https://doi.org/10.3390/pr10040660
APA StyleSantos, C. I. A. V., Barros, M. C. F., & Ribeiro, A. C. F. (2022). Diffusion of Ethanol in Supercritical Carbon Dioxide—Investigation of scCO2-Cosolvent Mixtures Used in Pharmaceutical Applications. Processes, 10(4), 660. https://doi.org/10.3390/pr10040660







