A Multi-Physic Modelling Insight into the Differences between Microwave and Conventional Heating for the Synthesis of TiO2 Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
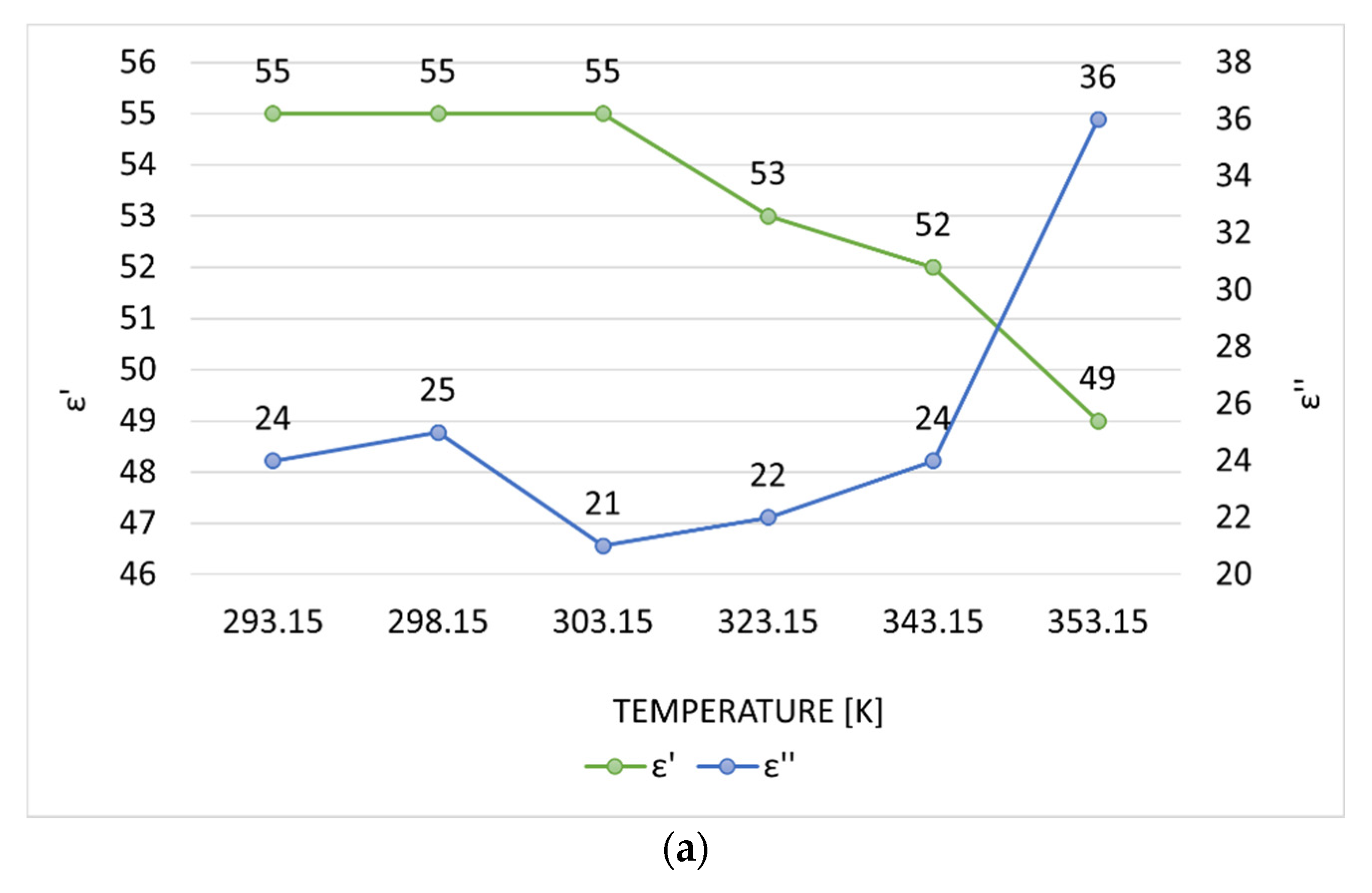
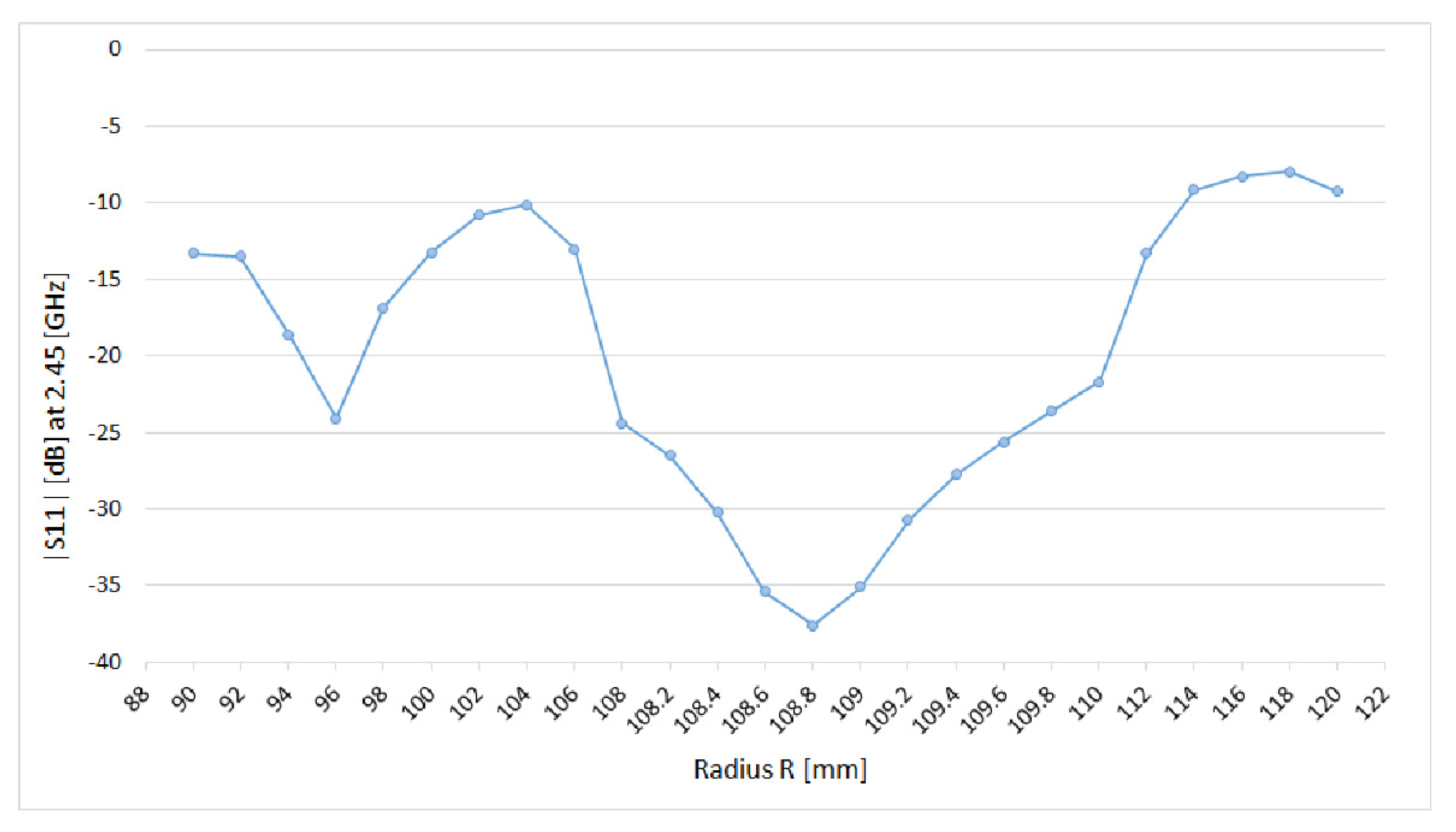
3.1. Preliminary Applicator Optimization
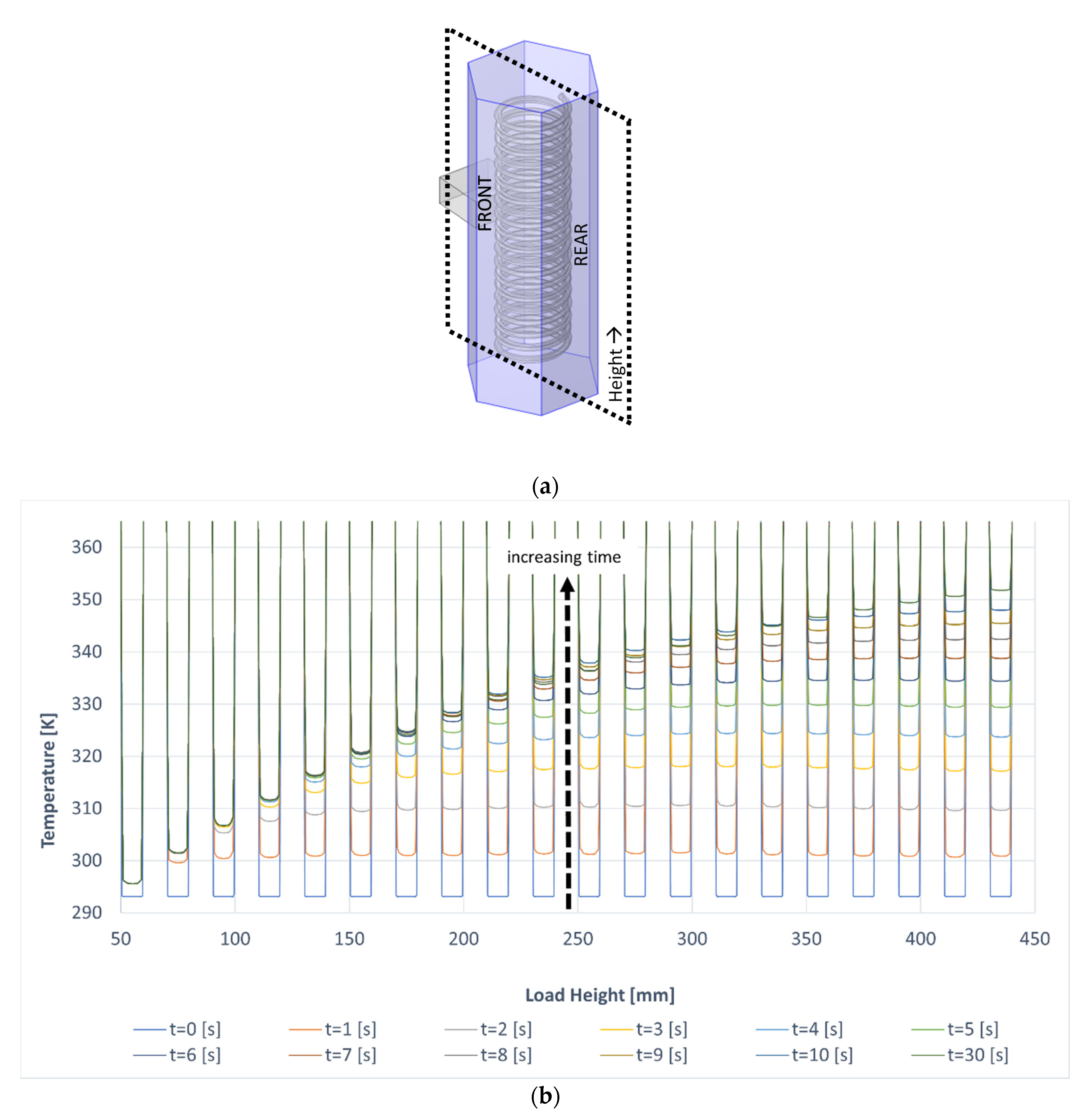
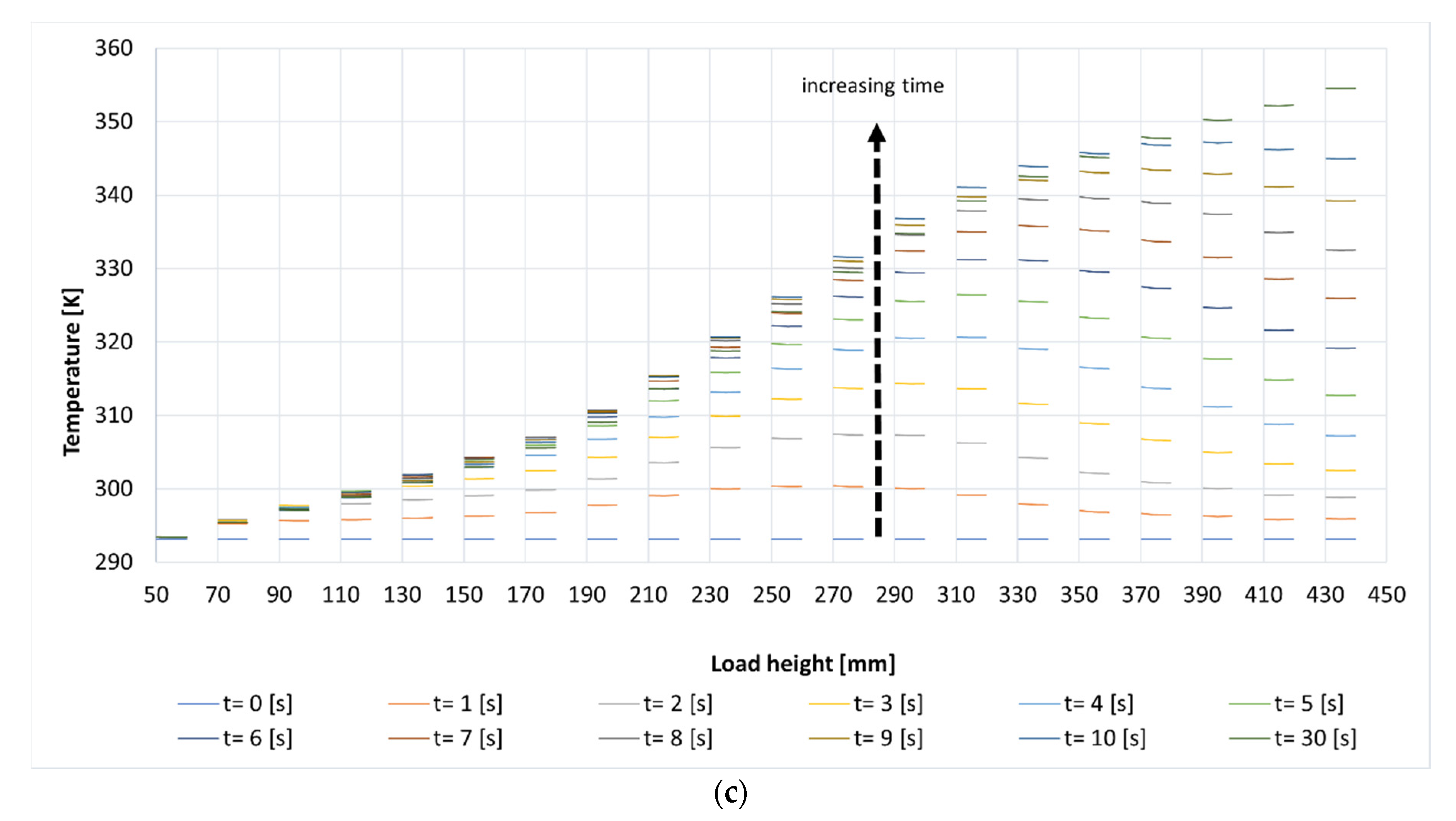
3.2. Comparison between Conventional and Microwave Heating
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Byranvand, M.M.; Kharat, A.N.; Fatholahi, L.; Beiranvand, Z.M. A Review on Synthesis of Nano-TiO2 via Different Methods. J. Nanostruct. 2013, 3, 1–9. [Google Scholar]
- Chen, X.; Mao, S.S. Synthesis of Titanium Dioxide (TiO2) Nanomaterials. J. Nanosci. Nanotechnol. 2006, 6, 906–925. [Google Scholar] [CrossRef] [PubMed]
- Karlsson, M.C.F.; Alvarez-Asencio, R.; Bordes, R.; Larsson, A.; Taylor, P.; Steenari, B.-M. Characterization of paint formulated using secondary TiO2 pigments recovered from waste paint. J. Coat. Technol. Res. Vol. 2019, 16, 607–614. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Selloni, A. Introduction: Titanium Dioxide (TiO2) Nanomaterials. Chem. Rev. 2014, 114, 9281–9282. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Wang, X.; Jia, Y.; Chen, X.; Han, H.; Li, C. Titanium Dioxide-Based Nanomaterials for Photocatalytic Fuel Generations. Chem. Rev. 2014, 114, 9987–10043. [Google Scholar] [CrossRef]
- Yun, H.J.; Lee, H.; Kim, N.D.; Lee, D.M.; Yu, S.; Yi, J. A Combination of Two Visible-Light Responsive Photocatalysts for Achieving the Z-Scheme in the Solid State. ACS Nano 2011, 5, 4084–4090. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Ci, S.; Mao, S.; Cui, S.; Lu, G.; Yu, K.; Luo, S.; He, Z.; Chen, J. TiO2 nanoparticles-decorated carbon nanotubes for significantly improved bioelectricity generation in microbial fuel cells. J. Power Sources 2013, 234, 100–106. [Google Scholar] [CrossRef]
- Hou, X.; Aitola, K.; Lund, P.D. TiO2 nanotubes for dye-sensitized solar cells—A review. Energy Sci. Eng. 2021, 9, 921–937. [Google Scholar] [CrossRef]
- Kong, F.; Dai, S.; Wang, K. Review of Recent Progress in Dye-Sensitized Solar Cells. Adv. Optoelectron. 2007, 2007, 075384. [Google Scholar] [CrossRef] [Green Version]
- Richards, B.S. Comparison of TiO2 and other dielectric Coatings for Buried-contact Solar Cells: A Review. Prog. Photovolt. Res. Appl. 2004, 12, 253–281. [Google Scholar] [CrossRef]
- Li, Z.; Yao, Z.; Haidry, A.A.; Plecenik, T.; Xie, L.; Sun, L.; Qawareen, F. Resistive-type hydrogen gas sensor based on TiO2: A review. Int. J. Hydrogen Energy 2018, 43, 21114–21132. [Google Scholar] [CrossRef]
- Ferroni, M.; Guidi, V.; Martinelli, G.; Faglia, G.; Nelli, P.; Sberveglieri, G. Characterization of a nanosized TiO2 gas sensor. Nanostruct. Mater. 1996, 7, 709–718. [Google Scholar] [CrossRef]
- Tang, H.; Prasad, K.; Sanjinés, R.; Lévy, F. TiO2 anatase thin films as gas sensors. Sens. Actuators B Chem. 1995, 26, 71–75. [Google Scholar] [CrossRef]
- Jin Choi, Y.; Seeley, Z.; Bandyopadhyay, A.; Bose, S.; Akbar, S.A. Aluminum-doped TiO2 nano-powders for gas sensors. Sens. Actuators B Chem. 2007, 124, 111–117. [Google Scholar] [CrossRef]
- Malallah Rzaij, J.; Mohsen Abass, A. Review on: TiO2 Thin Film as a Metal Oxide Gas Sensor. J. Chem. Rev. 2020, 2, 114–121. [Google Scholar] [CrossRef] [Green Version]
- Brezesinski, T.; Wang, J.; Polleux, J.; Dunn, B.; Tolbert, S.H. Templated Nanocrystal-Based Porous TiO2 Films for Next-Generation Electrochemical Capacitors. J. Am. Chem. Soc. 2009, 131, 1802–1809. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.K.; Choi, G.; Lee, S.Y.; Seo, M.; Lee, S.W.; Han, J.H.; Ahn, H.-S.; Han, S.; Hwang, C.S. Al-Doped TiO2 Films with Ultralow Leakage Currents for Next Generation DRAM Capacitors. Adv. Mater. 2008, 20, 1429–1435. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, W.; Tang, L.; Zhou, K.; Luo, H. High performance capacitors via aligned TiO2 nanowire array. Appl. Phys. Lett. 2017, 110, 133902. [Google Scholar] [CrossRef]
- Albertin, K.F.; Valle, M.A.; Pereyra, I. Study Of MOS Capacitors With TiO2 And SiO2/TiO2 Gate Dielectric. J. Integr. Circuits Syst. 2007, 2, 89–93. [Google Scholar] [CrossRef]
- Froehlich, K. TiO2-based structures for nanoscale memory applications. Mater. Sci. Semicond. Process. 2013, 16, 1186–1195. [Google Scholar] [CrossRef]
- Masalski, J.; Gluszek, J.; Furman, P. Titanium dioxide film obtained using the PACVD method on 316L steel. J. Mater. Sci. Lett. 1995, 14, 587–588. [Google Scholar] [CrossRef]
- Poulios, I.; Spathis, P.; Grigoriadou, A.; Delidou, K.; Tsoumparis, P. Protection of marbles against corrosion and microbial corrosion with TiO2 coatings. J. Environ. Sci. Health Part A 1999, 34, 1455–1471. [Google Scholar] [CrossRef]
- Meinert, K.; Uerpmann, C.; Matschullat, J.; Wolf, G.K. Corrosion and leaching of silver doped ceramic IBAD coatings on SS 316L under simulated physiological conditions. Surf. Coat. Technol. 1998, 103–104, 58–65. [Google Scholar] [CrossRef]
- Yun, H.; Li, J.; Chen, H.; Lin, C. A study on the N-, S- and Cl-modified nano-TiO2 coatings for corrosion protection of stainless steel. Electrochim. Acta 2007, 52, 6679–6685. [Google Scholar] [CrossRef]
- Shen, G.X.; Chen, Y.C.; Lin, C.J. Corrosion protection of 316 L stainless steel by a TiO2 nanoparticle coating prepared by sol–gel method. Thin Solid Film. 2005, 489, 130–136. [Google Scholar] [CrossRef]
- Shan, C.X.; Hou, X.; Choy, K. Corrosion resistance of TiO2 films grown on stainless steel by atomic layer deposition. Surf. Coat. Technol. 2008, 202, 2399–2402. [Google Scholar] [CrossRef]
- John, S.; Salam, A.; Maria, A.; Joseph, A. Corrosion inhibition of mild steel using chitosan/TiO2 nanocomposite coatings. Prog. Org. Coat. 2019, 129, 254–259. [Google Scholar] [CrossRef]
- Wöbkenberg, P.H.; Ishwara, T.; Nelson, J.; Bradley, D.D.C.; Haque, S.A.; Anthopoulos, T.D. TiO2 thin-film transistors fabricated by spray pyrolysis. Appl. Phys. Lett. 2010, 96, 58–61. [Google Scholar] [CrossRef]
- Okyay, A.K.; Oruç, F.B.; Çimen, F.; Aygün, L.E. TiO2 Thin Film Transistor by Atomic Layer Deposition. Proceedings 2013, 8626, 862616. [Google Scholar]
- Shih, W.S.; Young, S.J.; Ji, L.W.; Water, W.; Shiu, H.W. TiO2-Based Thin Film Transistors with Amorphous and Anatase Channel Layer. J. Electrochem. Soc. 2011, 158, 609–611. [Google Scholar] [CrossRef]
- Zhang, J.; Cui, P.; Lin, G.; Zhang, Y.; Sales, M.G.; Jia, M.; Li, Z.; Goodwin, C.; Beebe, T.; Gundlach, L.; et al. High performance anatase-TiO2 thin film transistors with a two-step oxidized TiO2 channel and plasma enhanced atomic layer-deposited ZrO2 gate dielectric. Appl. Phys. Express 2019, 12, 096502. [Google Scholar] [CrossRef]
- Ollis, D.F. Photocatalytic purification and remediation of contaminated air and water. Comptes Rendus l’Acad. Sci.-Ser. IIC-Chem. 2000, 3, 405–411. [Google Scholar] [CrossRef]
- Choi, W.; Ko, J.Y.; Park, H.; Chung, J.S. Investigation on TiO2-coated optical fibers for gas-phase photocatalytic oxidation of acetone. Appl. Catal. B Environ. 2001, 31, 209–220. [Google Scholar] [CrossRef]
- Ryu, J.; Choi, W. Effects of TiO2 Surface Modifications on Photocatalytic Oxidation of Arsenite: The Role of Superoxides. Environ. Sci. Technol. 2004, 38, 2928–2933. [Google Scholar] [CrossRef]
- Cho, Y.; Choi, W.; Lee, C.-H.; Hyeon, T.; Lee, H.-I. Visible Light-Induced Degradation of Carbon Tetrachloride on Dye-Sensitized TiO2. Environ. Sci. Technol. 2001, 35, 966–970. [Google Scholar] [CrossRef] [PubMed]
- Agrios, A.G.; Pichat, P. Recombination rate of photogenerated charges versus surface area: Opposing effects of TiO2 sintering temperature on photocatalytic removal of phenol, anisole, and pyridine in water. J. Photochem. Photobiol. A Chem. 2006, 180, 130–135. [Google Scholar] [CrossRef]
- Munusamy, S.; Aparna, R.s.l.; Prasad, V. Photocatalytic effect of TiO2 and the effect of dopants on degradation of brilliant green. Sustain. Chem. Process. 2013, 1, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.; Vaya, D. Photocatalytic activity of TiO2 nanomaterial. J. Chil. Chem. Soc. 2017, 62, 3683–3690. [Google Scholar] [CrossRef] [Green Version]
- Baldi, G.; Bitossi, M.; Barzanti, A. Method for the Preparation of Aqueous Dispersions of TiO in the Form of Nanoparticles, and Dispersions Obtainable with This Method. U.S. Patent 8,431,621, 30 April 2013. [Google Scholar]
- Cabello, G.; Davoglio, R.A.; Pereira, E.C. Microwave-assisted synthesis of anatase-TiO2 nanoparticles with catalytic activity in oxygen reduction. J. Electroanal. Chem. 2017, 794, 36–42. [Google Scholar] [CrossRef]
- Gressel-Michel, E.; Chaumont, D.; Stuerga, D. From a microwave flash-synthesized TiO2 colloidal suspension to TiO2 thin films. J. Colloid Interface Sci. 2005, 285, 674–679. [Google Scholar] [CrossRef]
- Addamo, M.; Bellardita, M.; Carriazo, D.; Di Paola, A.; Milioto, S.; Palmisano, L.; Rives, V. Inorganic gels as precursors of TiO2 photocatalysts prepared by low temperature microwave or thermal treatment. Appl. Catal. B Environ. 2008, 84, 742–748. [Google Scholar] [CrossRef]
- Bilecka, I.; Djerdj, I.; Niederberger, M. One-minute synthesis of crystalline binary and ternary metal oxide nanoparticles. Chem. Commun. 2008, 7, 886–888. [Google Scholar] [CrossRef] [PubMed]
- Schütz, M.B.; Xiao, L.; Lehnen, T.; Fischer, T.; Mathur, S. Microwave-assisted synthesis of nanocrystalline binary and ternary metal oxides. Int. Mater. Rev. 2018, 63, 341–374. [Google Scholar] [CrossRef]
- Dufour, F.; Cassaignon, S.; Durupthy, O.; Colbeau-Justin, C.; Chanéac, C. Do TiO2 nanoparticles really taste better when cooked in a microwave oven? Eur. J. Inorg. Chem. 2012, 2012, 2707–2715. [Google Scholar] [CrossRef]
- Imoisili, P.E.; Jen, T.-C.; Safaei, B. Microwave-assisted sol–gel synthesis of TiO2-mixed metal oxide nanocatalyst for degradation of organic pollutant. Nanotechnol. Rev. 2021, 10, 126–136. [Google Scholar] [CrossRef]
- Monti, D.; Ponrouch, A.; Estruga, M.; Palacín, M.R.; Ayllón, J.A.; Roig, A. Microwaves as a synthetic route for preparing electrochemically active TiO2 nanoparticles. J. Mater. Res. 2013, 28, 340–347. [Google Scholar] [CrossRef] [Green Version]
- Chung, C.C.; Chung, T.W.; Yang, T.C.K. Rapid synthesis of titania nanowires by microwave-assisted hydrothermal treatments. Ind. Eng. Chem. Res. 2008, 47, 2301–2307. [Google Scholar] [CrossRef]
- SIMPLIFY (Sonication and Microwave Processing of Material Feedstocks), EU Horizon 2020 (Call SPIRE-02-2018) Funded Project under the Grant Agreement No° 820716. Available online: https://www.spire2030.eu/simplify (accessed on 3 April 2021).
- Veronesi, P.; Colombini, E.; Salvatori, D.; Catauro, M.; Leonelli, C. Microwave Processing of PET Using Solid-State Microwave Generators. Macromol. Symp. 2021, 395, 2000204. [Google Scholar] [CrossRef]
- Scott, A.W. Understanding Microwaves; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993; ISBN 9780471745334. [Google Scholar]
- Saleh, T.A.; Majeed, S.; Nayak, A.; Bhushan, B. Principles and Advantages of Microwave-Assisted Methods for the Synthesis of Nanomaterials for Water Purification. In Advanced Nanomaterials for Water Engineering, Treatment, and Hydraulics; Saleh, T.A., Ed.; IGI Global: Hershey, PA, USA, 2017; pp. 40–57. [Google Scholar]
- Leonelli, C.; Lojkowski, W.; Veronesi, P. Temperature profile within a microwave irradiated batch. J. Mach. Constr. Maint. 2018, 3, 33–40. [Google Scholar]
- Baghbanzadeh, M.; Carbone, L.; Cozzoli, P.D.; Kappe, C.O. Microwave-assisted synthesis of colloidal inorganic nanocrystals. Angew. Chem.-Int. Ed. 2011, 50, 11312–11359. [Google Scholar] [CrossRef] [PubMed]
- Van Gerven, T.; Stankiewicz, A. Structure, Energy, Synergy, Time-The fundamentals of Process Intensification. Ind. Eng. Chem. Res. 2009, 48, 2465–2474. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poppi, G.; Colombini, E.; Salvatori, D.; Balestri, A.; Baldi, G.; Leonelli, C.; Veronesi, P. A Multi-Physic Modelling Insight into the Differences between Microwave and Conventional Heating for the Synthesis of TiO2 Nanoparticles. Processes 2022, 10, 697. https://doi.org/10.3390/pr10040697
Poppi G, Colombini E, Salvatori D, Balestri A, Baldi G, Leonelli C, Veronesi P. A Multi-Physic Modelling Insight into the Differences between Microwave and Conventional Heating for the Synthesis of TiO2 Nanoparticles. Processes. 2022; 10(4):697. https://doi.org/10.3390/pr10040697
Chicago/Turabian StylePoppi, Giulia, Elena Colombini, Diego Salvatori, Alessio Balestri, Giovanni Baldi, Cristina Leonelli, and Paolo Veronesi. 2022. "A Multi-Physic Modelling Insight into the Differences between Microwave and Conventional Heating for the Synthesis of TiO2 Nanoparticles" Processes 10, no. 4: 697. https://doi.org/10.3390/pr10040697
APA StylePoppi, G., Colombini, E., Salvatori, D., Balestri, A., Baldi, G., Leonelli, C., & Veronesi, P. (2022). A Multi-Physic Modelling Insight into the Differences between Microwave and Conventional Heating for the Synthesis of TiO2 Nanoparticles. Processes, 10(4), 697. https://doi.org/10.3390/pr10040697








