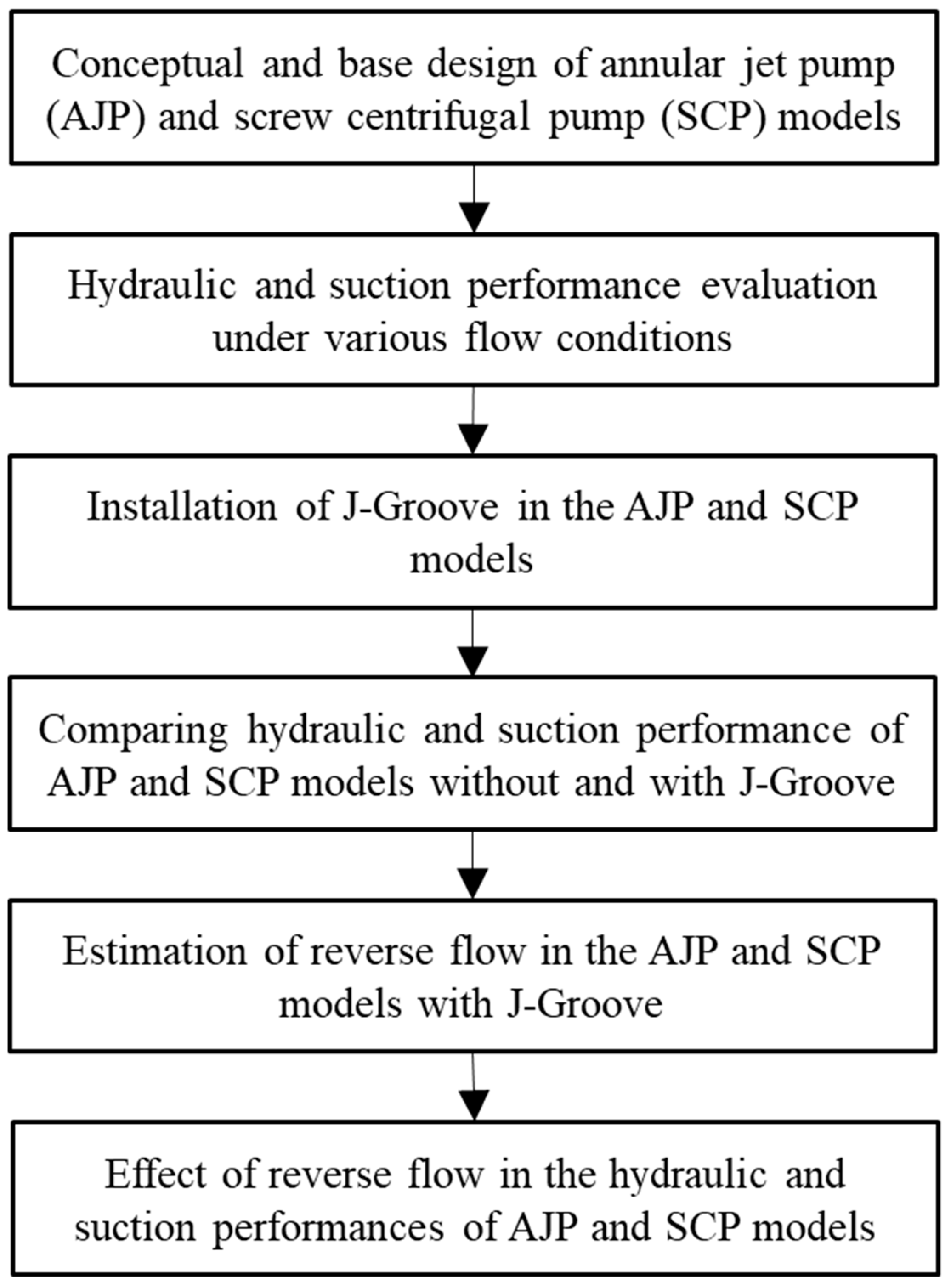
Estimation of Reverse Flow Rate in J-Groove Channel of AJP and SCP Models Using CFD Analysis
Abstract
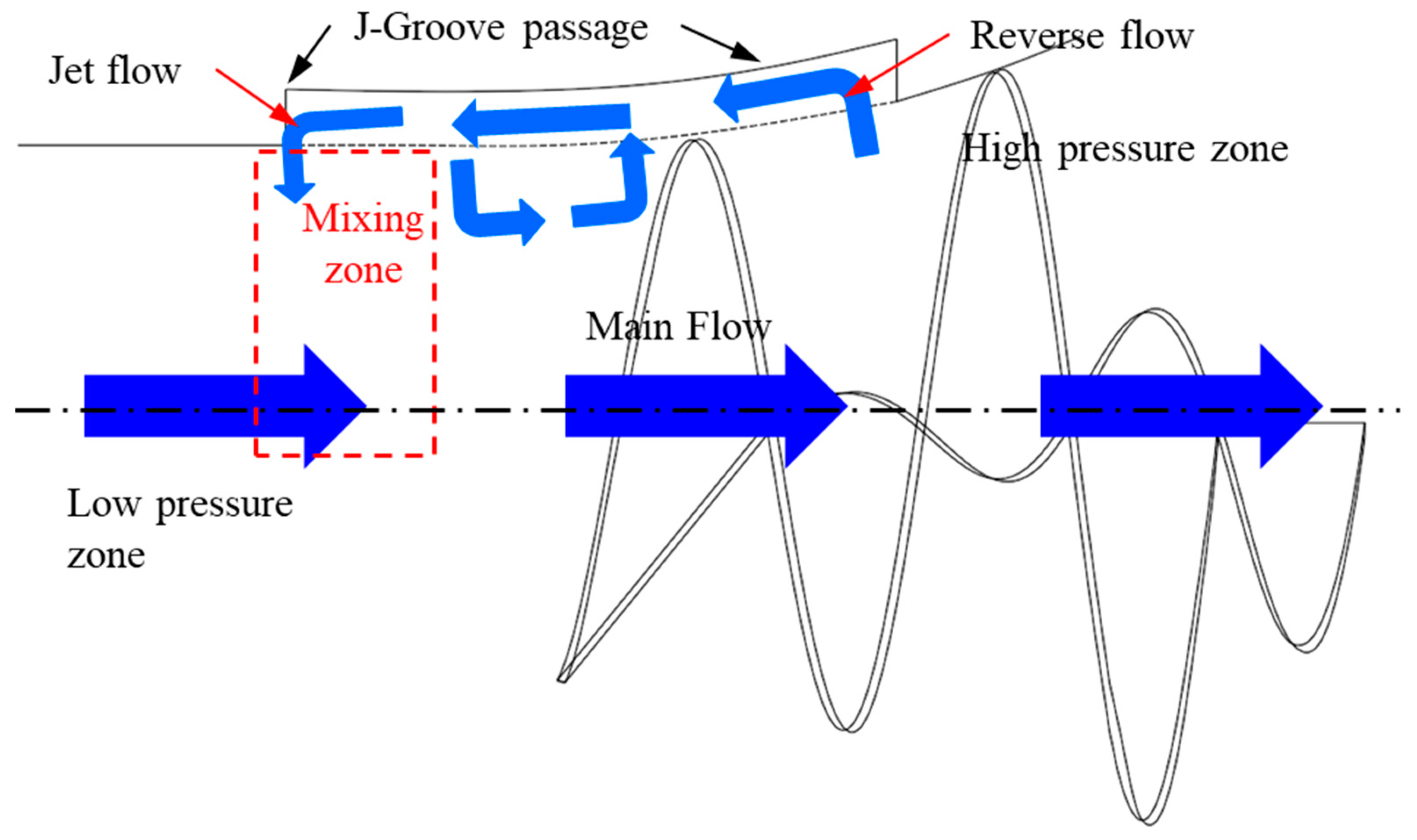
:1. Introduction
2. Test Pump Models and J-Groove Shape Configuration
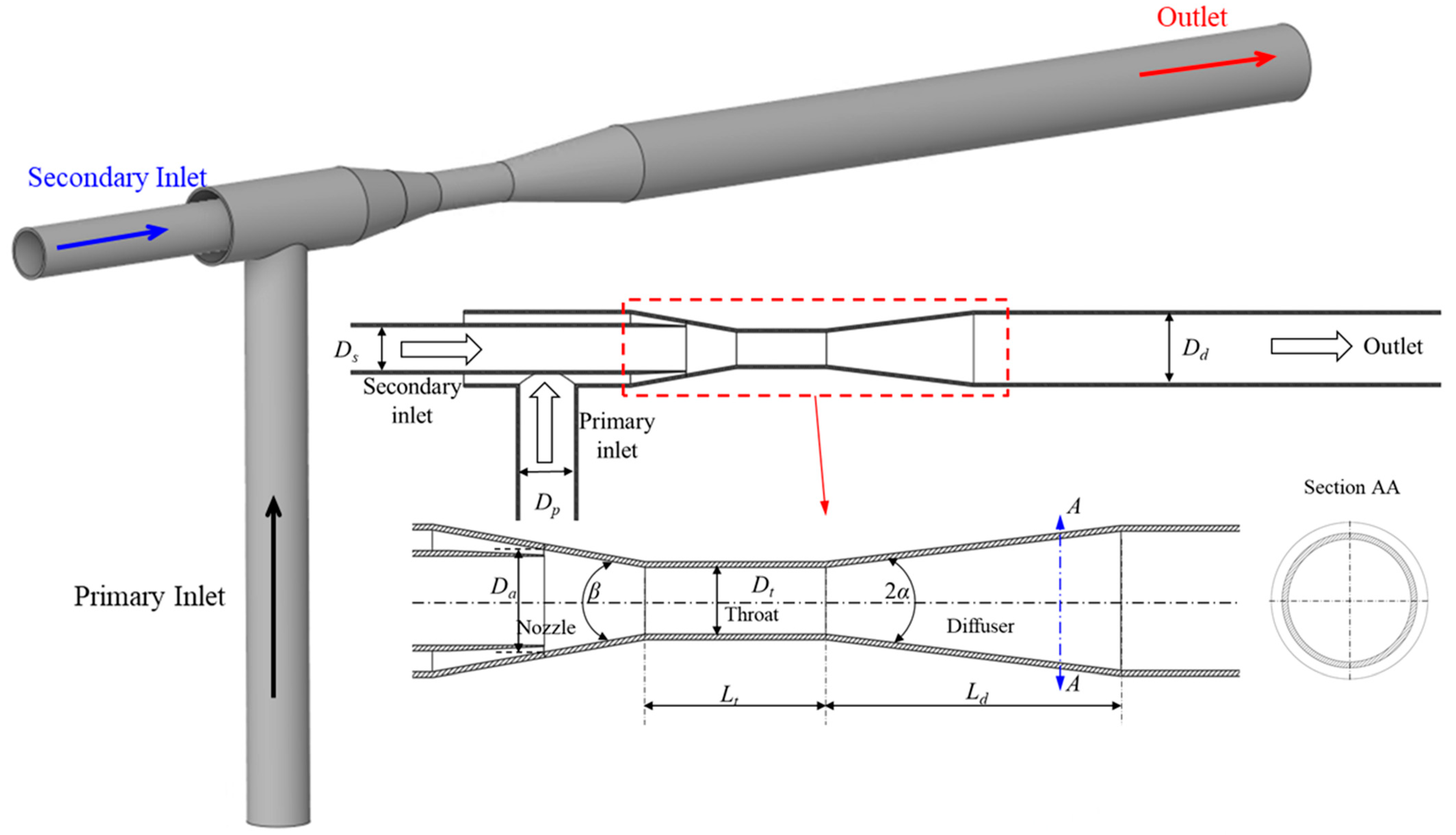
2.1. Annular Jet Pump Model
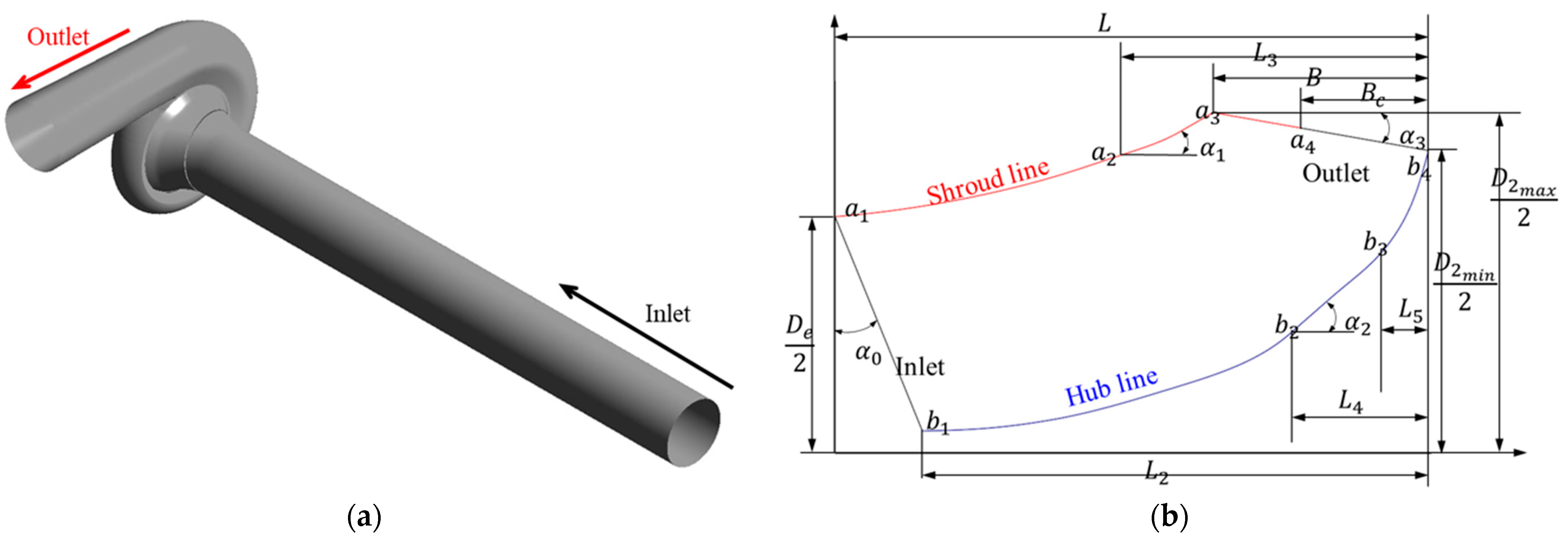
2.2. Screw Centrifugal Pump Model
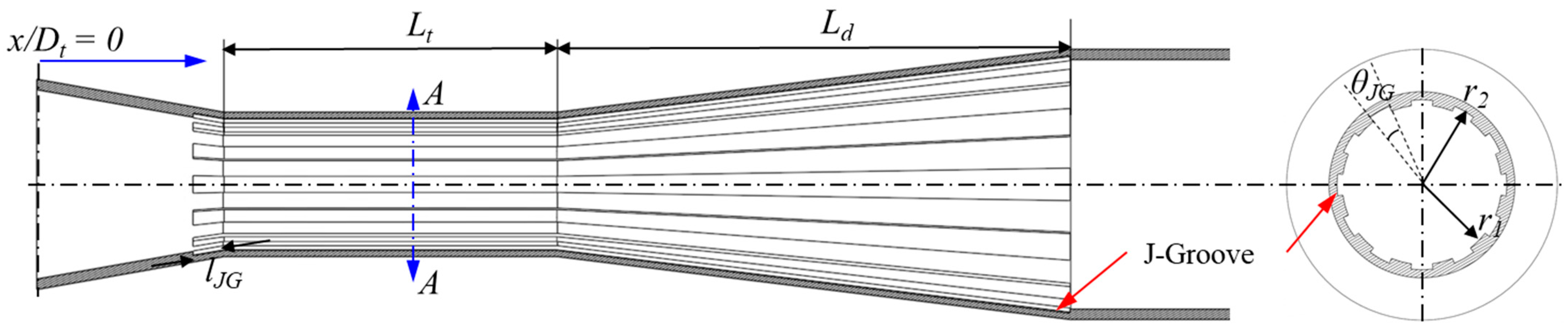
2.3. J-Groove Shape Parameters for AJP and SCP Models
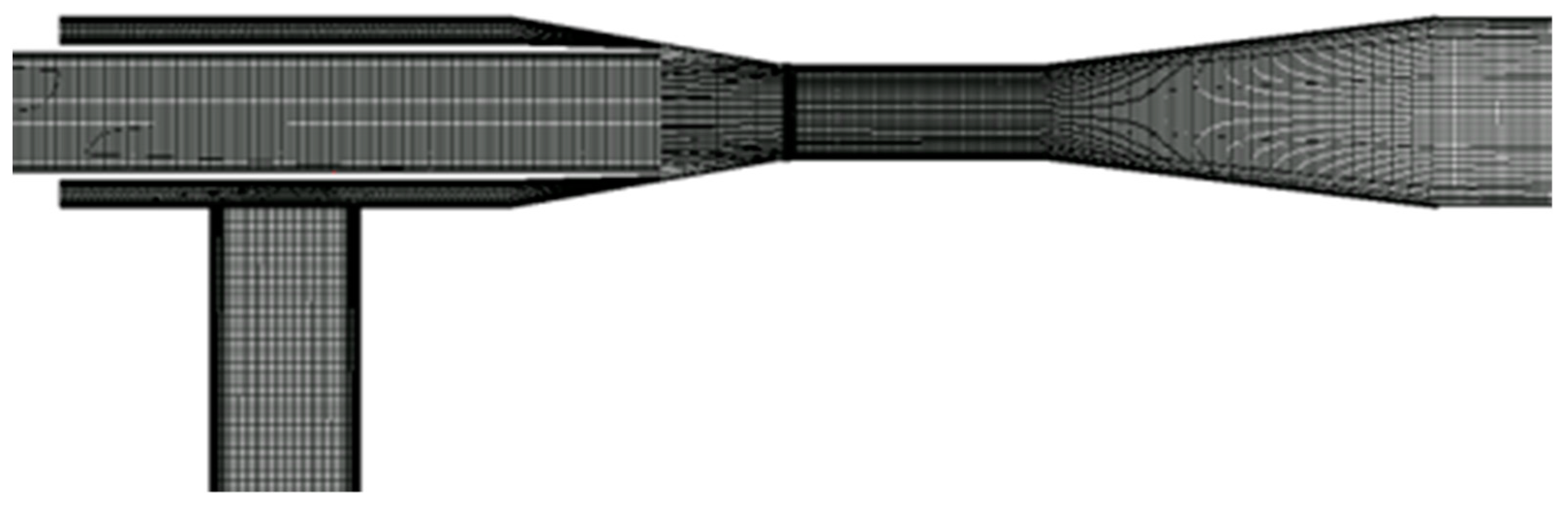
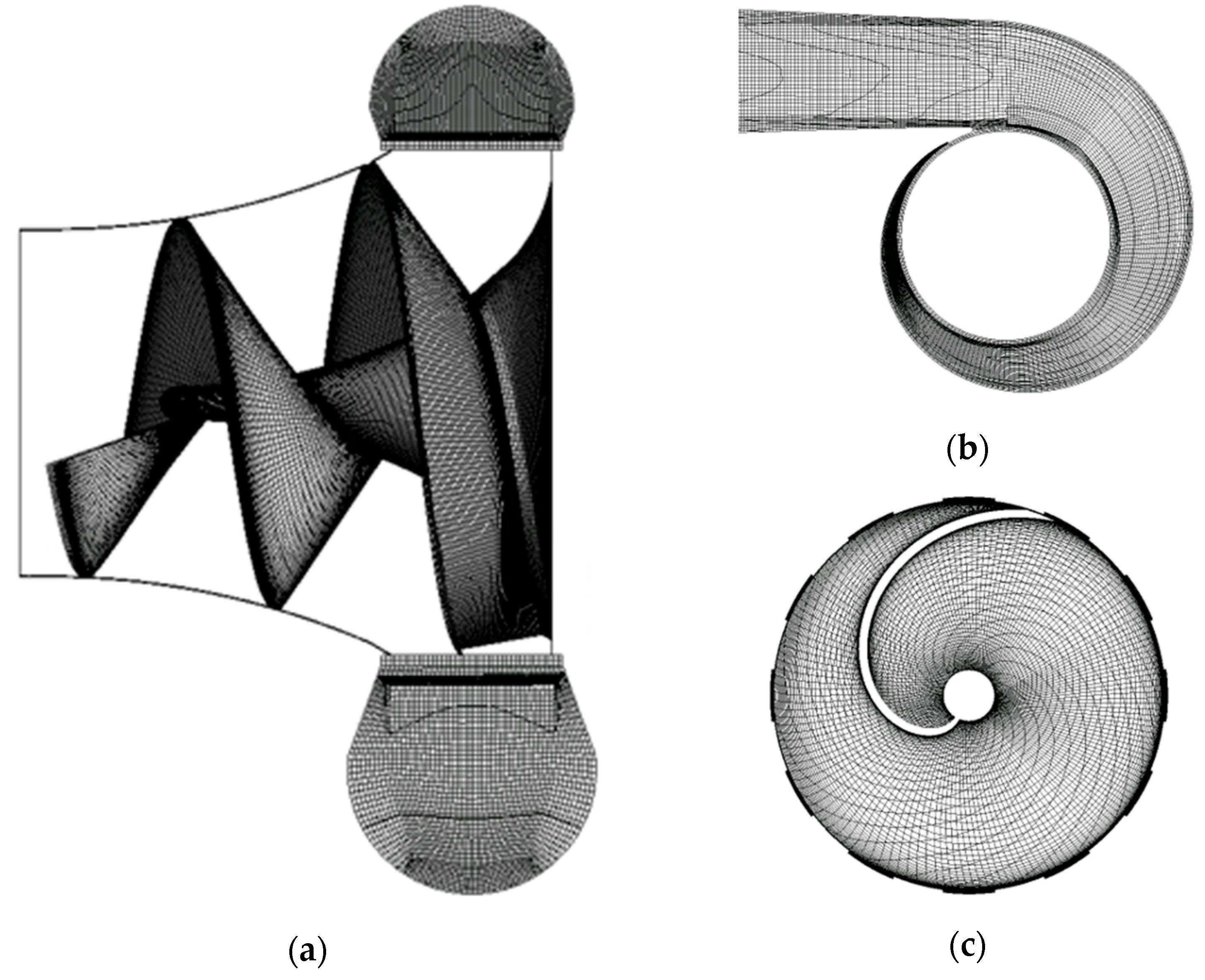
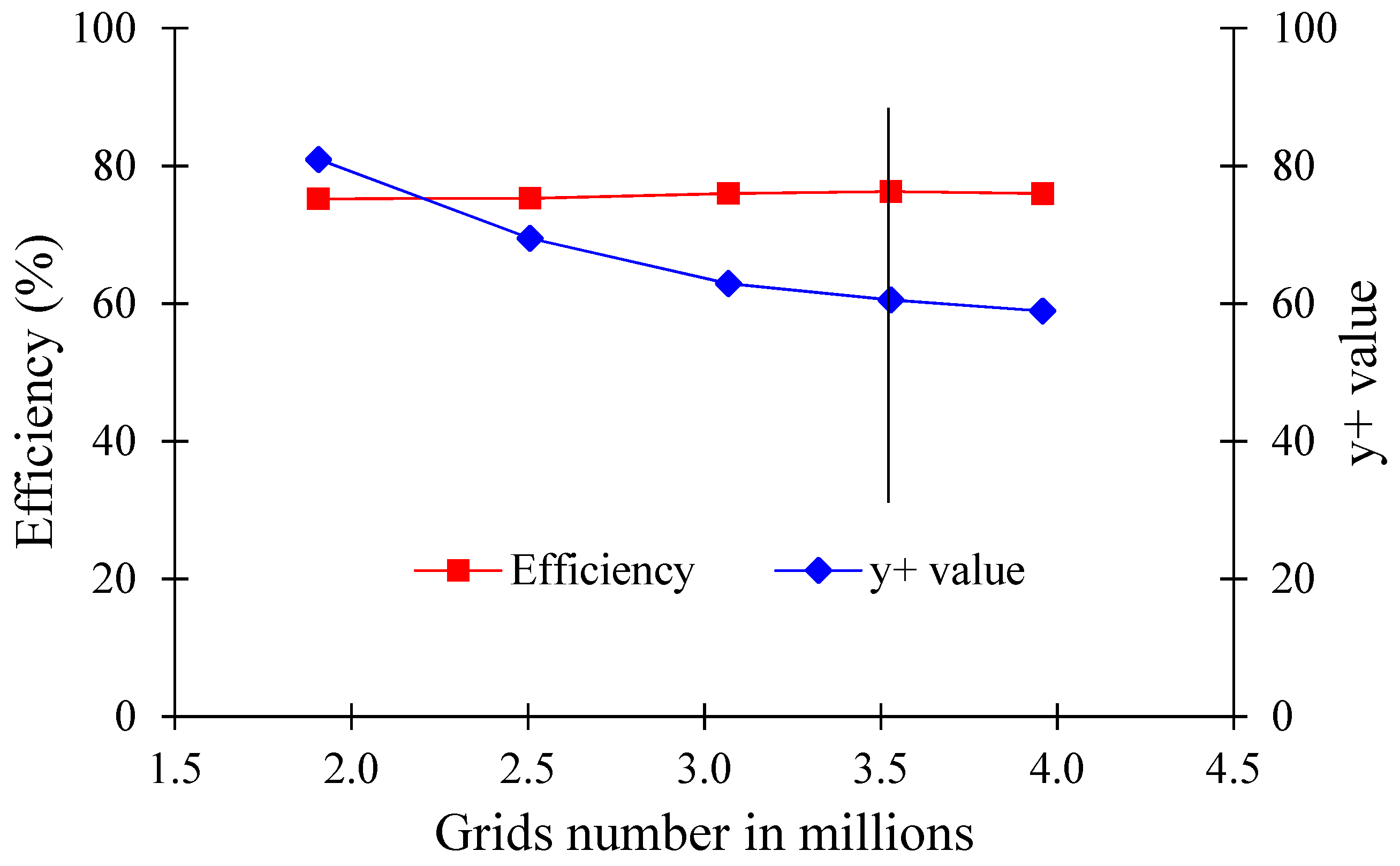
2.4. Numerical Methodology
3. Results and Discussion
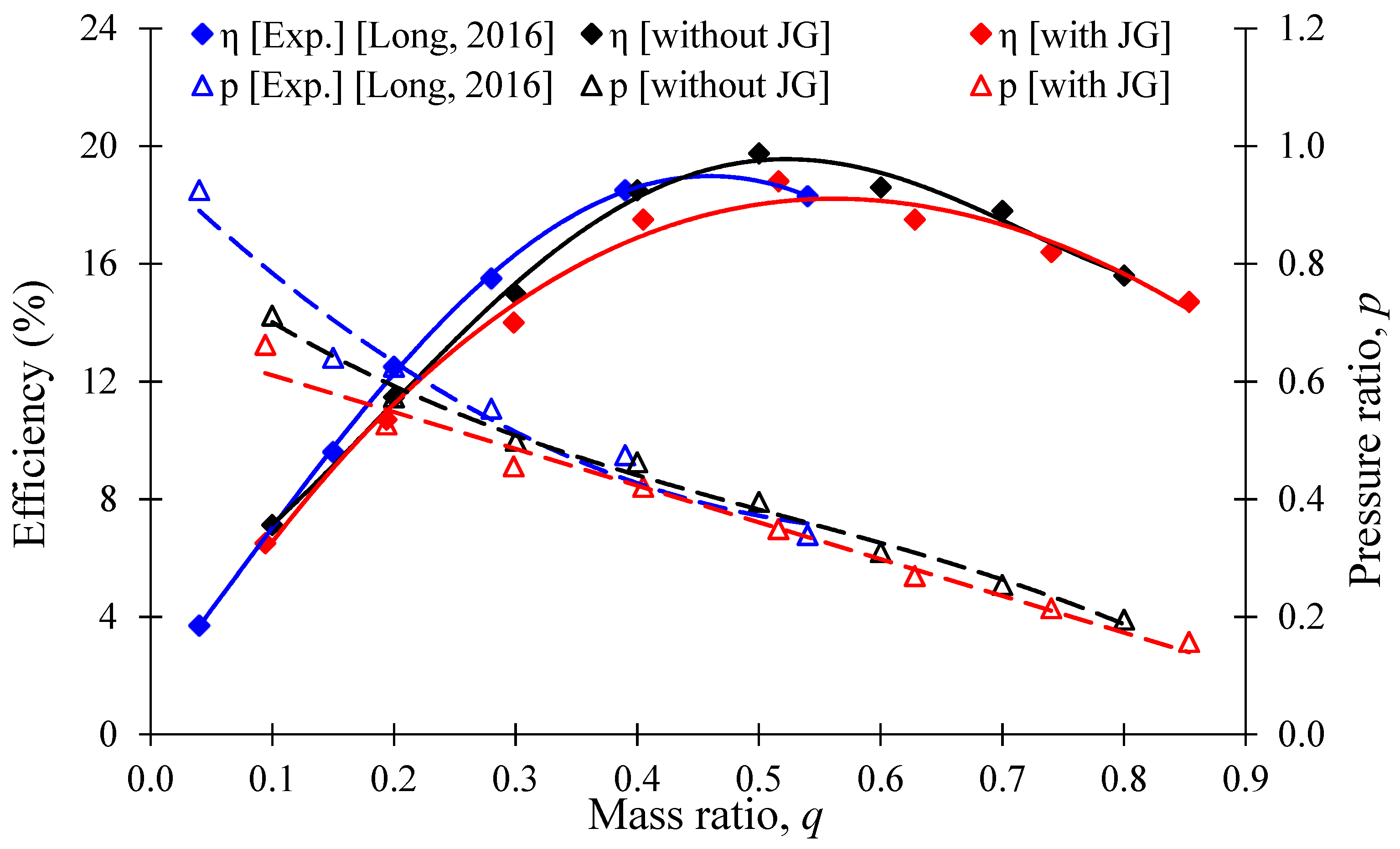
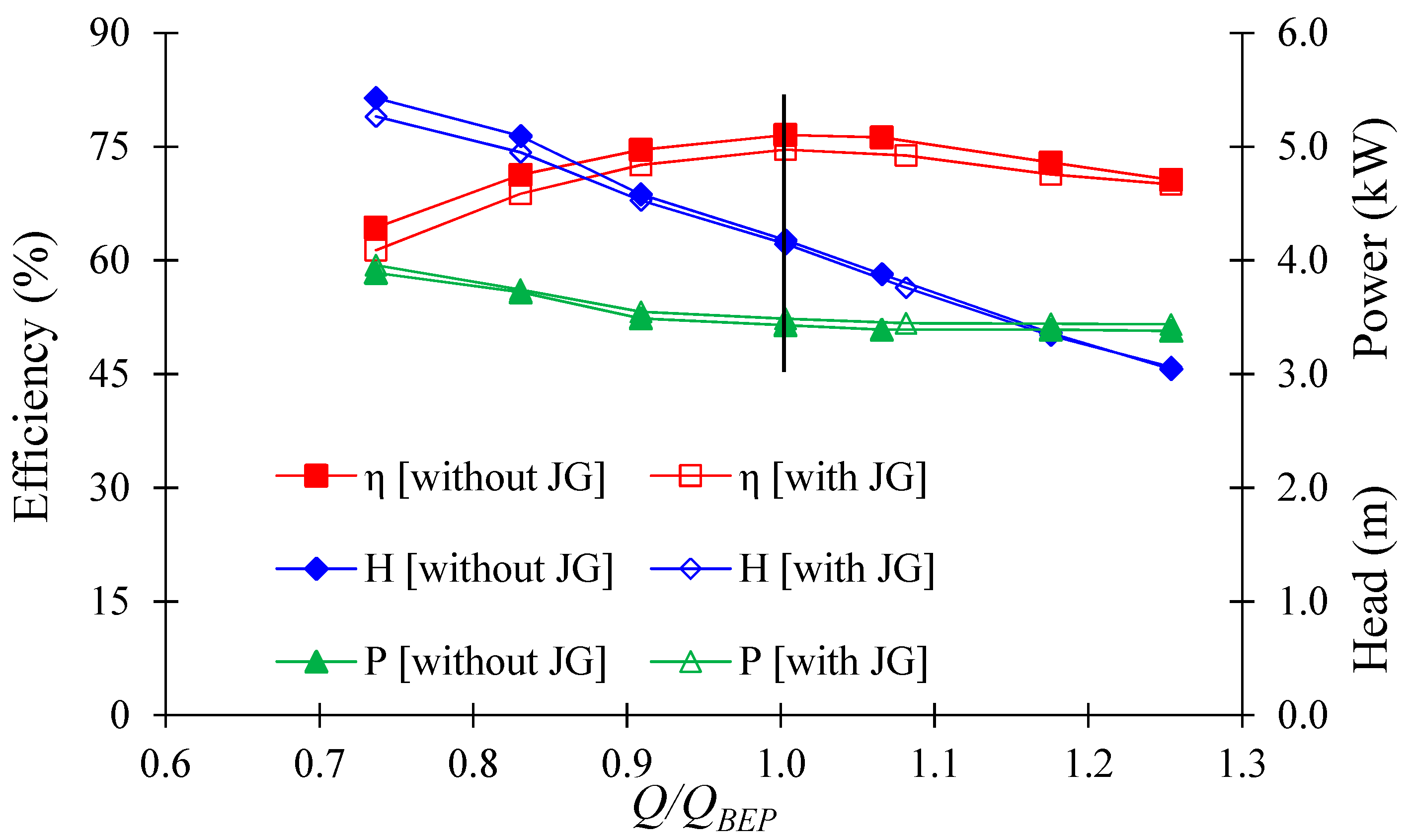
3.1. Pump Performance Curves of AJP and SCP Models
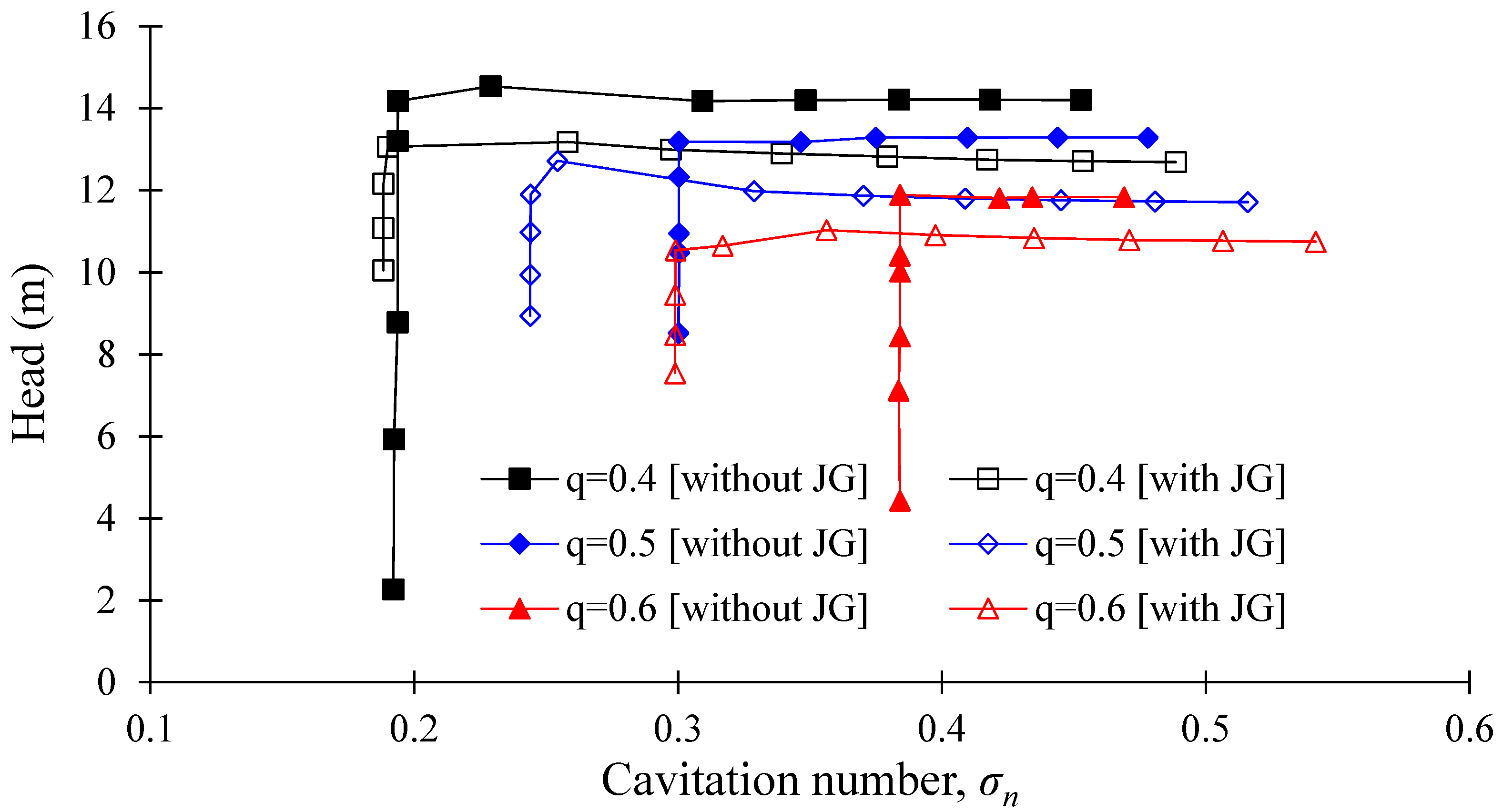
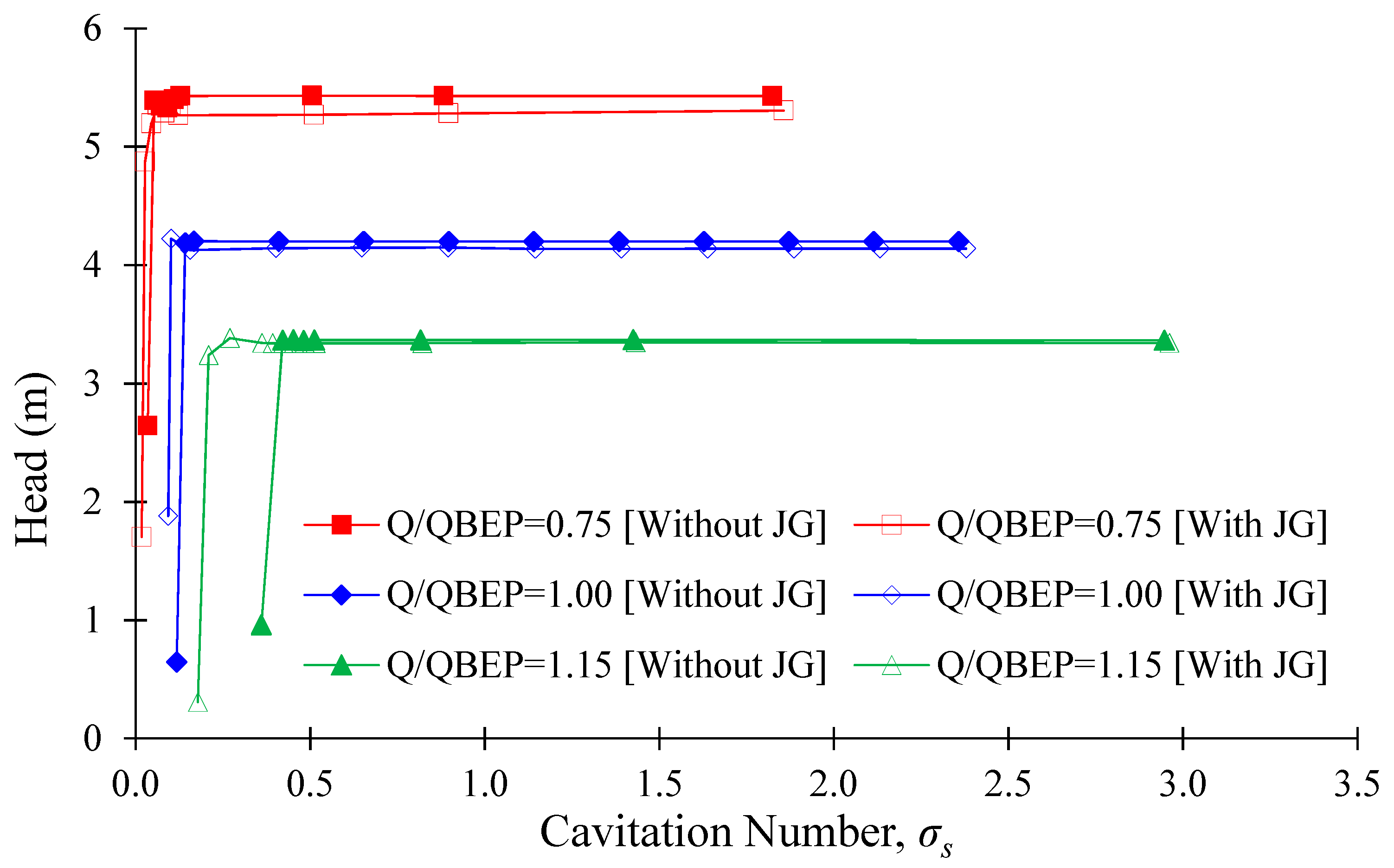
3.2. Suction Performance Curves of AJP and SCP Models
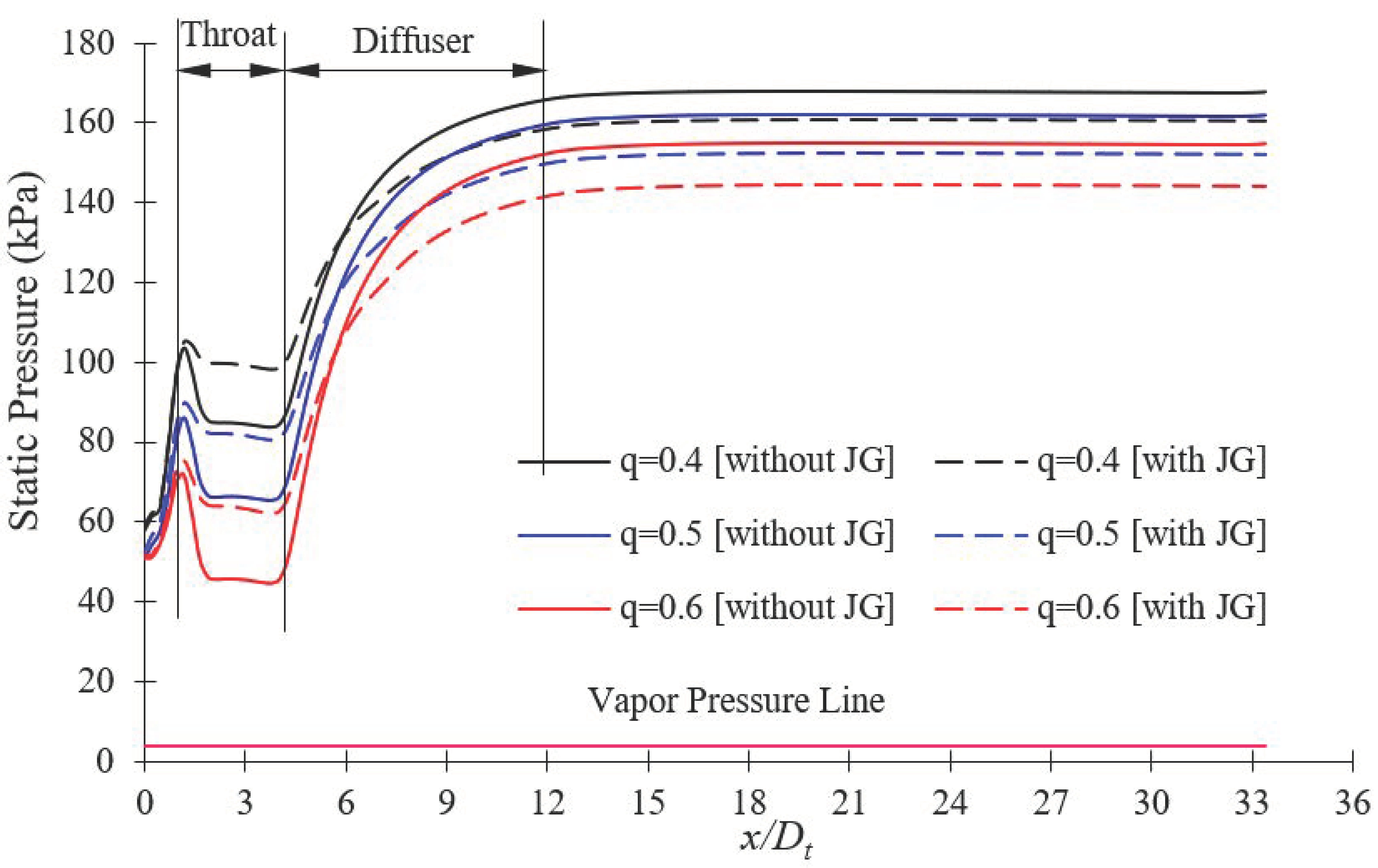
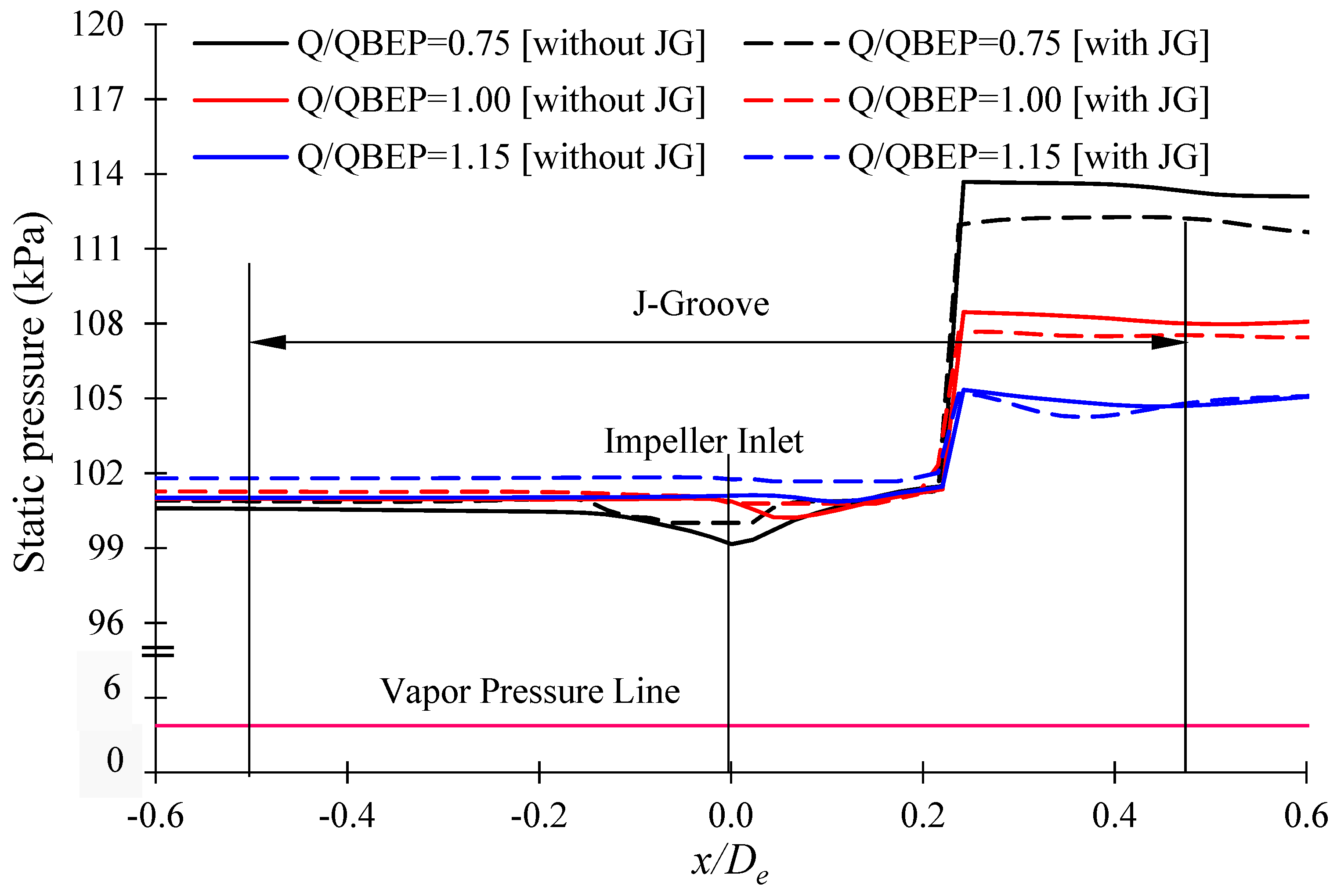
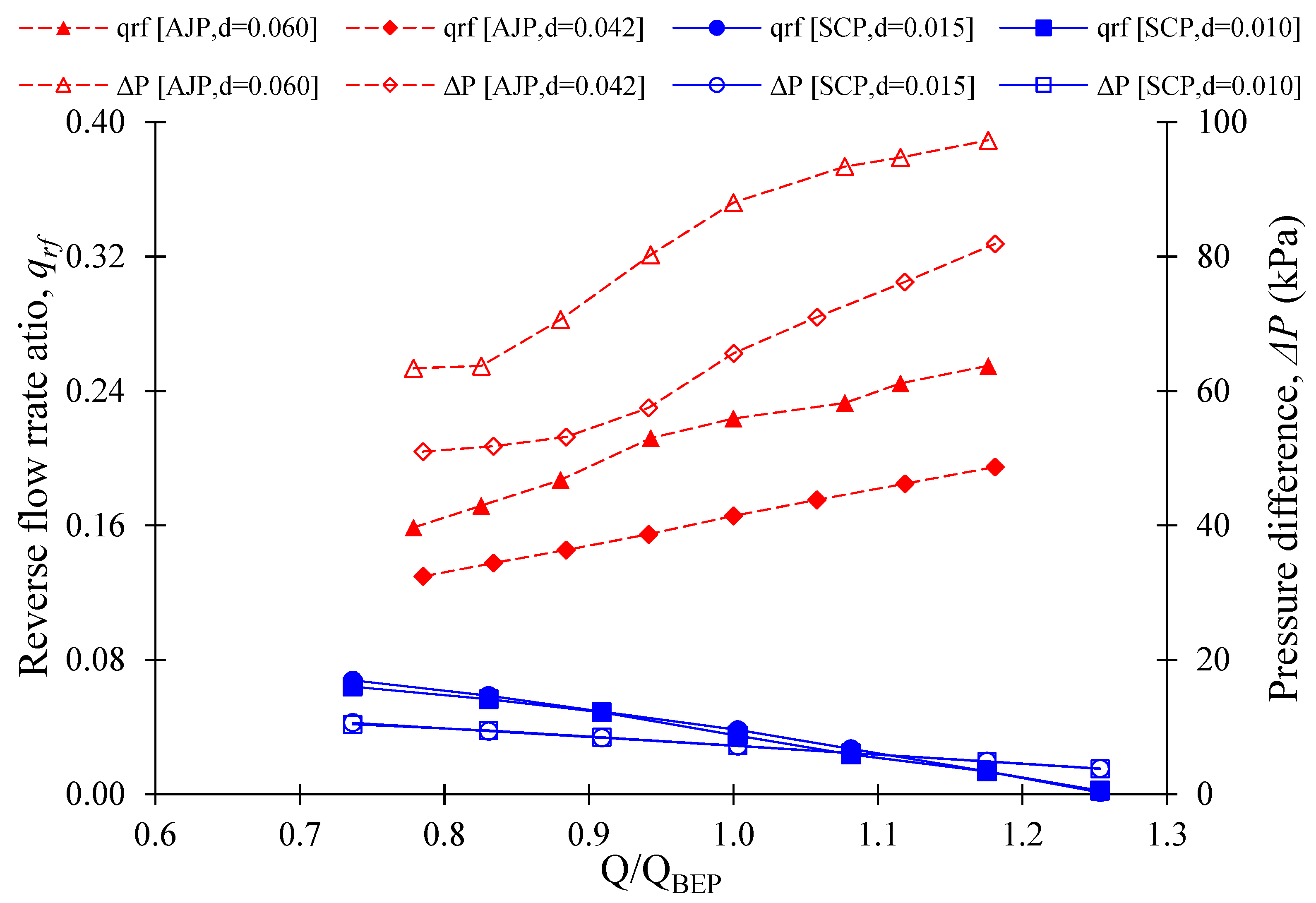
3.3. Estimation of Reverse Flow Rate by J-Groove Installation
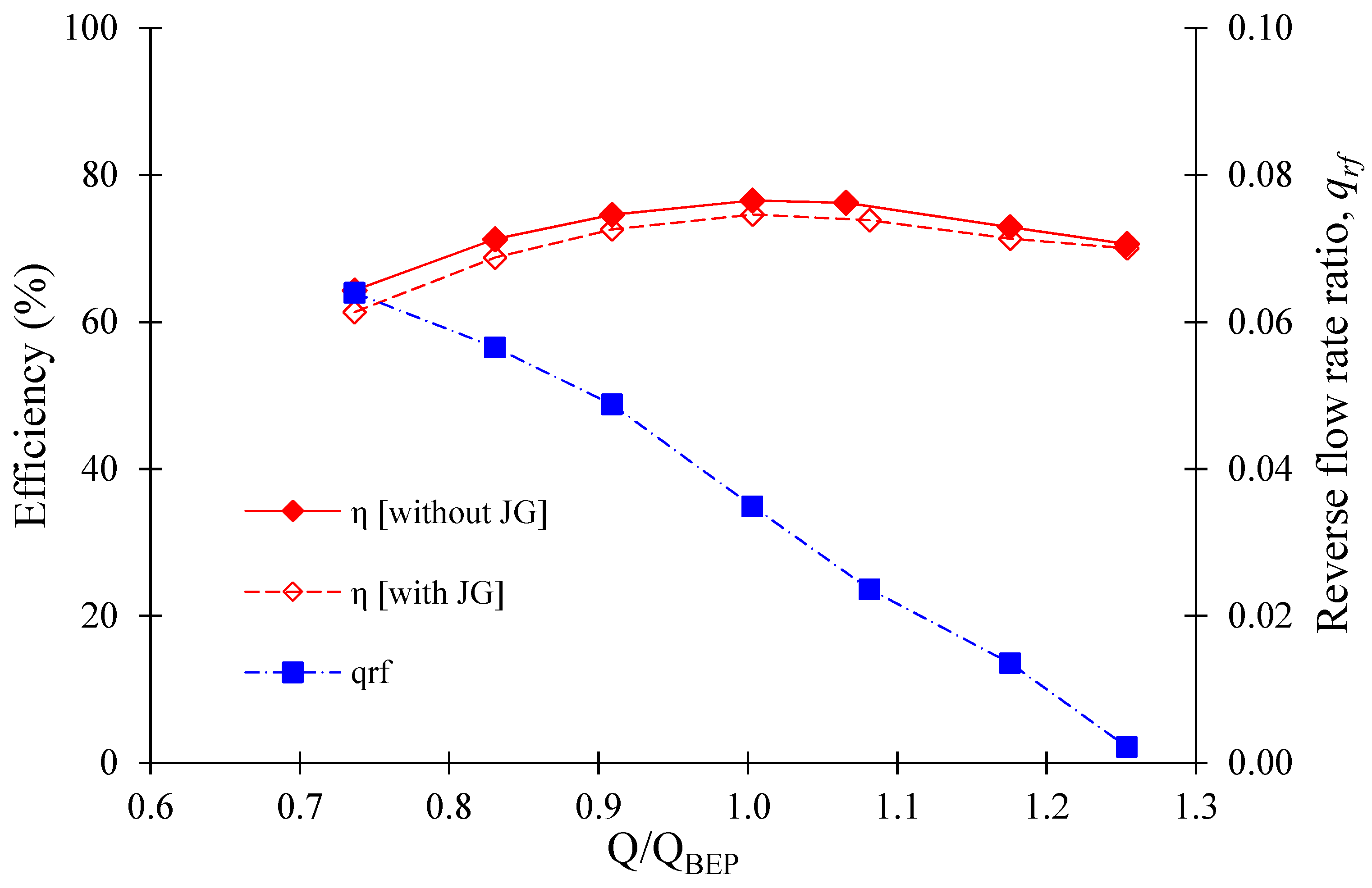
3.4. Relationship between Reverse Flow Rate in J-Groove Channel and Pump Performance
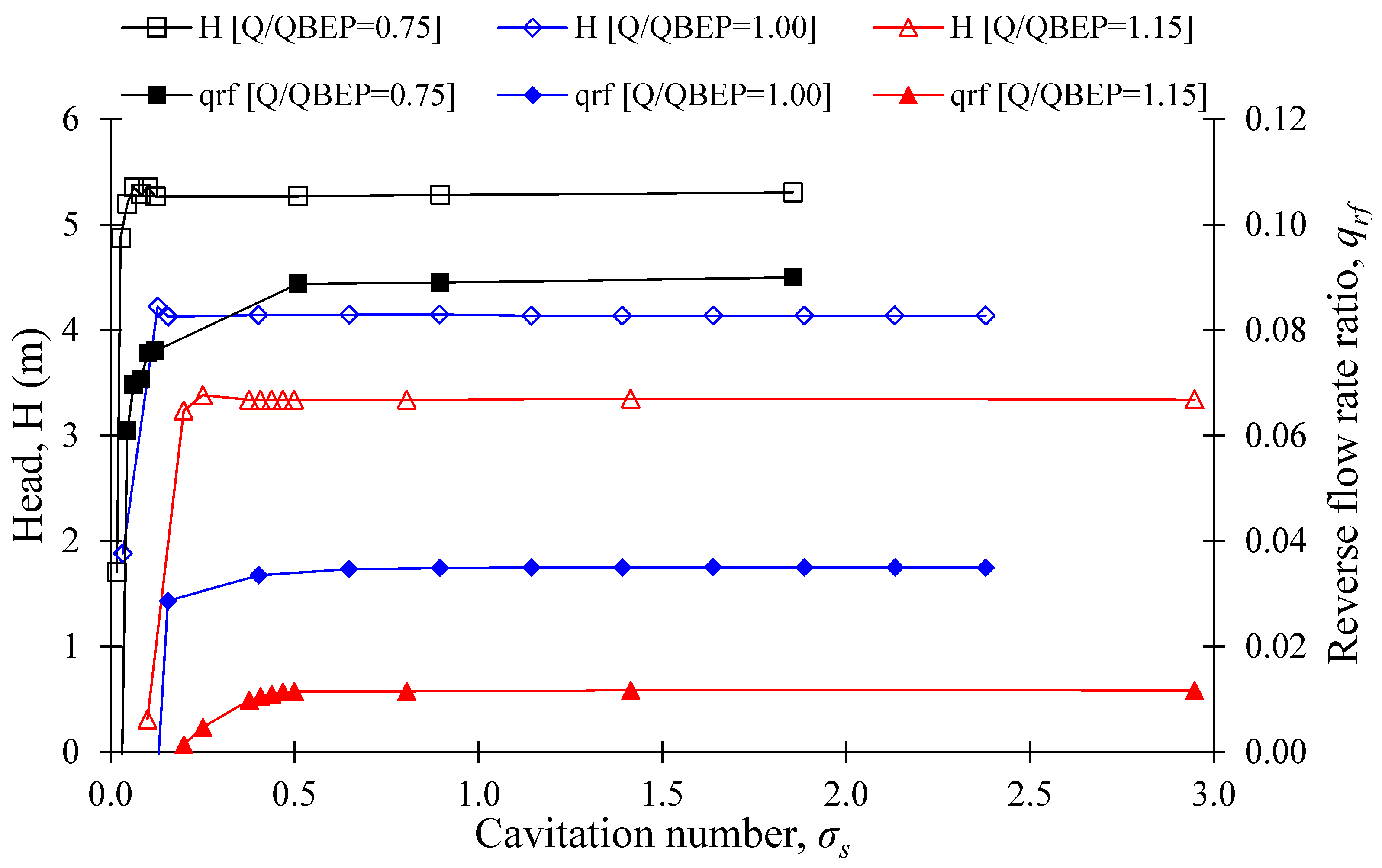
3.5. Relationship between Reverse Flow Rate in J-Groove Channel and Suction Performance
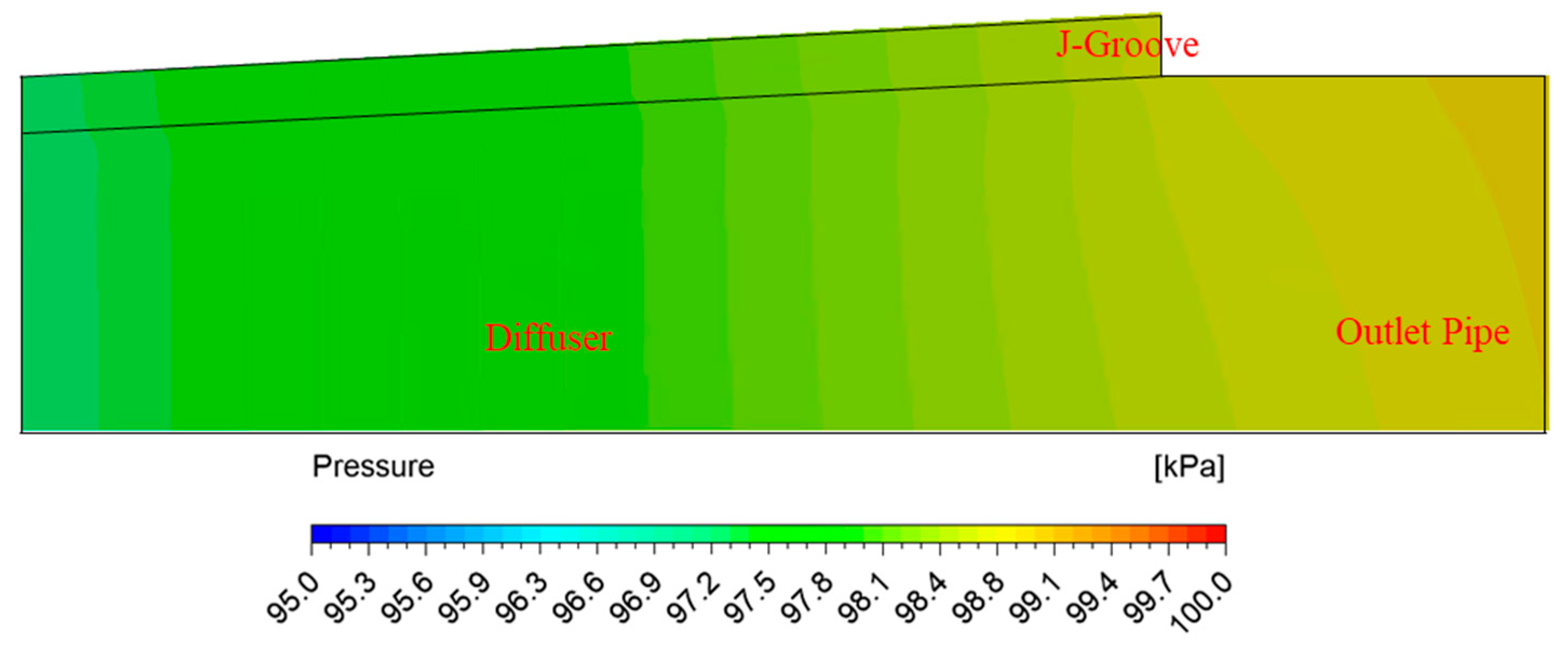
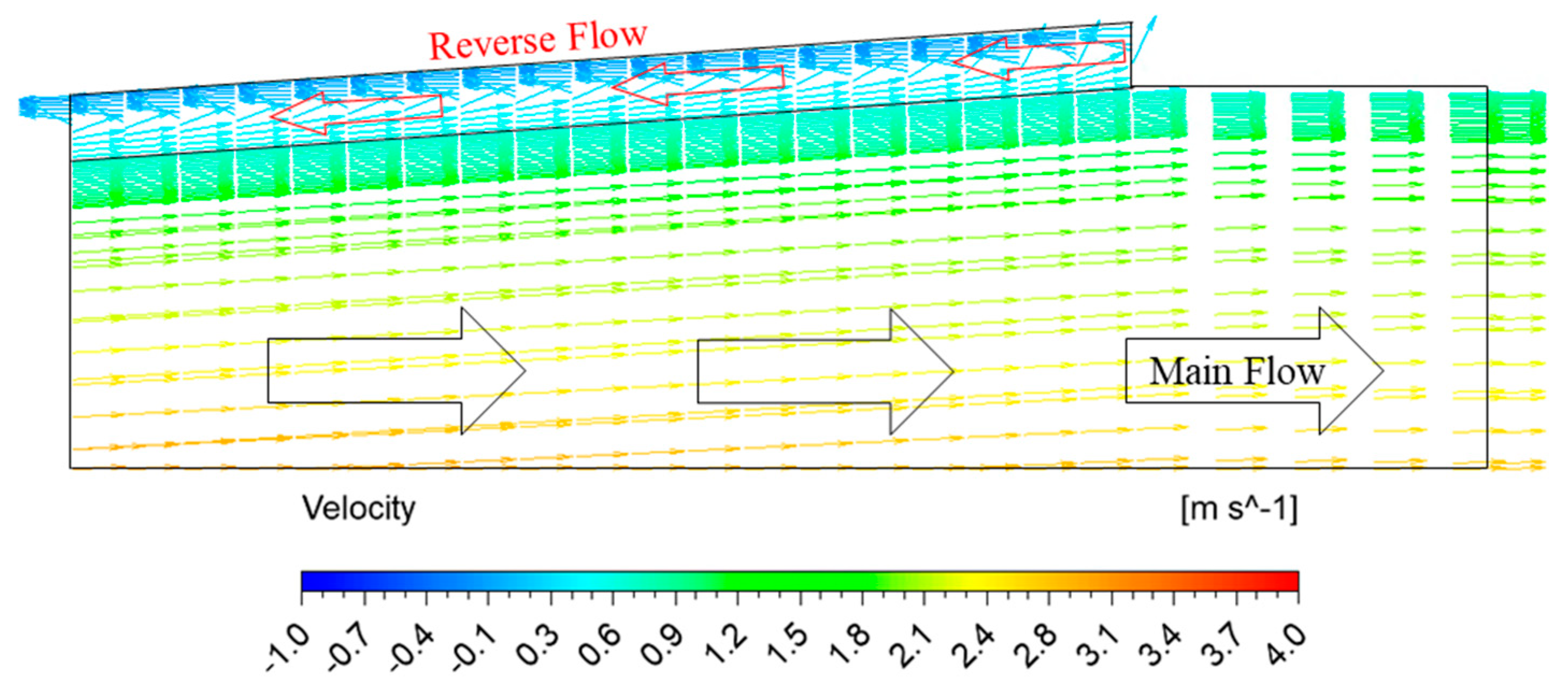
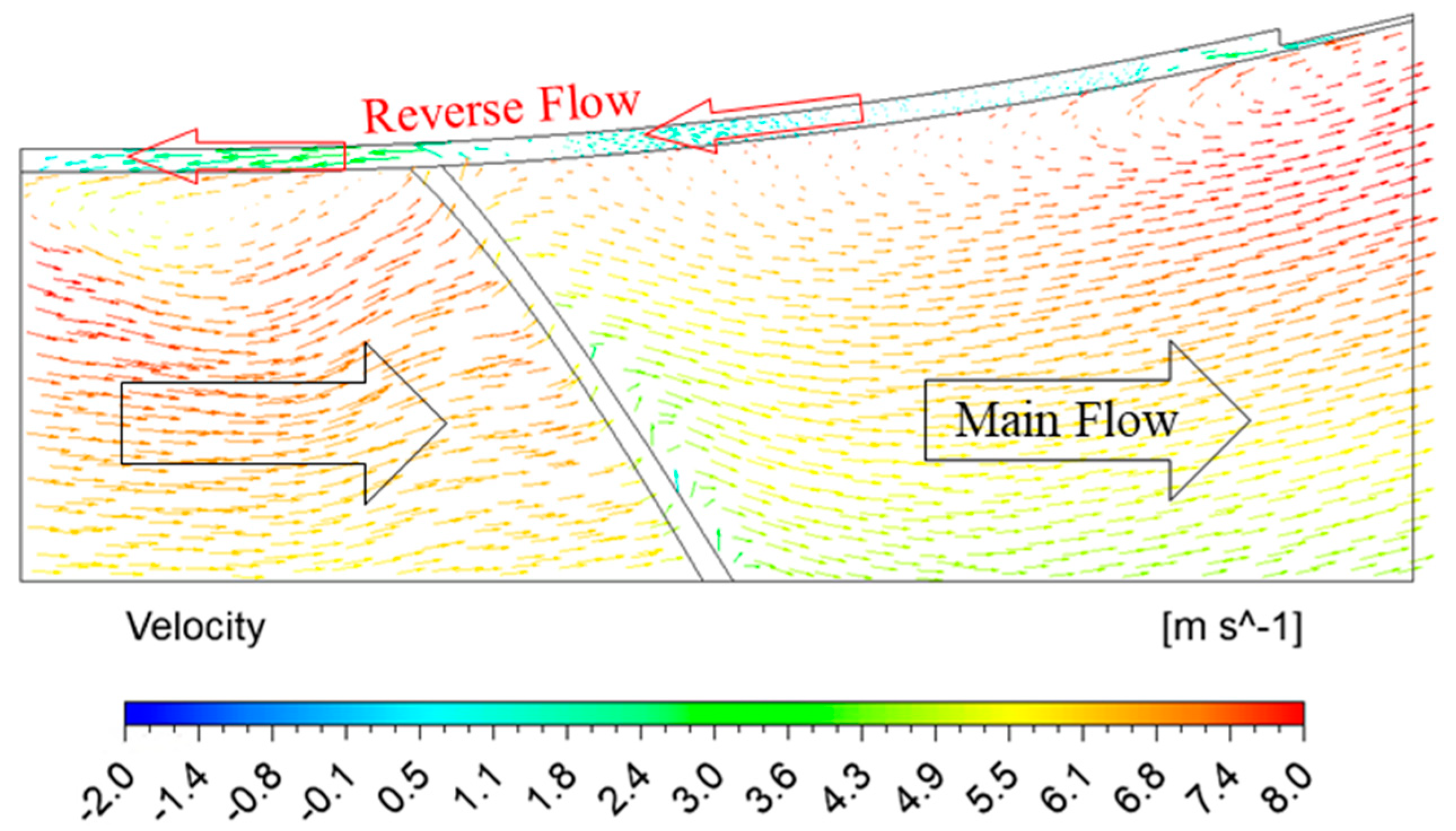
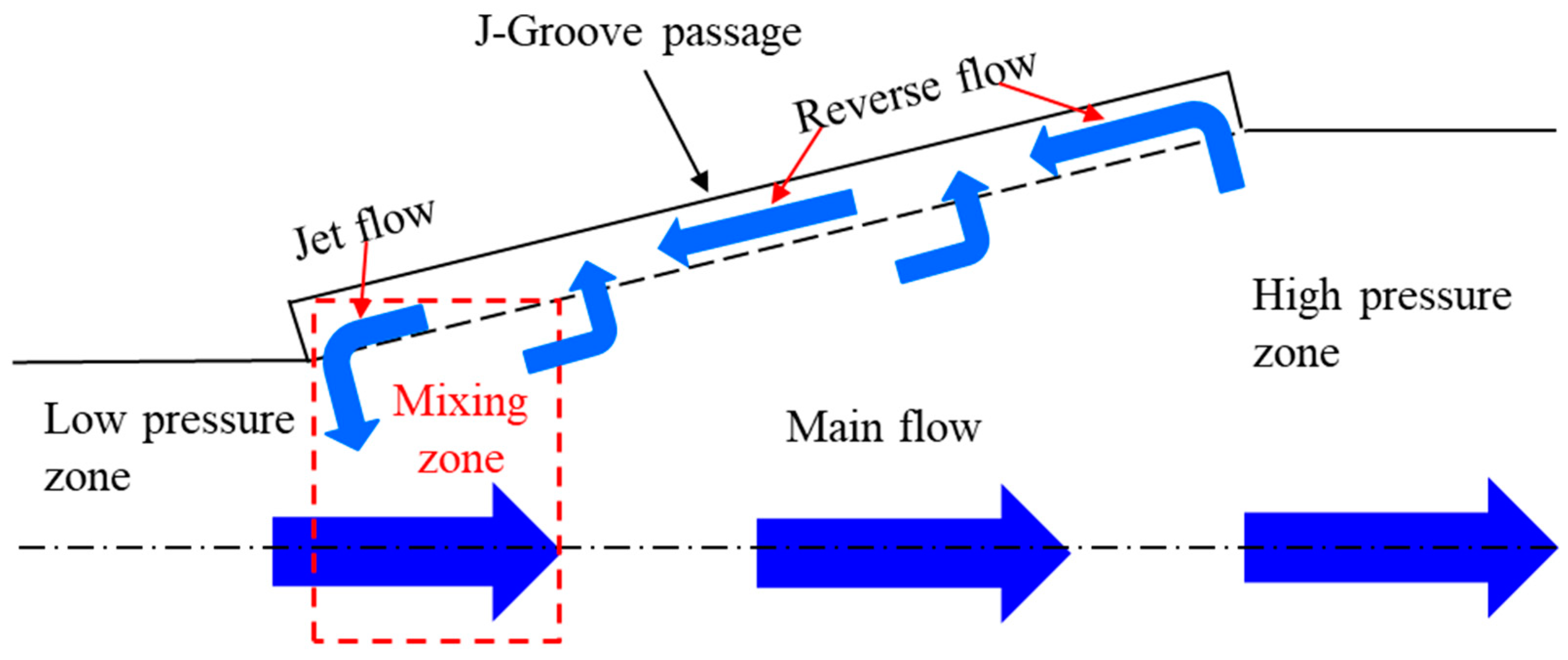
3.6. Mechanism of Reverse Flow Rate in AJP and SCP Models
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Elger, D.F.; Mclam, E.T.; Taylor, S.J. A new way to represent jet pump performance. J. Fluids Eng. 1991, 113, 439–444. [Google Scholar] [CrossRef]
- Deng, X.; Dong, J.; Wang, Z.; Tu, J. Numerical analysis of an annular water-air jet pump with self-induced oscillation mixing chamber. J. Comput. Multiph. Flows 2017, 9, 47–53. [Google Scholar] [CrossRef]
- Kryzhanivskyi, Y.I. The study on the flow’s kinematics in the jet pump’s mixing chamber. Geotech. Min. Mech. Eng. Mach. Build. 2019, 1, 62–68. [Google Scholar]
- Kim, Y.K.; Lee, D.Y.; Kim, H.D.; Ahn, J.H.; Kim, K.C. An experimental and numerical study on hydrodynamic characteristics of horizontal annular type water-air ejector. J. Mech. Sci. Technol. 2012, 26, 2773–2781. [Google Scholar] [CrossRef]
- Nilavalagan, S.; Ravindran, M.; RadhaKrishna, H.C. Analysis of mixing characteristics of flow in a jet pump using a finite-difference method. Chem. Eng. J. 1988, 39, 97–109. [Google Scholar] [CrossRef]
- Elger, D.F.; Taylor, S.J.; Liou, C.P. Recirculation in an annular-type jet pump. J. Fluids Eng. 1994, 116, 735–740. [Google Scholar] [CrossRef]
- Hatzlavramidls, D.T. Modeling and design of jet pumps. SPE Prod. Eng. 1991, 6, 413–419. [Google Scholar] [CrossRef]
- Narabayashi, T.; Yamazaki, Y.; Kobayashi, H.; Shakouchi, T. Flow analysis for single and multi-nozzle jet pump. JMSE Int. J. 2006, 49, 933–940. [Google Scholar] [CrossRef] [Green Version]
- Zhu, H.; Qiu, B.; Jia, Q.; Yang, X. Simulation analysis of hydraulic jet pump. Adv. Mater. Res. 2011, 204, 293–296. [Google Scholar] [CrossRef]
- Shimizu, Y.; Nakamura, S.; Kuzuhara, S.; Kurata, S. Studies of the configuration and performance of annular type jet pumps. J. Fluids Eng. 1987, 190, 205–212. [Google Scholar] [CrossRef]
- Hammoud, A.H. Effect of design and operational parameters on jet pump performance. In Proceedings of the 4th WSEAS International Conference on Fluid Mechanics and Aerodynamics, Elounda, Greece, 21 August 2006. [Google Scholar]
- Kwon, O.B.; Kim, M.K.; Kwon, H.C.; Bae, D.S. Two-dimensional numerical simulations on the performance of an annular jet pump. J. Vis. 2002, 5, 21–28. [Google Scholar] [CrossRef]
- Song, X.G.; Park, J.H.; Kim, S.G.; Park, Y.C. Performance comparison and erosion prediction of jet pumps by using a numerical method. Math. Comput. Model. 2013, 57, 245–253. [Google Scholar] [CrossRef]
- Guan, X.F. Modern Pump Theory and Design; China Astronaut: Beijing, China, 2011. (In Chinese) [Google Scholar]
- Kim, Y.; Tanaka, K.; Lee, Y.; Matsumoto, Y. Effects of entrained air on the characteristics of a small screw-type centrifugal pump. KSFM J. Fluid Mach. 2011, 2, 37–44. [Google Scholar]
- Tatebayashi, Y.; Tanaka, K. Influence of meridional shape on screw-type centrifugal pump performance. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, FEDSM2002-31183, Montreal, QC, Canada, 14–18 July 2002; pp. 769–776. [Google Scholar]
- Tatebayashi, Y.; Tanaka, K.; Kobayashi, T. Thrust prediction in screw-type centrifugal pump. In Proceedings of the 4th ASME_JSME Joint Fluid Engineering Conference, FEDSM2003-45105, Honolulu, HI, USA, 6–10 July 2003; pp. 621–626. [Google Scholar]
- Cheng, X.; Lia, R. Parameter equation study for screw centrifugal pump. Procedia Eng. 2012, 31, 914–921. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Choi, Y.-D. Design and CFD analysis of a screw centrifugal pump model. J. Korean Soc. Mar. Eng. 2017, 43, 640–647. [Google Scholar] [CrossRef]
- Franc, J.P. Partial cavity instabilities and re-entrant jet. In Proceedings of the 4th International Symposium on Cavitation, Grenoble, France; 2001. [Google Scholar]
- Xiao, L.; Long, X. Cavitating flow in annular jet pumps. Int. J. Multiph. Flow 2015, 71, 116–132. [Google Scholar] [CrossRef]
- Cunningham, R.G.; Hansen, A.G.; Na, T.Y. Jet Pump Cavitation. J. Basic Eng. 1970, 92, 483–492. [Google Scholar] [CrossRef]
- Long, X.; Xu, M.; Lyu, Q.; Zou, J. Impact of the internal flow in a jet fish pump on the fish. Ocean Eng. 2016, 126, 313–320. [Google Scholar] [CrossRef]
- Cochran, D.L.; Kline, S.J. Use of Short Flat Vanes for Producing Efficient Wide-Angle Two-dimensional Diffusers. NASA Tech. Note 1958, 4309, 1–130. [Google Scholar]
- Kurokawa, J.; Imamura, H.; Choi, Y.-D. Effect of J-groove on the suppression of swirl flow in a conical diffuser. J. Fluids Eng. 2010, 132, 071101. [Google Scholar] [CrossRef]
- Choi, Y.-D.; Kurokawa, J.; Imamura, H. Suppression of cavitation in inducers by J-Grooves. J. Fluids Eng. 2007, 129, 15–22. [Google Scholar] [CrossRef]
- Choi, Y.-D.; Shrestha, U. Cavitation performance improvement of an annular jet pump by J-groove. KSFM J. Fluid Mach. 2020, 26, 25–35. [Google Scholar] [CrossRef]
- Shrestha, U.; Choi, Y.-D. Effect of diffuser angle and J-groove depth on improvement in suction performance of annular jet pump model. J. Adv. Mar. Eng. Technol. 2020, 44, 385–394. [Google Scholar] [CrossRef]
- Shrestha, U.; Choi, Y.-D. Suction performance improvement of an annular jet pump by J-Groove passage shape optimization. J. Mech. Sci. Technol. 2021, 35, 5517–5527. [Google Scholar] [CrossRef]
- Hoang, T.H.M.; Truong, V.A.; Shrestha, U.; Choi, Y. Optimization of the Meridional Plane Shape Design Parameters in a Screw Centrifugal Pump Impeller. KSFM J. Fluid Mach. 2021, 24, 15–25. [Google Scholar] [CrossRef]
- ANSYS. ANSYS CFX Documentation; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng.-Trans. ASME 2008, 130, 078001. [Google Scholar]
- Franc, J. The Rayleigh-Plesset equation: A simple and powerful tool to understand various aspects of cavitation. In Fluid Dynamics of Cavitation and Cavitating Turbopumps; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–41. [Google Scholar]
- Xu, K.; Wang, G.; Wang, L.; Yun, F.; Sun, W.; Wang, X.; Chen, X. CFD-Based Study of Nozzle Section Geometry Effects on the Performance of an Annular Multi-Nozzle Jet Pump. Processes 2020, 8, 133. [Google Scholar] [CrossRef] [Green Version]





| Nomenclature | Size Ratio | Values |
|---|---|---|
| 2.08 | ||
| 1.67 | ||
| 1.33 | ||
| 1.53 | ||
| 1.00 | ||
| 8.33 | ||
| 2.7 | ||
| 3.5° | ||
| 20.0° | ||
| 1.75 |
| Nomenclature | Size Ratio | Value |
|---|---|---|
| 1.39 | ||
| 1.30 | ||
| 1.00 | ||
| 0.46 | ||
| 1.46 | ||
| 1.09 | ||
| 0.61 | ||
| 0.35 | ||
| 0.13 | ||
| 0.30 | ||
| 30.0° | ||
| 41.2° | ||
| 39.9° | ||
| 10.0° |
| Nomenclature | J-Groove in AJP Model | J-Groove in SCP Model | ||
|---|---|---|---|---|
| Size Ratio | Value | Size Ratio | Value | |
| 0.06 | 0.01 | |||
| 0.32 | 0.44 | |||
| 12° | 12° | |||
| 15 | 15 | |||
| 2.1766 | 2.1766 | 2.1766 | |
| 2.6461 | 2.6461 | 2.6461 | |
| 0.4486 | 0.3981 | 17.8600 | |
| 0.4484 | 0.4246 | 19.0400 | |
| 0.24 | 0.4118 | 18.6300 | |
| 0.0040 | −0.0128 | −0.4100 | |
| −0.0002 | 0.0265 | 1.1800 | |
| 0.8352 | 1.3240 | 1.4327 | |
| 0.4488 | 0.3880 | 17.4707 | |
| 0.847% | 3.441% | 4.311% | |
| 0.798% | 7.413% | 7.790% | |
| 0.044% | 3.168% | 2.724% |
| 1.095 | 1.095 | 1.095 | |
| 1.110 | 1.110 | 1.110 | |
| 73.414 | 2.912 | 2.478 | |
| 73.469 | 2.917 | 2.471 | |
| 72.879 | 2.876 | 2.466 | |
| −0.589 | −0.041 | −0.015 | |
| 0.055 | 0.005 | 0.003 | |
| 23.016 | 20.941 | 15.305 | |
| 73.489 | 2.919 | 2.482 | |
| 0.075% | 0.163% | 0.128% | |
| 0.102% | 0.217% | 0.159% | |
| 0.013% | 0.036% | 0.053% |
| Parameter/Boundary | Condition/Value | |
|---|---|---|
| AJP | SCP | |
| Primary Inlet | Total Pressure | Mass Flow Rate |
| Secondary Inlet | Mass Flow Rate | - |
| Outlet | Static Pressure | Static Pressure |
| Turbulence model | Realizable κ-ε | SST |
| Grid interface connection | General Grid Interface (GGI) | General Grid Interface (GGI) |
| Interface model | Steady State/Frozen rotor | Steady State/Frozen rotor |
| Walls | No slip wall (roughness: smooth) | No slip wall (roughness: smooth) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrestha, U.; Choi, Y.-D. Estimation of Reverse Flow Rate in J-Groove Channel of AJP and SCP Models Using CFD Analysis. Processes 2022, 10, 785. https://doi.org/10.3390/pr10040785
Shrestha U, Choi Y-D. Estimation of Reverse Flow Rate in J-Groove Channel of AJP and SCP Models Using CFD Analysis. Processes. 2022; 10(4):785. https://doi.org/10.3390/pr10040785
Chicago/Turabian StyleShrestha, Ujjwal, and Young-Do Choi. 2022. "Estimation of Reverse Flow Rate in J-Groove Channel of AJP and SCP Models Using CFD Analysis" Processes 10, no. 4: 785. https://doi.org/10.3390/pr10040785
APA StyleShrestha, U., & Choi, Y.-D. (2022). Estimation of Reverse Flow Rate in J-Groove Channel of AJP and SCP Models Using CFD Analysis. Processes, 10(4), 785. https://doi.org/10.3390/pr10040785







