Fracture Interference and Refracturing of Horizontal Wells
Abstract
:1. Introduction
1.1. Decline in Production Capacity and Low Recovery
1.2. Inter-Fracture Stress Interference
1.3. Fracturing Fluid Filtration Loss and Variation of Pore Pressure
2. Theory and Model Design
2.1. Calculation of Multi-Fracture Interference Stress Field
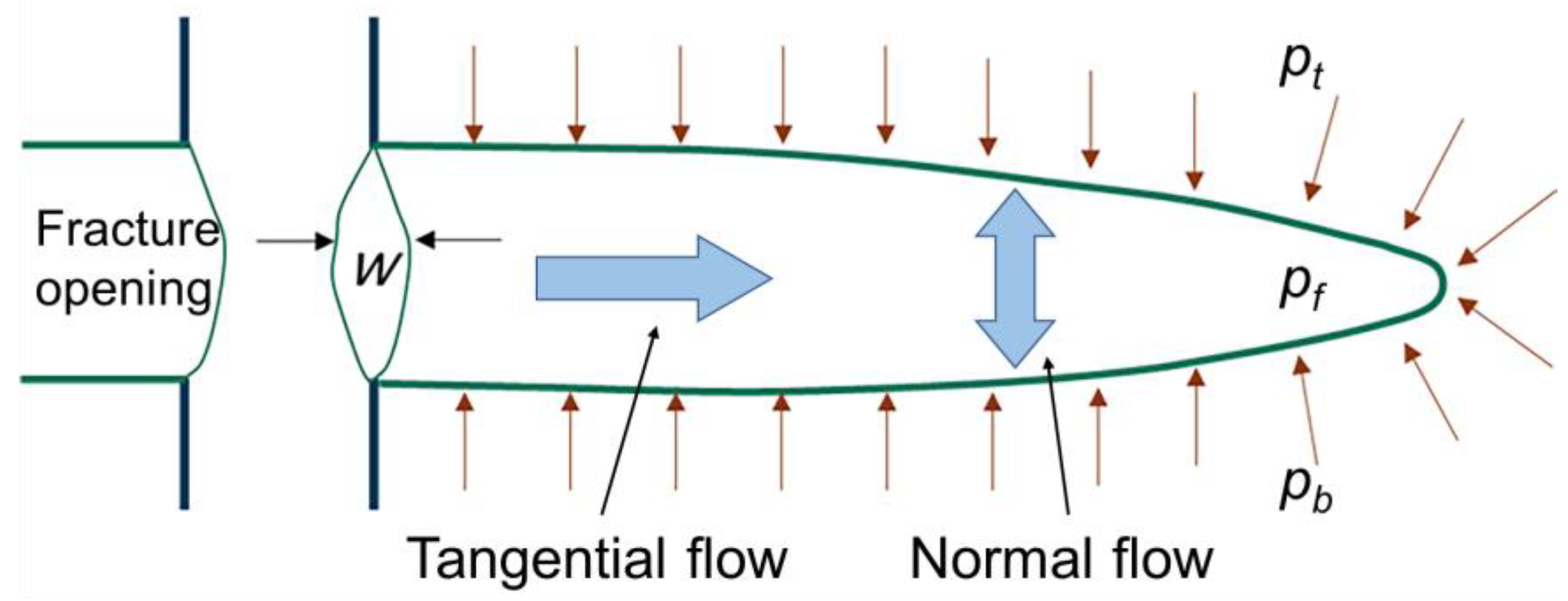
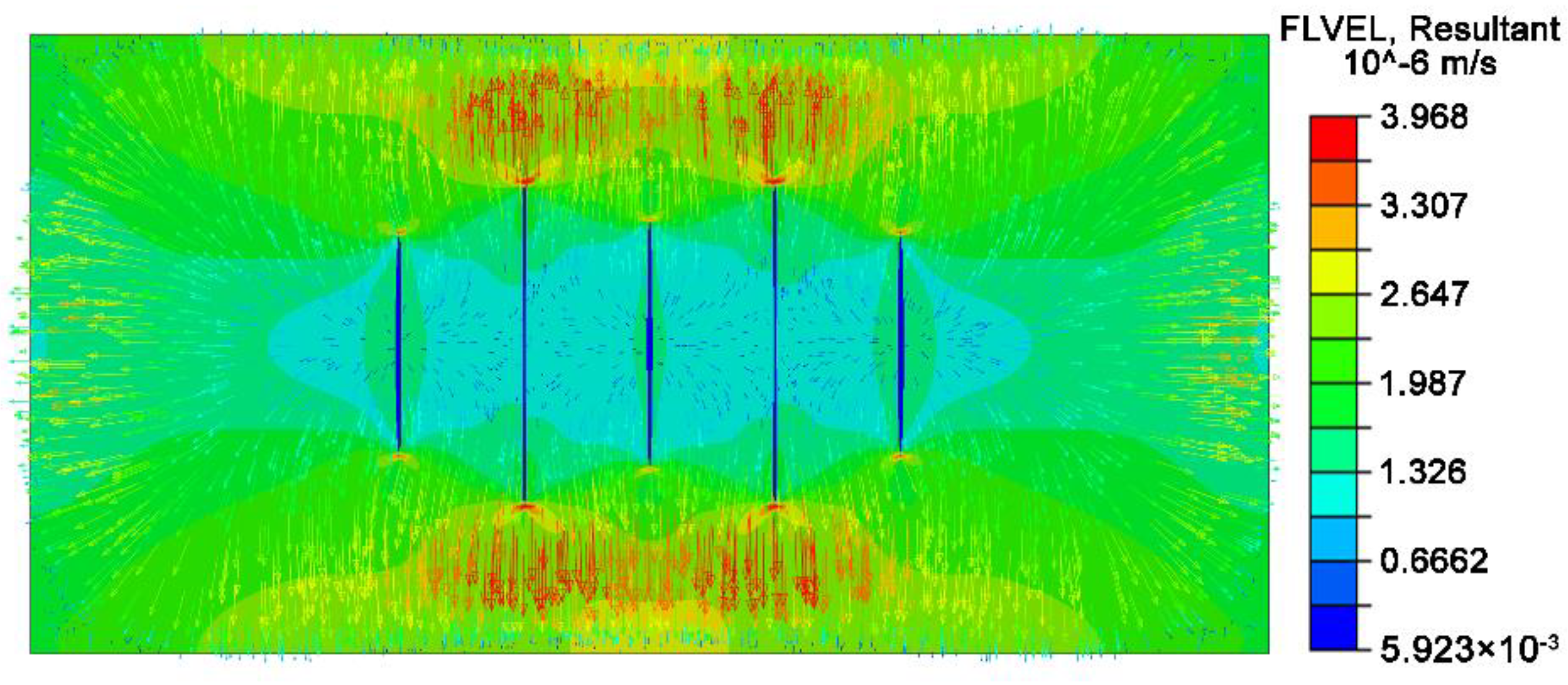
2.2. Fracturing Fluid Flow and Filtration
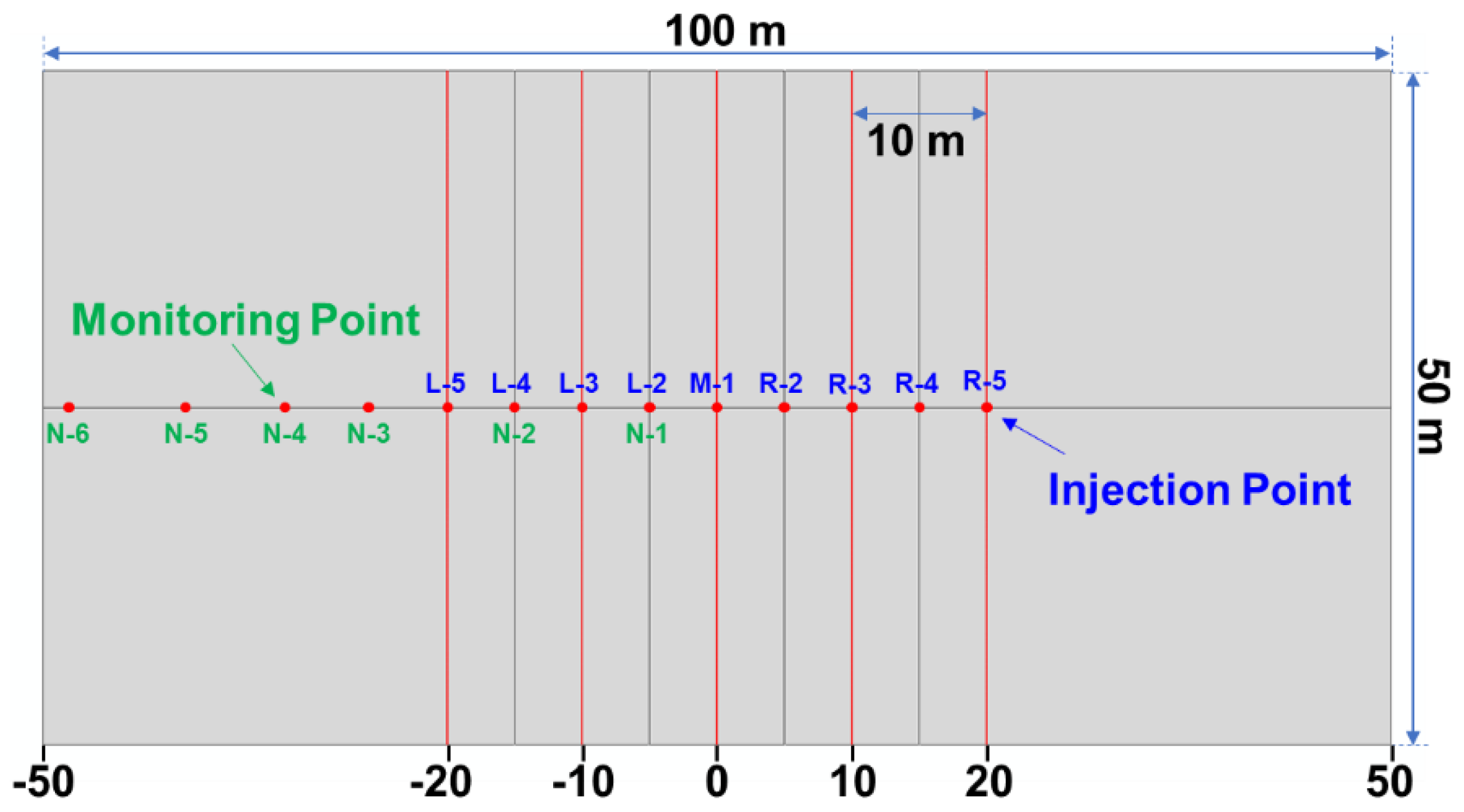
2.3. Establishment of Fracturing Model
3. Multi-Cluster Fracturing Simulation
3.1. Initial Fracturing Simulation
- Ground stress balance stage.
- Pump 150 m3 (70 min) fracturing fluid, the cracks open and extend forward, and then stop the pump.
- A 150-min simulation of fracturing fluid filtration loss and in situ stress field evolution.
3.2. Refracturing Simulation
4. Discussion
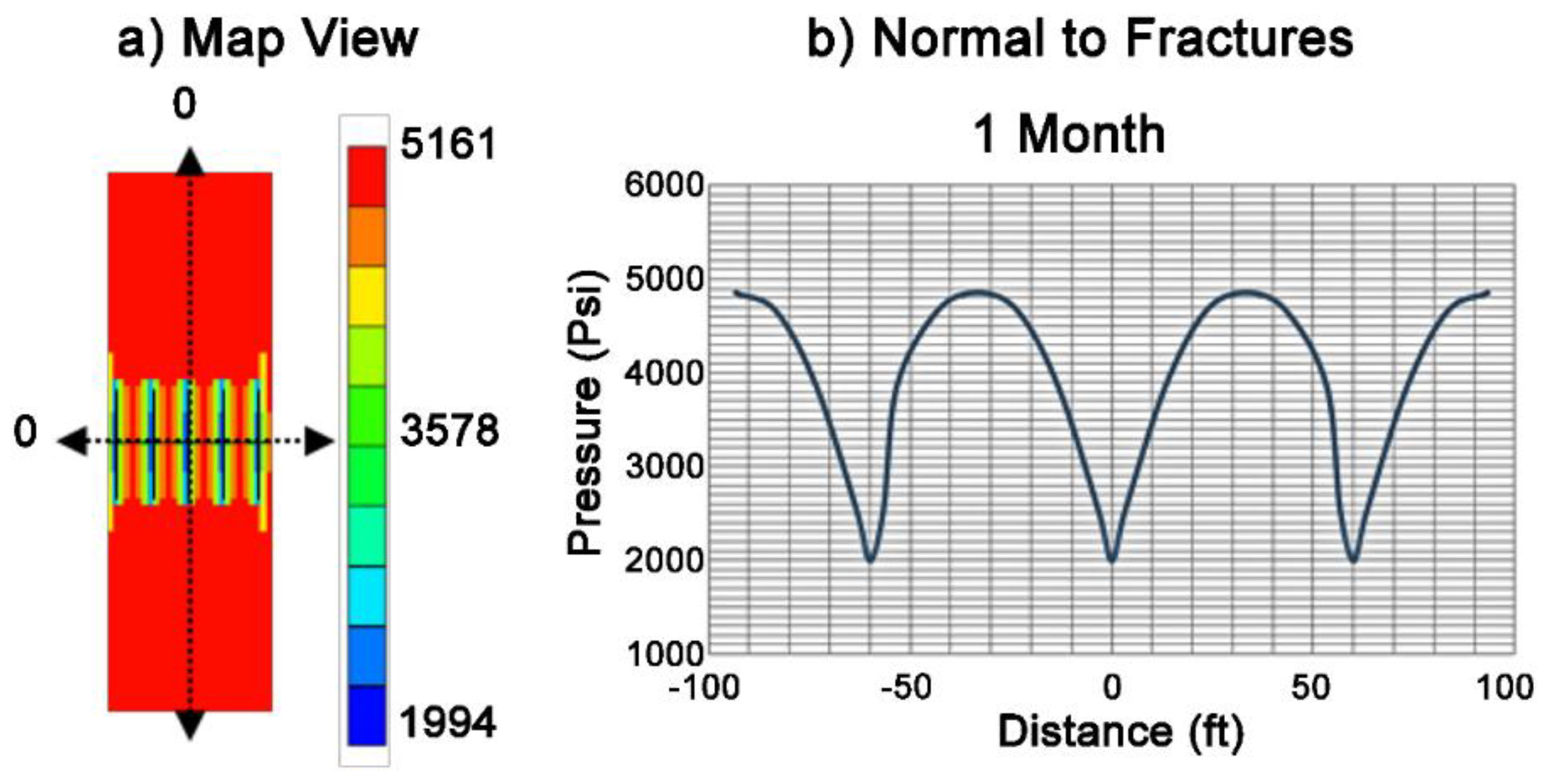
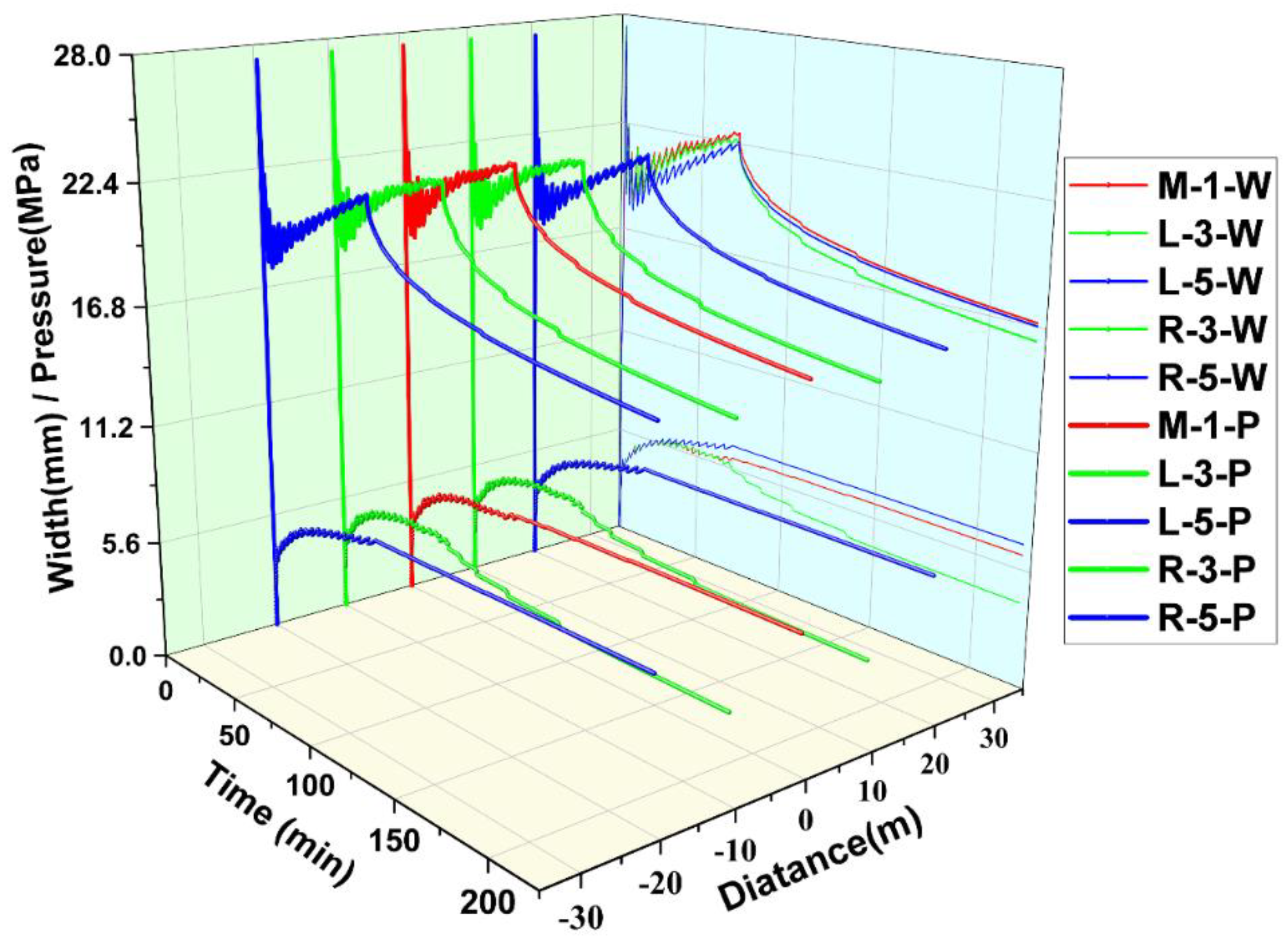
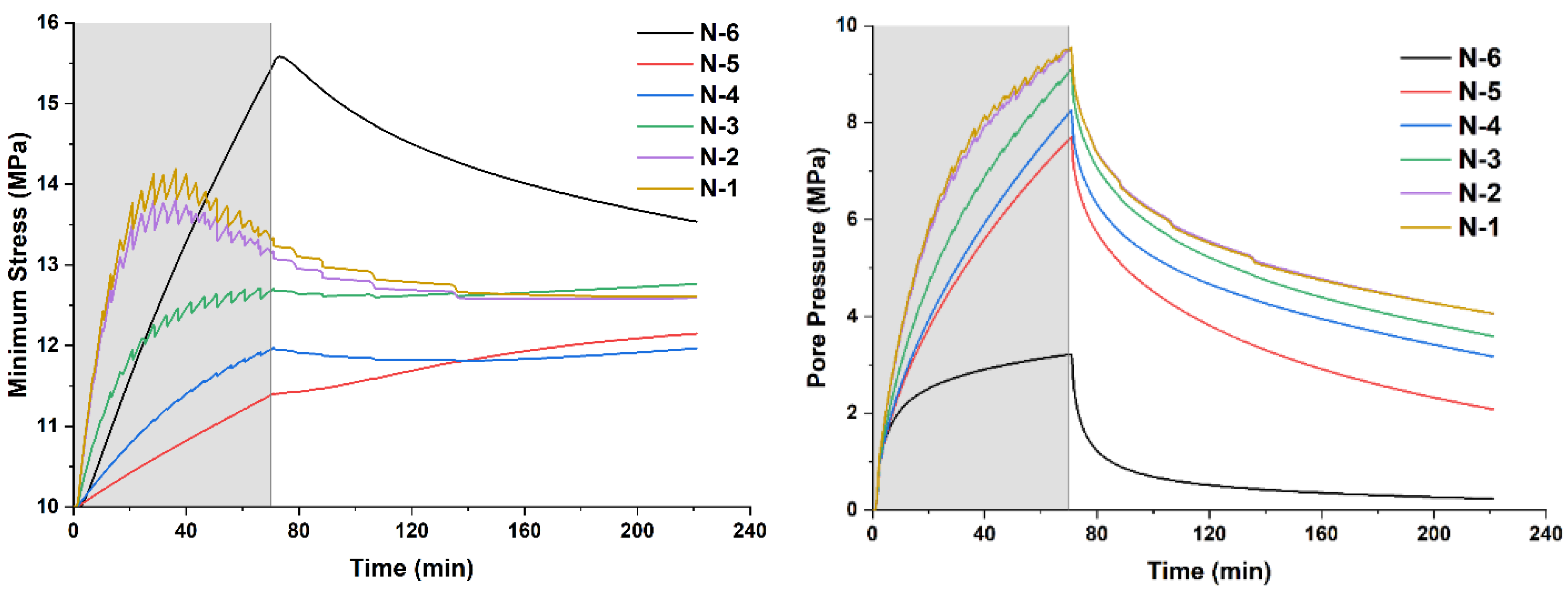
4.1. Fracturing Fluid Filtration Loss and Variation of Pore Pressure
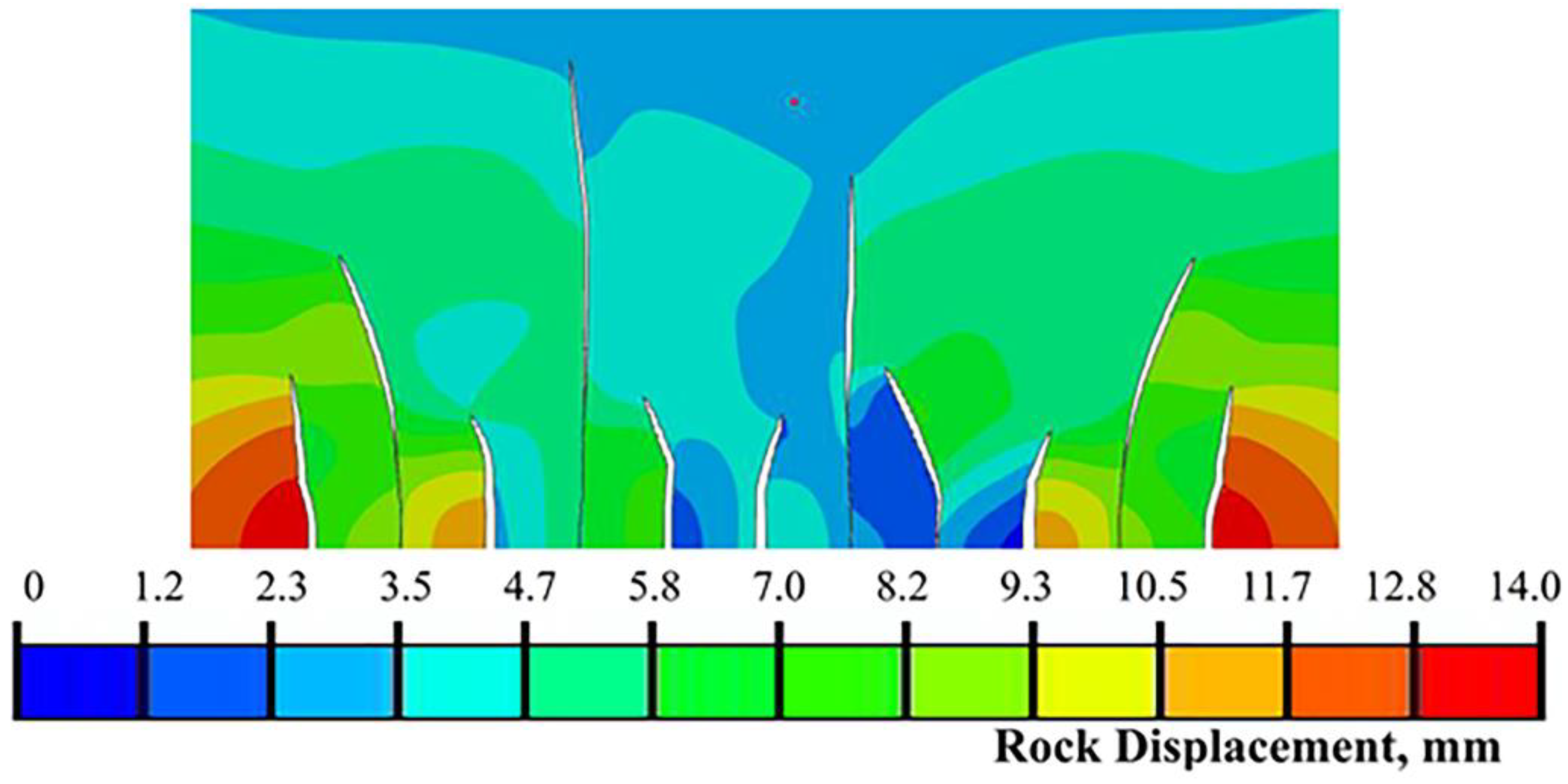
4.2. Changes of Fracture Size
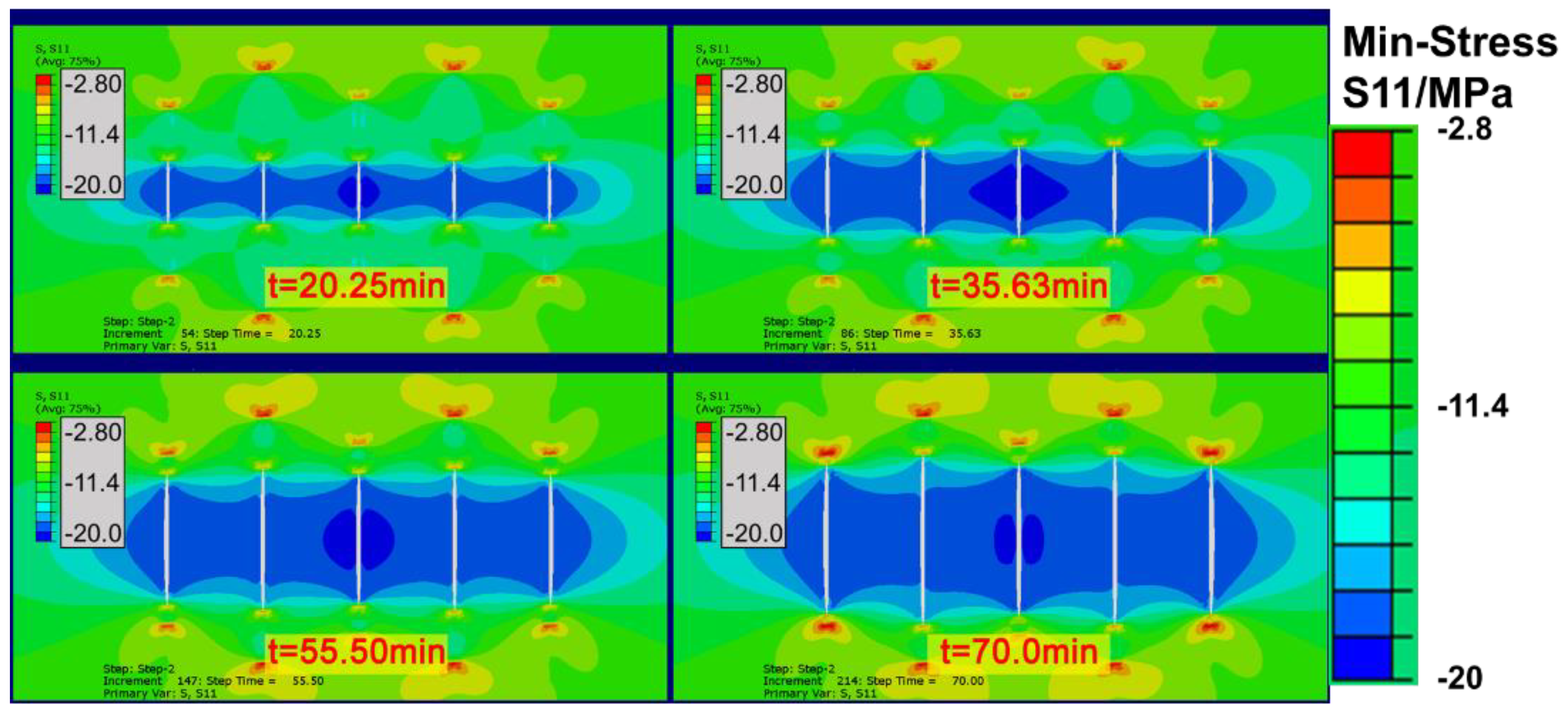
4.3. Evolution of Stress Field
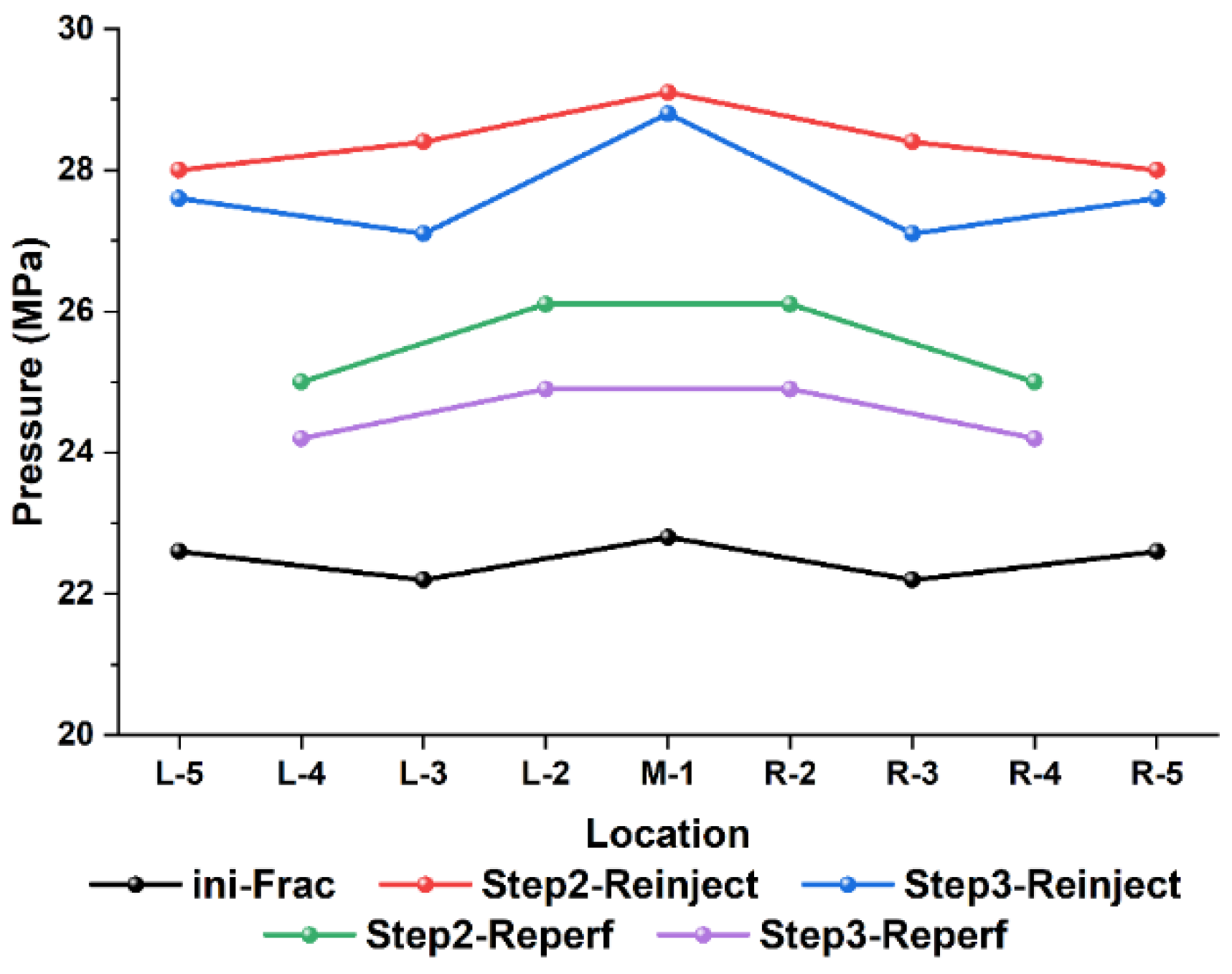
4.4. Refracturing
5. Conclusions
- There is stress concentration around the fractures during multi-cluster fracturing of horizontal wells due to formation deformation, which is more obvious between fractures. The hydraulic fracture’s effective influence radius on the external formation is about 15 m.
- The formation stress gradually recovers after the fracturing is completed, but it is still significantly higher than the original in situ stress. When refracturing is performed, it is recommended that stress relief be performed first, as this aids fracture initiation.
- Reperforating fracturing has a lower fracture extension pressure and a longer fracture length than in situ refracturing. As a result, it is recommended that reperforating fracturing be used first when refracturing is performed. With repeated stimulation, fracture temporary plugging technology increases the effective volume of reservoir stimulation and achieves high and stable production.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yew, C.H.; Li, Y. Fracturing of a Deviated Well. SPE Prod. Eng. 1988, 3, 429–437. [Google Scholar] [CrossRef]
- Chen, M.; Chen, Z.; Huang, R. Hydraulic Fracturing of Highly Deviated Wells. J. Univ. Pet. 1995, 19, 30–35. [Google Scholar]
- Zhang, G.; Chen, M.; Wang, Q. Three-dimensional model for space reorientation of hydraulic fractures near deflecting well bore. J. Univ. Pet. 2004, 28, 51–55. [Google Scholar]
- Pu, C.; Zheng, H.; Yang, Z.; Gao, Z. Research status and development trend of the formation mechanism of complex fractures by staged volume fracturing in horizontal wells. Acta Pet. Sin. 2020, 41, 1734–1743. [Google Scholar]
- Ahmed, M.; Rahim, Z.; Al-Anazi, H.; Al-Kanaan, A.; Mohiuddin, M. Development of Low Permeability Reservoir Utilizing Multi-Stage Fracture Completion in the Minimum Stress Direction. In Proceedings of the SPE Saudi Arabia Section Technical Symposium and Exhibition, Al-Khobar, Saudi Arabia, 8 April 2012; p. SPE-160848-MS. [Google Scholar]
- Dehghan, A.N. An Experimental Investigation into the Influence of Pre-Existing Natural Fracture on the Behavior and Length of Propagating Hydraulic Fracture. Eng. Fract. Mech. 2020, 240, 107330. [Google Scholar] [CrossRef]
- Wang, Y.; Dusseault, M.B. Defining SRV in Unconventional Reservoirs; How Is It Related to Production? In Proceedings of the 54th U.S. Rock Mechanics/Geomechanics Symposium Golden, CO, USA, 28 June–1 July 2020; OnePetro: The Woodlands, TX, USA, 2020. [Google Scholar]
- Xing, C. Numerical Simulation on Multi-Crack Initiation and Propagation under the Influence of Stress Shadow Effect. Master’s Thesis, Northeast Petroleum University, Daqing, China, 2017. [Google Scholar]
- Xu, Y.; Lei, Q.; Chen, M.; Wu, Q.; Yang, N.; Weng, D.; Li, D.; Jiang, H. Progress and development of volume stimulation techniques. Pet. Explor. Dev. 2018, 45, 932–947. [Google Scholar] [CrossRef]
- Ren, L. Fracture Network Propagation and Productivity Prediction Based on Fluid-Solid Fully Coupling of SRV-Fractured Horizontal Wells in Tight Oil Reservoirs. Ph.D. Thesis, China University of Petroleum (East China), Qingdao, China, 2016. [Google Scholar]
- Gale, J.F.W.; Laubach, S.E.; Olson, J.E.; Eichhubl, P.; Fall, A. Natural Fractures in Shale: A Review and New Observations. AAPG Bull. 2014, 98, 2165–2216. [Google Scholar] [CrossRef]
- Wang, D.; Qin, H.; Ma, H.; Li, J.; Sun, D. Numerical Simulation of Stress Shadow Effect of Multi-fractures via Finite Element Methods. J. Beijing Inst. Petrochem. Technol. 2020, 28, 22–28. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J. Numerical simulation of multiple fractures simultaneous propagation in horizontal wells. Acta Pet. Sin. 2015, 36, 1571–1579. [Google Scholar]
- Yu, Y.; Zhu, W.; Li, L.; Wei, C.; Dai, F.; Liu, S.; Wang, W. Analysis on stress shadow of mutual interference of fractures in hydraulic fracturing engineering. Chin. J. Rock Mech. Eng. 2017, 36, 2926–2939. [Google Scholar] [CrossRef]
- Khanal, A.; Weijermars, R. Pressure Depletion and Drained Rock Volume near Hydraulically Fractured Parent and Child Wells. J. Pet. Sci. Eng. 2019, 172, 607–626. [Google Scholar] [CrossRef]
- Raterman, K.T.; Liu, Y.; Warren, L. Analysis of a Drained Rock Volume: An Eagle Ford Example. In Proceedings of the Unconventional Resources Technology Conference (URTeC), Denver, Colorado, 22–24 July 2019; SEG Global Meeting Abstracts. pp. 4106–4125. [Google Scholar]
- Wang, H.; Sharma, M.M. Estimating Unpropped-Fracture Conductivity and Fracture Compliance From Diagnostic Fracture-Injection Tests. SPE J. 2018, 23, 1648–1668. [Google Scholar] [CrossRef]
- Khanal, A.; Weijermars, R. Distinguishing Fracture Conductivity and Fracture Flux: A Systematic Investigation of Individual Fracture Contribution to Well Productivity. In Proceedings of the 8th Unconventional Resources Technology Conference, Houston, TX, USA, 16–18 July 2021; American Association of Petroleum Geologists: Tulsa, OK, USA, 2020. [Google Scholar]
- Weijermars, R.; Nandlal, K.; Tugan, M.F.; Dusterhoft, R.; Stegent, N. Wolfcamp Hydraulic Fracture Test Site Drained Rock Volume and Recovery Factors Visualized by Scaled Complex Analysis Method (CAM): Emulating Multiple Data Sources (Production Rates, Water Cuts, Pressure Gauges, Flow Regime Changes, and b-Sigmoids). In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 20–22 July 2020; pp. 588–629. [Google Scholar]
- Weijermars, R. Improving Well Productivity—Ways to Reduce the Lag between the Diffusive and Convective Time of Flight in Shale Wells. J. Pet. Sci. Eng. 2020, 193, 107344. [Google Scholar] [CrossRef]
- Fu, W.; Morris, J.P.; Fu, P.; Huang, J.; Sherman, C.S.; Settgast, R.R.; Ryerson, F.J. Developing Upscaling Approach for Swarming Hydraulic Fractures Observed at Hydraulic Fracturing Test Site through Multiscale Simulations. SPE J. 2021, 26, 2670–2684. [Google Scholar] [CrossRef]
- Chang, F.F.; Bartko, K.; Dyer, S.; Aidagulov, G.; Suarez-Rivera, R.; Lund, J. Multiple Fracture Initiation in Openhole Without Mechanical Isolation: First Step to Fulfill an Ambition. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4 February 2014; p. SPE-168638-MS. [Google Scholar]
- Sneddon, I.N. The Distribution of Stress in the Neighborhood of a Crack in an Elastic Solid. Philos. Trans. R. Soc. Lond. Ser. A 1946, 187, 1934–1990. [Google Scholar]
- Warpinski, N.R.; Teufel, L.W. Influence of Geologic Discontinuities on Hydraulic Fracture Propagation (Includes Associated Papers 17011 and 17074 ). J. Pet. Technol. 1987, 39, 209–220. [Google Scholar] [CrossRef]
- Liu, H.; Hu, Y.; Zhao, J.; Li, W.; Liu, W.; Hu, G. Simulation Study of Induced Stress Field in Refracturing Gas Well. Chin. J. Rock Mech. Eng. 2004, 23, 4022–4027. [Google Scholar]
- Deng, Y. Research on the Mechanics Mechanism of Deng Yan Refracturing New Fractures. Ph.D. Thesis, Southwest Petroleum Institute, Chengdu, China, 2005. [Google Scholar]
- Cheng, Y. Boundary Element Analysis of the Stress Distribution Around Multiple Fractures: Implications for the Spacing of Perforation Clusters of Hydraulically Fractured Horizontal Wells. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 23–25 September 2009. [Google Scholar]
- Nagel, N.B.; Sanchez-Nagel, M. Stress Shadowing and Microseismic Events: A Numerical Evaluation; OnePetro: The Woodlands, TX, USA, 2011. [Google Scholar]
- Yoon, J.S.; Zimmermann, G.; Zang, A. Numerical Investigation on Stress Shadowing in Fluid Injection-Induced Fracture Propagation in Naturally Fractured Geothermal Reservoirs. Rock Mech. Rock Eng. 2015, 48, 1439–1454. [Google Scholar] [CrossRef]
- Wu, R.; Kresse, O.; Weng, X.; Cohen, C.; Gu, H. Modeling of Interaction of Hydraulic Fractures in Complex Fracture Networks; OnePetro: The Woodlands, TX, USA, 2012. [Google Scholar]
- Manchanda, R.; Olson, J.E.; Sharma, M.M. Mechanical, Failure And Flow Properties of Sands: Micro-Mechanical Models. OnePetro: The Woodlands, TX, USA, 2012. [Google Scholar]
- Cheng, W.; Jin, Y.; Chen, M.; Xu, T.; Zhang, Y.; Diao, C. A criterion for identifying hydraulic fractures crossing natural fractures in 3D space. Pet. Explor. Dev. 2014, 41, 371–376. [Google Scholar] [CrossRef]
- Zeng, Q. Numerical Simulation Study of Hydraulic Fracture Propagation in Shale and Tight Reservoirs. Ph.D. Thesis, China University of Petroleum (East China), Qingdao, China, 2016. [Google Scholar]
- Xia, L.; Zeng, Y. Stress shadow effect of alternative fracturing based on numerical simulation of PFC2D. Rock Soil Mech. 2018, 39, 4269–4281. [Google Scholar] [CrossRef]
- Wang, X. Horizontal Well Fracturing Multiple Fracture Stress Disturbance Size Simulation and Application Research. Master’s Thesis, China University of Petroleum (Beijing), Beijing, China, 2018. [Google Scholar]
- Gao, Q.; Han, S.; Cheng, Y.; Yan, C.; Sun, Y.; Han, Z. Effects of Non-Uniform Pore Pressure Field on Hydraulic Fracture Propagation Behaviors. Eng. Fract. Mech. 2019, 221, 106682. [Google Scholar] [CrossRef]
- Zuo, S.; Ge, Z.; Deng, K.; Zheng, J.; Wang, H. Fracture Initiation Pressure and Failure Modes of Tree-Type Hydraulic Fracturing in Gas-Bearing Coal Seams. J. Nat. Gas Sci. Eng. 2020, 77, 103260. [Google Scholar] [CrossRef]
- Shokouhi, P.; Jin, J.; Manogharan, P.; Wood, C.; Rivière, J.; Elsworth, D.; Marone, C. An Experimental Investigation of the Coupling Between Elastodynamic and Hydraulic Properties of Naturally Fractured Rock at the Laboratory Scale; American Rock Mechanics Association: Golden, CO, USA, 2020. [Google Scholar]
- Weijermars, R.; Wang, J.; Nelson, R. Stress Concentrations and Failure Modes in Horizontal Wells Accounting for Elastic Anisotropy of Shale Formations. Earth-Sci. Rev. 2020, 200, 102957. [Google Scholar] [CrossRef]
- Gholami, A.; Aghighi, M.A.; Rahman, S.S. Effect of Non-Uniform Pore Pressure Fields on Hydraulic Fracture Propagation. J. Pet. Sci. Eng. 2017, 159, 889–902. [Google Scholar] [CrossRef]
- Prabhakaran, R.; De Pater, H.; Shaoul, J. Pore Pressure Effects on Fracture Net Pressure and Hydraulic Fracture Containment: Insights from an Empirical and Simulation Approach. J. Pet. Sci. Eng. 2017, 157, 724–736. [Google Scholar] [CrossRef]
- Lian, P.; Cheng, L.; Deng, B. Simulation of Ground Stress Field and Fracture Anticipation with Effect of Pore Pressure. Theor. Appl. Fract. Mech. 2011, 56, 34–41. [Google Scholar] [CrossRef]
- Ikeda, R.; Tsukahara, H. Hydraulic Fracturing Technique: Pore Pressure Effect and Stress Heterogeneity. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 26, 471–475. [Google Scholar] [CrossRef]
- Weijermars, R.; Nandlal, K.; Khanal, A.; Tugan, M.F. Comparison of Pressure Front with Tracer Front Advance and Principal Flow Regimes in Hydraulically Fractured Wells in Unconventional Reservoirs. J. Pet. Sci. Eng. 2019, 183, 106407. [Google Scholar] [CrossRef]
- Jin, Y.; Chen, M.; Zhang, X. Hydraulic fracturing initiation pressure models for directional wells in naturally fractured formation. Acta Pet. Sin. 2006, 27, 124–126. [Google Scholar]
- Jia, C.; Li, M.; Deng, J.; Tian, C.; Chang, L. Large-Scale Three Dimensional Simulation Test For Directional Perforation And Fracturing In Deflected Well. J. Southwest Pet. Univ. 2007, 29, 135–137. [Google Scholar]
- Hou, B.; Zhang, R.; Diao, C.; Li, L.; Cheng, M. Experimental study on hydraulic fracture propagation in highly deviated wells. China Offshore Oil Gas 2016, 28, 85–91. [Google Scholar]
- Bérard, T.; Desroches, J.; Yang, Y.; Weng, X.; Olson, K. High-Resolution 3D Structural Geomechanics Modeling for Hydraulic Fracturing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015. [Google Scholar]
- Zhang, G.; Chen, M.; Yao, F.; Zhao, Z. Study on optimal re-fracturing timing in anisotropic formation and its influencing factors. Acta Pet. Sin. 2008, 29, 885–888, 893. [Google Scholar]
- Guo, T.; Zhang, S.; Wang, L.; Sui, W.; Wen, H. Optimization of proppant size for frac-pack completion based on a new equipment. J. Pet. Sci. Eng. 2012, 96–97, 1–9. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, W.; Qu, Z.; Guo, T.; Sun, Y.; Rabiei, M.; Cao, Q. Feasibility evaluation of hydraulic fracturing in hydrate-bearing sediments based on analytic hierarchy process-entropy method (AHP-EM). J. Nat. Gas Sci. Eng. 2020, 81, 103434. [Google Scholar] [CrossRef]
- Pham, T.; Weijermars, R. Solving Stress Tensor Fields around Multiple Pressure-Loaded Fractures Using a Linear Superposition Method (LSM). Appl. Math. Model. 2020, 88, 418–436. [Google Scholar] [CrossRef]
- Gaurina-Međimurec, N.; Brkić, V.; Topolovec, M.; Mijić, P. Fracturing Fluids and Their Application in the Republic of Croatia. Appl. Sci. 2021, 11, 2807. [Google Scholar] [CrossRef]
- Gaurina-Međimurec, N.; Pašić, B.; Mijić, P.; Medved, I. Drilling Fluid and Cement Slurry Design for Naturally Fractured Reservoirs. Appl. Sci. 2021, 11, 767. [Google Scholar] [CrossRef]








| Geological Oroperties | Numerical Value |
|---|---|
| Young’s modulus | 20 GPa |
| Poisson’s ratio | 0.25 |
| Porosity | 10% |
| Permeability | 1 mD |
| Tensile strength | 6 MPa |
| Horizontal minimum principal stress | 10 MPa |
| Horizontal maximum principal stress | 20 MPa |
| Injection Point | Breaking Pressure MPa | Fracture Pressure MPa | Average Fracture Width mm | Average Fracture Length m | |||
|---|---|---|---|---|---|---|---|
| Step2 | Step3 | Step2 | Step3 | Step2 | Step3 | ||
| L/R-5 | 27.6 | 22.6 | 16.9 | 6.9 | 6.8 | 18 | 18 |
| L/R-3 | 27.6 | 22.2 | 16.2 | 5.7 | 4 | 20 | 26 |
| M-1 | 27.6 | 22.8 | 17 | 6.2 | 6.3 | 20 | 20 |
| Data Information | Breaking Pressure/MPa | Extension Pressure/MPa | ||||
|---|---|---|---|---|---|---|
| Fracturing Method | Injection Point | Source of Stress Field | Injection Point | Source of Stress Field | ||
| Step2 | Step3 | Step2 | Step3 | |||
| reinject | M-1 | 33.5 | 32.5 | M-1 | 29.1 | 28.8 |
| L/R-3 | 33.5 | 32.5 | L/R-3 | 28.4 | 27.1 | |
| L/R-5 | 33.5 | 32.5 | L/R-5 | 28 | 27.6 | |
| reperforation | L/R-2 | 33.4 | 32 | L/R-2 | 26.1 | 24.9 |
| L/R-4 | 33.4 | 32 | L/R-4 | 25 | 24.2 | |
| Data Information | Average Fracture Width/mm | Average Fracture Length/m | ||||
| Fracturing Method | Injection Point | Source of Stress Field | Injection Point | Source of Stress Field | ||
| Step2 | Step3 | Step2 | Step3 | |||
| reinject | M-1 | 6.8 | 7.2 | M-1 | 17 | 17 |
| L/R-3 | 6.4 | 6.5 | L/R-3 | 18 | 18 | |
| L/R-5 | 7.4 | 7.4 | L/R-5 | 16 | 16 | |
| reperforation | L/R-2 | 6.3 | 6.4 | L/R-2 | 22 | 19 |
| L/R-4 | 6.7 | 6.3 | L/R-4 | 25 | 21 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, H.; Tian, Y.; Sun, Z.; Zhou, F. Fracture Interference and Refracturing of Horizontal Wells. Processes 2022, 10, 899. https://doi.org/10.3390/pr10050899
Lin H, Tian Y, Sun Z, Zhou F. Fracture Interference and Refracturing of Horizontal Wells. Processes. 2022; 10(5):899. https://doi.org/10.3390/pr10050899
Chicago/Turabian StyleLin, Hai, Yakai Tian, Zhenwei Sun, and Fujian Zhou. 2022. "Fracture Interference and Refracturing of Horizontal Wells" Processes 10, no. 5: 899. https://doi.org/10.3390/pr10050899
APA StyleLin, H., Tian, Y., Sun, Z., & Zhou, F. (2022). Fracture Interference and Refracturing of Horizontal Wells. Processes, 10(5), 899. https://doi.org/10.3390/pr10050899






