Causal Network Structure Learning Based on Partial Least Squares and Causal Inference of Nonoptimal Performance in the Wastewater Treatment Process
Abstract
:1. Introduction
- (1)
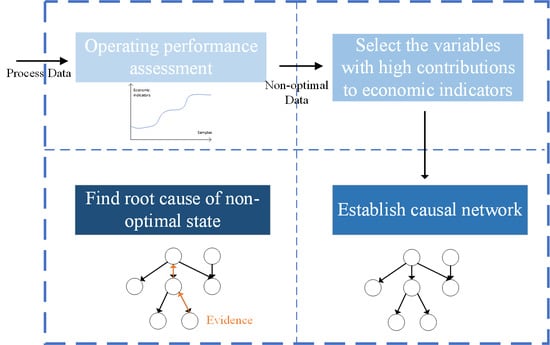
- A complete framework from operating performance assessment to nonoptimal cause identification is established. Process data are divided into multiple operating grades, so that field operators can detect operational states with poor economic benefits and adjust them in time.
- (2)
- In order to establish a causality network, contribution plots and Granger causality analysis are used in this paper, which avoid the NP-hard problem of searching for the causal network structure.
- (3)
- PLS-GC method is proposed to replace simple GC, which can remove false causalities caused by variable coupling and reduce the possibility of generating a cyclic structure in causal networks.
- (4)
- Through Bayesian network inference, both nonoptimal causes can be identified, and the transmission path of nonoptimal causes can be obtained.
2. Preliminaries
2.1. Granger Causality Analysis
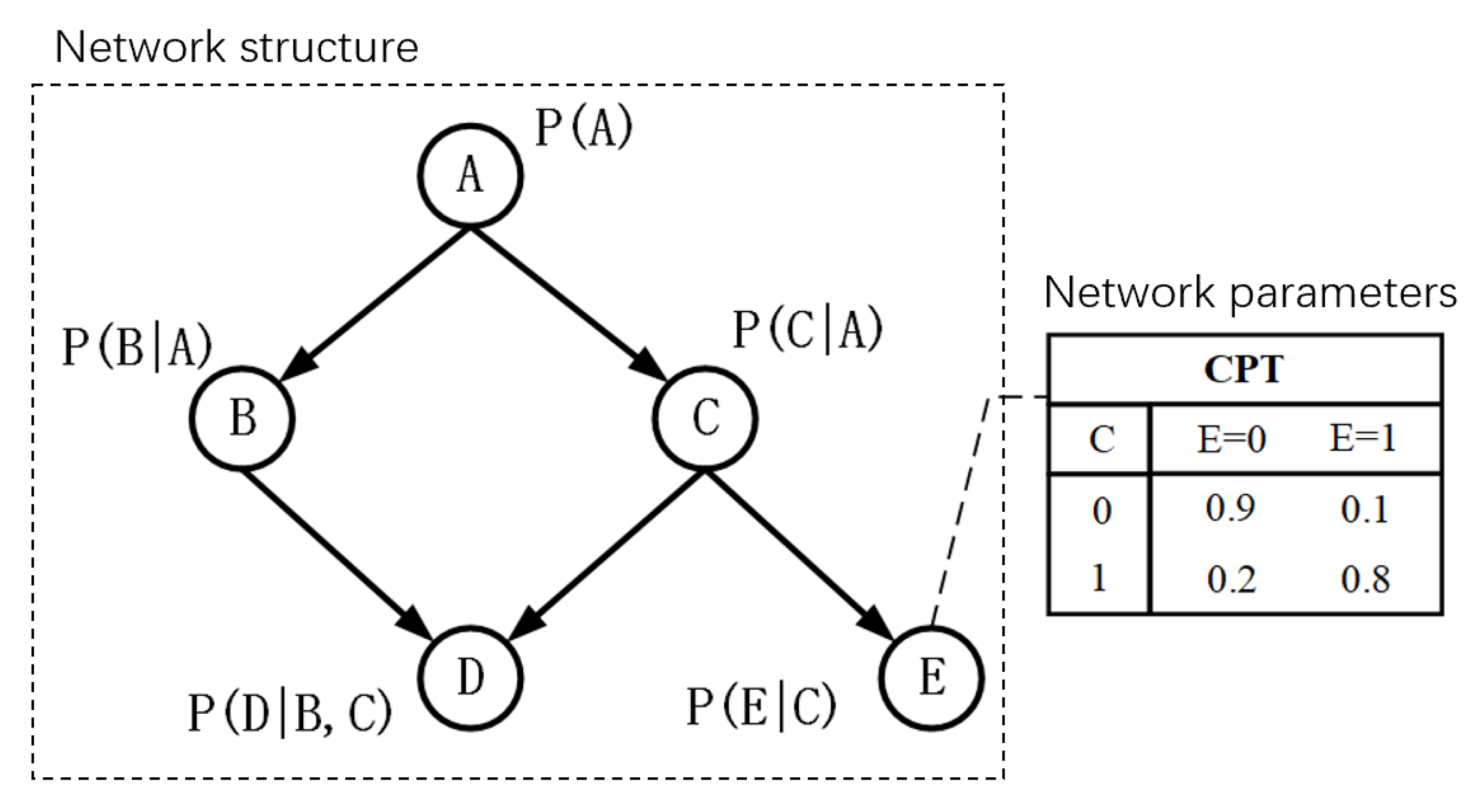
2.2. Bayesian Network
2.2.1. Fundamentals of Bayesian Networks
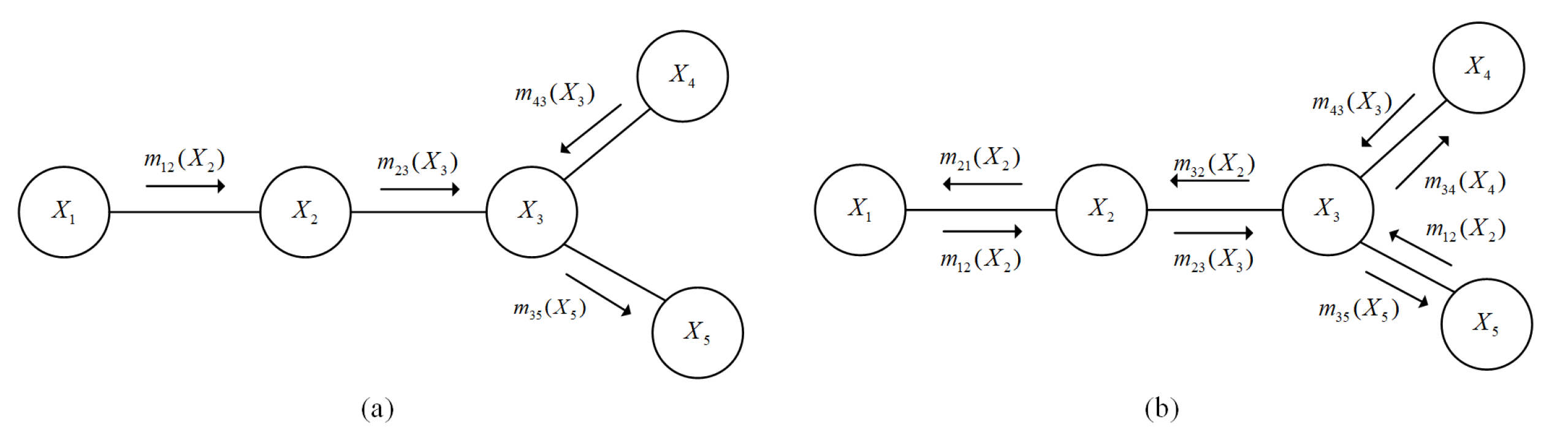
2.2.2. Inference Algorithm of Bayesian Network
3. Method Development
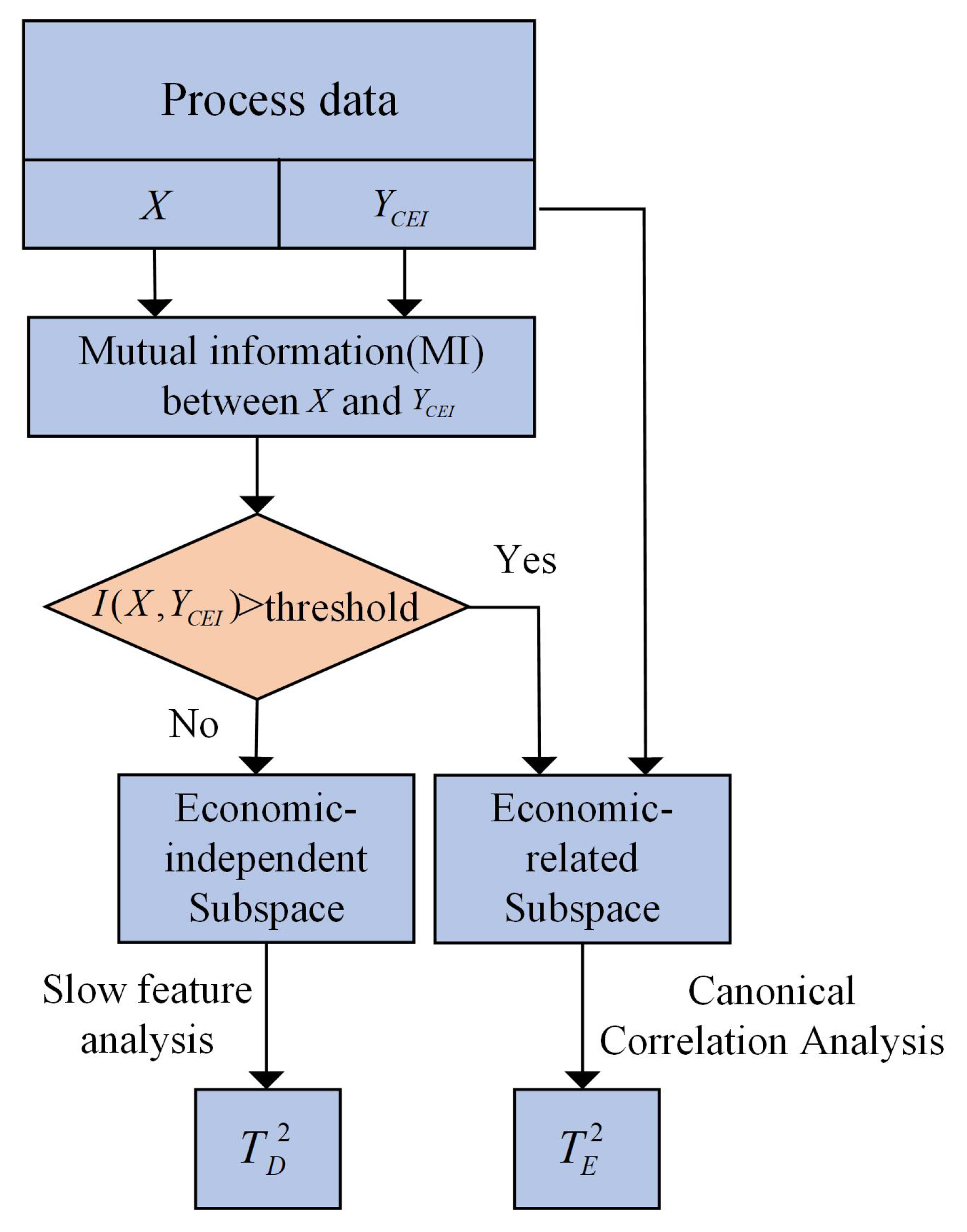
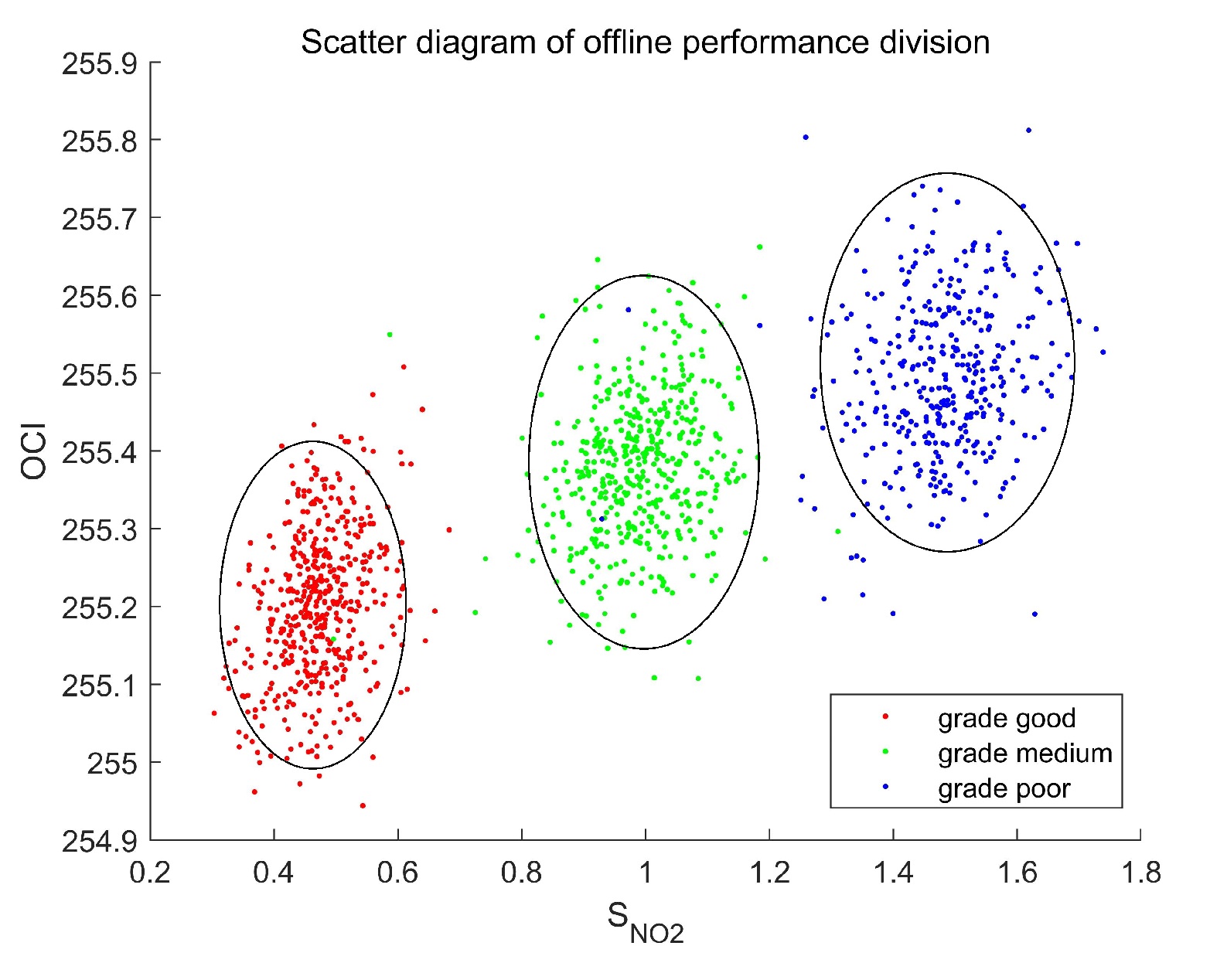
3.1. Establishment of Operating Optimality Assessment Model
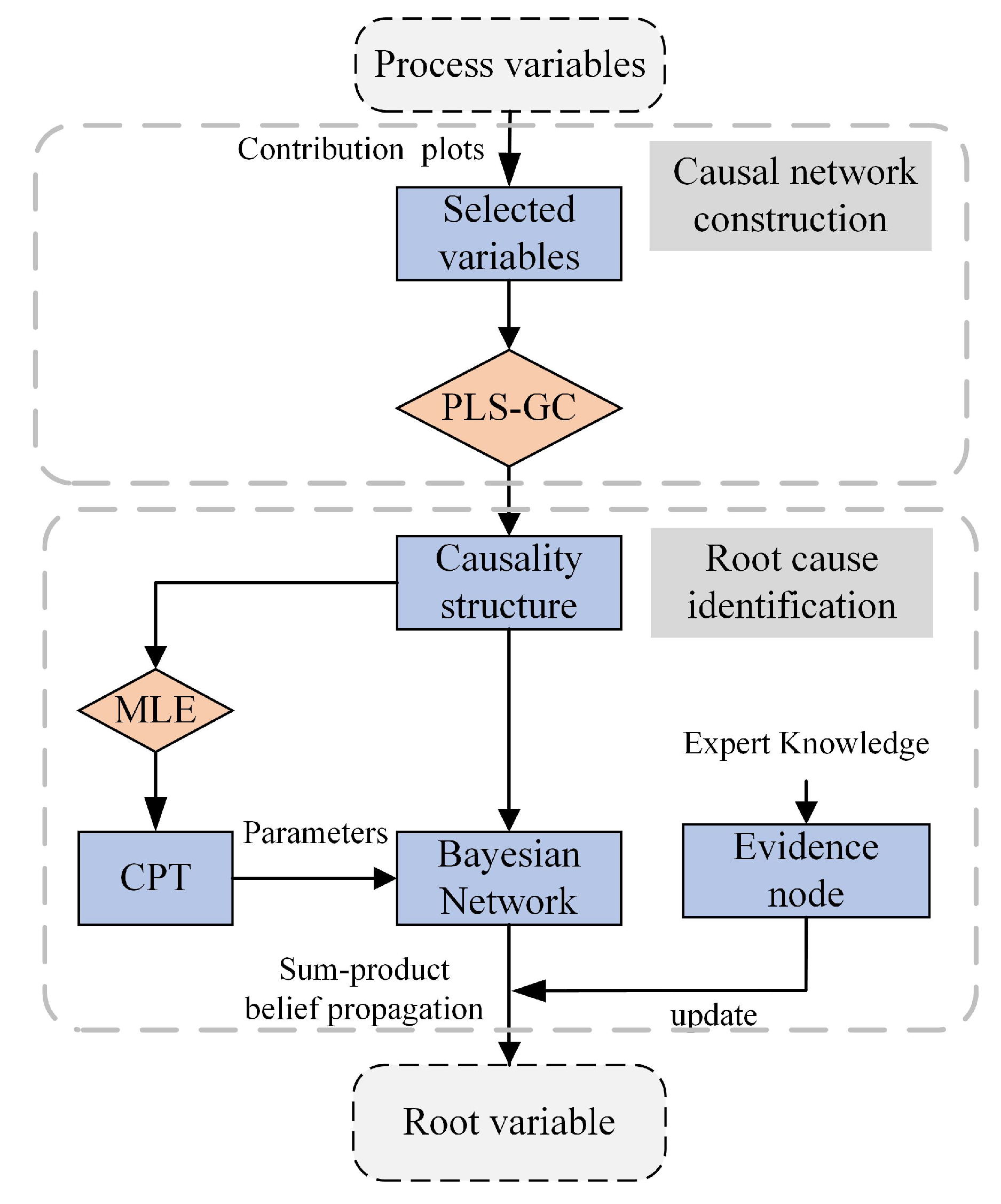
3.2. Nonoptimal Root Cause Identification
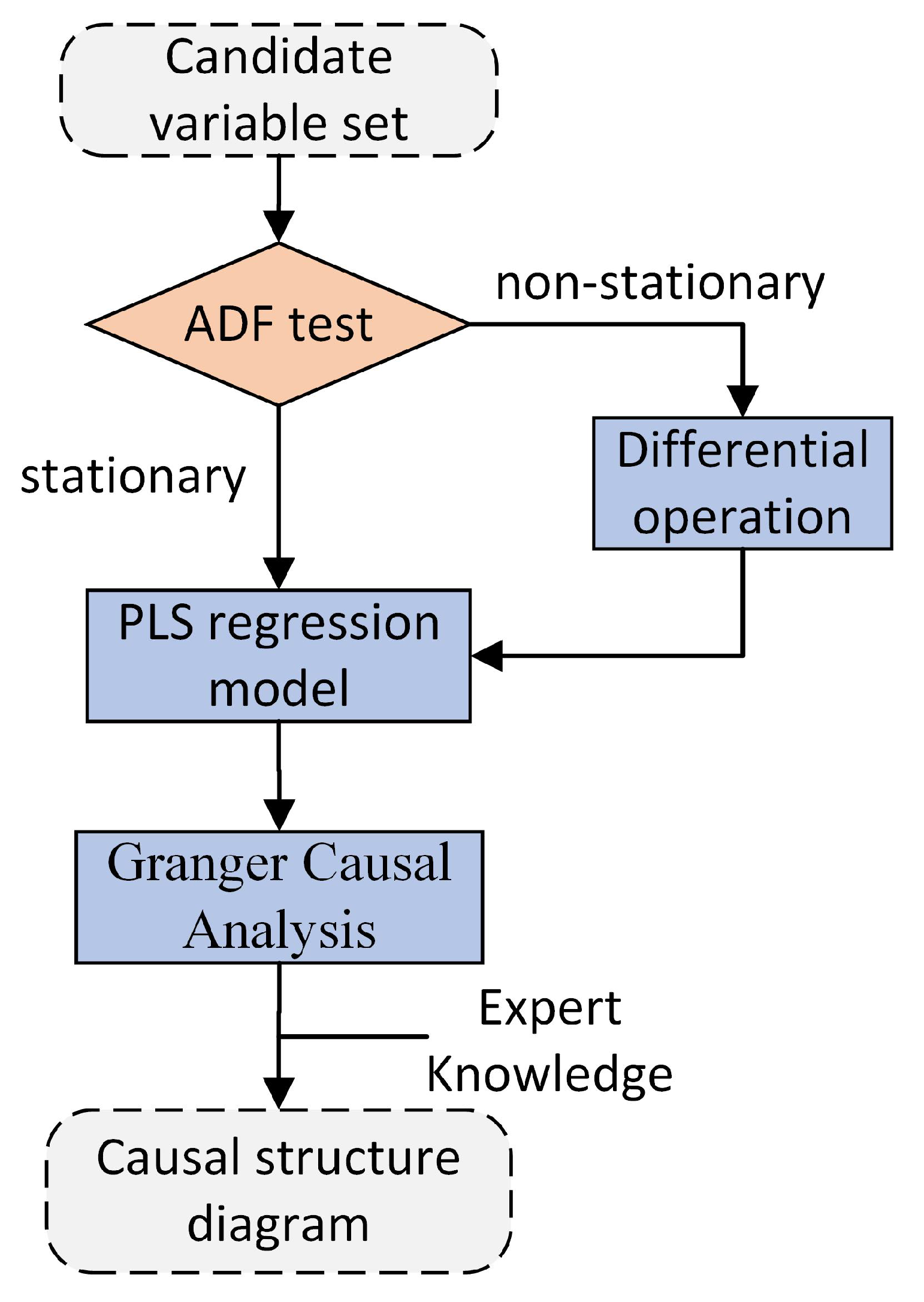
3.2.1. Causal Network Establishment
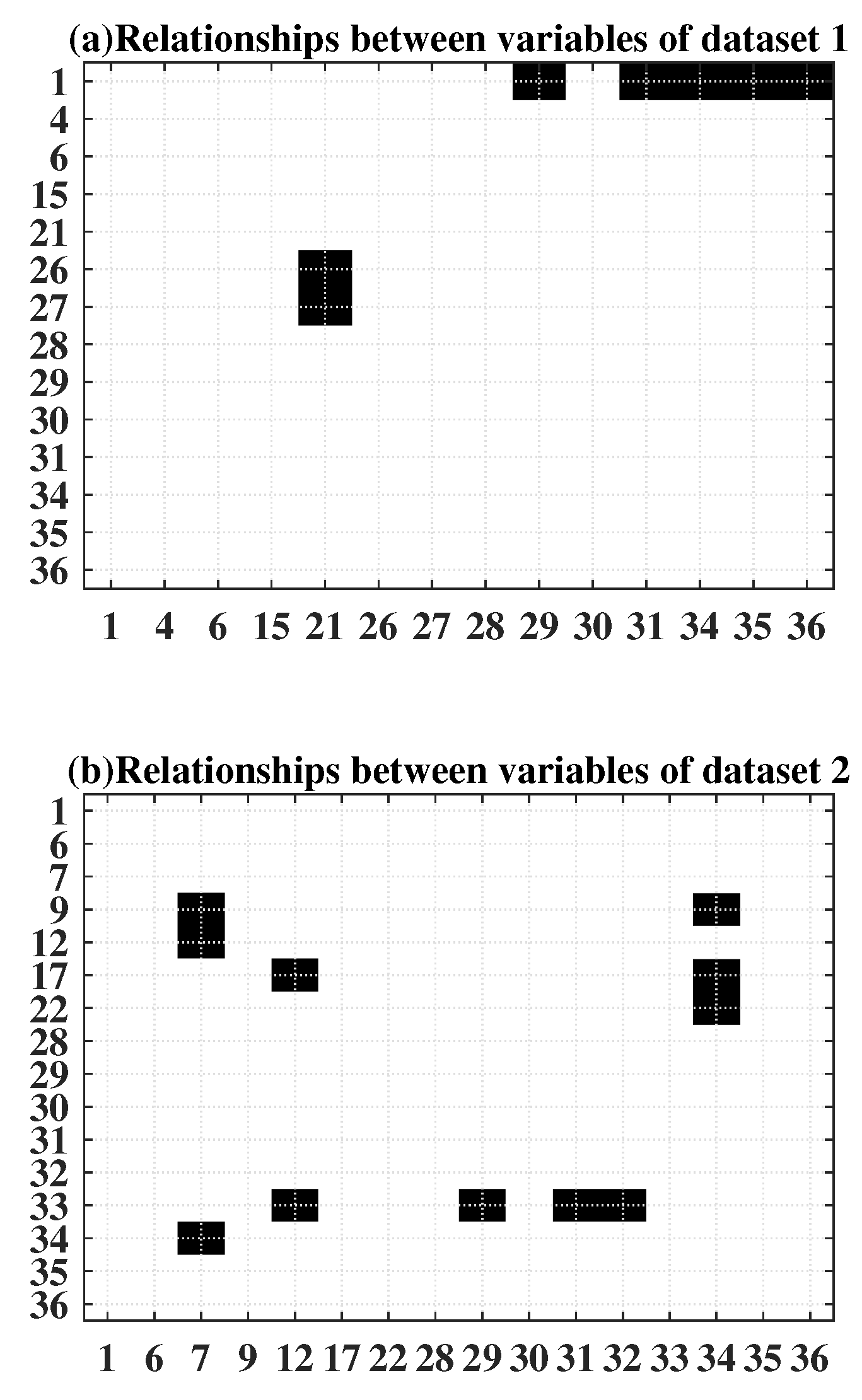
- Candidate variables are selected for causality structure construction by PCA contribution plots.
- ADF test is conducted to ensure that all variables are stationary
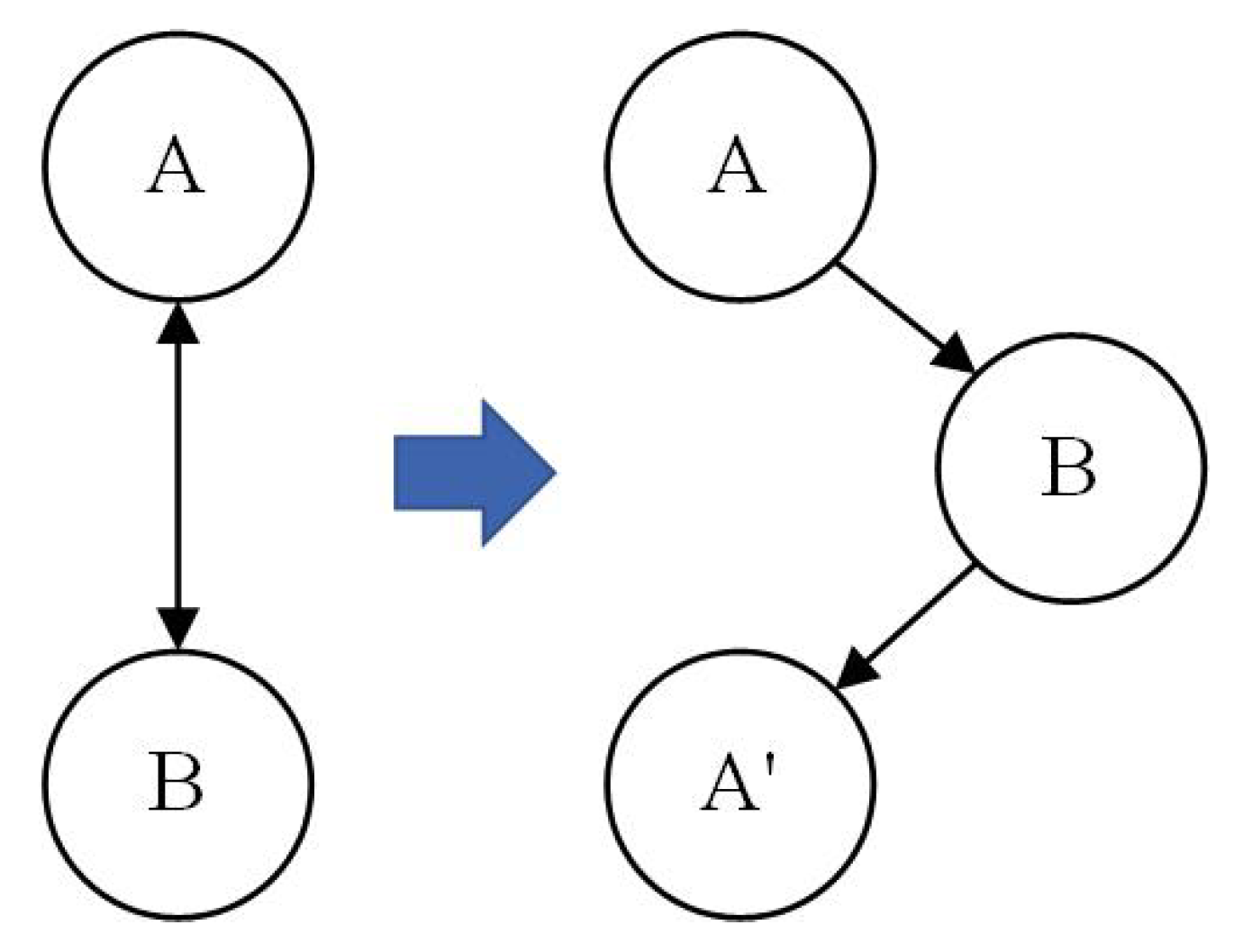
- For all stationary variables , we selected two variables and , , establish autoregression model and union-regression model by PLS and calculate F statistics. If p value of F statistic is in the confidence interval , there is a causal relationship from to . Such a causality test is conducted on each pair of variables in turn.
- A causal network structure is constructed and adjusted according to expert knowledge.
3.2.2. Nonoptimal Cause Identification
- On the basis of PCA contribution plots, select the candidate variable set.
- Construct the network structure on the basis of PLS-GC.
- Calculate the conditional probability and obtain CPT.
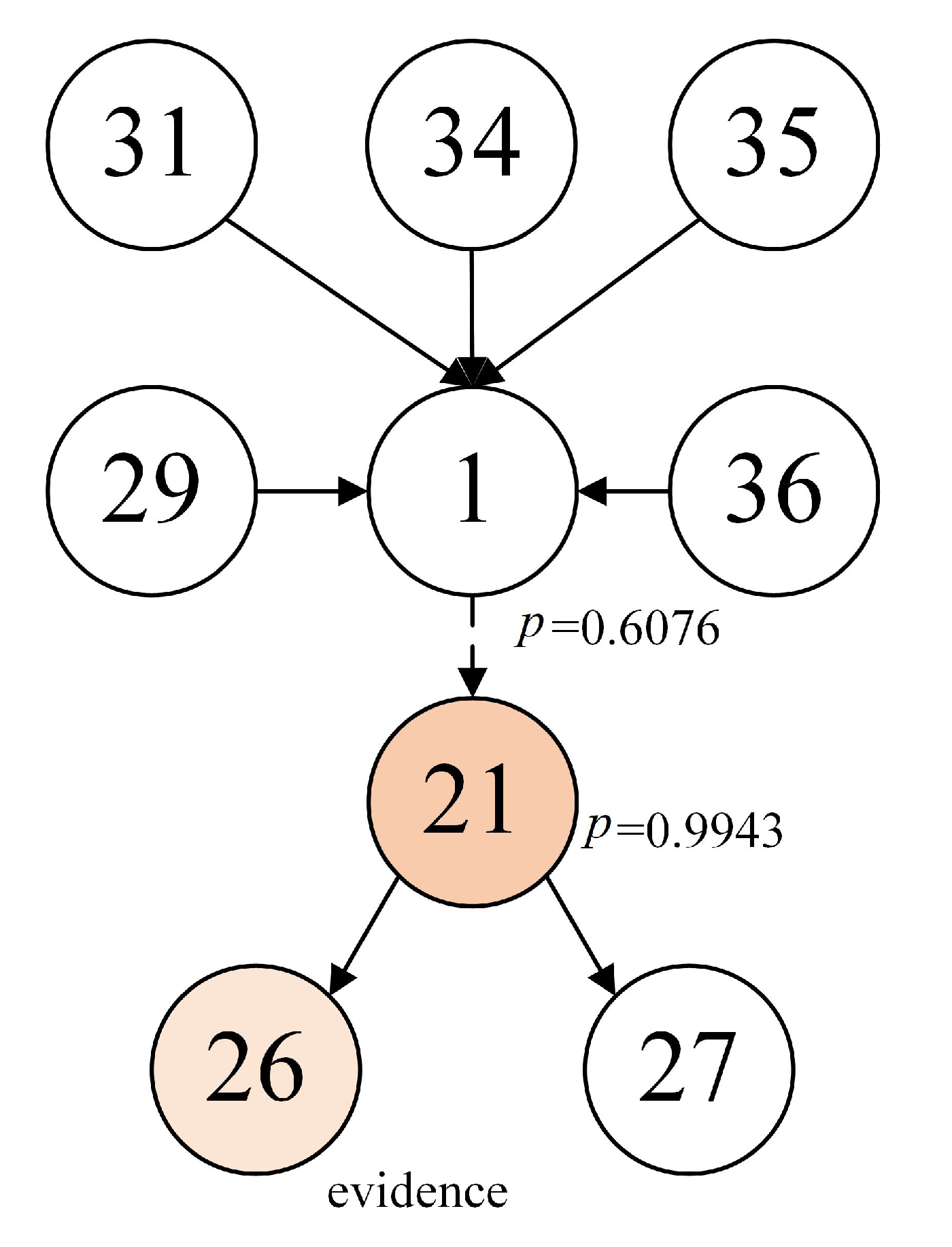
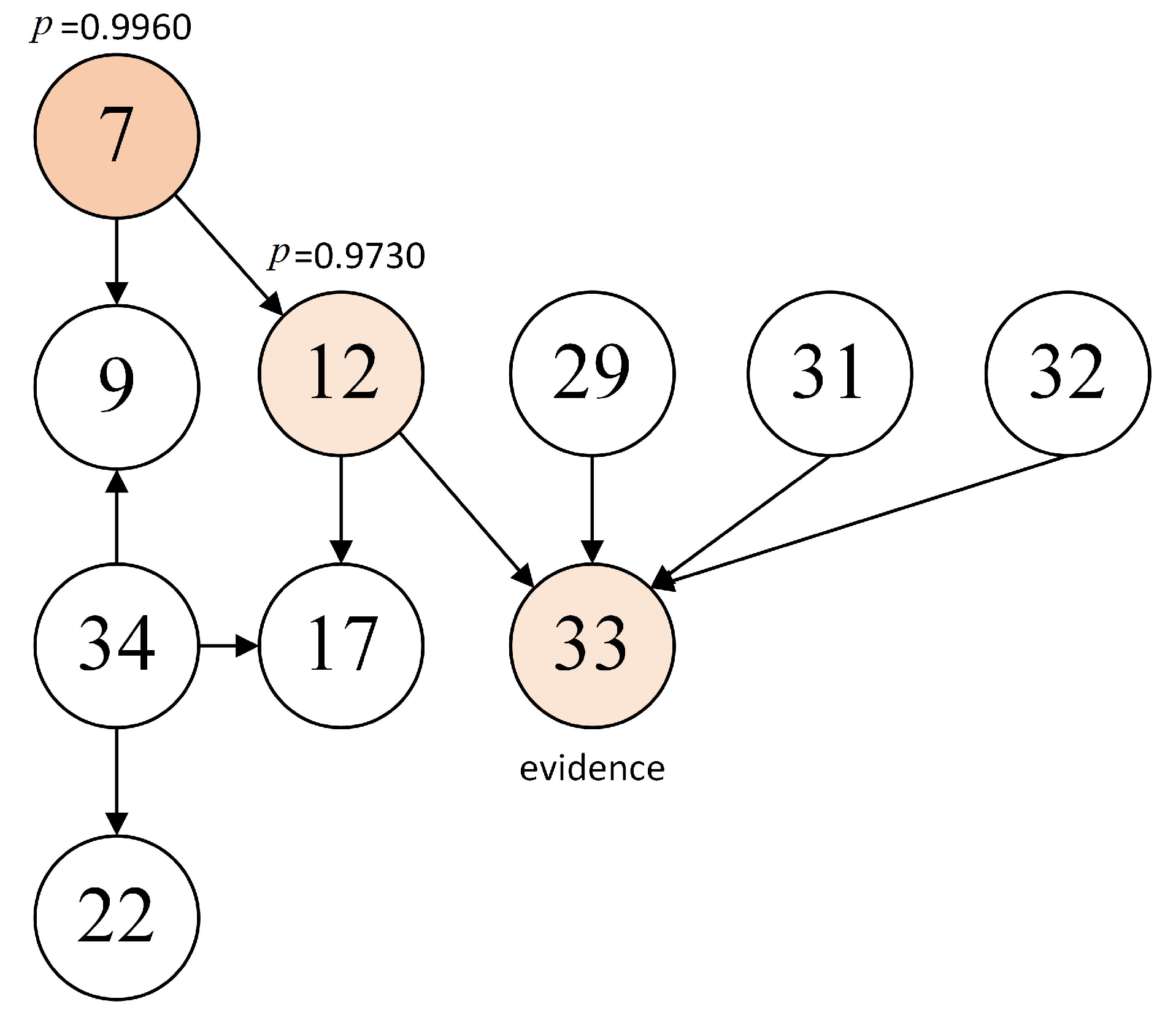
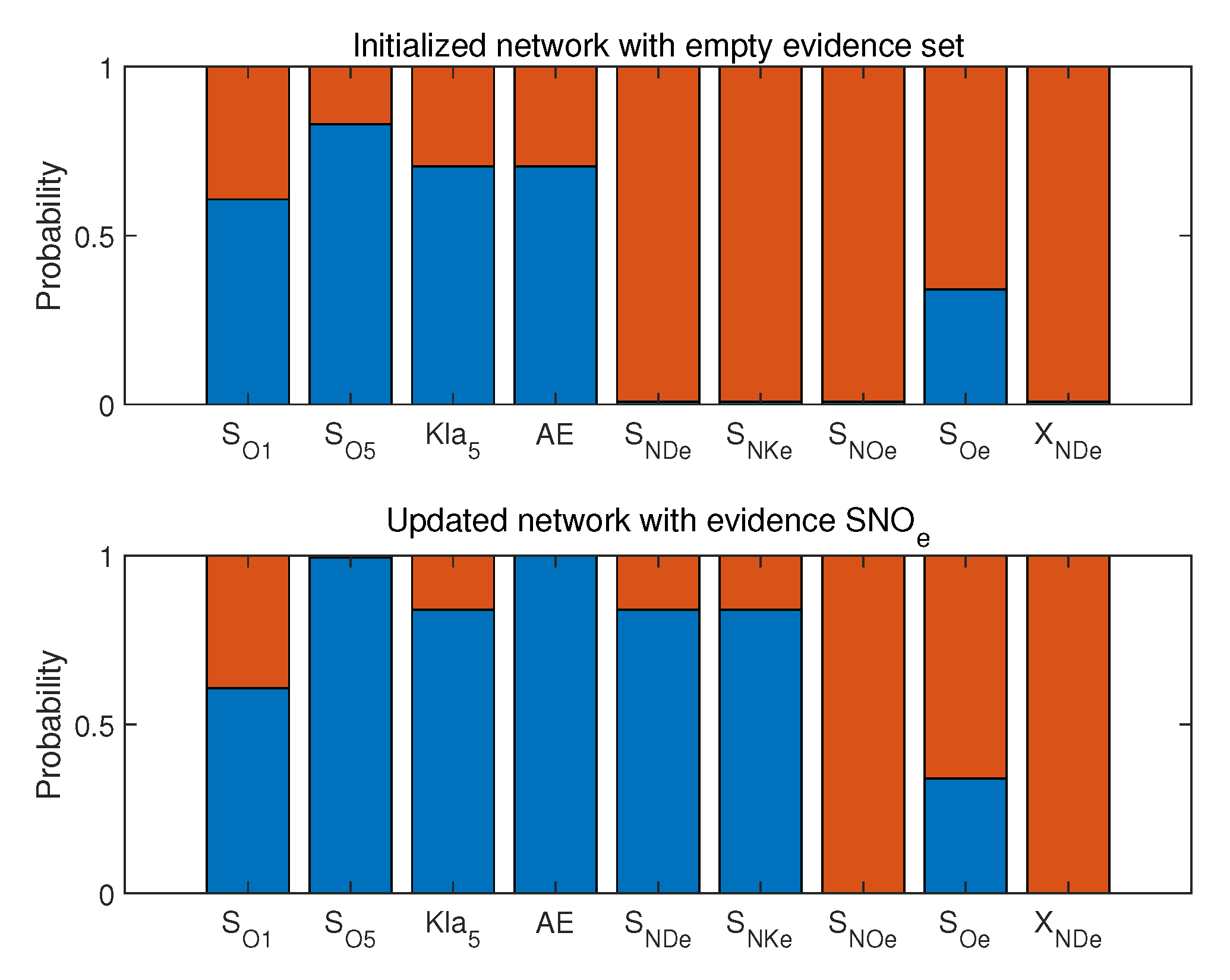
- Determine evidence variable according to industry field experience and contribution plots. Among the resulting variables in the causal network, the one with the largest contribution is the evidence node. Then, update the network parameters with the belief propagation method and identify the root nonoptimal variable.
4. Results and Discussion
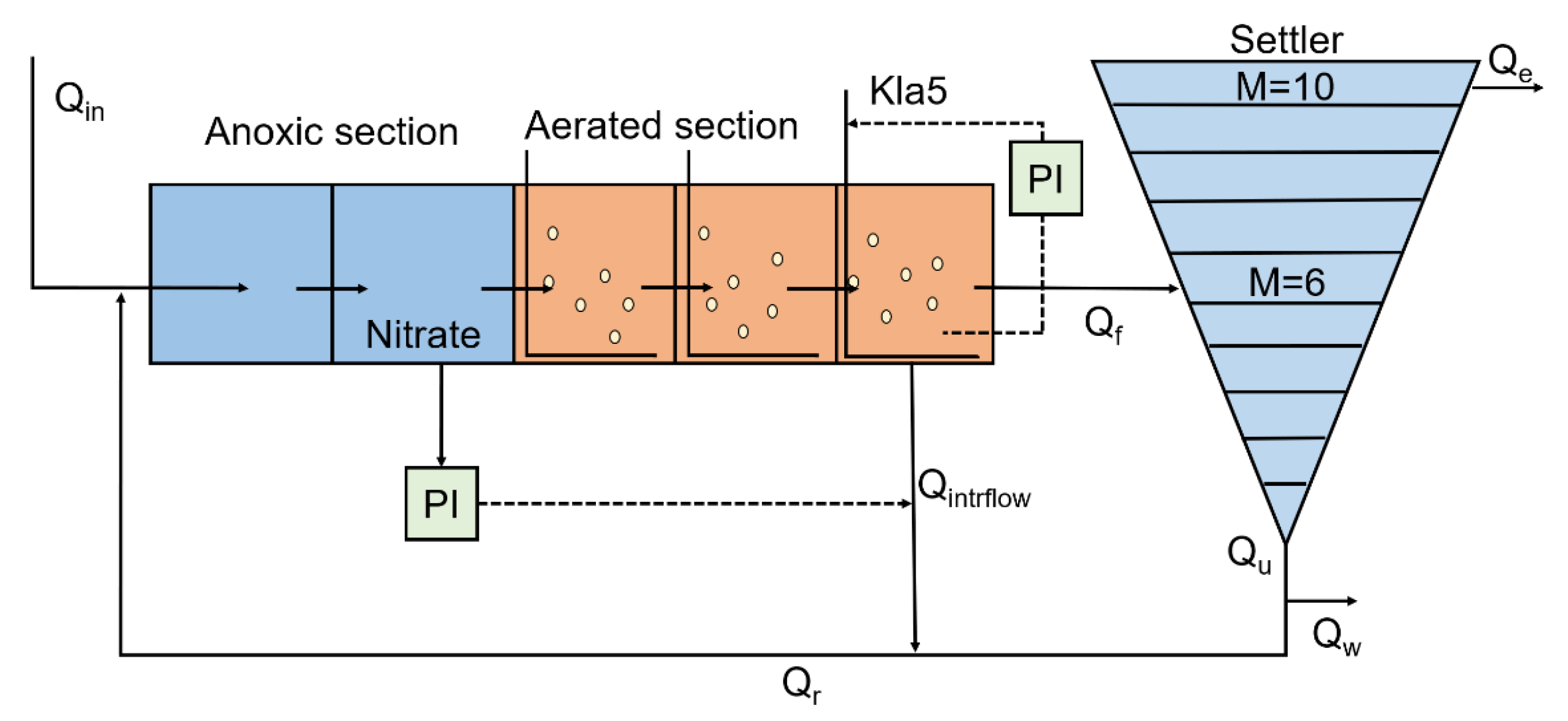
4.1. Process Description
4.2. Data Preparation
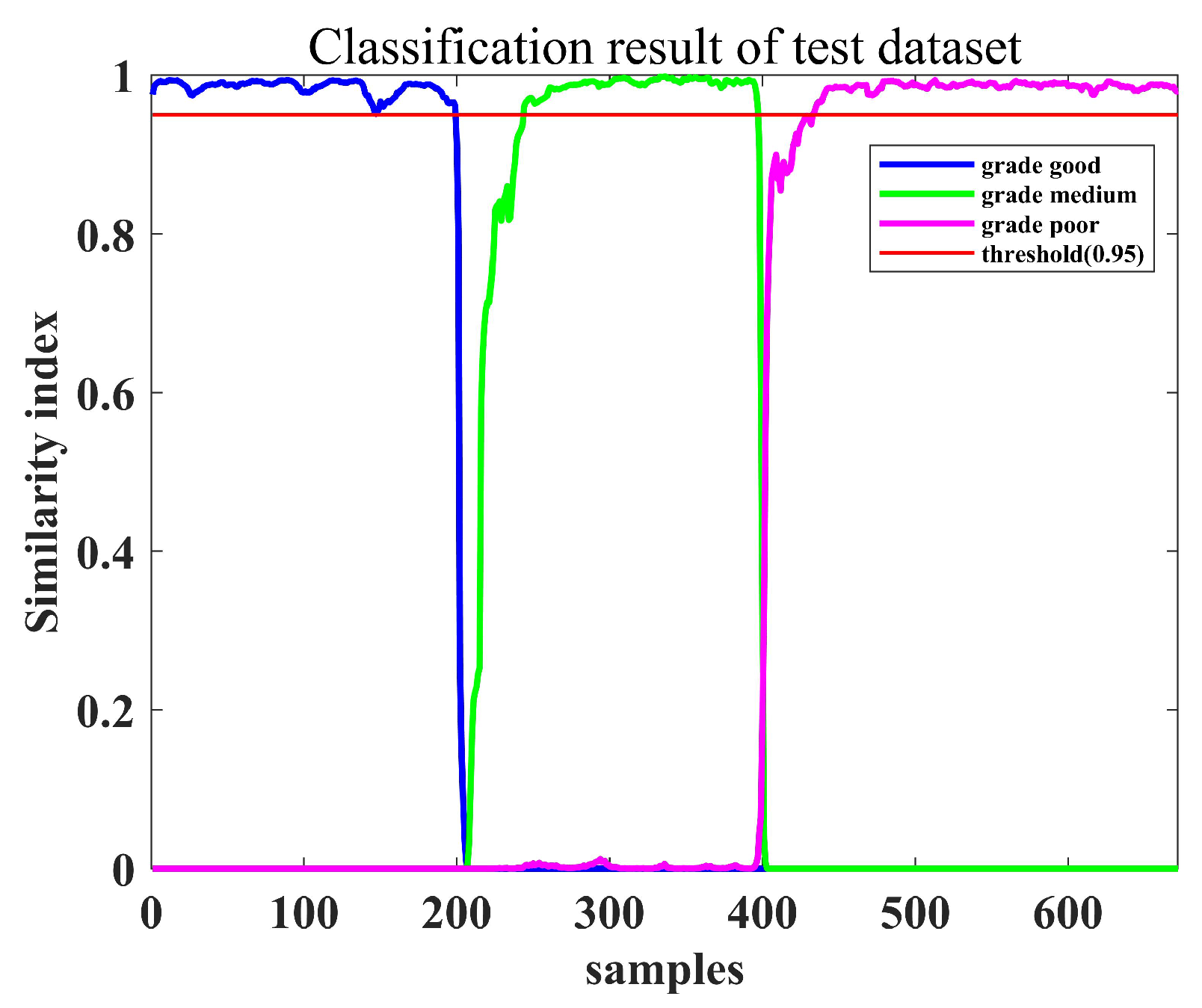
4.3. Operating Performance Assessment and Nonoptimal Cause Identification
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PCA | Principal component analysis |
| DAG | Directed acyclic graph |
| PLS | Partial least squares |
| GC | Granger causality |
| PLS-GC | Partial-least-squares-based Granger causality |
| BN | Bayesian network |
| CPT | Conditional probability table |
| CEI | Comprehensive economic indicatory |
| ERS | Economic subspace |
| EIS | Economic-independent subspace |
| MI | Mutual information |
| CCA | Canonical correlation analysis |
| SFA | Slow feature analysis |
| ADF test | Augmented Dickey–Fuller unit root test |
| MLE | Maximum likelihood estimation |
| BSM1 | Benchmark Simulation Model 1 |
| OCI | Overall cost index |
References
- Ye, L.; Liu, Y.; Fei, Z.; Liang, J. Online Probabilistic Assessment of Operating Performance Based on Safety and Optimality Indices for Multimode Industrial Processes. Ind. Eng. Chem. Res. 2009, 48, 10912–10923. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, Y.; Wang, F. Online process operating performance assessment and nonoptimal cause identification for industrial processes. J. Process Control 2014, 24, 1548–1555. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Chang, Y. Online Fuzzy Assessment of Operating Performance and Cause Identification of Nonoptimal Grades for Industrial Processes. Ind. Eng. Chem. Res. 2013, 52, 18022–18030. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Chang, Y. Operating optimality assessment based on optimality related variations and nonoptimal cause identification for industrial processes. J. Process Control 2016, 39, 11–20. [Google Scholar] [CrossRef]
- Chu, F.; Dai, W.; Shen, J. Online complex nonlinear industrial process operating optimality assessment using modified robust total kernel partial M-regression. Chin. J. Chem. Eng. 2018, 26, 775–785. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Gao, F. Hierarchical Multiblock T-PLS Based Operating Performance Assessment for Plant-Wide Processes. Ind. Eng. Chem. Res. 2018, 57, 14617–14627. [Google Scholar] [CrossRef]
- Chang, Y.; Zou, X.; Wang, F. Multi-mode plant-wide process operating performance assessment based on a novel two-level multi-block hybrid model. Chem. Eng. Res. Des. 2018, 136, 721–733. [Google Scholar] [CrossRef]
- Lu, Q.; Jiang, B.; Gopaluni, R.B.; Loewen, P.D.; Braatz, R.D. Locality preserving discriminative canonical variate analysis for fault diagnosis. Comput. Chem. Eng. 2018, 117, 309–319. [Google Scholar] [CrossRef]
- Venkatasubramanian, V.; Rengaswamy, R.; Yin, K.; Kavuri, S. A review of process fault detection and diagnosis: Part I: Quantitative model-based methods. Comput. Chem. Eng. 2003, 27, 293–311. [Google Scholar] [CrossRef]
- Zou, X.; Wang, F.; Chang, Y. Process operating performance optimality assessment and non-optimal cause identification under uncertainties. Chem. Eng. Res. Des. 2017, 120, 348–359. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Wu, J.; Liu, Y.; Huang, D. A novel fault identification and root-causality analysis of incipient faults with applications to wastewater treatment processes. Chemom. Intell. Lab. Syst. 2019, 188, 24–36. [Google Scholar] [CrossRef]
- Li, G.; Joe, S.; Tao, Y. Data-driven root cause diagnosis of faults in process industries. Chemom. Intell. Lab. Syst. 2019, 1859, 1–11. [Google Scholar] [CrossRef]
- Pearl, J. Causality; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Chen, H.S.; Yan, Z.; Zhang, X.; Liu, Y.; Yao, Y. Root cause diagnosis of process faults using conditional Granger causality analysis and Maximum Spanning Tree. IFAC-PapersOnLine 2018, 51, 381–386. [Google Scholar] [CrossRef]
- Kannan, R.; Tangirala, A.K. Correntropy-based partial directed coherence for testing multivariate Granger causality in nonlinear processes. Phys. Rev. E 2014, 89, 062144. [Google Scholar] [CrossRef]
- Chen, H.S.; Yan, Z.; Yuan, Y.; Huang, T.B.; Yi-Sern, W. Systematic Procedure for Granger-Causality-Based Root Cause Diagnosis of Chemical Process Faults. Ind. Eng. Chem. Res. 2018, 29, 9500–9512. [Google Scholar] [CrossRef]
- Lindner, B.; Auret, L.; Bauer, M. A Systematic Workflow for Oscillation Diagnosis Using Transfer Entropy. IEEE Trans. Control Syst. Technol. 2019, 28, 908–919. [Google Scholar] [CrossRef]
- Gharahbagheri, H.; Imtiaz, S.A.; Khan, F. Root cause diagnosis of process fault using KPCA and Bayesian network. Ind. Eng. Chem. Res. 2017, 56, 2054–2070. [Google Scholar] [CrossRef]
- Chen, G.; Ge, Z. Hierarchical Bayesian Network Modeling Framework for Large-Scale Process Monitoring and Decision Making. IEEE Trans. Control Syst. Technol. 2018, 28, 1–9. [Google Scholar] [CrossRef]
- Suresh, R.; Sivaram, A.; Venkatasubramanian, V. A hierarchical approach for causal modeling of process systems. Comput. Chem. Eng. 2019, 123, 170–183. [Google Scholar] [CrossRef]
- Gang, L.; Qin, S.J.; Zhou, D. Geometric properties of partial least squares for process monitoring. Automatica 2010, 46, 204–210. [Google Scholar]
- Stocchero, M.; De, N.M.; Scarpa, B. Geometric properties of partial least squares for process monitoring. Chemom. Intell. Lab. Syst. 2021, 216, 104374. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Artif. Intell. 1990, 48, 117–124. [Google Scholar]
- Cai, B.; Huang, L.; Xie, M. Bayesian networks in fault diagnosis. IEEE Trans. Ind. Inform. 2017, 13, 2227–2240. [Google Scholar] [CrossRef]
- Jin, S.; Liu, Y.; Lin, Z. A Bayesian network approach for fixture fault diagnosis in launch of the assembly process. Int. J. Prod. Res. 2012, 13, 6655–6666. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiao, F.; Wang, S. An intelligent chiller fault detection and diagnosis methodology using Bayesian belief network. Energy Build. 2020, 57, 278–288. [Google Scholar] [CrossRef]
- Sun, W.; Paiva, A.R.; Xu, P.; Braatz, R.D. Fault detection and identification using Bayesian recurrent neural networks. Comput. Chem. Eng. 2020, 141, 106991. [Google Scholar] [CrossRef]
- Yu, J.; Rashid, M.M. A novel dynamic bayesian network-based networked process monitoring approach for fault detection, propagation identification, and root cause diagnosis. AIChE J. 2013, 59, 2348–2365. [Google Scholar] [CrossRef]
- Lo, C.H.; Wong, Y.K.; Rad, A.B. Bond graph based Bayesian network for fault diagnosis. Appl. Soft Comput. 2011, 11, 1208–1212. [Google Scholar] [CrossRef]
- Khanafer, R.M.; Solana, B.; Triola, J.; Barco, R.; Moltsen, L.; Altman, Z.; Lazaro, P. Automated diagnosis for UMTS networks using Bayesian network approach. IEEE Trans. Veh. Technol. 2008, 57, 2451–2461. [Google Scholar] [CrossRef]
- Wentian, L. Slow Feature Analysis: Mutual information functions versus correlation functions. J. Stat. Phys. 1990, 60, 823–837. [Google Scholar]
- Hotelling, H. Relations Between Two Sets of Variates. Biometrika 1935, 28, 321–377. [Google Scholar] [CrossRef]
- Wiskott, L.; Sejnowski, T.J. Slow Feature Analysis: Unsupervised Learning of Invariances. Neural Comput. 2002, 14, 715–770. [Google Scholar] [CrossRef]
- Ge, Z.; Zhang, M.; Song, Z. Nonlinear process monitoring based on linear subspace and Bayesian inference. J. Process Control 2010, 57, 676–688. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the Estimators for Autoregressive Time Series With a Unit Root. J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Wu, P.; Lou, S.; Zhang, X.; He, J.; Gao, J. Novel Quality-Relevant Process Monitoring based on Dynamic Locally Linear Embedding Concurrent Canonical Correlation Analysis. Ind. Eng. Chem. Res. 2020, 59, 21439–21457. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, Y.; Huang, D. Development of a Novel Adaptive Soft-Sensor Using Variational Bayesian PLS with Accounting for Online Identification of Key Variables. Ind. Eng. Chem. Res. 2015, 54, 338–350. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Jeppsson, U.; Vanrolleghem, P.A.; Copp, J.B. Benchmarking of Control Strategies for Wastewater Treatment Plants; IWA Publishing: London, UK, 2014. [Google Scholar]
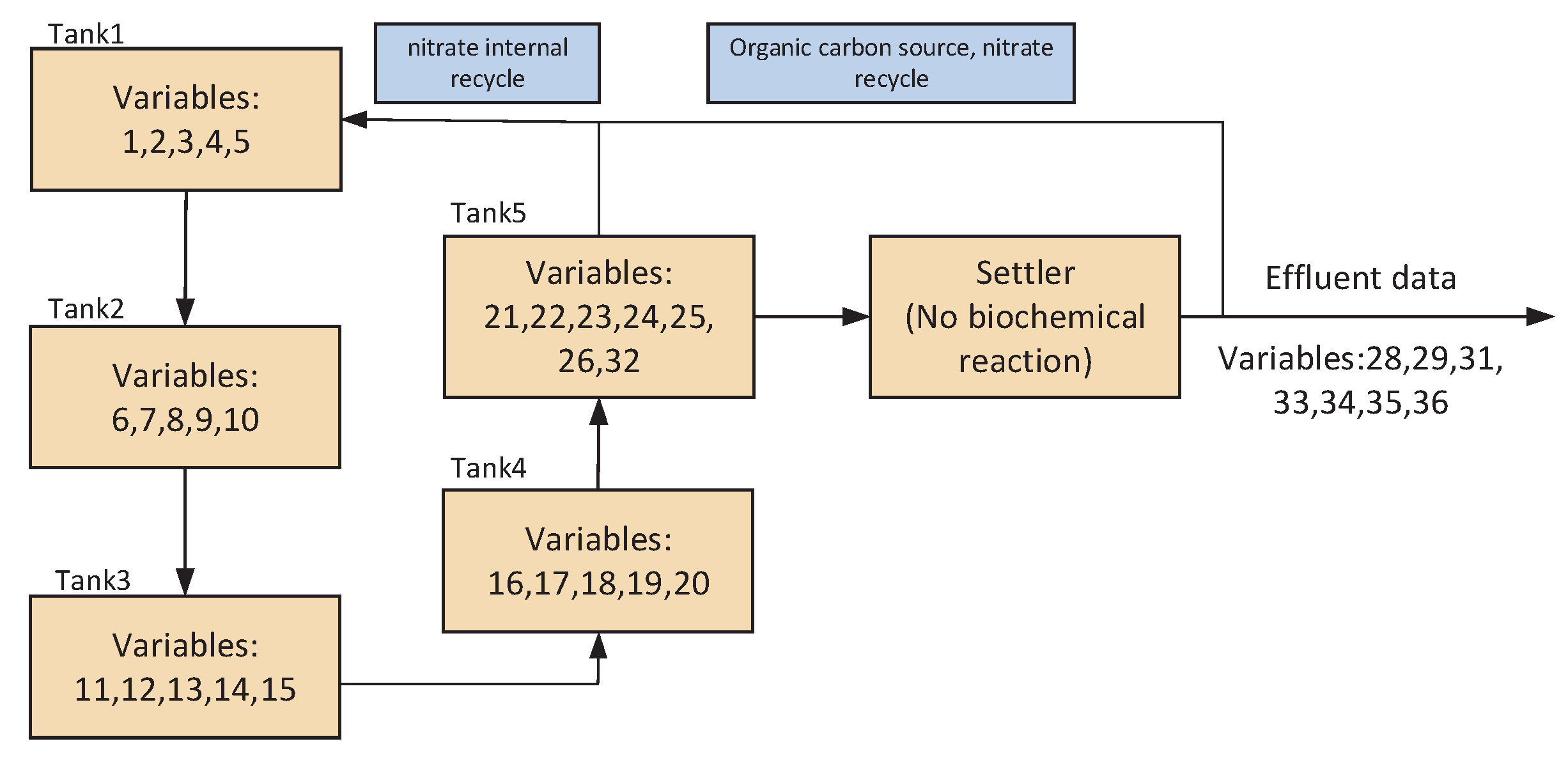


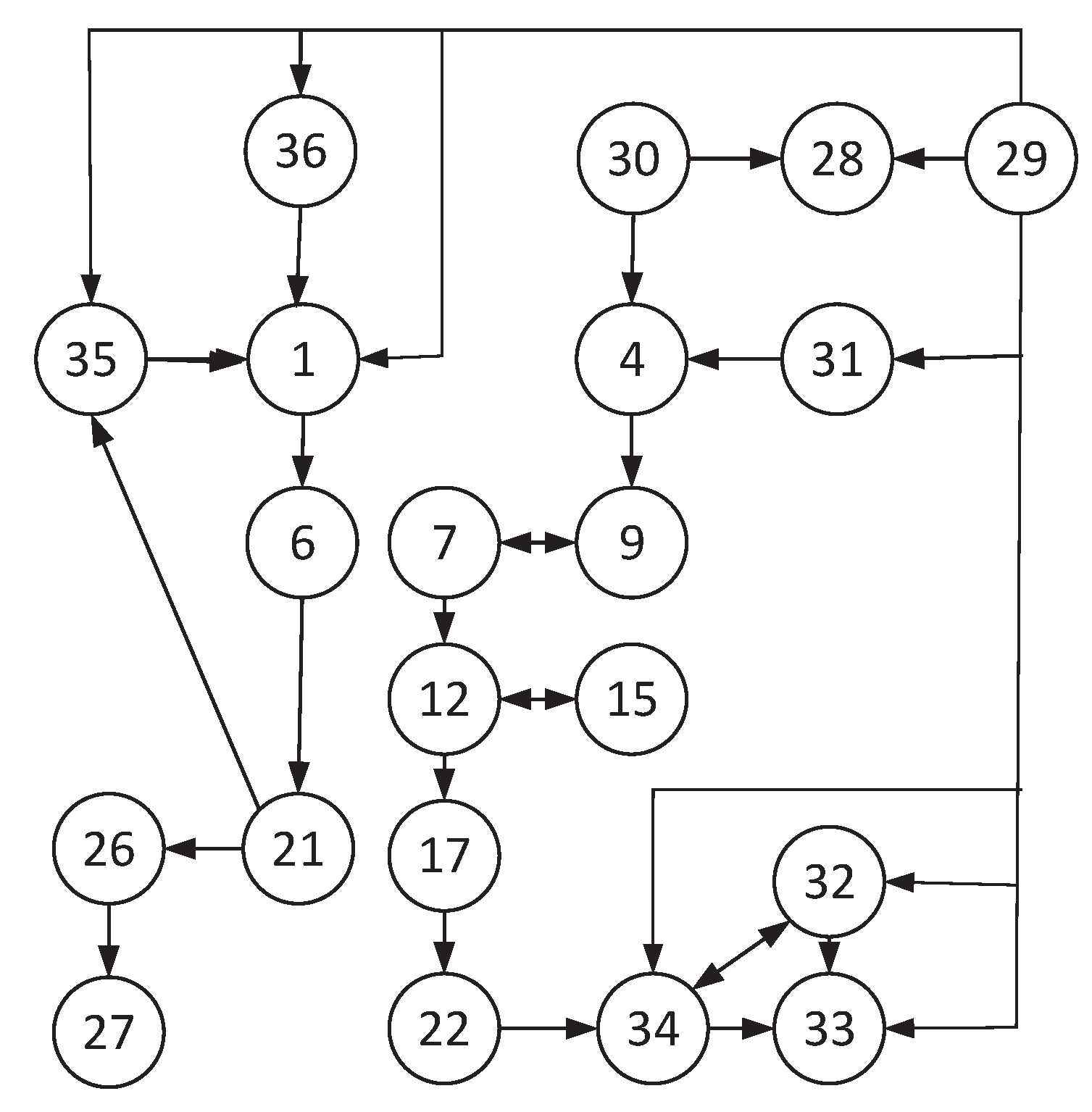

| Variable Number | Variable Name |
|---|---|
| 1, 6, 11, 16, 21 | Dissolved oxygen concentration of Tanks 1–5 |
| 2, 7, 12, 17, 22 | Nitrate and nitrite concentrations of Tanks 1–5 |
| 3, 8, 13, 18, 23 | Concentration of Tanks 1–5 |
| 4, 9, 14, 19, 24 | Soluble biodegradable organic nitrogen of Tanks 1–5 |
| 5, 10, 15, 20, 25 | Granular biodegradable organic nitrogen of Tanks 1–5 |
| 26 | Aeration intensity of fifth reaction tank |
| 27 | Aeration energy consumption, |
| 28 | Pump energy consumption, |
| 29 | Effluent speed |
| 30 | Internal reflux speed |
| 31 | Soluble biodegradable organic nitrogen in effluent |
| 32 | Effluent concentration of |
| 33 | Effluent Kjeldahl nitrogen concentration |
| 34 | Effluent concentration of nitrate and nitrite |
| 35 | Effluent concentration of dissolved oxygen |
| 36 | Effluent particulate biodegradable organic nitrogen |
| Grades | Accuracy of Proposed Method | Accuracy of Simple CCA | Accuracy of Simple SFA |
|---|---|---|---|
| grade good | 0.9896 | 0.9170 | 0.9010 |
| grade medium | 0.7601 | 0.6701 | 0.6963 |
| grade poor | 0.8741 | 0.8636 | 0.8601 |
| Variables | Initial Probability | Updated Probability | Difference |
|---|---|---|---|
| 0.6073 | 0.6076 | 0.0003 | |
| 0.8300 | 0.9943 | 0.1643 | |
| 0.7045 | 0.8392 | 0.1347 | |
| 0.7045 | 1 | 0.2955 | |
| 0.0081 | 0.8392 | 0.8311 | |
| 0.0081 | 0.8392 | 0.8311 | |
| 0.0081 | 0 | −0.0081 | |
| 0.3401 | 0.3401 | 0 | |
| 0.0081 | 0 | −0.0081 |
| Variables | Initial Probability | Updated Probability | Difference |
|---|---|---|---|
| 0.8178 | 0.9966 | 0.1788 | |
| 0.8178 | 0.9966 | 0.1788 | |
| 0.7585 | 0.9730 | 0.2145 | |
| 0.5424 | 0.6434 | 0.1010 | |
| 0.8178 | 0.9897 | 0.1719 | |
| 0.0127 | 0.0017 | −0.0110 | |
| 0.0042 | 0 | −0.0042 | |
| 0.1314 | 0.1433 | 0.0119 | |
| 0.7966 | 1 | 0.2034 | |
| 0.8263 | 1 | 0.1737 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Yang, D.; Peng, X.; Zhong, W.; Cheng, H. Causal Network Structure Learning Based on Partial Least Squares and Causal Inference of Nonoptimal Performance in the Wastewater Treatment Process. Processes 2022, 10, 909. https://doi.org/10.3390/pr10050909
Wang Y, Yang D, Peng X, Zhong W, Cheng H. Causal Network Structure Learning Based on Partial Least Squares and Causal Inference of Nonoptimal Performance in the Wastewater Treatment Process. Processes. 2022; 10(5):909. https://doi.org/10.3390/pr10050909
Chicago/Turabian StyleWang, Yuhan, Dan Yang, Xin Peng, Weimin Zhong, and Hui Cheng. 2022. "Causal Network Structure Learning Based on Partial Least Squares and Causal Inference of Nonoptimal Performance in the Wastewater Treatment Process" Processes 10, no. 5: 909. https://doi.org/10.3390/pr10050909
APA StyleWang, Y., Yang, D., Peng, X., Zhong, W., & Cheng, H. (2022). Causal Network Structure Learning Based on Partial Least Squares and Causal Inference of Nonoptimal Performance in the Wastewater Treatment Process. Processes, 10(5), 909. https://doi.org/10.3390/pr10050909