Numerical Simulations of a Postulated Methanol Pool Fire Scenario in a Ventilated Enclosure Using a Coupled FVM-FEM Approach
Abstract
:1. Introduction
2. Modeling and Simulation
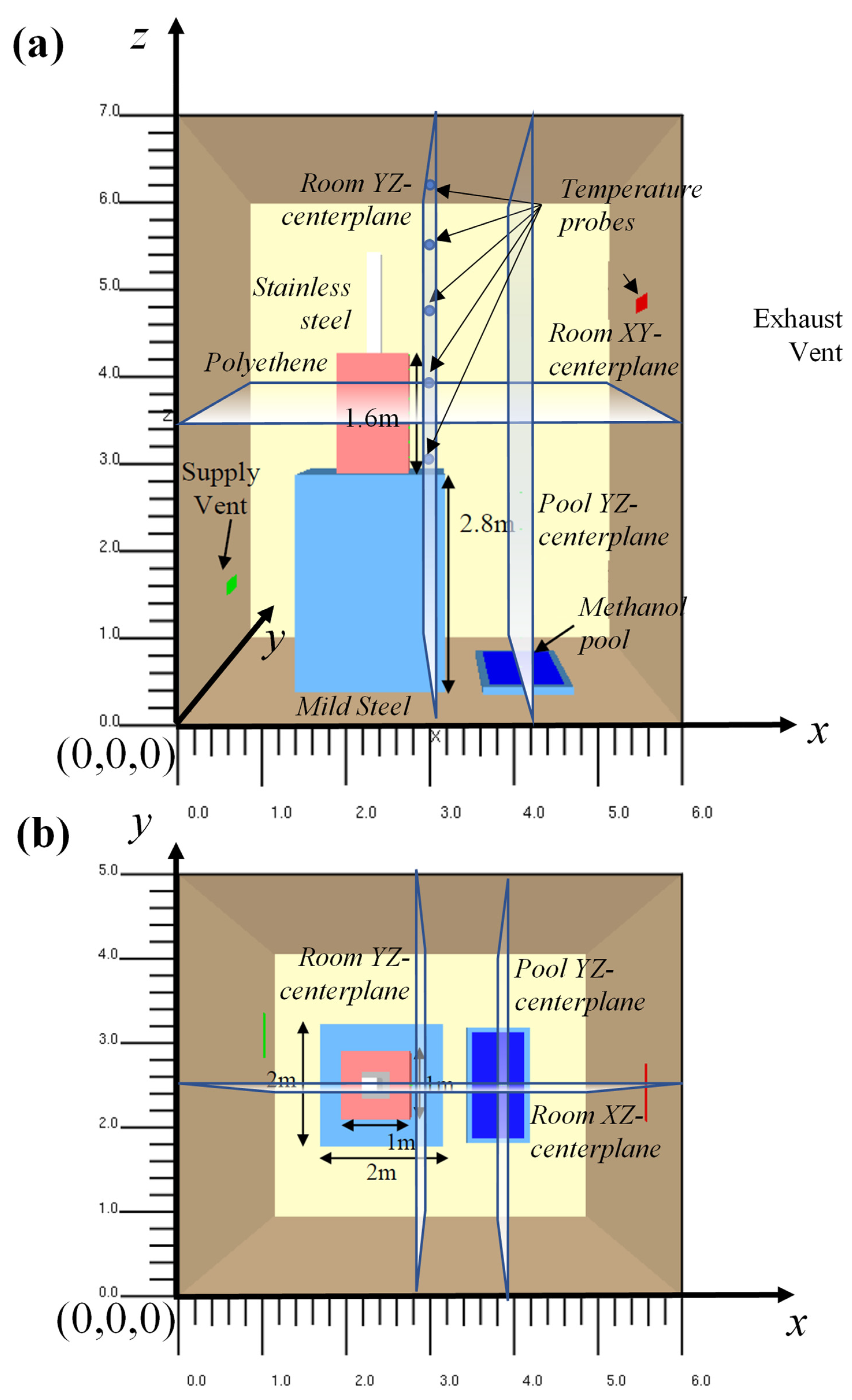
2.1. Problem Scenario
2.2. Model Description
2.3. Assessment Methodology
3. Governing Equations
3.1. Large Eddy Simulation (LES)
3.2. Fire Modeling
4. Validation of FDS
4.1. Geometry and Meshing
4.2. Boundary Conditions
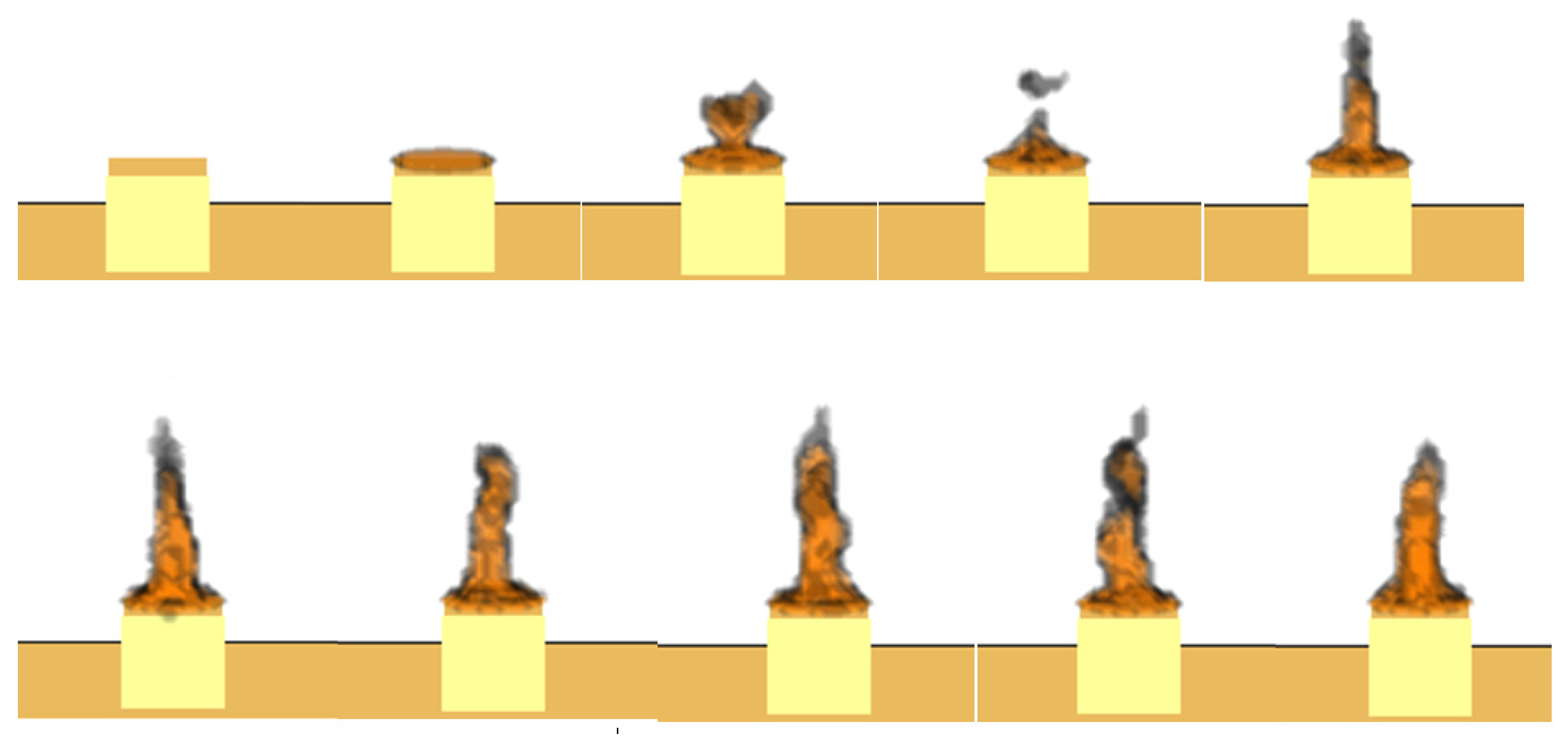
4.3. Fire Ignition
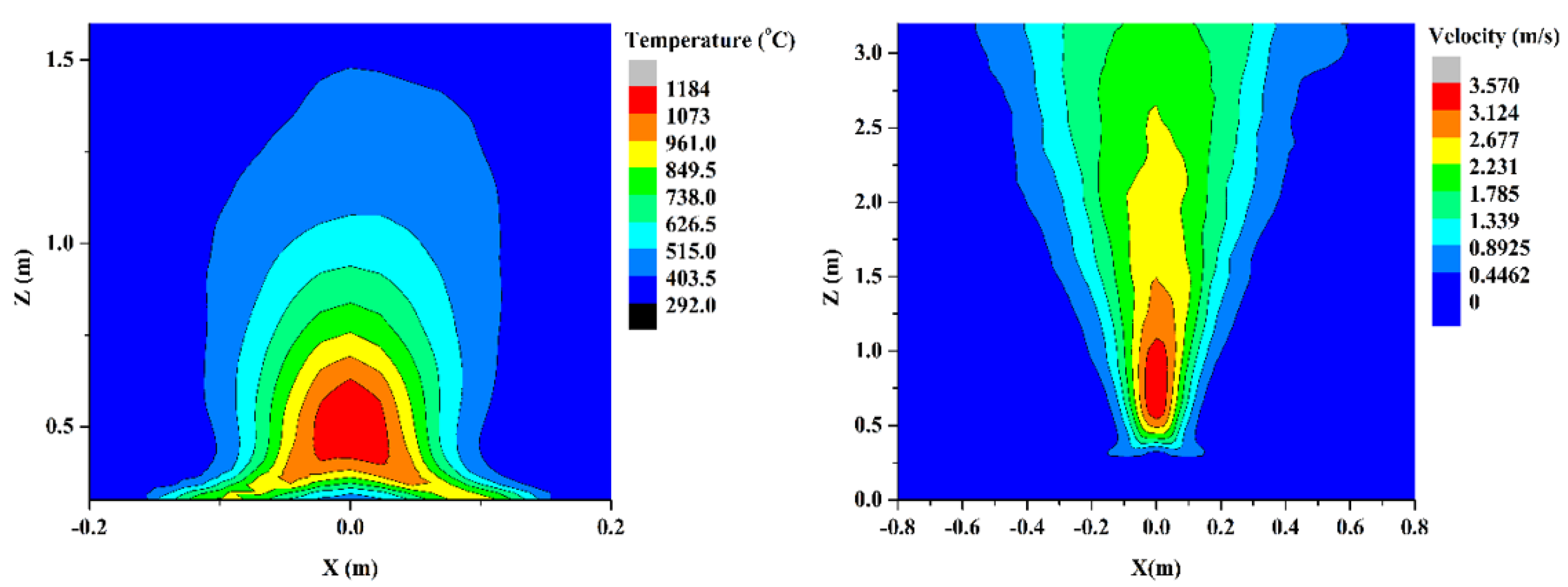
4.4. Velocity and Temperature Profiles
4.5. Sensitivity Analysis
5. Results and Discussion
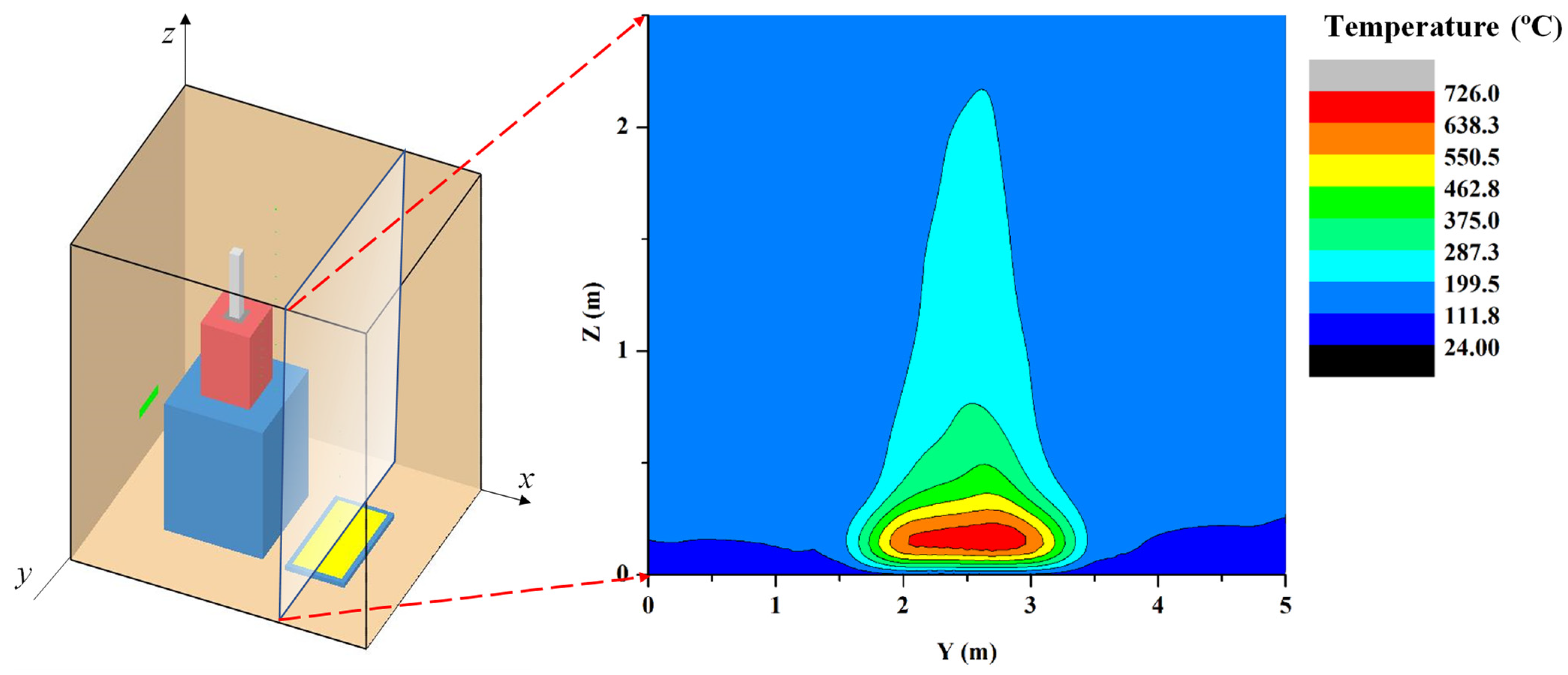
5.1. Results for the Postulated Scenario: Simulation I
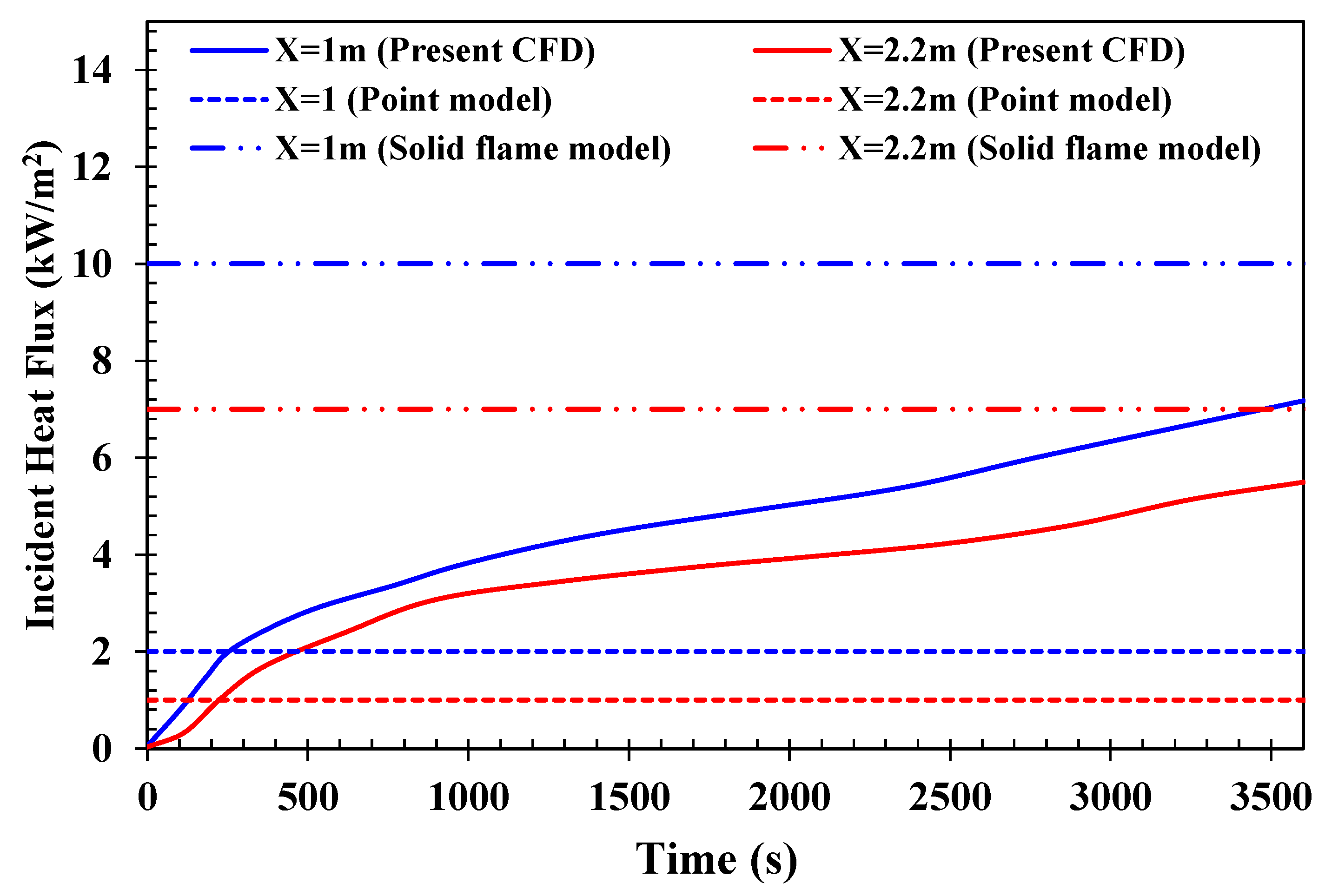
5.1.1. Incident Heat Flux
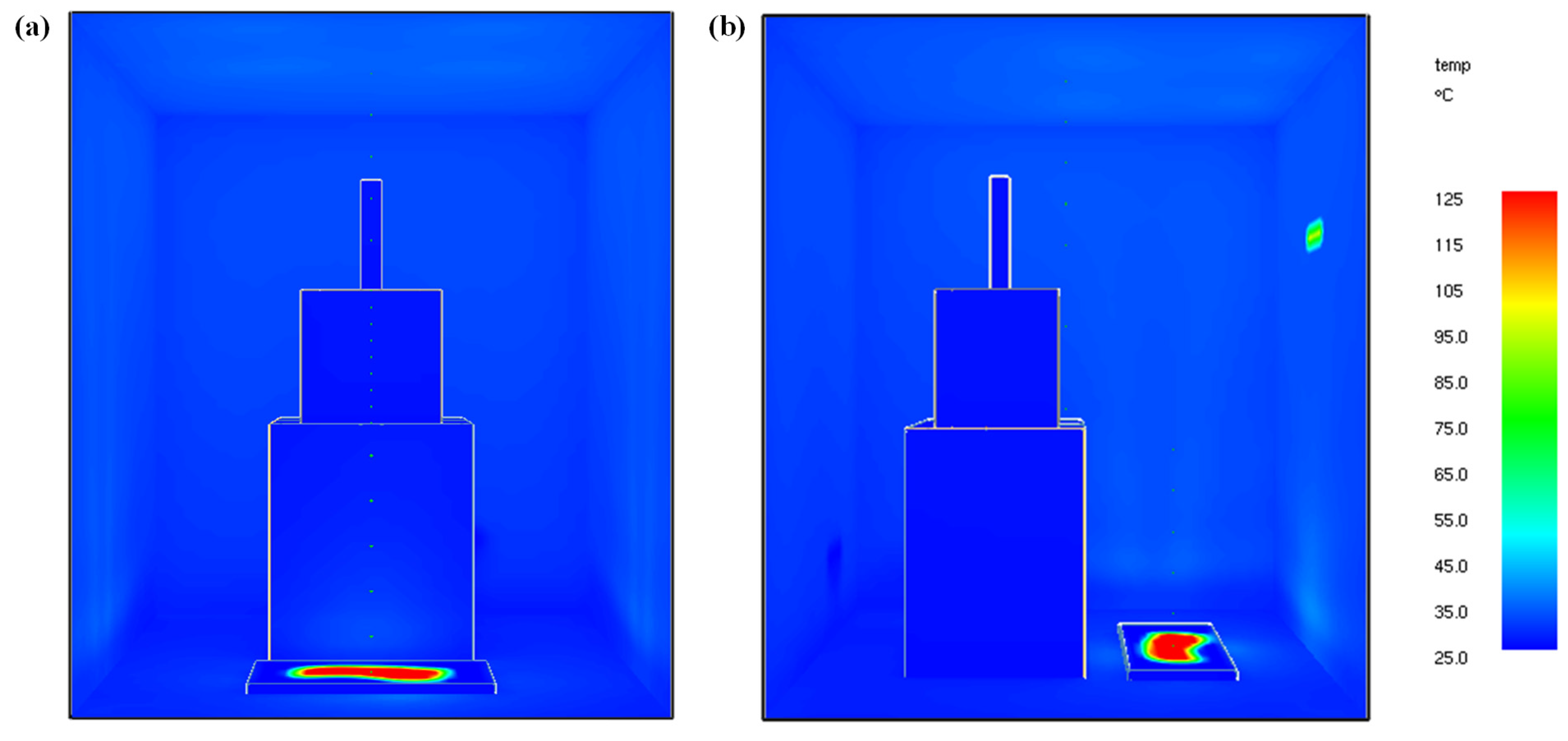
5.1.2. Enclosure Temperature
5.2. Results for the Postulated Scenario: Simulation II
5.2.1. Enclosure Temperature
5.2.2. Velocity Profile
5.2.3. Oxygen Availability
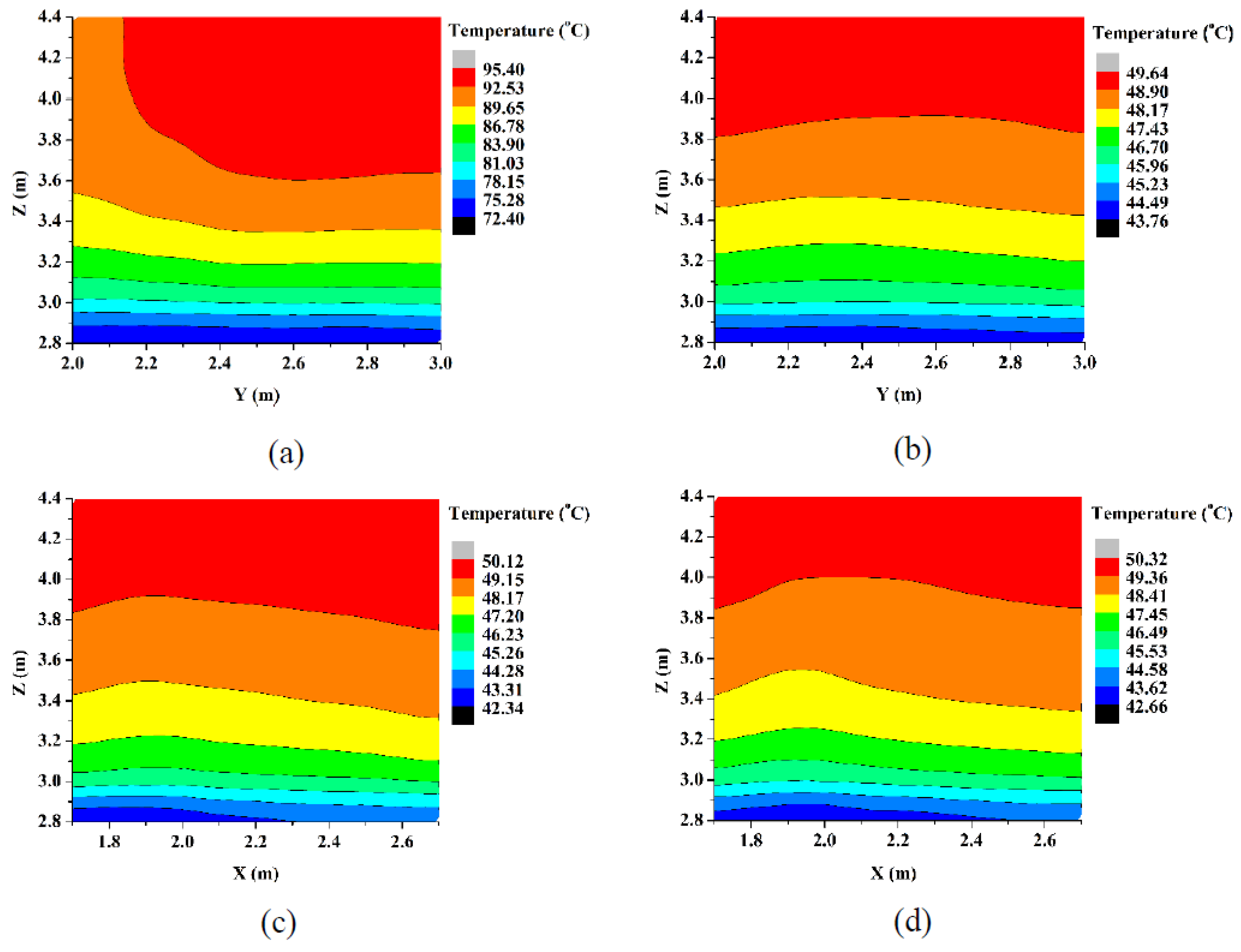
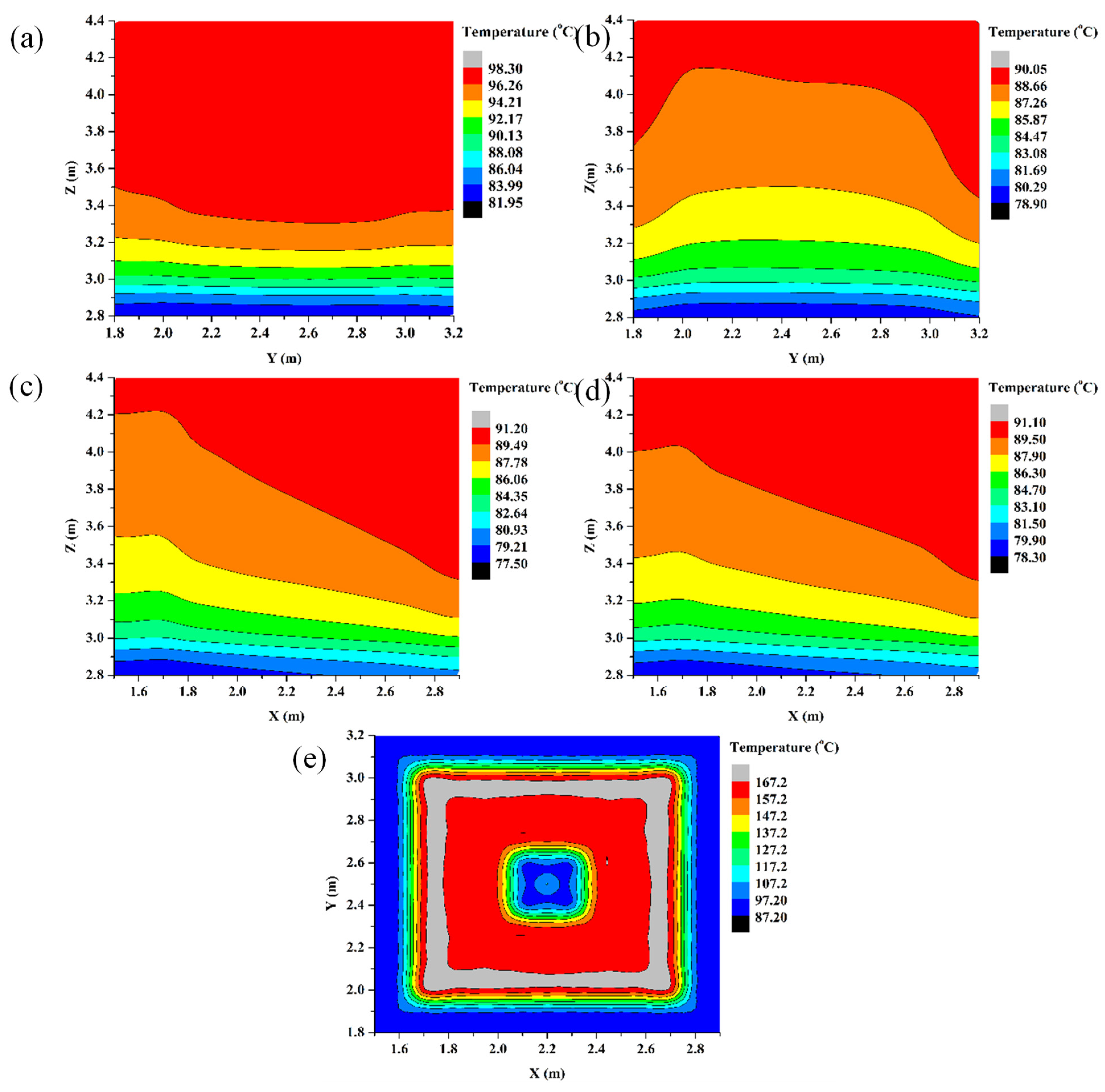
5.2.4. Vertical Temperature Profiles
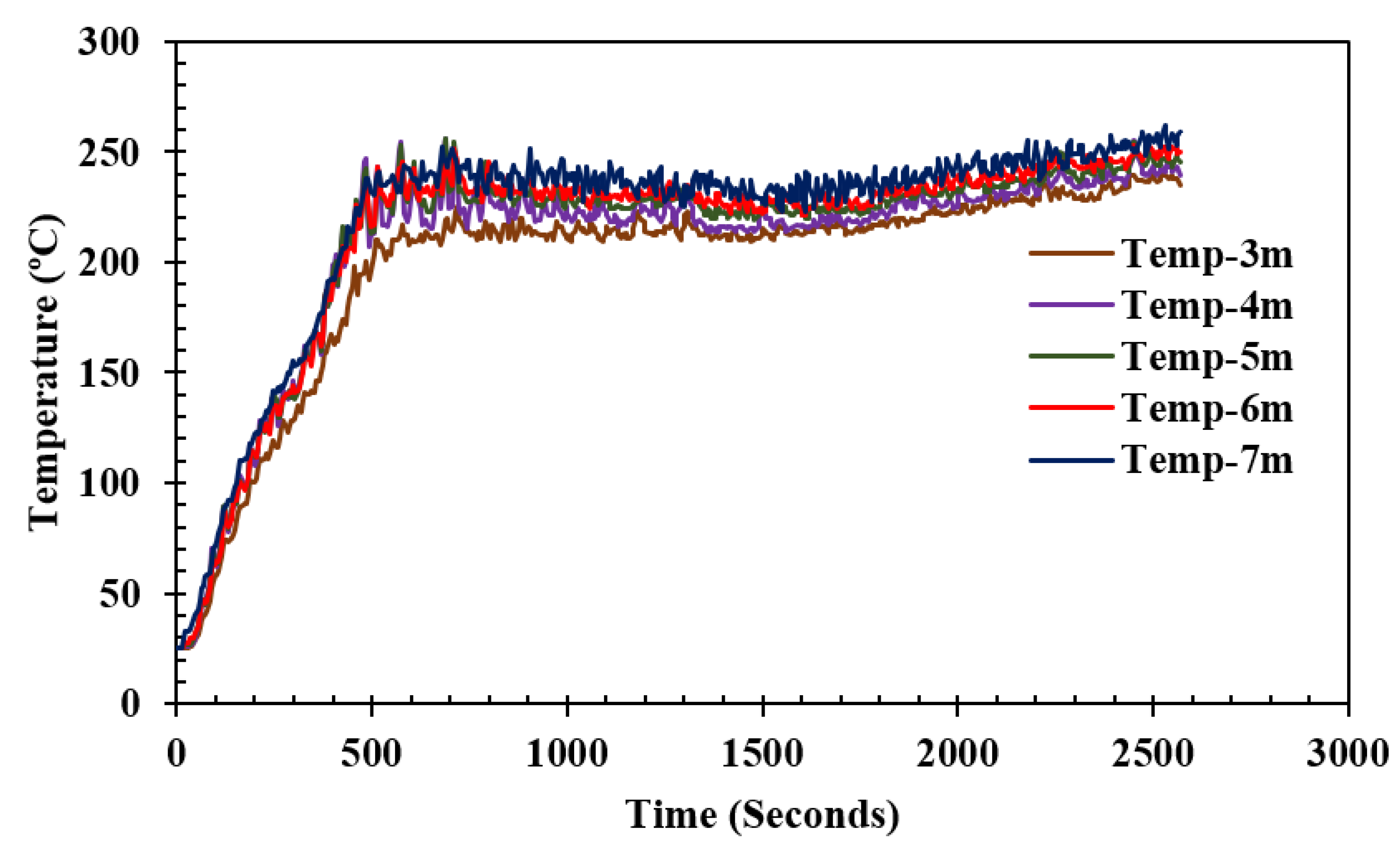
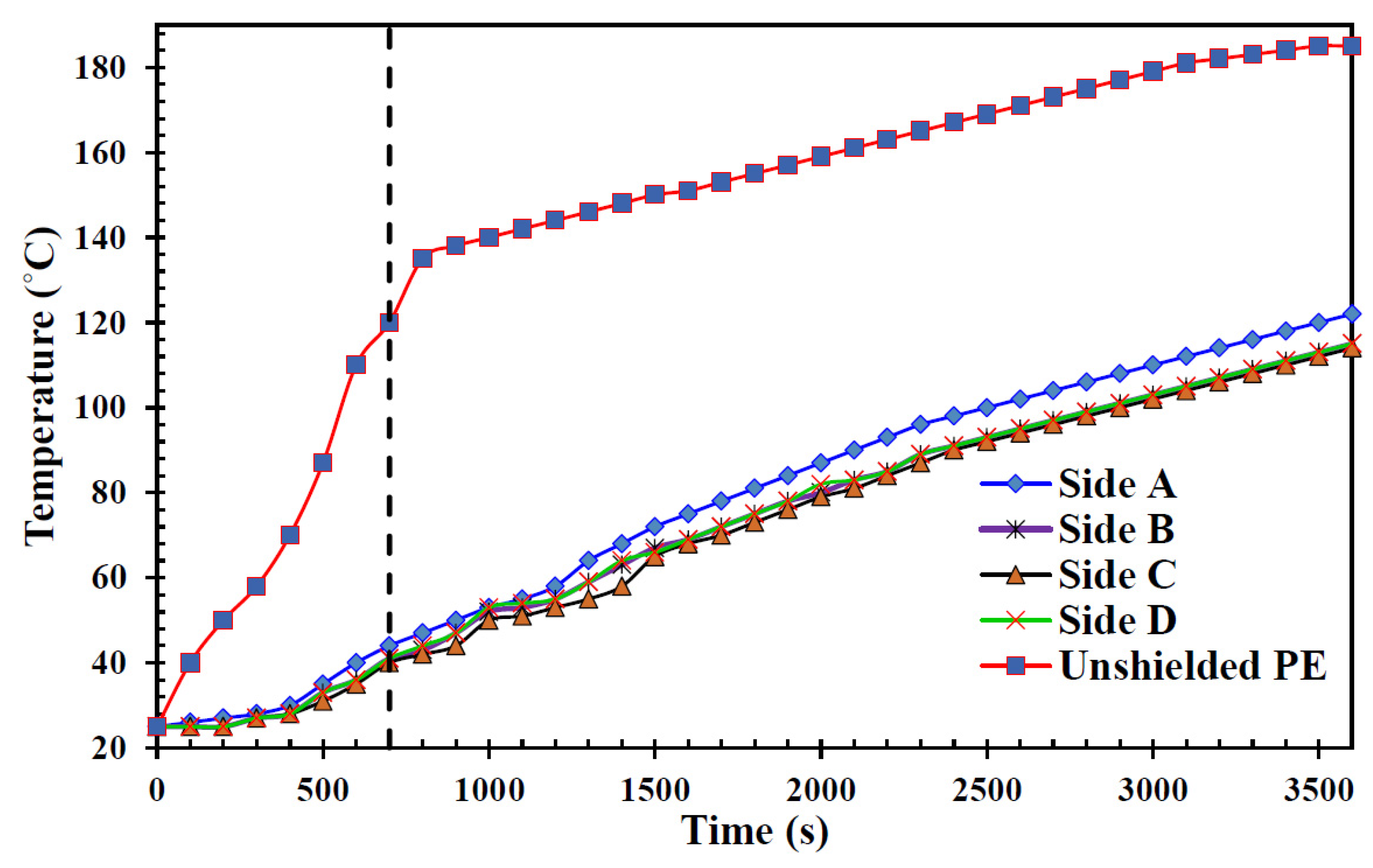
5.3. Temperatures on Each Side of the Shield
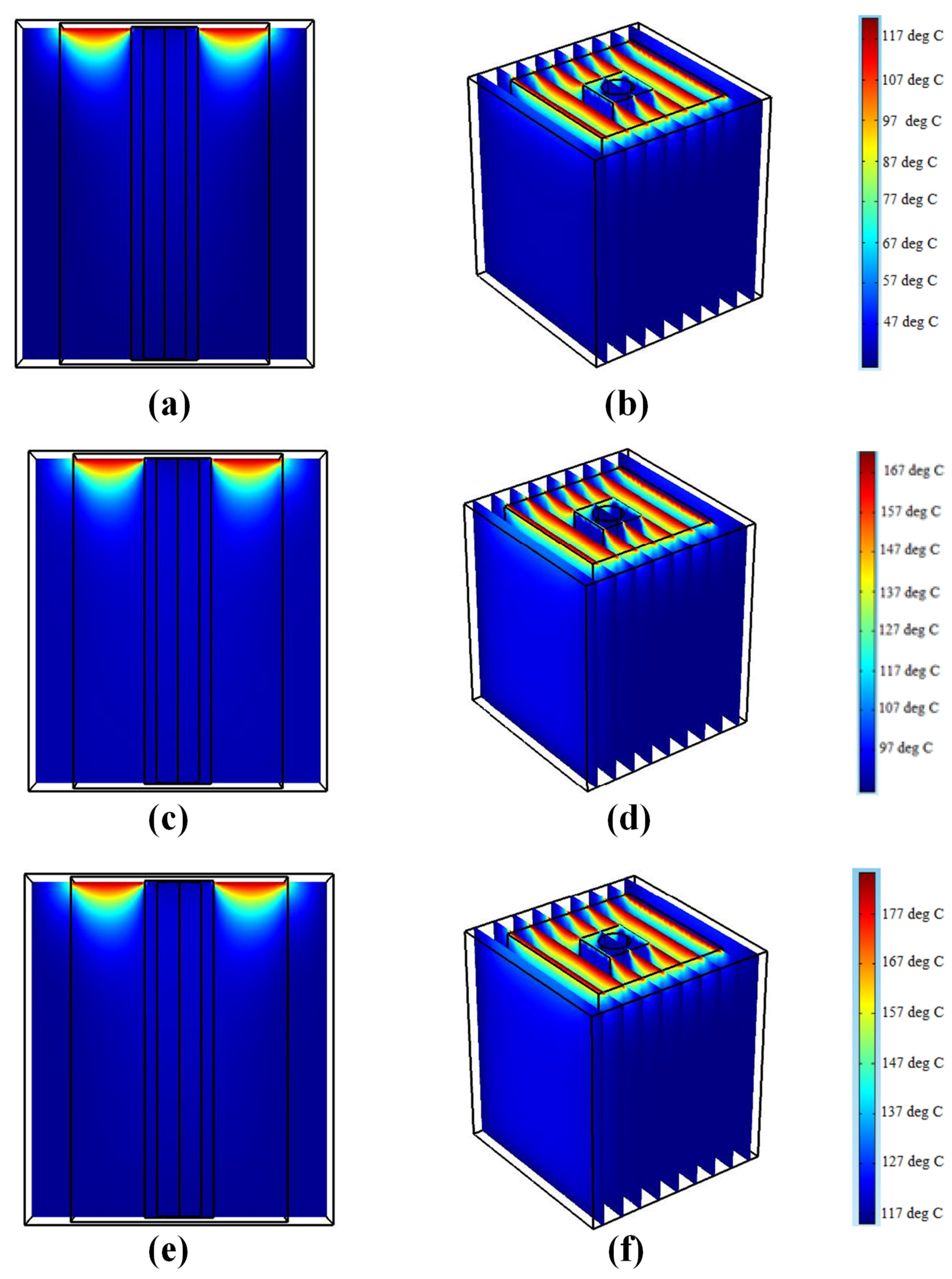
5.4. The Maximum Temperatures on the Shield
6. Conclusions
- Firstly, validation and corroboration studies were carried out for simulating methanol pool fires by comparing the results from the present large eddy simulations (carried out in Fire Dynamics Simulator) against experimental results from the literature. The predicted flame heights, centerline temperatures, and velocities are in good agreement with the experimental results.
- The validated mesh configuration was then used for simulating the postulated methanol pool fire scenario. The fire dynamics predicted from FDS were in line with the values obtained from empirical correlations.
- The predicted solid-body temperatures from FDS were used as input boundary conditions for FEM simulations which were then used for carrying out detailed three-dimensional heat transfer simulations to investigate the thermal conduction within the solid (mild steel and polyethylene shields).
- The proposed coupled FVM–FEM technique has been verified and tested in the present study. This technique will be helpful to practicing safety engineers and fire technologists to have a more detailed assessment of pool fires (considering all three modes of heat transfer) which will assist them in the safer design of rooms involving inflammable liquid inventories.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | pool area (m2) |
| total compartment interior surface area excluding area of vent openings (m2) | |
| total area of ventilation opening (m2) | |
| Smagorinsky Constant | |
| specific heat of ambient air at constant pressure (kJ/kg K) | |
| D | Pool diameter (m) |
| D* | characteristic fire diameter |
| Fr | Fire Froude number |
| f | external forces |
| g | acceleration due to gravity (m/s2) |
| heat of combustion (kJ/kg) | |
| effective heat of combustion (kJ/kg) | |
| heat of gasification (kJ/kg) | |
| compartment height (m) | |
| heat of formation of the burning material (kJ/kg) | |
| k | extinction coefficient (m−1) |
| kSGS | sub-grid scale turbulent kinetic energy |
| L | mean flame height (m) |
| compartment length (m) | |
| mass burning rate/mass loss rate of the fuel (kg/m2 s) | |
| gas mass flow rate out of the ventilation (kg/s) | |
| is mass burning rate for very large pool (kg/m2 s) | |
| mass production rate of the species α per unit volume | |
| heat release rate (kW) | |
| heat release rate of the pool (kW/m2) | |
| heat release rate per unit area (kW/m2) | |
| heat release rate per unit volume (kW/m3) | |
| radiant heat flux absorbed by the pool (kW/m2) | |
| convective heat flux to the pool (kW/m2) | |
| heat flux reradiated from the surface of the pool (kW/m2) | |
| wall conduction losses (kW/m2) | |
| heat release rate per unit volume (kW/m2) | |
| is the filtered strain rate | |
| strain rate tensor | |
| T | temperature (K) |
| centreline temperature (K) | |
| ambient temperature (K) | |
| hot gas layer temperature (K) | |
| t | time (s) |
| u | x-component of velocity (m/s) |
| average value of u at the grid cell center | |
| weighted average value of u over the adjacent cells | |
| dimensionless wind speed | |
| wind speed (m/s) | |
| centreline velocity (m/s) | |
| spatially filtered u velocity | |
| time-averaged u velocity | |
| turbulent component of velocity after time-averaging | |
| V | velocity magnitude (m/s) |
| v | y-component of velocity (m/s) |
| w | z-component of velocity (m/s) |
| compartment width (m) | |
| z | vertical distance from point source (m) |
| virtual origin (m) | |
| Stefan–Boltzmann’s constant | |
| mean beam length corrector | |
| Δ x, Δy and Δz | the grid sizes along the x, y and z directions |
| Δ | cut-off width used to filter out the eddies in LES |
| any flow variable in a turbulent field | |
| sub-grid scale eddy viscosity in LES | |
| eddy viscosity in RANS | |
| Reynolds stress | |
| spatially filtered stress tensor | |
| time-averaged stress tensor | |
| sub-grid-scale stress tensor | |
| ambient air density (1.18 kg/m3) |
References
- Vílchez, J.A.; Sevilla, S.; Montiel, H.; Casal, J. Historical Analysis of Accidents in Chemical Plants and in the Transportation of Hazardous Materials. J. Loss Prev. Process Ind. 1995, 8, 87–96. [Google Scholar] [CrossRef]
- Planas-Cuchi, E.; Montiel, H.; Casal, J. A Survey of the Origin, Type and Consequences of Fire Accidents in Process Plants and in the Transportation of Hazardous Materials. Process Saf. Environ. Prot. 1997, 75, 3–8. [Google Scholar] [CrossRef] [Green Version]
- Casal Fàbrega, J.; Gómez-Mares, M.; Muñoz, M.Á.; Palacios, A. Jet Fires: A “Minor” Major Accident? Chem. Eng. Trans. 2012, 26, 13–20. [Google Scholar] [CrossRef]
- Freeman, R.A. CCPS Guidelines for Chemical Process Quantitative Risk Analysis. Plant/Oper. Prog. 1990, 9, 231–235. [Google Scholar] [CrossRef]
- Sajid, Z.; Khan, M.K.; Rahnama, A.; Moghaddam, F.S.; Vardhan, K.; Kalani, R. Computational Fluid Dynamics (CFD) Modeling and Analysis of Hydrocarbon Vapor Cloud Explosions (VCEs) in Amuay Refinery and Jaipur Plant Using FLACS. Processes 2021, 9, 960. [Google Scholar] [CrossRef]
- Parihar, R. 12 Dead, over 200 Injured in Indian Oil Depot Fire in Jaipur. Available online: https://www.indiatoday.in/india/story/12-dead-over-200-injured-in-indian-oil-depot-fire-in-jaipur-59623-2009-10-29 (accessed on 22 December 2020).
- Gai, G.; Cancelliere, P. Design of a Pressurized Smokeproof Enclosure: CFD Analysis and Experimental Tests. Safety 2017, 3, 13. [Google Scholar] [CrossRef] [Green Version]
- Hehnen, T.; Arnold, L.; La Mendola, S. Numerical Fire Spread Simulation Based on Material Pyrolysis—An Application to the CHRISTIFIRE Phase 1 Horizontal Cable Tray Tests. Fire 2020, 3, 33. [Google Scholar] [CrossRef]
- Beyler, C.L. Fire hazard calculations for large, open hydrocarbon fires. In SFPE Handbook of Fire Protection Engineering; Hurley, M.J., Gottuk, D., Hall, J.R., Harada, K., Kuligowski, E., Puchovsky, M., Torero, J., Watts, J.M., Wieczorek, C., Eds.; Springer: New York, NY, USA, 2016; pp. 2591–2663. ISBN 978-1-4939-2565-0. [Google Scholar]
- Ganju, S.; Karanam, A.; Mishra, S.; Saha, N.; Gera, B.; Goyal, P.; Sharma, P.K.; Shelke, A.V. Application of CFD for assessment of containment safety. In Advances of Computational Fluid Dynamics in Nuclear Reactor Design and Safety Assessment; Elsevier: Amsterdam, The Netherlands, 2019; pp. 567–662. [Google Scholar]
- Sharma, P.K. Modeling of fire with CFD for nuclear power plants (NPPs). In Advances of Computational Fluid Dynamics in Nuclear Reactor Design and Safety Assessment; Woodhead Publishing: Sawston, UK, 2019; pp. 663–727. [Google Scholar]
- Woo, D.; Seo, J.K. Numerical Validation of the Two-Way Fluid-Structure Interaction Method for Non-Linear Structural Analysis under Fire Conditions. J. Mar. Sci. Eng. 2021, 9, 400. [Google Scholar] [CrossRef]
- Husain, Z.; Tiwari, S.S.; Pandit, A.B.; Joshi, J.B. Computational Fluid Dynamics Study of Biomass Cook Stove—Part 1: Hydrodynamics and Homogeneous Combustion. Ind. Eng. Chem. Res. 2020, 59, 4161–4176. [Google Scholar] [CrossRef]
- Husain, Z.; Tiwari, S.S.; Kataria, A.; Mathpati, C.S.; Pandit, A.B.; Joshi, J.B. Computational Fluid Dynamic Study of Biomass Cook Stove—Part 2: Devolatilization and Heterogeneous Combustion. Ind. Eng. Chem. Res. 2020, 59, 14507–14521. [Google Scholar] [CrossRef]
- Tiwari, M.K.; Gupta, A.; Kumar, R.; Mishra, R.K.; Chaudhary, A.; Sharma, P.K. Experimental Study on Elevated Methanol Pool Fires in a Compartment. Lect. Notes Mech. Eng. 2021, 29, 473–479. [Google Scholar] [CrossRef]
- Muñoz, M.; Arnaldos, J.; Casal, J.; Planas, E. Analysis of the Geometric and Radiative Characteristics of Hydrocarbon Pool Fires. Combust. Flame 2004, 139, 263–277. [Google Scholar] [CrossRef]
- Weckman, E.J.; Strong, A.B. Experimental Investigation of the Turbulence Structure of Medium-Scale Methanol Pool Fires. Combust. Flame 1996, 105, 245–266. [Google Scholar] [CrossRef]
- Chatris, J.M.; Quintela, J.; Folch, J.; Planas, E.; Arnaldos, J.; Casal, J. Experimental Study of Burning Rate in Hydrocarbon Pool Fires. Combust. Flame 2001, 126, 1373–1383. [Google Scholar] [CrossRef]
- Hamins, A.; Johnsson, E.; Donnelly, M.; Maranghides, A. Energy Balance in a Large Compartment Fire. Fire Saf. J. 2008, 43, 180–188. [Google Scholar] [CrossRef]
- Mosisa Wako, F.; Pio, G.; Salzano, E. Reduced Combustion Mechanism for Fire with Light Alcohols. Fire 2021, 4, 86. [Google Scholar] [CrossRef]
- Wen, J.X.; Kang, K.; Donchev, T.; Karwatzki, J.M. Validation of FDS for the Prediction of Medium-Scale Pool Fires. Fire Saf. J. 2007, 42, 127–138. [Google Scholar] [CrossRef]
- Chun, H.; Wehrstedt, K.-D.; Vela, I.; Schönbucher, A. Thermal Radiation of Di-Tert-Butyl Peroxide Pool Fires—Experimental Investigation and CFD Simulation. J. Hazard. Mater. 2009, 167, 105–113. [Google Scholar] [CrossRef]
- Chung, W. A CFD Investigation of Turbulent Buoyant Helium Plumes. Master’s Thesis, Applied Science in Mechanical Engineering, University of Waterloo, Waterloo, ON, Canada, 2007. [Google Scholar]
- Vasanth, S.; Tauseef, S.M.; Abbasi, T.; Abbasi, S.A. Assessment of Four Turbulence Models in Simulation of Large-Scale Pool Fires in the Presence of Wind Using Computational Fluid Dynamics (CFD). J. Loss Prev. Process Ind. 2013, 26, 1071–1084. [Google Scholar] [CrossRef]
- Tomaskova, M.; Pokorny, J.; Kucera, P.; Balazikova, M.; Marasova, D. Fire Models as a Tool for Evaluation of Energy Balance in Burning Space Relating to Building Structures. Appl. Sci. 2022, 12, 2505. [Google Scholar] [CrossRef]
- Lenz, S.; Geier, M.; Krafczyk, M. Simulation of Fire with a Gas Kinetic Scheme on Distributed GPGPU Architectures. Computation 2020, 8, 50. [Google Scholar] [CrossRef]
- Moon, M.-H.; Kim, H.-J.; Min, S.-G.; Kim, S.-C.; Park, W.-J. Simulation of Indoor Fire Dynamics of Residential Buildings with Full-Scale Fire Test. Sustainability 2021, 13, 4897. [Google Scholar] [CrossRef]
- Salamonowicz, Z.; Krauze, A.; Majder-Lopatka, M.; Dmochowska, A.; Piechota-Polanczyk, A.; Polanczyk, A. Numerical Reconstruction of Hazardous Zones after the Release of Flammable Gases during Industrial Processes. Processes 2021, 9, 307. [Google Scholar] [CrossRef]
- McGrattan, K.; Hostikka, S.; McDermott, R.; Floyd, J.; Vanella, M.; Weinschenk, C.; Overholt, K. Fire Dynamics Simulator User’s Guide; NIST Special Publication 1019; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2019. [Google Scholar]
- Fraga, G.C.; Centeno, F.R.; Petry, A.P.; Coelho, P.J.; França, F.H.R. On the Individual Importance of Temperature and Concentration Fluctuations in the Turbulence-Radiation Interaction in Pool Fires. Int. J. Heat Mass Transf. 2019, 136, 1079–1089. [Google Scholar] [CrossRef]
- Ma, L.; Nmira, F.; Consalvi, J.-L. Large Eddy Simulation of Medium-Scale Methanol Pool Fires—Effects of Pool Boundary Conditions. Combust. Flame 2020, 222, 336–354. [Google Scholar] [CrossRef]
- Xu, B.; Wen, J. The Effect of Convective Motion within Liquid Fuel on the Mass Burning Rates of Pool Fires—A Numerical Study. Proc. Combust. Inst. 2021, 38, 4979–4986. [Google Scholar] [CrossRef]
- Yang, D.; Hu, L.H.; Jiang, Y.Q.; Huo, R.; Zhu, S.; Zhao, X.Y. Comparison of FDS Predictions by Different Combustion Models with Measured Data for Enclosure Fires. Fire Saf. J. 2010, 45, 298–313. [Google Scholar] [CrossRef]
- Vasanth, S.; Tauseef, S.M.; Abbasi, T.; Abbasi, S.A. CFD Simulation of Pool Fires Situated at Differing Elevation. Process Saf. Environ. Prot. 2015, 94, 89–95. [Google Scholar] [CrossRef]
- Jain, S.; Kumar, S.; Kumar, S.; Sharma, T.P. Numerical Simulation of Fire in a Tunnel: Comparative Study of CFAST and CFX Predictions. Tunn. Undergr. Space Technol. 2008, 23, 160–170. [Google Scholar] [CrossRef]
- Vasanth, S.; Tauseef, S.M.; Abbasi, T.; Abbasi, S.A. Simulation of Multiple Pool Fires Involving Two Different Fuels. J. Loss Prev. Process Ind. 2017, 48, 289–296. [Google Scholar] [CrossRef]
- Chen, Z.; Wen, J.; Xu, B.; Dembele, S. Large Eddy Simulation of a Medium-Scale Methanol Pool Fire Using the Extended Eddy Dissipation Concept. Int. J. Heat Mass Transf. 2014, 70, 389–408. [Google Scholar] [CrossRef]
- Sengupta, A. Optimal Safe Layout of Fuel Storage Tanks Exposed to Pool Fire: One Dimensional Deterministic Modelling Approach. Fire Technol. 2019, 55, 1771–1799. [Google Scholar] [CrossRef]
- Sengupta, A.; Gupta, A.K.; Mishra, I.M. Engineering Layout of Fuel Tanks in a Tank Farm. J. Loss Prev. Process Ind. 2011, 24, 568–574. [Google Scholar] [CrossRef]
- Bale, S.; Tiwari, S.; Sathe, M.; Berrouk, A.S.; Nandakumar, K.; Joshi, J. Direct Numerical Simulation Study of End Effects and D/d Ratio on Mass Transfer in Packed Beds. Int. J. Heat Mass Transf. 2018, 127, 234–244. [Google Scholar] [CrossRef]
- Bale, S.; Tiwari, S.S.; Nandakumar, K.; Joshi, J.B. Effect of Schmidt Number and D/d Ratio on Mass Transfer through Gas-Solid and Liquid-Solid Packed Beds: Direct Numerical Simulations. Powder Technol. 2019, 354, 529–539. [Google Scholar] [CrossRef]
- Joshi, J.B.; Nandakumar, K.; Patwardhan, A.W.; Nayak, A.K.; Pareek, V.K.; Gumulya, M.M.; Wu, C.; Minocha, N.; Pal, E.; Kumar, M.; et al. Computational fluid dynamics. In Advances of Computational Fluid Dynamics in Nuclear Reactor Design and Safety Assessment; Woodhead Publishing: Cambridge, MA, USA, 2019; pp. 21–238. ISBN 978-0-08-102338-9. [Google Scholar]
- Tiwari, S.S.; Pal, E.; Bale, S.; Minocha, N.; Patwardhan, A.W.; Nandakumar, K.; Joshi, J.B. Flow Past a Single Stationary Sphere, 1. Experimental and Numerical Techniques. Powder Technol. 2020, 365, 115–148. [Google Scholar] [CrossRef]
- Tiwari, S.S.; Pal, E.; Bale, S.; Minocha, N.; Patwardhan, A.W.; Nandakumar, K.; Joshi, J.B. Flow Past a Single Stationary Sphere, 2. Regime Mapping and Effect of External Disturbances. Powder Technol. 2020, 365, 215–243. [Google Scholar] [CrossRef]
- Gajbhiye, B.D.; Kulkarni, H.A.; Tiwari, S.S.; Mathpati, C.S. Teaching Turbulent Flow through Pipe Fittings Using Computational Fluid Dynamics Approach. Eng. Rep. 2020, 2, e12093. [Google Scholar] [CrossRef] [Green Version]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Ghosal, S.; Moin, P. The Basic Equations for the Large Eddy Simulation of Turbulent Flows in Complex Geometry. J. Comput. Phys. 1995, 118, 24–37. [Google Scholar] [CrossRef]
- Deardorff, J.W. A Numerical Study of Three-Dimensional Turbulent Channel Flow at Large Reynolds Numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Siddapureddy, S.; Wehrstedt, K.-D.; Prabhu, S.V. Heat Transfer to Bodies Engulfed in Di-Tert-Butyl Peroxide Pool Fires—Numerical Simulations. J. Loss Prev. Process Ind. 2016, 44, 204–211. [Google Scholar] [CrossRef]
- Fernandes Oliveira, R.L.; Doubek, G.; Vianna, S.S.V. On the Behaviour of the Temperature Field around Pool Fires in Controlled Experiment and Numerical Modelling. Process Saf. Environ. Prot. 2019, 123, 358–369. [Google Scholar] [CrossRef]
- Pio, G.; Carboni, M.; Iannaccone, T.; Cozzani, V.; Salzano, E. Numerical Simulation of Small-Scale Pool Fires of LNG. J. Loss Prev. Process Ind. 2019, 61, 82–88. [Google Scholar] [CrossRef]
- Ahmadi, O.; Mortazavi, S.B.; Pasdarshahri, H.; Mohabadi, H.A. Consequence Analysis of Large-Scale Pool Fire in Oil Storage Terminal Based on Computational Fluid Dynamic (CFD). Process Saf. Environ. Prot. 2019, 123, 379–389. [Google Scholar] [CrossRef]
- Drysdale, D. An Introduction to Fire Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hodgman, C.D. CRC Handbook of Chemistry and Physics; CRC Press: Cleveland, OH, USA, 1978. [Google Scholar]
- Wood, W. DMIC Report 177: Thermal Radiative Properties of Selected Materials; Battelle Memorial Institute, Defense Metals Information Center: Columbus, OH, USA, 1962. [Google Scholar]
- Gubareff, G.G.; Janssen, J.E.; Torborg, R.H. Thermal Radiation Properties Survey: A Review of the Literature; Honeywell Research Center, Minneapolis-Honeywell Regulator Company: Minneapolis, MN, USA, 1960. [Google Scholar]
- Grooshandler, W.L. Radcal—A Narrow-Band Model for Radiation Calculations in a Combustion Environment. 1993. Available online: https://www.govinfo.gov/app/details/https%3A%2F%2Fwww.govinfo.gov%2Fapp%2Fdetails%2FGOVPUB-C13-d0301b96642f0167a45468dd42912cd7 (accessed on 17 April 2022).
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Torero, J.L.; Watts, J.M., Jr.; Wieczorek, C.J. (Eds.) SFPE Handbook of Fire Protection Engineering, 5th ed.; Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Peatross, M.J.; Beyler, C.L. Ventilation Effects on Compartment Fire Characterization. Fire Saf. Sci. 1997, 5, 403–414. [Google Scholar] [CrossRef] [Green Version]

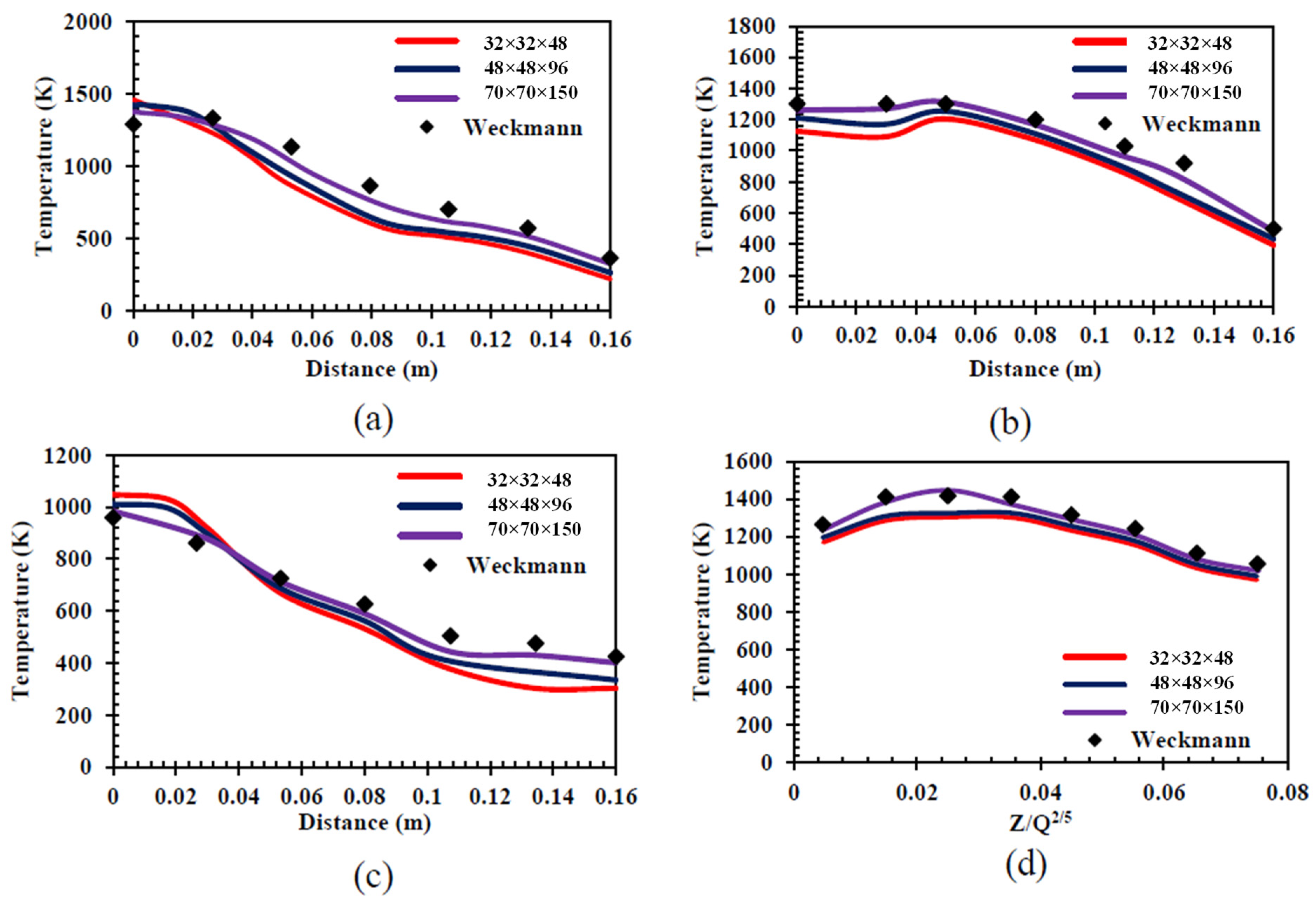





| Grid Size | Criterion of Classification | W × D × H | Size of Each Cell | Total No. of Cells |
|---|---|---|---|---|
| Coarse | 32 × 32 × 48 | 0.05 m | 49,152 | |
| Medium | 48 × 48 × 96 | 0.033 m | 22,184 | |
| Fine | 75 × 75 × 150 | 0.0218 m | 843,750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, S.S.; Bale, S.; Das, D.; Tripathi, A.; Tripathi, A.; Mishra, P.K.; Ekielski, A.; Suresh, S. Numerical Simulations of a Postulated Methanol Pool Fire Scenario in a Ventilated Enclosure Using a Coupled FVM-FEM Approach. Processes 2022, 10, 918. https://doi.org/10.3390/pr10050918
Tiwari SS, Bale S, Das D, Tripathi A, Tripathi A, Mishra PK, Ekielski A, Suresh S. Numerical Simulations of a Postulated Methanol Pool Fire Scenario in a Ventilated Enclosure Using a Coupled FVM-FEM Approach. Processes. 2022; 10(5):918. https://doi.org/10.3390/pr10050918
Chicago/Turabian StyleTiwari, Shashank S., Shivkumar Bale, Diptendu Das, Arpit Tripathi, Ankit Tripathi, Pawan Kumar Mishra, Adam Ekielski, and Sundaramurthy Suresh. 2022. "Numerical Simulations of a Postulated Methanol Pool Fire Scenario in a Ventilated Enclosure Using a Coupled FVM-FEM Approach" Processes 10, no. 5: 918. https://doi.org/10.3390/pr10050918







