Continuous-Flow Magnetic Fractionation of Red Blood Cells Based on Hemoglobin Content and Oxygen Saturation—Clinical Blood Supply Implications and Sickle Cell Anemia Treatment
Abstract
:1. Introduction
2. Theory
2.1. One and Two Phase Annular Flow
2.2. RBC Transport
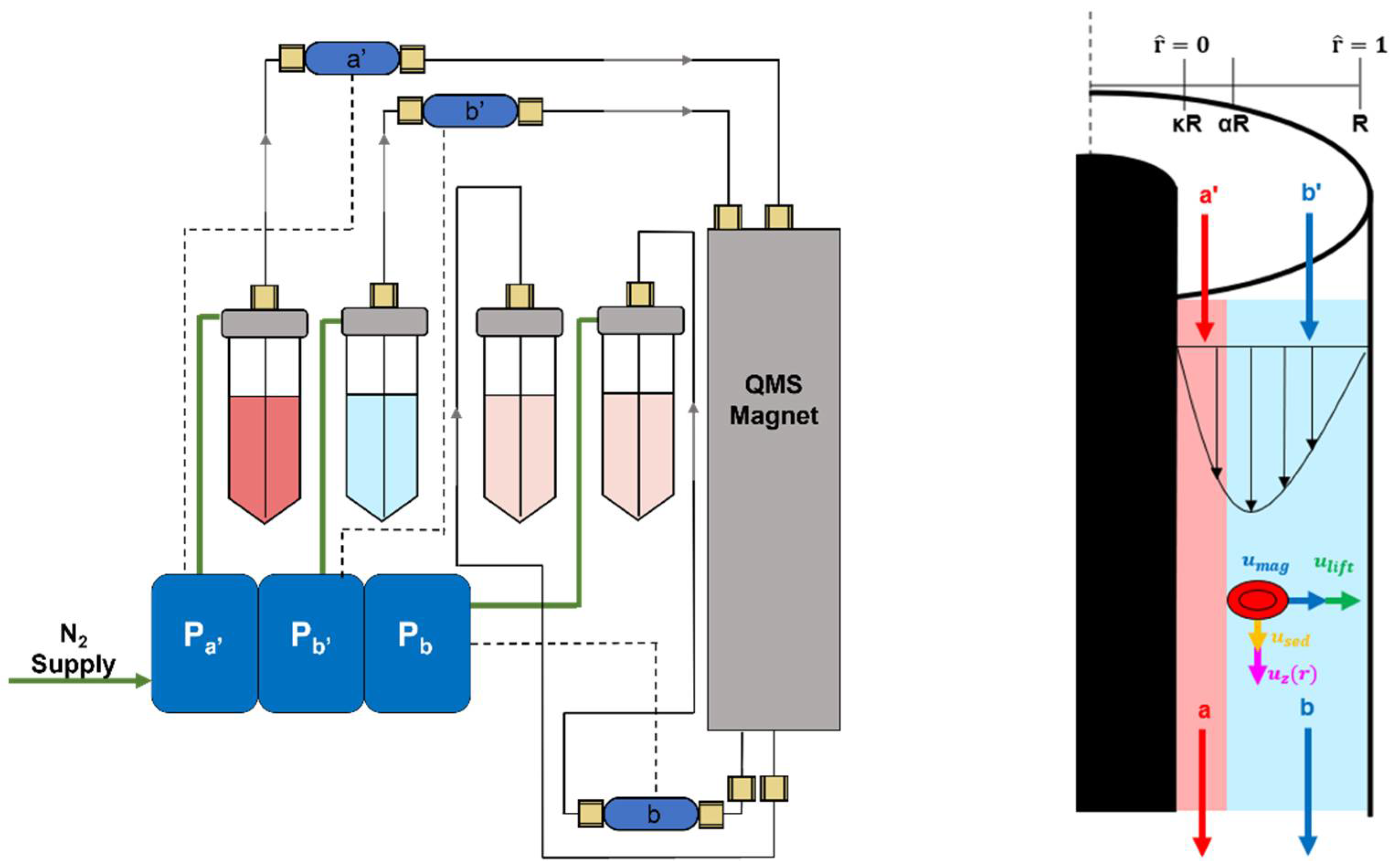
3. Materials and Methods
3.1. Sample Preparation and Analysis
3.2. Pressure Driven Flow System
3.3. Euler Method Crossover Model
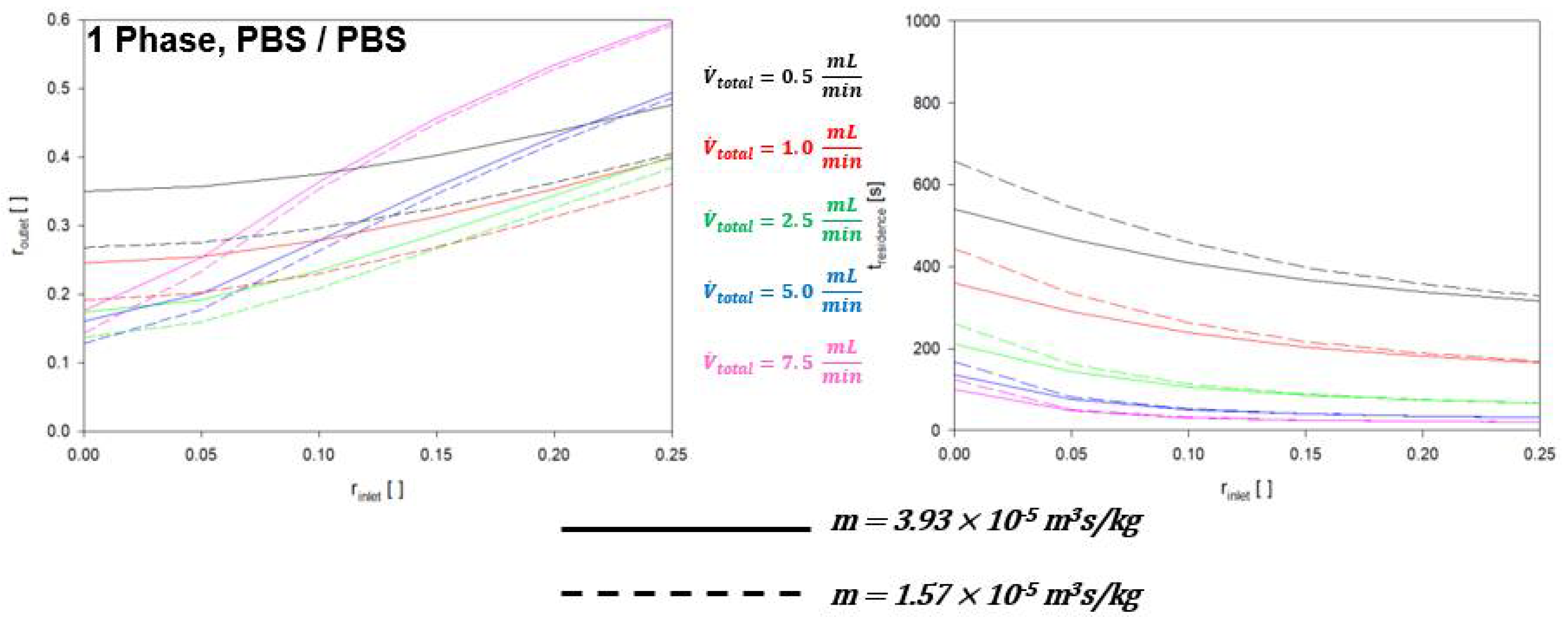
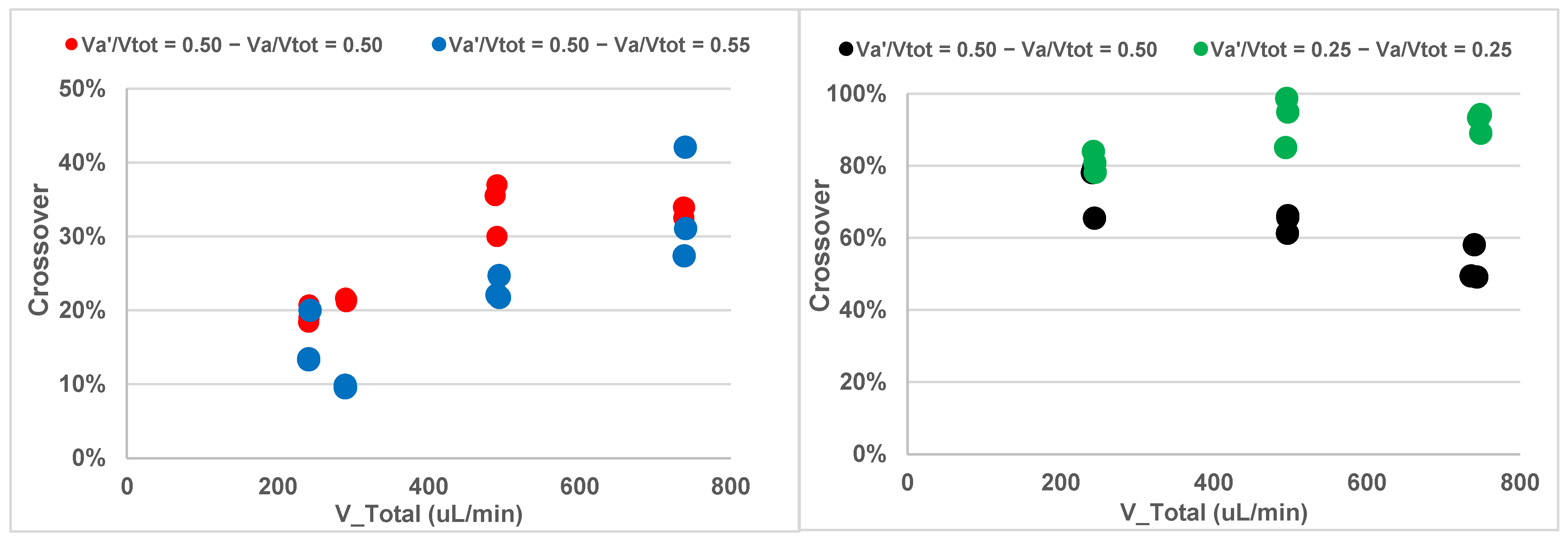
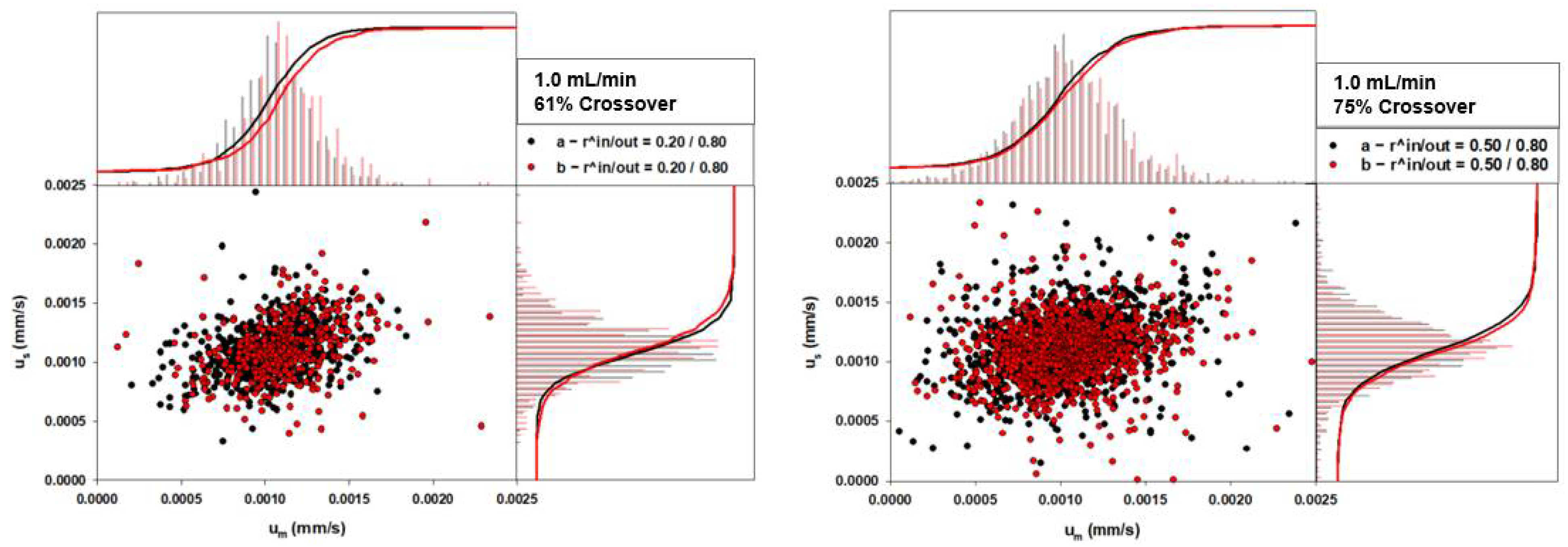
4. Results
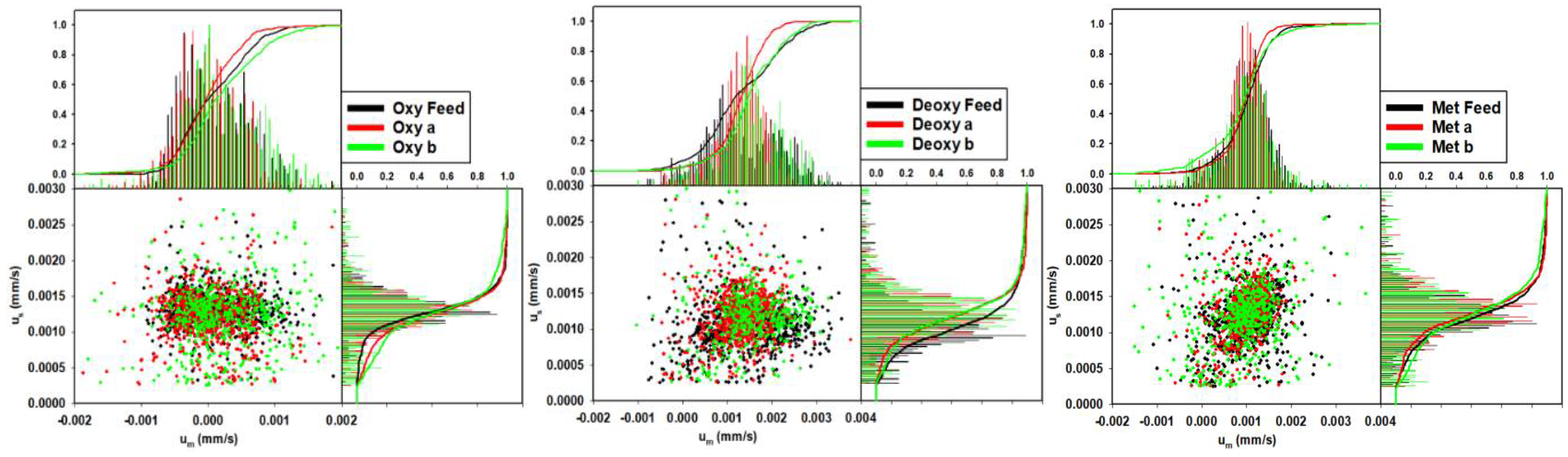
4.1. Single Phase RBC Crossover
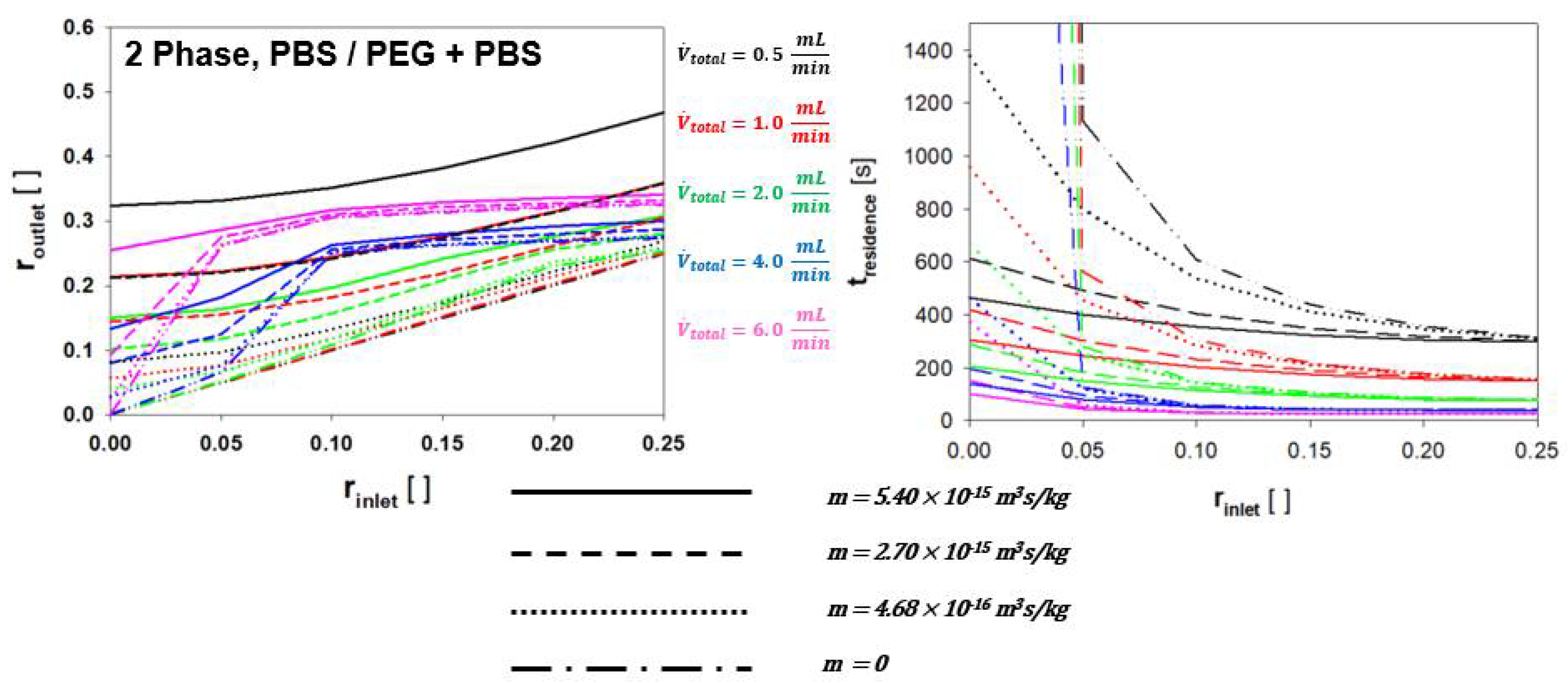
4.2. Two Phase RBC Crossover
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- American Red Cross. US Blood Supply Facts. Available online: https://www.redcrossblood.org/donate-blood/how-to-donate/how-blood-donations-help/blood-needs-blood-supply.html (accessed on 8 April 2022).
- McCullough, J. Transfusion Medicine, 3rd ed.; John Wiley & Sons, Inc.: New Jersey, NJ, USA, 2011. [Google Scholar]
- World Health Organization. Blood Safety and Availability. Available online: https://www.who.int/news-room/fact-sheets/detail/blood-safety-and-availability (accessed on 8 April 2022).
- Muteb, P.B.; Mamba, J.F.J.K.; Pfutila, P.M.; Bilo, V.; Mulefu, J.D.P.; Diallo, D.A. Effectiveness, safety, and cost of partial exchange transfusions in patients with sickle-cell anemia at a sickle cell disease center in sub-Saharan Africa. Med. Sante Trop. 2017, 27, 387–391. [Google Scholar]
- Luten, M.; Roerdinkholder-Stoelwinder, B.; Schaap, N.P.M.; de Grip, W.J.; Bos, H.J.; Bosman, G.J.C.G.M. Survival of red blood cells after transfusion: A comparison between red cells concentrates of different storage periods. Transfusion 2008, 48, 1478–1485. [Google Scholar] [PubMed]
- Piety, N.Z.; Gifford, S.C.; Yang, X.; Shevkoplyas, S.S. Quantifying Morphological Heterogeneity: A Study of More than 1,000,000 Individual Stored Red Blood Cells. Vox Sang. 2015, 109, 221–230. [Google Scholar]
- Eaton, W.A.; Bunn, H.F. Treating Sickle Cell Disease by Targeting HbS Polymerization. Blood 2017, 129, 2719–2726. [Google Scholar] [PubMed] [Green Version]
- Jacobs, J.W.; Booth, G.S. Blood Shortages and Changes to Massive Transfusion Protocols: Survey of Hospital Practices during the COVID-19 Pandemic. Transfus. Apher. Sci. 2022, 61, 103297. [Google Scholar] [CrossRef] [PubMed]
- Ware, R.E.; de Montalembert, M.; Tshilolo, L.; Abboud, M.R. Sickle Cell Disease. Lancet 2017, 390, 311–323. [Google Scholar] [PubMed]
- Gómez-Pastora, J.; Bringas, E.; Lázaro-Díez, M.; Ramos-Vivas, J.; Ortiz, I. The reverse of controlled release: Controlled sequestration of species and biotoxins into nanoparticles (NPs). In Drug Delivery Systems; Stroeve, P., Mahmoudi, M., Eds.; World Scientific: Hackensack, NJ, USA, 2017; pp. 207–244. [Google Scholar]
- González Fernández, C.; Gómez-Pastora, J.; Basauri, A.; Fallanza, M.; Bringas, E.; Chalmers, J.J.; Ortiz, I. Continuous-flow separation of magnetic particles from biofluids: How does the microdevice geometry determine the separation performance? Sensors 2020, 20, 3030. [Google Scholar]
- Roodan, V.A.; Gómez-Pastora, J.; Karampelas, I.H.; González-Fernández, C.; Bringas, E.; Ortiz, I.; Chalmers, J.J.; Furlani, E.P.; Swihart, M.T. Formation and manipulation of ferrofluid droplets with magnetic fields in a microdevice: A numerical parametric study. Soft Matter 2020, 16, 9506–9518. [Google Scholar]
- Chalmers, J.J.; Jin, X.; Palmer, A.F.; Yazer, M.H.; Moore, L.; Amaya, P.; Park, K.; Pan, X.; Zborowski, M. Femtogram Resolution of Iron Content on a per Cell Basis: Ex Vivo Storage of Human Red Blood Cells Leads to Loss of Hemoglobin. Anal. Chem. 2017, 89, 3702–3709. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Weigand, M.; Palmer, A.F.; Zborowski, M.; Yazer, M.H.; Chalmers, J.J. Single Cell Analysis of Aged RBCs: Quantitative Analysis of the Aged Cells and Byproducts. Analyst 2019, 144, 935–942. [Google Scholar]
- Eldeniz, C.; Binkley, M.M.; Fields, M.; Guilliams, K.; Ragan, D.K.; Chen, Y.; Lee, J.M.; Ford, A.L.; An, H. Bulk volume susceptibility difference between deoxyhemoglobin and oxyhemoglobin for HbA and HbS: A comparative study. Magn. Reson. Med. 2021, 85, 3383–3393. [Google Scholar] [CrossRef] [PubMed]
- Weigand, M.; Gómez-Pastora, J.; Strayer, J.; Wu, X.; Choe, H.; Lu, S.; Plencner, E.; Landes, K.; Palmer, A.; Zborowski, M.; et al. The Unique Magnetic Signature of Sickle Red Blood Cells: A Comparison Between the Red Blood Cells of Transfused and Non-Transfused Sickle Cell Disease Patients and Healthy Donors. IEEE Trans. Biomed. Eng. 2022; under review. [Google Scholar]
- Scrima, R.; Fugetto, S.; Capitanio, N.; Gatti, D.L. Hemoglobin Non-equilibrium Oxygen Dissociation Curve. bioRxiv 2019. [Google Scholar] [CrossRef]
- Moore, L.R.; Mizutani, D.; Tanaka, T.; Buck, A.; Yazer, M.; Zborowski, M.; Chalmers, J.J. Continuous, Intrinsic Magnetic Depletion of Erythrocytes from Whole Blood with a Quadrupole Magnet and Annular Flow Channel; Pilot Scale Study. Biotechnol. Bioeng. 2018, 115, 1521–1530. [Google Scholar] [CrossRef]
- Park, K.J.J.; Kim, J.; Testoff, T.; Adams, J.; Poklar, M.; Zborowski, M.; Venere, M.; Chalmers, J.J. Quantitative Characterization of the Regulation of Iron Metabolism in Glioblastoma Stem-like Cells Using Magnetophoresis. Biotechnol. Bioeng. 2019, 116, 1644–1655. [Google Scholar] [CrossRef]
- Moore, L.R.; Rodriguez, A.R.; Williams, P.S.; McCloskey, K.; Bolwell, B.J.; Nakamura, M.; Chalmers, J.J.; Zborowski, M. Progenitor Cell Isolation with a High-Capacity Quadrupole Magnetic Flow Sorter. J. Mag. Mag. Mater. 2001, 225, 277–284. [Google Scholar] [CrossRef]
- Williams, P.S.; Decker, K.; Nakamura, M.; Chalmers, J.J.; Moore, L.R.; Zborowski, M. Splitter Imperfections in Annular Split-Flow Thin Separation Channels: Experimental Study of Nonspecific Crossover. Anal. Chem. 2003, 75, 6687–6695. [Google Scholar] [CrossRef]
- Wu, X.; Gómez-Pastora, J.; Zborowski, M.; Chalmers, J. SPIONs Self-Assembly and Magnetic Sedimentation in Quadrupole Magnets: Gaining Insight into the Separation Mechanisms. Sep. Purif. Technol. 2022, 280, 119786. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Wu, X.; Sundar, N.; Alawi, J.; Nabar, G.; Winter, J.O.; Zborowski, M.; Chalmers, J. Self-assembly and sedimentation of 5 nm SPIONs using horizontal, high magnetic fields and gradients. Sep. Purif. Technol. 2020, 248, 117012. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N.; Klingenberg, D.J. Shell Momentum Balances and Velocity Distributions in Laminar Flow. In Introductory Transport Phenomena; Sayre, D., Ed.; Wiley: Hoboken, NJ, USA, 2014; pp. 57–58. [Google Scholar]
- Nam, K.H.; Chang, W.J.; Hong, H.; Lim, S.M.; Kim, D.I.; Koo, Y.M. Continuous-flow fractionation of animal cells in microfluidic device using aqueous two-phase extraction. Biomed. Microdevices 2005, 7, 189–195. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Effects of Aggregation on Blood Sedimentation and Conductivity. PLoS ONE 2015, 10, e0129337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González-Fernández, C.; Gómez-Pastora, J.; Bringas, E.; Zborowski, M.; Chalmers, J.J.; Ortiz, I. Recovery of Magnetic Catalysts: Advanced Design for Process Intensification. Ind. Eng. Chem. Res. 2022, 60, 16780–16790. [Google Scholar] [CrossRef]
- Kim, J.; Gómez-Pastora, J.; Weigand, M.; Potgieter, M.; Walters, N.A.; Reátegui, E.; Palmer, A.F.; Yazer, M.; Zborowski, M.; Chalmers, J.J. A Subpopulation of Monocytes in Normal Human Blood Has Significant Magnetic Susceptibility: Quantification and Potential Implications. Cytometry A 2019, 95, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Pastora, J.; Kim, J.; Multanen, V.; Weigand, M.; Walters, N.A.; Reátegui, E.; Palmer, A.F.; Yazer, M.H.; Zborowski, M.; Chalmers, J.J. Intrinsically magnetic susceptibility in human blood and its potential impact on cell separation: Non-classical and intermediate monocytes have the strongest magnetic behavior in fresh human blood. Exp. Hematol. 2021, 99, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Weigand, M.R.H.; Gómez-Pastora, J.; Kim, J.; Kurek, M.T.; Hickey, R.J.; Irwin, D.C.; Buehler, P.W.; Zborowski, M.; Palmer, A.F.; Chalmers, J.J. Magnetophoretic and spectral characterization of oxyhemoglobin and deoxyhemoglobin: Chemical versus enzymatic processes. PLoS ONE 2021, 16, e0257061. [Google Scholar] [CrossRef]
- Kim, J.; Gómez-Pastora, J.; Gilbert, C.J.; Weigand, M.; Walters, N.A.; Reátegui, E.; Palmer, A.F.; Yazer, M.; Zborowski, M.; Chalmers, J.J. Quantification of the mean and distribution of hemoglobin content in normal human blood using cell tracking velocimetry. Anal. Chem. 2020, 92, 1956–1962. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, S.; Yuan, D.; Alici, G.; Nguyen, N.T.; Warkiani, M.E.; Li, W. Fundamentals and Applications of Inertial Microfluidics: A Review. Lab Chip 2016, 16, 10–34. [Google Scholar] [CrossRef] [Green Version]
- Franco, R.S.; Puchulu-Campanella, M.E.; Barber, L.A.; Palascak, M.B.; Joiner, C.H.; Low, P.S.; Cohen, R.M. Changes in the Properties of Normal Human Red Blood Cells during in Vivo Aging. Am. J. Hematol. 2013, 88, 44–51. [Google Scholar] [CrossRef] [Green Version]
- Maruyama, T.; Fukata, M.; Fujino, T. Physiological and Pathophysiological Significance of Erythrocyte Senescence, Density and Deformability: Important but Unnoticed Trinity. J. Biorheol. 2020, 34, 61–70. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Weigand, M.; Kim, J.; Palmer, A.F.; Yazer, M.; Desai, P.C.; Zborowski, M.; Chalmers, J.J. Potential of Cell Tracking Velocimetry as an Economical and Portable Hematology Analyzer. Sci. Rep. 2022, 12, 1–12. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weigand, M.; Gomez-Pastora, J.; Palmer, A.; Zborowski, M.; Desai, P.; Chalmers, J. Continuous-Flow Magnetic Fractionation of Red Blood Cells Based on Hemoglobin Content and Oxygen Saturation—Clinical Blood Supply Implications and Sickle Cell Anemia Treatment. Processes 2022, 10, 927. https://doi.org/10.3390/pr10050927
Weigand M, Gomez-Pastora J, Palmer A, Zborowski M, Desai P, Chalmers J. Continuous-Flow Magnetic Fractionation of Red Blood Cells Based on Hemoglobin Content and Oxygen Saturation—Clinical Blood Supply Implications and Sickle Cell Anemia Treatment. Processes. 2022; 10(5):927. https://doi.org/10.3390/pr10050927
Chicago/Turabian StyleWeigand, Mitchell, Jenifer Gomez-Pastora, Andre Palmer, Maciej Zborowski, Payal Desai, and Jeffrey Chalmers. 2022. "Continuous-Flow Magnetic Fractionation of Red Blood Cells Based on Hemoglobin Content and Oxygen Saturation—Clinical Blood Supply Implications and Sickle Cell Anemia Treatment" Processes 10, no. 5: 927. https://doi.org/10.3390/pr10050927
APA StyleWeigand, M., Gomez-Pastora, J., Palmer, A., Zborowski, M., Desai, P., & Chalmers, J. (2022). Continuous-Flow Magnetic Fractionation of Red Blood Cells Based on Hemoglobin Content and Oxygen Saturation—Clinical Blood Supply Implications and Sickle Cell Anemia Treatment. Processes, 10(5), 927. https://doi.org/10.3390/pr10050927







