Economic Optimization Dispatch Model of a Micro-Network with a Solar-Assisted Compressed Air Energy Storage Hub, with Consideration of Its Operationally Feasible Region
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Novelty and Contributions
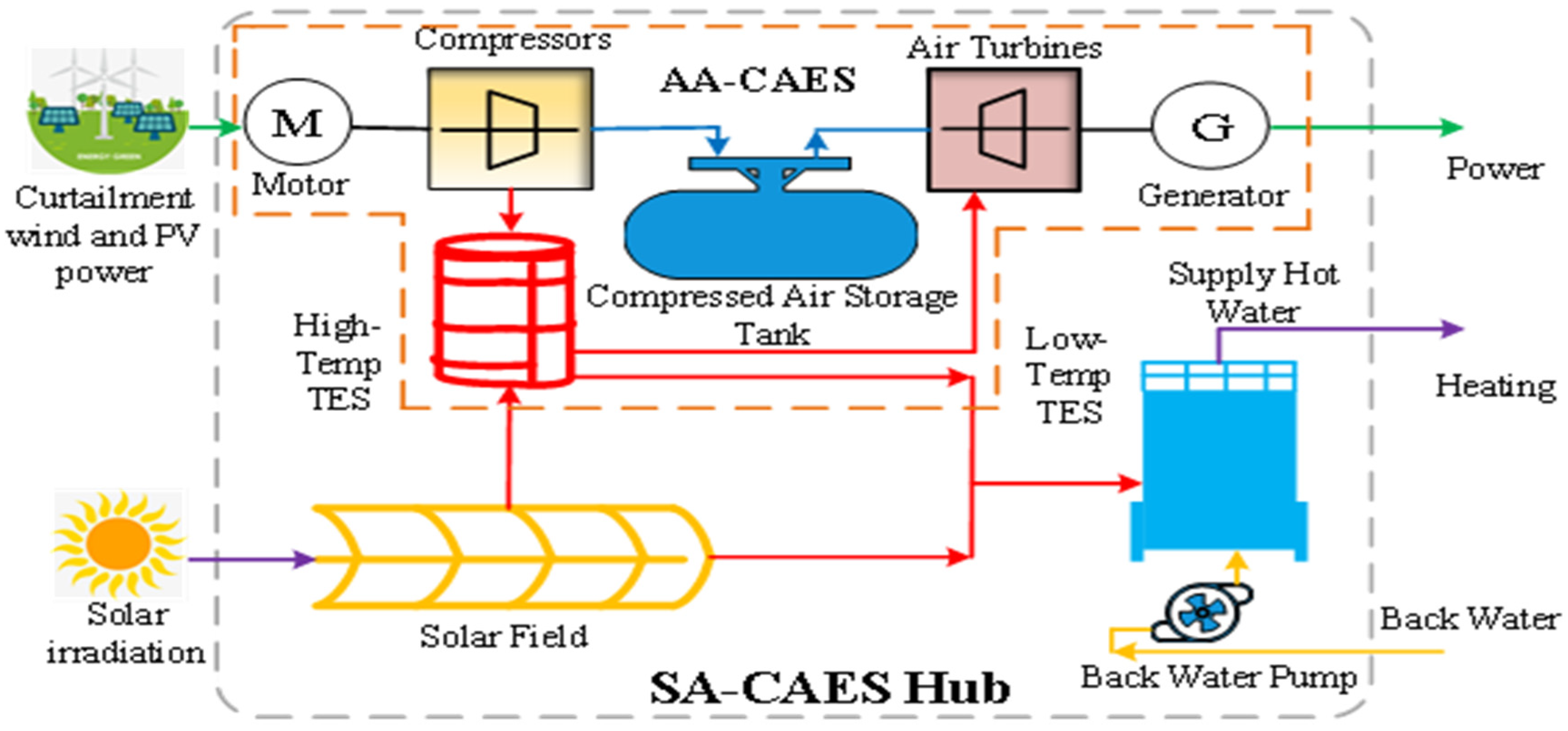
2. The Design Scheme of the SA-CAES Hub
3. Economic Dispatch Model of a MEN
3.1. SA-CAES Hub Formulation
3.2. PDN Formulation
3.3. DHN Formulation
3.4. Objective
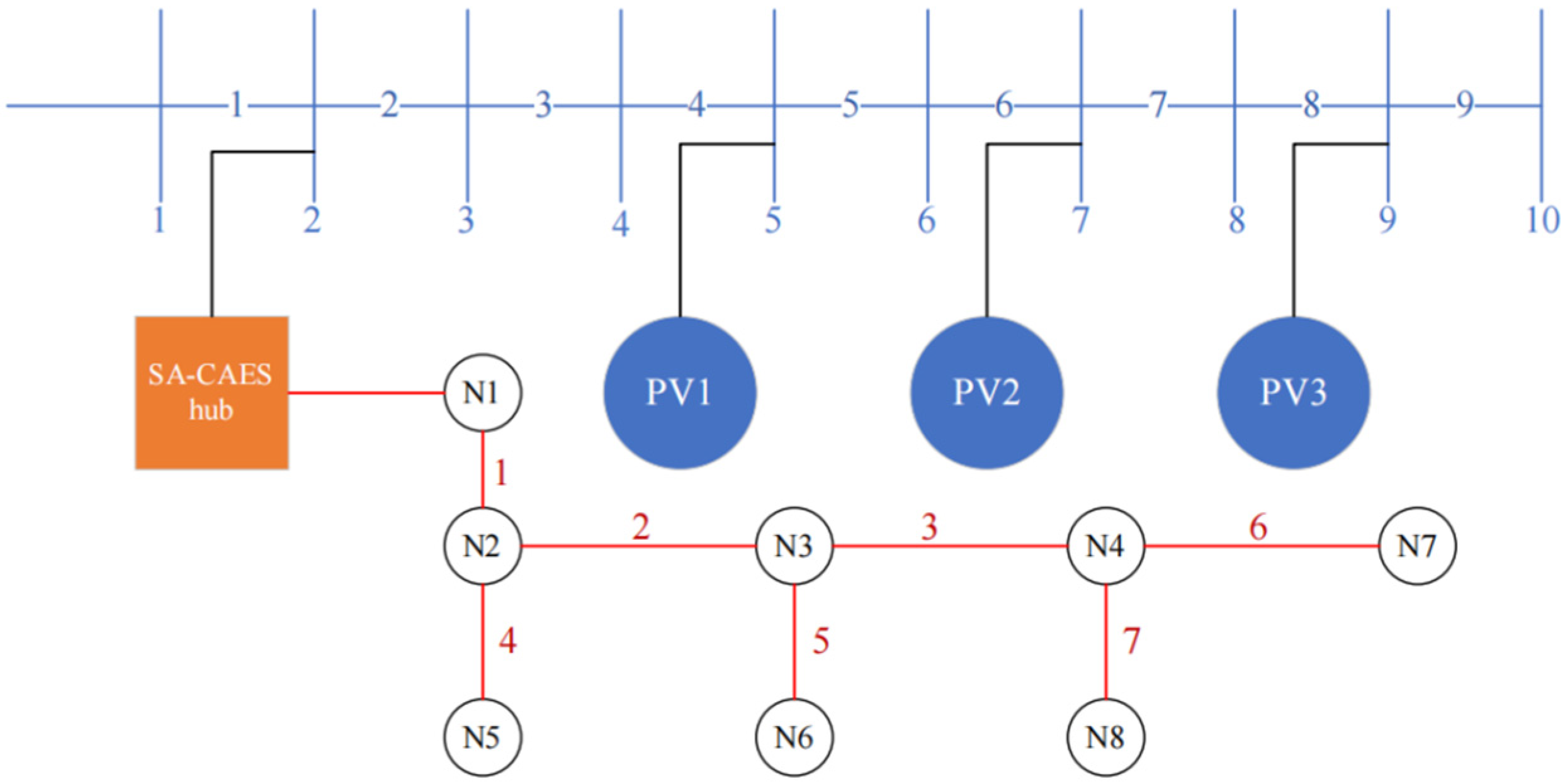
4. Case Studies
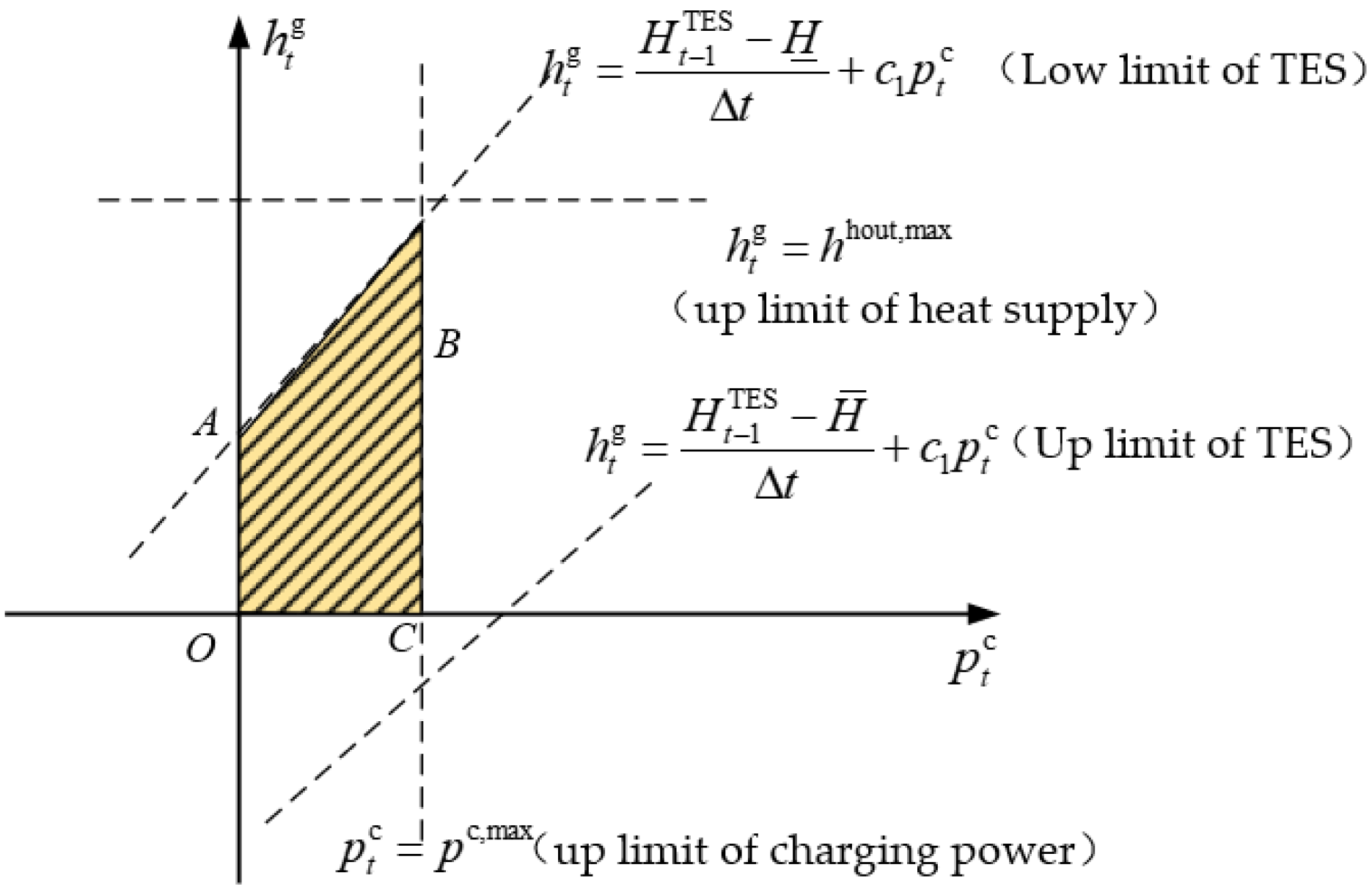
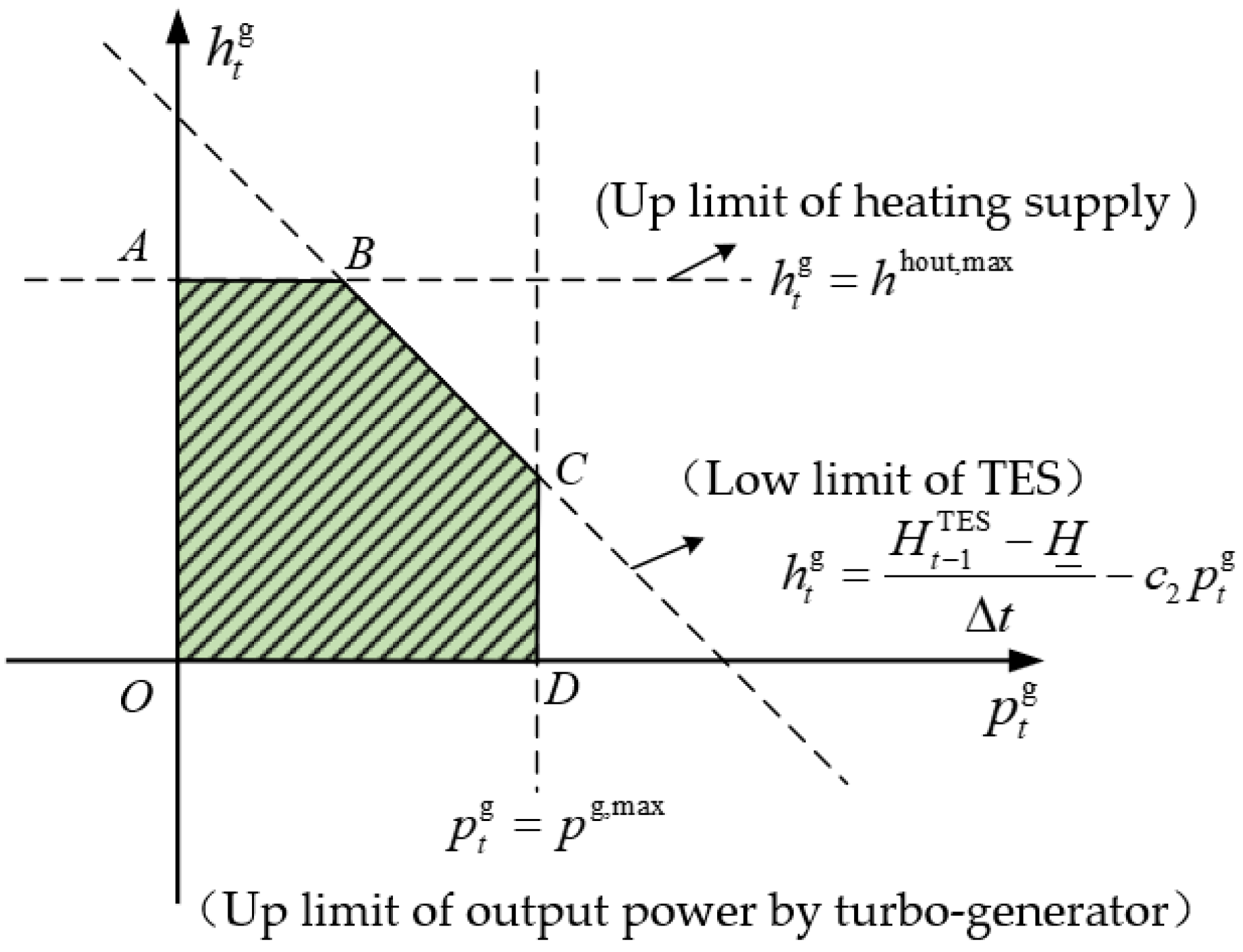
4.1. Operationally Feasible Region Based on Thermodynamic Analysis
- The compressed air in the system is treated as the ideal gas;
- The SA-CAES operates in a steady-state condition;
- The pressure drop of each heat exchanger is 2%, and heat loss is ignored;
- The adiabatic efficiency of the compressors and air turbine is constant;
- The heat loss in the TES is ignored.
4.2. Simulation Results
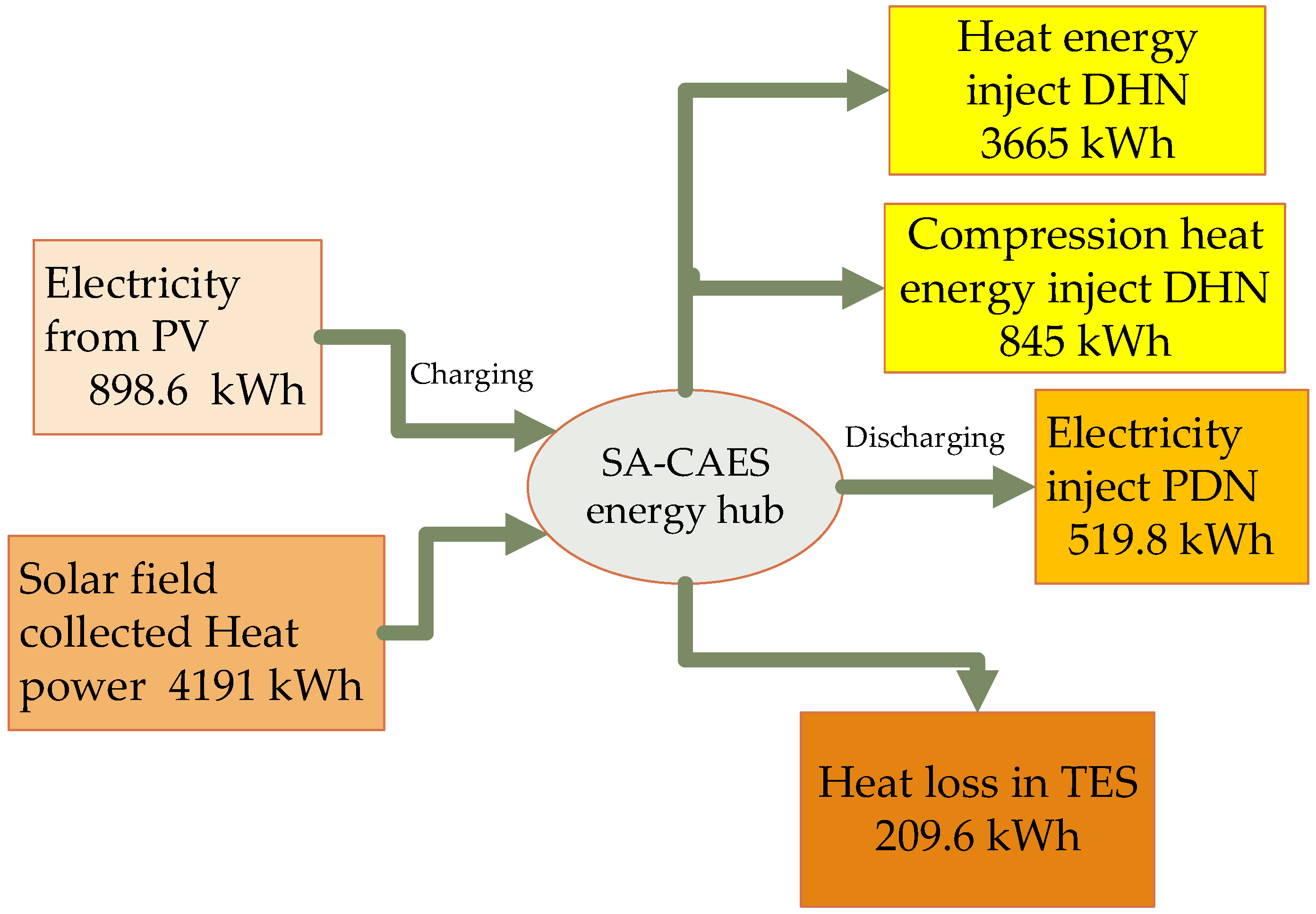
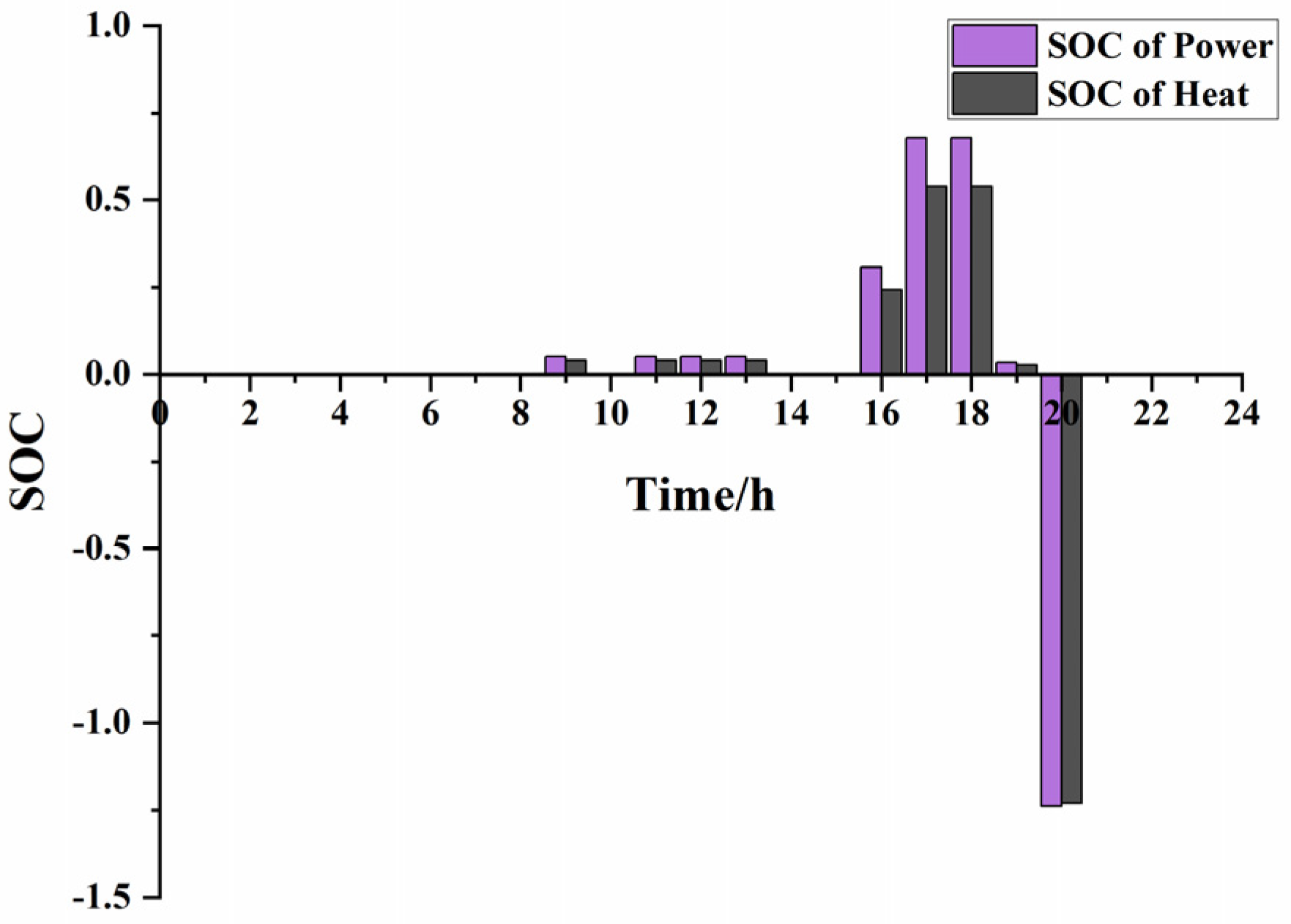
4.2.1. Operation of the SA-CAES
4.2.2. Operation Costs
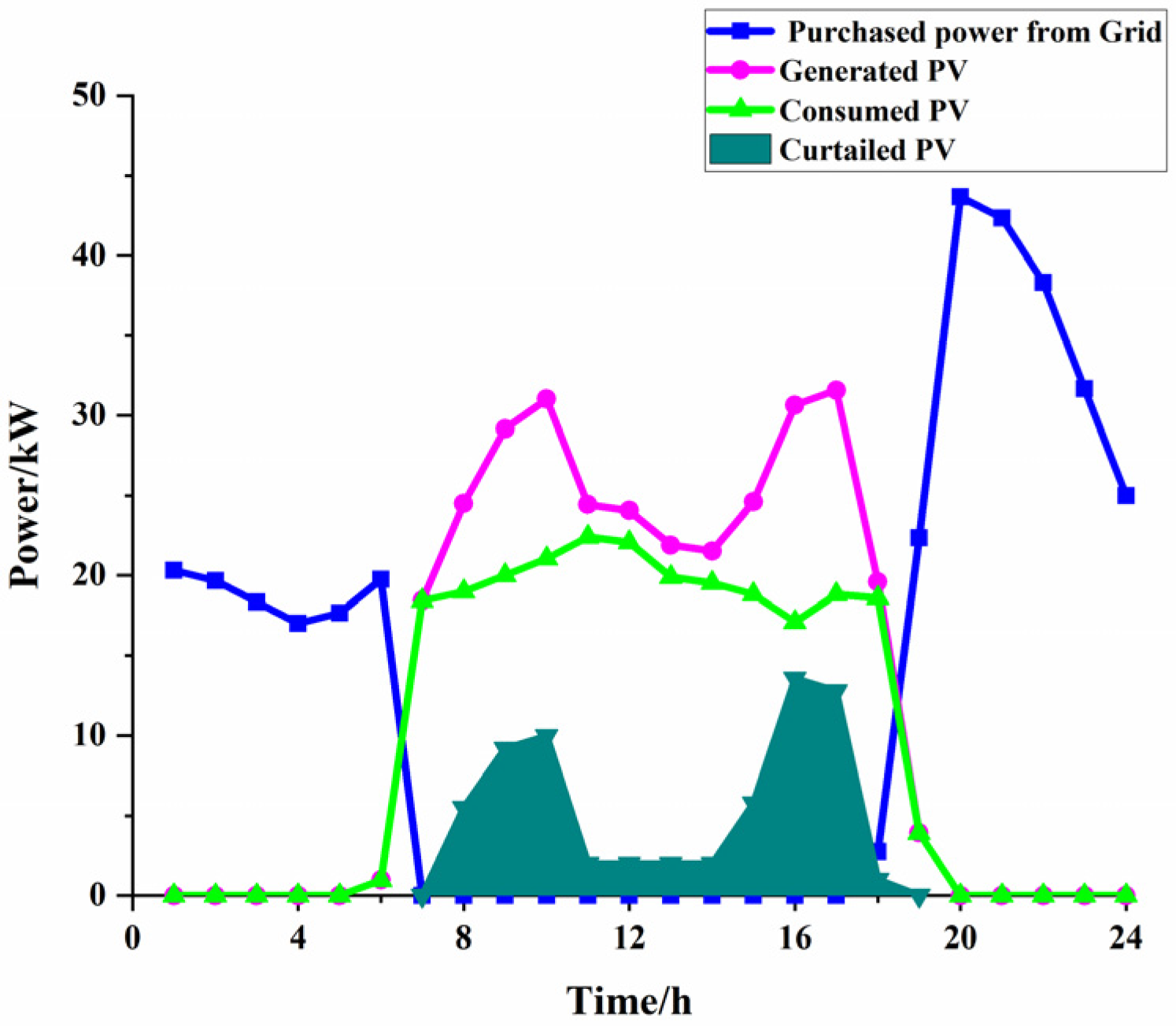
4.2.3. Solar Power Curtailment
4.2.4. Optimal Temperature Distribution in the DHN
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| SA-CAES | Solar-Assisted Compressed Air Energy Storage System |
| PDN | Power distribution network |
| DHN | District heating network |
| RES | Renewable energy source |
| DG | Distributed generator |
| DES | Distributed energy system |
| MEN | Micro-energy network |
| CHP | Cooling–Heating and Power |
| AA-CAES | Advanced Adiabatic Compressed Air Energy Storage |
| RES | Renewable energy source |
| DG | Distributed generation |
| ST-CAES | Hybrid external solar thermal energy and CAES |
| CAES | Compressed air energy storage |
| TES | Thermal energy storage |
| PV | Photovoltaic power |
| MINLP | Mixed integer nonlinear programming |
| MILP | Mixed integer linear programming |
| Symbols | |
| W | Work (kWh) |
| Nc and Ne | The stage number of compressors and the turbine |
| The mass flow rate of the compressor at time τ (kg/s) | |
| h | Specific enthalpy (kJ/kg) |
| p | Pressure (MPa) |
| and | Boolean quantities indicating the operating state |
| U | Voltage (kV) |
| P | Active Power (kW) |
| Q | Reactive power (kVar) |
| τ | Time (h) |
References
- Li, G.; Li, Q.; Liu, Y.; Liu, H.; Song, W.; Ding, R. A cooperative Stackelberg game based energy management considering price discrimination and risk assessment. Int. J. Electr. Power Energy Syst. 2021, 135, 107461. [Google Scholar] [CrossRef]
- Coronavirus and Climate Change-C-CHANGE Harvard, T.H. Chan School of Public Health. Available online: https://www.hsph.harvard.edu/c-change/subtopics/coronavirus-and-climate-change/ (accessed on 1 January 2021).
- Geidl, M.; Andersson, G. Optimal power flow of multiple energy carriers. IEEE Trans. Power Syst. 2007, 22, 145–155. [Google Scholar] [CrossRef]
- Geidl, M.; Koeppel, G.; Favre-Perrod, P.; Klockl, B.; Andersson, G.; Frohlich, K. Energy hubs for the future. IEEE Power Energy Mag. 2006, 5, 24–30. [Google Scholar] [CrossRef]
- Mohammadi, M.; Noorollahi, Y.; Mohammadi-Ivatloo, B.; Yousefi, H. Energy hub: From a model to a concept—A review. Renew. Sustain. Energy Rev. 2017, 80, 1512–1527. [Google Scholar] [CrossRef]
- Nakhamkin, M.; Daniel, C. Available compressed air energy storage (CAES) plant concepts. Energy 2010, 4100, 81. [Google Scholar]
- Chen, X.; Zhang, T.; Xue, X.; Chen, L.; Li, Q.; Mei, S. A Solar–Thermal-Assisted Adiabatic Compressed Air Energy Storage System and Its Efficiency Analysis. Appl. Sci. 2018, 8, 1390. [Google Scholar] [CrossRef] [Green Version]
- Ji, W.; Zhou, Y.; Sun, Y.; Zhang, W.; An, B.; Wang, J. Thermodynamic analysis of a novel hybrid wind-solar-compressed air energy storage system. Energy Convers. Manag. 2017, 142, 176–187. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Ran, P.; Li, Z.; Ni, W. Thermodynamic analysis of a hybrid thermal-compressed air energy storage system for the integration of wind power. Appl. Therm. Eng. 2014, 66, 519–527. [Google Scholar] [CrossRef]
- Houssainy, S.; Janbozorgi, M.; Ip, P.; Kavehpour, P. Thermodynamic analysis of a high temperature hybrid compressed air energy storage (HTH-CAES) system. Renew Energy 2018, 115, 1043–1054. [Google Scholar] [CrossRef]
- Wang, S.; Chen, G.; Fang, M.; Fang, M.; Wang, Q. A new compressed air energy storage refrigeration system. Energy Convers. Manag. 2006, 47, 3408–3416. [Google Scholar] [CrossRef]
- Lund, H.; Salgi, G. The role of compressed air energy storage (CAES) in future sustainable energy systems. Energy Convers. Manag. 2009, 50, 1172–1179. [Google Scholar] [CrossRef]
- Bai, J.; Chen, L.; Liu, F.; Mei, S. Interdependence of electricity and heat distribution systems coupled by an AA-CAES-based energy hub. IET Renew. Power Gener. 2019, 14, 399–407. [Google Scholar] [CrossRef]
- Ni, C.; Xue, X.; Mei, S.; Zhang, X.-P.; Chen, X. Technological Research of a Clean Energy Router Based on Advanced Adiabatic Compressed Air Energy Storage System. Entropy 2020, 22, 1440. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Wei, W.; Shengwei, M. Efficiency Analysis of AA-CAES Based Energy Hub Considering Combined Cooling, Heating and Power. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiwun, China, 22–24 October 2021; pp. 131–136. [Google Scholar]
- Han, Z.; Sun, Y.; Li, P.; Hu, Q. Thermo-Economic Analysis of Trigeneration System Based on Aa-CaeS. Acta Energ. Sol. Sin. 2022, 43, 97. [Google Scholar]
- Chen, X.; Xue, X.; Si, Y.; Liu, C.; Chen, L.; Guo, Y.; Mei, S. Thermodynamic analysis of a hybrid trigenerative compressed air energy storage system with solar thermal energy. Entropy 2020, 22, 764. [Google Scholar] [CrossRef]
- Mei, S.; Li, R.; Xue, X.; Chen, Y.; Lu, Q.; Chen, X.; Ahrens, C.D.; Li, R.; Chen, L. Paving the way to smart micro energy grid: Concepts, design principles, and engineering practices. CSEE J. Power Energy Syst. 2017, 3, 440–449. [Google Scholar] [CrossRef]
- Daneshi, H.; Srivastava, A.K.; Daneshi, A. Generation scheduling with integration of wind power and compressed air energy storage. In Proceedings of the 2010 IEEE PES Trans and Distribution Conference and Exposit, New Orleans, LA, USA, 19–22 April 2010; pp. 19–22. [Google Scholar]
- Liu, B.; Chen, L.J.; Zhang, Y.; Chen, L.; Zhang, Y.; Fang, C.; Mei, S.; Zhou, Y. Modeling and analysis of unit commitment considering RCAES system. In Proceedings of the 33rd Hinese Control Conference (CCC’14), Nanjing, China, 28–30 July 2014; pp. 7478–7482. [Google Scholar]
- Wen, P.; Xie, Y.; Huo, L.; Tohidi, A. Optimal and stochastic performance of an energy hub-based microgrid consisting of a solar-powered compressed-air energy storage system and cooling storage system by modified grasshopper optimization algorithm. Int. J. Hydrogen Energy 2022, 47, 13351–13370. [Google Scholar] [CrossRef]
- Yaowang, L.I.; Shihong, M.I.A.O.; Binxin, Y.I.N.; Shixu Zhang, S.Z. Optimal Dispatch Model for Micro Integrated Energy System Considering Multi-carrier Energy Generation Characteristic of Advanced Adiabatic Compressed Air Energy Storage. Power Gener. Technol. 2020, 41, 41–49. [Google Scholar]
- Liu, B.; Lin, Q.; Zheng, T.; Chen, L.; Mei, S. Low carbon economic dispatch for multi-energy distribution network with compressed air energy storage system as energy hub. In Proceedings of the 36th Chinese Control Conference (CCC), Dalian, China, 26 July 2017; pp. 3083–3088. [Google Scholar]
- Wu, D.; Bai, J.; Wei, W.; Chen, L.; Mei, S. Optimal bidding and scheduling of AA-CAES based energy hub considering cascaded consumption of heat. Energy 2021, 233, 121133. [Google Scholar] [CrossRef]
- Li, J.; Fang, J.; Zeng, Q.; Chen, Z. Optimal operation of the integrated electrical and heating systems to accommodate the intermittent renewable sources. Appl. Energy 2016, 167, 244–254. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Shahidehpour, M.; Wang, J.; Zhang, B. Combined Heat and Power Dispatch Considering Pipeline Energy Storage of District Heating Network. IEEE Trans. Sustain. Energy 2016, 7, 12–22. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Wang, J.; Zhang, B.; Zheng, T. Transmission-Constrained Unit Commitment Considering Combined Electricity and District Heating Networks. IEEE Trans. Sustain. Energy 2015, 7, 480–492. [Google Scholar] [CrossRef]
- Arabkoohsar, A.; Andresen, G.B. Dynamic energy, exergy and market modeling of a High Temperature Heat and Power Storage System. Energy 2017, 126, 430–443. [Google Scholar] [CrossRef]
- Li, R.; Wei, W.; Mei, S.; Hu, Q.; Wu, Q. Participation of an energy hub in electricity and heat distribution markets: An MPEC approach. IEEE Trans. Smart Grid 2018, 10, 3641–3653. [Google Scholar] [CrossRef]
- Najafi, A.; Falaghi, H.; Contreras, J.; Ramezani, M. A Stochastic Bilevel Model for the Energy Hub Manager Problem. IEEE Trans. Smart Grid 2017, 8, 2394–2404. [Google Scholar] [CrossRef]
- Davatgaran, V.; Saniei, M.; Mortazavi, S.S. Optimal bidding strategy for an energy hub in energy market. Energy 2018, 148, 482–493. [Google Scholar] [CrossRef]
- Farivar, M.; Low, S.H. Branch flow model: Relaxations and convexification—Part I. IEEE Trans. Power Syst 2013, 28, 2554–2564. [Google Scholar] [CrossRef]
- Li, R.; Chen, L.; Yuan, T.; Li, C. Optimal dispatch of zero-carbon-emission micro Energy Internet integrated with non-supplementary fired compressed air energy storage system. J. Mod. Power Syst. Clean Energy 2016, 4, 566–580. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D. Qinghai Development and Reform Commission. 2020. Available online: http://fgw.qinghai.gov.cn/zfxxgk/sdzdgknr/fgwwj/202012/t20201218_76157.html (accessed on 26 April 2022).
- Mei, S.; Wang, J.; Tian, F.; Chen, L.; Xue, X.; Lu, Q.; Zhou, Y.; Zhou, X. Design and engineering implementation of non-supplementary fired compressed air energy storage system: TICC-500. Sci. China Technol. Sci. 2015, 58, 600–611. [Google Scholar] [CrossRef]
- Cheayb, M.; Gallego, M.M.; Tazerout, M.; Poncet, S. A techno-economic analysis of small-scale trigenerative compressed air energy storage system. Energy 2020, 239, 121842. [Google Scholar] [CrossRef]
- Yu, M.; Li, S.; Zhang, X.; Zhao, Y. Techno-economic analysis of air source heat pump combined with latent thermal energy storage applied for space heating in China. Appl. Therm. Eng. 2021, 185, 116434. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Mass flow of compressor air, kg/s | 0.33 |
| Mass flow of turbine air, kg/s | 1.167 |
| Air adiabatic exponent | 1.4 |
| The stage of compressor and turbine | 4 and 3 |
| Air storage tank volume, | 100 |
| Ambient temperature, °C | 20 |
| Ambient pressure, MPa | 0.1 |
| The temperature of the hot, HTF °C | 250 |
| The store thermal energy capacity, MJ | 447.4 |
| The temperature of the cold HTF, °C | 150 |
| The inlet compressed air temperature of the air turbine, °C | 200 |
| The area of the solar thermal energy collection field, | 2200 |
| The average solar irradiance in winter spring/fall and summer, | 838.2 / 991.4 / 1105.5 |
| The duration time of the collection, h | 5 |
| Efficiency of the solar thermal energy collection field | 64.2% |
| Charging time, h | 5 |
| Discharging time, h | 1.4 |
| Typical Solar hours/day, h in winter scenario | 12/20 (20 January) |
| Typical Solar hours/day, h in spring/fall scenarios | 3/20 and 9/23 (March and September) |
| Compressor | (MPa) | (MPa) | P (kW) | |||
|---|---|---|---|---|---|---|
| 1-stage | 0.1013 | 0.309 | 20 | 143.7 | 41.67 | 88.43% |
| 2-stage | 0.303 | 0.924 | 45 | 178.8 | 46.11 | 88.44% |
| 3-stage | 0.91 | 2.73 | 45 | 177.3 | 45.57 | 88.46% |
| 4-stage | 2.68 | 8.16 | 45 | 179.6 | 46.37 | 88.25% |
| Turbine | (MPa) | (MPa) | P (kW) | |||
|---|---|---|---|---|---|---|
| 1-stage | 2.846 | 0.95 | 200 | 90 | 123.9 | 86.95% |
| 2-stage | 0.93 | 0.31 | 200 | 90 | 123.7 | 86.92% |
| 3-stage | 0.304 | 0.013 | 200 | 90 | 123.6 | 86.92% |
| Scenarios Season | Mode | PDN (USD) | DHN (USD) | SUM (USD) |
|---|---|---|---|---|
| Winter | MEN with SA-CAES | 2282.2 | 4690.2 | 6972.4 |
| Conventional MEN | 2688.5 | 4616.9 | 7305.4 | |
| Spring and Fall | MEN with SA-CAES | 1982.2 | 2690.2 | 4672.4 |
| Conventional MEN | 2186.4 | 2760.3 | 4946.7 | |
| Summer | MEN with SA-CAES | 1893.2 | 2135.2 | 4028.4 |
| Conventional MEN | 2065.3 | 2332.4 | 4397.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Zong, M.; Chen, X.; Si, Y.; Chen, L.; Guo, Y.; Mei, S. Economic Optimization Dispatch Model of a Micro-Network with a Solar-Assisted Compressed Air Energy Storage Hub, with Consideration of Its Operationally Feasible Region. Processes 2022, 10, 963. https://doi.org/10.3390/pr10050963
Yang L, Zong M, Chen X, Si Y, Chen L, Guo Y, Mei S. Economic Optimization Dispatch Model of a Micro-Network with a Solar-Assisted Compressed Air Energy Storage Hub, with Consideration of Its Operationally Feasible Region. Processes. 2022; 10(5):963. https://doi.org/10.3390/pr10050963
Chicago/Turabian StyleYang, Libin, Ming Zong, Xiaotao Chen, Yang Si, Laijun Chen, Yongqing Guo, and Shengwei Mei. 2022. "Economic Optimization Dispatch Model of a Micro-Network with a Solar-Assisted Compressed Air Energy Storage Hub, with Consideration of Its Operationally Feasible Region" Processes 10, no. 5: 963. https://doi.org/10.3390/pr10050963






