Novel Approaches Concerning the Numerical Modeling of Particle and Cell Separation in Microchannels: A Review
Abstract
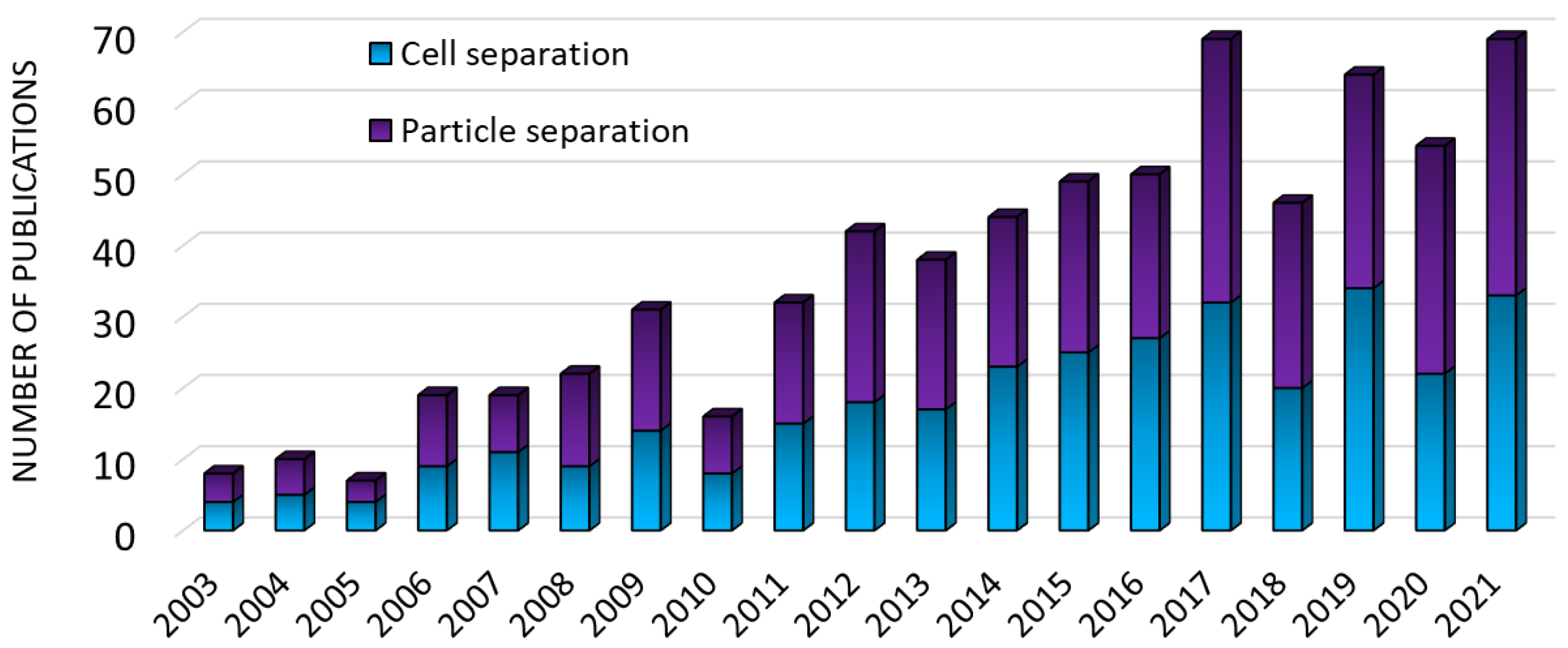
:1. Introduction
2. Principles and Numerical Modeling of the Active Microfluidic Particle Separation
2.1. Approaches to Model the Microfluidic Separation of Suspended Particles/Cells
2.2. Forces Acting on the Material
2.2.1. Fluid and Gravity Forces
2.2.2. Separation Forces
Magnetic Forces
Electric Forces
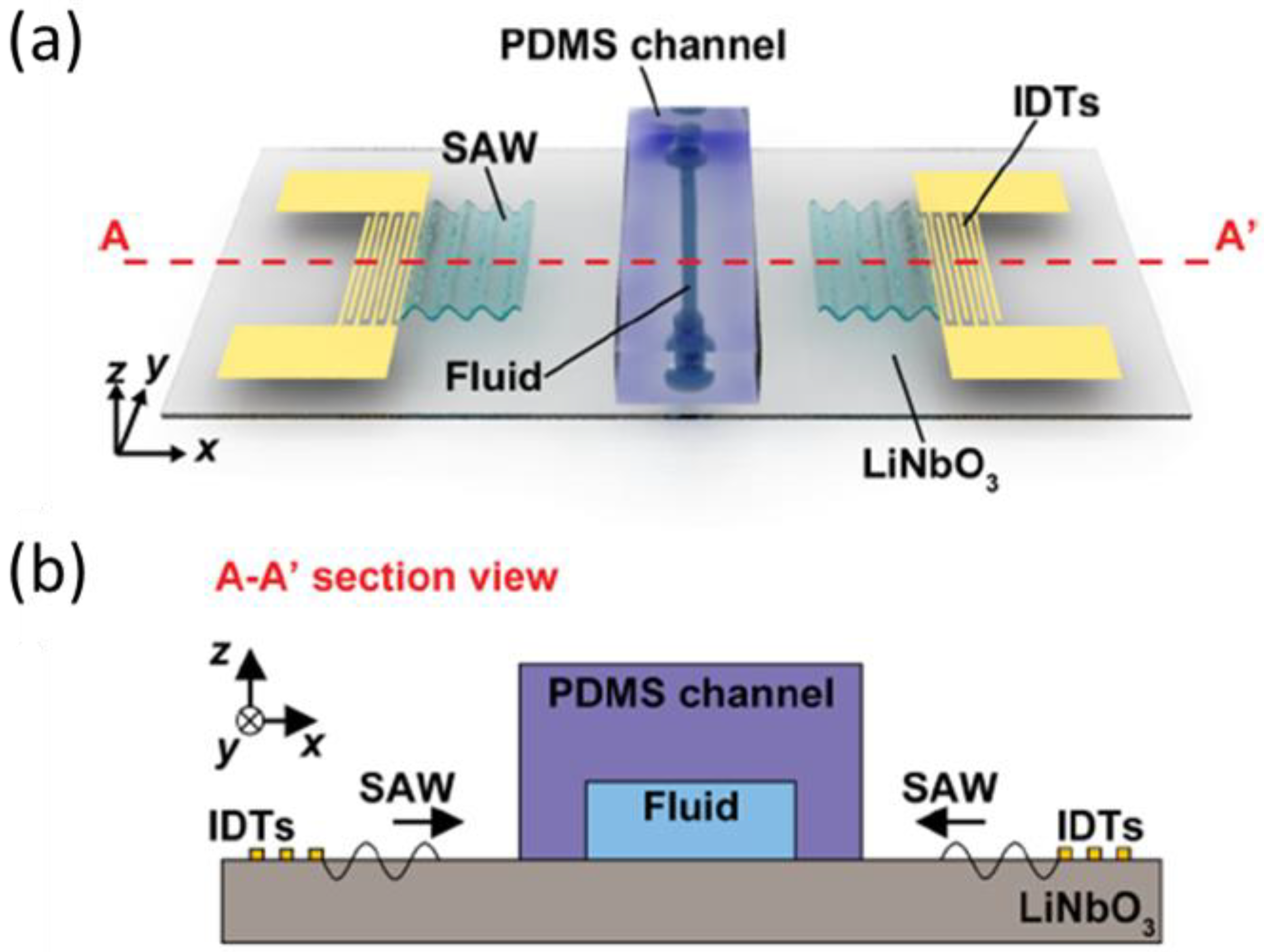
Acoustic Forces
2.3. Numerical Methods
2.3.1. Finite Element Method
2.3.2. Finite Volume Method
2.3.3. Mesh Dependency Analysis
3. Recent Simulation Studies
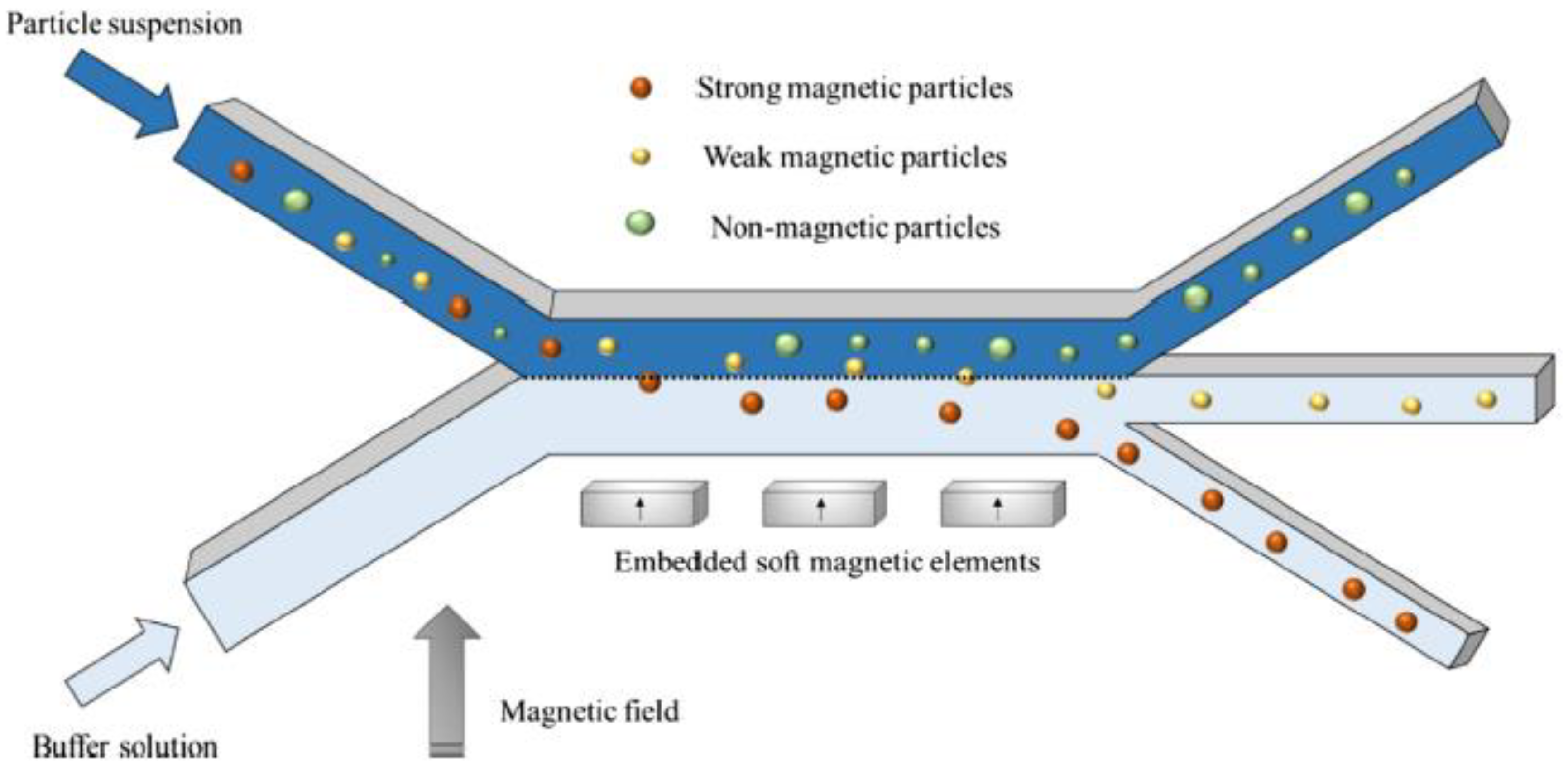
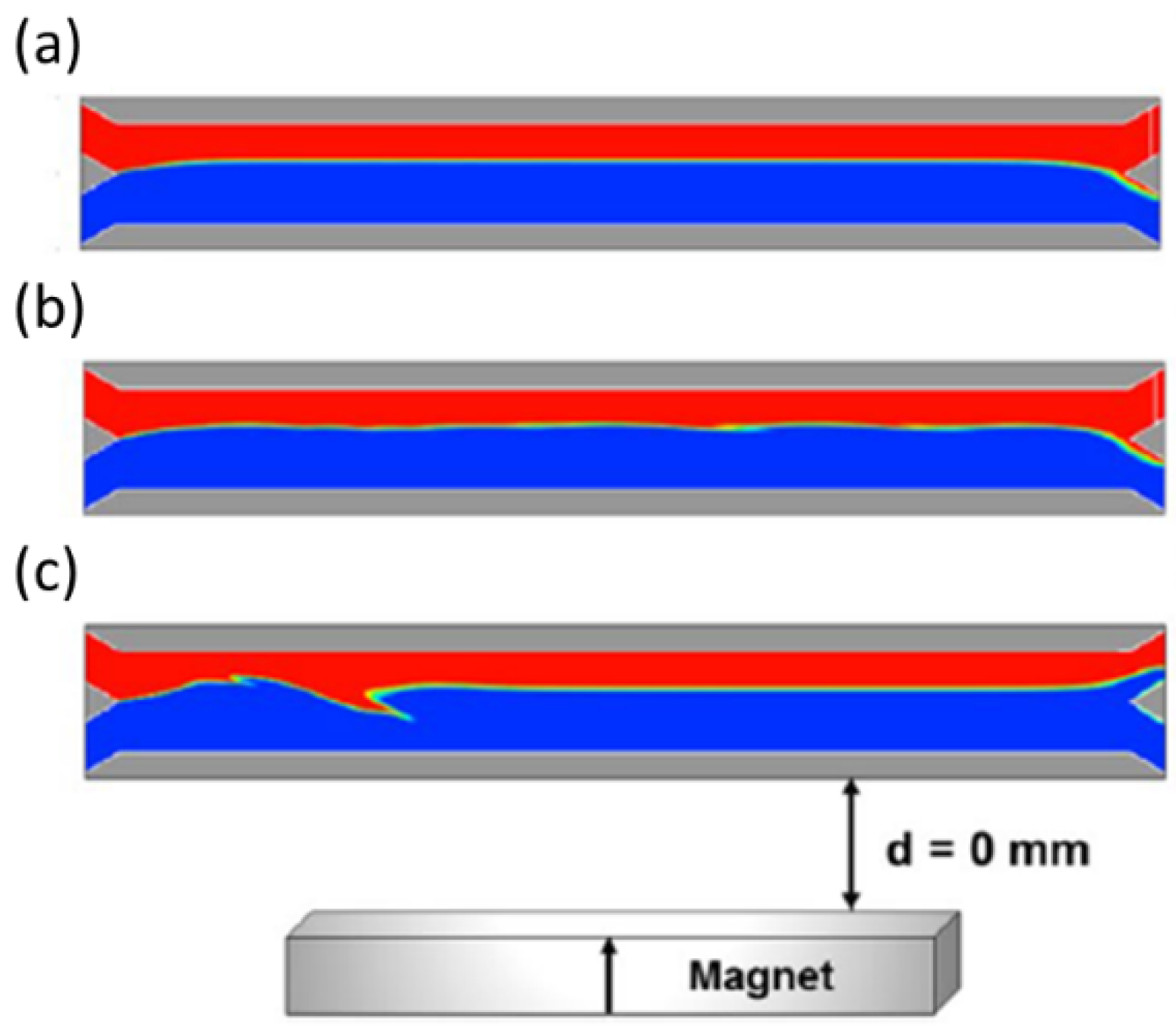
3.1. Magnetic Separation
3.2. Dielectrophoretic Separation
3.3. Acoustophoretic Separation
4. Conclusions and Further Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Richard, C.; Fakhfouri, A.; Colditz, M.; Striggow, F.; Kronstein-Wiedemann, R.; Tonn, T.; Medina-Sánchez, M.; Schmidt, O.G.; Gemming, T.; Winkler, A. Blood platelet enrichment in mass-producible surface acoustic wave (SAW) driven microfluidic chips. Lab. Chip 2019, 19, 4043. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yousuff, C.M.; Pavithra devi, E.; Swetha, C.; Ramya, R. Acoustic Based Separation of Blood Cells Using Microfluidic Device. In 2021 Seventh International Conference on Bio Signals, Images, and Instrumentation (ICBSII); IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Rahman, M.R.U.; Kwak, T.J.; Woehl, J.C.; Chang, W.J. Quantitative analysis of the three-dimensional trap stiffness of a dielectrophoretic corral trap. Electrophoresis 2021, 42, 644–655. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Pastora, J.; Bringas, E.; Lázaro-Díez, M.; Ramos-Vivas, J.; Ortiz, I. The reverse of controlled release: Controlled sequestration of species and biotoxins into nanoparticles (NPs). In Drug Delivery Systems; Stroeve, P., Mahmoudi, M., Eds.; World Scientific: Hackensack, NJ, USA, 2017; pp. 207–244. [Google Scholar]
- Collins, D.J.; O’Rorke, R.; Neild, A.; Han, J.; Ai, Y. Acoustic fields and microfluidic patterning around embedded micro-structures subject to surface acoustic waves. Soft Matter 2019, 15, 8691. [Google Scholar] [CrossRef]
- González Fernández, C.; Gómez-Pastora, J.; Basauri, A.; Fallanza, M.; Bringas, E.; Chalmers, J.J.; Ortiz, I. Continuous-flow separation of magnetic particles from biofluids: How does the microdevice geometry determine the separation performance? Sensors 2020, 20, 3030. [Google Scholar] [CrossRef] [PubMed]
- Weigand, M.; Gómez-Pastora, J.; Palmer, A.; Zborowski, M.; Desai, P.; Chalmers, J. Continuous-Flow Magnetic Fractionation of Red Blood Cells Based on Hemoglobin Content and Oxygen Saturation—Clinical Blood Supply Implications and Sickle Cell Anemia Treatment. Processes 2022, 10, 927. [Google Scholar] [CrossRef]
- Taatizadeh, E.; Dalili, A.; Rellstab-Sanchez, P.I.; Tahmooressi, H.; Ravishankara, A.; Tasnim, N.; Najjaran, H.; Li, I.T.S.; Hoorfar, M. Micron-sized particle separation with standing surface acoustic wave—Experimental and numerical approaches. Ultrason. Sonochem. 2021, 76, 105651. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X. Blood cells separation microfluidic chip based on dielectrophoretic force. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 206. [Google Scholar] [CrossRef]
- Kim, J.; Gómez-Pastora, J.; Weigand, M.; Potgieter, M.; Walters, N.A.; Reátegui, E.; Palmer, A.F.; Yazer, M.; Zborowski, M.; Chalmers, J.J. A Subpopulation of Monocytes in Normal Human Blood Has Significant Magnetic Susceptibility: Quantification and Potential Implications. Cytometry A 2019, 95, 478–487. [Google Scholar] [CrossRef]
- Rahman, M.R.U.; Kwak, T.J.; Woehl, J.C.; Chang, W.J. Characterization of stiffness of micro-particle trapped in dielectrophoretic-microfluidic device. In 2020 2nd International Conference on Advanced Information and Communication Technology (ICAICT); IEEE: Piscataway, NJ, USA, 2020; pp. 94–98. [Google Scholar] [CrossRef]
- Weigand, M.R.H.; Gómez-Pastora, J.; Kim, J.; Kurek, M.T.; Hickey, R.J.; Irwin, D.C.; Buehler, P.W.; Zborowski, M.; Palmer, A.F.; Chalmers, J.J. Magnetophoretic and spectral characterization of oxyhemoglobin and deoxyhemoglobin: Chemical versus enzymatic processes. PLoS ONE 2021, 16, e0257061. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Kim, J.; Multanen, V.; Weigand, M.; Walters, N.A.; Reátegui, E.; Palmer, A.F.; Yazer, M.H.; Zborowski, M.; Chalmers, J.J. Intrinsically magnetic susceptibility in human blood and its potential impact on cell separation: Non-classical and intermediate monocytes have the strongest magnetic behavior in fresh human blood. Exp. Hematol. 2021, 99, 21–31. [Google Scholar] [CrossRef]
- Simon, G.; Andrade, M.A.B.; Desmulliez, M.P.Y.; Riehle, M.O.; Bernassau, A.L. Theoretical Framework of Radiation Force in Surface Acoustic Waves for Modulated Particle Sorting. Period. Polytech. Electr. Eng. Comput. Sci. 2019, 63, 77–84. [Google Scholar] [CrossRef]
- Ettehad, H.M.; Zarrin, P.S.; Hölzel, R.; Wenger, C. Dielectrophoretic Immobilization of Yeast Cells Using CMOS Integrated Microfluidics. Micromachines 2020, 11, 501. [Google Scholar] [CrossRef] [PubMed]
- Gupta, T.; Ghosh, R.; Ganguly, R. Acoustophoretic separation of infected erythrocytes from blood plasma in a microfluidic platform using biofunctionalized, matched-impedance layers. Int. J. Numer. Method. Biomed. Eng. 2018, 34, e2943. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Gómez-Pastora, J.; Gilbert, C.J.; Weigand, M.; Walters, N.A.; Reátegui, E.; Palmer, A.F.; Yazer, M.; Zborowski, M.; Chalmers, J.J. Quantification of the mean and distribution of hemoglobin content in normal human blood using cell tracking velocimetry. Anal. Chem. 2020, 92, 1956–1962. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Weigand, M.; Kim, J.; Palmer, A.F.; Yazer, M.; Desai, P.C.; Zborowski, M.; Chalmers, J.J. Potential of Cell Tracking Velocimetry as an Economical and Portable Hematology Analyzer. Sci. Rep. 2022, 12, 1692. [Google Scholar] [CrossRef]
- Liu, G.; He, F.; Li, Y.; Zhao, H.; Li, X.; Tang, H.; Li, Z.; Yang, Z.; Zhang, Y. Effects of two surface acoustic wave sorting chips on particles multi-level sorting. Biomed. Microdevices 2019, 21, 59. [Google Scholar] [CrossRef]
- Siani, O.Z.; Targhi, M.Z.; Sojoodi, M.; Movahedin, M. Dielectrophoretic separation of monocytes from cancer cells in a microfluidic chip using electrode pitch optimization. Bioprocess Biosyst. Eng. 2020, 43, 1573–1586. [Google Scholar] [CrossRef]
- González-Fernández, C.; Gómez-Pastora, J.; Bringas, E.; Zborowski, M.; Chalmers, J.J.; Ortiz, I. Recovery of Magnetic Catalysts: Advanced Design for Process Intensification. Ind. Eng. Chem. Res. 2022, 60, 16780–16790. [Google Scholar] [CrossRef]
- Wu, X.; Gómez-Pastora, J.; Zborowski, M.; Chalmers, J. SPIONs Self-Assembly and Magnetic Sedimentation in Quadrupole Magnets: Gaining Insight into the Separation Mechanisms. Sep. Purif. Technol. 2022, 280, 119786. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Bringas, E.; Ortiz, I. Design of novel adsorption processes for the removal of arsenic from polluted groundwater employing functionalized magnetic nanoparticles. Chem. Eng. Trans. 2016, 47, 241–246. [Google Scholar]
- Lei, J.; Cheng, F.; Li, K.; Guo, Z. Numerical simulation of continuous separation of microparticles in two-stage acousto-microfluidic systems. Appl. Math. Model. 2020, 83, 342–356. [Google Scholar] [CrossRef]
- Roodan, V.A.; Gómez-Pastora, J.; Karampelas, I.H.; González-Fernández, C.; Bringas, E.; Ortiz, I.; Chalmers, J.J.; Furlani, E.P.; Swihart, M.T. Formation and manipulation of ferrofluid droplets with magnetic fields in a microdevice: A numerical parametric study. Soft Matter 2020, 16, 9506–9518. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.V.; Manh, T.L.; Nguyen, T.S.; Le, V.T.; Hieu, N.V. Applied electric field analysis and numerical investigations of the continuous cell separation in a dielectrophoresis-based microfluidic channel. J. Sci. Adv. Mater. Devices 2021, 6, 11–18. [Google Scholar] [CrossRef]
- Khashan, S.A.; Alazzam, A.; Mathew, B.; Hamdan, M. Mixture model for biomagnetic separation in microfluidic systems. J. Magn. Magn. Mater. 2017, 442, 118–127. [Google Scholar] [CrossRef]
- Scopus Database. Available online: www.scopus.com (accessed on 2 January 2022).
- Castillo-Torres, K.Y.; McLamore, E.S.; Arnold, D.P. A High-Throughput Microfluidic Magnetic Separation (µFMS) Platform for Water Quality Monitoring. Micromachines 2020, 11, 16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Omer, S.; Suhyrani, I.; Deng, Y. Cell Separation Using Simple Microchip Configuration Experimental and Simulation Analysis. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017; pp. 378–382. [Google Scholar] [CrossRef]
- Golozar, M.; Molki, M.; Darabi, J. Computational and performance analysis of a continuous magnetophoretic bioseparation chip with alternating magnetic fields. Microfluid. Nanofluid. 2017, 21, 73. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; González-Fernández, C.; Real, E.; Iles, A.; Bringas, E.; Furlani, E.P.; Ortiz, I. Computational modeling and fluorescence microscopy characterization of a two-phase magnetophoretic microsystem for continuous-flow blood detoxification. Lab Chip 2018, 18, 1593–1606. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Karampelas, I.H.; Bringas, E.; Furlani, E.P.; Ortiz, I. Numerical analysis of bead magnetophoresis from flowing blood in a continuous-flow microchannel: Implications to the bead-fluid interactions. Sci. Rep. 2019, 9, 7265. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Moore, L.; Xue, W.; Kim, J.; Zborowski, M.; Chalmers, J.J. Correlation of simulation/finite element analysis to the separation of intrinsically magnetic spores and red blood cells using a microfluidic magnetic deposition system. Biotechnol. Bioeng. 2018, 115, 1288–1300. [Google Scholar] [CrossRef]
- Cao, Q.; Li, Z.; Wang, Z.; Qi, F.; Han, X. Disaggregation and separation dynamics of magnetic particles in a microfluidic flow under an alternating gradient magnetic field. J. Phys. D Appl. Phys. 2018, 51, 195002. [Google Scholar] [CrossRef]
- Civelekoglu, O.; Wang, N.; Boya, M.; Ozkaya-Ahmadov, T.; Liu, R.; Sarioglu, A.F. Electronic profiling of membrane antigen expression via immunomagnetic cell manipulation. Lab Chip 2019, 19, 2444. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cardoso, V.F.; Miranda, D.; Botelho, G.; Minas, G.; Lanceros-Méndez, S. Highly effective clean-up of magnetic nanoparticles using microfluidic technology. Sens. Actuators B Chem. 2018, 255, 2384–2391. [Google Scholar] [CrossRef]
- Munaz, A.; Shiddiky, M.J.A.; Nguyen, N.T. Magnetophoretic separation of diamagnetic particles through parallel ferrofluid streams. Sens. Actuators B Chem. 2018, 275, 459–469. [Google Scholar] [CrossRef]
- Samla, G.; Gan, K.B.; Then, S.M. Modeling microfluidic DNA extraction using superparamagnetic bead particles in COMSOL multiphysics simulation. Microsyst. Technol. 2017, 23, 4435–4440. [Google Scholar] [CrossRef]
- Balakrishnan, S.G.; Ahmad, M.R.; Koloor, S.S.R.; Petrů, M. Separation of ctDNA by superparamagnetic bead particles in microfluidic platform for early cancer detection. J. Adv. Res. 2021, 33, 109–116. [Google Scholar] [CrossRef]
- Kasetsirikul, S.; Srituravanich, W.; Piyaviriyakul, P.; Pimpin, A. Separation of Magnetic Particles Using an Array of Magnets —A Model of a Separation Device for Malaria-Infected Blood Cells. Sens. Mater. 2017, 29, 281–291. [Google Scholar]
- Gauri, S.; Gan, K.B.; Then, S.M. Simulation of DNA extraction and separation from salivary fluid by superparamagnetic beads and electromagnetic field in microfluidic platform. Microsyst. Technol. 2019, 25, 1379–1385. [Google Scholar] [CrossRef]
- Wu, J.; Yan, Q.; Xuan, S.; Gong, X. Size—Selective separation of magnetic nanospheres in a microfluidic channel. Microfluid. Nanofluid. 2017, 21, 47. [Google Scholar] [CrossRef]
- Fikar, P.; Georgiev, V.; Lissorgues, G.; Holubova, M.; Lysak, D.; Georgiev, D. 2DEP cytometry: Distributed dielectrophoretic cytometry for live cell dielectric signature measurement on population level. Biomed. Microdevices 2018, 20, 12. [Google Scholar] [CrossRef]
- Rafiefard, N.; Sasanpour, P.; Fardindoost, S.; Irajizad, A. A Novel Approach for Microparticle Separation Based on Dielectrophoresis Method. Biomed. Phys. Eng. Express 2019, 5, 035004. [Google Scholar] [CrossRef]
- Kumar, C.L.; Juliet, A.V.; Ramakrishna, B.; Chakraborty, S.; Mohammed, M.A.; Sunny, K.A. Computational Microfluidic Channel for Separation of Escherichia coli from Blood-Cells. Comput. Mater. Contin. 2021, 67, 1369–1384. [Google Scholar]
- Praveenkumar, S.; Srigitha, S.N.; Dinesh, R.G.; Ramesh, R. Computational Modeling of Dielectrophoretic Microfluidic Channel for Simultaneous Separation of Red Blood Cells and Platelets. Curr. Signal Transduct. Ther. 2020, 15, 243–251. [Google Scholar] [CrossRef]
- Teoh, B.Y.; Lee, P.F.; Thong, Y.L.; Lim, Y.M. Design Of DC-Dielectrophoresis Microfluidic Channel For Particle and Biological Cell Separation Using 3D Printed PVA Material. In 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES); IEEE: Piscataway, NJ, USA, 2018; pp. 566–570. [Google Scholar] [CrossRef]
- Tirapu-Azpiroz, J.; Temiz, Y.; Delamarche, E. Dielectrophoretic microbead sorting using modular electrode design and capillary-driven microfluidics. Biomed. Microdevices 2017, 19, 95. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, X. Dielectrophoretic microfluidic device for separation of red blood cells and platelets: A model—Based study. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 89. [Google Scholar] [CrossRef]
- Chiriac, E.; Avram, M.; Bălan, C. Dielectrophoretic separation of Circulating Tumor Cells and Red Blood Cells in a microfluidic device. In Proceedings of the 2020 International Semiconductor Conference (CAS), Sinaia, Romania, 7–9 October 2020; pp. 211–214. [Google Scholar] [CrossRef]
- Chen, L.; Liu, X.; Zheng, X.; Zhang, X.; Yang, J.; Tian, T.; Liao, Y. Dielectrophoretic Separation of Particles Using Microfluidic Chip with Composite Three-Dimensional Electrode. Micromachines 2020, 11, 700. [Google Scholar] [CrossRef] [PubMed]
- Thomas, R.S.W.; Mitchell, P.D.; Oreffo, R.O.C.; Morgan, H.; Green, N.G. Image-based sorting and negative dielectrophoresis for high purity cell and particle separation. Electrophoresis 2019, 40, 2718–2727. [Google Scholar] [CrossRef]
- Valijam, S.; Salehi, A. Influence of the obstacles on dielectrophoresis—Assisted separation in microfluidic devices for cancerous cells. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 134. [Google Scholar] [CrossRef]
- Rashid, N.F.A.; Deivasigamani, R.; Wee, M.F.M.R.; Hamzah, A.A.; Buyong, M.R. Integration of a Dielectrophoretic Tapered Aluminum Microelectrode Array with a Flow Focusing Technique. Sensors 2021, 21, 4957. [Google Scholar] [CrossRef]
- Chiriac, E.; Avram, M.; Bălan, C. Manipulation of particles using dielectrophoresis in a microchannel. Rom. J. Inf. Sci. Technol. 2021, 24, 213–221. [Google Scholar]
- Shamloo, A.; Kamali, A. Numerical Analysis of a Dielectrophoresis Field-flow Fractionation Device for the Separation of Multiple Cell Types. J. Sep. Sci. 2017, 40, 4067–4075. [Google Scholar] [CrossRef]
- Derakhshan, R.; Ramiar, A.; Ghasemi, A. Numerical investigation into continuous separation of particles and cells in a two-component fluid flow using dielectrophoresis. J. Mol. Liq. 2020, 310, 113211. [Google Scholar] [CrossRef]
- Davanlou, A.; Reddy, V. Numerical Simulation and Optimization of Electric Field-Based Sorting in Particle Laden Flows in Microchannels. In Proceedings of the ASME 2018 5th Joint US-European Fluids Engineering Division Summer Meeting, Montreal, QC, Canada, 24 October 2018; Volume 2. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, X.; Ren, Y.; Yan, Y.; Wu, A. Numerical simulation of circulating tumor cell separation in a dielectrophoresis based Y-Y shaped microfluidic device. Sep. Purif. Technol. 2021, 255, 117343. [Google Scholar] [CrossRef]
- Aghaamoo, M.; Aghilinejad, A.; Chen, X. Numerical study of insulator-based dielectrophoresis method for circulating tumor cell separation. In Proceedings of the SPIE 10061, Microfluidics, BioMEMS, and Medical Microsystems XV, San Francisco, CA, USA, 28 January 2017; p. 100611A. [Google Scholar] [CrossRef]
- Ansar, M.Z.B.I.; Tirth, V.; Yousuff, C.M.; Shukla, N.K.; Islam, S.; Irshad, K.; Aarif, M.K.O. Simulation Guided Microfluidic Design for Multitarget Separation Using Dielectrophoretic Principle. BioChip J. 2020, 14, 390–404. [Google Scholar]
- Alnaimat, F.; Mathew, B.; Alazzam, A. Simulation of a microfluidic device employing dielectrophoresis for liquid biopsy. Med. Eng. Phys. 2020, 81, 130–135. [Google Scholar] [CrossRef]
- Sahin, O.; Elitas, M.; Yapici, M.K. Simulation of Dielectrophoresis based Separation of Red Blood Cells (RBC) from Bacteria Cells. In 2020 21st International Conference on Thermal, Mechanical and Multi-Physics Simulation and Experiments in Microelectronics and Microsystems (EuroSimE); IEEE: Piscataway, NJ, USA, 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Song, Y.; Han, X.; Li, D.; Liu, Q.; Li, D. Simultaneous and continuous particle separation and counting via localized DC-dielectrophoresis in a microfluidic chip. RSC Adv. 2021, 11, 3827. [Google Scholar] [CrossRef]
- Ettehad, H.M.; Yadav, R.K.; Guha, S.; Wenger, C. Towards CMOS Integrated Microfluidics Using Dielectrophoretic Immobilization. Biosensors 2019, 9, 77. [Google Scholar] [CrossRef] [Green Version]
- Shirmohammadli, V.; Manavizadeh, N. Application of Differential Electrodes in a Dielectrophoresis-Based Device for Cell Separation. IEEE Trans. Electron Devices 2019, 66, 4075–4080. [Google Scholar] [CrossRef]
- Jiang, T.; Ren, Y.; Liu, W.; Tang, D.; Tao, Y.; Xue, R.; Jiang, H. Dielectrophoretic separation with a floating-electrode array embedded in microfabricated fluidic networks. Phys. Fluids 2018, 30, 112003. [Google Scholar] [CrossRef]
- Nada, A.; Omar, M.; Sayed, A.M. Separation Modeling of Blood Cells using Dielectrophoretic Field Flow. Int. J. Comput. Appl. 2018, 181, 36–41. [Google Scholar] [CrossRef]
- Samandari, M.; Abrinia, K.; Sanati-Nezhad, A. Acoustic Manipulation of Bio-Particles at High Frequencies: An Analytical and Simulation Approach. Micromachines 2017, 8, 290. [Google Scholar] [CrossRef] [Green Version]
- Shamloo, A.; Boodaghi, M. Design and simulation of a microfluidic device for acoustic cell separation. Ultrasonics 2018, 84, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Baek, J.; Kang, B.; Rhyou, C.; Lee, H. Effect of the sound speed mismatch between fluid and channel on the particle alignment in a standing surface acoustic wave device. Sens. Actuators B Chem. 2021, 346, 130442. [Google Scholar] [CrossRef]
- Karthick, S.; Sen, A.K. Improved Understanding of Acoustophoresis and Development of an Acoustofluidic Device for Blood Plasma Separation. Phys. Rev. Appl. 2018, 10, 034037. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, X. Particle separation in microfluidics using different modal ultrasonic standing waves. Ultrason. Sonochem. 2021, 75, 105603. [Google Scholar] [CrossRef]
- Klymkovych, T.; Bokla, N.; Matviykiv, O.; Stakhiv, V. Simulation and Analysis of Microparticles Acoustophoretic Separation in Multi-Channel Lab-Chip Device. In 2021 IEEE 16th International Conference on the Experience of Designing and Application of CAD Systems (CADSM); IEEE: Piscataway, NJ, USA, 2021; pp. 29–33. [Google Scholar] [CrossRef]
- Wang, Z.; Qian, L.; Jiang, Z.; Xue, X.; Reddy, K. Vibration effects of standing surface acoustic wave for separating suspended particles in lubricating oil. AIP Adv. 2020, 10, 045013. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Pastora, J.; Wu, X.; Chalmers, J.J. Magnetic separation of micro- and nanoparticles for water treatment processes. In Solid-Liquid Separation Technologies; CRC Press: Boca Raton, FL, USA, 2022; pp. 211–232. [Google Scholar]
- Furlani, E.P. Magnetic Biotransport: Analysis and Applications. Materials 2010, 3, 2412–2446. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Pastora, J.; Xue, X.; Karampelas, I.H.; Bringas, E.; Furlani, E.P.; Ortiz, I. Analysis of separators for magnetic beads recovery: From large systems to multifunctional microdevices. Sep. Purif. Technol. 2017, 172, 16–31. [Google Scholar] [CrossRef]
- Douglas, T.A.; Cemazar, J.; Balani, N.; Sweeney, D.C.; Schmelz, E.M.; Davalos, R.V. A feasibility study for enrichment of highly aggressive cancer subpopulations by their biophysical properties via dielectrophoresis enhanced with synergistic fluid flow. Electrophoresis 2017, 38, 1507–1514. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Karampelas, I.H.; Xue, X.; Bringas, E.; Furlani, E.P.; Ortiz, I. Magnetic bead separation from flowing blood in a two-phase continuous-flow magnetophoretic microdevice: Theoretical analysis through computational fluid dynamics simulation. J. Phys. Chem. C 2017, 121, 7466–7477. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Wu, X.; Sundar, N.; Alawi, J.; Nabar, G.; Winter, J.O.; Zborowski, M.; Chalmers, J. Self-assembly and sedimentation of 5 nm SPIONs using horizontal, high magnetic fields and gradients. Sep. Purif. Technol. 2020, 248, 117012. [Google Scholar] [CrossRef]
- Rapp, B.E. Microfluidics: Modeling, Mechanics and Mathematics; Elsevier: Oxford, UK, 2017. [Google Scholar]
- Weigand, M.; Gómez-Pastora, J.; Strayer, J.; Wu, X.; Choe, H.; Lu, S.; Plencner, E.; Landes, K.; Palmer, A.; Zborowski, M.; et al. The Unique Magnetic Signature of Sickle Red Blood Cells: A Comparison between the Red Blood Cells of Transfused and Non-Transfused Sickle Cell Disease Patients and Healthy Donors. IEEE Trans. Biomed. Eng. 2022, under review. [Google Scholar] [CrossRef]
- Gómez-Pastora, J.; Amiri Roodan, V.; Karampelas, I.H.; Alorabi, A.Q.; Tarn, M.D.; Iles, A.; Bringas, E.; Paunov, V.N.; Pamme, N.; Furlani, E.P.; et al. Two-step numerical approach to predict ferrofluid droplet generation and manipulation inside multilaminar flow chambers. J. Phys. Chem. C 2019, 123, 10065–10080. [Google Scholar] [CrossRef]


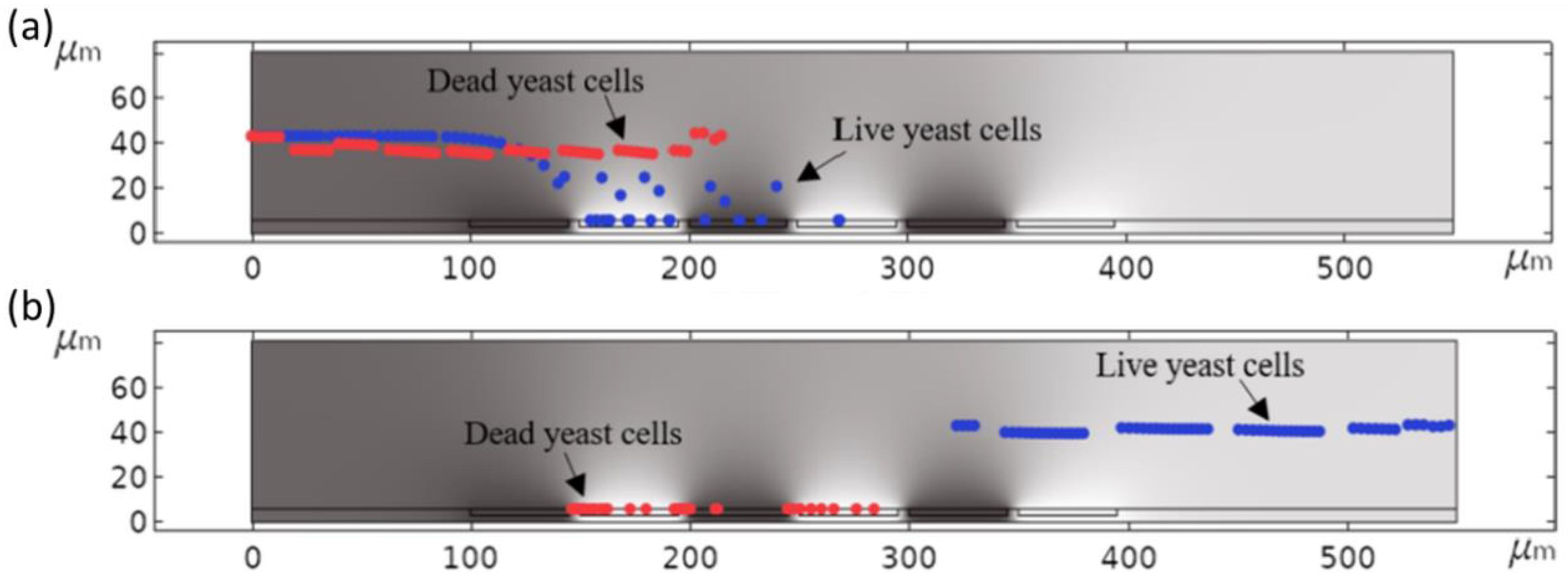
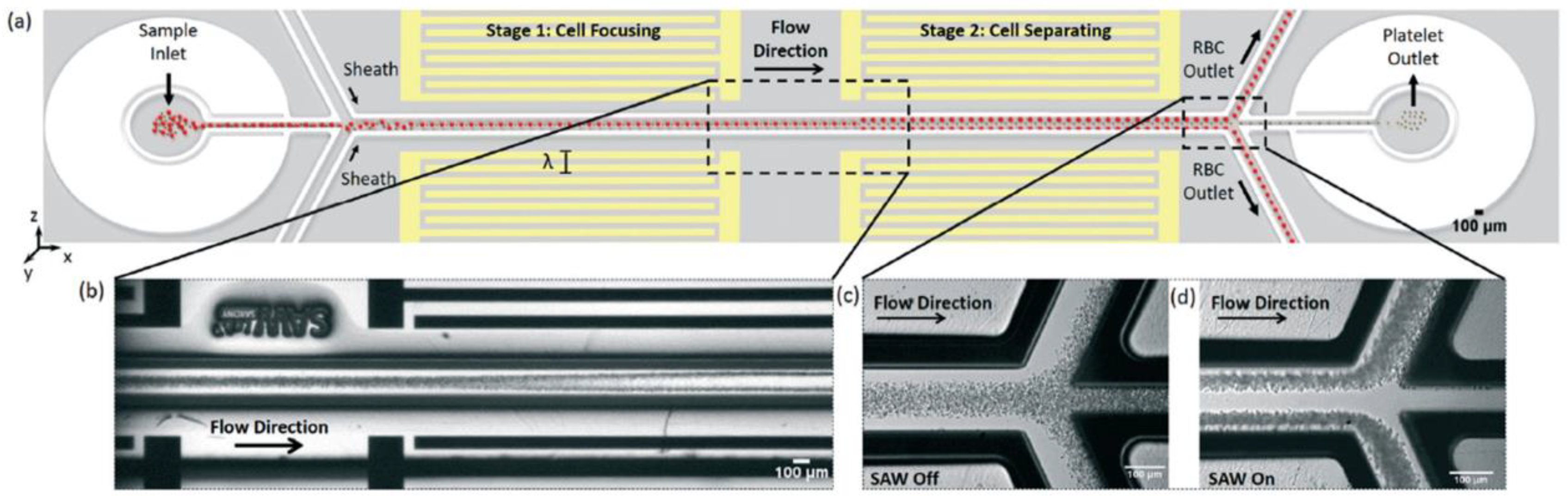
| Material to Be Separated | Fluid Medium | Fluid Velocity or Flow Rate | Magnetic Field Source | Simulation Software | Experimental Validation | Reference |
|---|---|---|---|---|---|---|
| Bacteria (E. coli) conjugated to magnetic disks (1.5 µm) | Aqueous solution | 5–120 µL/s | 3 × 3 NdFeB magnets | COMSOL Multiphysics | Yes | [29] |
| Circulating tumor cells (CTCs, MCF-7) conjugated to magnetic beads | Aqueous solution | - | Permanent magnet | COMSOL Multiphysics | Yes | [30] |
| Magnetic beads (1–4.5 µm) conjugated to cells (10–30 µm) | Aqueous solution | 100–250 mL/h | 16 NdFeB magnets | OpenFOAM | Yes | [31] |
| Magnetic beads (2.29 and 4.9 µm) | Blood and aqueous solution | Up to 1.5 µL/s | Permanent magnet | Flow-3D | Yes | [32] |
| Magnetic beads (5 µm) | Blood and aqueous solution | Up to 3.5 cm/s | Permanent magnet | Flow-3D | No | [33] |
| Red blood cells (RBCs) and Bacillus spores | Aqueous solution | 0.1–10 mL/h | Permanent magnets | Custom program (Maple and MATLAB) | Yes | [34] |
| Magnetic beads (4 and 8 µm) | Water | 1 mm/s | Electromagnetic coils | - | No | [35] |
| Cancer cells (MCF-7 and MDA-MB-231) attached to magnetic beads (1 µm) | Aqueous solution | - | NdFeB magnet | COMSOL Multiphysics | Yes | [36] |
| Iron oxide nanoparticles (10 nm) | Aqueous solution | 5–100 µL/min | NdFeB magnet | COMSOL Multiphysics | Yes | [37] |
| Diamagnetic (polyethylene) beads (3.2 and 4.8 µm) | Ferrofluid | 0.5–2 µL/min | 5 NdFeB magnets | COMSOL Multiphysics | Yes | [38] |
| Magnetic beads (1.05 and 2.8 µm) | Aqueous solution | 3 mm/s | Soft magnetic elements (Permalloy) externally magnetized (NdFeB magnet) | ANSYS FLUENT | No | [27] |
| DNA attached to magnetic beads (2.8 µm) | Aqueous solution | 5–10 µL/min | Magnet array | COMSOL Multiphysics | No | [39] |
| DNA attached to magnetic beads (1 µm) | Aqueous solution | 5–10 µL/min | Permanent magnet | COMSOL Multiphysics | No | [40] |
| Malaria infected RBCs and magnetic particles (4.8 and 9.6 µm) | Water | 0.18–20 µL/min | Magnet array | COMSOL Multiphysics and MATLAB | Yes | [41] |
| DNA attached to magnetic beads (2.8 µm) | Water | 5–15 µL/min | Electromagnetic coil | COMSOL Multiphysics and MATLAB | No | [42] |
| Magnetic particles (40–280 nm) | Aqueous solution | 0.01–0.04 mL/h | NdFeB magnet | COMSOL Multiphysics and MATLAB | Yes | [43] |
| Material to Be Separated | Fluid Medium | Fluid Velocity or Flow Rate | Electric Field (Frequency/Voltage) | Simulation Software | Experimental Validation | Reference |
|---|---|---|---|---|---|---|
| Polystyrene (PE) beads (8 µm) and leukemia cells (K562, KG1) | Aqueous solutions | 40–50 nL/s | F = 300 kHz, 10 MHz (0.5–5 V) | COMSOL Multiphysics | Yes | [44] |
| PE beads (2, 6, 8 µm) | Water | 0.13 mm/s | F = 500 kHz (0.2 V) | FEM algorithm | Yes | [45] |
| CTCs (MDA-MB-231 breast cancer cells) from RBCs | Phosphate buffer saline (PBS) | 0.5–2.5 µL/min | F = 1 kHz (10 V) | COMSOL Multiphysics | No | [2] |
| Platelets, white blood cells (WBCs) and RBCs | Aqueous solutions | 100–800 µm/s | F = 0.1–1000 kHz (3–5 V) | COMSOL Multiphysics | Yes | [9] |
| PE beads (0.5–2 µm) | Water | No flow | F = 1 MHz (6 V) | COMSOL Multiphysics | Yes | [11] |
| E. coli from RBCs and platelets | Aqueous solutions | 134–853 µm/s | F = 1 Hz to 1 THz (0–130 V) | COMSOL Multiphysics | Yes | [46] |
| Platelets and RBCs from blood | Plasma | 150–850 µm/s | F = 100 kHz (5 V) | COMSOL Multiphysics | No | [47] |
| Cancer cells (Raji cells) from PE beads | Aqueous solutions | 1 mL/min | 0.5–2.5 V | ANSYS Inc. software | Yes | [48] |
| Live and dead yeast cells (Saccharomyces cerevisiae RXII) | Water | 1 µm/s | F = 1 kHz–20 MHz (Up to 20 V) | COMSOL Multiphysics | Yes | [15] |
| PE beads (5 and 10 µm) | Water | 300 µm/s | F = 1 MHz (6–22 V) | COMSOL Multiphysics | Yes | [49] |
| RBCs and platelets | Aqueous solutions | 134–853 µm/s | F = 100 kHz (3–7 V) | COMSOL Multiphysics | Yes | [50] |
| RBCs and CTCs (MDA-MB-231, breast cancer cell) | Water | 500 µm/s | F = 100 kHz (10 V) | COMSOL Multiphysics | No | [51] |
| Monocytes from T-cell acute lymphoblastic leukemia (RPMI-8402) | Aqueous solutions | 0.8 mL/h | F = 110 kHz (up to 16.5 V) | COMSOL Multiphysics | Yes | [20] |
| PE beads (5, 10 and 20 µm) | PBS | 0.5–6 µL/min | F = 1 MHz (up to 40 V) | COMSOL Multiphysics | Yes | [52] |
| PE beads (5.5 and 15.6 µm) and osteosarcoma (MG-63 cells), and bone marrow cells | PBS | 20–100 nL/min | F = 1–5 MHz (5–12 V) | FlexPDE software | Yes | [53] |
| CTCs (MDA-MB231) and RBCs | Water | 134–800 µm/s | F = 10 kHz (8–12 V) | COMSOL Multiphysics | No | [54] |
| PE beads (1, 3.2, 10 µm) | Aqueous solutions | 100–500 µL/min | F = 150 kHz (10 V) | COMSOL Multiphysics | Yes | [55] |
| CTCs (MDA-MB-231) and RBCs | PBS | 180- 500 µm/s | F = 100 kHz (10 V) | COMSOL Multiphysics | Yes | [56] |
| Cancer cells (MD-231, HT-29) T-lymphocytes, RBCs and platelets | Aqueous solutions | 134–853 µm/s | F = 5–100 kHz (up to 13 V) | Custom FEM solver | Yes | [57] |
| PE beads (2, 3, 3.5, 5 µm) and RBCs, WBCs and cancer cells (MDA-MB-231) | PBS | 20–200 µm/s | F = 100–270 kHz (up to 29 V) | OpenFOAM | Yes | [58] |
| Beads (1.8, 5 µm) | Water | 0.01–4 mm/s | F = 100 kHz (0.5–8 V) | STAR-CCM+ | No | [59] |
| Cancer cells (HOP-62, HOP-92, NCI-H226, NCIH23, EKVX) from blood cells | Aqueous solutions | 200–400 µm/s | F = 100 kHz (1.6–2.2 V) | - | No | [60] |
| CTCs (MDA-231) and WBCs (granulocytes) | Aqueous solutions | - | F = 100 kHz | COMSOL Multiphysics | No | [61] |
| PE beads (4.42 µm) | Water | No flow | F = 1 MHz (6–10 V) | COMSOL Multiphysics | Yes | [3] |
| Particles emulating blood cells (3, 7, 15, 20, 25 μm) | PBS | 750–1600 µm/s | F = 110 kHz (4.8–44 V) | COMSOL Multiphysics | No | [62] |
| CTCs from blood cells | Water | Up to 5 mm/s | 1–15 V | ANSYS Fluent | No | [63] |
| RBCs from bacteria (Clostridium difficile) cells | Aqueous solutions | 10–40 µm/s | F = 250 kHz–50 MHz (0.1–0.5 V) | COMSOL Multiphysics | No | [64] |
| PE beads (3, 4, 6, 7 µm) | PBS | 42.5–400 µm/s | V= 80–90 V | - | Yes | [65] |
| Beads (0.5, 3.5, 10 µm) | Water | 30–50 µm/s | F = 1–10 MHz (1–8 V) | COMSOL Multiphysics | No | [66] |
| CTCs (MCF-7) from WBCs and RBCs | Plasma | 100 µm/s | 2–3 V | COMSOL Multiphysics | No | [67] |
| Yeasts and PE beads (4 µm) | Aqueous solutions | 1 mm/s | F = 0.1–10 MHz (30–60 V) | COMSOL Multiphysics | No | [68] |
| Platelets from RBCs | Aqueous solutions | 134–1500 µm/s | F = 0.1–1 MHz (10–20 V) | COMSOL Multiphysics | No | [69] |
| Material to Be Separated | Fluid Medium | Fluid Velocity or Flow Rate | Acoustic Field (Frequency/Wavelength) | Simulation Software | Experimental Validation | Reference |
|---|---|---|---|---|---|---|
| Particles (10 µm in size) | Water | No flow | λ = 60 µm | COMSOL Multiphysics | No | [70] |
| Malaria infected RBCs | Plasma | No flow | F = 0.985–1.007 MHz | COMSOL Multiphysics | Yes | [16] |
| PE and iron oxide particles | Water | No flow | F = 13.3 MHz | COMSOL Multiphysics | Yes | [14] |
| Blood cells (2–30 µm) | Water | 0.01 m/s | F = 50 MHz | COMSOL Multiphysics | No | [2] |
| RBCs and platelets | Plasma | 0.5 µL/min | F = 12.7–13 MHz | COMSOL Multiphysics | Yes | [1] |
| RBCs, WBCs, and platelets | Water | 15 mm/s | F = 7.4 MHz | Custom FEM code | Yes | [71] |
| PE beads (10 µm) | Acetic acid, water, ethanol | No flow | F = 14 MHz | COMSOL Multiphysics | Yes | [72] |
| PE beads (1, 5, 10 µm) | Water | 4–5 mm/s | F = 19.8 MHz | COMSOL Multiphysics and MATLAB | Yes | [19] |
| Blood cells | Plasma | 22–100 μL/min | F = 1.03 MHz | COMSOL Multiphysics | Yes | [73] |
| PE beads (5, 10 µm) | - | No flow | λ = 100–200 µm | COMSOL Multiphysics | Yes | [8] |
| PE beads (3, 5, 7, 10, 15 µm) | Water | 3–67 mm/s | F = 2–5 MHz | COMSOL Multiphysics | No | [24] |
| PE beads (1.8, 5 µm) | Water | No flow | Λ = 200, 300 and 600 µm | COMSOL Multiphysics | No | [74] |
| Particles (0.1–150 µm) | Water | 2 mm/s | F = 3 MHz | CAD/CAE software | No | [75] |
| Particles (10 µm) | Oil | 1–10 mm/s | F = 3–20 MHz | COMSOL Multiphysics | Yes | [76] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karampelas, I.H.; Gómez-Pastora, J. Novel Approaches Concerning the Numerical Modeling of Particle and Cell Separation in Microchannels: A Review. Processes 2022, 10, 1226. https://doi.org/10.3390/pr10061226
Karampelas IH, Gómez-Pastora J. Novel Approaches Concerning the Numerical Modeling of Particle and Cell Separation in Microchannels: A Review. Processes. 2022; 10(6):1226. https://doi.org/10.3390/pr10061226
Chicago/Turabian StyleKarampelas, Ioannis H., and Jenifer Gómez-Pastora. 2022. "Novel Approaches Concerning the Numerical Modeling of Particle and Cell Separation in Microchannels: A Review" Processes 10, no. 6: 1226. https://doi.org/10.3390/pr10061226
APA StyleKarampelas, I. H., & Gómez-Pastora, J. (2022). Novel Approaches Concerning the Numerical Modeling of Particle and Cell Separation in Microchannels: A Review. Processes, 10(6), 1226. https://doi.org/10.3390/pr10061226






