Determining the Drawing Force in a Wire Drawing Process Considering an Arbitrary Hardening Law

Abstract

The present paper considers the wire drawing process through a conical die and provides an approximate solution for the drawing force, assuming an arbitrary hardening law. The solution is based on the upper bound theorem. However, this theorem does not apply to the stationary flow of strain-hardening materials. Therefore, an adopted engineering approach is to replace the original material model with a non-homogeneous, perfectly plastic model. The kinematically admissible velocity field is derived from an exact semi-analytical solution for the flow through an infinite channel, which increases the accuracy of the solution. The solution for the homogeneous perfectly plastic material compares with an available solution. The general solution is valid for any die angle. The numerical example focuses on the range of angles used in wire drawing. Since the material model is pressure-independent, it is straightforward to adopt the solution for calculating the force in extrusion.

1. Introduction

Wire drawing is a commonly used metal forming process characterized by its high deformation rate and excellent surface quality [1,2,3]. During the process, metal or alloy billets with high tensile strength, such as copper, aluminum, steel, etc., are reshaped through the conical drawing die. The products are widely used in different industry sectors, such as construction, electrical, chemical, and automotive [4,5,6,7]. Papers [8,9,10,11] have pointed out the importance and influence of some wire drawing process parameters, including the reduction ratio, die angle, drawing speed, and friction.

Several approximate analytical methods are available for calculating wire drawing process parameters. One of these methods employs analytical solutions for material flow in infinite converging conical channels. The first solution of this class has been derived in [12]. This rigid perfectly plastic solution is valid for any isotropic pressure-independent yield criterion. Paper [13] has studied some mathematical features of the solution [12] for the von Mises and Tresca yield criteria. Paper [14] has extended the solution [12] to linear hardening materials, assuming the von Mises yield criterion. An approach to using radial flows to analyze drawing processes has been developed in [15]. The corresponding approximate solutions are valid for any hardening law, but small die angle and friction.

Another widely used method for calculating wire drawing process parameters is based on the upper bound theorem. The first solution of this class has been presented in [16]. Other solutions have been derived in [17,18,19]. A distinguishing feature of the solution [17] is that the kinematically admissible velocity field is continuous. Paper [18] has focused on the formation of a rigid region near the friction surface. The singular velocity field in the vicinity of maximum friction surfaces derived in [20] has been employed in [19]. Upper bound solutions are also available for non-conical dies (see, for example, [21,22,23]).

A disadvantage of the upper bound method is that it does not apply to stationary processes for strain-hardening materials. Several papers have calculated the yield stress at the exit from the die by replacing the equivalent strain in the hardening law with the extrusion ratio [24,25,26]. An extension of this method allows average yield stress in each cross-section of the wire to be calculated using geometric parameters [27,28]. This method allows one to replace a strain-hardening material model with the corresponding model of non-homogeneous perfectly plastic material. The upper bound theorem is valid for the latter model. The present paper adopts this approach to develop a new approximate solution for the drawing force. In addition, the velocity field found in [12] is used as a kinematically admissible velocity field in the plastic region. Therefore, the stress equations are satisfied in this region in the case of homogeneous perfectly plastic material, which increases the accuracy of the solution. A comparison with the solution [16] is made.

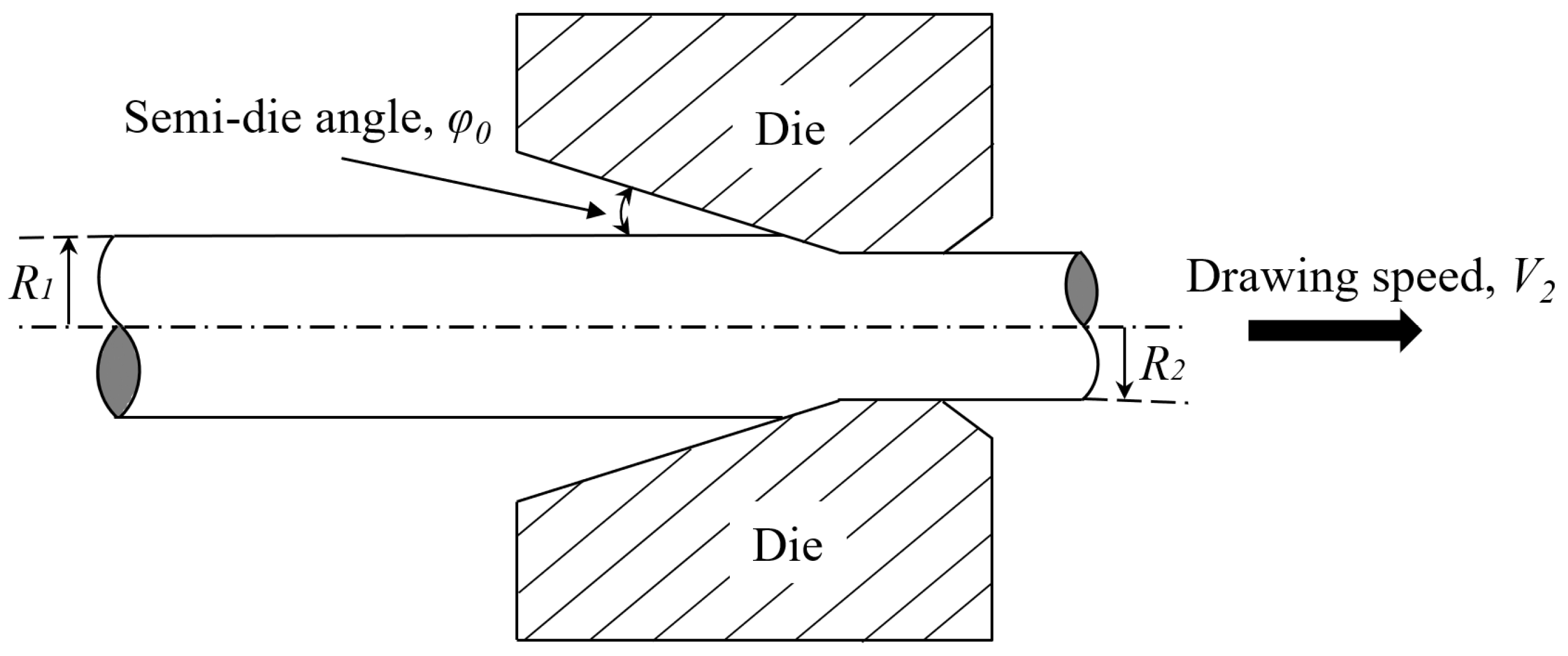
2. Statement of the Problem

A schematic diagram of the wire drawing process through a conical die is shown in Figure 1. The initial and final radii of the wire are denoted as $R_1$ and $R_2$, respectively. The die angle is $2{\phi }_0$, and the drawing speed is $V_2$. It is required to calculate the drawing force F.

The material is regarded as rigid/plastic, and incompressible. In the case of perfectly plastic material, the von Mises yield criterion reads:

$${\sigma }_{eq}={\sigma }_0.$$

(1)

Here ${\sigma }_{eq}$ is the equivalent stress and ${\sigma }_0$ is the yield stress in tension. The latter is a constitutive parameter. The friction stress between the conical die and material is taken as:

$${\tau }_f=m\frac{{\sigma }_0}{\sqrt{3}}.$$

(2)

Here $m$ is the constant friction factor. Its value may vary in the range $0\le m\le 1$. A consequence of the incompressibility equation is:

$$V_1{R}_1^2=V_2{R}_2^2.$$

(3)

Here $V_1$ is the velocity of the wire before entering the die.

The solution is based on the upper bound theorem [29]. Therefore, strictly speaking, strain-hardening models cannot be considered because the process is stationary. The von Mises yield criterion of strain-hardening materials is represented as:

$${\sigma }_{eq}={\sigma }_0\Phi \left({\epsilon }_{eq}\right)$$

(4)

where ${\epsilon }_{eq}$ is the equivalent strain and $\Phi \left({\epsilon }_{eq}\right)$ is an arbitrary function of its argument satisfying the conditions $\Phi \left(0\right)=1$ and $\frac{d\Phi \left({\epsilon }_{eq}\right)}{d{\epsilon }_{eq}}\ge 0$ for all ${\epsilon }_{eq}$. An engineering approach to account for strain hardening has been proposed in [28] for linear strain-hardening materials. According to this approach, the equivalent strain in the hardening law is replaced with an average strain defined as:

$${\epsilon }_a=ln\left(\frac{A_0}{A}\right)$$

(5)

where $A_0$ is the cross-sectional area of the wire before entering the die and $A$ is the cross-sectional area of the wire at any distance from the entrance. It is evident from (5) that ${\epsilon }_a=0$ at $A=A_0$. Therefore, it follows from (4) that ${\sigma }_{eq}={\sigma }_0$ at the entrance to the die. Paper [28] assumes that $\Phi \left({\epsilon }_{eq}\right)$ is a linear function of its argument. However, it is straightforward to extend this approach to any function. Then, Equation (4) becomes:

$${\sigma }_{eq}={\sigma }_0\Phi \left({\epsilon }_a\right).$$

(6)

Since ${\epsilon }_a$ is a known function of position, the corresponding model can be regarded as rigid perfectly plastic with a known nonuniform yield stress distribution. The upper bound theorem applies to such a model. Equation (2) becomes:

$${\tau }_f=m\frac{\Phi \left({\epsilon }_a\right)}{\sqrt{3}}.$$

(7)

3. Kinematically Admissible Velocity Field

It is natural to use a spherical coordinate system $\left(r,\hspace{0.17em}\phi ,\hspace{0.17em}\varphi \right)$. The solution is independent of $\varphi$. The shear stress in the spherical coordinate system is denoted as ${\sigma }_{r\phi }$. The equation of the die surface is $\phi ={\phi }_0$ (Figure 2). The boundary conditions (2) and (7) become:

$${\sigma }_{r\phi }=m\frac{{\sigma }_0}{\sqrt{3}} \mathrm{and} {\sigma }_{r\phi }=m\frac{{\sigma }_0\Phi \left({\epsilon }_a\right)}{\sqrt{3}}$$

(8)

for $\phi ={\phi }_0$, respectively. Axial symmetry demands

$${\sigma }_{r\phi }=0$$

(9)

for $\phi =0$. The spherical coordinate system and the general structure of the kinematically admissible velocity field are shown in Figure 2. The kinematically admissible velocity field consists of a plastic region and two rigid regions. The rigid/plastic boundaries are velocity discontinuity lines in meridian planes.

3.1. Kinematically Admissible Velocity Field in the Plastic Region

Choosing a kinematically admissible velocity field that satisfies the stress equations when combined with the associated flow rule is advantageous. Semi-analytical solutions to boundary value problems supply such velocity fields. In particular, the solution presented in [12] can be used in the case under consideration. This solution is valid for any pressure-independent yield criterion. The present paper employs the solution for the von Mises yield criterion. The dimensionless shear stress $\tau =\frac{\sqrt{3}{\sigma }_{r\phi }}{{\sigma }_0}$ satisfies the following Equation [12]:

$$\frac{d\tau }{d\phi }+\tau cot\phi +2\sqrt{3}\sqrt{1-{\tau }^2}=c.$$

(10)

Here $c$ is constant. Its value should be found from the solution. It is convenient to put:

$$\tau =sin\psi \mathrm{and} \sqrt{1-{\tau }^2}=cos\psi .$$

(11)

Equations (10) and (11) combine to give:

$$\frac{d\psi }{d\phi }=\frac{c-sin\psi cot\phi -2\sqrt{3}cos\psi }{cos\psi }.$$

(12)

The first equation in (8) and (9) become $\tau =m$ for $\phi ={\phi }_0$ and $\tau =0$ for $\phi =0$, respectively. Using (11), one can transform these boundary conditions to:

$$\psi =0$$

(13)

for $\phi =0$ and:

$$\psi ={\psi }_f=arcsin m$$

(14)

for $\phi ={\phi }_0$. It is seen from (13) that the term $sin\psi cot\phi$ involved in (12) reduces to the expression $\frac{0}{0}$ at $\phi =0$. Assume that $\psi$ is a linear function of $\phi$ in the vicinity of $\phi =0$. This function must satisfy (13). Substituting it into (12) and expanding the right-hand side of the resulting equation in a power series, one obtains

$$\psi =\frac{\left(c-2\sqrt{3}\right)}{2}\phi +o\left(\phi \right)$$

(15)

as $\phi \to 0$. Equation (12) should be solved numerically using (15). The solution depends on c. The boundary condition (14) supplies the equation to determine c. Figure 3 illustrates the dependence of c on m and ${\phi }_0$. In what follows, it is assumed that $\psi$ is a known function of $\phi$.

The only non-vanishing velocity component is the radial velocity. The latter is given by [12]

$$u=-\frac{\beta V{R}^2}{r^2}exp\left[-2\sqrt{3}{{\displaystyle \int }}_{{\phi }_0}^{\phi }\frac{\tau }{\sqrt{1-{\tau }^2}}d\gamma \right].$$

(16)

Here $\beta >0$ is constant whose value should be found from the solution. In (16) and what follows, the quantity $V{R}^2$ may be represented as $V_1{R}_1^2$ or $V_2{R}_2^2$ due to (3). Using (11), one transforms (16) to

$$u=-\frac{\beta V{R}^2}{r^2}q\left(\phi \right)$$

(17)

where

$$q\left(\phi \right)=exp\left[-2\sqrt{3}{{\displaystyle \int }}_{{\phi }_0}^{\phi }tan\psi d\gamma \right].$$

(18)

A consequence of the incompressibility equation is:

$$\pi V{R}^2=-2\pi {{\displaystyle \int }}_0^{{\phi }_0}u{r}^{2}sin\phi d\phi .$$

(19)

Eliminating here u using (17), one arrives at the following equation for $\beta$:

$$1=2\beta {{\displaystyle \int }}_0^{{\phi }_0}q\left(\phi \right)sin\phi d\phi .$$

(20)

In what follows, it is assumed that $\beta$ has been calculated. Therefore, the kinematically admissible velocity field in the plastic region has been determined.

3.2. Velocity Discontinuity Lines

There are the two velocity discontinuity lines shown in Figure 4 (BB₁ and AA₁). Two orthogonal systems of unit vectors associated with line BB₁ are depicted in this figure. A similar system of vectors may be associated with line AA₁. The derivation below is valid for both lines.

The base vectors of the spherical coordinate system are denoted as ${\mathit{e}}_{\mathit{r}}$ and ${\mathit{e}}_{\mathsf{\phi }}$. The vectors directed along the normal and tangent to the velocity discontinuity line are denoted as $\mathit{n}$ and $\mathsf{\tau }$, respectively. Moreover, $\mathit{i}$ is the unit vector directed along the axis of symmetry. It follows from the geometry of Figure 4 that the relationships between the unit vectors are:

$$\mathit{n}={\mathit{e}}_{\mathit{r}}cos\gamma +{\mathit{e}}_{\mathsf{\phi }}sin\gamma , \mathsf{\tau }=-{\mathit{e}}_{\mathit{r}}sin\gamma +{\mathit{e}}_{\mathsf{\phi }}cos\gamma , \mathit{i}={\mathit{e}}_{\mathit{r}}cos\phi -{\mathit{e}}_{\mathsf{\phi }}sin\phi .$$

(21)

Here $\gamma$ is the inclination of the vector $\mathit{n}$ to the r-axis, measured clockwise. The velocity vectors in the plastic and rigid regions are represented as:

$${\mathit{U}}_{\mathit{p}}=u{\mathit{e}}_{\mathit{r}} \mathrm{and} {\mathit{U}}_{\mathit{r}}=-V\mathit{i},$$

(22)

respectively. Here, and in what follows, V should be replaced with V₁ for line BB₁ and with V₂ for line AA₁. The normal velocity must be continuous across the velocity discontinuity line. Therefore, ${\mathit{U}}_{\mathit{p}}\cdot \mathit{n}={\mathit{U}}_{\mathit{r}}\cdot \mathit{n}$. Upon substitution from (21) and (22), this equation becomes:

$$\frac{u}{V}=-\frac{cos\left(\gamma +\phi \right)}{cos\gamma }.$$

(23)

The amount of velocity jump across the velocity discontinuity line is $\left[u\right]={\mathit{U}}_{\mathit{r}}\cdot \mathsf{\tau }-{\mathit{U}}_{\mathit{p}}\cdot \mathsf{\tau }$. Upon substitution from (21) and (22), this equation becomes:

$$\frac{\left[u\right]}{V}=\frac{u}{V}sin\gamma +sin\left(\gamma +\phi \right).$$

(24)

Eliminating here u using (23), one obtains:

$$\frac{\left[u\right]}{V}=\frac{sin\phi }{cos\gamma }.$$

(25)

An infinitesimal length element of the velocity discontinuity line is:

$$dl=\sqrt{{\left(dr\right)}^2+{\left(rd\phi \right)}^2}=r\sqrt{{\left(\frac{dr}{rd\phi }\right)}^2+1}d\phi .$$

(26)

It follows from the geometry of Figure 4 that:

$$tan\gamma =-\frac{dr}{rd\phi }.$$

(27)

Equations (26) and (27) combine to give:

$$dl=\frac{r}{cos\gamma }d\phi .$$

(28)

Using (17), one can transform Equation (23) to:

$$\frac{\beta R^2}{r^2}q\left(\phi \right)=\frac{cos\left(\gamma +\phi \right)}{cos\gamma }.$$

(29)

Employing trigonometric identities and (27), one rewrites this equation as:

$$\frac{ds}{d\phi }=\frac{2}{sin\phi }\left[\beta q\left(\phi \right)-scos\phi \right]$$

(30)

where $s=\frac{r^2}{R^2}.$ Here $R=R_1$ for line BB₁ and $R=R_2$ for line AA₁. Equation (30) determines the velocity discontinuity line. This line must pass through point B or A (Figure 4). Therefore, the boundary condition to Equation (30) is:

$$s=\frac{1}{{sin}^2{\phi }_0}$$

(31)

for $\phi ={\phi }_0$. The general solution of Equation (30) is:

$$s=\frac{1}{{sin}^2\phi }\left[2\beta {{\displaystyle \int }}_0^{\phi }sin\chi q\left(\chi \right)d\chi +s_0\right].$$

(32)

Here $s_0$ is constant. The value of s must be finite at $\phi =0$. Otherwise, the velocity discontinuity line does not reach the symmetry axis. Therefore, it is necessary to put $s_0=0$. Then, Equation (32) becomes:

$$s=\frac{2\beta }{{sin}^2\phi }S\left(\phi \right), S\left(\phi \right)={{\displaystyle \int }}_0^{\phi }sin\chi q\left(\chi \right)d\chi .$$

(33)

This solution reduces to the expression $\frac{0}{0}$ at $\phi =0$. Applying L’Hospital’s rule leads to:

$$s=\beta q_0$$

(34)

at $\phi ={\phi }_0$. Here $q_0$ is the value of q at $\phi =0$. It follows from (18) that:

$$q_0=exp\left[2\sqrt{3}{{\displaystyle \int }}_0^{{\phi }_0}tan\psi d\gamma \right].$$

(35)

It is seen from (20) and (33) that (31) is satisfied.

An infinitesimal area element of the velocity discontinuity surface is determined from (28) as:

$$d\Sigma =\frac{r^{2}sin\phi }{cos\gamma }d\phi d\varphi .$$

(36)

Using the definition for s and (33), one transforms this equation to:

$$d\Sigma =\frac{2\beta R^{2}S\left(\phi \right)}{cos\gamma sin\phi }d\phi d\varphi .$$

(37)

4. Plastic Work Rate

It is necessary to calculate the plastic work rate (i) in the plastic region, (ii) at two velocity discontinuity surfaces, and (iii) at the friction surface.

4.1. Plastic Work Rate in the Plastic Region

The infinitesimal volume element is $d\Omega =r^{2}sin\phi drd\phi d\varphi$. Using the definition for s, one transforms this equation to:

$$d\Omega =\frac{R^3\sqrt{s}sin\phi }{2}dsd\phi d\varphi .$$

(38)

The plastic work rate is defined as:

$$W_{\Omega }={{\displaystyle \iiint }}_{\Omega }{\sigma }_{eq}{\xi }_{eq}d\Omega .$$

(39)

Here ${\xi }_{eq}$ is the equivalent plastic strain rate. In the case under consideration, it is given by:

$${\xi }_{eq}=\sqrt{\frac{2}{3}}\sqrt{{\xi }_{rr}^2+{\xi }_{\phi \phi }^2+{\xi }_{\varphi \varphi }^2+2{\xi }_{r\phi }^2}.$$

(40)

The strain rate components are expressed through the radial velocity as:

$${\xi }_{rr}=\frac{\partial u}{\partial r}, {\xi }_{\phi \phi }={\xi }_{\varphi \varphi }=\frac{u}{r},\hspace{0.17em}{\xi }_{r\phi }=\frac{1}{2r}\frac{\partial u}{\partial \phi }.$$

(41)

Equations (17), (18) and (41) combine to give:

$${\xi }_{rr}=\frac{2\beta V{R}^2}{r^3}q\left(\phi \right), {\xi }_{\phi \phi }={\xi }_{\varphi \varphi }=-\frac{\beta V{R}^2}{r^3}q\left(\phi \right), {\xi }_{r\phi }=\frac{\sqrt{3}\beta V{R}^2}{r^3}q\left(\phi \right)tan\psi .$$

(42)

Substituting (41) into (40) and using the definition for s yields:

$${\xi }_{eq}=\frac{2\beta Vq\left(\phi \right)}{Rs\sqrt{s}cos\psi }.$$

(43)

Equations (38), (39) and (43) combine to give:

$$w_{\Omega }=\frac{W_{\Omega }}{\pi V{R}^2{\sigma }_0}=2\beta {{\displaystyle \int }}_0^{{\phi }_0}{{\displaystyle \int }}_{s_1\left(\phi \right)}^{s_2\left(\phi \right)}\frac{{\sigma }_{eq}}{{\sigma }_0}\frac{q\left(\phi \right)sin\phi }{scos\psi }dsd\phi .$$

(44)

This equation involves both velocity discontinuity lines. Therefore, it is necessary to adopt the same definition for s. Assuming that $R=R_2$ and using (33) results in:

$$s_1\left(\phi \right)=\frac{2\beta }{{sin}^2\phi }{{\displaystyle \int }}_0^{\phi }sin\chi q\left(\chi \right)d\chi \mathrm{and} s_2\left(\phi \right)=\frac{2\beta }{{sin}^2\phi }{\left(\frac{R_1}{R_2}\right)}^2{{\displaystyle \int }}_0^{\phi }sin\chi q\left(\chi \right)d\chi .$$

(45)

The first equation determines the velocity discontinuity line through A and the second through B (Figure 4). The equations in (45) allow the integral in (44) to be evaluated numerically. In the case of homogeneous properties, Equation (1) is valid, and Equations (44) and (45) yield:

$$w_{\Omega }=4\beta ln\left(\frac{R_1}{R_2}\right){{\displaystyle \int }}_0^{{\phi }_0}\frac{q\left(\phi \right)sin\phi }{cos\psi }d\phi .$$

(46)

In the case of non-homogeneous properties, Equation (6) is valid, and Equation (44) yields:

$$w_{\Omega }=2\beta {{\displaystyle \int }}_0^{{\phi }_0}{{\displaystyle \int }}_{s_1\left(\phi \right)}^{s_2\left(\phi \right)}\frac{\Phi \left({\epsilon }_a\right)q\left(\phi \right)sin\phi }{scos\psi }dsd\phi .$$

(47)

In the spherical coordinate system, Equation (5) becomes:

$${\epsilon }_a=2ln\left(\frac{R_1}{rsin{\phi }_0}\right).$$

(48)

Using the definition for s, one can transform this equation to:

$${\epsilon }_a=2ln\left(\frac{R_1}{R_{2}sin{\phi }_0\sqrt{s}}\right).$$

(49)

Eliminating ${\epsilon }_a$ in (47) using (49), one represents the integrand as a function of s and $\phi$.

4.2. Plastic Work Rate at the Velocity Discontinuity Surfaces

The plastic work rate at each velocity discontinuity surface is given by:

$$W_d=\frac{1}{\sqrt{3}}{{\displaystyle \iint }}_{\Sigma }{\sigma }_{eq}\left[u\right]d\Sigma .$$

(50)

Using (25) and (37), one transforms this equation to:

$$w_d=\frac{W_d}{\pi V{R}^2{\sigma }_0}=\frac{4\beta }{\sqrt{3}}{{\displaystyle \int }}_0^{{\phi }_0}\frac{{\sigma }_{eq}}{{\sigma }_0{cos}^2\gamma }S\left(\phi \right)d\phi .$$

(51)

This equation is valid for both velocity discontinuity surfaces. In the case of homogeneous properties, Equation (51) becomes:

$$w_d=\frac{4\beta }{\sqrt{3}}{{\displaystyle \int }}_0^{{\phi }_0}\frac{S\left(\phi \right)}{{cos}^2\gamma }d\phi$$

(52)

for each velocity discontinuity surface. In the case of non-homogeneous properties, Equation (51) becomes:

$$w_d=\frac{4\beta }{\sqrt{3}}{{\displaystyle \int }}_0^{{\phi }_0}\frac{\Phi \left({\epsilon }_a\right)}{{cos}^2\gamma }S\left(\phi \right)d\phi .$$

(53)

Here ${\epsilon }_a$ should be regarded as a function of $\phi$. One derives this function by replacing s in (49) with $s_1\left(\phi \right)$ or $s_2\left(\phi \right)$. Therefore, the plastic work rate is not the same at the two velocity discontinuity surfaces.

Equations (52) and (53) involve ${cos}^2\gamma$. It follows from (27) and (30) that:

$$tan\gamma =\frac{scos\phi -\beta q\left(\phi \right)}{ssin\phi }.$$

(54)

The right-hand side of this equation is a known function of $\phi$ due to (33). Therefore, ${cos}^2\gamma$ is determined as a function of $\phi$ using (54) and the identity ${cos}^2\gamma ={\left(1+{tan}^2\gamma \right)}^{-1}$.

4.3. Plastic Work Rate at the Friction Surface

The radial velocity at the friction surface is determined from (17) and (18) as:

$$u_f=-\frac{\beta V{R}^2}{r^2}.$$

(55)

The plastic work rate is:

$$W_f=\frac{2\pi m}{\sqrt{3}}{{\displaystyle \int }}_{R_{2}sin{\phi }_0}^{R_{1}sin{\phi }_0}{\sigma }_{eq}\left|u_f\right|rsin{\phi }_{0}dr.$$

(56)

Equations (55) and (56) combine to give:

$$w_f=\frac{W_f}{\pi V{R}^2{\sigma }_0}=\frac{2m\beta sin{\phi }_0}{\sqrt{3}}{{\displaystyle \int }}_{R_{2}sin{\phi }_0}^{R_{1}sin{\phi }_0}\frac{{\sigma }_{eq}}{{\sigma }_0}\frac{dr}{r}.$$

(57)

In the case of homogeneous properties, this equation becomes:

$$w_f=\frac{2m\beta sin{\phi }_0}{\sqrt{3}}ln\left(\frac{R_1}{R_2}\right).$$

(58)

In the case of non-homogeneous properties, Equation (57) becomes:

$$w_f=\frac{2m\beta sin{\phi }_0}{\sqrt{3}}{{\displaystyle \int }}_{R_{2}sin{\phi }_0}^{R_{1}sin{\phi }_0}\frac{\Phi \left({\epsilon }_a\right)}{r}dr.$$

(59)

Here one should eliminate ${\epsilon }_a$ using (48).

5. Drawing Force

Let F be the drawing force. It follows from the upper bound theorem that:

$$F{V}_2\ge W_{\Omega }+W_{d1}+W_{d2}+W_f.$$

(60)

Here $W_{d1}$ is $W_d$ calculated at the velocity discontinuity line through A, and $W_{d2}$ is $W_d$ calculated at the velocity discontinuity line through B (Figure 4). Using (44), (51) and (57), one transforms Equation (60) to:

$$f_u=\frac{F_u}{\pi R_2^2{\sigma }_0}=w_{\Omega }+w_{d1}+w_{d2}+w_f.$$

(61)

Here $F_u$ is the upper bound on F and $f_u$ is its dimensionless representation. The right-hand side of Equation (61) has been calculated in the previous section for both homogeneous and non-homogeneous materials. Quantitative results can be obtained after prescribing the function $\Phi \left({\epsilon }_{eq}\right)$ and evaluating the integrals numerically.

6. Numerical Examples

The right-hand side of Equation (61) has been calculated using the corresponding build-in commands in Wolfram Mathematica (version 11.3). The present section illustrates these results and emphasizes the effect of the reduction ratio, the die angle, and the friction factor on the drawing force. Even though the general solution is valid for any values of these parameters, the quantitative results focus on their typical ranges in the drawing of thin wires. In the case of strain-hardening material, the stress–strain curve of AISI-316 stainless steel is approximated by the equation:

$$\Phi \left({\epsilon }_{eq}\right)={\left(1+84.75{\epsilon }_{eq}\right)}^{0.52}.$$

(62)

The constitutive parameter ${\sigma }_0$ involved in (4) and required to calculate the drawing force F after determining f is ${\sigma }_0=119$ MPa.

Figure 5 compares the present solution for rigid perfectly plastic material and the solution provided in [16]. The former is shown by the solid lines, and the latter by the broken lines. The difference is invisible in the figure. It is worthy of note that the solution [16] has been specifically derived for small die angles. The present solution is more general and is valid for any die angle. Figure 5 demonstrates that this advantageous feature of the solution does not affect its accuracy.

Figure 6, Figure 7, Figure 8 and Figure 9 show the effect of process parameters on the dimensionless drawing force. Each figure shows the effect of the die angle for several friction factor values. The effect of the reduction ratio is revealed by comparing the results depicted in all these figures. The effect of strain hardening is revealed by comparing the results depicted in Figure 5 and Figure 6. All results coincide with physical expectations. In particular, the processing of strain-hardening materials requires a larger force than materials with no hardening. In the case under consideration, this difference is considerable. It is because of the hardening law (62). It is seen from each figure that an optimal die angle (i.e., the drawing force attains a minimum at this angle) exists if the other process parameters are kept constant. Its value depends on these other process parameters and may be outside the typical ranges considered. The drawing force increases as the friction factor increases.

7. Discussion

The present paper has developed an engineering approach that allows one to use the upper bound technique for analyzing the stationary metal forming processes for strain-hardening materials. This development is important because the upper bound solutions are in good agreement with finite element solutions when the upper bound theorem is valid. It has been demonstrated in [30] in the case of wire drawing processes. It is unsurprising because the upper bound theorem provides an accurate result, even from comparatively crude kinematically admissible velocity fields [31]. The present solution is based on the kinematically admissible velocity field that, in conjunction with the associated flow rule, satisfies all the fundamental and constitutive equations in the plastic region in the case of rigid perfectly plastic material. This kinematically admissible velocity field feature increases the solution’s accuracy.

The solution found shows the effect of process parameters on the drawing force. It is straightforward to use this solution for other applications. Examples of such applications are the prediction of central bursting defects using the approaches proposed in [32,33], and the prediction of fracture initiation using the extended Bernoulli’s theorem [34] in conjunction with uncoupled ductile fracture criteria. A review of such criteria is available, for example, in [35].

8. Conclusions

The process of wire drawing through a conical die has been investigated. A new theoretical solution for the drawing force has been derived, assuming an arbitrary strain- hardening law. The solution is based on the upper bound theorem, although it is not an upper bound solution for the standard model of rigid plastic strain-hardening material. The reason for it is that the theorem does not apply to the stationary flow of rigid plastic strain-hardening materials. An engineering approach has been used to overcome this difficulty. In particular, the equivalent strain in the strain-hardening law is replaced with an average strain in each cross-section of the wire. The latter is calculated using geometric parameters of the die. As a result, the original material model is replaced with the rigid perfectly plastic model with a non-homogeneous yield stress distribution. The upper bound theorem applies to such a model.

The solution has been reduced to several ordinary integrals that should be evaluated numerically. Section 6 illustrates the effect of process parameters on the dimensionless drawing force, assuming the hardening law (62). The behavior of the solution agrees with physical expectations. The solution practically coincides with solution [16] (Figure 5). The latter has been developed for small die angles. The new solution is valid for any die angle. An advantage of this solution is that the kinematically admissible velocity field is taken from the exact solution for material flow through an infinite channel [12].

Since the material is pressure-independent, it is straightforward to adopt the solution provided for calculating the extrusion force. To this end, it is necessary to add the same hydrostatic stress to all normal stresses such that the drawing force vanishes. Front and back forces can be included similarly.