A Primary Support Design for Deep Shaft Construction Based on the Mechanism of Advanced Sequential Geopressure Release
Abstract
:1. Introduction
2. The Primary Support Principle for the Prestress-Relieved Zone
3. Field and Laboratory Studies
4. Primary Support Design of Xincheng Shaft
5. Comparison and Verification of Numerical Simulation between the Original Support and Proposed Support
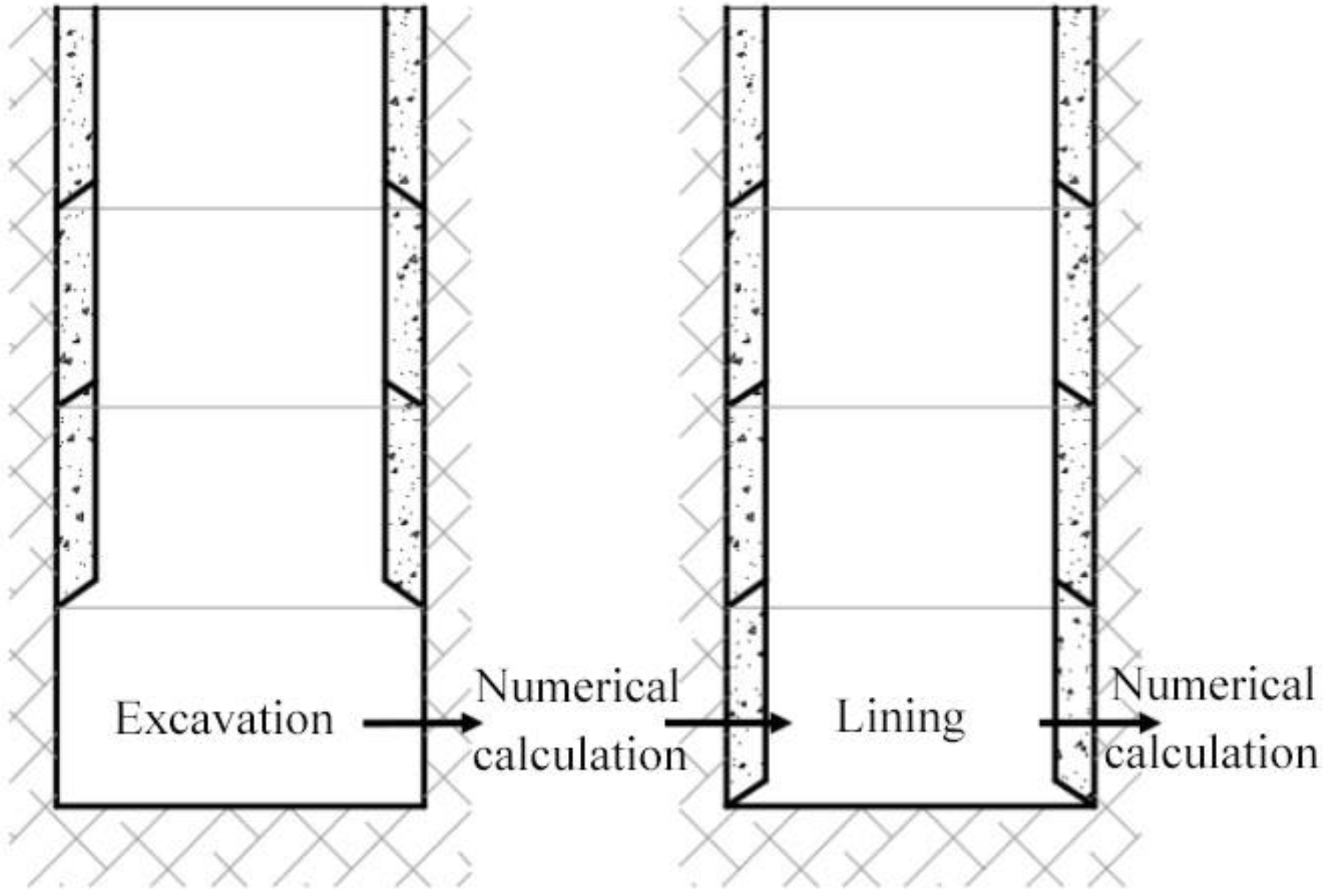
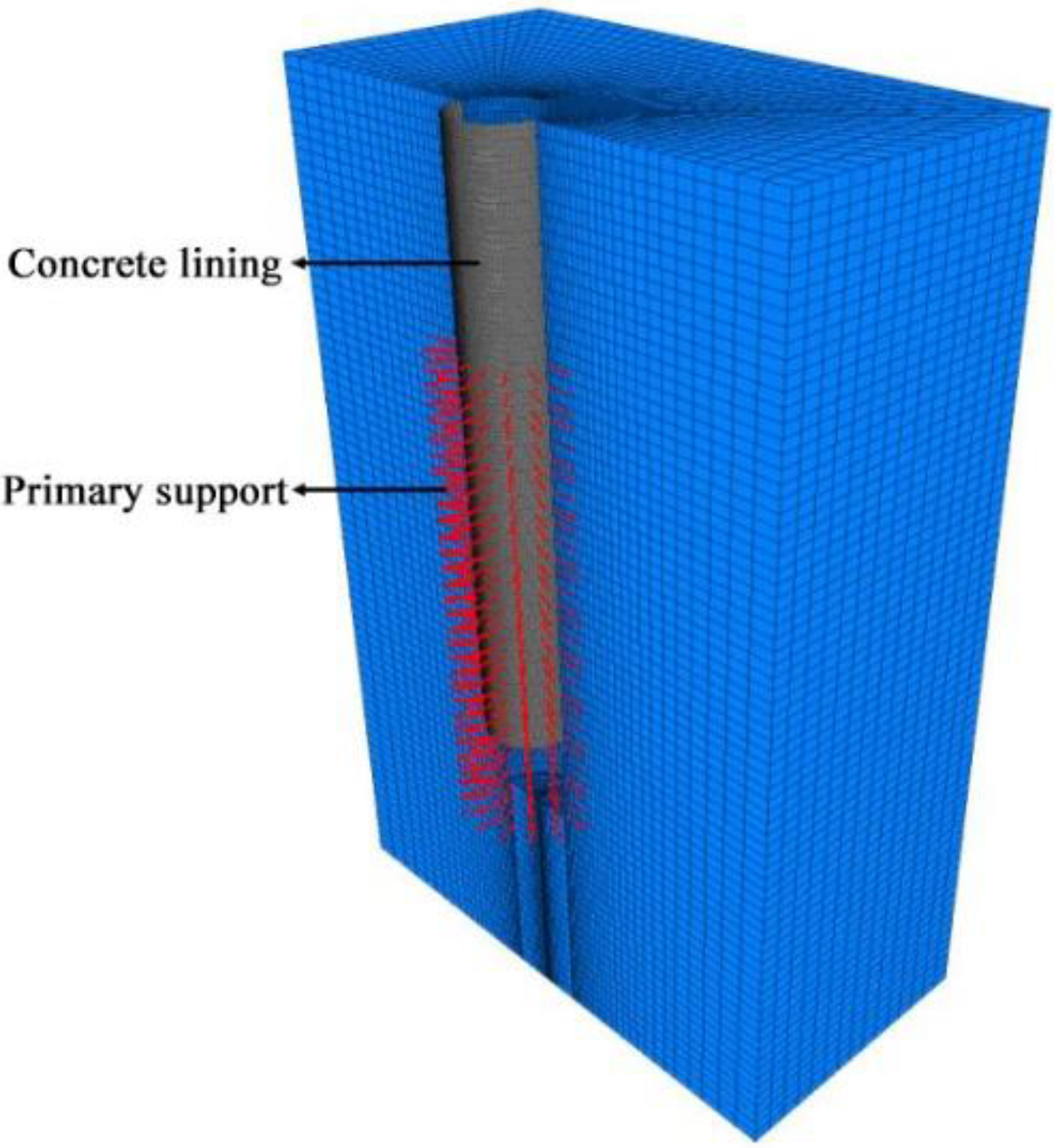
5.1. Design of the Numerical Modeling Scheme
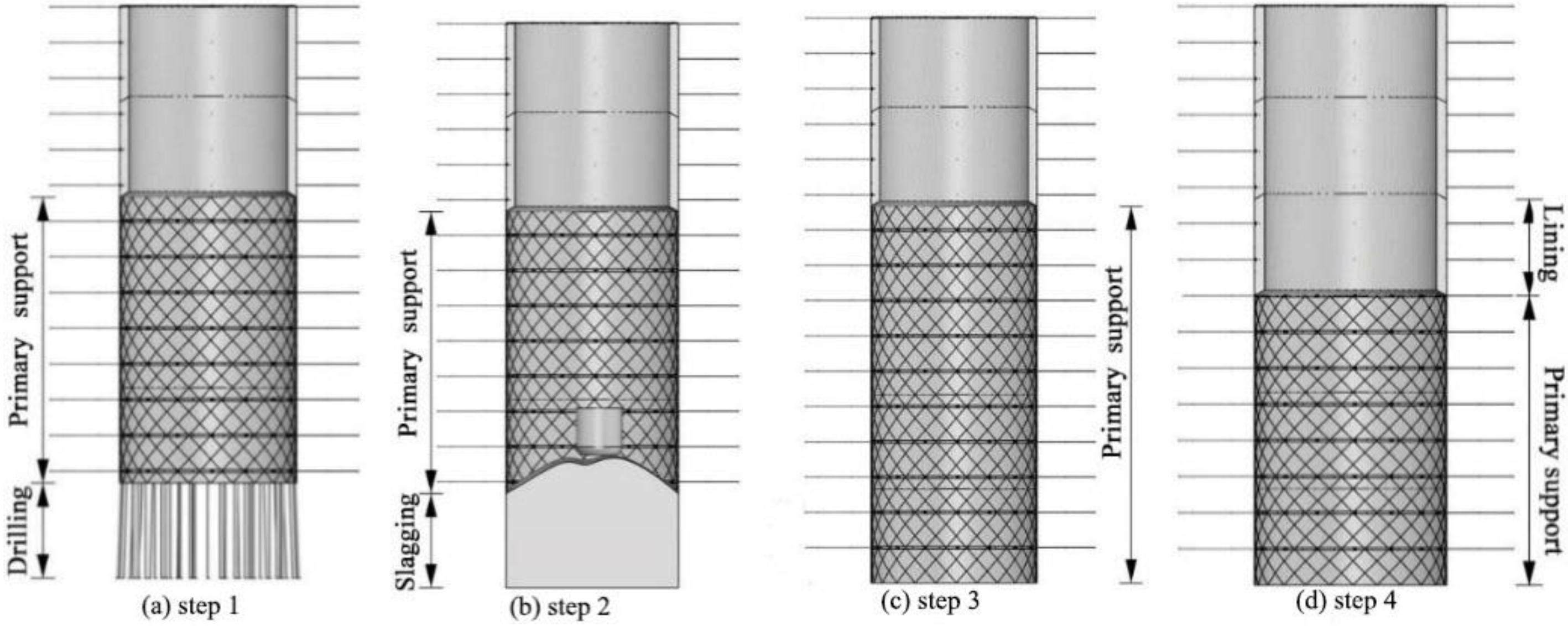
5.1.1. Excavation and Support Construction of the Original Scheme
5.1.2. Improve the Construction of Excavation and Support
5.2. Numerical Modeling Results and Analysis
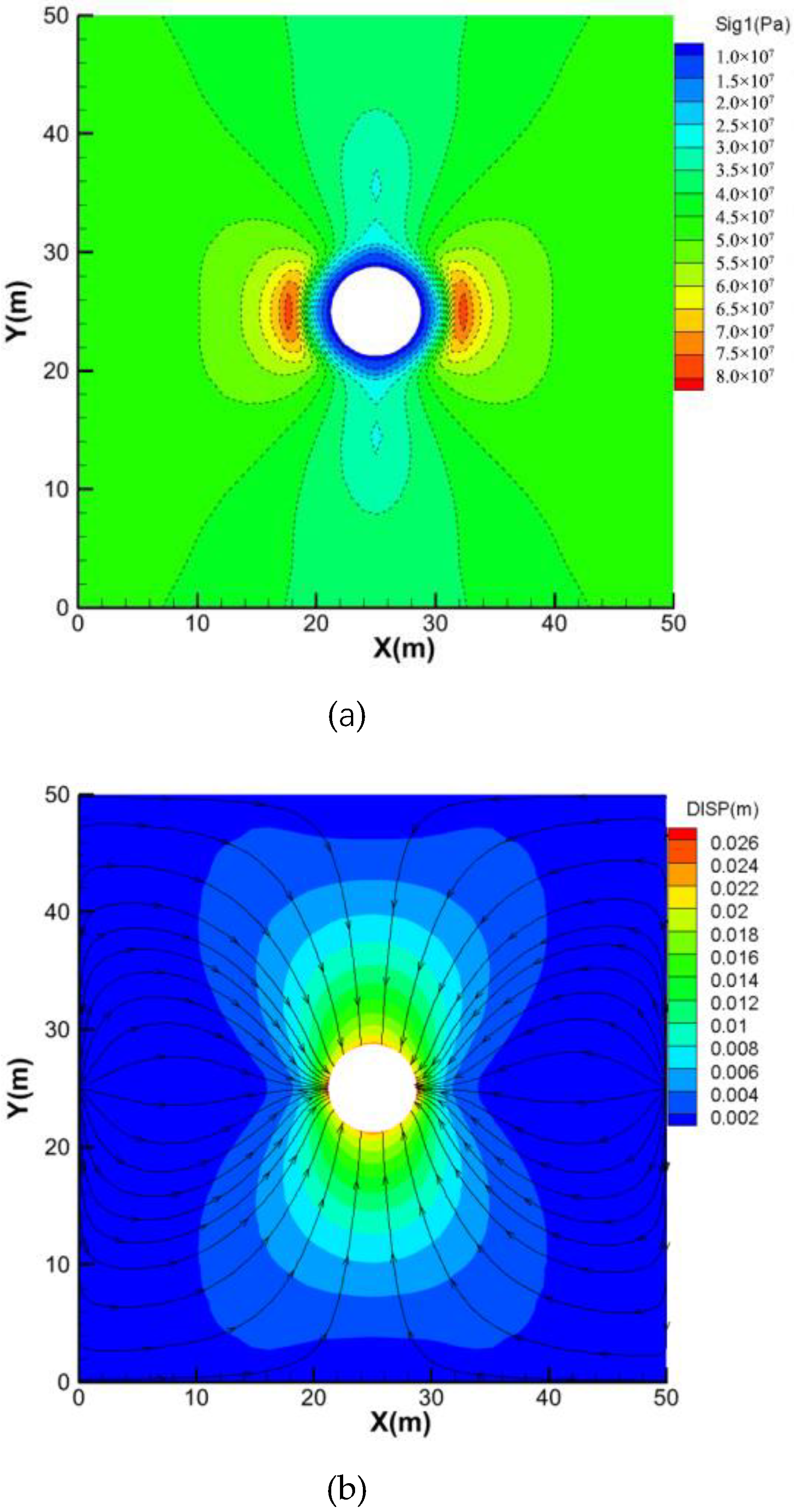
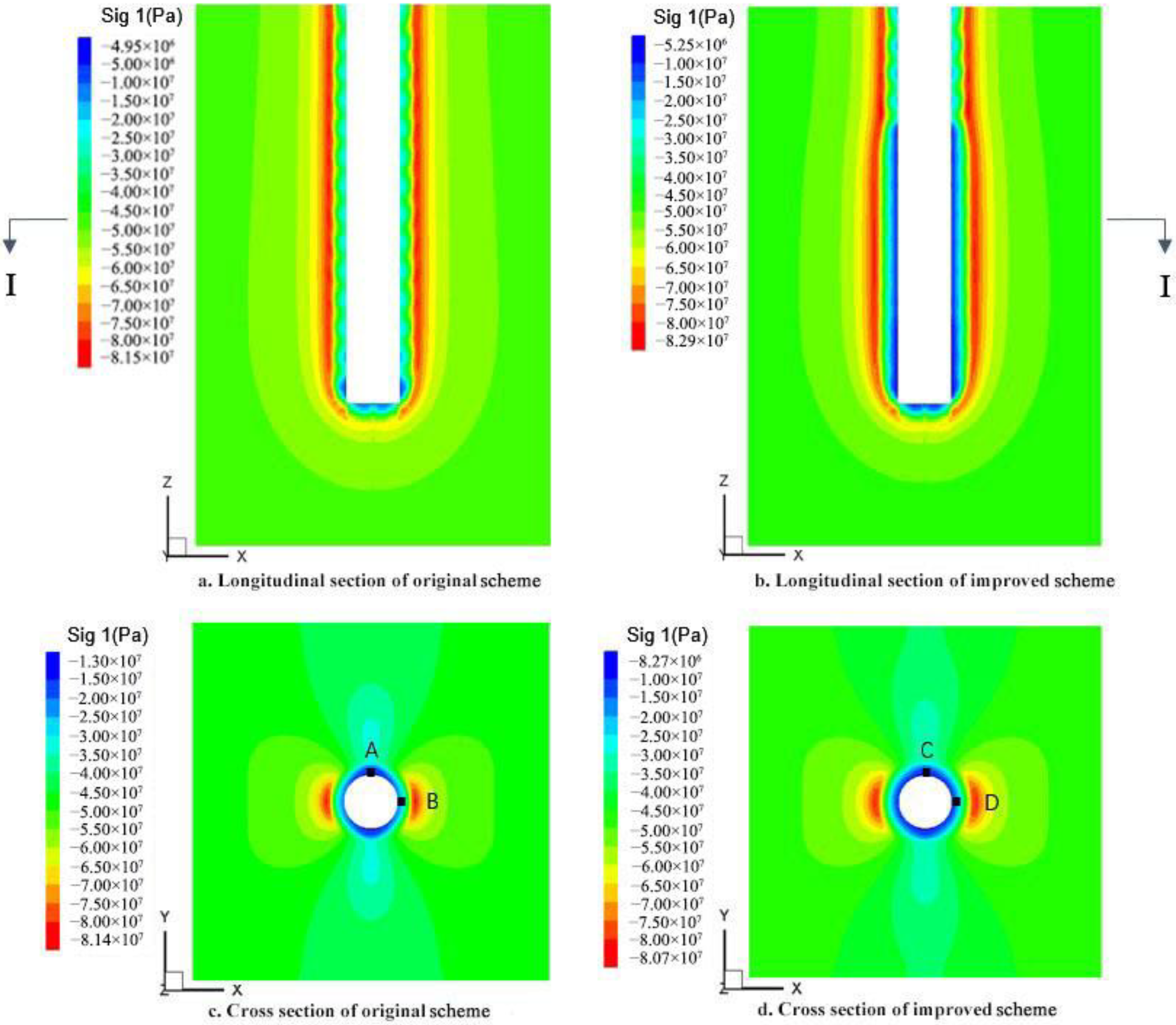
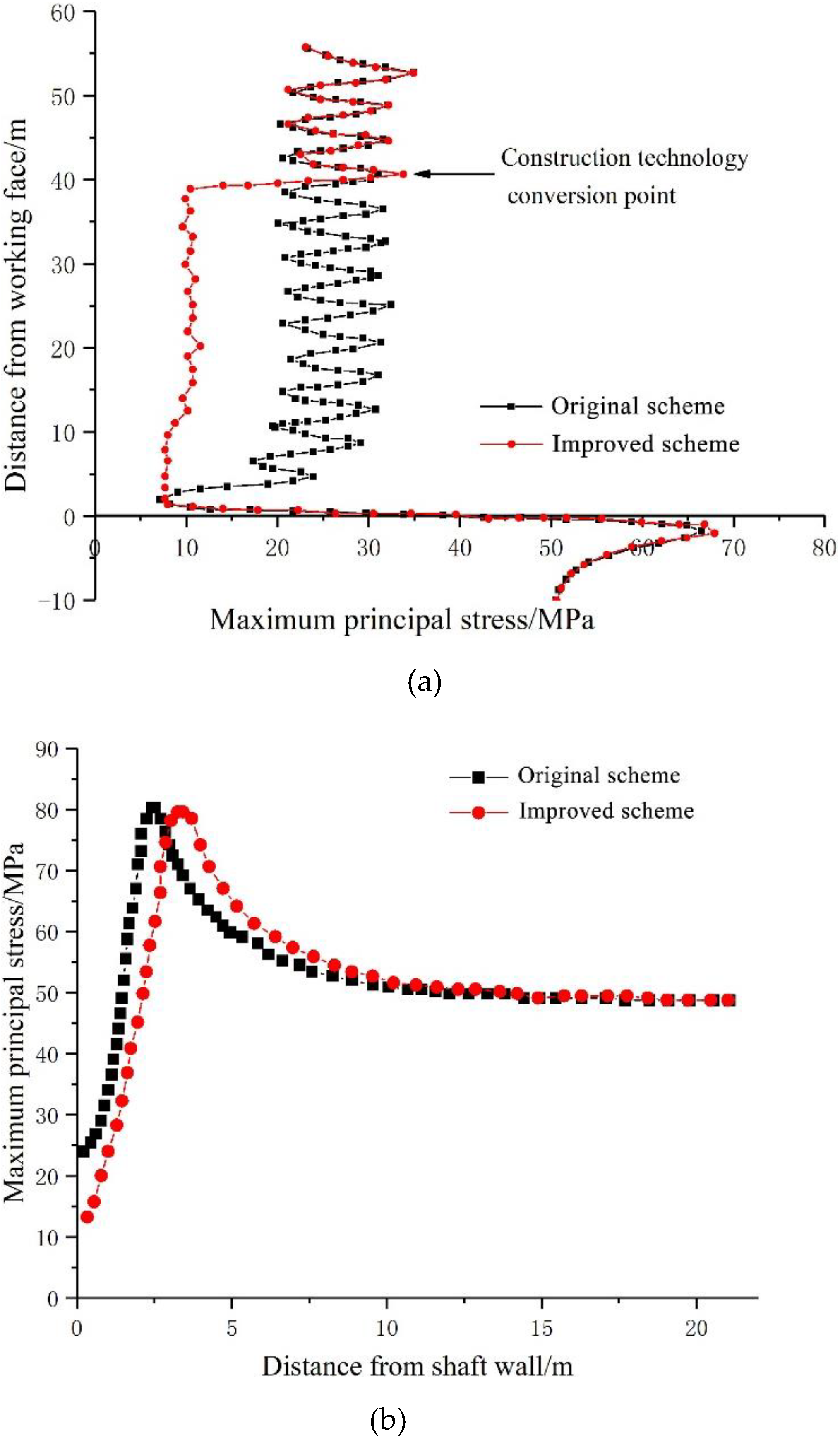
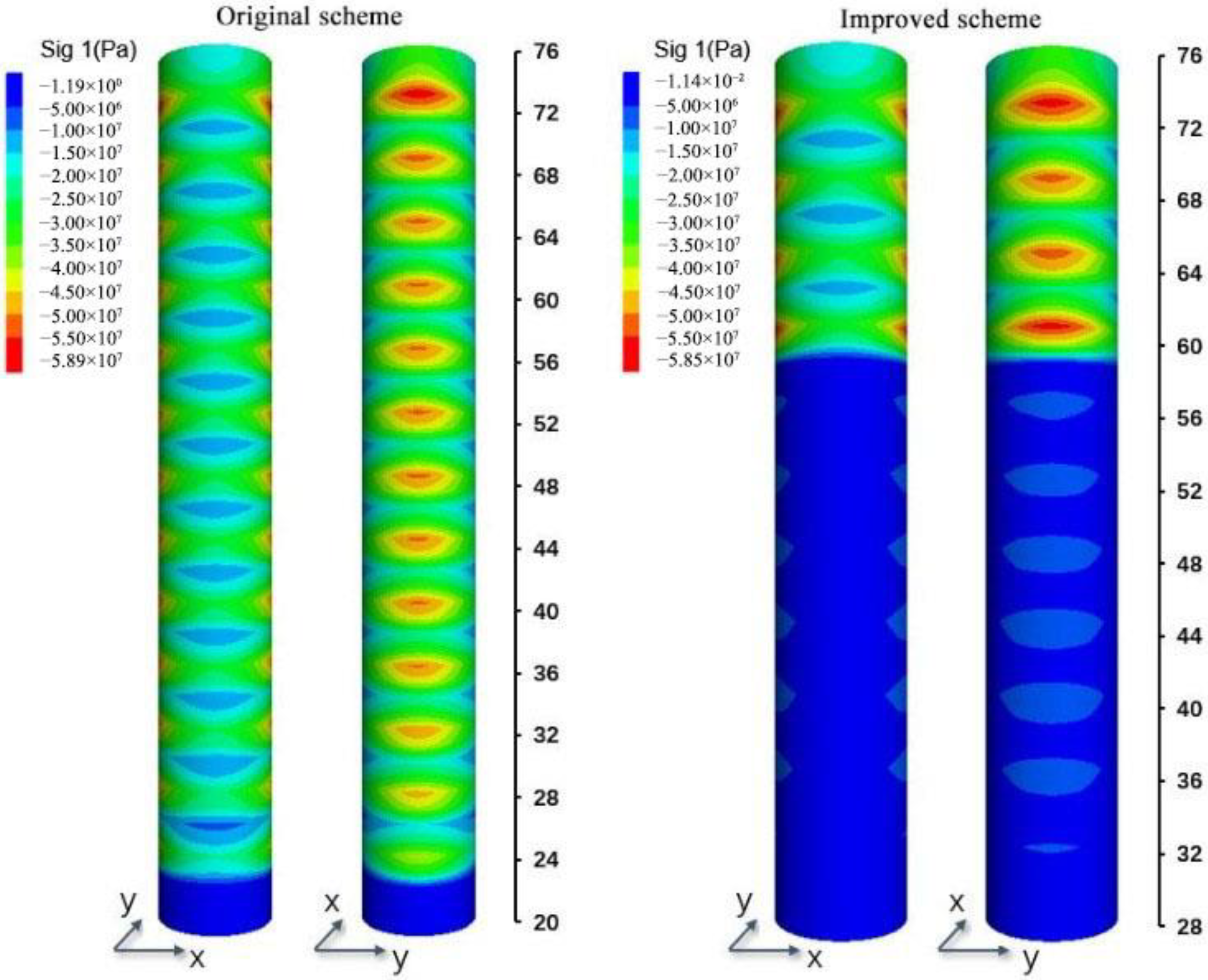
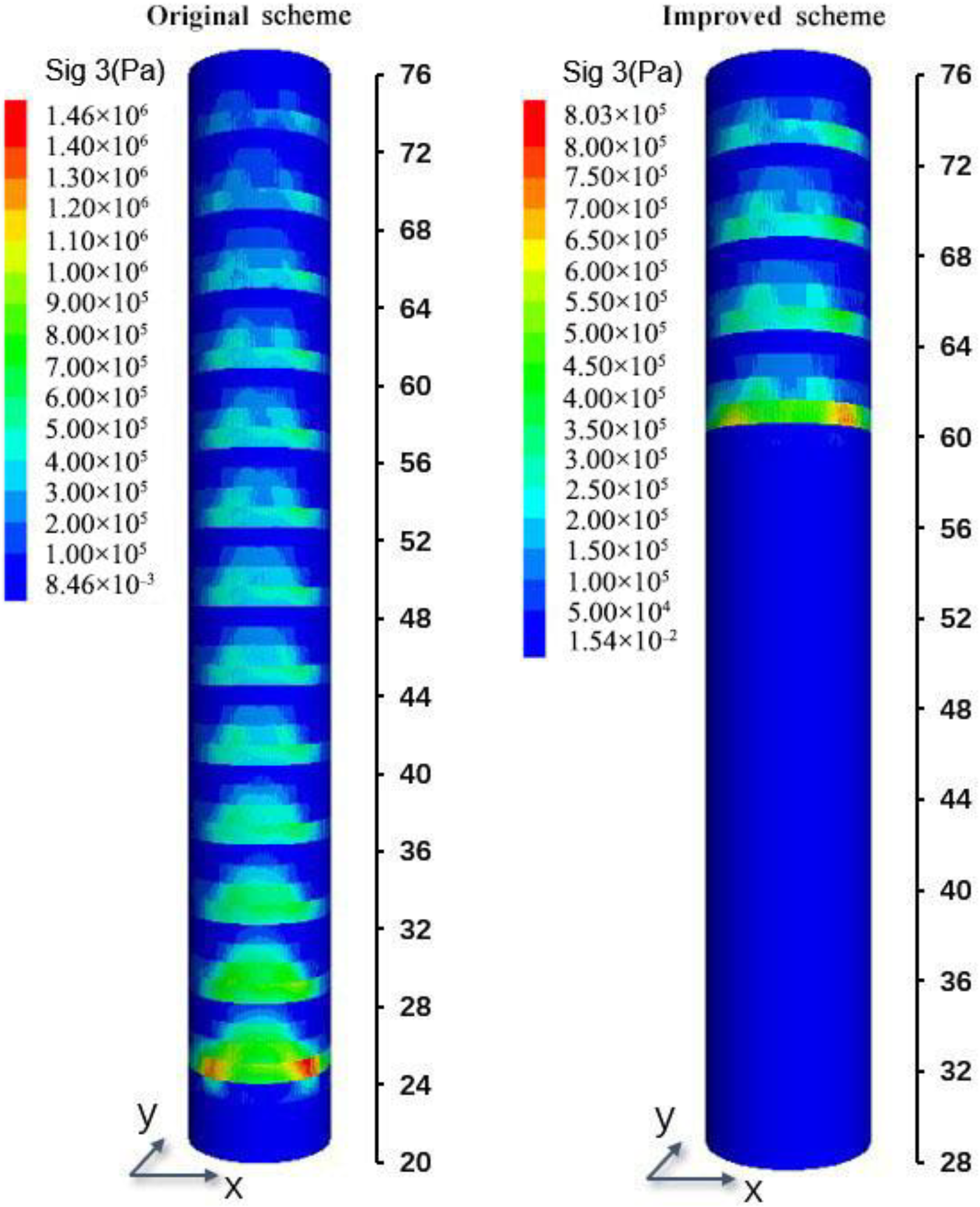
5.2.1. Stress Analysis of Surrounding Rock
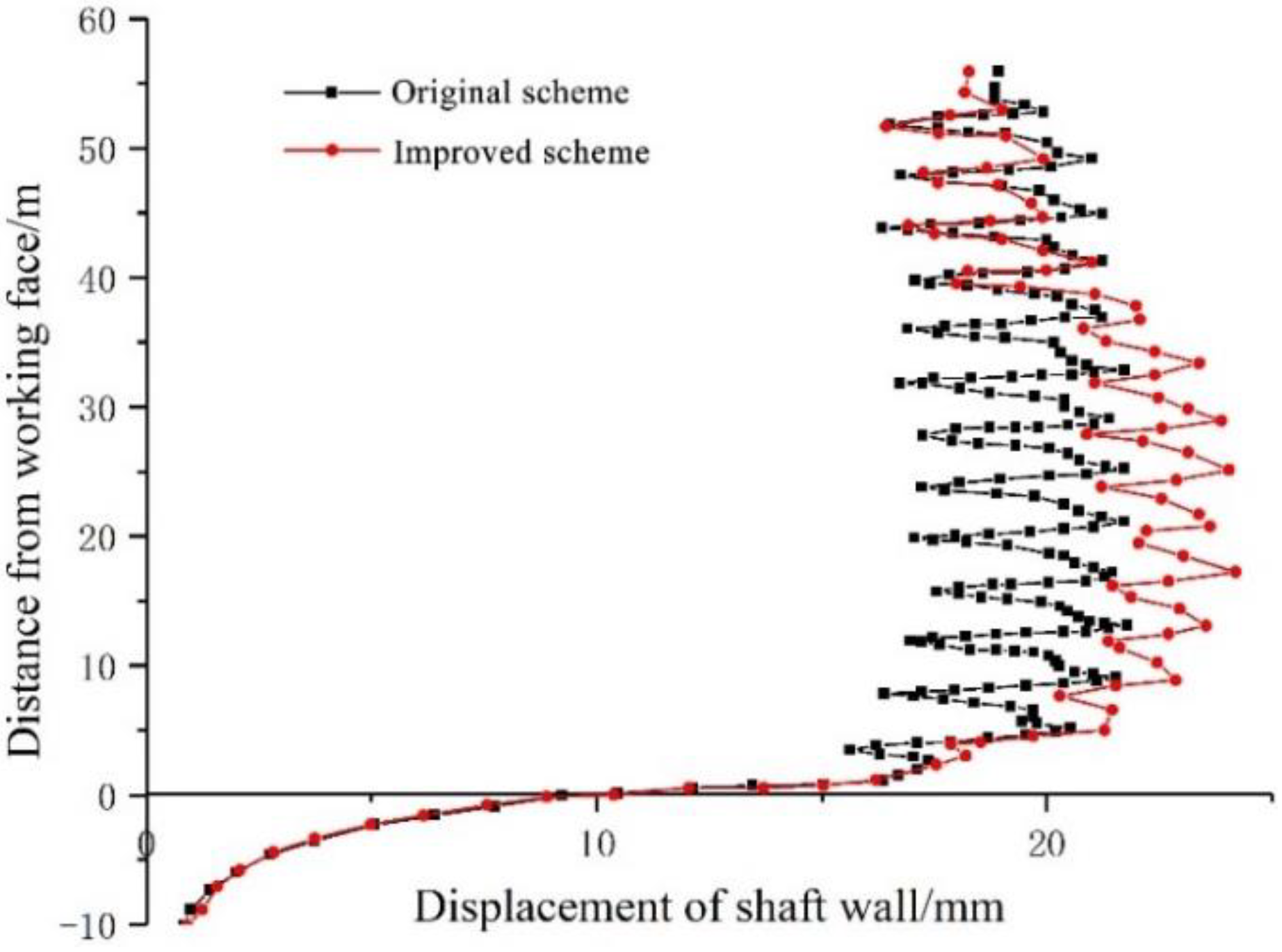
5.2.2. Displacement Analysis of the Surrounding Rock
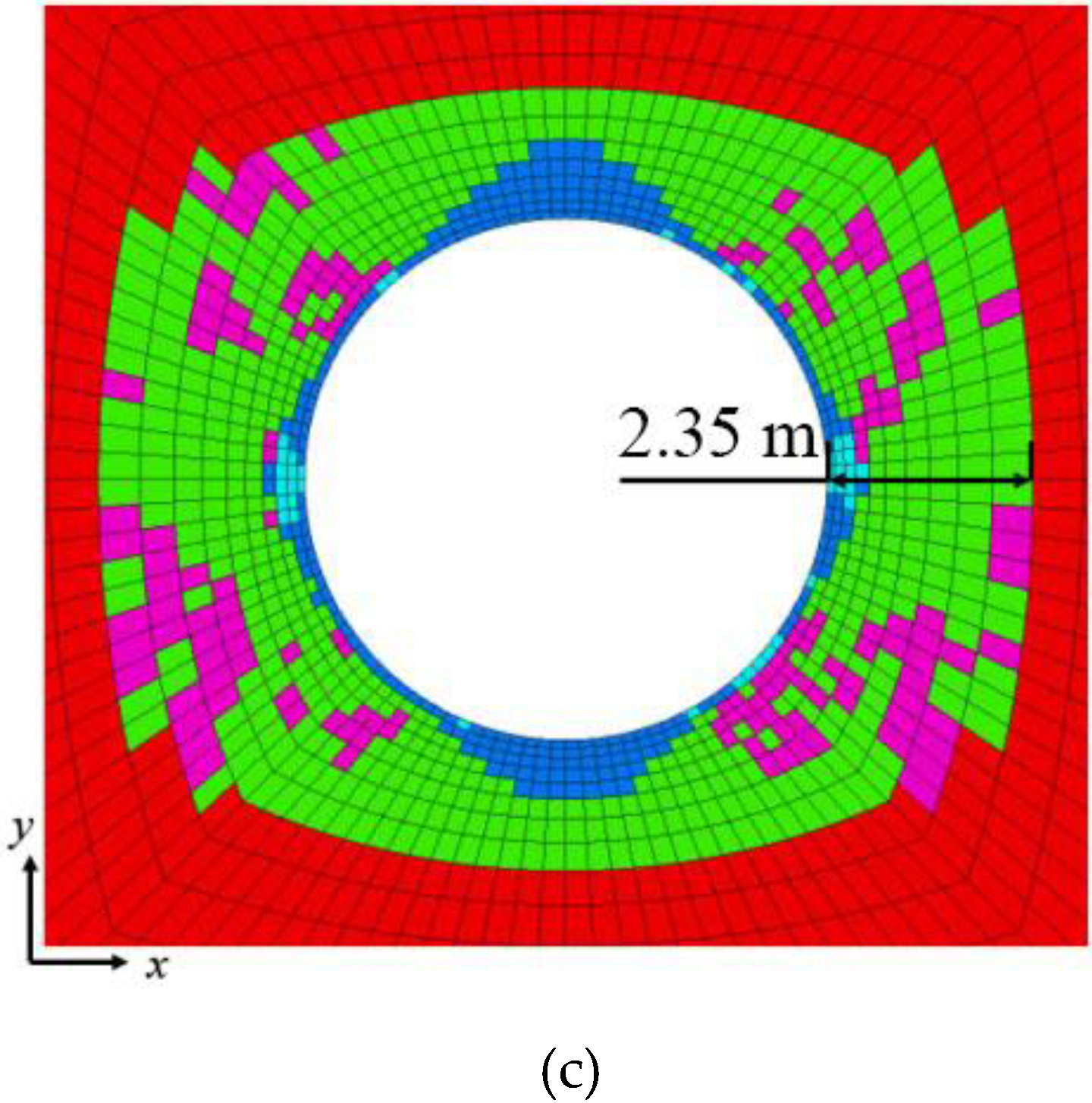
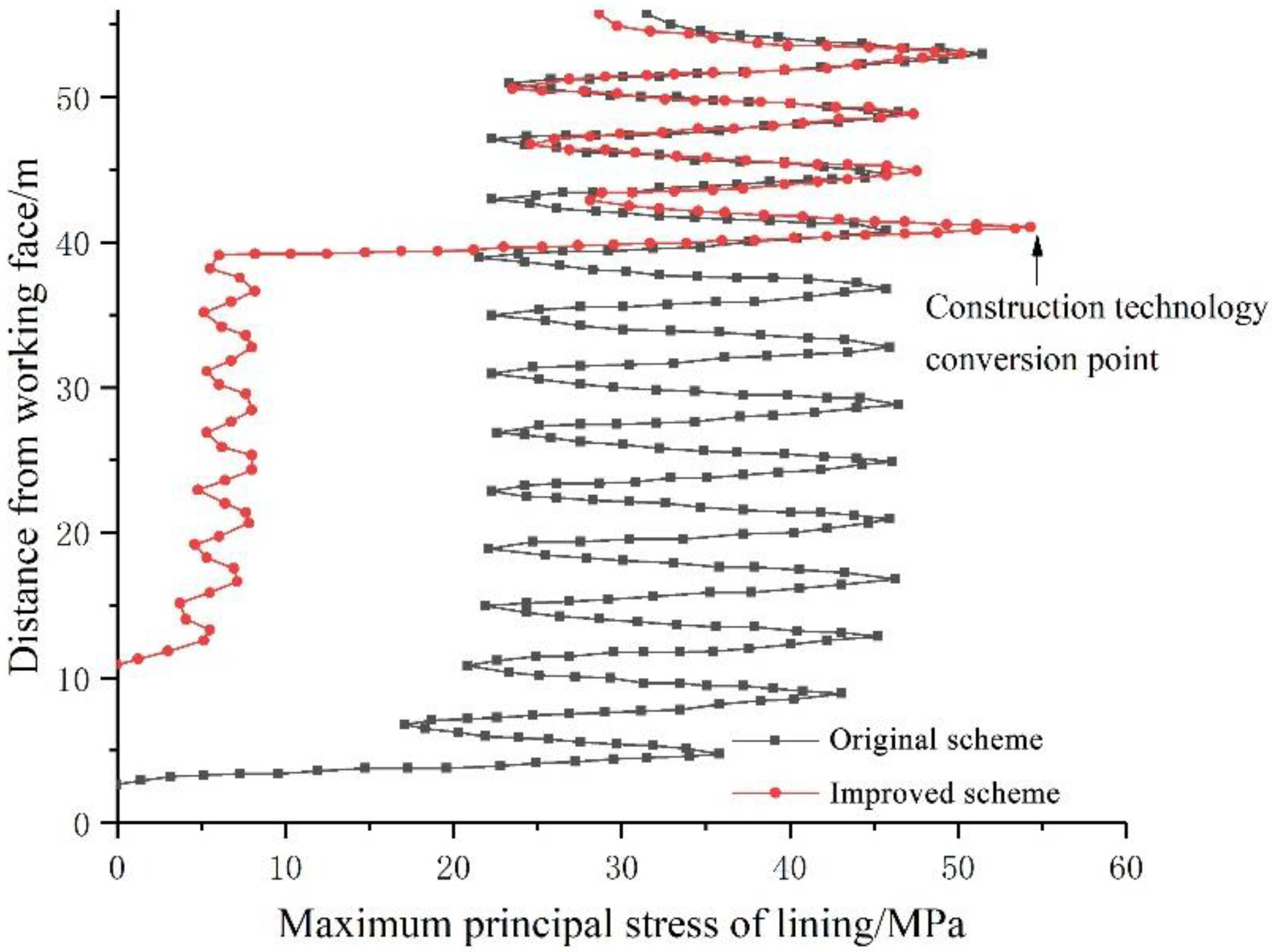
5.2.3. Lining Analysis
6. Conclusions
- In the original scheme, due to the spatial effect of the excavation face, the surrounding rock stress near the excavation face is not completely released. If lining support is installed very early, the excavation face effect will decrease as the excavation face advances. If the stress of the surrounding rock is not released completely, the displacement of the surrounding rock will be prevented by the lining, which leads to the stress concentration in the lining.
- Considering the actual stress release tie of the surrounding rock and foreign experience in shaft construction, the support distance is determined to be 12 m, with an interval of three operation cycles.
- In the proposed scheme, when the lining is 12 m away from the excavation face, the improved support scheme is used for the surrounding rock of the unlined section, which makes the rock surrounding the shaft have enough ties and space to release the stress and displacement. Therefore, the stress distribution in the lining is more uniform, and the lining compressive safety factor is increased to 2.0.
Author Contributions
Funding
Conflicts of Interest
References
- Owens, B. Mining: Extreme prospects. Nature 2013, 495, S4–S6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, J.; Wang, S. Rock mechanics and rock engineering in China: Developments and current state-of-the-art. Int. J. Rock Mech. Min. Sci. 2000, 37, 447–465. [Google Scholar] [CrossRef]
- Jiang, Q.; Su, G.; Feng, X.-T.; Chen, G.; Zhang, M.-Z.; Liu, C. Excavation Optimization and Stability Analysis for Large Underground Caverns Under High Geostress: A Case Study of the Chinese Laxiwa Project. Rock Mech. Rock Eng. 2019, 52, 895–915. [Google Scholar] [CrossRef]
- Xie, H.P.; Gao, F.; Ju, Y. Research and Development of Rock mechanics in Deep Ground Engineering. Chin. J. Rock Mech. Eng. 2015, 34, 2161–2178. [Google Scholar] [CrossRef]
- Xie, H. Research framework and anticipated results of deep rock mechanics and mining theory. Adv. Eng. Sci. 2017, 49, 1–16. [Google Scholar] [CrossRef]
- Foderà, G.; Voza, A.; Barovero, G.; Tinti, F.; Boldini, D. Factors influencing overbreak volumes in drill-and-blast tunnel excavation. A statistical analysis applied to the case study of the Brenner Base Tunnel—BBT. Tunn. Undergr. Space Technol. 2020, 105, 103475. [Google Scholar] [CrossRef]
- Yang, J.; Yao, C.; Jiang, Q.; Lu, W. 2D numerical analysis of rock damage induced by dynamic in-situ stress redistribution and blast loading in underground blasting excavation. Tunn. Undergr. Space Technol. 2017, 70, 221–232. [Google Scholar] [CrossRef]
- Zhou, Y.-C.; Liu, J.-H.; Huang, S.; Yang, H.-T.; Ji, H.-G. Performance change of shaft lining concrete under simulated coastal ultra-deep mine environments. Constr. Build. Mater. 2019, 230, 116909. [Google Scholar] [CrossRef]
- Xue, W.; Yao, Z.; Jing, W.; Tang, B.; Kong, G.; Wu, H. Experimental study on permeability evolution during deformation and failure of shaft lining concrete. Constr. Build. Mater. 2019, 195, 564–573. [Google Scholar] [CrossRef]
- Manríquez, A.L.; Sepehrnoori, K. The diffusivity equation for geopressure prediction using well logs. J. Pet. Sci. Eng. 2015, 134, 186–198. [Google Scholar] [CrossRef]
- Martyushev, D.A.; Galkin, S.V.; Shelepov, V.V. The Influence of the Rock Stress State on Matrix and Fracture Permeability under Conditions of Various Lithofacial Zones of the Tournaisian–Fammenian Oil Fields in the Upper Kama Region. Mosc. Univ. Geol. Bull. 2019, 74, 573–581. [Google Scholar] [CrossRef]
- Martyushev, D. Rock stress state influence on permeability of carbonate reservoirs. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2020, 331, 24–33. [Google Scholar] [CrossRef]
- Wang, J. Calculation of shaft wall stress under negative friction. J. Hefei Univ. Technol. 1995, 18, 117–121. [Google Scholar]
- Su, J.; Cheng, Y. Theoretical analysis of additional wellbore force in hydrophobic subsidence formation. Chin. J. Rock Mech. Eng. 2000, 19, 310–313. [Google Scholar]
- Su, J. Non-linear mechanical analysis of shaft lining in stratum settlement resulted from water drainage. Chin. J. Rock Mech. Eng. 2005, 24, 139–143. [Google Scholar]
- Zhou, Y.; Zhou, G. Strict axisymmetric deformation analysis of shaft linings considering shaft-curing load. Chin. J Geo. Eng. 2008, 30, 170–174. [Google Scholar]
- Ozturk, H.; Guler, E. A methodology for lining design of circular mine shafts in different rock masses. Int. J. Min. Sci. Technol. 2016, 26, 761–768. [Google Scholar] [CrossRef]
- Brady, B.; Brown, E. Rock Mechanics for Underground Mining; George Allen Unwin: London, UK, 2006. [Google Scholar] [CrossRef]
- Zhao, X.; Li, Y. Estimation of support requirement for a deep shaft at the Xincheng Gold Mine, China. Bull. Eng. Geol. Environ. 2021, 80, 6863–6876. [Google Scholar] [CrossRef]
- Auld, F. Design of concrete shaft linings. Proc. Inst. Civ. Eng. 1979, 67 Pt 2, 817–832. [Google Scholar] [CrossRef]
- Ozturk, H.; Unal, E. Estimation of lining thickness around circular shafts. In Proceedings of the International Mining Congress and Exhibition of Turkey (17th)—IMCET2001, Chamber of Mining Engineers of Turkey, Ankara, Turkey, 22 June 2001; pp. 437–444. [Google Scholar]
- He, M. Research progress of deep shaft construction mechanics. J. China Coal Soc. 2021, 46, 726–746. [Google Scholar] [CrossRef]
- Yu, Q.; Yin, K.; Ma, J.; Shimada, H. Vertical Shaft Support Improvement Studies by Strata Grouting at Aquifer Zone. Adv. Civ. Eng. 2018, 2018, 5365987. [Google Scholar] [CrossRef]
- Ma, F.-S.; Deng, Q.-H.; Cunningham, D.; Yuan, R.-M.; Zhao, H.-J. Vertical shaft collapse at the Jinchuan Nickel Mine, Gansu Province, China: Analysis of contributing factors and causal mechanisms. Environ. Earth Sci. 2012, 69, 21–28. [Google Scholar] [CrossRef]
- Hu, X.; He, C.; Walton, G.; Chen, Z. A Combined Support System Associated with the Segmental Lining in a Jointed Rock Mass: The Case of the Inclined Shaft Tunnel at the Bulianta Coal Mine. Rock Mech. Rock Eng. 2020, 53, 2653–2669. [Google Scholar] [CrossRef]
- Monteiro, V.M.D.A.; Silva, F.D.A. The use of the Barcelona test as quality control of fiber reinforced shotcrete for underground mining. Constr. Build. Mater. 2020, 262, 120719. [Google Scholar] [CrossRef]
- Unrug, K. Construction of Development Openings; Society for Mining, Metallurgy, and Exploration, Inc.: Littleton, CO, USA, 1992. [Google Scholar]
- Yang, L.; Yao, Z.; Xue, W.; Wang, X.; Kong, W.; Wu, T. Preparation, performance test and microanalysis of hybrid fibers and microexpansive high-performance shaft lining concrete. Constr. Build. Mater. 2019, 223, 431–440. [Google Scholar] [CrossRef]
- Xue, W. Research on Coupled Damage Evolution Mechanism and Strength Characteristics of Shaft Lining Concrete under High Pressure Water; Anhui University of Science and Technology: Huainan, China, 2017. [Google Scholar]
- Zhou, X.; He, Z.; Ji, H. Design method of freezing rock wall under high water pressure. J. China Coal Soc. 2011, 36, 2121–2126. [Google Scholar]
- Huang, W.; Wang, X.; Shen, Y.; Feng, F.; Wu, K.; Li, C. Application of concrete-filled steel tubular columns in gob-side entry retaining under thick and hard roof stratum: A case study. Energy Sci. Eng. 2019, 7, 2540–2553. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Z.; Sun, W.; Chen, S.; Yin, D.; Liu, H.; Chen, B. Determination of critical criterion of tensile-shear failure in Brazilian disc based on theoretical analysis and meso-macro numerical simulation. Comput. Geotech. 2021, 134, 104096. [Google Scholar] [CrossRef]
- Vergne, J. The Hard Rock Miner’s Handbook, 3rd ed.; McIntosh Engineering Limited: North Bay, ON, Canada, 2003. [Google Scholar]
- Cai, M.; Brown, E.T. Challenges in the Mining and Utilization of Deep Mineral Resources. Engineering 2017, 3, 432–433. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Wang, Q.; Liu, S. Vertical Shaft Excavation Shaping and Surrounding Rock Control Technology Under the Coupling Action of High Ground Stress and Fracture Formation. J. Perform. Constr. Facil. 2020, 34, 04020116. [Google Scholar] [CrossRef]
- Mu, W.; Wang, D.; Li, L.; Yang, T.; Feng, Q.; Wang, S.; Xiao, F. Cement flow in interaction rock fractures and its corresponding new construction process in slope engineering. Constr. Build. Mater. 2021, 303, 124533. [Google Scholar] [CrossRef]
- Ostrowski, W. Design considerations for modern shaft linings. Can. Min. Metall. Bull. 1972, 65, 58–72. [Google Scholar]
- Zhao, X.; Li, Y.; Zhang, S.; Chen, Y.; Wang, C.; Wang, X. Analysis and application of disturbance stress reaction mechanism of surrounding rock during sinking ultra-deep shaft. Hazards Control Tunn. Undergr. Eng. 2020, 2, 19–28. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. Rock Eng. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Grimstad, E.; Barton, N. Updating the Q-system for NMT. In Proceedings of the International Symposium on Sprayed Concrete-Modern Use of Wet Mix Sprayed Concrete for Underground Support, Fagemes, Oslo, Norway, 22–26 October 1993; pp. 46–66. [Google Scholar]
- Barton, N. Some new Q-value correlations to assist in site characterization and tunnel design. Int. J. Rock Mech. Min. Sci. 2002, 39, 185–216. [Google Scholar] [CrossRef]
- Bieniawski, Z. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 333–343. [Google Scholar]
- Bieniawski, Z. Engineering Rock Mass Classifications; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Hormazabal, E.; Soto, C.; Russo, A.; Carranza-Torres, C. Estimation of support requirement for large diameter ventilation shaft at Chuquicamata underground mine in Chile. In Proceedings of the Harmonising Rock Engineering and the Environment—12th ISRM International Congress on Rock Mechanics, Beijing, China, 18–21 October 2011; pp. 1511–1520. [Google Scholar] [CrossRef]
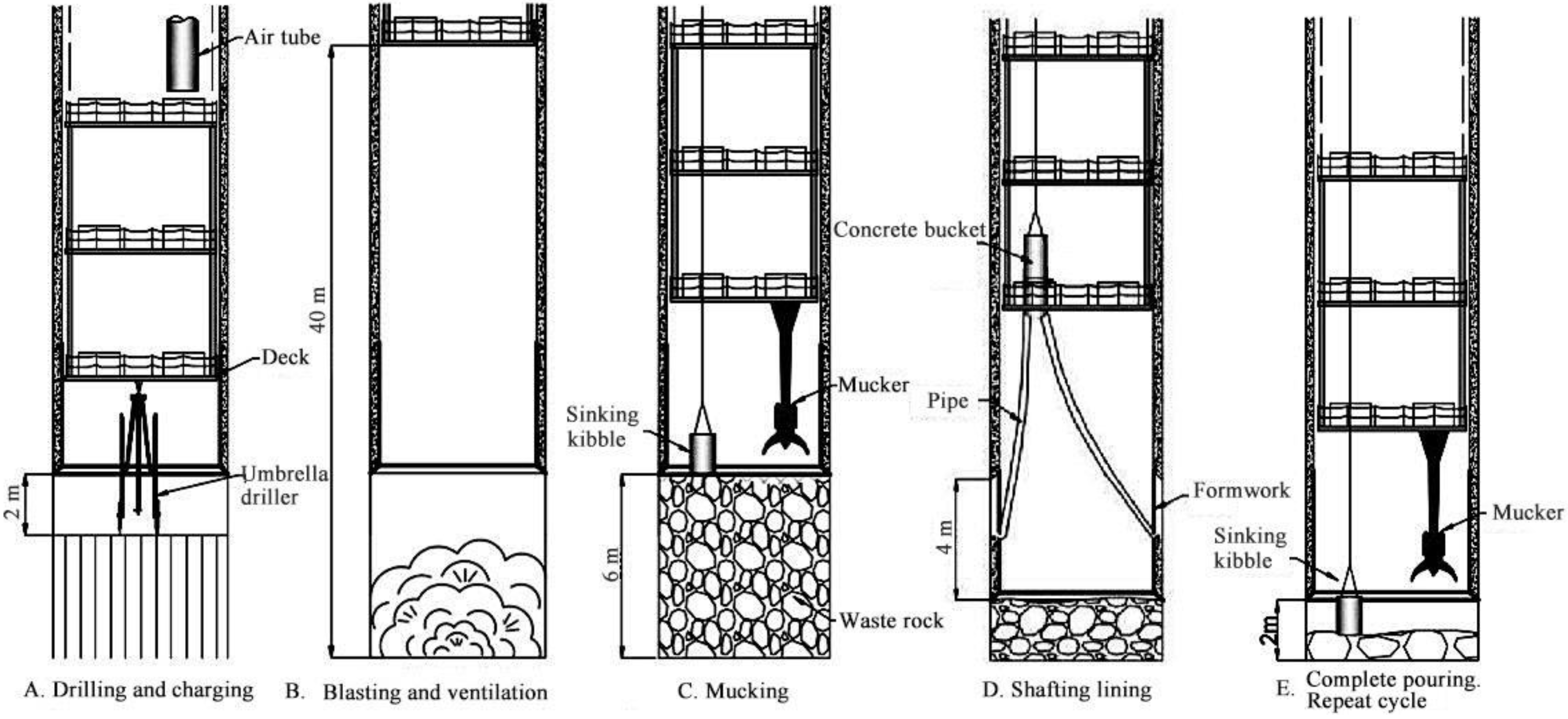
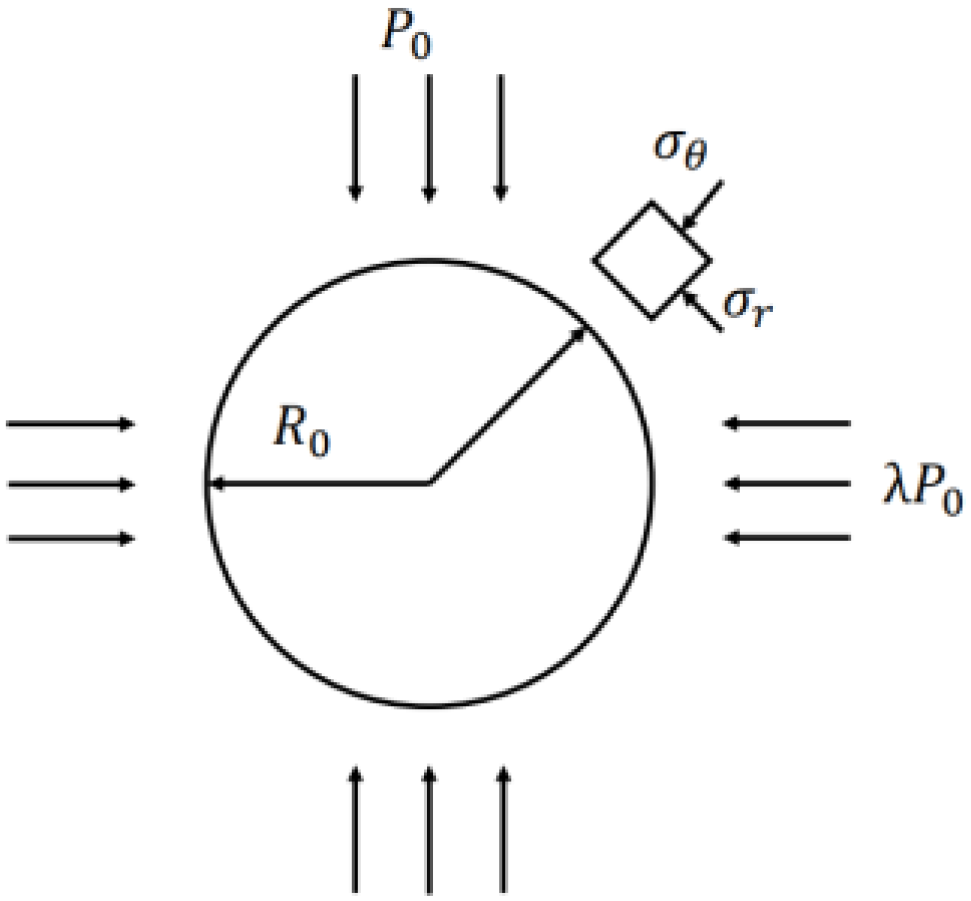

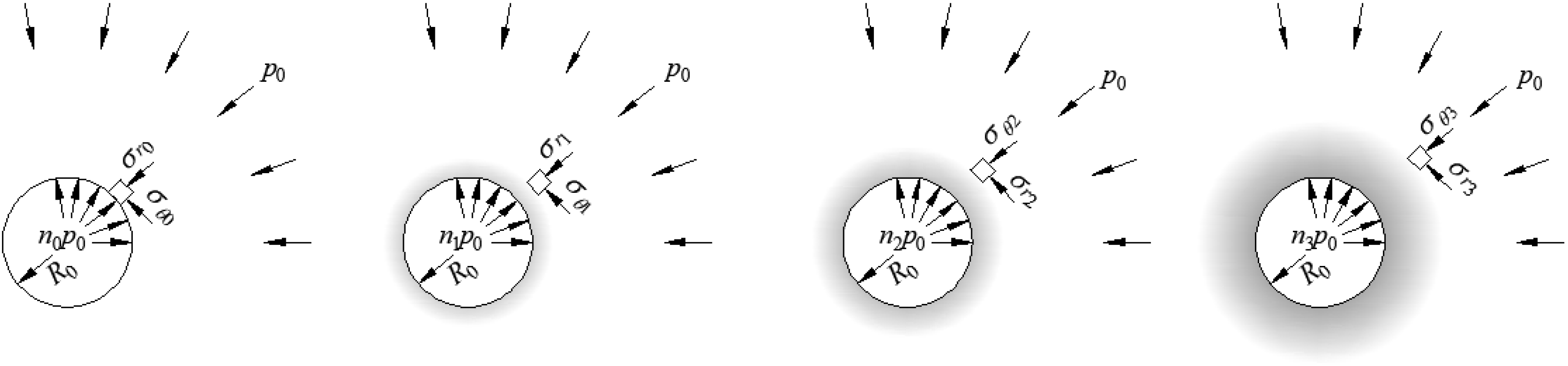
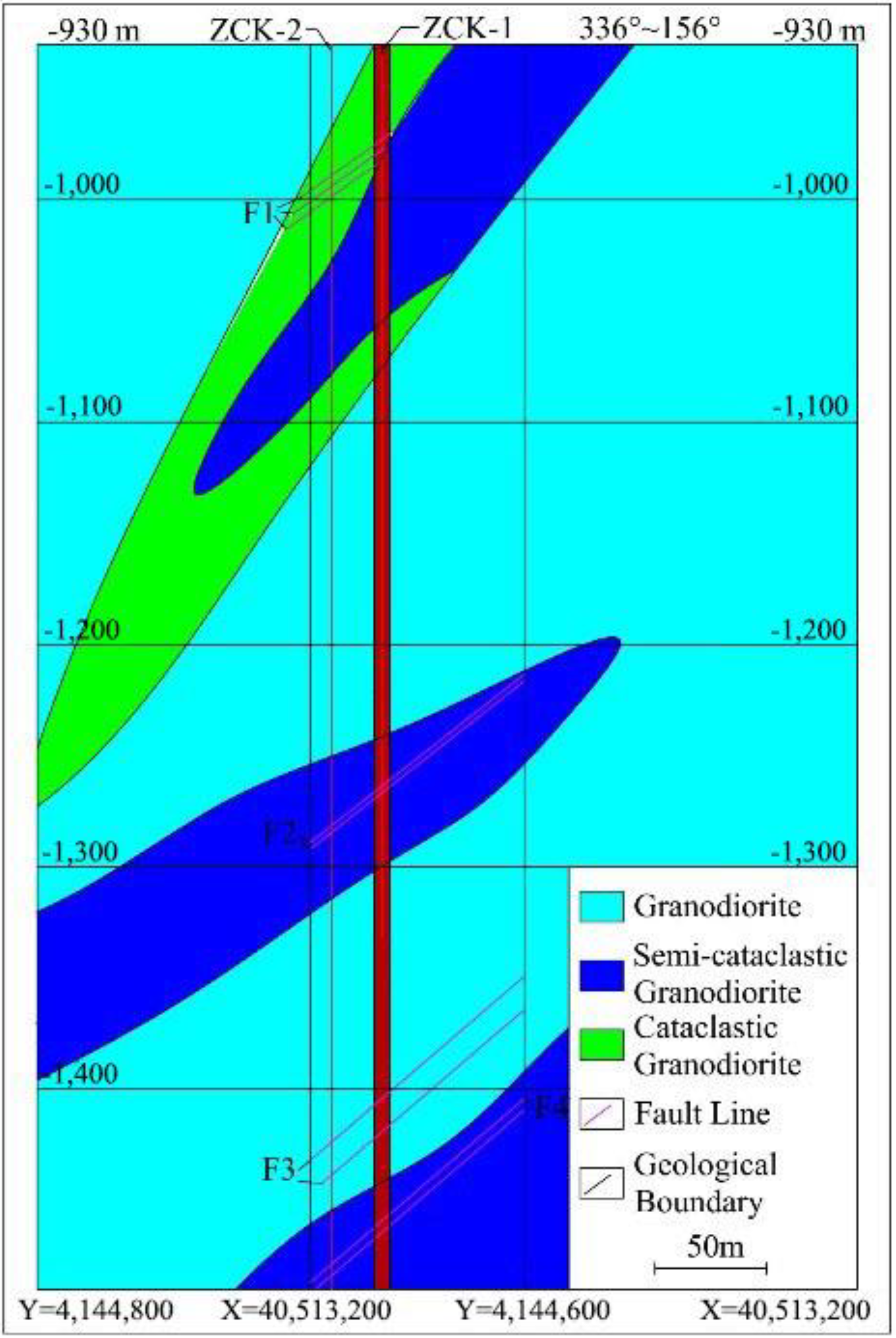



| Depth/m | Lithology | RQD | Rock Quality |
|---|---|---|---|
| −930~−987 | Cataclastic Granodiorite | 83% | Good |
| −987~−1101 | Granodiorite, Semicataclastic Granodiorite and Cataclastic Granodiorite | 55% | Fair |
| −1101~−1167 | Granodiorite | 81% | Good |
| −1167~−1199 | Granodiorite | 71% | Fair |
| −1199~−1254 | Granodiorite | 87% | Good |
| −1254~−1276 | Semicataclastic Granodiorite | 59% | Fair |
| Depth/m | Number of Joint Sets |
|---|---|
| −930.00~−972.00 | 2~3 |
| −972.00~−987.00 | 3 |
| −987.00~−1050.00 | 3 |
| −1050.00~−1073.00 | 3 |
| −1073.00~−1102.00 | 3 |
| −1102.00~−1153.00 | 2 |
| −1153.00~−1207.00 | 3 |
| −1207.00~−1250.00 | 2 |
| −1250.00~−1271.00 | 3 |
| Rock | Density g/cm3 | UCS/MPa | c/MPa | φ/° | E/GPa | |
|---|---|---|---|---|---|---|
| Granite | 2.66 | 102.5 | 24.3 | 49.94 | 70.8 | 0.29 |
| Depth/m | RQD | Jn | Jr | Ja | Jw | SRF | Q | Rock Rating | Rock Quality |
|---|---|---|---|---|---|---|---|---|---|
| −930.0~−972.0 | 86 | 6 | 1~1.5 | 1 | 1.0 | 20 | 1.1 | Ⅳ | poor |
| −972.0~−987.0 | 76 | 9 | 1~1.5 | 1 | 1.0 | 20 | 0.6 | Ⅳ | poor |
| −987.0~−1050.0 | 51 | 9 | 1~1.5 | 1 | 1.0 | 20 | 0.4 | Ⅳ | poor |
| −1050.0~−1073.0 | 71 | 6 | 1~1.5 | 1 | 1.0 | 20 | 0.9 | Ⅳ | poor |
| −1073.0~−1102.0 | 52 | 6 | 1~1.5 | 1 | 1.0 | 20 | 0.7 | Ⅳ | poor |
| −1102.0~−1153.0 | 80 | 6 | 1~1.5 | 1 | 1.0 | 20 | 1 | Ⅳ | poor |
| −1153.0~−1207.0 | 77 | 9 | 1~1.5 | 1 | 1.0 | 20 | 0.6 | Ⅳ | poor |
| −1207.0~−1250.0 | 87 | 9 | 1~1.5 | 1 | 1.0 | 20 | 0.7 | Ⅳ | poor |
| −1250.0~−1271.0 | 68 | 9 | 1~1.5 | 1 | 1.0 | 20 | 0.6 | Ⅳ | poor |
| Depth/m | UCS/MPa | RQD | Spacing/m | Joint Condition | Ground Water | Revision | Score | Rock Rating | Rock Quality |
|---|---|---|---|---|---|---|---|---|---|
| −930.0~−972.0 | 12 | 17 | 10 | 25 | 15 | −5 | 74 | Ⅱ | good |
| −972.0~−987.0 | 12 | 17 | 10 | 25 | 15 | −5 | 74 | Ⅱ | good |
| −987.0~−1050.0 | 12 | 13 | 10 | 25 | 15 | −5 | 70 | Ⅱ | good |
| −1050.0~−1073.0 | 12 | 13 | 10 | 25 | 15 | −5 | 70 | Ⅱ | good |
| −1073.0~−1102.0 | 12 | 13 | 8 | 25 | 15 | −5 | 68 | Ⅱ | good |
| −1102.0~−1153.0 | 12 | 17 | 10 | 25 | 15 | −5 | 74 | Ⅱ | good |
| −1153.0~−1207.0 | 12 | 17 | 8 | 25 | 15 | −5 | 72 | Ⅱ | good |
| −1207.0~−1250.0 | 12 | 17 | 10 | 25 | 15 | −5 | 74 | Ⅱ | good |
| −1250.0~−1271.0 | 12 | 13 | 10 | 25 | 15 | −5 | 70 | Ⅱ | good |
| Depth/m | c/MPa | φ/° | Em/GPa | ||
|---|---|---|---|---|---|
| −930.0~−972.0 | 7.28 | 39.61 | 10.50 | 0.224 | 20.73 |
| −972.0~−987.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
| −987.0~−1050.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
| −1050.0~−1073.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
| −1073.0~−1102.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
| −1102.0~−1153.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
| −1153.0~−1207.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
| −1207.0~−1250.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
| −1250.0~−1271.0 | 6.55 | 37.08 | 7.16 | 0.141 | 16.12 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Deng, L.; Zhou, X.; Zhao, Y.; Guo, Z. A Primary Support Design for Deep Shaft Construction Based on the Mechanism of Advanced Sequential Geopressure Release. Processes 2022, 10, 1376. https://doi.org/10.3390/pr10071376
Zhao X, Deng L, Zhou X, Zhao Y, Guo Z. A Primary Support Design for Deep Shaft Construction Based on the Mechanism of Advanced Sequential Geopressure Release. Processes. 2022; 10(7):1376. https://doi.org/10.3390/pr10071376
Chicago/Turabian StyleZhao, Xingdong, Lei Deng, Xin Zhou, Yifan Zhao, and Zhenpeng Guo. 2022. "A Primary Support Design for Deep Shaft Construction Based on the Mechanism of Advanced Sequential Geopressure Release" Processes 10, no. 7: 1376. https://doi.org/10.3390/pr10071376
APA StyleZhao, X., Deng, L., Zhou, X., Zhao, Y., & Guo, Z. (2022). A Primary Support Design for Deep Shaft Construction Based on the Mechanism of Advanced Sequential Geopressure Release. Processes, 10(7), 1376. https://doi.org/10.3390/pr10071376






