Cable Fault Location in VSC-HVDC System Based on Improved Local Mean Decomposition

Abstract

Aiming at the problem of low positioning accuracy caused by modal aliasing and noise interference in DC cable fault location analysis of a VSC-HVDC system, a double-ended fault location method for flexible DC cables based on improved local mean decomposition is proposed. Firstly, the local mean decomposition (LMD) is used to decompose the six-mode voltage signal to obtain the product function (PF) component; then, to overcome the problem that the instantaneous frequency function of the LMD is limited by the extreme value, the Hilbert transform is performed on the PF1 to obtain the instantaneous frequency curve, and the arrival time of the voltage traveling wave head is determined from the mutation information. Finally, the fault distance is obtained by using the principle of double-ended traveling wave fault location. Different fault conditions are simulated, analyzed, and compared with wavelet transform and Hilbert–Huang transform. The results show that the proposed method has a positioning error within 1%, and it is less affected by interference noise and transition resistance.

1. Introduction

In the context of the development of the dual-carbon policy, the large-scale and effective use of renewable energy and distributed energy has promoted the development of flexible DC transmission projects. China has also successfully built flexible DC transmission projects such as Shanghai Nanhui, Zhejiang Zhoushan, and Fujian Xiamen [1]. It has broad application scenarios in terms of island power supply and asynchronous interconnection [2]. As an important link for reliable and continuous output of electric energy, transmission lines are mostly laid in cable trenches or directly buried underground, which is more reliable than overhead lines. The line cannot be directly followed, and the repair speed and excavation range put forward higher requirements for the measurement of fault distance.

At present, the available methods for distance measurement of DC transmission lines include the traveling wave method, fault analysis method, and natural frequency method. From the three dimensions of time, space, and frequency, the distance equation between fault distance and electrical quantity is constructed. The fault analysis method establishes the ranging equation system according to the system parameters and the fault recording data and solves the fault distance [3]. Reference [4] calculates the resistance value of the transition resistance according to the voltage distribution along the line and the current distribution along the line and uses the minimum variance of the transition resistance value at the fault point to locate the fault. Reference [5] is based on the time-domain model, considering the distribution parameters of HVDC transmission lines with infinitely small multi-order distances, and uses the particle swarm algorithm to search for the corresponding distance with the smallest voltage distribution difference along the entire line, which is the actual fault distance. However, the line model is required to be more accurate. Reference [6] considers the frequency-dependent characteristics of DC transmission line parameters, extracts each frequency component in the transient process, and uses the corresponding line parameters to locate faults at each frequency point, which improves the accuracy of the model to a certain extent. Some scholars have used different methods to extract the principal components of the natural frequency to calculate the fault distance, which can avoid the error caused by wave head identification. Reference [7] first obtains the natural frequency principal component interval of the fault traveling wave signal through wavelet transform and then comprehensively considers the extreme point distribution of the wavelet transform coefficients on each decomposition scale to obtain a more accurate natural frequency principal component. References [8,9] use the multiple signal classification (MUSIC) method to extract the natural frequency principal components of transient voltages and currents. Reference [10] improves the aliasing phenomenon in the MUSIC algorithm, combining the fast Fourier transform (FFT) and the MUSIC algorithm to obtain a more accurate second-order natural frequency principal component. Based on FFT, References [11,12] combine with the Prony algorithm and the rotation-invariant technology signal parameter estimation algorithm and the total least squares method to extract the natural frequency accurately. However, when the natural frequency method is in a high-resistance fault, the reflected traveling wave energy decreases rapidly, which will significantly reduce the ranging accuracy [13]; when the fault point is close to the line terminal, the frequency of the main component of the traveling wave spectrum is extremely high (exceeding the sampling rate of traveling wave acquisition), resulting in a dead zone for ranging. To reduce the influence of accurate wave velocity errors and solve the problem of high-resistance faults, deep learning methods such as convolutional neural networks [14] and deep belief networks [15] provide new solutions for research in the field of HVDC transmission. Reference [16] uses wavelet packet decomposition to extract traveling wave features from fault signals, which are used as input samples of a radial basis function neural network to map to line fault locations. References [17,18] both use Hilbert–Huang transform (HHT) to capture fault features and use them as input samples for support vector machines and convolutional neural networks to achieve fault location. However, the training of neural network models requires a large amount of fault data. If this condition is not met, the positioning results will not be as accurate as expected, and there are great challenges in practical application. The traveling wave method utilizes the time difference and wave speed between the fault traveling wave and the fault point to and from the measurement terminal to realize the fault location. Although the single-ended traveling wave method [19] is lower in cost than the double-ended traveling wave method, it has a principal defect; it cannot locate complex line structures and fault conditions, and there is a problem with positioning dead zones. The wave method is not as high as the double-ended traveling wave method in terms of reliability and positioning accuracy.

Accurately detecting the arrival time of the traveling wave head is one of the key issues of the traveling wave method. At present, although these nonlinear analysis methods have achieved good detection results in the process of wave head detection, they also have some problems. For example, the detection effect of wavelet transform [20] is not only restricted by the Heisenberg uncertainty principle but also depends on the selection of the basis function and the decomposition scale, which cannot guarantee the optimal decomposition effect; S transform [21,22] is an easy way to describe the distribution of amplitude and phase with time according to the magnitude matrix of the S matrix, but it is difficult to examine the distribution of fault signal frequency with time. The morphological spectrum in multi-scale morphology [23] can be used to characterize the characteristics of the wave head reaching the monitoring point, but the size of the morphological spectrum under each scale is greatly affected by the amplitude and shape of the structure function and the sampling frequency. HHT [24] first uses empirical mode decomposition (EMD) to decompose the complex signal into the sum of several intrinsic mode functions (IMF) and then uses Hilbert transform to obtain the frequency and amplitude of each IMF component. Although this method has good self-adaptation, it will cause serious pollution to the amplitude-frequency data in the process of multiple iterations, which will affect the detection accuracy of the disturbance amplitude and frequency. The local mean decomposition method [25] obtains the product function by iterative division, and the process of obtaining the product function component has fewer iterations and less end effect, and so the degree of inward contamination of the instantaneous amplitude and frequency data is lesser. However, for the positioning of the arrival time of the traveling wave head, it is often necessary to observe the amplitude mutation point of the instantaneous frequency curve. The value of the frequency-modulated (FM) signal must be kept between −1 and 1 to be effective, but the corresponding value of the wave head arrival time is often far greater. If the valid range is required, it should be set to −1 or 1. The instantaneous frequency curve obtained after processing has no obvious change in the sudden change time and amplitude from its adjacent time value and amplitude, and so accurate positioning cannot be carried out.

Based on the above analysis, an improved local mean decomposition method (ILMD) is proposed. Aiming at the problem that the instantaneous frequency function in the general local mean decomposition method is limited by the extreme value and cannot be accurately located, the method of extracting the instantaneous frequency function after the Hilbert transform of the product function component is proposed to solve the problem. The first frequency mutation point of the frequency curve is used to determine the moment when the first wave head of the traveling wave arrives at the measurement point. Simulation verification proves that the proposed ranging method has high accuracy.

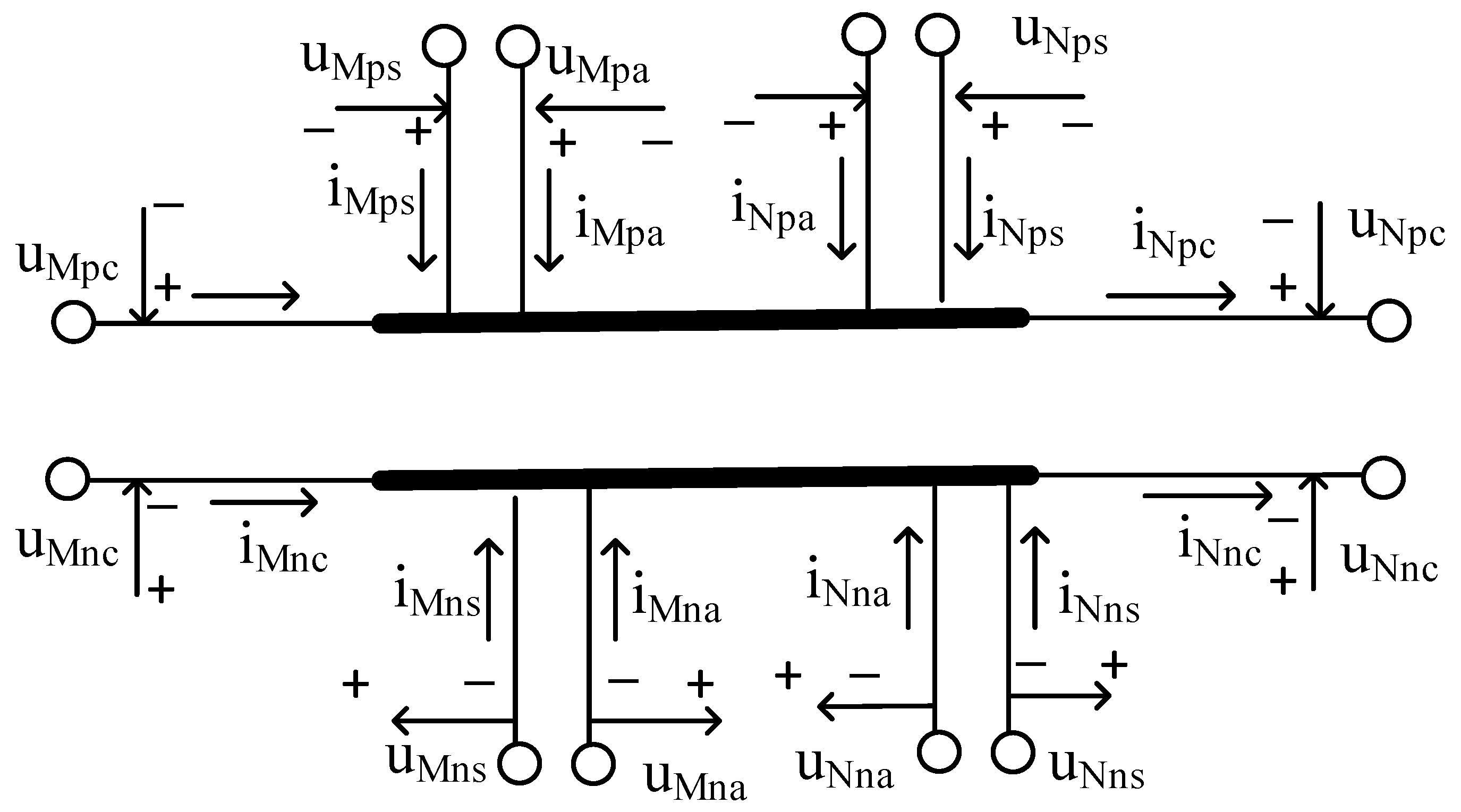
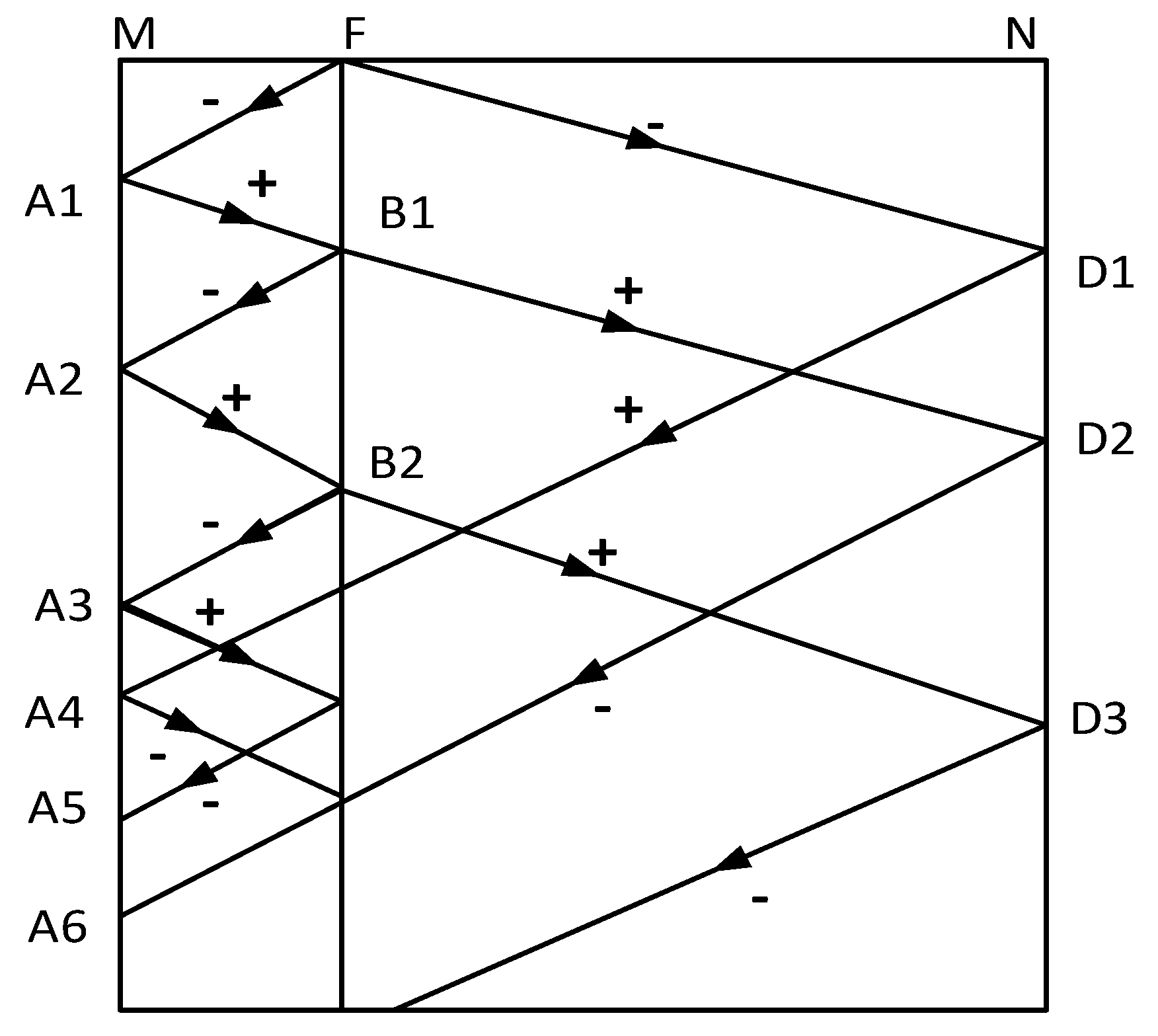
2. DC Cable Phase-Mode Conversion

This article takes a single-core XLPE cable with an armored layer as an example. The single-core XLPE cable is composed of a cable core, an insulating layer, and an armoring layer. Regardless of whether they are in normal operation or the fault stage, the positive and negative poles have a strong coupling degree, and the six groups of voltage and current interfere with each other. To eliminate the difference between these parameters, they must be decoupled first. The voltages of the core layer, insulation layer, and armor layer of the DC cable are, respectively, recorded as ${\mathrm{U}}_{\mathrm{MPc}}$, ${\mathrm{U}}_{\mathrm{Mps}}$, ${\mathrm{U}}_{\mathrm{Mpa}}$ and ${\mathrm{U}}_{\mathrm{Nnc}}$, ${\mathrm{U}}_{\mathrm{Nns}}$, ${\mathrm{U}}_{\mathrm{Nna}}$, and the DC currents of them are, respectively, recorded as ${\mathrm{I}}_{\mathrm{MPc}}$, ${\mathrm{I}}_{\mathrm{Mps}}$, ${\mathrm{I}}_{\mathrm{Mpa}}$ and ${\mathrm{I}}_{\mathrm{Nnc}}$, ${\mathrm{I}}_{\mathrm{Nns}}$, ${\mathrm{I}}_{\mathrm{Nna}}$. The specific reference direction is shown in Figure 1.

The wave process equation of the cable is:

$$\{\begin{array}{l}\frac{\partial {\mathrm{U}}_{\mathrm{M}}}{\partial x}=-{\mathrm{RI}}_{\mathrm{M}}-\mathrm{L}\frac{\partial {\mathrm{I}}_{\mathrm{M}}}{\partial \mathrm{t}}\\ \frac{\partial {\mathrm{I}}_{\mathrm{M}}}{\partial x}=-{\mathrm{GU}}_{\mathrm{M}}-\mathrm{C}\frac{\partial {\mathrm{U}}_{\mathrm{M}}}{\partial \mathrm{t}}\end{array}$$

(1)

Here, ${\mathrm{U}}_{\mathrm{M}}=[u_{\mathrm{Mpc}}{u}_{\mathrm{Mnc}}{u}_{\mathrm{Mps}}{u}_{\mathrm{Mns}}{u}_{\mathrm{Mpa}}{u}_{\mathrm{Mna}}]$, ${\mathrm{I}}_{\mathrm{M}}=[i_{\mathrm{Mpc}}{i}_{\mathrm{Mnc}}{i}_{\mathrm{Mps}}{i}_{\mathrm{Mns}}{i}_{\mathrm{Mpa}}{i}_{\mathrm{Mna}}]$.

Converting R, L, G, and C into a diagonal matrix gives the phase-mode transformation matrix of the DC voltage [26].

$$P=K\otimes \left[\begin{array}{ccc}I& I& I\\ I& I& 0\\ I& 0& 0\end{array}\right]$$

(2)

$$K=\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$

(3)

where 0 and I are the second-order zero matrix and identity matrix, respectively, and K is the Karenbauer transformation matrix.

Let $\mathrm{Q}={\mathrm{P}}^{-\mathrm{T}}$. $\mathrm{Q}$ is the phase-mode transformation matrix of the cable current; then the wave process equation of the cable is transformed into

$$\{\begin{array}{l}\frac{\partial {\mathrm{U}}_{\mathrm{m}}}{\partial x}=-{\mathrm{P}}^{-1}{\mathrm{RQI}}_{\mathrm{m}}-{\mathrm{P}}^{-1}\mathrm{LQ}\frac{\partial {\mathrm{I}}_{\mathrm{m}}}{\partial \mathrm{t}}\\ \frac{\partial {\mathrm{I}}_{\mathrm{m}}}{\partial x}=-{\mathrm{Q}}^{-1}{\mathrm{GPU}}_{\mathrm{m}}-{\mathrm{Q}}^{-1}\mathrm{CP}\frac{\partial {\mathrm{U}}_{\mathrm{m}}}{\partial \mathrm{t}}\end{array}$$

(4)

Among them, the modulo voltage and current vectors after phase-mode transformation are shown in Equations (5) and (6). The six sets of voltage and current parameters in the bipolar cable are converted into six independent moduli.

$${\mathrm{U}}_{\mathrm{M}}{}_{\mathrm{m}}={\mathrm{P}}^{-1}{\mathrm{U}}_{\mathrm{M}}=\left[\begin{array}{c}{\mathrm{U}}_{1\mathrm{m}}\\ {\mathrm{U}}_{2\mathrm{m}}\\ {\mathrm{U}}_{3\mathrm{m}}\\ {\mathrm{U}}_{4\mathrm{m}}\\ {\mathrm{U}}_{5\mathrm{m}}\\ {\mathrm{U}}_{6\mathrm{m}}\end{array}\right]=\left[\begin{array}{c}{u}_{Mpa}+u_{Mna}\\ u_{Mpa}-u_{Mna}\\ u_{Mps}+u_{Mns}-u_{Mps}-u_{Mna}\\ u_{Mps}-u_{Mns}-u_{Mps}+u_{Mna}\\ u_{Mpc}+u_{Mnc}^{}-u_{Mps}-u_{Mns}\\ u_{Mpc}-u_{Mnc}-u_{Mps}+u_{Mns}\end{array}\right]$$

(5)

$${\mathrm{I}}_{\mathrm{Mm}}{=\mathrm{Q}}^{-1}{\mathrm{I}}_{\mathrm{M}}=\left[\begin{array}{c}{\mathrm{I}}_{1\mathrm{m}}\\ {\mathrm{I}}_{2\mathrm{m}}\\ {\mathrm{I}}_{3\mathrm{m}}\\ {\mathrm{I}}_{4\mathrm{m}}\\ {\mathrm{I}}_{5\mathrm{m}}\\ {\mathrm{I}}_{6\mathrm{m}}\end{array}\right]=\left[\begin{array}{c}{i}_{\mathrm{Mpc}}+i_{\mathrm{Mnc}}+i_{\mathrm{Mps}}+i_{\mathrm{Mns}}+i_{\mathrm{Mpa}}+i_{\mathrm{Mna}}\\ i_{\mathrm{Mpc}}-i_{\mathrm{Mnc}}+i_{\mathrm{Mps}}-i_{\mathrm{Mns}}+i_{\mathrm{Mpa}}-i_{\mathrm{Mna}}\\ i_{\mathrm{Mpc}}+i_{\mathrm{Mnc}}+i_{\mathrm{Mps}}+i_{\mathrm{Mns}}\\ i_{\mathrm{Mpc}}-i_{\mathrm{Mnc}}+i_{\mathrm{Mps}}-i_{\mathrm{Mns}}\\ i_{\mathrm{Mpc}}+i_{\mathrm{Mnc}}\\ i_{\mathrm{Mpc}}-i_{\mathrm{Mnc}}\end{array}\right]$$

(6)

3. Traveling Wave Transmission Characteristics

When a short-circuit fault occurs somewhere in the cable, the magnetic field energy and electric field energy around the fault point are transformed into each other, and then voltage and current traveling waves are generated to the lines at both ends. According to the superposition principle, it can be equivalent to the normal component and the fault component voltage at the fault point. The additional voltage source generates fault voltage traveling waves with rich frequencies to both ends of the cable. When the fault voltage traveling wave propagates in the DC cable, its own refraction occurs at the fault point, and the polarity of the traveling wave will be changed by reflection instead of refraction. The grid is shown in Figure 2.

In the DC cable, the characteristic impedance (wave impedance) $Z_{cm}$ of each modulus and the modulus propagation coefficient ${\gamma }_m$ are calculated as follows [27]:

$$Z_{cm}=\sqrt{\frac{Z_m}{Y_m}}=\sqrt{\frac{(R_m+jw{L}_m)}{(G_m+jw{C}_m)}}$$

(7)

$$\begin{array}{l}{\gamma }_m={\alpha }_{\mathrm{m}}+j{\beta }_{\mathrm{m}}=\sqrt{Z_m{Y}_m}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\sqrt{(R_m+jw{L}_m)(G_m+jw{C}_m)}\end{array}$$

(8)

$R_m,G_m,L_m,C_m$ are the modulus resistance, modulus conductance, modulus inductance, and modulus capacitance per unit length of the line, respectively.

Combining the above two formulas, we obtain:

$$\begin{array}{l}{\alpha }_m=\sqrt{\frac{1}{2}[-{\omega }^2{L}_m{C}_m+R_m{G}_m+\sqrt{(R_{\mathrm{m}}^2+{\omega }^2{L}_{\mathrm{m}}^2)(G_{\mathrm{m}}^2+{\omega }^2{C}_{\mathrm{m}}^2)}]}\\ {\beta }_m=\sqrt{\frac{1}{2}[-{\omega }^2{L}_m{C}_m-R_m{G}_m+\sqrt{(R_{\mathrm{m}}^2+{\omega }^2{L}_{\mathrm{m}}^2)(G_{\mathrm{m}}^2+{\omega }^2{C}_{\mathrm{m}}^2)}]}\end{array}$$

(9)

In the formula, ${\alpha }_m$ is the attenuation constant of each modulus, characterizing the attenuation characteristics of the traveling wave of each modulus; ${\beta }_m$ is the phase constant of each modulus, characterizing the phase change characteristics of the traveling wave of each modulus; w is the signal angular frequency; $w=2\mathrm{f}\pi$.

Then, the formula for calculating the frequency-dependent wave velocity (propagation along the line) of each modulus of the DC cable is:

$$v_m=\frac{w}{{\beta }_m}=\frac{2\pi f}{\sqrt{\frac{1}{2}[w^2{L}_m{C}_m-R_m{G}_m+\sqrt{(R_m^2+w^2{L}_m^2)(G_m^2+w^2{C}_m^2)}]}}$$

(10)

The fault traveling wave signal can be decomposed into traveling wave components in different frequency segments. From Equations (9) and (10), it can be known that when different frequency components of traveling waves with different moduli propagate on the transmission line, the attenuation constant and propagation speed are different. This will cause traveling wave attenuation and dispersion, which will distort the traveling wave waveform. The higher the frequency of the traveling wave component, the more serious is the attenuation; that is, during the propagation process, the highest frequency component of the initial traveling wave head has the most serious attenuation. Under the attenuation of the initial wave head, the frequency band of the second traveling wave head will be reduced (the farther the distance is, the more the reduction will be); the speed of the traveling wave component and the singularity of the wave head will be weakened. The travel time of the component’s traveling wave to the measurement point increases. The detection of the second traveling wave head will directly cause errors in the ranging accuracy, and so using the double-ended traveling wave method to identify the first traveling wave head at both ends of the line will have a higher ranging accuracy.

If the total length of the line is L, it is assumed that, at the time $t_{\mathrm{f}}$, a short-circuit fault occurs at a distance d from the cable to the rectifier side, and the time when the initial traveling wave of the fault reaches the rectifier side and the inverter side is $t_M$ and $t_N$, respectively. The propagation velocity of the voltage traveling wave in the cable is v; then the distance from the fault point to the rectifier terminal is shown in Equation (11).

$$\mathrm{d}=\frac{(L-(t_N-t_M)v)}{2}$$

(11)

The relative positioning error is defined as Equation (12). Among them, L_m represents the measured fault distance, L_a represents the actual fault distance, and L₀ represents the full length of the line.

$$\epsilon =\left|\frac{L_{\mathrm{m}}-L_a}{L_0}\right|\times 100\%$$

(12)

In this paper, the six-mode voltage is used as the ranging parameter; the propagation speed and attenuation constant of the six-mode voltage in the cable are comprehensively considered, and the fixed reference wave speed is selected as v = 1.978 × 10⁸ m/s.

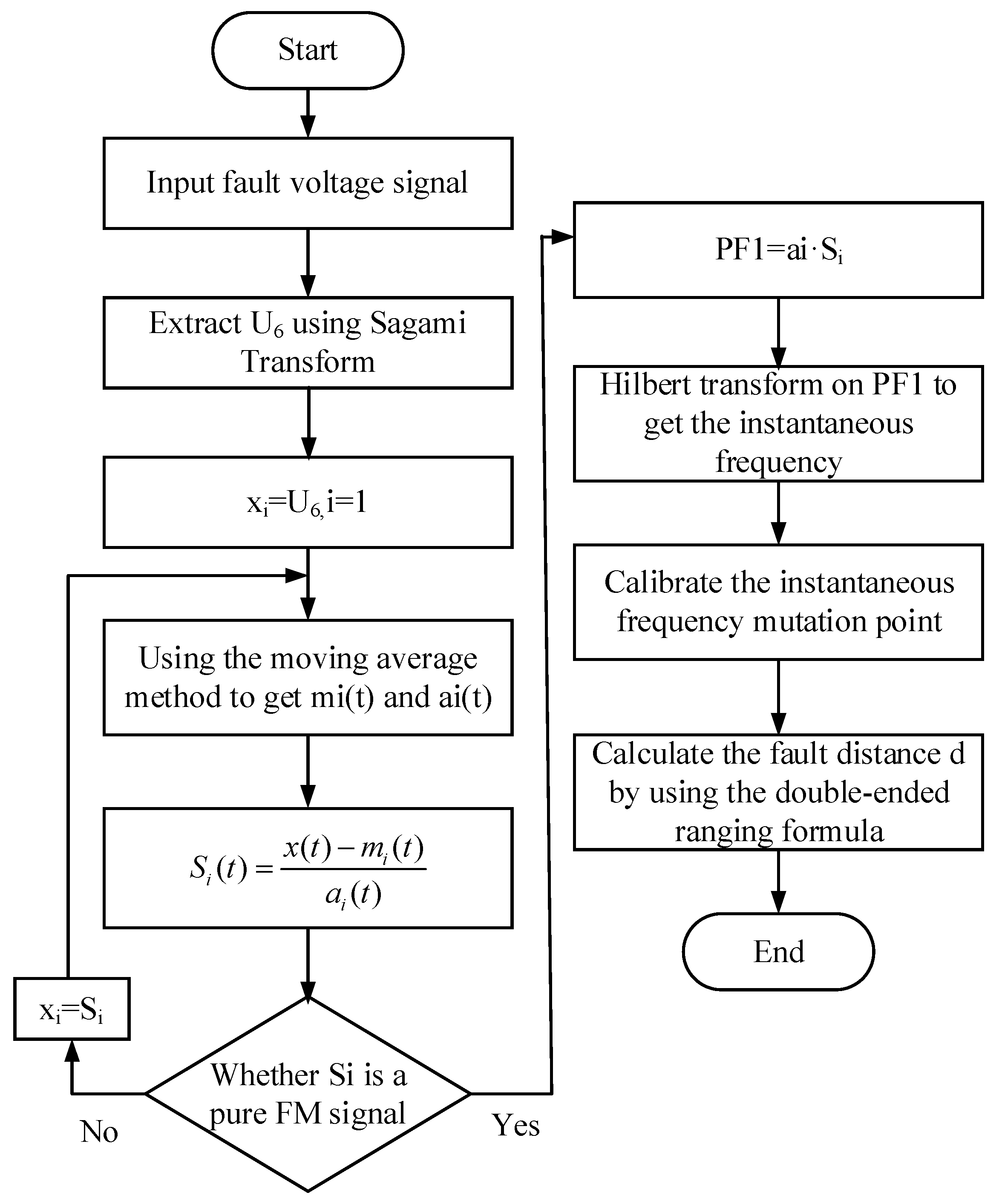
4. The Principle of ILMD

4.1. The Principle of LMD

The local mean decomposition signal processing process [28] is as follows.

(1) For an original signal, determine all local extreme points in the signal, and calculate the average value of any two adjacent local extreme points and the estimated value of the amplitude envelope.

$$m_i=(n_i+n_{i+1})/2$$

(13)

$$a_i=\left|n_i-n_{i+1}\right|/2$$

(14)

(2) Connect the adjacent local mean points $m_i$ and $m_{i+1}$ and the amplitude envelope estimates $a_i$ and $a_{i+1}$, and then smooth them with the moving average method to obtain the local mean function $m_{11}(t)$ and the amplitude envelope estimation function $a_{11}(t)$, respectively. The calculation formula of moving average processing is as follows.

$$y_s(i)=\frac{1}{2n+1}\left[y(i+n)+y(i+n-1)+\cdots +y(i-n)\right]$$

(15)

Among them, $y(i)$ is the original sequence of data, and $2n+1$ is the sliding width. When $i<n$, the span should be reduced accordingly, and the limit should not exceed the endpoint of the sequence.

(3) Separate the local mean function $m_{11}(t)$ from the original signal $x(t)$ to obtain the signal $h_{11}(t)$.

$$h_{11}(t)=x(t)-m_{11}(t)$$

(16)

(4) Divide $h_{11}(t)$ by the magnitude envelope estimation function $a_{11}(t)$ to obtain the FM signal $s_{11}(t)$.

$$s_{11}(t)=\frac{h_{11}(t)}{a_{11}(t)}$$

(17)

Repeat the above steps $s_{11}(t)$. If the amplitude envelope estimation function $a_{12}(t)=1$ is obtained, this means that $s_{11}(t)$ is a pure FM signal. If $a_{12}(t)\ne 1$, the above iterative process needs to be repeated until $s_{1n}(t)$ is a pure FM signal, as shown in the following formula.

$$\{\begin{array}{ll}{h}_{11}(t)& =x(t)-m_{11}(t)\\ h_{12}(t)& =s_{11}(t)-m_{12}(t)\\ & ⋮\\ h_{1n}(t)& =s_{1(n-1)}(t)-m_{1n}(t)\end{array}$$

(18)

$$\{\begin{array}{ll}{s}_{11}(t)& =\frac{h_{11}(t)}{a_{11}(t)}\\ s_{12}(t)& =\frac{h_{12}(t)}{a_{12}(t)}\\ & ⋮\\ s_{1n}(t)& =\frac{h_{1n}(t)}{a_{1n}(t)}\end{array}$$

(19)

The conditions for iterative termination are as shown in Equation (20). In practical applications, in order to avoid excessive decomposition times, an iteration termination threshold Δ is set. When $1-\Delta \le a_{1n}(t)\le 1+\Delta$, the iteration terminates.

$$\underset{n\to \infty }{\lim }{a}_{1n}(t)=1$$

(20)

(5) Multiply all the amplitude envelope estimation functions generated in the iterative process to obtain the instantaneous amplitude function $a_1(t)$.

$$a_1(t)=a_{11}(t)a_{12}(t)\cdots a_{1n}(t)={\displaystyle \prod _{k=1}^n{a}_{1k}(t)}$$

(21)

(6) Multiply $a_1(t)$ and $s_{1n}(t)$ to obtain the first product function component of the original signal x(t).

$$P{F}_1(t)=a_1(t)s_{1n}(t)$$

(22)

(7) After separating the first product function component from the original signal $x(t)$, the remaining signal $u_1(t)$ is obtained, and the above steps are repeated with $u_1(t)$ as the new initial signal until $u_k(t)$ is a monotonic function. The calculation process is as follows.

$$\{\begin{array}{ll}{u}_1(t)=& x(t)-P{F}_1(t)\\ u_2(t)=& u_1(t)-P{F}_2(t)\\ & ⋮\\ u_k(t)=& u_{k-1}(t)-P{F}_k(t)\end{array}$$

(23)

The final original signal can be reconstructed from $u_k(t)$ and all product function components.

$$x(t)={\displaystyle \sum _{i=1}^{k}P{F}_i(t)}+u_k(t)$$

(24)

4.2. Hilbert Transform

Perform Hilbert transform on the product function components of the original signal x(t).

$${\overline{PF}}_i(t)=\frac{1}{\pi }{\displaystyle {\int }_{-\infty }^{+\infty }\frac{P{F}_i(\tau )}{t-\tau }}d\tau$$

(25)

The corresponding analytical signal can be expressed by Equations (26) and (27).

$$Y_i(t)=P{F}_i(t)+j{\overline{PF}}_i(t)={a^{\prime }}_i(t)e^{j{\varphi }_i(t)}$$

(26)

$${\varphi }_i(t)=\arctan \frac{{\overline{PF}}_i^{}(t)}{P{F}_i(t)}$$

(27)

Derivation of the phase function gives the instantaneous frequency function.

$$f_i(t)=\frac{1}{2\pi }{\omega }_i(t)=\frac{1}{2\pi }\cdot d\left[\arctan \frac{{\overline{PF}}_i^{}(t)}{P{F}_i(t)}\right]/dt$$

(28)

Figure 3 is the flowchart of the fault location of DC cables based on the improved LMD algorithm. The input fault signal is first decomposed by local mean value; the obtained amplitude envelope signal A is used as the final instantaneous amplitude function, and the PF1 component is used for Hilbert transform to obtain the instantaneous frequency function. The sudden change point of the instantaneous frequency curve is the moment when the wave head reaches the measurement end, and then the fault distance is calculated.

4.3. Comparison of Mathematical Methods

There is a significant difference in the solution methods for the local mean functions EMD and LMD. EMD uses cubic spline interpolation for all extreme points to obtain the upper envelope and lower envelope of the original signal and then uses the average method to obtain the local mean function. For LMD to solve the local mean function, the average of two adjacent extreme values is obtained, and the moving average algorithm is used to smooth it; we take a mathematical signal as an example and use LMD and EMD to decompose and then reconstruct. Observe Figure 4c and Figure 5b; compared with the original signal, the frequency and amplitude after EMD resynthesis are quite different, and the decomposition result of LMD is more accurate.

The LMD decomposition results are as follows:

Figure 4. Decomposition result of LMD. (a) Original signal. (b) PF component. (c) Comparison of the resynthesized signal with the original signal.

Figure 4. Decomposition result of LMD. (a) Original signal. (b) PF component. (c) Comparison of the resynthesized signal with the original signal.

The EMD decomposition results are as follows:

Figure 5. Decomposition result of EMD. (a) IMF component. (b) Comparison of the resynthesized signal with the original signal.

Figure 5. Decomposition result of EMD. (a) IMF component. (b) Comparison of the resynthesized signal with the original signal.

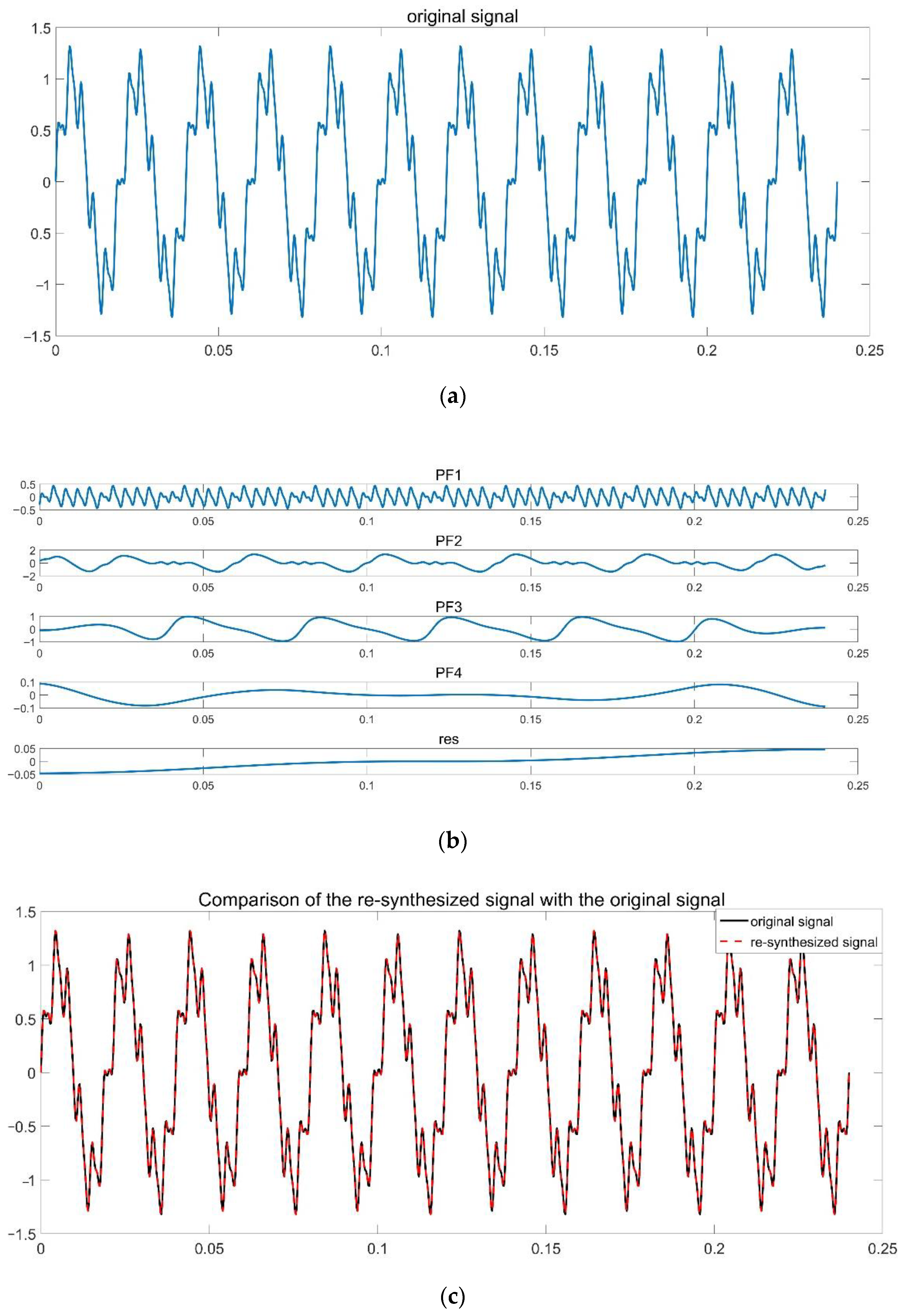
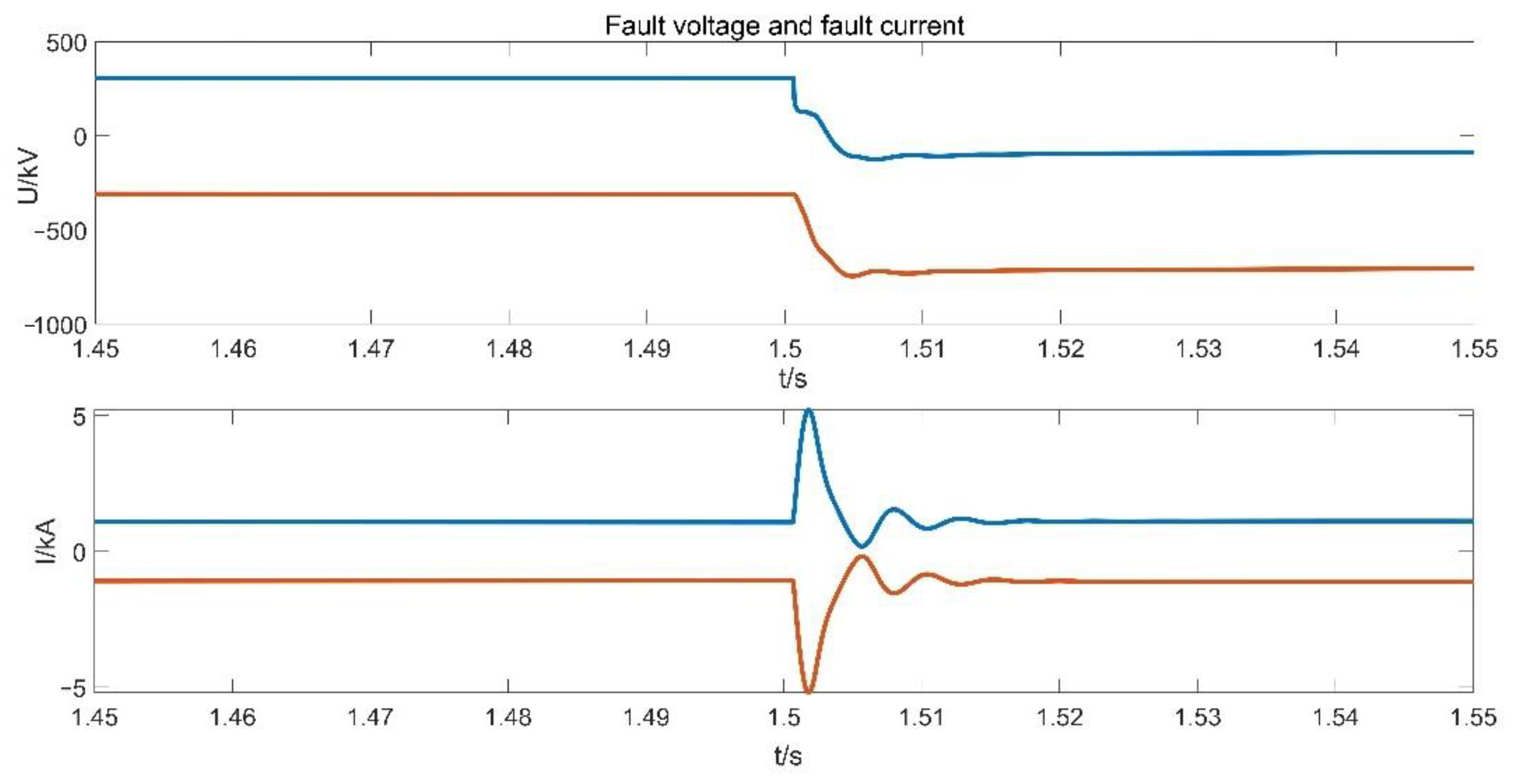
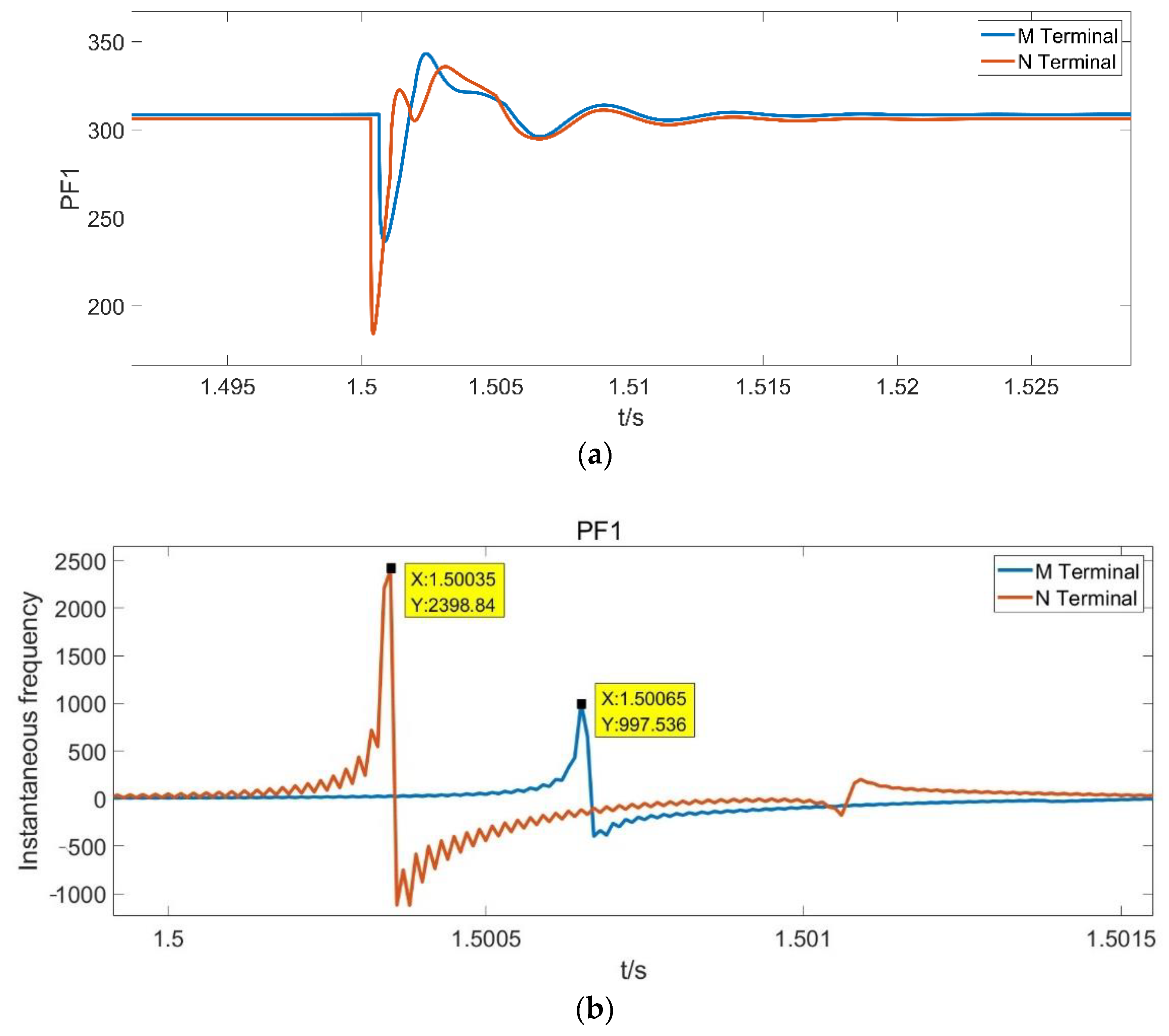
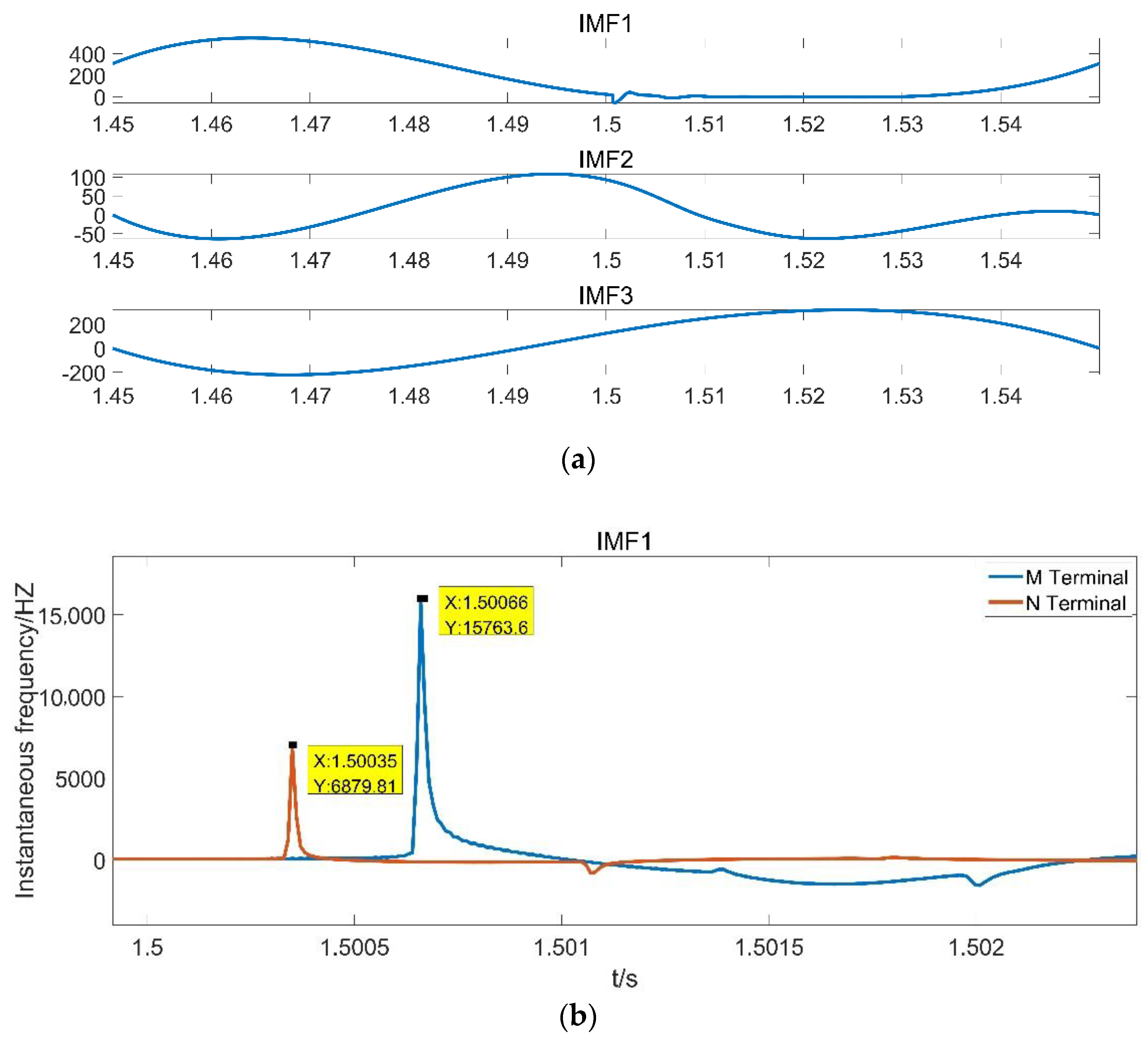
5. Simulation Results

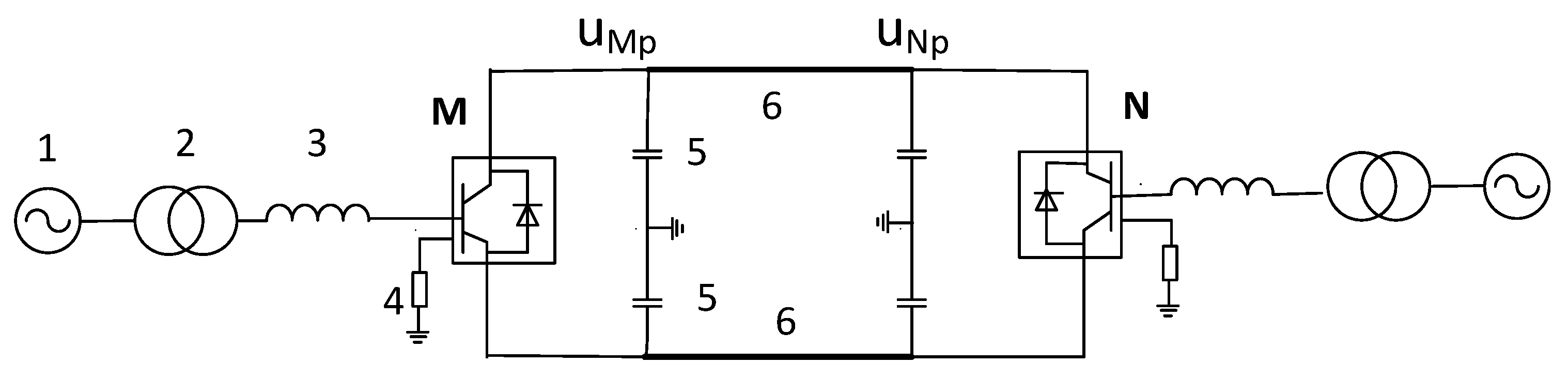
5.1. Power Transmission Model Construction

At present, there are three types of HVDC transmission model: distributed parameter model, equivalent thermal circuit model, and finite element model. When the wavelength of the electromagnetic wave is much smaller than the physical size of the corresponding network, it is necessary to use the distributed parameter model to characterize the power network, and so the distributed parameter model is more used in practical applications. The VSC-HVDC simulation system model established by PSCAD is shown in Figure 6. The AC system voltage is 50 Hz; the rated voltage is 220 kV; the rated DC voltage is ±320 kV; and the rated transmission power is 1000 MW. The three-phase fully controlled bridge circuit and the SPWM modulation control circuit are used. There is constant DC voltage and constant AC voltage control; the receiving end adopts constant active power and constant reactive power control; the rated DC voltage is set to 640 kV; the rated transmission active power is 1000 MW; and the reactive power is 0 Mvar. The single-core XLPE DC cable model adopts the armored frequency domain model, and the total cable length is 200 km.

Among them, ① represents the AC power supply; ② represents the converter transformer; ③ represents the converter reactor; ④ represents the AC filter; ⑤ represents the DC side capacitor; and ⑥ represents the DC cable.

5.2. ILMD Method Validation

Using the above-mentioned building model, faults are set at different positions, and the improved LMD method is used for testing. Set the fault start time to 1.5 s, the fault duration to 0.02 s, and the sampling frequency to 0.1 MHz. Taking the metal ground fault 130 km away from the rectifier side as an example, take 1.45–1.55 s for data analysis. The corresponding fault current and fault voltage waveforms are shown in Figure 7, and the six-mode voltage waveform obtained by decoupling the rectifier side voltage is shown in Figure 8.

The six-mode voltage is decomposed by LMD to obtain the high-frequency component PF1 as shown in Figure 9a, and the Hilbert analysis is performed to obtain its instantaneous frequency function curve, as shown in Figure 9b. The frequency mutation points of the M-terminal and N-terminal correspond to the moments of 1.50065 s and 1.50035 s, respectively. Putting them into Equation (11), the theoretical value of the fault distance is 129.6699 km; the error distance is 0.33 km, and the error percentage is 0.165%.

The IMF component obtained by using HHT for the six-mode voltage component is shown in Figure 10a, and the instantaneous frequency of Hilbert transform of IMF1 is shown in Figure 10b. The frequency mutation points of the M-terminal and N-terminal appear at 1.50066 s and 1.50035 s, respectively. Putting them into Equation (11), the theoretical value of fault distance is 130.6590 km; the error distance is 0.659 km, and the error percentage is 0.3295%. Compared with HHT, ILMD has a high precision of 329 m, and, in the case of partial fault distance, the amplitude-frequency information, including the high-frequency feature quantity, is seriously polluted in the process of EMD decomposition, which makes it impossible to accurately locate.

In the fault location problem, the initial traveling wave front is the singular point, and the wavelet mode maxima can be used to identify the singular point. In the fault data in Figure 6, the wavelet modulus maxima are obtained by discrete stationary wavelet transform. The wavelet basis function and the number of decomposition layers are Daubechies (db4) and three layers, respectively, and the modulus maxima of the voltage at both ends are obtained as shown in Figure 11.

It can be seen from Figure 11 that the time when the initial traveling wave head reaches the M end and the N end corresponds to the 5069th and 5038th sampling points, respectively, and the corresponding time difference between the two sampling points is 0.00031 s. It can be calculated that the theoretical value of the fault distance is 130.6605 km; the error distance is 0.6605 km, and the relative error percentage is 0.3302%.

For metallic ground faults, the fault time is set to 1.5 s~1.52 s; the fault location is performed for different fault distance points; and the accuracy is compared with the methods using wavelet analysis and HHT. It can be obtained that the error of fault location using ILMD is significantly reduced compared with that of other methods. The corresponding experimental simulation data are shown in

Table 1. Comparison of ILMD and other ranging methods.

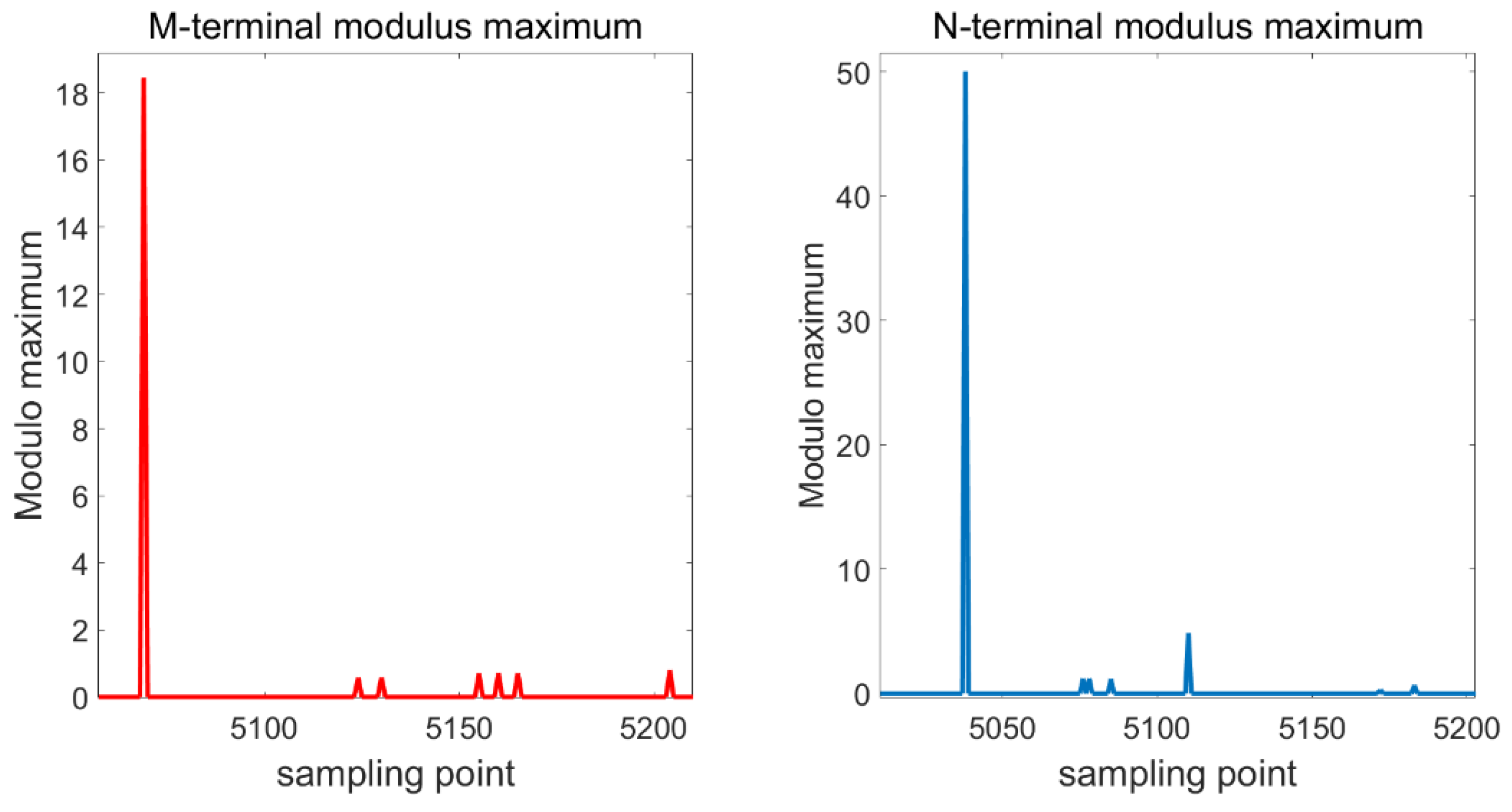
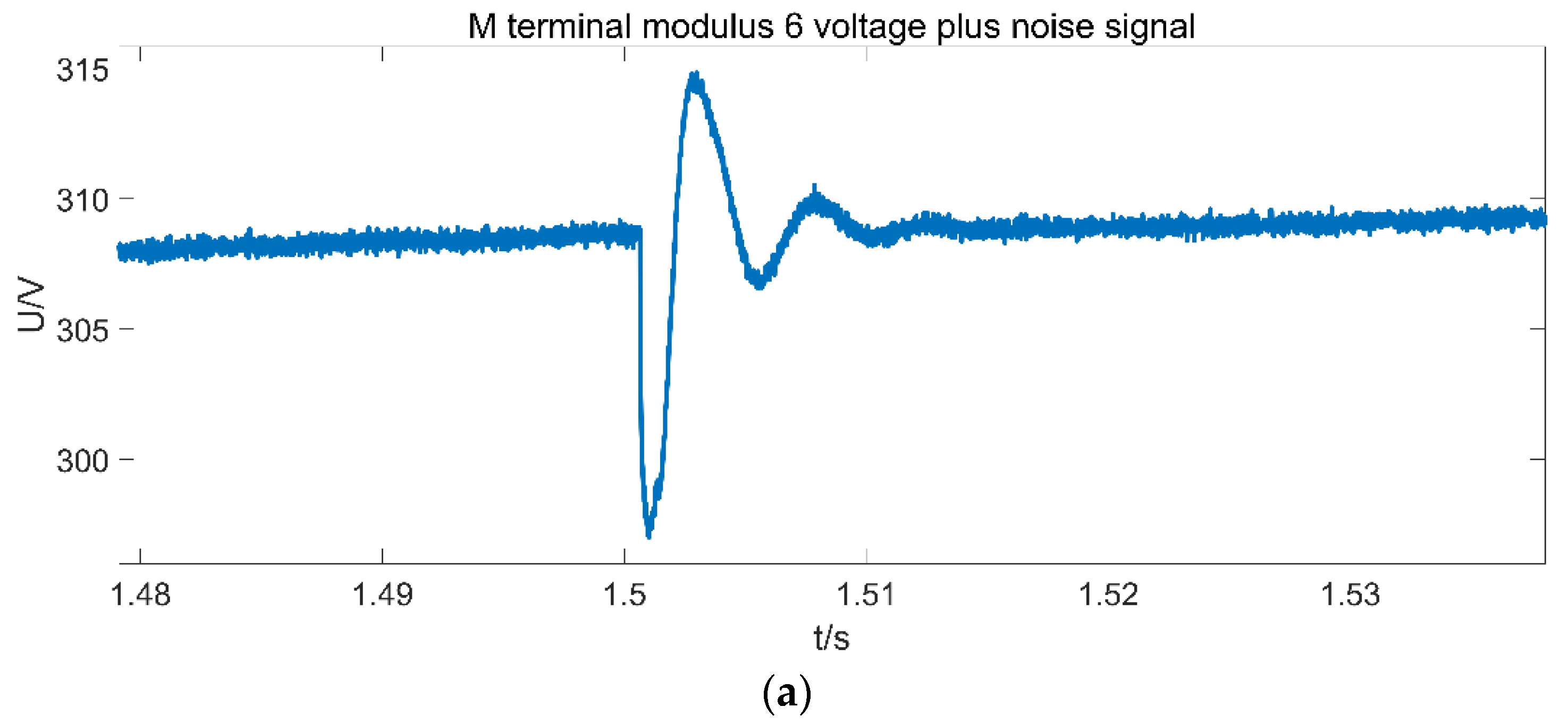
Fault Distance (km)	Wavelet Transform (km)	Error (%)	HHT (km)	Error (%)	ILMD (km)	Error (%)
0	1.0536	0.5268	0.9886	0.4943	0.7742	0.3871
10	8.0183	0.9909	Error	-	9.0119	0.4940
50	49.5584	0.2208	49.3350	0.3325	49.9350	0.0325
85	84.1760	0.4120	Error	-	85.1642	0.0821
100	100.0125	0.0063	100	0.0063	100	0
130	130.6605	0.3303	130.6590	0.3295	129.6699	0.1650
150	150.5415	0.2708	150.6392	0.3196	150.4390	0.2195
180	182.0910	1.0455	182.0870	1.0435	180.7391	0.3695
200	198.6750	0.6625	201.3762	0.6881	198.9653	0.5173

. Taking China as an example, according to the ‘National Electric Power Dispatching System “Tenth Five-Year” Science and Technology Development Plan Outline’ issued by State Grid, the comprehensive error should not exceed 1%. Due to technical and economic constraints, the ranging error cannot be too small. From a practical point of view, an absolute ranging error of less than 1 km can better meet the field requirements. The error in the ranging method proposed in this paper is up to more than 900 m under high impedance, and the error is smaller in most cases, which can meet the actual requirements of engineering.

The fault time is set as 1.5 s~1.52 s, and it is grounded through different transition resistances under different fault distances. The ILMD distance measurement results are shown in

Table 2. Algorithm ranging accuracy verification under different transition impedances.

Fault Distance (km)	Transition Impedance (Ω)	ILMD (km)	Error (%)
10	0	9.0119	0.4940
	100	8.0229	0.9885
	1000	8.0229	0.9885
	2000	8.0229	0.9885
50	0	49.9350	0.0325
	100	49.9350	0.0325
	1000	49.9350	0.0325
	2000	49.6609	0.1695
85	0	85.1642	0.0821
	100	85.1658	0.0829
	1000	85.1658	0.0829
	2000	85.1650	0.0825
130	0	129.6699	0.1650
	100	130.6590	0.3295
	1000	130.6590	0.3295
	2000	130.6590	0.3295
180	0	180.7391	0.3695
	100	180.7391	0.3695
	1000	180.7391	0.3695
	2000	181.0980	181.0980

. It can be seen from Table 2 that, at the same fault point, the error only increases by a few meters in the case of high-impedance grounding; that is, the result of fault location is hardly affected by the transition resistance.

5.3. Noise Immunity Test

Cables generally use transformers to collect fault traveling wave signals, but the detection of transformers is susceptible to noise interference. The influencing factors and sources of noise can be divided into external factors and internal factors. External factors include line construction, electrical equipment interference, etc., while internal factors generally originate from random fluctuations within the transformer itself.

Take the metallic ground fault 130 km away from the rectifier side as an example, and add noise interference with a signal-to-noise ratio (SNR) of 20 dB to the voltage traveling wave signal, as shown in Figure 12a. Gaussian white noise with signal-to-noise ratios of 10 dB, 15 dB, 25 dB, and 40 dB is added to the fault signal, and the instantaneous frequency is obtained by ILMD analysis, as shown in Figure 12b. The 2037th and 2067th sampling points appear at the M-terminal and N-terminal frequency mutation points, respectively, corresponding to 1.50065 s and 1.50034 s. Putting them into formula (11), the theoretical value of the fault distance can be obtained as 129.6699 km, and the error is 0.3301 km. A large number of fault points are added with different proportions of noise for testing, and the results are shown in

Table 3. Algorithm ranging accuracy verification under different proportions of noise.

Fault Distance (km)	SNR (dB)	Ranging Results (km)	Error (%)
10	40/25/15	9.0119	0.4940
50	40/25/15	49.9350	0.0325
85	40/25/15	85.1642	0.0821
100	40/25/15	100	0
130	40/25/15	129.6699	0.1650
180	40/25/15	180.7391	0.3695

. When the signal-to-noise ratio (SNR) is less than 10 dB, the instantaneous frequency mutation point caused by the arrival of the wave head will be submerged, and accurate detection cannot be performed. When the signal-to-noise ratio SNR ≥ 15 dB, the ranging accuracy is high.

6. Conclusions

(1) This paper proposes a new fault location method for HVDC cable lines which combines LMD and Hilbert transform. It not only inherits the advantages of LMD in the decomposition process of the weak endpoint effect and of less pollution of amplitude-frequency information but also takes into account the ability of the Hilbert transform to completely retain the mutation information of the instantaneous frequency function. Through a large number of experimental verifications, the error of the proposed positioning method is within 1%; the positioning accuracy is high, and it is hardly affected by transition resistance and interference noise.

(2) Compared with HHT, the method in this paper has a small endpoint effect and less iteration processing, which avoids the large difference in the instantaneous frequency function extracted by HHT in some cases. Compared with wavelet transform, it overcomes the large positioning error in the case of high-resistance near-end faults, and the ranging accuracy meets the requirements of on-site operation and maintenance accuracy.