Theoretical-Experimental Analysis of the Performance of Geothermal Heat Pumps for Air Conditioning Greenhouses in Arid Zones
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Instrumentation
2.2. Methods
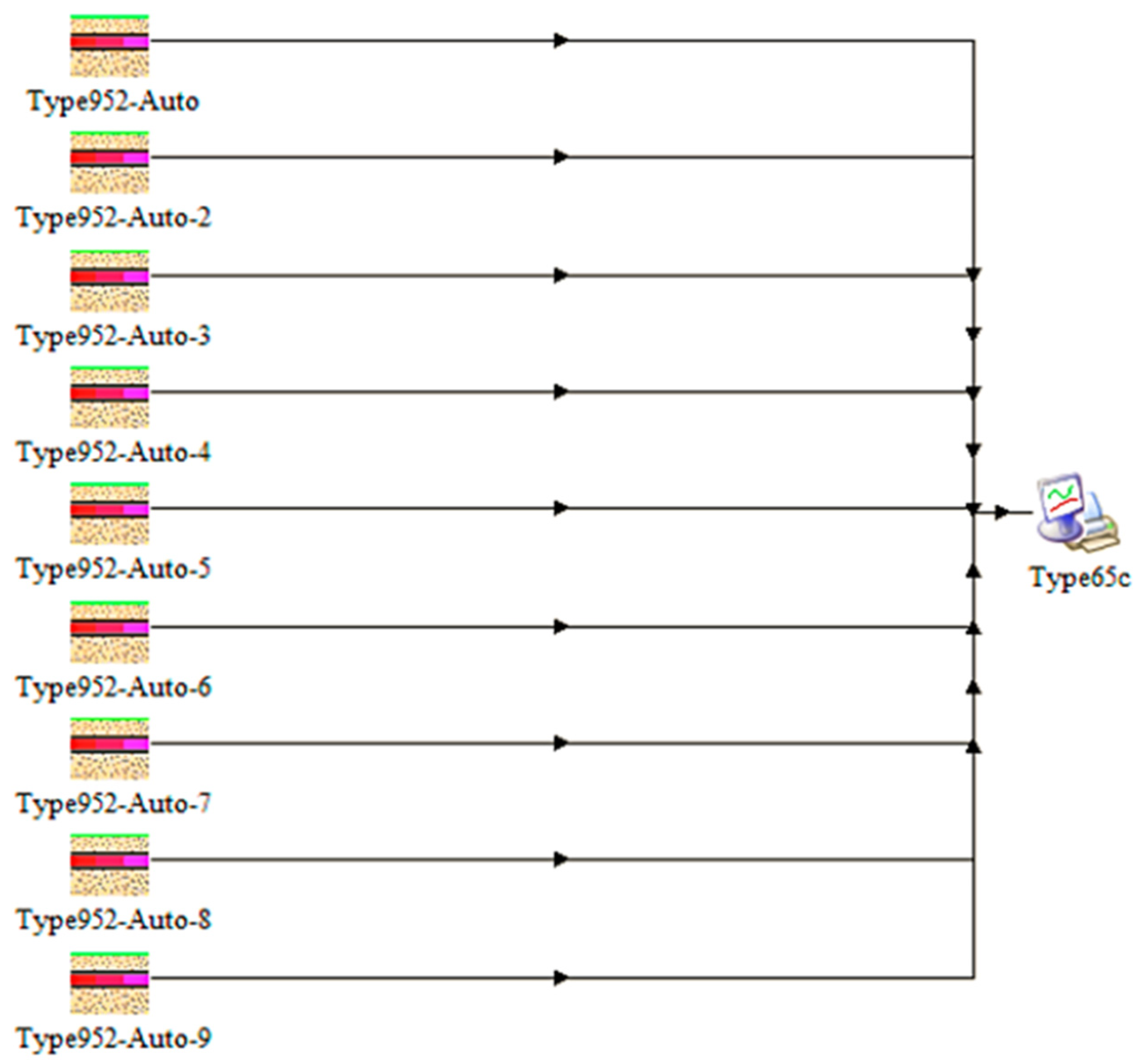
Simulator Considerations
3. Mathematical Model
4. Results
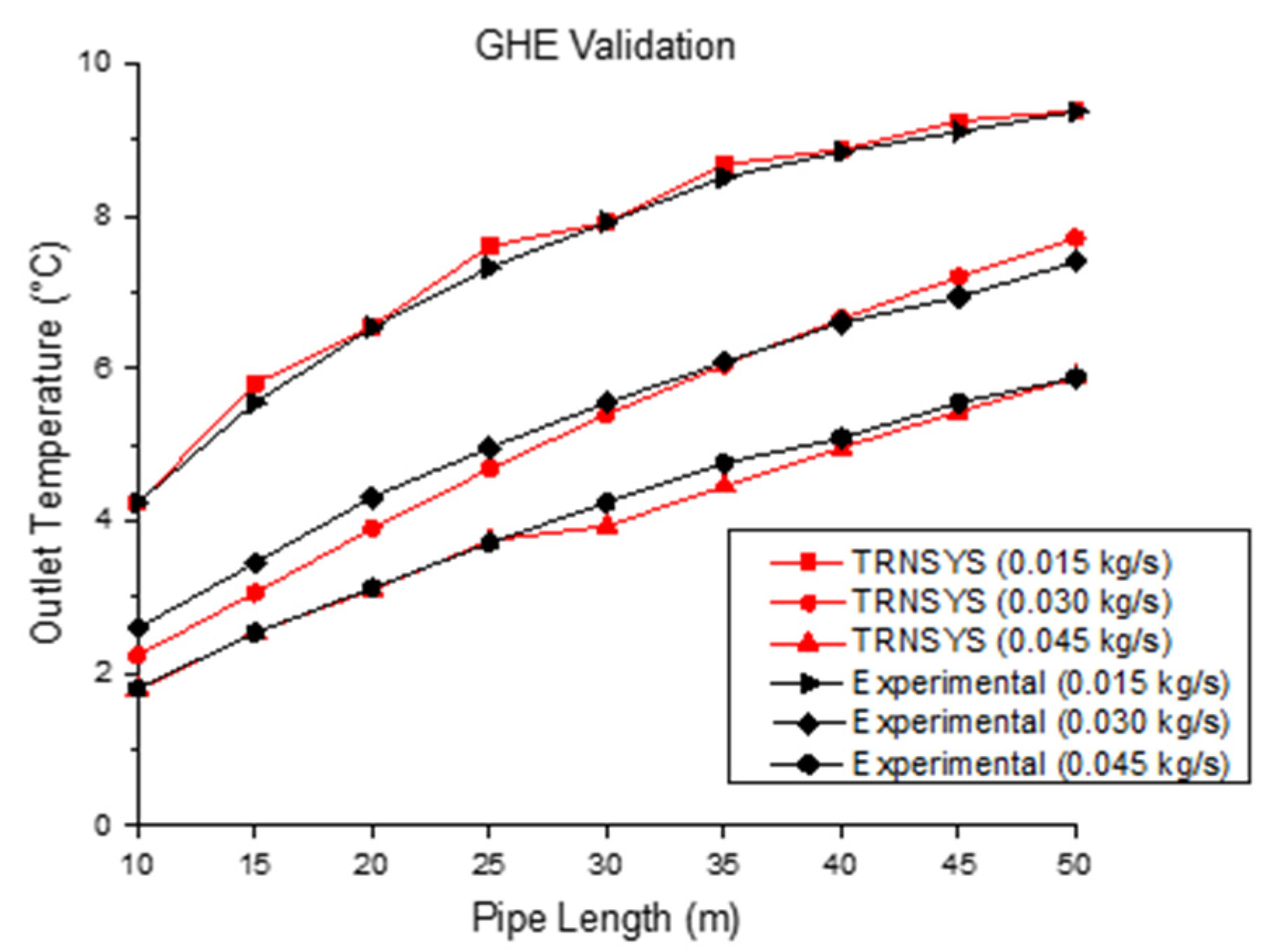
4.1. Simulator Validation
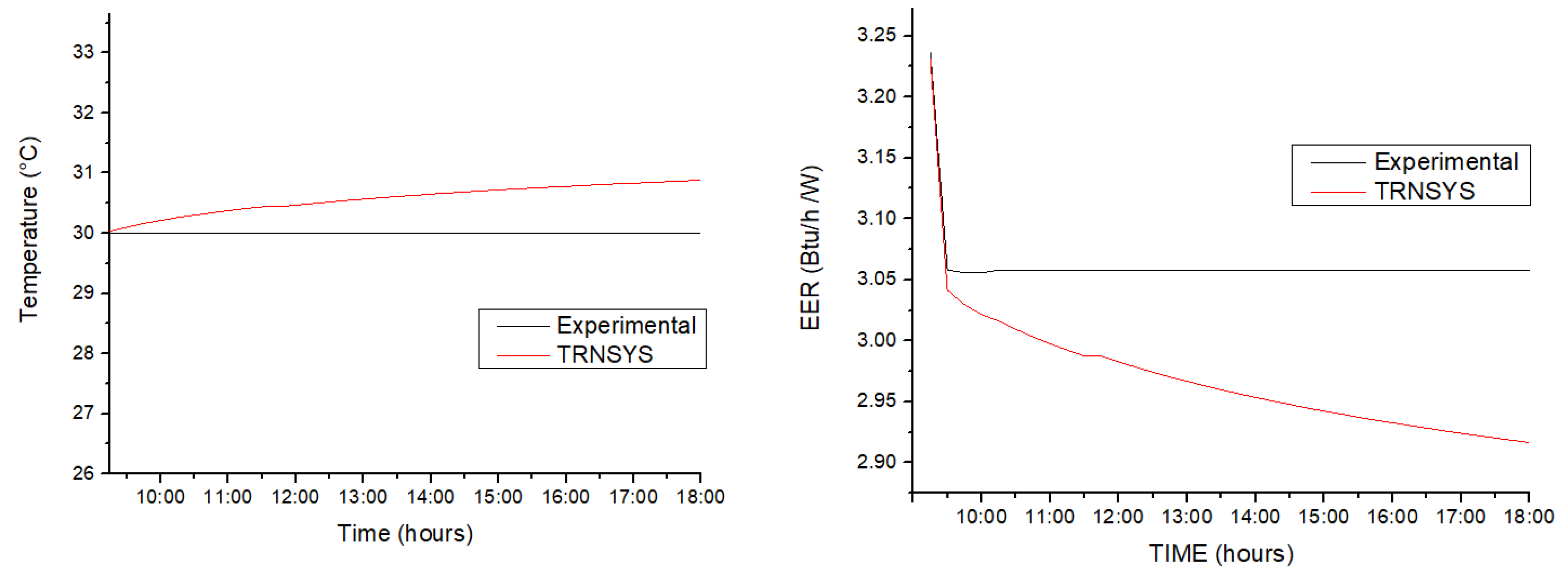
4.2. Experimental Validation
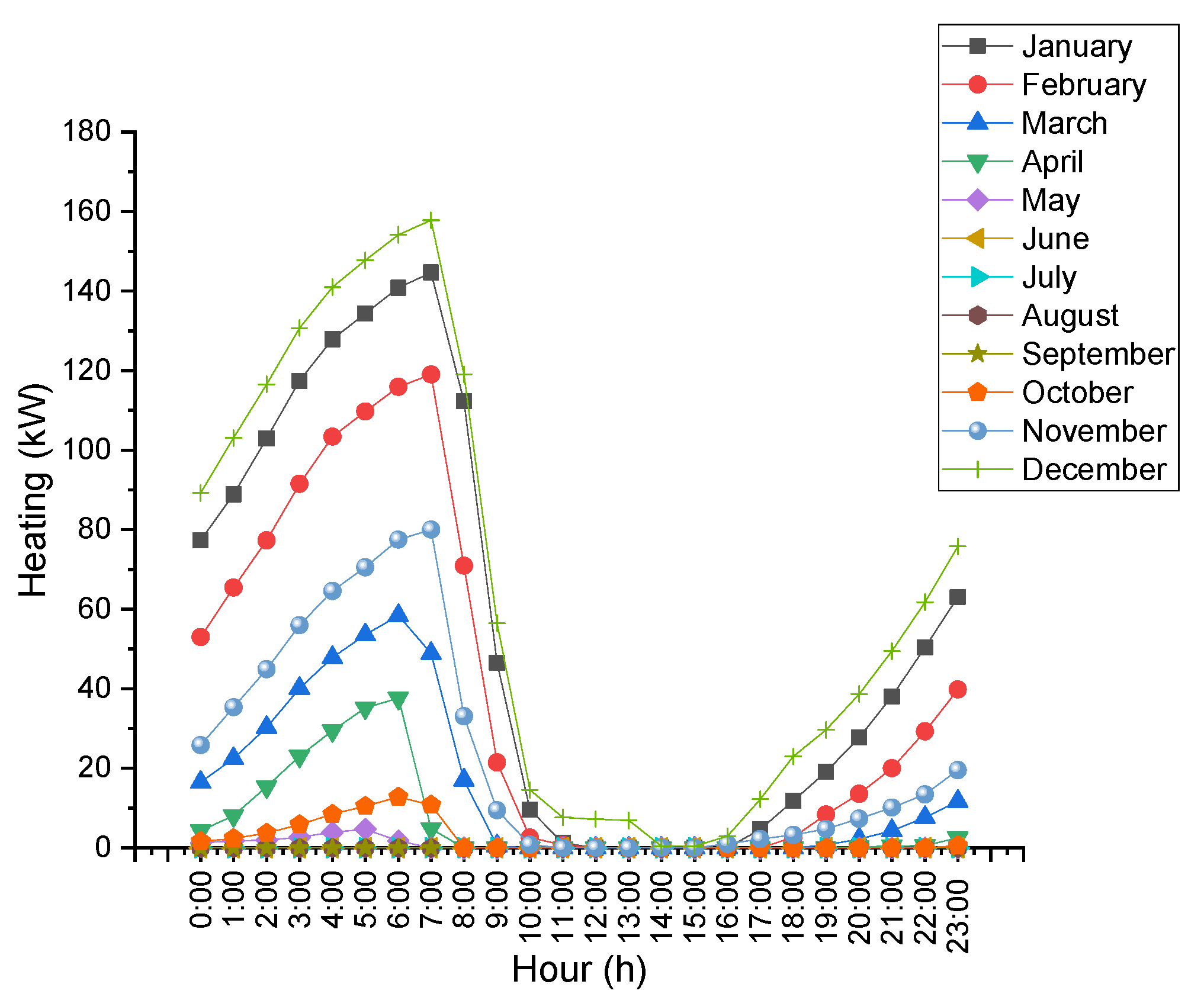
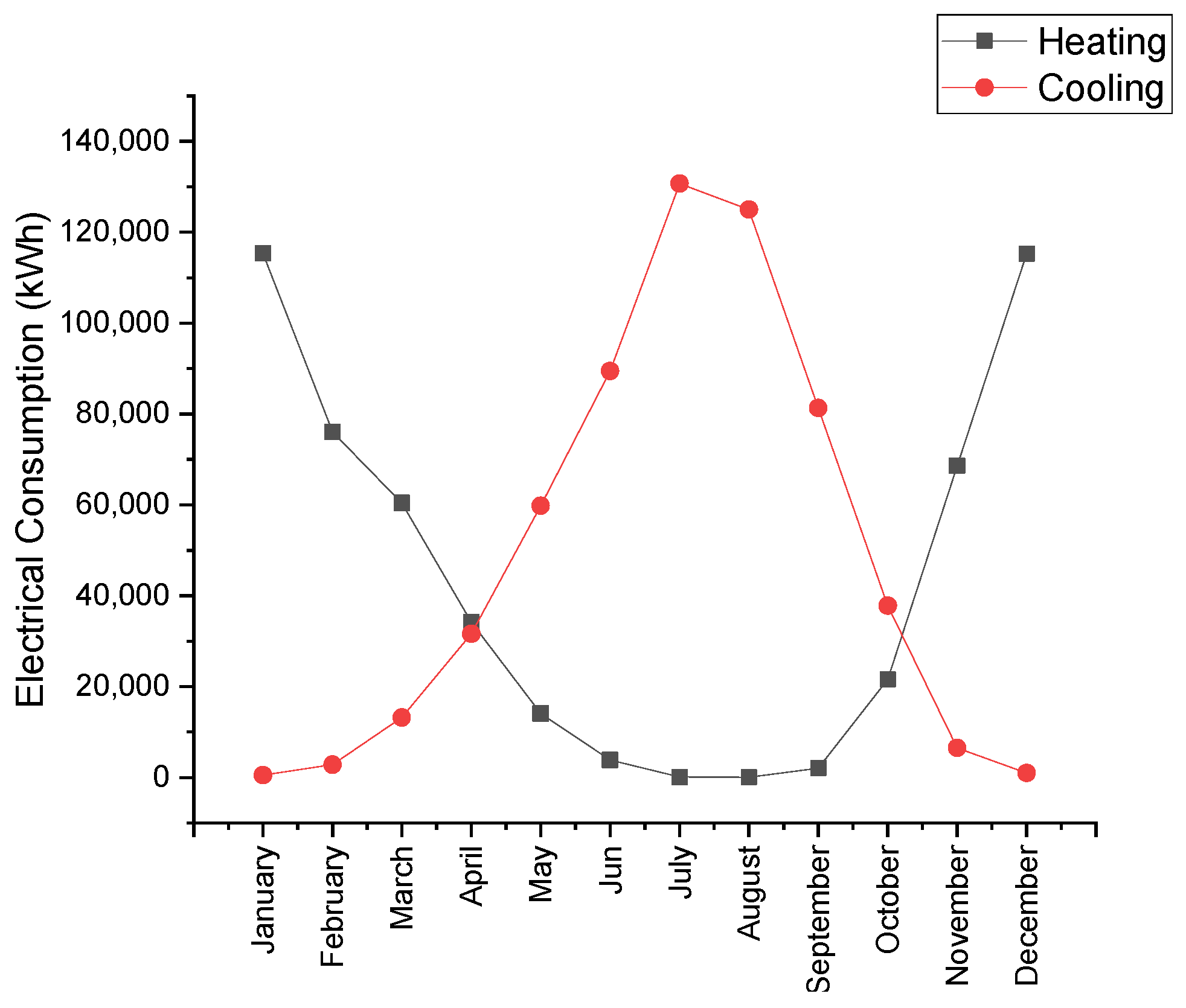
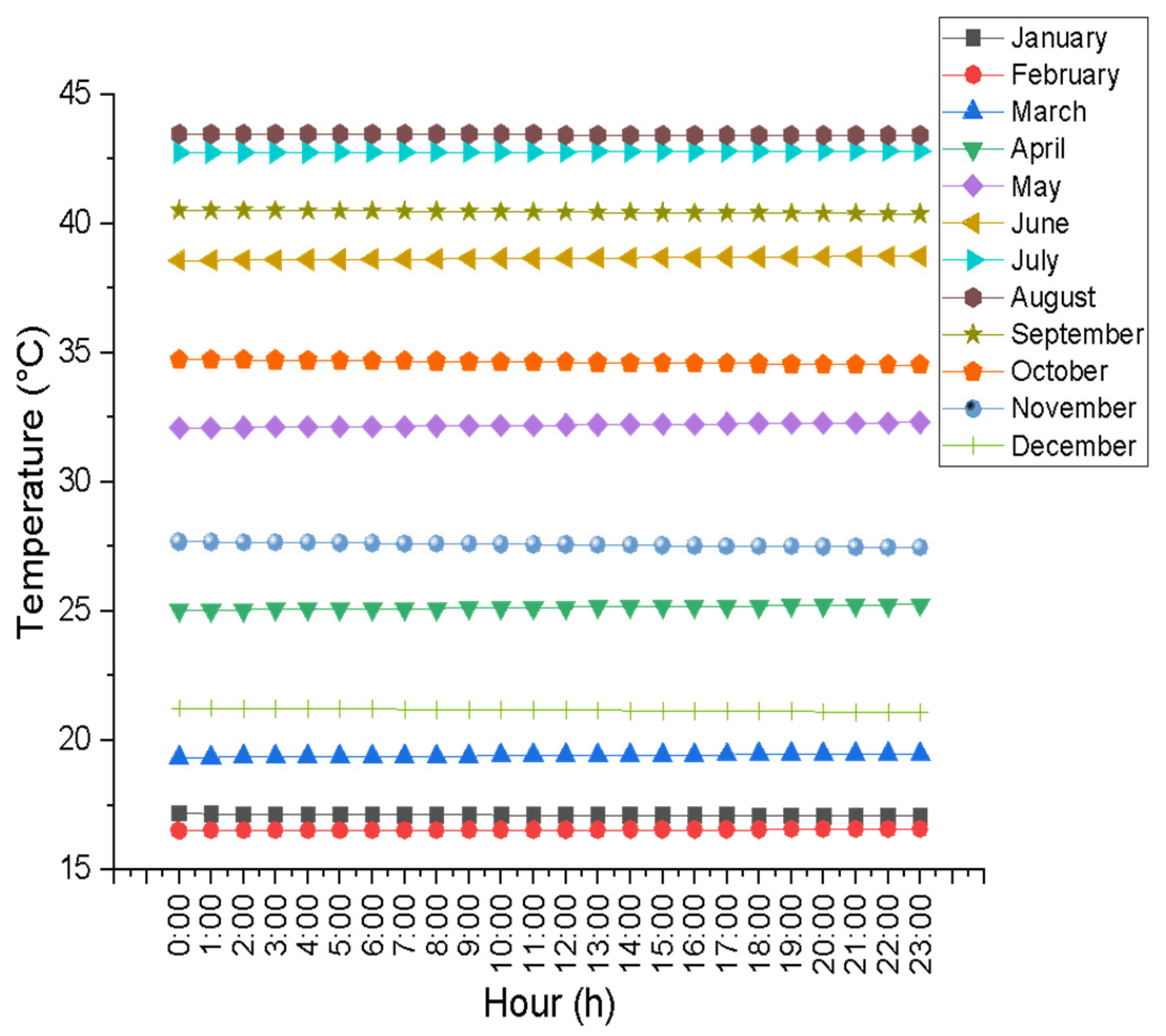
4.3. Temperatures and Electrical Consumption
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boughanmi, H.; Lazaar, M.; Guizani, A. A performance of a heat pump system connected a new conic helicoidal geothermal heat exchanger for a greenhouse heating in the north of Tunisia. Sol. Energy 2018, 171, 343–353. [Google Scholar] [CrossRef]
- Ouammi, A. Model predictive control for optimal energy management of connected cluster of microgrids with net zero energy multi-greenhouses. Energy 2021, 234, 121274. [Google Scholar] [CrossRef]
- Mehrpooya, M.; Hemmatabady, H.; Ahmadi, M.H. Optimization of performance of Combined Solar Collector-Geothermal Heat Pump Systems to supply thermal load needed for heating greenhouses. Energy Convers. Manag. 2015, 97, 382–392. [Google Scholar] [CrossRef]
- Zuquim, M.D.P.; Zarrouk, S.J. Nursery greenhouses heated with geothermal energy—A case study from Rotorua New Zealand. Geothermics 2021, 95, 102123. [Google Scholar] [CrossRef]
- Esen, M.; Yuksel, T. Experimental evaluation of using various renewable energy sources for heating a greenhouse. Energy Build. 2013, 65, 340–351. [Google Scholar] [CrossRef]
- Boughanmi, H.; Lazaar, M.; Bouadila, S.; Farhat, A. Thermal performance of a conic basket heat exchanger coupled to a geothermal heat pump for greenhouse cooling under Tunisian climate. Energy Build. 2015, 104, 87–96. [Google Scholar] [CrossRef]
- Mirzamohammadi, S.; Jabarzadeh, A.; Shahrabi, M.S. Long-term planning of supplying energy for greenhouses using renewable resources under uncertainty. J. Clean. Prod. 2020, 264, 121611. [Google Scholar] [CrossRef]
- Anifantis, A.; Colantoni, A.; Pascuzzi, S. Thermal energy assessment of a small scale photovoltaic, hydrogen and geothermal stand-alone system for greenhouse heating. Renew. Energy 2017, 103, 115–127. [Google Scholar] [CrossRef]
- Aljubury, I.M.A.; Ridha, H.D. Enhancement of evaporative cooling system in a greenhouse using geothermal energy. Renew. Energy 2017, 111, 321–331. [Google Scholar] [CrossRef]
- Mahmoudi, H.; Spahis, N.; Goosen, M.F.; Ghaffour, N.; Drouiche, N.; Ouagued, A. Application of geothermal energy for heating and fresh water production in a brackish water greenhouse desalination unit: A case study from Algeria. Renew. Sustain. Energy Rev. 2010, 14, 512–517. [Google Scholar] [CrossRef]
- Seo, Y.; Seo, U.-J. Ground source heat pump (GSHP) systems for horticulture greenhouses adjacent to highway interchanges: A case study in South Korea. Renew. Sustain. Energy Rev. 2020, 135, 110194. [Google Scholar] [CrossRef]
- Cuce, E.; Harjunowibowo, D.; Cuce, P.M. Renewable and sustainable energy saving strategies for greenhouse systems: A comprehensive review. Renew. Sustain. Energy Rev. 2016, 64, 34–59. [Google Scholar] [CrossRef]
- Romo-Jones, J.M.; García-Gutiérrez, A. Mexico Country Report and Direct Use Update, Workshop on Geothermal Direct Use for a Green Economy. In Proceedings of the International Energy Agency, Geothermal Implementation Agreement (IEA–GIA), KIGAM, Daejeon, Korea, 9 November 2018. [Google Scholar]
- Incropera, F.; DeWitt, D. Introduction to Heat Transfer; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1985. [Google Scholar]











| Instrumentation | Measurement Ranges | Deviation |
|---|---|---|
| Analog Thermometer Analog | 0–100 °C | +/−1.6 of range of measurement |
| Manometer Analog Flowmeter | 0–700 kPa | +/−0.01 |
| Analog | 0–75 LPM | +/−0.05 |
| Ammeter | 0–100 A | +/−0.01 |
| Temperatures Along the GHE | Temperature (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Incropera | TRNSYS | Deviation % | |||||||
| 0.015 kg/s | 0.030 kg/s | 0.045 kg/s | 0.015 kg/s | 0.030 kg/s | 0.045 kg/s | 0.015 kg/s | 0.030 kg/s | 0.045 kg/s | |
| T(10 m) | 4.24 | 2.59 | 1.80 | 4.23 | 2.36 | 1.79 | 0% | 9% | 1% |
| T(15 m) | 5.55 | 3.45 | 2.53 | 5.80 | 3.22 | 2.53 | −5% | 7% | 0% |
| T(20 m) | 6.54 | 4.31 | 3.12 | 6.55 | 3.90 | 3.09 | 0% | 9% | 1% |
| T(25 m) | 7.33 | 4.96 | 3.71 | 7.60 | 4.68 | 3.74 | −4% | 6% | −1% |
| T(30 m) | 7.92 | 5.55 | 4.24 | 7.92 | 5.40 | 3.93 | 0% | 3% | 7% |
| T(35 m) | 8.51 | 6.08 | 4.76 | 8.67 | 6.05 | 4.46 | −2% | 0% | 6% |
| T(40 m) | 8.84 | 6.60 | 5.09 | 8.87 | 6.65 | 4.96 | 0% | −1% | 3% |
| T(45 m) | 9.11 | 6.94 | 5.55 | 9.24 | 7.20 | 5.43 | −1% | −4% | 2% |
| T(50 m) | 9.37 | 7.40 | 5.88 | 9.38 | 7.71 | 5.88 | 0% | −4% | 0% |
| Hour | Tout (Experimental) | Tout (TRNSYS) | Deviation (%) | EER (Experimental) | EER (TRNSYS) | Deviation (%) |
|---|---|---|---|---|---|---|
| 9:15 | 30 | 30.03 | 0.11 | 3.24 | 3.23 | 0.17 |
| 10:00 | 30 | 30.21 | 0.71 | 3.06 | 3.02 | 1.13 |
| 11:00 | 30 | 30.38 | 1.25 | 3.06 | 3.00 | 1.98 |
| 12:00 | 30 | 30.47 | 1.56 | 3.06 | 2.98 | 2.47 |
| 13:00 | 30 | 30.57 | 1.89 | 3.06 | 2.97 | 2.99 |
| 14:00 | 30 | 30.65 | 2.17 | 3.06 | 2.95 | 3.42 |
| 15:00 | 30 | 30.72 | 2.40 | 3.06 | 2.94 | 3.79 |
| 16:00 | 30 | 30.78 | 2.60 | 3.06 | 2.93 | 4.10 |
| 17:00 | 30 | 30.83 | 2.78 | 3.06 | 2.92 | 4.38 |
| 18:00 | 30 | 30.88 | 2.93 | 3.06 | 2.92 | 4.63 |
| Hour | Tout (Experimental) | Tout (TRNSYS) | Deviation (%) | EER (Experimental) | EER (TRNSYS) | Deviation (%) |
|---|---|---|---|---|---|---|
| 9:15 | 30 | 30.04 | 0.15 | 1.74 | 1.74 | 0.19 |
| 10:00 | 30 | 30.06 | 0.21 | 1.74 | 1.74 | 0.26 |
| 11:00 | 30 | 30.08 | 0.27 | 1.74 | 1.73 | 0.34 |
| 12:00 | 30 | 30.10 | 0.34 | 1.74 | 1.73 | 0.42 |
| 13:00 | 30 | 30.12 | 0.39 | 1.74 | 1.73 | 0.49 |
| 14:00 | 30 | 30.13 | 0.44 | 1.74 | 1.73 | 0.56 |
| 15:00 | 30 | 30.15 | 0.49 | 1.74 | 1.73 | 0.61 |
| 16:00 | 30 | 30.16 | 0.54 | 1.74 | 1.73 | 0.67 |
| 17:00 | 30 | 30.17 | 0.58 | 1.74 | 1.73 | 0.72 |
| 18:00 | 30 | 30.18 | 0.62 | 1.74 | 1.73 | 0.77 |
| Hour | Tout (Experimental) | Tout (TRNSYS) | Deviation (%) | EER (Experimental) | EER (TRNSYS) | Deviation (%) |
|---|---|---|---|---|---|---|
| 9:15 | 30 | 30.07 | 0.25 | 3.09 | 3.07 | 0.67 |
| 10:00 | 30 | 30.42 | 1.39 | 2.99 | 2.87 | 3.80 |
| 11:00 | 30 | 30.66 | 2.19 | 3.05 | 2.87 | 5.98 |
| 12:00 | 30 | 30.81 | 2.70 | 3.05 | 2.83 | 7.37 |
| 13:00 | 30 | 30.90 | 2.99 | 3.05 | 2.80 | 8.16 |
| 14:00 | 30 | 30.99 | 3.30 | 3.05 | 2.78 | 9.01 |
| 15:00 | 30 | 31.07 | 3.56 | 3.05 | 2.75 | 9.70 |
| 16:00 | 30 | 31.13 | 3.77 | 3.05 | 2.74 | 10.29 |
| 17:00 | 30 | 31.19 | 3.96 | 3.05 | 2.72 | 10.79 |
| 18:00 | 30 | 31.24 | 4.12 | 3.05 | 2.71 | 11.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubalcaba Velasco, J.O.; Acuña Ramírez, A.; Quintal López, J.A.; Mercado Herrera, A.; Suástegui Macías, J.A.; Ruelas Puente, A.H.; Lara Chávez, F.; Rosales Escobedo, P.F.; Corona Sánchez, J.A. Theoretical-Experimental Analysis of the Performance of Geothermal Heat Pumps for Air Conditioning Greenhouses in Arid Zones. Processes 2022, 10, 1682. https://doi.org/10.3390/pr10091682
Rubalcaba Velasco JO, Acuña Ramírez A, Quintal López JA, Mercado Herrera A, Suástegui Macías JA, Ruelas Puente AH, Lara Chávez F, Rosales Escobedo PF, Corona Sánchez JA. Theoretical-Experimental Analysis of the Performance of Geothermal Heat Pumps for Air Conditioning Greenhouses in Arid Zones. Processes. 2022; 10(9):1682. https://doi.org/10.3390/pr10091682
Chicago/Turabian StyleRubalcaba Velasco, Jesús Octavio, Alexis Acuña Ramírez, Jammin Abdi Quintal López, Abelardo Mercado Herrera, José Alejandro Suástegui Macías, Adolfo Heriberto Ruelas Puente, Fernando Lara Chávez, Pedro Francisco Rosales Escobedo, and José Armando Corona Sánchez. 2022. "Theoretical-Experimental Analysis of the Performance of Geothermal Heat Pumps for Air Conditioning Greenhouses in Arid Zones" Processes 10, no. 9: 1682. https://doi.org/10.3390/pr10091682
APA StyleRubalcaba Velasco, J. O., Acuña Ramírez, A., Quintal López, J. A., Mercado Herrera, A., Suástegui Macías, J. A., Ruelas Puente, A. H., Lara Chávez, F., Rosales Escobedo, P. F., & Corona Sánchez, J. A. (2022). Theoretical-Experimental Analysis of the Performance of Geothermal Heat Pumps for Air Conditioning Greenhouses in Arid Zones. Processes, 10(9), 1682. https://doi.org/10.3390/pr10091682







