Next Article in Journal
Cultivation of Nitrifying and Nitrifying-Denitrifying Aerobic Granular Sludge for Sidestream Treatment of Anaerobically Digested Sludge Centrate
Previous Article in Journal
Vibration Characteristics Analysis of O-Shaped Damping Ring to Balance Damping Gear Transmission System for Three-Cylinder Engine
Previous Article in Special Issue
Special Issue “Optimization Technology of Greenhouse Gas Emission Reduction”
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 10
Issue 9
10.3390/pr10091686
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Application of a Single Multilayer Perceptron Model to Predict the Solubility of CO2 in Different Ionic Liquids for Gas Removal Processes

by
Elías N. Fierro
1,
Claudio A. Faúndez
1,
Ariana S. Muñoz
2,* and
Patricio I. Cerda
1
1
Departamento de Física, Universidad de Concepción, Casilla 160-C, Concepción 3349001, Chile
2
Facultad de Ingeniería, Universidad Autónoma de Chile, 5 Poniente 1670, Talca 3480094, Chile
*
Author to whom correspondence should be addressed.
Processes 2022, 10(9), 1686; https://doi.org/10.3390/pr10091686
Submission received: 23 July 2022 / Revised: 7 August 2022 / Accepted: 12 August 2022 / Published: 25 August 2022
(This article belongs to the Special Issue Optimization Technology of Greenhouse Gas Emission Reduction)
Browse Figures
Review Reports Versions Notes

Abstract

:
In this work, 2099 experimental data of binary systems composed of CO2 and ionic liquids are studied to predict solubility using a multilayer perceptron. The dataset includes 33 different types of ionic liquids over a wide range of temperatures, pressures, and solubilities. The main objective of this work is to propose a procedure for the prediction of CO2 solubility in ionic liquids by establishing four stages to determine the model parameters: (1) selection of the learning algorithm, (2) optimization of the first hidden layer, (3) optimization of the second hidden layer, and (4) selection of the input combination. In this study, a bound is set on the number of model parameters: the number of model parameters must be less than the amount of predicted data. Eight different learning algorithms with (4,m,n,1)-type hidden two-layer architectures (m = 2, 4, …, 10 and n = 2, 3, …, 10) are studied, and the artificial neural network is trained with three input combinations with three combinations of thermodynamic variables such as temperature (T), pressure (P), critical temperature (Tc), critical pressure, the critical compressibility factor (Zc), and the acentric factor (ω). The results show that the 4-6-8-1 architecture with the input combination T-P-Tc-Pc and the Levenberg–Marquard learning algorithm is a very acceptable and simple model (95 parameters) with the best prediction and a maximum absolute deviation close to 10%.

1. Introduction

The impact of greenhouse gas emissions on the atmosphere has motivated important technological developments in recent decades [1,2]. This is because our planet’s environmental problems threaten not only our natural environment but also our health and the world economy [3,4,5]. Currently, the main factor responsible for global warming and climate change is carbon dioxide produced by fossil fuels, which are used to generate energy. The need to prevent carbon dioxide emissions has been accepted by many industries. For that reason, industrial processes have incorporated technologies to reduce the amount of carbon dioxide emitted into the atmosphere [6,7,8].
Currently, research is focused on three main alternatives for CO2 capture: precombustion, oxy-combustion, and postcombustion [9,10]. In particular, postcombustion capture has been widely used for CO2 capture in natural gas, refinery off-gases, and synthesis gas processing [11,12]. Current postcombustion technologies contemplate the use of amines such as monoethanolamine, diethanolamine, methyldiethanolamine, and 2-amino-2-, ethyl-1-propanol [13]. However, the amine-based afterburning method has certain drawbacks, such as the creation of corrosive byproducts due to amine degradation, solvent loss, and high energy demand for sorbent regeneration [14,15,16].
An alternative is the so-called ionic liquids (ILs) [17,18,19]. This new class of nonaqueous fluids consists of an asymmetric organic cation and an organic or inorganic anion. Ionic liquids are usually defined as organic salts that remain a liquid at room temperature. Their properties include high thermal stability, low vapor pressure and toxicity, a low melting point, and easy recycling. In addition, it is possible to control their physical and chemical properties by manipulating the cation. Compared with current technology based on aqueous amines, ionic liquids require less energy to regenerate them and remove the captured CO2 [20].
Several experimental studies have estimated the solubility of polluting gases such as CO2 in ionic liquids. Huang and Peng (2017) studied the solubility of carbon dioxide in three low-viscosity ILs by the volumetric method in a temperature range of 298.0–373.2 K and a pressure range of 0–300 KPa [21]. Kodama et al. (2017) measured the CO2 solubility in ionic liquid mixtures of (bmim)(PF6) and (bmim)(TFSA) at 313.15 K and a pressure up to 8.5 MPa using a volume-variable high-pressure apparatus [22]. Turnaoglu et al. (2019) investigated the phase behavior of carbon dioxide in three pyrrolidinium-based ILs using both gravimetric and volumetric methods at 298.15, 318.15, and 338.15 K and a pressure of up to 20 MPa [23]. These experimental results indicate that ILs are efficient at removing carbon dioxide.
Unfortunately, experimentally measuring the solubility of CO2 in ILs is expensive and, in some cases, dangerous. For these reasons, different theoretical and computational models have been proposed to predict the solubility of binary mixtures of CO2 and ILs. Breure et al. (2007) applied a group contribution equation of state (GC-EOS) to predict the phase behavior of binary ionic liquid systems of the homologous hexafluorophosphate and 1-alkyl-3-methylimidazolium tetrafluoroborate families with CO2 [24]. Yokoseki and Shiflett (2010) showed that the experimental data of gas solubility (CO2, CF3-CFH2, SO2, and NH3) in ionic liquids at room temperature are well correlated with the van der Waals EOS model [25]. Kamgar and Rahimpour (2016) used the UNIQUAC model and the quantum model, based on the COSMO-RS theory of interacting molecular surface charge, to determine the solubility of CO2 in six ionic liquids [26]. Mirzaei et al. (2018) correlated the experimental data of CO2 and methane solubility in (Hmim)(NO3) with the extended Henry’s law model and the activity coefficient of the gases, and the interaction parameters of the model were estimated as a function of the temperature [27].
Within computational forecasting methods, artificial intelligence-based tools have received attention in recent times. Machine learning techniques such as genetic algorithms, support vector machines, and artificial neural networks have reported acceptable results in the prediction of thermodynamic properties [13,28,29,30,31,32,33]. Yusuf et al. (2021) showed that the ANN approach is the most widely used approach among machine learning techniques in the prediction of the various properties of ILs [34]. Among the ANN models, the multilayer perceptron (MLP) stands out for its easy application to different nonlinear problems. This method consists of a network of units called neurons, characterized by numerical parameters called weights and bias. Currently, there is no specific rule to establish the number of neurons and the value of the weights and biases. For this reason, many authors use trial and error to establish the network architecture. After several iterations, the architecture that offers the best statistical results is selected. However, this has led authors to select unreasonable architectures for the prediction of thermodynamic properties. Often, the number of model parameters is larger than the data used to evaluate the predictive ability of the ANN. Tatar et al. (2016) used two ANN models to predict the solubility of CO2 in 14 LIs. The MLP model reported by these authors had 162 parameters, while the prediction set had 146 data points [13]. Mesbah et al. (2018) presented the (5,23,1) architecture as the best MLP model for predicting the solubility of 20 binary mixtures of CO2 and Lis [35]. The model was composed of 261 parameters and was used to predict 208 experimental data. Recently, Ouaer et al. (2019) proposed an ANN model with a (6,11,11,9,1) architecture to predict the solubility of CO2 in 13 different LIs. This complex 327-parameter model was used for the prediction of 149 data [36]. On the other hand, Song et al. (2020) employed an ANN and support vector machine to develop group contribution models [32]. From a database of 10,116 data, they obtained a reasonable artificial neural network model with a (53,7,1) architecture of 386 parameters to predict 2023 experimental data. More recently, Daryayehsalameh et al. (2021) used 6 different artificial intelligence techniques to study the solubility of 548 CO2 data in (Bmim)(BF4) [37]. Table 1 details some ANN models reported in the last 10 years to predict CO2 solubility in LIs. It is known that the use of complex architectures leads to overfitting of the model. Hence, a complex model is not synonymous with a good model. For this reason, it is necessary to establish a criterion to control the complexity of a model based on an MLP.
In this work, 2099 experimental data of binary systems composed of CO2 and ionic liquids are studied to predict solubility using a multilayer perceptron. Architectures with two hidden layers are used, and four stages are established to determine the model parameters: (1) selection of the learning algorithm, (2) optimization of the first hidden layer, (3) optimization of the second hidden layer, and (4) selection of the input combination. In addition to the usual statistical criteria, a new criterion is added: the number of model parameters must be less than the amount of predicted data. The findings show that it is possible to obtain a model that meets these criteria for the prediction of the solubility of binary mixtures of CO2 and ionic liquids.

2. Prediction of Solubility by Using a Multilayer Perceptron

The multilayer perceptron is an artificial neural network composed of three types of layers: the input layer, hidden layer, and output layer. Figure 1 shows the diagram of the MLP used in this work. In this model, the output a k + 1 of the one-neuron in hidden layer (k + 1) of a network with M layers is given by Equation (1) [40,41]:
a k + 1 ( l ) = f k + 1 ( ∑ j = 1 N k w k + 1 ( l , j ) a k ( j ) + b k + 1 ( l ) ) ; k = 1 , 2 , 3 … ( M − 1 )
The activation function for the hidden layers is the tansing function given by Equation (2), and that for the output layer is the linear purelin function given by Equation (3):
f t ( x ) = e x − e − x e x + e − x
f p ( x ) = n
The objective function is the mean square error (MSE), which is given by Equation (4) and is optimized by updating the values of the weights and bias with the learning algorithm:
M S E = 1 N ∑ i = 1 n ( X i − Y i ) 2
To ensure that the ANN did not predict individual solubilities that are negative or greater than one, the maximum absolute deviation for each run was studied, in addition to determining the average deviations. The individual absolute deviations, average absolute deviations, and average relative deviations of the solubilities calculated with respect to the experimental data are determined using Equations (4)–(6):
| Δ x % | = 100 ( x i c a l − x i e x p x i e x p )
| Δ x 1 ¯ % | = 100 N ∑ i = 1 N | x i c a l − x i e x p x i e x p |
Δ x 1 ¯ % = 100 N ∑ i = 1 N ( x i c a l − x i e x p x i e x p )
We terminated the iterative process when a maximum of 900 iterations was reached or when consecutive errors of up to 1 × 10−4 were observed. Architectures with two hidden layers were studied, and the optimal number of neurons was determined by trial and error. To avoid overfitting, a limit of up to 10 neurons per hidden layer was considered, and three sets of data were defined: a training set, testing set, and prediction set [42,43]. A multilayer perceptron was built using MATLAB© R2014a software [44] (MATLAB (R2014a)) with code already presented in previous works [45].

3. Results

In the present work, binary systems composed of CO2 in different ionic liquids are studied. The following 33 ionic liquids were considered: (Bmim)(PF6), (Bmim)(NO3), (Omim)(BF4), (Pmim)(TF2N), (Bmim)(PF6), (Bmim)(DCA), (Emim)(TF2N), (Hmim)(TF2N), (Hmim)(PF6), (Emim)(AC), (Emim)(TfO), (Bmim)(TfO), (Omim)(TfO), (Omim)(TF2N), (Hmim)(TfO), (Hmim)(BF4), (Emim)(SCN), (Emim)(N(CN)2), (Emim)(C(CN)3), (P(14)666)(DCA), (HMMIM)(TF2N), (Bmim)(BF4), (Bmim)(SCN), (BMP)(Tf2N), (TBMA)(MeSO4), (P14,6,6,6)(TF2N), (Bmim)(Cl), (Bmmim)(TF2N), (Emim)(NFBS), (Emim)(BF4), (PMPY)(TF2N), (Omim)(PF6), and (Hmim)(NO3). The temperatures varied between 273.15 K and 449.41 K, the pressure varied between 0.010 MPa and 100.120 MPa, and the solubility varied between 0.1000 and 0.8456. This study included 269 isotherms with a total of 2099 experimental data points (P-T-x data). In Table 2, the temperature, pressure, and solubility ranges used in this work are presented, indicating the literature sources from which the experimental data were taken.
The experimental dataset was used to predict the solubility using a multilayer perceptron. The original available data were divided into three sets: 1890 data for training (90%), 105 data for testing (5%), and 104 data points randomly selected as a network prediction set (5%). In this study, four steps were considered to obtain the best network learning: selection of the best learning algorithm, optimization of two hidden layers, studying different input combinations, and selection of the best model. Figure 2 shows the diagram of each step and the criteria used in this work.

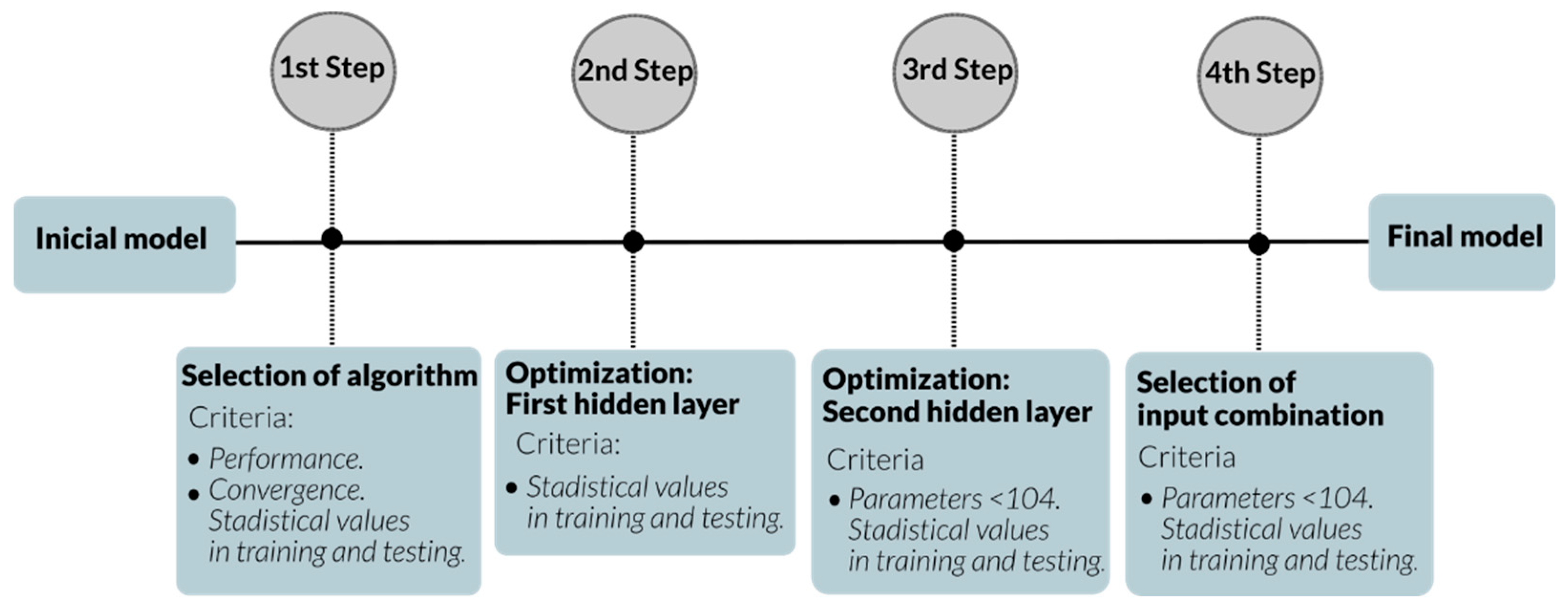
3.1. Selection of Learning Algorithms for Artificial Neural Networks

The artificial neural network can be trained using different learning algorithms. For the purpose of choosing the most suitable method, in this paper, seven learning algorithms were applied to predict the solubility of binary systems of CO2 in ionic liquids. The experimental data used were carefully selected by analyzing the experimental errors reported by the authors of each set of data. The experimental results were calculated with MATLAB R2014a by employing the following algorithms: BFGS Quasi-Newton, Resilient Backpropagation, Scaled Conjugate Gradient, Conjugate Gradient with P/B R, Polak–Ribiére Conjugate Gradient, One-Step Secant, Variable Learning Rate Backpropagation, and Levenberg–Marquartd [44]. Table 3 shows a training function and iterative equation for each algorithm used.
The criteria used were the performance, convergence, and statistical values. A simple (4,m,n,1) architecture was used to investigate the results of the eight algorithms. The network consisted of four layers: an input layer, in which each neuron in this layer corresponded to one input signal (four neurons), two hidden layers of neurons that adjusted in order to represent a relationship (m = 2 and n = 2 neurons), and an output layer, in which each neuron in this layer corresponded to one output signal (one neuron). In this stage, the input corresponded to the experimental temperature and pressure, as well as the critical temperature and pressure. The number of epochs for training the algorithms was set to 900.
From Figure 3, the training step using the LM algorithm converged faster than the other algorithms studied. In Table 3, we can see that the three best performances were obtained with the Levenberg–Marquard, BFGS Quasi-Newton, and Fletch–Powell Conjugate Gradient algorithms, being 0.03645, 0.03873, and 0.03874, respectively.
The resulting statistical values in Table 3 also indicate that the Levenberg–Marquard algorithm provided a more accurate nonlinear predictive model (with average absolute deviations of 16.09% and 11.36% in the training and testing sets, respectively). This was followed by the Polak–Riére Conjugate Gradient (with an average absolute deviation of 16.16% and 12.25% in the training and testing sets, respectively) and Scaled Conjugate Gradient (with average absolute deviations of 16.18% and 12.09% in the training and testing sets, respectively). The results show that the Levenberg–Marquardt algorithm performed slightly better than the other algorithms and was the fastest.

3.2. Optimization of the First Hidden Layer

Architectures with two hidden layers of the form (4,m,n,1) were considered in this step (m = 2,3, …,10 represents the neurons of the first hidden layer, and n = 2, 4, 6, …, 10 represents the neurons of the second hidden layer). Each hidden layer was optimized separately using the Levenberg–Marquard algorithm. Four inputs were considered in this step: T, P, Tc, and Pc. To optimize the first hidden layer, a fixed value n = 2 was considered, and (4,m,2,1)-type architectures were studied. The findings show that for m = 6, an acceptable average absolute deviation was achieved (6.74% in the training dataset, 4.38% in the testing dataset, and 3.94% in the prediction dataset). Although this architecture did not present the best training results, it is a simple model. Figure 4 presents the results obtained with the (4,m,2,1)-type architecture with m = 1, 2, …, 10. Then, to optimize the second hidden layer, a fixed value m = 6 was considered for the next step.

3.3. Optimization of the Second Hidden Layer

For each architecture of the form (4,6,n,1), 50 executions were run. To ensure that the artificial neural network did not predict individual solubilities that were negative or greater than one, in addition to the average deviations, the maximum absolute deviation for each run is shown. Table 4 presents the run with the lowest average absolute deviation during training, testing, and prediction that was selected for each architecture. From the table, it is clear that the two best models were the (4,6,8,1) and (4,6,10,1) architectures. Model (4,6,10,1) obtained the best average absolute deviation in training and testing at 3.44% and 1.98%, respectively. However, it exceeded the number of parameters allowed (123 parameters). On the other hand, model (4,6,8,1) obtained the best prediction with an average absolute deviation of 2.29% and a maximum absolute deviation of 10.76%. Moreover, this model employed 95 parameters. Thus, it was selected as the most suitable architecture to predict the solubility of CO2 in ionic liquids.

3.4. Selection of the Input Combination

In addition, different combinations of training variables were considered. The most appropriate variables for use as independent variables in an MLP for solubility prediction have not been previously determined in the literature. However, the experimental temperature and pressure of the binary system (T and P), critical temperature (Tc), critical pressure (Pc), the acentric factor (ω), and the compressibility factor (Zc) are commonly used in ANN models [38,39,42,72,73]. Table 5 shows the values of the critical properties used in this work.
In this step, three input combinations were considered: T-P-Tc-Pc, T-P-Tc, Pc-ω, and T-P-Tc-Pc-Zc. For all three cases, the number of parameters met the condition of being less than 104. As noted above, when using the training variables T, P, Tc, and Pc, the (4,6,8,1) architecture presented the lowest deviation and absolute average the prediction set. In Figure 5, we can see that with this input and architecture combination, a reasonable correlation between the experimental and calculated solubilities was obtained. On the other hand, adding the acentric factor (101 parameters) slightly improved the results in training (average absolute deviations of 3.52% and maximum average deviation of 40.88%). However, the prediction and testing sets presented absolute average deviations of 2.40% and 2.68%, respectively. Finally, when considering training variables P, Tc, Pc, and Zc (101 parameters), an increase in the prediction set was observed (absolute average deviation of 3.55%) along with a decrease in the training and testing sets (absolute average deviation of 3.55% and 2.18 respectively). Figure 6 and Figure 7 show the correlation between the experimental and calculated solubilities with T-P-Tc-Pc-w and T-P-Tc-Pc-Zc. In three cases in the training set, the largest relative deviations were found in the low-solubility region, as shown in Figure 8. This was reasonable due to the experimental uncertainty inherent in these measurements. With these results, we could consider the combination T, P, Tc, and Pc as a reasonable choice of input. Although this combination did not present the best training results, it is a simple model (95 parameters) with the best prediction and a maximum absolute deviation closer to 10%. The values of the artificial neural network parameters for the architecture (4,6,8,1) are shown in Table 6, Table 7 and Table 8.

4. Conclusions

In this work, 2099 experimental solubility data regarding binary mixtures composed of CO2 and ILs were studied with an artificial neural network model. The dataset included 33 different types of ionic liquids, where the temperature ranged from 273.15 K to 449.41 K, the pressure ranged from 0.010 MPa to 100.120 MPa, and the solubility ranged from 0.1000 to 0.8456. The solubility was predicted using a multilayer perceptron (MLP) consisting of four stages to determine the model parameters of the (4,m,n,1)-type architecture. In addition to the usual statistical criteria, a new criterion was added: the amount of model parameters had to be less than the amount of predicted data. This allowed the following main conclusions to be drawn. (1) The resulting statistical values indicate that the Levenberg–Marquard algorithm provided a more accurate nonlinear predictive model. (2) For m = 6, an acceptable average absolute deviation was achieved (6.74% in the training dataset, 4.38% in the test dataset, and 3.94% in the prediction dataset using the (4,m,2,1)-type architecture). (3) For n = 8, the best prediction was obtained with an average absolute deviation of 2.29% and a maximum absolute deviation of 10.76% using the (4,6,n,1)-type architecture. (4) The combination of T, P, Tc, and Pc is a reasonable choice of input with 95 parameters and the best prediction.

Author Contributions

Conception and design of study, E.N.F. and C.A.F.; acquisition of data, A.S.M. and E.N.F.; analysis and interpretation of data: E.N.F., C.A.F., A.S.M. and P.I.C.; drafting the manuscript, E.N.F., C.A.F. and A.S.M.; revising the manuscript critically for important intellectual content, E.N.F., C.A.F., A.S.M. and P.I.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by ANID grant number 21171075, research grant DIUA 238-2022 of the VRID and research grant VRID 219011062-INV.

Acknowledgments

The authors are grateful for the support of their respective institutions and grants. E.N.F. thanks the support of ANID scholarship 21171075. C.A.F. and A.S.M. thank María A. Rodríguez of Research and Development of the University of Concepcion for the support through the research grant VRID N° 219.011.062-INV. The authors acknowledge the DIUA 238-2022 project of the VRID for supporting part of this work. ASM thanks the research group GEMA Res.180/2019 VRI-UA for special support.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Jordaan, S.M.; Romo-Rabago, E.; McLeary, R.; Reidy, L.; Nazari, J.; Herremans, I.M. The role of energy technology innovation in reducing greenhouse gas emissions: A case study of Canada. Renew. Sustain. Energy Rev. 2017, 78, 1397–1409. [Google Scholar] [CrossRef]
  2. Fernández, Y.F.; López, M.F.; Blanco, B.O. Innovation for sustainability: The impact of R&D spending on CO2 emissions. J. Clean. Prod. 2018, 172, 3459–3467. [Google Scholar]
  3. Mendelsohn, R.; Neumann, J.E. (Eds.) The Impact of Climate Change on the United States Economy; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
  4. McMichael, A.J.; Woodruff, R.E.; Hales, S. Climate change and human health: Present and future risks. Lancet 2006, 367, 859–869. [Google Scholar] [CrossRef]
  5. Kjellstrom, T. Impact of climate conditions on occupational health and related economic losses: A new feature of global and urban health in the context of climate change. Asia Pac. J. Public Health 2016, 28 (Suppl. 2), 28S–37S. [Google Scholar] [CrossRef] [PubMed]
  6. Beller, M.; Steinberg, M. Liquid Fuel Synthesis Using Nuclear Power in a Mobile Energy Depot System (No. BNL-955); Brookhaven National Lab.: Upton, NY, USA, 1965. [Google Scholar]
  7. Lackner, K.; Ziock, H.J.; Grimes, P. Carbon Dioxide Extraction from Air: Is it an Option? (No. LA-UR-99-583); Los Alamos National Lab.: Los Alamos, NM, USA, 1999. [Google Scholar]
  8. Keith, D.W.; Holmes, G.; Angelo, D.S.; Heidel, K. A process for capturing CO2 from the atmosphere. Joule 2018, 2, 1573–1594. [Google Scholar] [CrossRef]
  9. Kanniche, M.; Gros-Bonnivard, R.; Jaud, P.; Valle-Marcos, J.; Amann, J.M.; Bouallou, C. Pre-combustion, post-combustion and oxy-combustion in thermal power plant for CO2 capture. Appl. Therm. Eng. 2010, 30, 53–62. [Google Scholar] [CrossRef]
  10. Adams, T.A.; Hoseinzade, L.; Madabhushi, P.B.; Okeke, I.J. Comparison of CO2 capture approaches for fossil-based power generation: Review and meta-study. Processes 2017, 5, 44. [Google Scholar] [CrossRef]
  11. Kohl, A.L.; Nielsen, R. Gas Purification; Elsevier: Amsterdam, The Netherlands, 1997. [Google Scholar]
  12. Astarita, G.; Savage, D.W.; Longo, J.M. Promotion of CO2 mass transfer in carbonate solutions. Chem. Eng. Sci. 1981, 36, 581–588. [Google Scholar] [CrossRef]
  13. Tatar, A.; Naseri, S.; Bahadori, M.; Hezave, A.Z.; Kashiwao, T.; Bahadori, A.; Darvish, H. Prediction of carbon dioxide solubility in ionic liquids using MLP and radial basis function (RBF) neural networks. J. Taiwan Inst. Chem. Eng. 2016, 60, 151–164. [Google Scholar] [CrossRef]
  14. Romeo, L.M.; Minguell, D.; Shirmohammadi, R.; Andrés, J.M. Comparative analysis of the efficiency penalty in power plants of different amine-based solvents for CO2 capture. Ind. Eng. Chem. Res. 2020, 59, 10082–10092. [Google Scholar] [CrossRef]
  15. Gouedard, C.; Picq, D.; Launay, F.; Carrette, P.L. Amine degradation in CO2 capture. I. A review. Int. J. Greenh. Gas Control. 2012, 10, 244–270. [Google Scholar] [CrossRef]
  16. Zhang, J.; Nwani, O.; Tan, Y.; Agar, D.W. Carbon dioxide absorption into biphasic amine solvent with solvent loss reduction. Chem. Eng. Res. Des. 2011, 89, 1190–1196. [Google Scholar] [CrossRef]
  17. Zeng, S.; Zhang, X.; Bai, L.; Zhang, X.; Wang, H.; Wang, J.; Zhang, S. Ionic-liquid-based CO2 capture systems: Structure, interaction and process. Chem. Rev. 2017, 117, 9625–9673. [Google Scholar] [CrossRef] [PubMed]
  18. Taimoor, A.A.; Al-Shahrani, S.; Muhammad, A. Ionic liquid (1-butyl-3-metylimidazolium methane sulphonate) corrosion and energy analysis for high pressure CO2 absorption process. Processes 2018, 6, 45. [Google Scholar] [CrossRef]
  19. Leonzio, G.; Zondervan, E. Surface-Response Analysis for the Optimization of a Carbon Dioxide Absorption Process Using [hmim][Tf2N]. Processes 2020, 8, 1063. [Google Scholar] [CrossRef]
  20. Brennecke, J.F.; Gurkan, B.E. Ionic liquids for CO2 capture and emission reduction. J. Phys. Chem. Lett. 2010, 1, 3459–3464. [Google Scholar] [CrossRef]
  21. Huang, K.; Peng, H.L. Solubilities of Carbon Dioxide in 1-Ethyl-3-methylimidazolium Thiocyanate, 1-Ethyl-3-methylimidazolium Dicyanamide, and 1-Ethyl-3-methylimidazolium Tricyanomethanide at (298.2 to 373.2) K and (0 to 300.0) kPa. J. Chem. Eng. Data 2017, 62, 4108–4116. [Google Scholar] [CrossRef]
  22. Kodama, D.; Sato, K.; Watanabe, M.; Sugawara, T.; Makino, T.; Kanakubo, M. Density, Viscosity, and CO2 Solubility in the Ionic Liquid Mixtures of [bmim][PF6] and [bmim][TFSA] at 313.15 K. J. Chem. Eng. Data 2017, 63, 1036–1043. [Google Scholar] [CrossRef]
  23. Turnaoglu, T.; Minnick, D.L.; Morais, A.R.C.; Baek, D.L.; Fox, R.V.; Scurto, A.M.; Shiflett, M.B. High-pressure vapor− liquid equilibria of 1-alkyl-1-methylpyrrolidinium bis (trifluoromethylsulfonyl) imide ionic liquids and CO2. J. Chem. Eng. Data 2019, 64, 4668–4678. [Google Scholar] [CrossRef]
  24. Breure, B.; Bottini, S.B.; Witkamp, G.J.; Peters, C.J. Thermodynamic modeling of the phase behavior of binary systems of ionic liquids and carbon dioxide with the group contribution equation of state. J. Phys. Chem. B 2007, 111, 14265–14270. [Google Scholar] [CrossRef]
  25. Yokozeki, A.; Shiflett, M.B. Gas solubilities in ionic liquids using a generic van der Waals equation of state. J. Supercrit. Fluids 2010, 55, 846–851. [Google Scholar] [CrossRef]
  26. Kamgar, A.; Rahimpour, M.R. Prediction of CO2 solubility in ionic liquids with QM and UNIQUAC models. J. Mol. Liq. 2016, 222, 195–200. [Google Scholar] [CrossRef]
  27. Mirzaei, M.; Mokhtarani, B.; Badiei, A.; Sharifi, A. Solubility of carbon dioxide and methane in 1-hexyl-3-methylimidazolium nitrate ionic liquid, experimental and thermodynamic modeling. J. Chem. Thermodyn. 2018, 122, 31–37. [Google Scholar] [CrossRef]
  28. Venkatraman, V.; Alsberg, B.K. Predicting CO2 capture of ionic liquids using machine learning. J. CO2 Util. 2017, 21, 162–168. [Google Scholar] [CrossRef]
  29. Mehraein, I.; Riahi, S. The QSPR models to predict the solubility of CO2 in ionic liquids based on least-squares support vector machines and genetic algorithm-multi linear regression. J. Mol. Liq. 2017, 225, 521–530. [Google Scholar] [CrossRef]
  30. Xia, L.; Wang, J.; Liu, S.; Li, Z.; Pan, H. Prediction of CO2 solubility in ionic liquids based on multi-model fusion method. Processes 2019, 7, 258. [Google Scholar] [CrossRef]
  31. Xia, L.; Liu, S.; Pan, H. Prediction of the Solubility of CO2 in Imidazolium Ionic Liquids Based on Selective Ensemble Modeling Method. Processes 2020, 8, 1369. [Google Scholar] [CrossRef]
  32. Song, Z.; Shi, H.; Zhang, X.; Zhou, T. Prediction of CO2 solubility in ionic liquids using machine learning methods. Chem. Eng. Sci. 2020, 223, 115752. [Google Scholar] [CrossRef]
  33. Nabipour, N.; Mosavi, A.; Baghban, A.; Shamshirband, S.; Felde, I. Extreme learning machine-based model for Solubility estimation of hydrocarbon gases in electrolyte solutions. Processes 2020, 8, 92. [Google Scholar] [CrossRef]
  34. Yusuf, F.; Olayiwola, T.; Afagwu, C. Application of Artificial Intelligence-based predictive methods in Ionic liquid studies: A review. Fluid Phase Equilibria 2021, 531, 112898. [Google Scholar] [CrossRef]
  35. Mesbah, M.; Shahsavari, S.; Soroush, E.; Rahaei, N.; Rezakazemi, M. Accurate prediction of miscibility of CO2 and supercritical CO2 in ionic liquids using machine learning. J. CO2 Util. 2018, 25, 99–107. [Google Scholar] [CrossRef]
  36. Ouaer, H.; Hosseini, A.H.; Nait Amar, M.; El Amine Ben Seghier, M.; Ghriga, M.A.; Nabipour, N.; Shamshirband, S. Rigorous connectionist models to predict carbon dioxide solubility in various ionic liquids. Appl. Sci. 2019, 10, 304. [Google Scholar] [CrossRef]
  37. Daryayehsalameh, B.; Nabavi, M.; Vaferi, B. Modeling of CO2 capture ability of [Bmim][BF4] ionic liquid using connectionist smart paradigms. Environ. Technol. Innov. 2021, 22, 101484. [Google Scholar] [CrossRef]
  38. Sedghamiz, M.A.; Rasoolzadeh, A.; Rahimpour, M.R. The ability of artificial neural network in prediction of the acid gases solubility in different ionic liquids. J. CO2 Util. 2015, 9, 39–47. [Google Scholar] [CrossRef]
  39. Eslamimanesh, A.; Gharagheizi, F.; Mohammadi, A.H.; Richon, D. Artificial neural network modeling of solubility of supercritical carbon dioxide in 24 commonly used ionic liquids. Chem. Eng. Sci. 2011, 66, 3039–3044. [Google Scholar] [CrossRef]
  40. Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed]
  41. Minsky, M.; Papert, S. Perceptron: An Introduction to Computational Geometry; MIT Press: Cambridge, UK, 1969. [Google Scholar]
  42. Faúndez, C.A.; Campusano, R.A.; Valderrama, J.O. Misleading results on the use of artificial neural networks for correlating and predicting properties of fluids. A case on the solubility of refrigerant R-32 in ionic liquids. J. Mol. Liq. 2020, 298, 112009. [Google Scholar] [CrossRef]
  43. Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
  44. MATLAB (R2014a). MathWorks. Available online: https://www.mathworks.com/ (accessed on 2 September 2014).
  45. Fierro, E.N.; Faúndez, C.A.; Muñoz, A.S. Influence of thermodynamically inconsistent data on modeling the solubilities of refrigerants in ionic liquids using an artificial neural network. J. Mol. Liq. 2021, 337, 116417. [Google Scholar] [CrossRef]
  46. Blanchard, L.A.; Gu, Z.; Brennecke, J.F. High-pressure phase behavior of ionic liquid/CO2 systems. J. Phys. Chem. B 2001, 105, 2437–2444. [Google Scholar] [CrossRef]
  47. Carvalho, P.J.; Álvarez, V.H.; Machado, J.J.; Pauly, J.; Daridon, J.L.; Marrucho, I.M.; Coutinho, J.A. High pressure phase behavior of carbon dioxide in 1-alkyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide ionic liquids. J. Supercrit. Fluids 2009, 48, 99–107. [Google Scholar] [CrossRef]
  48. Carvalho, P.J.; Álvarez, V.H.; Marrucho, I.M.; Aznar, M.; Coutinho, J.A. High pressure phase behavior of carbon dioxide in 1-butyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide and 1-butyl-3-methylimidazolium dicyanamide ionic liquids. J. Supercrit. Fluids 2009, 50, 105–111. [Google Scholar] [CrossRef]
  49. Raeissi, S.; Peters, C.J. Carbon dioxide solubility in the homologous 1-alkyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide family. J. Chem. Eng. Data 2009, 54, 382–386. [Google Scholar] [CrossRef]
  50. Ren, W.; Sensenich, B.; Scurto, A.M. High-pressure phase equilibria of {carbon dioxide (CO2)+ n-alkyl-imidazolium bis (trifluoromethylsulfonyl) amide} ionic liquids. J. Chem. Thermodyn. 2010, 42, 305–311. [Google Scholar] [CrossRef]
  51. Shariati, A.; Peters, C.J. High-pressure phase behavior of systems with ionic liquids: Part III. The binary system carbon dioxide+ 1-hexyl-3-methylimidazolium hexafluorophosphate. J. Supercrit. Fluids 2004, 30, 139–144. [Google Scholar] [CrossRef]
  52. Shiflett, M.B.; Yokozeki, A. Phase behavior of carbon dioxide in ionic liquids:[emim][acetate], [emim][trifluoroacetate], and [emim][acetate] + [emim][trifluoroacetate] mixtures. J. Chem. Eng. Data 2009, 54, 108–114. [Google Scholar] [CrossRef]
  53. Shin, E.K.; Lee, B.C. High-pressure phase behavior of carbon dioxide with ionic liquids: 1-alkyl-3-methylimidazolium trifluoromethanesulfonate. J. Chem. Eng. Data 2008, 53, 2728–2734. [Google Scholar] [CrossRef]
  54. Shin, E.K.; Lee, B.C.; Lim, J.S. High-pressure solubilities of carbon dioxide in ionic liquids: 1-alkyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide. J. Supercrit. Fluids 2008, 45, 282–292. [Google Scholar] [CrossRef]
  55. Yim, J.H.; Lim, J.S. CO2 solubility measurement in 1-hexyl-3-methylimidazolium ([HMIM]) cation based ionic liquids. Fluid Phase Equilibria 2013, 352, 67–74. [Google Scholar] [CrossRef]
  56. Safarov, J.; Hamidova, R.; Stephan, M.; Schmotz, N.; Kul, I.; Shahverdiyev, A.; Hassel, E. Carbon dioxide solubility in 1-butyl-3-methylimidazolium-bis (trifluormethylsulfonyl) imide over a wide range of temperatures and pressures. J. Chem. Thermodyn. 2013, 67, 181–189. [Google Scholar] [CrossRef]
  57. Kim, J.E.; Kim, H.J.; Lim, J.S. Solubility of CO2 in ionic liquids containing cyanide anions:[c2mim][SCN],[c2mim][N (CN) 2],[c2mim][C (CN) 3]. Fluid Phase Equilibria 2014, 367, 151–158. [Google Scholar] [CrossRef]
  58. Jalili, A.H.; Safavi, M.; Ghotbi, C.; Mehdizadeh, A.; Hosseini-Jenab, M.; Taghikhani, V. Solubility of CO2, H2S, and their mixture in the ionic liquid 1-octyl-3-methylimidazolium bis (trifluoromethyl) sulfonylimide. J. Phys. Chem. B 2012, 116, 2758–2774. [Google Scholar] [CrossRef]
  59. Afzal, W.; Liu, X.; Prausnitz, J.M. High solubilities of carbon dioxide in tetraalkyl phosphonium-based ionic liquids and the effect of diluents on viscosity and solubility. J. Chem. Eng. Data 2014, 59, 954–960. [Google Scholar] [CrossRef]
  60. Hwang, S.; Park, Y.; Park, K. Phase equilibria of the 1-hexyl-2, 3-dimethylimidazolium bis (trifluoromethylsulfonyl) imide and carbon dioxide binary system and 1-octyl-2, 3-dimethylimidazolium bis (trifluoromethylsulfonyl) imide and carbon dioxide binary system. J. Chem. Eng. Data 2012, 57, 2160–2164. [Google Scholar] [CrossRef]
  61. Revelli, A.L.; Mutelet, F.; Jaubert, J.N. High carbon dioxide solubilities in imidazolium-based ionic liquids and in poly (ethylene glycol) dimethyl ether. J. Phys. Chem. B 2010, 114, 12908–12913. [Google Scholar] [CrossRef] [PubMed]
  62. Yim, J.H.; Song, H.N.; Yoo, K.P.; Lim, J.S. Measurement of CO2 solubility in ionic liquids:[BMP][Tf2N] and [BMP][MeSO4] by measuring bubble-point pressure. J. Chem. Eng. Data 2011, 56, 1197–1203. [Google Scholar] [CrossRef]
  63. Yim, J.H.; Ha, S.J.; Lim, J.S. Measurement and Correlation of CO2 Solubility in 1-Ethyl-3-methylimidazolium ([EMIM]) Cation-Based Ionic Liquids:[EMIM][Ac],[EMIM][Cl], and [EMIM][MeSO4]. J. Chem. Eng. Data 2018, 63, 508–518. [Google Scholar] [CrossRef]
  64. Ramdin, M.; Vlugt, T.J.; de Loos, T.W. Solubility of CO2 in the ionic liquids [TBMN][MeSO4] and [TBMP][MeSO4]. J. Chem. Eng. Data 2012, 57, 2275–2280. [Google Scholar] [CrossRef]
  65. Song, H.N.; Lee, B.C.; Lim, J.S. Measurement of CO2 solubility in ionic liquids: [BMP][TfO] and [P14, 6, 6, 6][Tf2N] by measuring bubble-point pressure. J. Chem. Eng. Data 2010, 55, 891–896. [Google Scholar] [CrossRef]
  66. Jang, S.; Cho, D.W.; Im, T.; Kim, H. High-pressure phase behavior of CO2+ 1-butyl-3-methylimidazolium chloride system. Fluid Phase Equilibria 2010, 299, 216–221. [Google Scholar] [CrossRef]
  67. Tagiuri, A.; Sumon, K.Z.; Henni, A. Solubility of carbon dioxide in three [Tf2N] ionic liquids. Fluid Phase Equilibria 2014, 380, 39–47. [Google Scholar] [CrossRef]
  68. Watanabe, M.; Kodama, D.; Makino, T.; Kanakubo, M. CO2 absorption properties of imidazolium based ionic liquids using a magnetic suspension balance. Fluid Phase Equilibria 2016, 420, 44–49. [Google Scholar] [CrossRef]
  69. Zoubeik, M.; Mohamedali, M.; Henni, A. Experimental solubility and thermodynamic modeling of CO2 in four new imidazolium and pyridinium-based ionic liquids. Fluid Phase Equilibria 2016, 419, 67–74. [Google Scholar] [CrossRef]
  70. Safavi, M.; Ghotbi, C.; Taghikhani, V.; Jalili, A.H.; Mehdizadeh, A. Study of the solubility of CO2, H2S and their mixture in the ionic liquid 1-octyl-3-methylimidazolium hexafluorophosphate: Experimental and modelling. J. Chem. Thermodyn. 2013, 65, 220–232. [Google Scholar] [CrossRef]
  71. Ebrahiminejadhasanabadi, M.; Nelson, W.M.; Naidoo, P.; Mohammadi, A.H.; Ramjugernath, D. Experimental measurement of carbon dioxide solubility in 1-methylpyrrolidin-2-one (NMP)+ 1-butyl-3-methyl-1H-imidazol-3-ium tetrafluoroborate ([bmim][BF4]) mixtures using a new static-synthetic cell. Fluid Phase Equilibria 2018, 477, 62–77. [Google Scholar] [CrossRef]
  72. Baghban, A.; Ahmadi, M.A.; Shahraki, B.H. Prediction carbon dioxide solubility in presence of various ionic liquids using computational intelligence approaches. J. Supercrit. Fluids 2015, 98, 50–64. [Google Scholar] [CrossRef]
  73. Faúndez, C.A.; Fierro, E.N.; Valderrama, J.O. Solubility of hydrogen sulfide in ionic liquids for gas removal processes using artificial neural networks. J. Environ. Chem. Eng. 2016, 4, 211–218. [Google Scholar] [CrossRef]
  74. Valderrama, J.O.; Forero, L.A.; Rojas, R.E. Extension of a group contribution method to estimate the critical properties of ionic liquids of high molecular mass. Ind. Eng. Chem. Res. 2015, 54, 3480–3487. [Google Scholar] [CrossRef]
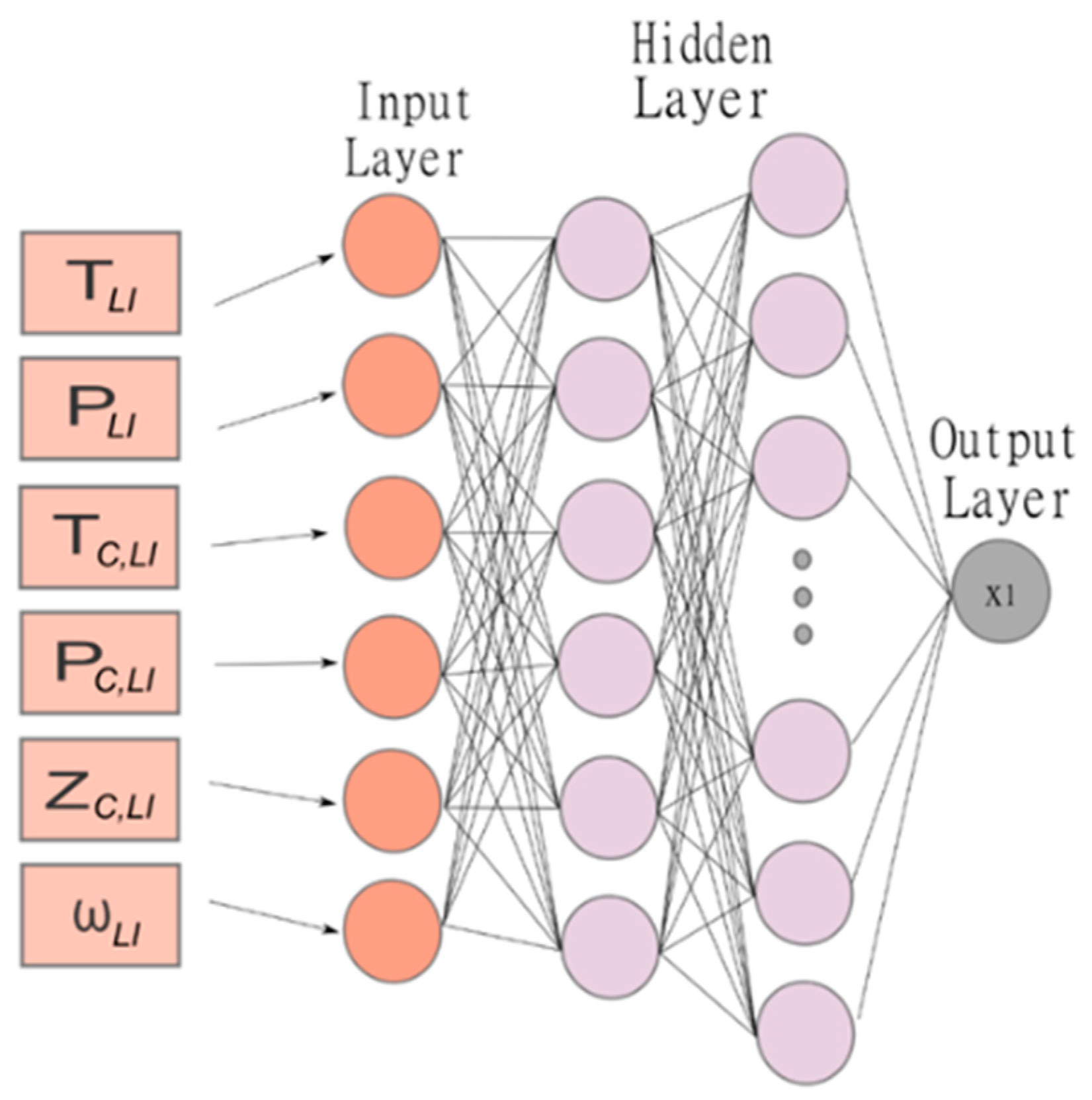
Processes 10 01686 g001 550
Figure 1. Schematic diagram of the multilayer perceptron with the variables of training, hidden, and output layers used in this study.
Figure 1. Schematic diagram of the multilayer perceptron with the variables of training, hidden, and output layers used in this study.
Processes 10 01686 g001
Processes 10 01686 g002 550
Figure 2. Schematic diagram of each step used in this study.
Figure 2. Schematic diagram of each step used in this study.
Processes 10 01686 g002
Processes 10 01686 g003 550
Figure 3. Convergence of the 8 algorithms used in the training of the (4,2,2,1) architecture.
Figure 3. Convergence of the 8 algorithms used in the training of the (4,2,2,1) architecture.
Processes 10 01686 g003
Processes 10 01686 g004 550
Figure 4. Optimization of the first hidden layer for architectures of type (4,m,2,1) with m = 1, 2, 3, …, 10.
Figure 4. Optimization of the first hidden layer for architectures of type (4,m,2,1) with m = 1, 2, 3, …, 10.
Processes 10 01686 g004
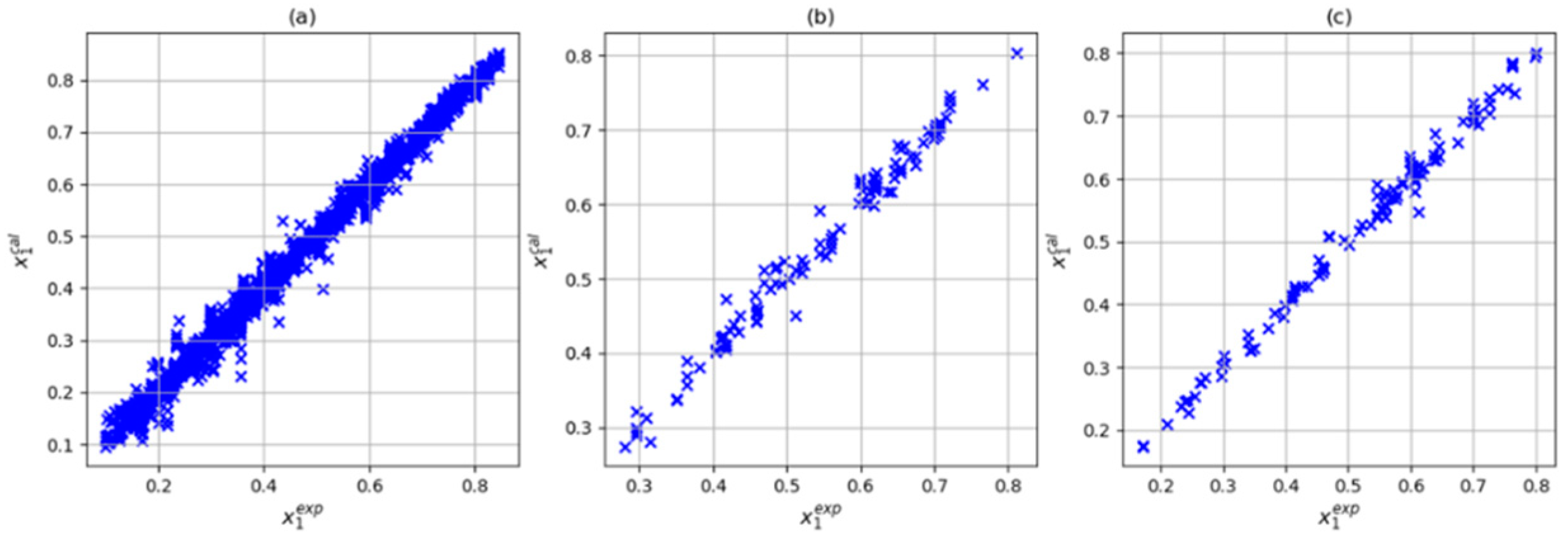
Processes 10 01686 g005 550
Figure 5. Correlation between experimental data and those calculated by ANN using T, P, Tc, and Pc inputs with (4,6,8,1) architecture: (a) training dataset, (b) testing dataset, and (c) prediction dataset.
Figure 5. Correlation between experimental data and those calculated by ANN using T, P, Tc, and Pc inputs with (4,6,8,1) architecture: (a) training dataset, (b) testing dataset, and (c) prediction dataset.
Processes 10 01686 g005
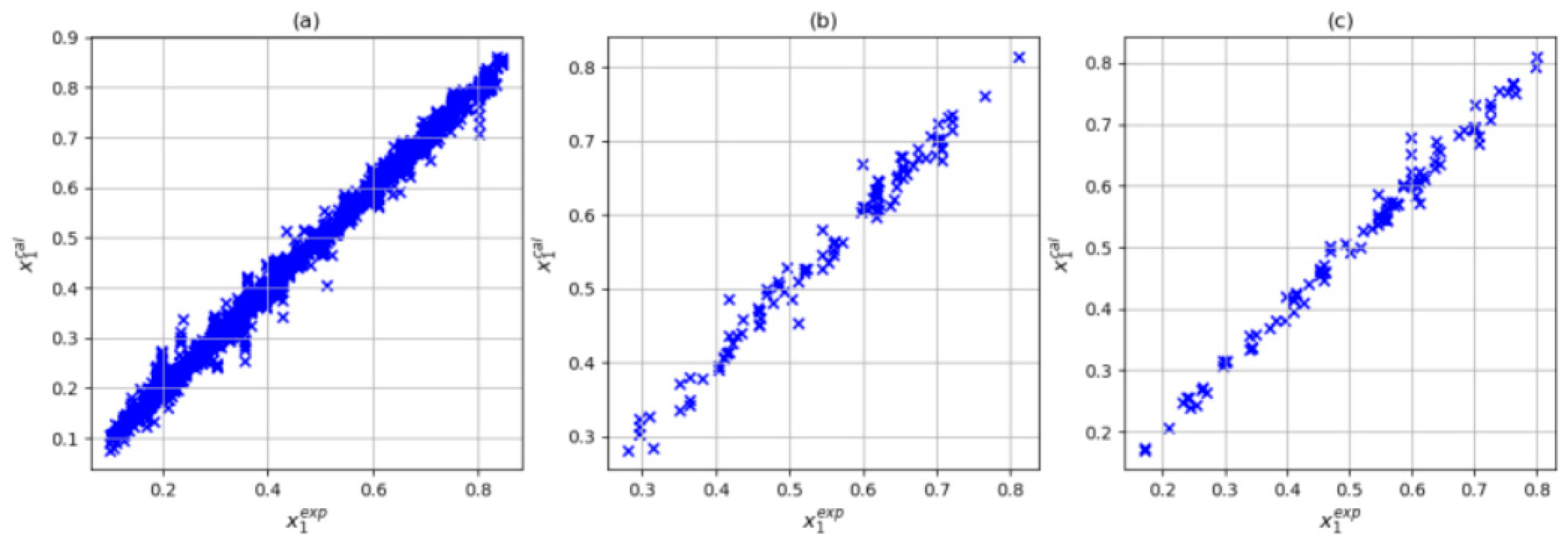
Processes 10 01686 g006 550
Figure 6. Correlation between experimental data and those calculated by ANN using T, P, Tc, Pc, and ω inputs with (5,6,8,1) architecture: (a) training dataset, (b) testing dataset, and (c) prediction dataset.
Figure 6. Correlation between experimental data and those calculated by ANN using T, P, Tc, Pc, and ω inputs with (5,6,8,1) architecture: (a) training dataset, (b) testing dataset, and (c) prediction dataset.
Processes 10 01686 g006
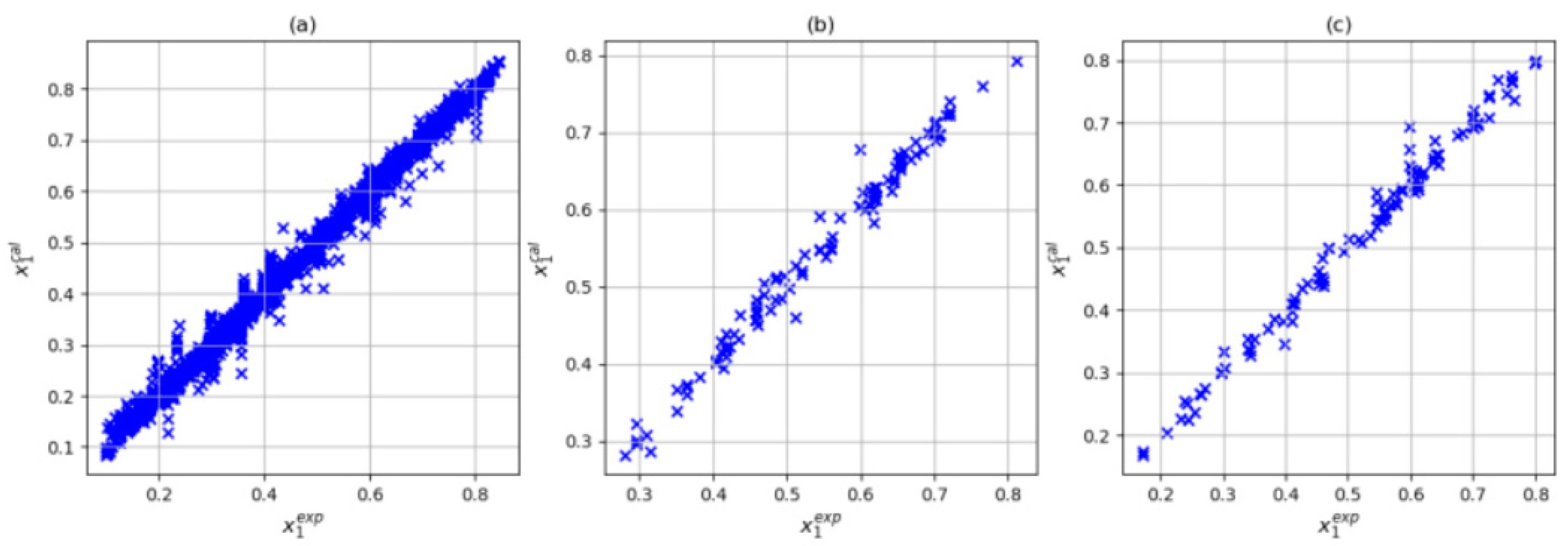
Processes 10 01686 g007 550
Figure 7. Correlation between experimental data and those calculated by ANN using T, P, Tc, Pc, and Zc inputs with (5,6,8,1) architecture: (a) training dataset, (b) testing dataset, and (c) prediction dataset.
Figure 7. Correlation between experimental data and those calculated by ANN using T, P, Tc, Pc, and Zc inputs with (5,6,8,1) architecture: (a) training dataset, (b) testing dataset, and (c) prediction dataset.
Processes 10 01686 g007
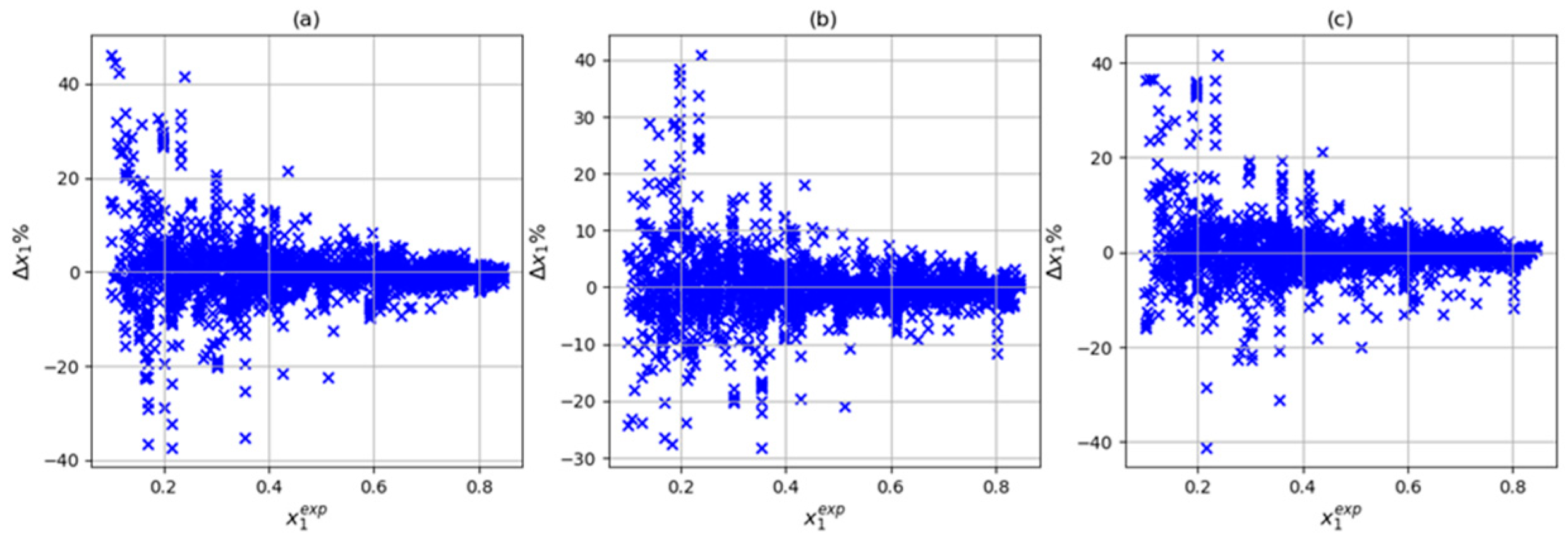
Processes 10 01686 g008 550
Figure 8. Dispersion of training in three input combination studies with (4,6,8,1) architecture: (a) T, P, Tc, and Pc, (b) T, P, Tc, Pc, and ω, and (c) T, P, Tc, Pc, and Zc.
Figure 8. Dispersion of training in three input combination studies with (4,6,8,1) architecture: (a) T, P, Tc, and Pc, (b) T, P, Tc, Pc, and ω, and (c) T, P, Tc, Pc, and Zc.
Processes 10 01686 g008
Table
Table 1. Detail of some models reported to predict the solubility of binary mixtures composed of CO2 and ILs using an MLP.
Table 1. Detail of some models reported to predict the solubility of binary mixtures composed of CO2 and ILs using an MLP.
AuthorData Point StudiedData Point PredictedSystemR2ArchitectureInputNp*
Ouaer et al., 2019 [36]744149130.9971(6,11,11,9,1)T, P, Mw, Tc, Pc, w327
Sedghamiz et al., 2015 [38]2930440390.9947(5,23,1)T, P, Tc, Pc, w162
Tatar et al., 2016 [13]728146140.998272(5,23,1)T, P, Tc, Pc, w162
Mesbah et al., 2018 [35]1386208200.9987(5,15,10,1)Mw, Tc, Pc, T, P261
Eslamimaneash et al., 2011 [39]1128112240.0995(5,19,1)T, P, Tc, Pc, w134
Song et al., 2020 [32]10,11620231240.0202(53,7,1)51 group numbers, T and P386
Daryayehsalameh et al., 2021 [37]548110170.98684(2,6,1)T and P25
Table
Table 2. All the data considered in this work.
Table 2. All the data considered in this work.
SystemsnT(K)P (MPa)x1Ref.
(Bmim)(PF6)7313.001.5170-9.56700.2310-0.7290[46]
7323.001.7380-9.24600.2360-0.6750
7333.001.5790-9.30100.2280-0.6670
(Bmim)(NO3)7313.001.5470-9.20000.1960-0.5130
7323.001.7120-9.26200.1690-0.5300
7333.001.8370-9.31700.1830-0.5220
(Omim)(BF4)7313.001.7260-9.29000.1970-0.7080
7323.001.5610-9.22800.1910-0.6710
7333.001.5610-9.37300.1600-0.6510
(Emim)(Tf2N)9292.16-293.650.6200-16.07600.2210-0.7500[47]
9297.70-298.550.7250-19.04800.2210-0.7500
9303.25-303.540.8370-22.13000.2210-0.7500
9313.19-313.591.0830-28.18700.2210-0.7500
9323.09-323.271.3450-33.78700.2210-0.7500
9332.88-333.231.6450-38.89800.2210-0.7500
9343.08-343.301.9570-43.56500.2210-0.7500
9353.02-353.222.2760-47.85000.2210-0.7500
8363.17-363.552.6800-30.85800.2210-0.7000
(Pmim)(Tf2N)9293.30-293.760.6180-27.46000.2120-0.8020
9298.37-298.770.7200-30.09800.2120-0.8020
9303.33-303.610.7990-32.88100.2120-0.8020
9312.85-313.571.0440-38.29900.2120-0.8020
9322.52-323.351.2520-43.22500.2120-0.8020
9332.54-333.561.5250-47.96000.2120-0.8020
9342.47-343.371.7800-52.43100.2120-0.8020
9352.65-353.492.1240-56.14600.2120-0.8020
9362.95-363.292.3700-59.80500.2120-0.8020
(Bmim)(Tf 2N)9292.65-293.530.6290-33.26300.2310-0.8010[48]
9303.05-303.310.7860-39.37300.2310-0.8010
9313.10-313.320.2310-44.74000.2310-0.8010
9323.09-323.301.3030-49.99000.2310-0.8010
8333.10-333.281.5740-33.69300.2310-0.7710
8342.87-343.251.8740-38.08100.2310-0.7710
8353.09-353.222.1790-42.03000.2310-0.7710
8362.99-363.182.4850-46.01000.2310-0.7710
(Bmim)(DCA)5293.36-293.501.0180-32.60600.2000-0.6010
5302.91-303.451.3600-39.86600.2000-0.6010
5313.03-313.361.7710-46.74900.2000-0.6010
5322.93-323.472.2600-53.17400.2000-0.6010
5332.72-333.282.6440-59.00700.2000-0.6010
5343.01-343.343.1080-64.21700.2000-0.6010
5353.09-353.013.7450-69.00200.2000-0.6010
5363.11-363.254.3280-73.64000.2000-0.6010
(Bmim)(Tf2N)6371.43-371.592.2020-13.95900.1886-0.5852[49]
4380.99-381.222.4330-11.62500.1886-0.5257
5390.86-390.952.6680-12.87400.1886-0.5257
4400.59-400.642.9120-14.09900.1886-0.5257
4410.37-410.523.1580-13.47300.1886-0.4866
3420.12-420.213.3980-8.93300.1886-0.3818
3429.86-429.893.6480-9.54800.1886-0.3818
3439.60-439.653.8880-10.19800.1886-0.3818
3449.36-449.414.1330-10.83300.1886-0.3818
(EMIm)(Tf2N)7298.151.2350-14.79400.2800-0.7820[50]
(HMIm)(Tf2N)8298.152.0150-14.80400.3960-0.8230
9323.153.7160-12.95900.4870-0.7790
7343.152.7540-24.70800.2390-0.7710
(Hmim)(PF6)3358.45-358.652.9200-8.41000.1980-0.4100[51]
6347.65-348.632.5700-76.90000.1980-0.7110
9337.82-338.472.2600-92.50000.1980-0.7270
9327.74-328.581.9400-87.58000.1980-0.7270
9318.03-318.551.6500-82.80000.1980-0.7270
3303.34-303.481.2700-3.37000.1980-0.4100
3308.35-308.481.4000-3.80000.1980-0.4100
2298.31-298.451.1500-3.05000.1980-0.4100
(Emim)(Ac)9298.100.0100-1.99980.1890-0.4280[52]
8323.100.0499-1.99960.2030-0.3900
8348.10-348.200.0501-1.99960.1570-0.3210
(Emim)(TfO)11303.850.8000-14.90000.1794-0.6268[53]
11314.051.0000-21.00000.1794-0.6268
11324.151.1500-27.00000.1794-0.6268
11334.351.3000-32.60000.1794-0.6268
11344.551.5500-37.80000.1794-0.6268
(Bmim)(TfO)13303.850.8500-16.00000.2182-0.6720
13314.051.0200-22.00000.2182-0.6720
13324.151.1500-27.40000.2182-0.6720
13334.351.3500-32.40000.2182-0.6720
13344.551.9000-37.50000.2182-0.6720
(Omim)(TfO)13303.850.6800-18.00000.2166-0.7414
13314.050.8000-22.00000.2166-0.7414
13324.151.0800-25.80000.2166-0.7414
13334.351.3500-29.80000.2166-0.7414
13344.551.6500-34.00000.2166-0.7414
(Emim)(Tf2N)12344.403.0600-43.20000.2330-0.7610[54]
12334.202.6600-36.50000.2330-0.7610
12324.002.2000-30.90000.2330-0.7610
12313.901.8300-25.30000.2330-0.7610
12303.701.5300-18.80000.2330-0.7610
22292.90-295.401.2200-17.06000.2330-0.8032
13303.70-303.901.8400-22.45000.3970-0.8032
13313.902.1400-28.07000.3970-0.8032
13324.002.4500-33.35000.3970-0.8032
13334.202.9200-38.25000.3970-0.8032
13344.403.6400-42.80000.3970-0.8032
(Hmim)(Tf2N)18303.701.4000-20.40000.3221-0.8333
18313.901.7500-25.30000.3221-0.8333
18324.002.1000-30.20000.3221-0.8333
18334.202.5200-34.50000.3221-0.8333
18344.402.9600-39.00000.3221-0.8333
(Omim)(Tf2N)7297.40-298.801.2300-14.80000.3762-0.8456
9299.80-301.300.6800-6.70000.3019-0.8120
16303.700.7200-17.00000.3019-0.8456
16313.900.8200-22.00000.3019-0.8456
16324.000.9600-26.00000.3019-0.8456
16334.201.2800-30.70000.3019-0.8456
16344.401.6000-34.80000.3019-0.8456
(HMIM)(Tf2N)8303.150.4200-11.49000.1650-0.8240[55]
8313.150.5800-18.27000.1650-0.8240
8323.150.6700-22.63000.1650-0.8240
8333.150.8000-27.80000.1650-0.8240
8343.150.9600-31.27000.1650-0.8240
8353.151.0900-36.63000.1650-0.8240
8363.151.2400-42.89000.1650-0.8240
8373.151.3800-45.28000.1650-0.8240
(HMIM)(TfO)8303.151.4200-67.97000.2670-0.8160
8313.151.7600-73.95000.2670-0.8160
8323.152.2500-78.00000.2670-0.8160
8333.152.6500-81.73000.2670-0.8160
8343.153.1000-86.12000.2670-0.8160
8353.153.6600-89.89000.2670-0.8160
8363.154.0200-95.31000.2670-0.8160
8373.154.4600-100.12000.2670-0.8160
(HMIM)(BF4)6303.151.2000-8.77000.2120-0.6220
6313.151.5300-16.20000.2120-0.6220
6323.151.9300-22.28000.2120-0.6220
6333.152.3200-27.16000.2120-0.6220
6343.152.6800-32.26000.2120-0.6220
6353.153.1400-36.05000.2120-0.6220
6363.153.4700-39.35000.2120-0.6220
6373.153.7600-41.69000.2120-0.6220
(Hmim)(PF6)6303.150.3000-26.54000.2160-0.6910
6313.150.5300-34.01000.2160-0.6910
6323.150.8600-39.52000.2160-0.6910
6333.151.2200-43.91000.2160-0.6910
6343.151.5300-47.47000.2160-0.6910
6353.151.7200-50.25000.2160-0.6910
6363.151.9400-53.28000.2160-0.6910
6373.152.1900-55.63000.2160-0.6910
(HMIM)(NTf2)3273.150.3990-2.47900.1852-0.6425[56]
4293.150.4270-4.15500.6555-0.1401
4313.150.4460-4.35100.1095-0.5665
3333.151.2340-4.47100.2153-0.4921
3353.151.2610-4.54700.2454-0.4393
3373.151.2810-4.60300.1632-0.3966
3393.151.2980-4.64300.1455-0.3683
3413.151.3110-4.67400.1342-0.3481
(Emim)(SCN)9303.151.3000-74.41000.1690-0.4740[57]
9313.151.6800-79.53000.1690-0.4740
9323.151.9800-83.90000.1690-0.4740
9333.152.4000-88.00000.1690-0.4740
9343.152.8500-90.46000.1690-0.4740
9353.153.3700-93.00000.1690-0.4740
9363.153.8900-94.40000.1690-0.4740
9373.154.4700-95.34000.1690-0.4740
(Emim)(N(CN)2)10303.150.8800-61.08000.1710-0.5850
10313.151.0600-67.48000.1710-0.5850
10323.151.3400-73.22000.1710-0.5850
10333.151.5700-78.78000.1710-0.5850
10343.151.9000-83.67000.1710-0.5850
10353.152.2800-88.15000.1710-0.5850
10363.152.5800-92.29000.1710-0.5850
10373.152.8900-96.20000.1710-0.5850
(Emim)(C(CN)3)10303.150.5900-46.96000.1700-0.7030
10313.150.9100-54.24000.1700-0.7030
10323.151.2100-60.31000.1700-0.7030
10333.151.4100-66.77000.1700-0.7030
10343.151.6500-72.85000.1700-0.7030
10353.151.9500-78.44000.1700-0.7030
10363.152.2100-83.49000.1700-0.7030
10373.152.4300-88.29000.1700-0.7030
(Omim)(Tf2N)5303.150.4147-1.58930.1380-0.4012[58]
5313.150.4405-1.69220.1297-0.3846
5323.150.4649-1.79090.1227-0.3685
5333.150.4880-1.88560.1170-0.3562
5343.150.5101-1.97600.1123-0.3445
5353.150.5314-2.06280.1087-0.3433
(P(14)666)(DCA)5298.00-299.000.7920-2.65400.2250-0.5270[59]
5303.00-304.000.8240-2.77400.2180-0.5170
5313.000.8860-3.00800.2020-0.4980
5322.00-323.000.9370-3.22900.1920-0.4810
(HMMIM)(Tf2N)5298.201.1050-6.34300.2106-0.8014[60]
7303.201.2040-6.64000.1642-0.8014
7308.201.3190-6.87900.1642-0.8014
7313.201.4110-7.07200.1642-0.8014
7318.201.5770-7.19600.1642-0.8014
3323.201.9100-5.49700.2106-0.5991
(BMIM)(BF4)6293.15-293.751.0500-7.30000.1410-0.6100[61]
6303.15-303.851.2000-8.10000.1410-0.6100
6313.25-314.051.3900-10.50000.1410-0.6100
|6322.65-324.151.5800-14.10000.1410-0.6100
6333.05-333.951.7800-16.20000.1410-0.6100
6342.75-343.752.0300-18.85000.1410-0.6100
6352.05-354.252.4100-22.33000.1410-0.6100
6362.85-363.152.7200-24.60000.1410-0.6100
5373.15-373.453.0300-19.80000.1410-0.5000
5382.95-383.153.8000-23.50000.1410-0.5000
(BMIM)(SCN)4292.35-293.651.0500-4.35000.1260-0.2960
5302.55-303.351.3100-5.50000.1260-0.3370
6312.75-313.651.6000-9.90000.1260-0.4300
6322.75-324.651.9200-12.80000.1260-0.4300
6332.95-333.652.3100-16.70000.1260-0.4300
6342.55-344.152.6800-20.50000.1260-0.4300
6352.85-353.553.0500-24.20000.1260-0.4300
6361.45-363.353.5500-27.50000.1260-0.4300
6372.55-373.354.0800-31.50000.1260-0.4300
5381.95-384.154.4600-12.11000.1260-0.3370
(BMP)(Tf2N)9303.150.6800-35.16000.2276-0.8029[62]
9313.150.9900-39.34000.2276-0.8029
9323.151.2300-44.54000.2276-0.8029
9333.151.4000-48.40000.2276-0.8029
9343.151.5600-52.75000.2276-0.8029
9353.151.8200-56.23000.2276-0.8029
9363.152.0400-59.44000.2276-0.8029
9373.152.2600-62.77000.2276-0.8029
(EMIM)(Ac)8303.150.4500-5.87000.2950-0.5750[63]
8313.150.5700-7.63000.2950-0.5750
8323.150.7400-9.46000.2950-0.5750
8333.150.9300-11.82000.2950-0.5750
8343.151.1800-14.61000.2950-0.5750
8353.151.4400-17.85000.2950-0.5750
8363.151.7000-20.96000.2950-0.5750
8373.152.0100-24.64000.2950-0.5750
(TBMA)(MeSO4)3338.40-338.412.4500-8.02900.1530-0.3680[64]
3343.29-343.442.6100-8.57400.1530-0.3680
3348.36-348.482.7600-9.17400.1530-0.3680
3353.35-353.532.9300-9.74100.1530-0.3680
3358.43-358.563.0800-10.33700.1530-0.3680
3363.41-363.503.1960-10.95300.1530-0.3680
3368.41-368.633.4010-11.52800.1530-0.3680
(P14,6,6,6)(Tf2N)10293.35-296.551.4300-6.99000.3603-0.8258[65]
10303.15-304.450.6400-8.27000.3603-0.8258
10313.05-314.950.7200-10.45000.3603-0.8258
10322.95-324.350.7900-12.47000.3603-0.8258
10333.15-335.150.9000-14.72000.3603-0.8258
10343.35-345.051.0100-16.60000.3603-0.8258
10353.45-355.451.1300-18.64000.3603-0.8258
10363.15-365.151.2400-20.36000.3603-0.8258
10372.65-375.351.3700-22.20000.3603-0.8258
(Bmim)(Cl)9353.152.4540-29.36400.1306-0.4060[66]
9358.152.5250-31.19000.1306-0.4060
9363.152.6670-33.01700.1306-0.4060
9368.152.8090-34.94700.1306-0.4060
9373.152.9690-36.94600.1306-0.4060
(bmmim)(Tf2N)7298.150.5001-1.89970.1270-0.3820[67]
7313.150.5001-1.89970.1000-0.3110
5343.150.9996-1.89970.1250-0.2110
(Emim)(NFBS)5313.151.0050-5.99400.1730-0.5920[68]
(Emim)(BF4)5313.151.9990-5.98600.1760-0.3840
(PMPY)(TF2N)5313.150.7000-1.89970.1370-0.3170[69]
8323.150.7001-1.90080.1180-0.2760
8333.150.6997-1.89960.1000-0.2320
(Omim)(PF6)5303.150.4889-1.45730.1148-0.3149[70]
5313.150.5178-1.53350.1074-0.3071
5323.150.5455-1.61850.1012-0.2961
4333.150.8442-1.69850.1404-0.2875
4343.150.8816-1.77550.1349-0.2804
4353.150.9178-1.85010.1308-0.2752
(Bmim)(BF4)10298.12-298.180.6440-2.12800.1001-0.2753[71]
4313.14-313.161.0350-1.81300.1168-0.1896
6323.13-323.171.0850-2.20100.1040-0.1924
2333.15-333.161.6060-1.92800.1259-0.1477
2348.13-348.151.6640-2.74200.1067-0.1658
(Hmim)(NO3)6293.151.0560-3.20000.1465-0.3539[27]
6303.151.1520-3.49600.1347-0.3285
6313.151.2420-3.77900.1258-0.3115
6323.151.3290-4.04900.1181-0.2983
6333.151.4100-4.29200.1117-0.2873
6343.151.4880-4.56400.1060-0.2752
Table
Table 3. Characteristics and results of the algorithms used in this work.
Table 3. Characteristics and results of the algorithms used in this work.
AlgorithmDescriptionTraining FunctionBest Performance|Δx1%|Training |Δx1%|Testing
Levenberg–MarquartLike the quasi-Newton methods, the Levenberg–Marquardt algorithm is designed to approach second-order training speed without having to compute the Hessian matrix.trainlm0.0364516.0911.36
BFGS Quasi-NewtonThis algorithm requires more computation in each iteration and more storage than the conjugate gradient methods, although it generally converges in fewer iterations. The approximate Hessian must be stored, and its dimensions are n × n, where n is equal to the number of weights and biases in the network.trainbfg0.0387316.6811.96
One-Step SecantThis method is an attempt to bridge the gap between the conjugate gradient algorithms and the quasi-Newton (secant) algorithms. This algorithm does not store the complete Hessian matrix; it assumes that at each iteration, the previous Hessian was the identity matrix.trainoss0.0446217.1214.35
Resilient BackpropagationThe purpose of this algorithm is to eliminate the harmful effects of the magnitudes of the partial derivatives. Only the sign of the derivative can determine the direction of the weight update. The magnitude of the derivative has no effect on the weight update.trainrp0.0443017.6113.88
Scaled Conjugate GradientThis algorithm is based on conjugate directions, but this algorithm does not perform a line search at each iteration.trainscg0.0388016.1812.09
Fletch–Powell Conjugate GradientThe algorithm can train any network as long as its weight, net input, and transfer functions have derivative functions.traincgf0.0387416.2011.99
Polak–Ribiére Conjugate GradientThis routine has performance similar to traincgf. It is difficult to predict which algorithm will perform best for a given problem. The storage requirements for Polak–Ribiére (four vectors) are slightly larger than those for Fletcher–Reeves.traincgp0.0390116.1612.25
Variable Learning RateThis function combines the adaptive learning rate with momentum training. It is invoked in the same way as traingda, except that it has the momentum coefficient as an additional training parameter.traingdx0.0485417.9914.08
Table
Table 4. Results of the 6,n,1 architecture using T, P, Tc and Pc training variables in step 2 (Np: parameters number).
Table 4. Results of the 6,n,1 architecture using T, P, Tc and Pc training variables in step 2 (Np: parameters number).
Training VariablesArchitectureNpRunTraining
(1890 Data Point)		Testing
(105 Data Point)		Predicted
(104 Data Point)
|Δx1%||Δx1%|max|Δx1%||Δx1%|max|Δx1%||Δx1%|max
T, P, Tc and Pc(4,6,2,1)47376.7488.834.3821.193.9418.2
(4,6,3,1)55255.9085.944.3322.003.6819.13
(4,6,4,1)63445.3964.703.0721.143.3513.02
(4,6,5,1)71274.7850.042.9818.312.5413.75
(4,6,6,1)79464.4852.732.9317.222.5114.61
(4,6,7,1)87264.3639.752.5812.162.7113.33
(4,6,8,1)95323.8746.152.4513.452.2910.76
(4,6,9,2)103333.3945.602.6613.722.3912.07
(4,6,10,1)123123.4446.481.9811.092.3612.00
Table
Table 5. Critical properties, acentric factors, and compressibility factors of all the substances used in this study.
Table 5. Critical properties, acentric factors, and compressibility factors of all the substances used in this study.
SystemTcPcωZcRef.
(Bmim)(PF6)719.417.30.79170.2203
(Bmim)(NO3)954.827.30.64360.2224
(Omim)(BF4)737.016.021.02870.231
(Emim)(Tf2N)1249.332.70.21570.2753
(Pmim)(Tf2N)1281.125.60.34440.2521
(Bmim)(Tf2N)1269.927.60.30040.2592
(Bmim)(DCA) 1035.824.40.84190.2017
(HMIm)(Tf2N)1292.823.90.38930.2454
(Hmim)(PF6)764.915.50.86970.2137
(Emim)(Ac)807.129.20.58890.2367
(Emim)(TfO)992.335.80.32550.2765
(Bmim)(TfO)1023.529.50.40460.26
(Omim)(TfO)1088.721.60.57660.2336
(Omim)(Tf2N)1317.821.00.48110.2333
(HMIM)(TfO)1055.625.00.48900.2459[74]
(HMIM)(BF4)690.017.940.96250.2406
(Emim)(SCN)1013.622.30.39310.176
(Emim)(N(CN)2)999.029.10.76610.2095
(Emim)(C(CN)3)1149.424.60.85090.1756
(P(14)666)(DCA)1505.87.71.03190.1388
(HMMIM)(Tf2N)1305.522.20.45780.2374
(BMIM)(BF4)643.220.40.88770.2496
(BMIM)(SCN)1047.419.40.47810.1738
(BMP)(Tf2N)1093.124.30.34670.2802
(TBMA)(MeSO4)966.320.00.68180.2545
(P14,6,6,6)(Tf2N)1536.58.51.56630.1716
(Bmim)(Cl)789.027.90.49140.2415
(bmmim)(Tf2N)1281.125.50.36690.2502
(Emim)(NFBS)993.419.40.42390.2088
(Emim)(BF4)596.223.60.80870.2573
(PMPY)(TF2N)1228.927.50.27230.2645
(Omim)(PF6)810.814.10.93850.2065
(Hmim)(NO3)991.823.20.72420.2135
Table
Table 6. Weights and bias of the optimized ANN architecture for the input to the first hidden layer.
Table 6. Weights and bias of the optimized ANN architecture for the input to the first hidden layer.
jwj1wj2wj3wj4bj
11.3233−0.31851.50810.821−2.1911
2−1.9445−0.6198−0.62210.49881.3147
3−1.76150.1466−1.2828−0.17590.4382
4−1.52231.57260.0288−0.0974−0.4382
5−0.802−0.67541.19551.5074−1.3147
6−1.5749−0.5344−0.3818−1.3746−2.1911
Table
Table 7. Weights and bias of the optimized ANN architecture for the first hidden layer to the second hidden layer.
Table 7. Weights and bias of the optimized ANN architecture for the first hidden layer to the second hidden layer.
jwj1wj2wj3wj4wj5wj6bj
1−0.65271.0697−0.7910.42920.3184−1.19931.9799
2−0.1462−0.09240.99731.09330.2437−1.280914.142
30.3816−0.00830.9227−0.0774−0.29011.6831−0.8485
40.9293−0.03090.9174−1.1957−0.6295−0.6227−0.2828
5−0.0842−0.73761.19420.335−0.1937−1.339−0.2828
6−0.1463−0.9691−0.8425−0.6288−1.14540.7364−0.8485
70.7699−1.3529−0.33180.08580.3403−1.12421.4142
8−0.07160.86651.07220.5021.02180.8475−1.9799
Table
Table 8. Weights and bias of the optimized ANN architecture for the second hidden layer to the output layer.
Table 8. Weights and bias of the optimized ANN architecture for the second hidden layer to the output layer.
jwj1wj2wj3wj4wj5wj6wj7wj8bj
1−0.8092−0.29490.18680.17040.33540.2961−0.1333−0.72050.5039
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Fierro, E.N.; Faúndez, C.A.; Muñoz, A.S.; Cerda, P.I. Application of a Single Multilayer Perceptron Model to Predict the Solubility of CO2 in Different Ionic Liquids for Gas Removal Processes. Processes 2022, 10, 1686. https://doi.org/10.3390/pr10091686

AMA Style

Fierro EN, Faúndez CA, Muñoz AS, Cerda PI. Application of a Single Multilayer Perceptron Model to Predict the Solubility of CO2 in Different Ionic Liquids for Gas Removal Processes. Processes. 2022; 10(9):1686. https://doi.org/10.3390/pr10091686

Chicago/Turabian Style

Fierro, Elías N., Claudio A. Faúndez, Ariana S. Muñoz, and Patricio I. Cerda. 2022. "Application of a Single Multilayer Perceptron Model to Predict the Solubility of CO2 in Different Ionic Liquids for Gas Removal Processes" Processes 10, no. 9: 1686. https://doi.org/10.3390/pr10091686

APA Style

Fierro, E. N., Faúndez, C. A., Muñoz, A. S., & Cerda, P. I. (2022). Application of a Single Multilayer Perceptron Model to Predict the Solubility of CO2 in Different Ionic Liquids for Gas Removal Processes. Processes, 10(9), 1686. https://doi.org/10.3390/pr10091686

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop