Descriptor Representation-Based Guaranteed Cost Control Design Methodology for Polynomial Fuzzy Systems

Abstract

This paper presents a descriptor representation-based guaranteed cost design methodology for polynomial fuzzy systems. This methodology applies the descriptor representation for presenting the closed-loop system of the polynomial fuzzy model with a parallel distributed compensation (PDC) based fuzzy controller. By the utility of descriptor representation, the guaranteed cost control (GCC) design analysis can utilize polynomial fuzzy slack matrices for obtaining less conservative results. The proposed GCC design is presented as the sum-of-squares (SOS) conditions. The application of polynomial fuzzy slack matrices leads to the double fuzzy summation issue in the control design. Accordingly, the copositive relaxation works out the problem well and is adopted in the control design analysis. The GCC design minimizes the upper limit of a predesignated cost function. According to the performance function, two simulation examples are provided to demonstrate the validity of the proposed GCC design. In these two examples, the proposed design obtains superior results.

1. Introduction

In recent decades, the Takagi–Sugeno (T-S) fuzzy model has been quite celebrated for its ability to represent nonlinear dynamical systems [1], and widely discussed in numerous studies [2,3,4]. The parallel distributed compensation (PDC) technique [5] applying the same membership functions of the T-S fuzzy model for the fuzzy controller is usually utilized for the control design of T-S fuzzy systems. It is well known that the control design is expressed as linear matrix inequality (LMI) conditions for T-S fuzzy systems [6]. Moreover, it is mentioned in [7] that the double fuzzy summation (DFS) issue exists in the control design analysis of T-S fuzzy systems with PDC control.

In [8], the T-S fuzzy system relied on the PDC control is transformed as a descriptor representation. The descriptor representation reduced the DFS issue in the PDC-based control design analysis to a single fuzzy summation issue. This way, the number of control design conditions can be dramatically reduced, especially for the T-S fuzzy systems with many fuzzy rules. Because of the great advantage mentioned above, the descriptor representation-based design for T-S fuzzy systems has been done by some research [9,10,11].

Besides the descriptor representation for T-S fuzzy systems, a polynomial form of the T-S fuzzy model was also proposed as the polynomial fuzzy model (PFM) [12]. Instead of only constants in the T-S fuzzy model, polynomials are contained in the system matrices of the PFM. Control design for polynomial fuzzy systems is usually associated with Lyapunov function candidates, which contain polynomial matrices [13,14,15]. Furthermore, the analysis and design conditions for polynomial fuzzy systems are demonstrated in sum-of-squares (SOS) rather than LMIs. During the decade, the polynomial fuzzy system has been widely studied [16,17,18,19,20,21,22,23,24,25,26,27,28]. A typical type of study for PFM-based control systems aims to acquire relaxed stabilization conditions [23,24,25]. The study [26] investigates the observer-based control for positive PFMs with unknown time delay. In [27], to control velocity and position in marine equipment, nonlinear system dynamics are built in a PFM-based structure. Additionally, the descriptor representation-based design has also been applied to polynomial fuzzy control systems [28].

For T-S and polynomial fuzzy systems, different control issues such as $H_{\infty }$ control [18,29,30], robust control [31,32,33], adaptive control [34,35], and optimization control [36,37,38] have been studied. In the optimization control issues, guaranteed cost control (GCC), which minimizes the upper limit of a predesignated cost function, has been applied in diversified fields [39,40,41]. It guarantees the system stability and ensures a performance index value shall never exceed the upper limit. Besides, GCC has also been designed for T-S fuzzy systems [42] and polynomial fuzzy systems [43]. In [44], a descriptor representation-based GCC approach for T-S fuzzy systems is also proposed. Nevertheless, no study contains the GCC design based on the descriptor representation for polynomial fuzzy systems.

This study proposes a descriptor representation-based GCC design methodology for polynomial fuzzy systems. At the beginning of this design methodology, the closed-loop system of PFM applying the PDC-based control is converted into the descriptor representation. By taking advantage of descriptor representation, less conservative results are obtained by introducing fuzzy slack matrices. Because of introducing fuzzy slack matrices, the DFS issue comes about in the control design analysis. Thus, the copositivity relaxation approach is adopted to cope with the DFS issue. The GCC design is represented as an SOS-based optimization problem to minimize the upper limit of a predesignated cost function with a known initial condition. The novelties of this paper are enumerated as follows:

• A descriptor representation-based methodology is proposed for the GCC design of PFM;
• The operation domain is considered in the proposed GCC design for solving the negative highest order term infeasible issue, which frequently happens in the SOS-based GCC design of [43];
• The fuzzy slack matrices are applied to descriptor representation-based GCC design for relaxation.

To the authors’ knowledge, this work is the first study to design GCC for polynomial fuzzy systems based on the descriptor representation. Moreover, the design examples given in this paper demonstrate some superior results compared with the existing design.

Throughout this paper, a matrix $\mathsf{\Omega }\succ 0$ ($\mathsf{\Omega }⪰0$) represents $\mathsf{\Omega }$ is a positive definite (semidefinite) matrix. A function in the form of $x_1^{e_1}{x}_2^{e_2}\cdots x_n^{e_n}$ is defined as a monomial in $\mathit{x}=[x_1{x}_2\cdots$$x_n{]}^T$, where $e_1,e_2,\cdots ,e_n$ are nonnegative integers [45]. The degree of a monomial is $e={\sum }_{j=1}^n{e}_j$. A linear combination of finite monomials with real coefficients is defined as a polynomial. If the polynomial $p\left(\mathit{x}\right)$ is an SOS, it means that there exist polynomials $f_1\left(\mathit{x}\right),f_2\left(\mathit{x}\right),\cdots ,f_m\left(\mathit{x}\right)$ such that $p\left(\mathit{x}\right)={\sum }_{i=1}^m{f}_i^2\left(\mathit{x}\right)$. Manifestly, a SOS $p\left(\mathit{x}\right)$ means $p\left(\mathit{x}\right)\ge 0$ for all $\mathit{x}\in {\mathbb{R}}^n$.

2. Descriptor Representation of the Closed-Loop Polynomial Fuzzy System

Consider the PFM [12] as the following equation:

$$\begin{array}{c}\hfill \mathbf{Model}\mathbf{rule}i\\ \hfill & \mathrm{If}{z}_1\left(t\right)\mathrm{is}{M}_{i1}\mathrm{and}\cdots \mathrm{and}{z}_p\left(t\right)\mathrm{is}{M}_{ip}\hfill \\ \hfill & \mathrm{then}\dot{\mathit{q}}\left(t\right)={\mathit{A}}_i\left(\mathit{q}\left(t\right)\right)\hat{\mathit{q}}\left(\mathit{q}\left(t\right)\right)+{\mathit{B}}_i\left(\mathit{q}\left(t\right)\right)\mathit{u}\left(t\right)\hfill \end{array}$$

(1)

where $i=1,2,\dots ,r$ and $z_i\left(t\right)$ are the premise variables; $r$ denotes the number of model rules; $M_{ij}$ is the membership function that links the ith model rule and jth premise variable; ${\mathit{A}}_i\left(\mathit{q}\left(t\right)\right)\in {\mathbb{R}}^{n\times N}$ and ${\mathit{B}}_i\left(\mathit{q}\left(t\right)\right)\in {\mathbb{R}}^{n\times m}$ are polynomial system matrices in $\mathit{q}\left(t\right)$; $\mathit{q}\left(t\right)\in {\mathbb{R}}^n$ is the state vector; $\mathit{u}\left(t\right)\in {\mathbb{R}}^m$ is the input vector, and $\hat{\mathit{q}}\left(\mathit{q}\left(t\right)\right)\in {\mathbb{R}}^N$ is a column vector whose entries are all monomials in $\mathit{q}\left(t\right)$ such that $\hat{\mathit{q}}\left(\mathit{q}\left(t\right)\right)=0$ iff $\mathit{q}\left(t\right)=0$. The defuzzification output of the PFM (1) can be represented as

$$\dot{\mathit{q}}\left(t\right)=\sum _{i=1}^r{h}_i\left(\mathit{z}\left(t\right)\right)\{{\mathit{A}}_i\left(\mathit{q}\left(t\right)\right)\hat{\mathit{q}}\left(\mathit{q}\left(t\right)\right)+{\mathit{B}}_i\left(\mathit{q}\left(t\right)\right)\mathit{u}\left(t\right)\},$$

(2)

where $\mathit{z}\left(t\right)=[z_1\left(t\right)\cdots z_p\left(t\right)]$ and

$$\begin{array}{cc}\hfill & h_i\left(\mathit{z}\left(t\right)\right)=\frac{{\prod }_{j=1}^p{M}_{ij}\left(z_j\left(t\right)\right)}{{\sum }_{k=1}^r{\prod }_{j=1}^p{M}_{kj}\left(z_j\left(t\right)\right)},\hfill \end{array}$$

with the following properties:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & \sum _{i=1}^r{h}_i\left(\mathit{z}\left(t\right)\right)=1,\hfill \\ \hfill & h_i\left(\mathit{z}\left(t\right)\right)\ge 0\forall i.\hfill \end{array}\right.\end{array}$$

(3)

We presume the PFM (1) is built in the following operation domain containing $\mathit{q}\left(t\right)=0$:

$$D_{op}=\{\mathit{q}\left(t\right):q_k^{min}\le q_k\left(t\right)\le q_k^{max},k=1,\cdots ,n\},$$

(4)

where $q_k^{min}$ and $q_k^{max}$ are the lower and upper bound of the operation domain for the state $q_k\left(t\right)$, respectively. For control design, the PDC-based fuzzy controller sharing the identical membership functions of the PFM (1) is applied:

$$\mathit{u}\left(t\right)=\sum _{i=1}^r{h}_i\left(z\left(t\right)\right){\mathit{F}}_i\left(\mathit{q}\left(t\right)\right)\mathit{q}\left(t\right),$$

(5)

where ${\mathit{F}}_i\left(\mathit{q}\left(t\right)\right)$ is the local feedback gain. In order to turn the fuzzy system into the descriptor representation, the fuzzy controller (1) is altered to

$$0=\sum _{i=1}^r{h}_i\left(z\left(t\right)\right)\{{\mathit{F}}_i\left(\mathit{q}\left(t\right)\right)\mathit{q}\left(t\right)-\mathit{u}\left(t\right)\}.$$

(6)

Moreover, the transformation matrix $\mathit{T}\left(\mathit{q}\right(t\left)\right)$ [28] represents the relevance between $\mathit{q}\left(t\right)$ and $\hat{\mathit{q}}\left(\mathit{q}\left(t\right)\right)$ as

$$\hat{\mathit{q}}\left(\mathit{q}\left(t\right)\right)=\mathit{T}\left(\mathit{q}\left(t\right)\right)\mathit{q}\left(t\right).$$

(7)

Applying (7), the descriptor representation for the closed-loop system of the PFM (2) with the PDC-based fuzzy controller (6) can be obtained as

$${\mathit{E}}^{*}{\dot{\mathit{q}}}^{*}\left(\mathit{q}\left(t\right)\right)=\sum _{i=1}^r{h}_i\left(z\left(t\right)\right){\mathit{A}}_i^{*}\left(\mathit{q}\left(t\right)\right){\mathit{q}}^{*}\left(\mathit{q}\left(t\right)\right),$$

(8)

where

$${\mathit{E}}^{*}=\left[\begin{array}{ccc}\mathit{I}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right],{\mathit{q}}^{*}=\left[\begin{array}{c}\mathit{q}\left(t\right)\\ \hat{\mathit{q}}\left(\mathit{q}\left(t\right)\right)\\ \mathit{u}\left(t\right)\end{array}\right],$$

$${\mathit{A}}_i^{*}\left(\mathit{q}\left(t\right)\right)=\left[\begin{array}{ccc}0& {\mathit{A}}_i\left(\mathit{q}\left(t\right)\right)& {\mathit{B}}_i\left(\mathit{q}\left(t\right)\right)\\ \mathit{T}\left(\mathit{q}\right(t\left)\right)& -\mathit{I}& 0\\ {\mathit{F}}_i\left(\mathit{q}\left(t\right)\right)& 0& -\mathit{I}\end{array}\right].$$

From here on, the notation concerning time t is neglected for conciseness. For instance, $\mathit{q}$ will be used instead of $\mathit{q}\left(t\right)$.

3. Guaranteed Cost Control Design

The objective of this study is to design GCC for the PFM (2) based on the descriptor representation (8). The outputs for the PFM (2) are defined as

$$\mathit{y}=\sum _{i=1}^r{h}_i\left(\mathit{z}\right){\mathit{C}}_i\left(\mathit{q}\right)\hat{\mathit{q}}\left(\mathit{q}\right),$$

(9)

where ${\mathit{C}}_i\left(\mathit{q}\right)\in {\mathbb{R}}^{p\times N}$ are polynomial output matrices. Moreover, the cost function in the following equation is considered:

$$\mathit{J}={\int }_0^{\infty }{\hat{\mathit{y}}}^T\left[\begin{array}{cc}\mathit{W}& 0\\ 0& \mathit{S}\end{array}\right]\hat{\mathit{y}}\mathrm{d}t,$$

(10)

where $\mathit{W}$ and $\mathit{S}$ are positive definite matrices and

$$\hat{\mathit{y}}=\sum _{i=1}^r{h}_i\left(\mathit{z}\right)\left[\begin{array}{c}{\mathit{C}}_i\left(\mathit{q}\right)\\ {-\mathit{F}}_i\left(\mathit{q}\right)\end{array}\right]\hat{\mathit{q}}\left(\mathit{q}\right).$$

(11)

The GCC aims to stabilize the closed-loop polynomial fuzzy system and minimize the upper limit of the cost function (10).

For introducing the Lyapunov function candidate, let $\mathit{K}=k_1,k_2,\cdots ,k_m$ denote the row indices of ${\mathit{B}}_i\left(\mathit{q}\right)$ whose corresponding row is equal to zero, and define $\tilde{\mathit{q}}={[q_{k_1}{q}_{k_2}\cdots q_{k_m}]}^T$. The Lyapunov function candidate applied in this study is given as

$$V\left(\mathit{q}\right)={\mathit{q}}^T{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\mathit{q},$$

(12)

where $\mathit{Q}\left(\tilde{\mathit{q}}\right)$ is a symmetric positive definite polynomial matrix in $\tilde{\mathit{q}}$. In order to apply the descriptor representation (8) for the GCC design, the Lyapunov function candidate (12) is rewritten as

$$V\left(\mathit{q}\right)={\mathit{q}}^T\left(\mathit{q}\right){\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\mathit{q}={\mathit{q}}^{*T}\left(\mathit{q}\right){\mathit{E}}^{*}{\Phi }^{-1}(\mathit{h},\mathit{q}){\mathit{q}}^{*}\left(\mathit{q}\right)$$

(13)

where $\mathit{h}={[h_1\left(\mathit{z}\right)h_2\left(\mathit{z}\right)\cdots h_r\left(\mathit{z}\right)]}^T$,

$$\mathsf{\Phi }(\mathit{h},\mathit{q})=\left[\begin{array}{ccc}\mathit{Q}\left(\tilde{\mathit{q}}\right)& 0& 0\\ {\overline{\mathit{Q}}}_{21}(\mathit{h},\mathit{q})& {\overline{\mathit{Q}}}_{22}(\mathit{h},\mathit{q})& {\overline{\mathit{Q}}}_{23}(\mathit{h},\mathit{q})\\ {\overline{\mathit{Q}}}_{31}(\mathit{h},\mathit{q})& {\overline{\mathit{Q}}}_{32}(\mathit{h},\mathit{q})& {\overline{\mathit{Q}}}_{33}(\mathit{h},\mathit{q})\end{array}\right],$$

(14)

in which

$${\overline{\mathit{Q}}}_{jk}(\mathit{h},\mathit{q})=\sum _{i=1}^r{h}_i\left(\mathit{z}\right){\mathit{Q}}_{jki}\left(\mathit{q}\right),j=2,3,k=1,2,3,$$

(15)

are fuzzy slack matrices and ${\mathit{Q}}_{jki}\left(\mathit{q}\right)$ are polynomial matrices in $\mathit{q}$.

Since the fuzzy slack matrices (15) are introduced for obtaining less conservative results, the problem of DFS appears in the control design analysis. It is well known that copositive relaxation is an efficient method to cope with the DFS issue [19]. The copositive relaxation [45] is described as follows. The copositivity of a given matrix $\mathit{U}=\left[U_{ij}\right]\in {\mathbb{R}}^{r\times r}$ can be verified by checking whether

$${\mathit{w}}^T\mathit{U}\mathit{w}=\sum _{i=1}^r\sum _{j=1}^r{w}_i{w}_j{U}_{ij}\ge 0,$$

(16)

for $\mathit{w}\left(t\right)={[w_1{w}_2\cdots w_r]}^T\in {\mathbb{R}}^r$ and $w_i\ge 0\forall i$. The copositivity checking can be done by writing $w_i={\hat{w}}_i^2$ and examining if

$${\mathit{Y}}^s\left(\hat{\mathit{w}}\right)={\left(\sum _{k=1}^r{\hat{\mathit{w}}}_k^2\right)}^s\sum _{i=1}^r\sum _{j=1}^r{\hat{\mathit{w}}}_i^2{\hat{\mathit{w}}}_j^2{U}_{ij}is\mathit{SOS},$$

(17)

where $\hat{\mathit{w}}={[\widehat{w_1}\widehat{w_2}\cdots \widehat{w_1}]}^T$, and s is a nonnegative integer.

Based on the descriptor representation (8) and the Lyapunov candidate (12), the proposed GCC design is provided in the subsequent theorem.

Theorem 1.

The closed-loop system of the PFM (2) and the PDC-based fuzzy controller (6) with the outputs (11) is asymptotically stable in the operation domain (4). Furthermore, the upper limit of the cost function (10) is minimized if polynomial matrices ${\mathit{M}}_i\left(\mathit{q}\right)$ and ${\mathit{Q}}_{jki}\left(\mathit{q}\right)$, a symmetric polynomial matrix $\mathit{Q}\left(\tilde{\mathit{q}}\right)$ and polynomials ${\sigma }_{ij\delta }\left(\mathit{q}\right)$ exist to be the solutions for the following optimization problem:

$$\underset{\mathit{Q}\left(\tilde{\mathit{q}}\right),{\mathit{M}}_i\left(\mathit{q}\right),{\mathit{Q}}_{jki}\left(\mathit{q}\right),{\sigma }_{ij\delta }\left(\mathit{q}\right)}{min}\lambda \mathrm{subject}\mathrm{to}$$

$${\mathit{v}}_1^T({\hat{\mathit{Q}}}_i\left(\mathit{q}\right)-{ϵ}_1\left(\mathit{q}\right)\mathit{I}){\mathit{v}}_{1}is\mathit{SOS},i=1,\cdots ,r,$$

(18)

$${\sigma }_{ij\delta }\left(\mathit{q}\right)is\mathit{SOS},i,j=1,\cdots ,r,\delta =1,\cdots ,n,$$

(19)

$$-{\left(\sum _{k=1}^r{\hat{h}}_k^2\right)}^s\sum _{i=1}^r\sum _{j=1}^r{\hat{h}}_i^2{\hat{h}}_j^2{\mathit{v}}_2^T{\mathit{N}}_{ij}\left(\mathit{q}\right){\mathit{v}}_{2}is\mathit{SOS},$$

(20)

$${\mathit{v}}_3^T\left[\begin{array}{cc}\lambda & {\mathit{q}}^T\left(0\right)\\ \mathit{q}\left(0\right)& {\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\left(0\right)\right)\end{array}\right]{\mathit{v}}_{3}is\mathit{SOS},$$

(21)

where ${\mathit{v}}_1$, ${\mathit{v}}_2$ and ${\mathit{v}}_3$ are vectors being independent of $\mathit{q}$; s is a nonnegative integer; polynomial ${ϵ}_1\left(\mathit{q}\right)>0$ for $\mathit{q}\ne 0$, and

$${\hat{\mathit{Q}}}_i\left(\mathit{q}\right)=\left[\begin{array}{ccc}\mathit{Q}\left(\tilde{\mathit{q}}\right)& 0& 0\\ {\mathit{Q}}_{21i}\left(\mathit{q}\right)& {\mathit{Q}}_{22i}\left(\mathit{q}\right)& {\mathit{Q}}_{23i}\left(\mathit{q}\right)\\ {\mathit{Q}}_{31i}\left(\mathit{q}\right)& {\mathit{Q}}_{32i}\left(\mathit{q}\right)& {\mathit{Q}}_{33i}\left(\mathit{q}\right)\end{array}\right]$$

$$\begin{gathered} \begin{array}{c}{\mathit{N}}_{ij}\left(\mathit{q}\right)=\hfill \\ \left[\begin{array}{cc}\left(\begin{array}{c}{\mathit{A}}_j\left(\mathit{q}\right){\mathit{Q}}_{21i}\left(\mathit{q}\right)+{\mathit{B}}_j\left(\mathit{q}\right){\mathit{Q}}_{31i}\left(\mathit{q}\right)\\ +{\mathit{Q}}_{21i}^T\left(\mathit{q}\right){\mathit{A}}_j^T\left(\mathit{q}\right)+{\mathit{Q}}_{31i}^T\left(\mathit{q}\right){\mathit{B}}_j^T\left(\mathit{q}\right)\\ -\sum _{k\in K}\frac{\partial \mathit{Q}}{\partial {\mathit{q}}_k}\left(\tilde{\mathit{q}}\right){\mathit{A}}_j^k\left(\mathit{q}\right)\hat{\mathit{q}}\left(\mathit{q}\right)\\ -\sum _{\delta =1}^n{\sigma }_{ij\delta }\left(\mathit{q}\right)O_{\delta }\left(\mathit{q}\right)\mathit{I}+{ϵ}_{2ij}\left(\mathit{q}\right)\mathit{I}\end{array}\right)& \left(\begin{array}{c}{\mathit{Q}}^T\left(\tilde{\mathit{q}}\right){\mathit{T}}^T\left(\mathit{q}\right)-{\mathit{Q}}_{21i}^T\left(\mathit{q}\right)+\\ {\mathit{A}}_j\left(\mathit{q}\right){\mathit{Q}}_{22i}\left(\mathit{q}\right)+{\mathit{B}}_j\left(\mathit{q}\right){\mathit{Q}}_{32i}\left(\mathit{q}\right)\end{array}\right)\\ \\ \left(\begin{array}{c}\mathit{T}\left(\mathit{q}\right)\mathit{Q}\left(\tilde{\mathit{q}}\right)-{\mathit{Q}}_{21i}\left(\mathit{q}\right)+\\ {\mathit{Q}}_{22i}^T\left(\mathit{q}\right){\mathit{A}}_j^T\left(\mathit{q}\right)+{\mathit{Q}}_{32i}^T\left(\mathit{q}\right){\mathit{B}}_j^T\left(\mathit{q}\right)\end{array}\right)& (-{\mathit{Q}}_{22i}\left(\mathit{q}\right)-{\mathit{Q}}_{22i}^T\left(\mathit{q}\right))\\ \\ \left(\begin{array}{c}{\mathit{M}}_j\left(\mathit{q}\right)-{\mathit{Q}}_{31i}\left(\mathit{q}\right)+\\ {\mathit{Q}}_{23i}^T\left(\mathit{q}\right){\mathit{A}}_j^T\left(\mathit{q}\right)+{\mathit{Q}}_{33i}^T\left(\mathit{q}\right){\mathit{B}}_j^T\left(\mathit{q}\right)\end{array}\right)& (-{\mathit{Q}}_{32i}\left(\mathit{q}\right)-{\mathit{Q}}_{23i}^T\left(\mathit{q}\right))\\ \\ {\mathit{C}}_j\left(\mathit{q}\right){\mathit{Q}}_{21i}\left(\mathit{q}\right)& {\mathit{C}}_j\left(\mathit{q}\right){\mathit{Q}}_{22i}\left(\mathit{q}\right)\\ \\ {\mathit{M}}_j\left(\mathit{q}\right)& 0\end{array}\right.\hfill \end{array} \\ \left.\begin{array}{ccccc}& & \left(\begin{array}{c}{\mathit{M}}_j^T\left(\mathit{q}\right)-{\mathit{Q}}_{31i}^T\left(\mathit{q}\right)+\\ {\mathit{A}}_j\left(\mathit{q}\right){\mathit{Q}}_{23i}\left(\mathit{q}\right)+{\mathit{B}}_j\left(\mathit{q}\right){\mathit{Q}}_{33i}\left(\mathit{q}\right)\end{array}\right)& {\mathit{Q}}_{21i}^T\left(\mathit{q}\right){\mathit{C}}_j^T\left(\mathit{q}\right)& {\mathit{M}}_j^T\left(\mathit{q}\right)\\ \\ & & -{\mathit{Q}}_{32i}^T\left(\mathit{q}\right)-{\mathit{Q}}_{23i}\left(\mathit{q}\right)& {\mathit{Q}}_{22i}^T\left(\mathit{q}\right){\mathit{C}}_j^T\left(\mathit{q}\right)& 0\\ \\ & & -{\mathit{Q}}_{33i}\left(\mathit{q}\right)-{\mathit{Q}}_{33i}^T\left(\mathit{q}\right)& {\mathit{Q}}_{23i}^T\left(\mathit{q}\right){\mathit{C}}_j^T\left(\mathit{q}\right)& 0\\ \\ & & {\mathit{C}}_j\left(\mathit{q}\right){\mathit{Q}}_{23i}\left(\mathit{q}\right)& -{\mathit{W}}^{-1}& 0\\ \\ & & 0& 0& -{\mathit{S}}^{-1}\end{array}\right] \end{gathered}$$

in which ${ϵ}_{2ij}\left(\mathit{q}\right)$ > 0 for $\mathit{q}\ne 0$ and

$$O_{\delta }\left(\mathit{q}\right)=(q_{\delta }-q_{\delta }^{max})(q_{\delta }-q_{\delta }^{min}),\delta =1,\cdots ,n.$$

Moreover, the local feedback gains of the PDC-based fuzzy controller (5) achieving the GCC can be designed as ${\mathit{F}}_j\left(\mathit{q}\right)={\mathit{M}}_j\left(\mathit{q}\right){\mathit{Q}}^{-1}\left(\mathit{q}\right)$.

Proof of Theorem 1.

Considering the Lyapunov candidate (12) for which $\mathit{Q}\left(\tilde{\mathit{q}}\right)$ being positive definite is guaranteed if (18) holds. The time derivative of $V\left(\mathit{q}\right)$ is obtained as the following equation:

$$\begin{array}{cc}\hfill \dot{V}\left(\mathit{q}\right)& ={\dot{\mathit{q}}}^T{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\mathit{q}+{\mathit{q}}^T{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\dot{\mathit{q}}+{\mathit{q}}^T{\dot{\mathit{Q}}}^{-1}\left(\tilde{\mathit{q}}\right)\mathit{q}\hfill \\ \hfill & ={\dot{\mathit{q}}}^T{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\mathit{q}+{\mathit{q}}^T{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\dot{\mathit{q}}+{\mathit{q}}^T\sum _{k=1}^n\frac{\partial {\mathit{Q}}^{-1}}{\partial q_k}\left(\tilde{\mathit{q}}\right){\dot{\mathit{q}}}_k.\hfill \end{array}$$

(22)

Let ${\mathit{A}}_i^k\left(\mathit{q}\left(t\right)\right)$ expresses the kth row of ${\mathit{A}}_i\left(\left(\mathit{q}\left(t\right)\right)\right)$. Since $\mathit{K}$ denotes the row indices of ${\mathit{B}}_i\left(\mathit{q}\right)$ whose corresponding row is equivalent to zero, it can be obtained that

$${\dot{\mathit{q}}}_k=\sum _{i=1}^r{h}_i\left(z\right){\mathit{A}}_i^k\left(\mathit{q}\right)\hat{\mathit{q}}\left(\mathit{q}\right)$$

(23)

for $k\in \mathit{K}$, and

$$\frac{\partial {\mathit{Q}}^{-1}}{\partial q_i}\left(\tilde{\mathit{q}}\right)=0$$

(24)

for $i\notin \mathit{K}$. Furthermore, due to ${\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\mathit{Q}\left(\tilde{\mathit{q}}\right)=\mathit{I}$, the following equation holds [12]:

$$\frac{\partial {\mathit{Q}}^{-1}}{\partial q_k}\left(\tilde{\mathit{q}}\right)=-{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\frac{\partial \mathit{Q}}{\partial q_k}\left(\tilde{\mathit{q}}\right){\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)$$

(25)

By applying (14) with (22)–(25), we can rewrite the time derivative of $\dot{V}\left(\mathit{q}\right)$ as

$$\begin{array}{cc}\hfill \dot{V}\left(\mathit{q}\right)& ={\dot{\mathit{q}}}^{*T}\left(\mathit{q}\right){\mathit{E}}^{*}{\mathsf{\Phi }}^{-1}(\mathit{h},\mathit{q}){\mathit{q}}^{*}\left(\mathit{q}\right)+{\mathit{q}}^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-T}(\mathit{h},\mathit{q}){\mathit{E}}^{*}{\dot{\mathit{q}}}^{*}\left(\mathit{q}\right)-\hfill \\ \hfill & {\mathit{q}}^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-T}(\mathit{h},\mathit{q})\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathsf{\Gamma }}_j\left(\mathit{q}\right){\Phi }^{-1}\left(\mathit{h},\mathit{q}\right){\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \\ \hfill & =\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathit{q}}^{*T}\left(\mathit{q}\right){\mathit{A}}_j^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right){\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \\ \hfill & +{\mathit{q}}^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right)\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathit{A}}_j^{*}\left(\mathit{q}\right){\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \\ \hfill & -{\mathit{q}}^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right)\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathsf{\Gamma }}_j\left(\mathit{q}\right){\Phi }^{-1}\left(\mathit{h},\mathit{q}\right){\mathit{q}}^{*}\left(\mathit{q}\right),\hfill \end{array}$$

(26)

where

$${\mathsf{\Gamma }}_j\left(\mathit{q}\right)=\left[\begin{array}{ccc}\sum _{k\in K}\frac{\partial Q}{\partial q_k}\left(\tilde{\mathit{q}}\right){\mathit{A}}_j^k\left(\mathit{q}\right)\hat{\mathit{q}}\left(\mathit{q}\right)& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right].$$

From (11) and (26), it can be obtained that

$$\begin{array}{cc}\hfill & \dot{V}\left(\mathit{q}\right)+{\hat{\mathit{y}}}^T\left[\begin{array}{cc}\mathit{W}& 0\\ 0& \mathit{S}\end{array}\right]\hat{\mathit{y}}\hfill \\ \hfill & =\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathit{q}}^{*T}\left(\mathit{q}\right)[{\mathit{A}}_j^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)\hfill \\ \hfill & +{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathit{A}}_j^{*}\left(\mathit{q}\right)-{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathsf{\Gamma }}_j\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)]{\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \\ \hfill & +\sum _{i=1}^r\sum _{j=1}^r{h}_i\left(\mathit{z}\right)h_j\left(\mathit{z}\right){\hat{\mathit{q}}}^T\left(\mathit{q}\right)[{\mathit{C}}_i^T\left(\mathit{q}\right)\mathit{W}{\mathit{C}}_j\left(\mathit{q}\right)+{\mathit{F}}_i^T\left(\mathit{q}\right)\mathit{S}{\mathit{F}}_j\left(\mathit{q}\right)]\hat{\mathit{q}}\left(\mathit{q}\right)\hfill \\ \hfill & =\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathit{q}}^{*T}\left(\mathit{q}\right)[{\mathit{A}}_j^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)\hfill \\ \hfill & +{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathit{A}}_j^{*}\left(\mathit{q}\right)-{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathsf{\Gamma }}_j\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)]{\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \\ \hfill & +\sum _{i=1}^r\sum _{j=1}^r{h}_i\left(\mathit{z}\right)h_j\left(\mathit{z}\right){\mathit{q}}^{*T}\left(\mathit{q}\right)[{\mathit{C}}_i^{*T}\left(\mathit{q}\right)\mathit{W}{\mathit{C}}_j^{*}\left(\mathit{q}\right)+{\mathit{F}}_i^{*T}\left(\mathit{q}\right)\mathit{S}{\mathit{F}}_j^{*}\left(\mathit{q}\right)]{\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \\ \hfill & \le \sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathit{q}}^{*T}\left(\mathit{q}\right)[{\mathit{A}}_j^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)\hfill \\ \hfill & +{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathit{A}}_j^{*}\left(\mathit{q}\right)-{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathsf{\Gamma }}_j\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)]{\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \\ \hfill & +\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathit{q}}^{*T}\left(\mathit{q}\right)[{\mathit{C}}_j^{*T}\left(\mathit{q}\right)\mathit{W}{\mathit{C}}_j^{*}\left(\mathit{q}\right)+{\mathit{F}}_j^{*T}\left(\mathit{q}\right)\mathit{S}{\mathit{F}}_j^{*}\left(\mathit{q}\right)]{\mathit{q}}^{*}\left(\mathit{q}\right)\hfill \end{array}$$

(27)

where

$${\mathit{C}}_j^{*}\left(\mathit{q}\right)=\left[\begin{array}{ccc}0& {\mathit{C}}_j\left(\mathit{q}\right)& 0\end{array}\right],{\mathit{F}}_j^{*}\left(\mathit{q}\right)=\left[\begin{array}{ccc}{\mathit{F}}_j\left(\mathit{q}\right)& 0& 0\end{array}\right].$$

(28)

Moreover, in the operation domain $D_{op}$ (4), the following inequality is fulfilled:

$$\begin{array}{cc}\hfill \upsilon (\mathit{h},\mathit{q})=& -\sum _{i=1}^r\sum _{j=1}^r\sum _{\delta =1}^n{h}_i\left(\mathit{z}\right)h_j\left(\mathit{z}\right){\sigma }_{ij\delta }\left(\mathit{q}\right)O_{\delta }\left(\mathit{q}\right)\ge 0\hfill \end{array}$$

(29)

where ${\sigma }_{ij\delta }\left(\mathit{q}\right)\ge 0$ being guaranteed by (19). Let

$$\mathsf{{\rm Y}}(\mathit{h},\mathit{q})=\left[\begin{array}{ccc}(\upsilon (\mathit{h},\mathit{q})+{ϵ}_2(\mathit{h},\mathit{q}))\mathit{I}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right].$$

where ${ϵ}_2(\mathit{h},\mathit{q})={\sum }_{i=1}^r{\sum }_{j=1}^r{h}_i\left(\mathit{z}\right)h_j\left(\mathit{z}\right){ϵ}_{2ij}\left(\mathit{q}\right)$ and ${ϵ}_{2ij}\left(\mathit{q}\right)>0$ for $\mathit{q}\ne 0$. From the membership function property (3), we have ${ϵ}_2(\mathit{h},\mathit{q})>0$ for $\mathit{q}\ne 0$. Since $\mathit{Q}\left(\tilde{\mathit{q}}\right)$ is a symmetric positive definite matrix and (29) holds in $D_{op}$, the following inequality holds for $D_{op}-\left\{0\right\}$:

$$-{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)(\upsilon (\mathit{h},\mathit{q})+{ϵ}_2(\mathit{h},\mathit{q}))\mathit{I}{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)<0.$$

(30)

By (30), the following inequality holds for $D_{op}-\left\{0\right\}$:

$$\dot{V}\left(\mathit{q}\right)+{\hat{\mathit{y}}}^T\left[\begin{array}{cc}\mathit{W}& 0\\ 0& \mathit{S}\end{array}\right]\hat{\mathit{y}}<0$$

(31)

if

$$\dot{V}\left(\mathit{q}\right)+{\hat{\mathit{y}}}^T\left[\begin{array}{cc}\mathit{W}& 0\\ 0& \mathit{S}\end{array}\right]\hat{\mathit{y}}\le -{\mathit{q}}^T{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)(\upsilon (\mathit{h},\mathit{q})+{ϵ}_2(\mathit{h},\mathit{q}))\mathit{I}{\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\right)\mathit{q}.$$

(32)

The inequality (32) can be rewritten as

$$\dot{V}\left(\mathit{q}\right)+{\hat{\mathit{y}}}^T\left[\begin{array}{cc}\mathit{W}& 0\\ 0& \mathit{S}\end{array}\right]\hat{\mathit{y}}+{\mathit{q}}^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-T}(\mathit{h},\mathit{q})\mathsf{{\rm Y}}(\mathit{h},\mathit{q}){\mathsf{\Phi }}^{-1}(\mathit{h},\mathit{q}){\mathit{q}}^{*}\left(\mathit{q}\right)\le 0.$$

(33)

According to (27), the inequality (33) holds if

$$\begin{array}{cc}\hfill & {\mathit{q}}^{*T}\left\{\sum _{j=1}^r{h}_j\left(\mathit{z}\right)[{\mathit{A}}_j^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)+{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathit{A}}_j^{*}\left(\mathit{q}\right)-{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathsf{\Gamma }}_j\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)]\right.\hfill \\ \hfill & +\left.\sum _{j=1}^r{h}_j\left(\mathit{z}\right)[{\mathit{C}}_j^{*T}\left(\mathit{q}\right)\mathit{W}{\mathit{C}}_j^{*}\left(\mathit{q}\right)+{\mathit{F}}_j^{*T}\left(\mathit{q}\right)\mathit{S}{\mathit{F}}_j^{*}\left(\mathit{q}\right)]+{\mathsf{\Phi }}^{-T}(\mathit{h},\mathit{q})\mathsf{{\rm Y}}(\mathit{h},\mathit{q}){\mathsf{\Phi }}^{-1}(\mathit{h},\mathit{q})\right\}{\mathit{q}}^{*}\le 0\hfill \end{array}$$

(34)

which is able to be guaranteed by

$$\begin{array}{cc}\hfill & \sum _{j=1}^r{h}_j\left(\mathit{z}\right)[{\mathit{A}}_j^{*T}\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)+{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathit{A}}_j^{*}\left(\mathit{q}\right)-{\mathsf{\Phi }}^{-T}\left(\mathit{h},\mathit{q}\right){\mathsf{\Gamma }}_j\left(\mathit{q}\right){\mathsf{\Phi }}^{-1}\left(\mathit{h},\mathit{q}\right)]\hfill \\ \hfill & +\sum _{j=1}^r{h}_j\left(\mathit{z}\right)[{\mathit{C}}_j^{*T}\left(\mathit{q}\right)\mathit{W}{\mathit{C}}_j^{*}\left(\mathit{q}\right)+{\mathit{F}}_j^{*T}\left(\mathit{q}\right)\mathit{S}{\mathit{F}}_j^{*}\left(\mathit{q}\right)]+{\mathsf{\Phi }}^{-T}(\mathit{h},\mathit{q})\mathsf{{\rm Y}}(\mathit{h},\mathit{q}){\mathsf{\Phi }}^{-1}(\mathit{h},\mathit{q})\le 0\hfill \end{array}$$

(35)

Multiply (35) from left and right sides by ${\mathsf{\Phi }}^T(\mathit{h},\mathit{q})$ and $\mathsf{\Phi }(\mathit{h},\mathit{q})$ respectively, it is obtained that

$$\begin{array}{cc}\hfill & \sum _{j=1}^r{h}_j\left(\mathit{z}\right)[{\mathsf{\Phi }}^T(\mathit{h},\mathit{q}){\mathit{A}}_j^{*T}\left(\mathit{q}\right)+{\mathit{A}}_j^{*}\left(\mathit{q}\right)\mathsf{\Phi }(\mathit{h},\mathit{q})-{\mathsf{\Gamma }}_j\left(\mathit{q}\right)]\hfill \\ \hfill & +\sum _{j=1}^r{h}_j\left(\mathit{z}\right){\mathsf{\Phi }}^T(\mathit{h},\mathit{q})[{\mathit{C}}_j^{*T}\left(\mathit{q}\right)\mathit{W}{\mathit{C}}_j^{*}\left(\mathit{q}\right)+{\mathit{F}}_j^{*T}\left(\mathit{q}\right)\mathit{S}{\mathit{F}}_j^{*}\left(\mathit{q}\right)]\mathsf{\Phi }(\mathit{h},\mathit{q})+\mathsf{{\rm Y}}(\mathit{h},\mathit{q})\le 0\hfill \end{array}$$

(36)

which is equivalent to

$$\begin{array}{cc}\hfill & -\sum _{j=1}^r{h}_j\left(\mathit{z}\right)[{\mathsf{\Phi }}^T(\mathit{h},\mathit{q}){\mathit{A}}_j^{*T}\left(\mathit{q}\right)+{\mathit{A}}_j^{*}\left(\mathit{q}\right)\mathsf{\Phi }(\mathit{h},\mathit{q})-{\mathsf{\Gamma }}_j\left(\mathit{q}\right)]-\mathsf{{\rm Y}}(\mathit{h},\mathit{q})\hfill \\ \hfill & -\sum _{j=1}^r{h}_j\left(\mathit{z}\right)\left[\begin{array}{cc}{\mathsf{\Phi }}^T(\mathit{h},\mathit{q}){\mathit{C}}_j^{*T}\left(\mathit{q}\right)& {\mathsf{\Phi }}^T(\mathit{h},\mathit{q}){\mathit{F}}_j^{*T}\left(\mathit{q}\right)\end{array}\right]\left[\begin{array}{cc}\mathit{W}& 0\\ 0& \mathit{S}\end{array}\right]\left[\begin{array}{c}{\mathit{C}}_j^{*}\left(\mathit{q}\right)\mathsf{\Phi }(\mathit{h},\mathit{q})\\ {\mathit{F}}_j^{*}\left(\mathit{q}\right)\mathsf{\Phi }(\mathit{h},\mathit{q})\end{array}\right]\ge 0\hfill \end{array}$$

(37)

Applying Schur complement and letting ${\mathit{M}}_j\left(\mathit{q}\right)={\mathit{F}}_j\left(\mathit{q}\right)\mathit{Q}\left(\tilde{\mathit{q}}\right)$, the inequality (37) holds if

$$\sum _{i=1}^r\sum _{j=1}^r{h}_i\left(\mathit{z}\right)h_j\left(\mathit{z}\right)(-{\mathit{N}}_{ij}\left(\mathit{q}\right))\ge 0$$

(38)

which is able to be guaranteed by

$$\sum _{i=1}^r\sum _{j=1}^r{h}_i\left(\mathit{z}\right)h_j\left(\mathit{z}\right){\mathit{v}}_2^T(-{\mathit{N}}_{ij}\left(\mathit{q}\right)){\mathit{v}}_2\ge 0,\forall {\mathit{v}}_2\in {\mathbb{R}}^{2n+2m+p}.$$

(39)

Through the copositive relaxation (16) and (17), the condition (38) is fulfilled by (20). As a short summary, if the solutions are found to satisfy (20), then (31) holds for $D_{op}-\left\{0\right\}$. Since $\mathit{W}$ and $\mathit{S}$ are positive definite matrices, the condition (31) holding for $D_{op}-\left\{0\right\}$ implies $\dot{V}\left(\mathit{q}\right)<0$ for $D_{op}-\left\{0\right\}$. Therefore, the closed-loop system of the PFM (2) with the PDC-based fuzzy controller (6) is asymptotically stable. Furthermore, it is noted that (31) is equivalent to

$${\hat{\mathit{y}}}^T\left[\begin{array}{cc}\mathit{W}& \mathit{0}\\ \mathit{0}& \mathit{S}\end{array}\right]\hat{\mathit{y}}<-\dot{V}\left(\mathit{q}\right).$$

(40)

Since the system is asymptotically stable, by integrating the condition (40) from 0 to ∞, it can be obtained that

$$\mathit{J}={\int }_0^{\infty }{\hat{\mathit{y}}}^T\left[\begin{array}{cc}\mathit{W}& 0\\ 0& \mathit{S}\end{array}\right]\hat{\mathit{y}}{\mathrm{d}t<-V\left(\mathit{q}\right)|}_0^{\infty }=-{\mathit{q}}^T\left(\mathit{q}\left(0\right)\right){\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\left(0\right)\right)\mathit{q}\left(\mathit{q}\left(0\right)\right)$$

(41)

For minimizing the upper limit of the cost function J, the following relation is considered:

$$\mathit{J}<{\mathit{q}}^T\left(0\right){\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\left(0\right)\right)\mathit{q}\left(0\right)\le \lambda$$

(42)

By Schur complement, the inequality

$${\mathit{q}}^T\left(0\right){\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\left(0\right)\right)\mathit{q}\left(0\right)\le \lambda$$

(43)

can be rewritten as

$$\left[\begin{array}{cc}\lambda & {\mathit{q}}^T\left(0\right)\\ \mathit{q}\left(0\right)& {\mathit{Q}}^{-1}\left(\tilde{\mathit{q}}\left(0\right)\right)\end{array}\right]\ge 0$$

(44)

which can be guaranteed by (21). In conclusion, if the SOS conditions (18)–(21) are satisfied, then the closed-loop polynomial fuzzy system is asymptotically stable and $J\le \lambda$ is fulfilled. Therefore, by minimizing $\lambda$ subject to (18)–(21), the GCC can be designed to minimize the upper limit of the cost function J. □

4. Design Examples

In this section, two design examples are given to validate the viability and effectiveness of the proposed GCC design methodology. For a PFM in the first example, the cost function of the proposed descriptor representation-based GCC design methodology is less (better) than the existing GCC approach. The second example clarifies that the proposed Theorem 1 could acquire more relaxed results than the existing SOS-based GCC design method.

4.1. Example 1

The PFM (2) is considered with $r=2$, $\hat{\mathit{q}}\left(\mathit{q}\right)=\mathit{q}={\left[q_1{q}_2\right]}^T$ and the following system matrices

$$\begin{array}{cc}\hfill & {\mathit{A}}_1\left(\mathit{q}\right)=\left[\begin{array}{cc}-1+q_1+q_1^2+q_1{q}_2-q_2^2& 1\\ 0& -1\end{array}\right],\hfill \\ \hfill & {\mathit{A}}_2\left(\mathit{q}\right)=\left[\begin{array}{cc}-1+q_1+q_1^2+q_1{q}_2-q_2^2& 1\\ 0.2172& -1\end{array}\right],\hfill \\ \hfill & {\mathit{B}}_1\left(\mathit{q}\right)=\left[\begin{array}{c}{q}_1\\ 0\end{array}\right],{\mathit{B}}_2\left(\mathit{q}\right)=\left[\begin{array}{c}{q}_1\\ 0\end{array}\right],\hfill \\ \hfill & {\mathit{C}}_1\left(\mathit{q}\right)=\left[10\right],{\mathit{C}}_2\left(\mathit{q}\right)=\left[10\right].\hfill \end{array}$$

The membership functions with $\mathit{z}=q_1$ are given below:

$$h_1\left(\mathit{z}\right)=\frac{sin\left(q_1\right)+0.2172q_1}{1.2172q_1},h_2\left(\mathit{z}\right)=\frac{q_1-sin\left(q_1\right)}{1.2172q_1}.$$

In addition, we consider the following operation domain:

$$D_{op}=\{\mathit{q}:-5\le q_k\le 5,k=1,2\}.$$

For $\mathit{W}=\mathit{I}$, $\mathit{S}=\mathit{I}$ and the initial condition $\mathit{q}\left(0\right)={\left[44\right]}^T$, the cost function values J given by the guaranteed cost controllers designed by the proposed and existing methods are shown in

Table 1. Comparison of the cost function value J in Example 1.

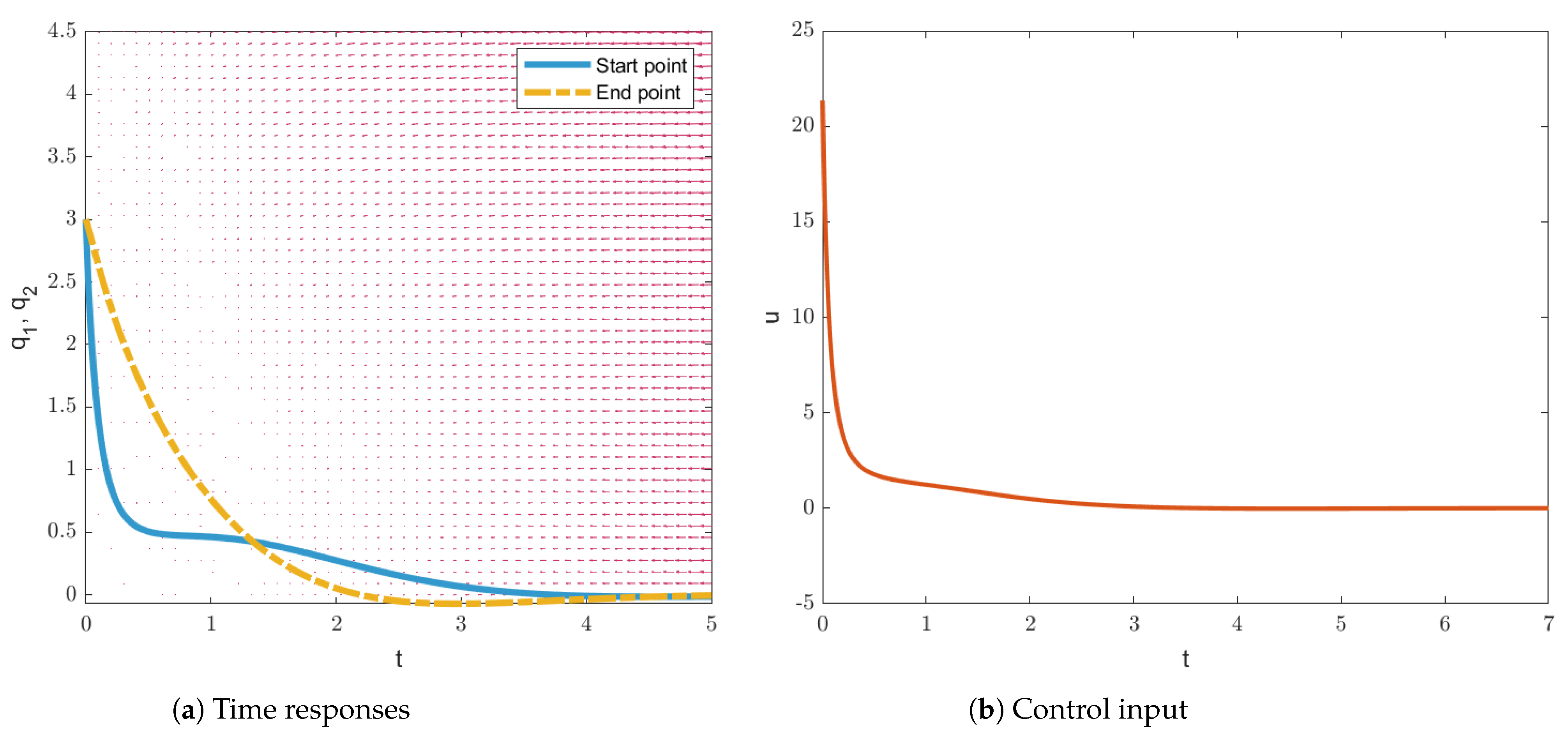
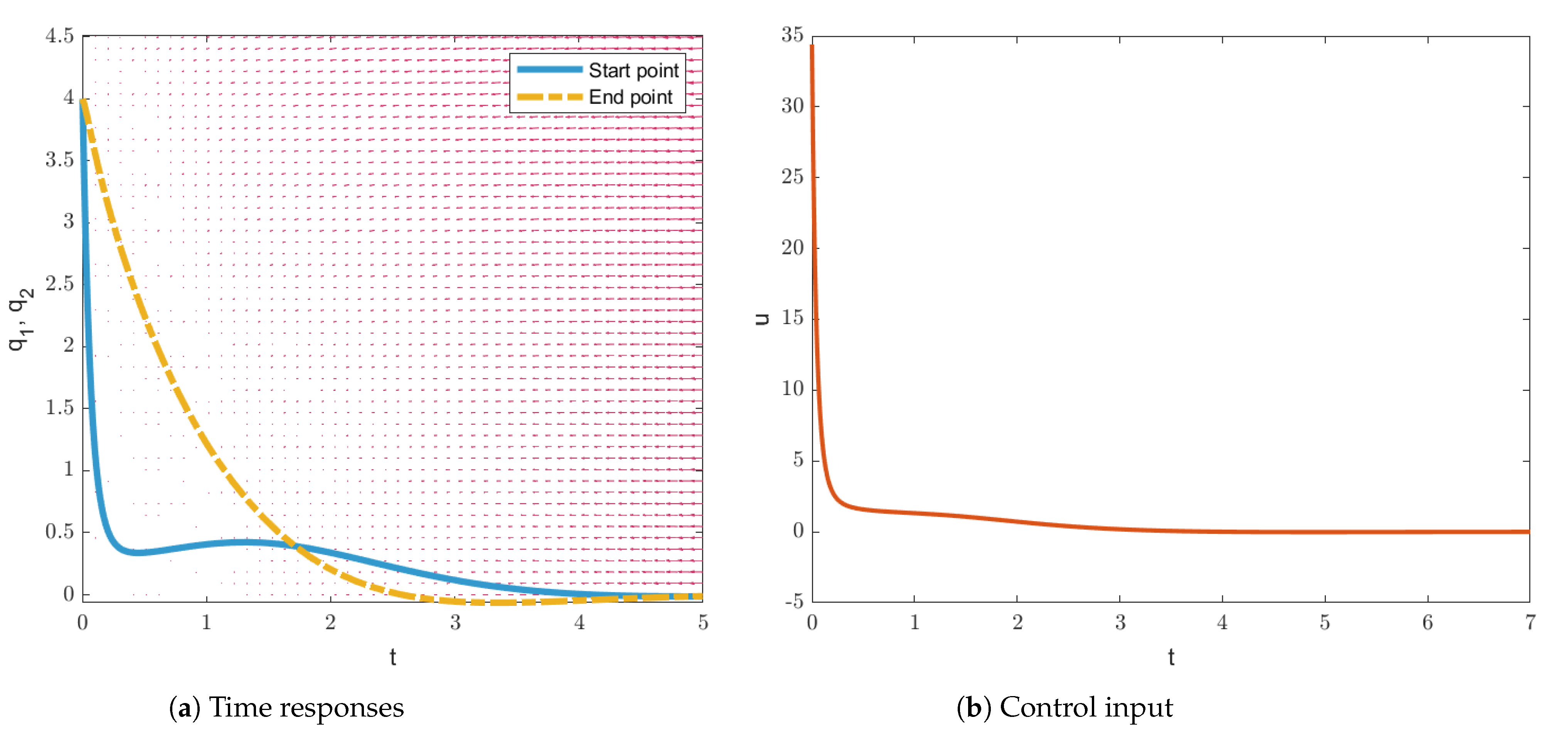
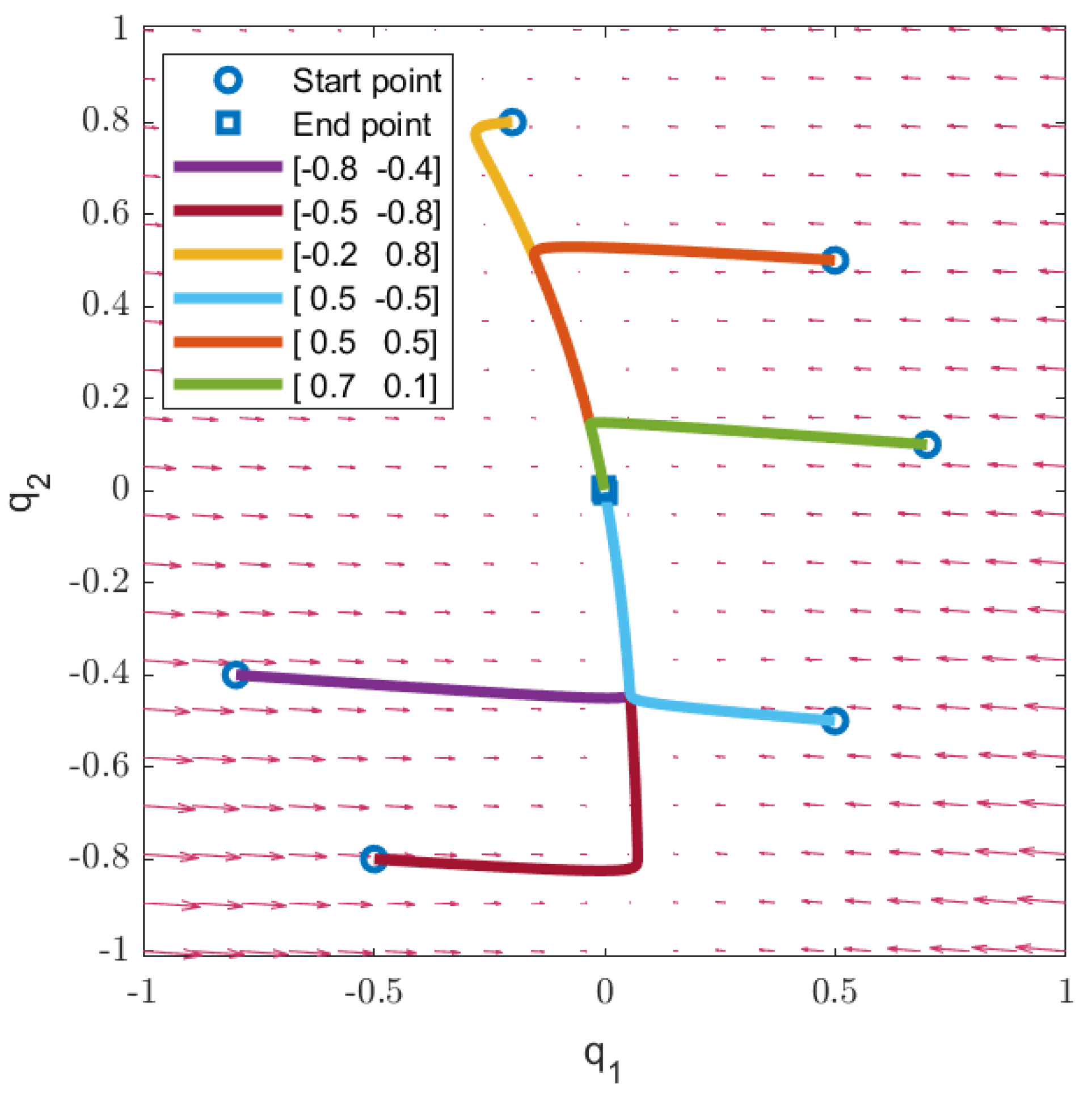
Initial Condition $\mathit{q}\left(0\right)$	Cost Function Value J of Theorem 1 of [43]	Cost Function Value J of The Proposed Theorem 1
${\left[33\right]}^T$	32.81	26.60
${\left[44\right]}^T$	60.79	41.94

. From Table 1, for the same initial conditions, it could be noticed that the cost function values J of the proposed design are about two-thirds of the values of the existing one [43]. It means that the proposed design is superior to the compared one for this example. Besides, Figure 1 and Figure 2 present the time responses and control inputs of the proposed guaranteed cost controllers with two different initial conditions. It is seen from Figure 1 and Figure 2 that the controlled systems are asymptotically stable.

4.2. Example 2

The PFM (2) is considered with $r=3$, $\hat{\mathit{q}}\left(\mathit{q}\right)=\mathit{q}={\left[q_1{q}_2\right]}^T$ and the following system matrices

$$\begin{array}{cc}\hfill & {\mathit{A}}_1=\left[\begin{array}{cc}1.59& -7.29\\ 0.01& 0\end{array}\right],{\mathit{A}}_2=\left[\begin{array}{cc}0.02& -4.64\\ 0.35& 0.21\end{array}\right],{\mathit{A}}_3=\left[\begin{array}{cc}-2& -4.33\\ 0& 0.05\end{array}\right]\hfill \\ \hfill & {\mathit{B}}_1=\left[\begin{array}{c}1\\ 0\end{array}\right],{\mathit{B}}_2=\left[\begin{array}{c}8\\ 0\end{array}\right],{\mathit{B}}_3=\left[\begin{array}{c}5\\ -1\end{array}\right]\hfill \\ \hfill & {\mathit{C}}_1=\left[10\right],{\mathit{C}}_2=\left[10\right],{\mathit{C}}_3=\left[10\right]\hfill \end{array}$$

The membership functions with $\mathit{z}=q_2$ are given below:

$$h_1\left(\mathit{z}\right)=\frac{1+sin\left(q_2\right)}{3},h_2\left(\mathit{z}\right)=h_3\left(\mathit{z}\right)=\frac{2-sin\left(q_2\right)}{6}$$

In addition, we consider the following operation domain:

$$D_{op}=\{\mathit{q}:-1\le q_k\le 1,k=1,2\}$$

In this case, no solution can be found by applying the existing SOS-based GCC design method (i.e., Theorem 1 of [43]). By contrast, utilizing the proposed Theorem 1 with $\mathit{W}=\mathit{I}$ and $\mathit{S}=\mathit{0}.\mathit{01}\mathit{I}$, the cost function values J for six different initial conditions are given in

Table 2. The cost function values J of the proposed GCC design methodology with six different initial conditions in Example 2.

Initial Condition $\mathit{q}\left(0\right)$	Cost Function Value J
${[-0.8-0.4]}^T$	0.1245
${[-0.5-0.8]}^T$	0.1663
${[-0.20.8]}^T$	0.1052
${[0.5-0.5]}^T$	0.1677
${\left[0.50.5\right]}^T$	0.0234
${\left[0.70.1\right]}^T$	0.0230

. Therefore, the proposed Theorem 1 has more relaxed results in this example. Moreover, Figure 3 shows the phase plot of trajectories for the six initial conditions mentioned in Table 2. According to Figure 3, the closed-loop system is asymptotically stable. To show the robustness of the proposed design, the two matrices of $A_1$ and $A_2$ are exchanged for further simulation. With the six same initial conditions,

Table 3. The cost function values J of the proposed GCC design methodology by exchanging $A_1$ and $A_2$ in Example 2.

Initial Condition $\mathit{q}\left(0\right)$	Cost Function Value J
${[-0.8-0.4]}^T$	0.0602
${[-0.5-0.8]}^T$	0.1747
${[-0.20.8]}^T$	0.0401
${[0.5-0.5]}^T$	0.0130
${\left[0.50.5\right]}^T$	0.0215
${\left[0.70.1\right]}^T$	0.0228

and Figure 4 show the cost function values J and the phase plot for the simulation results with exchanging $A_1$ and $A_2$. From Table 3 and Figure 4, it shows that the proposed GCC design is still feasible and the controlled systems are still asymptotically stable.

5. Conclusions

This paper has presented a descriptor representation-based guaranteed cost design methodology for polynomial fuzzy systems. The design methodology converts the closed-loop polynomial fuzzy system applying the PDC-based fuzzy control into the descriptor representation. The polynomial fuzzy slack matrices are taken into the GCC design analysis to obtain less conservative results by taking advantage of the descriptor representation. The proposed GCC design has relied on the SOS decomposition of multivariate polynomials. The DFS issue comes about in the control design analysis owing to the application of polynomial fuzzy slack matrices. Accordingly, the copositive relaxation is adopted and works out well for the DFS issue in the control design analysis. As a result, the GCC design can minimize the upper limit of a provided cost function for the polynomial fuzzy system. Eventually, two simulation examples have been given to illustrate that the proposed methodology is effectual and has obtained superior results.