Precision Calorimeter Model Development: Generative Design Approach
Abstract
:1. Introduction
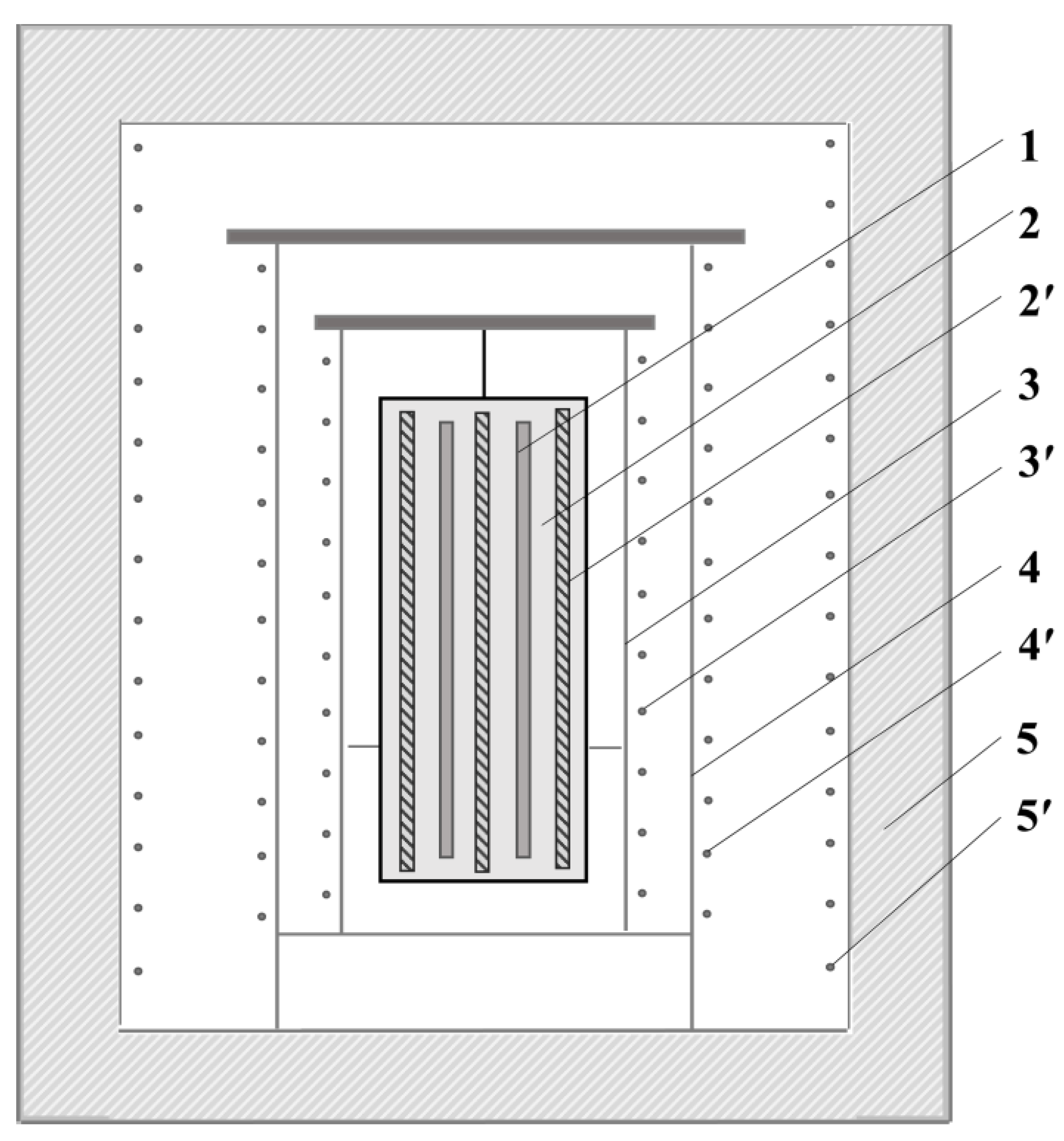
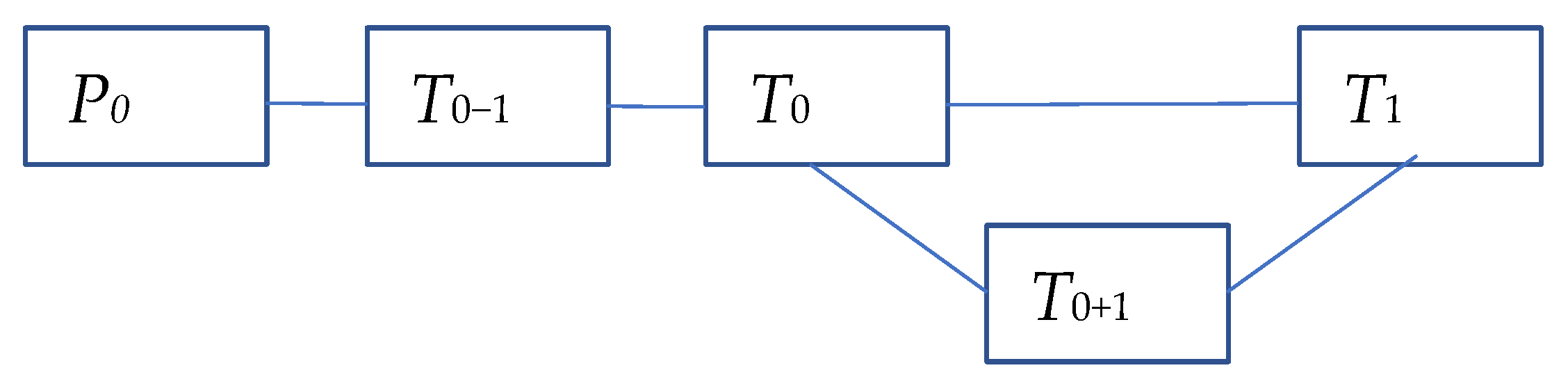
2. Model Building
3. Generating Optimized Model
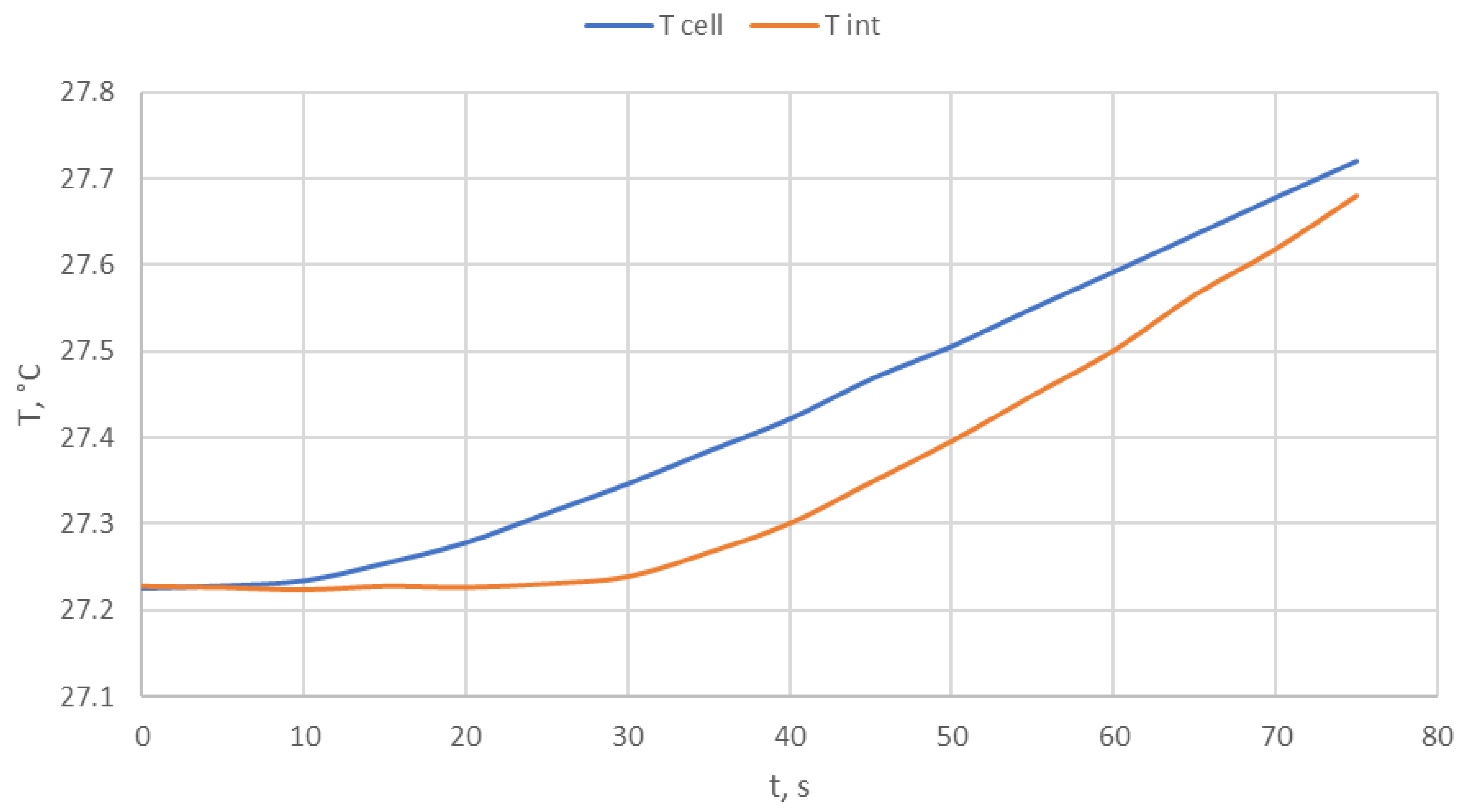
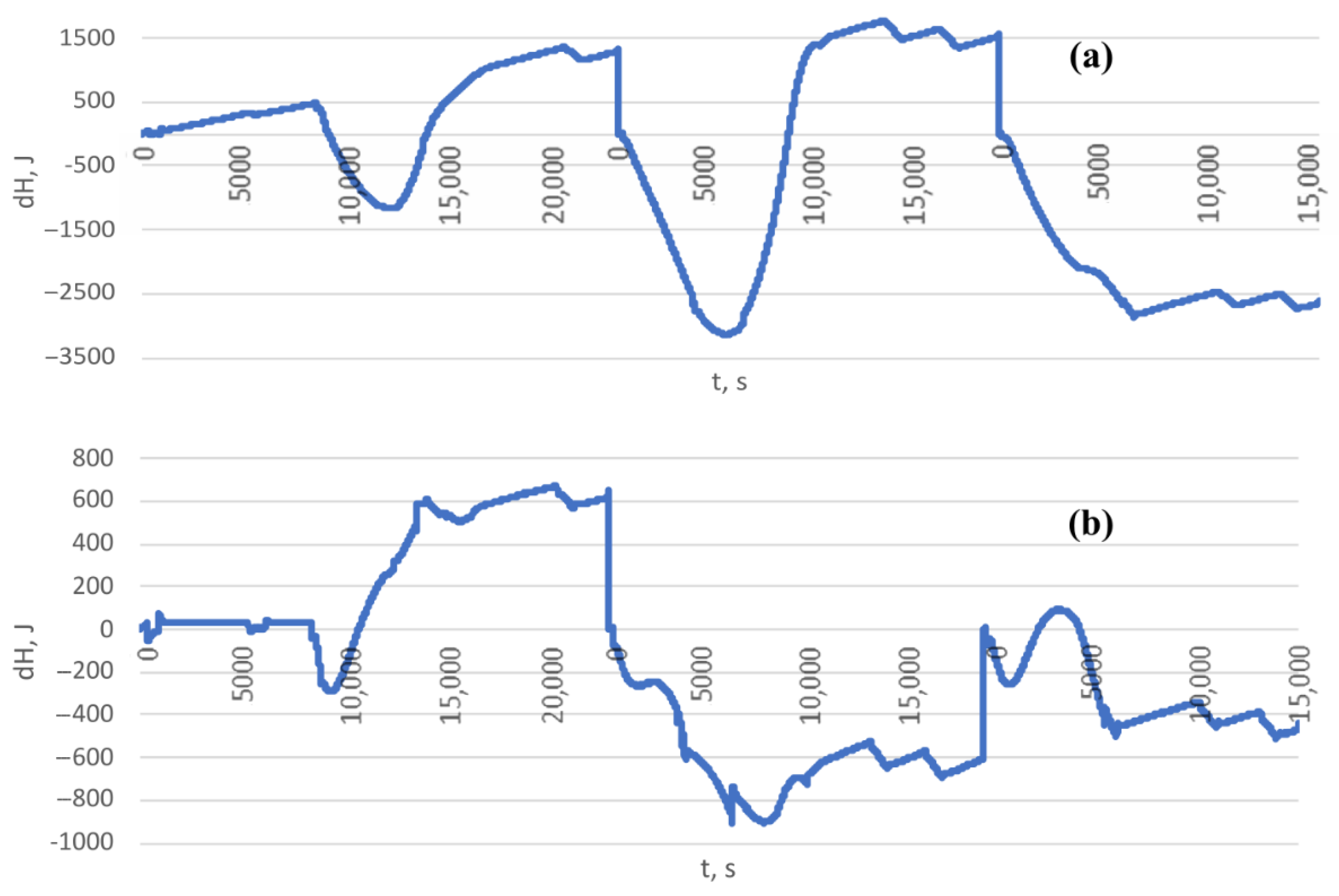
3.1. Starting Point
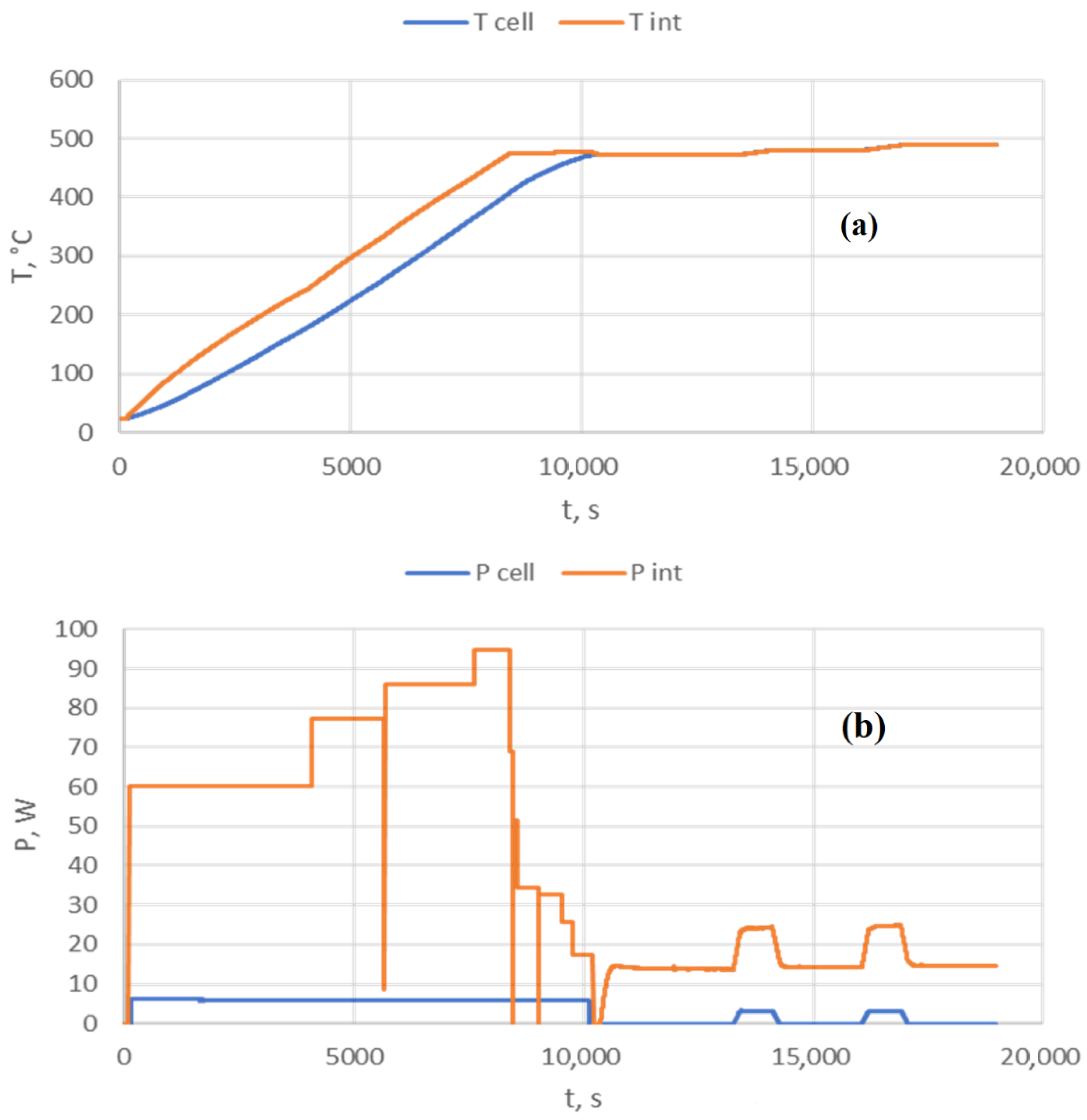
3.2. Generative Design. Generalization of Dependencies and Structure
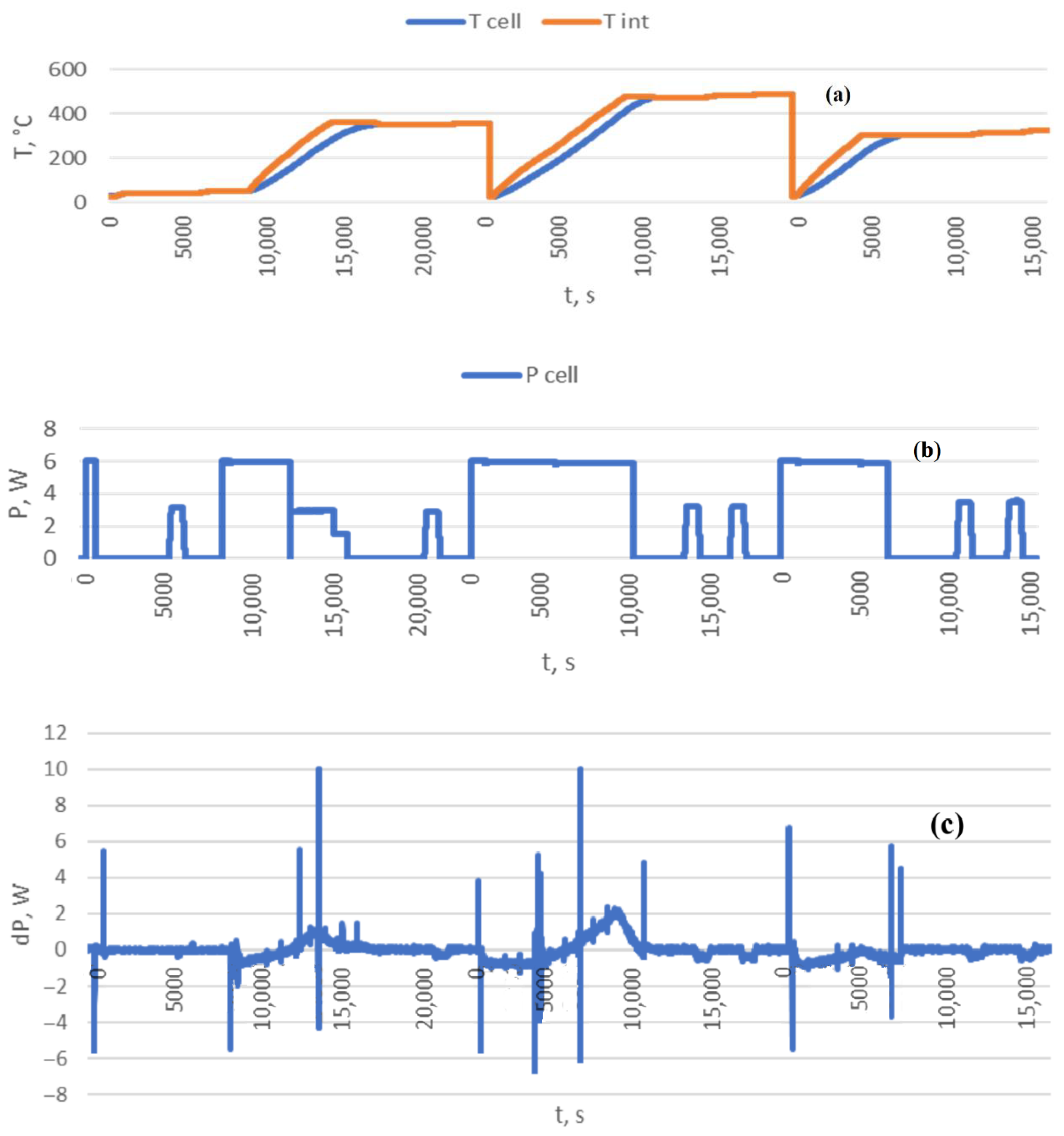
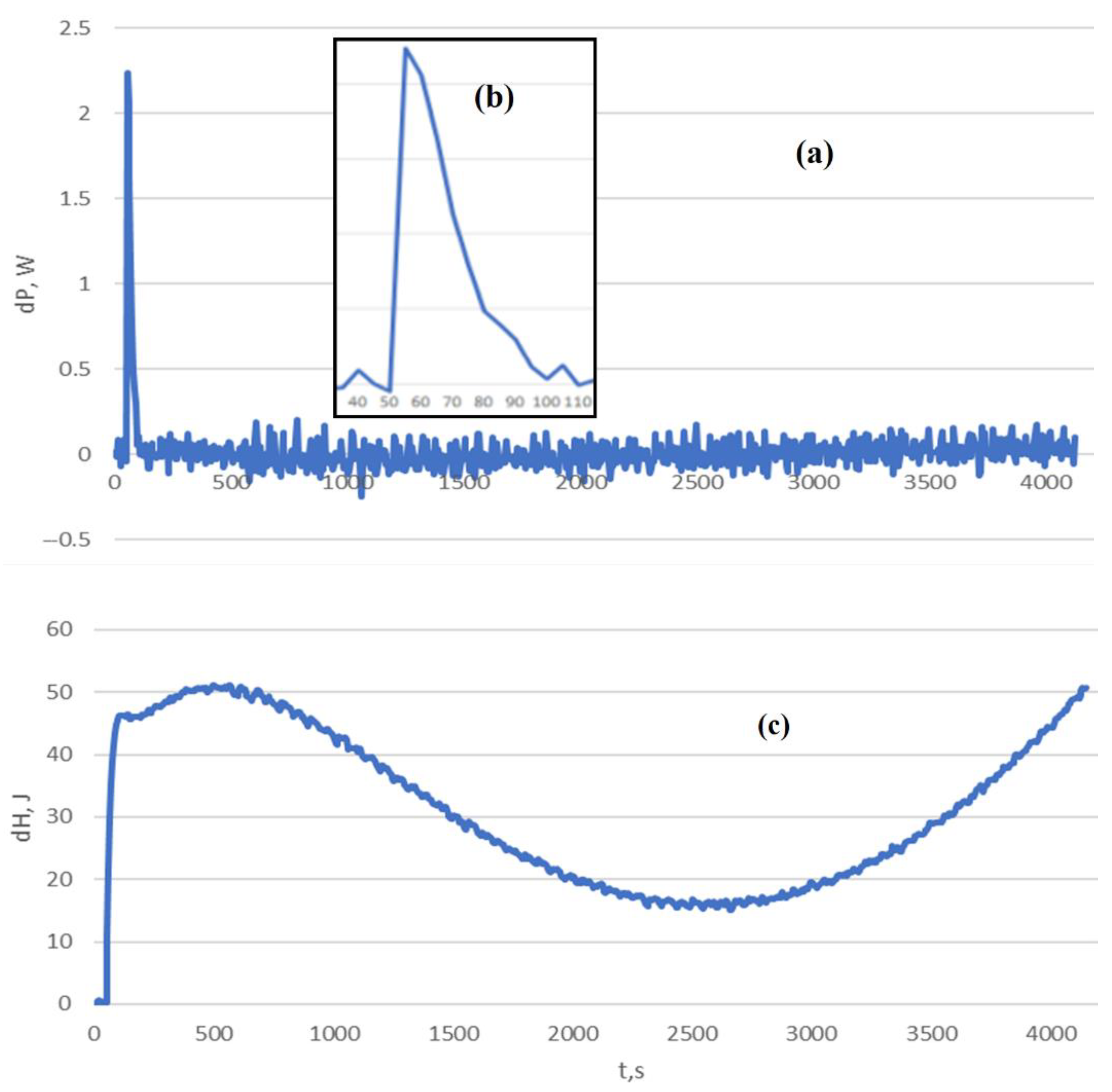
3.3. Generative Design. Expansion
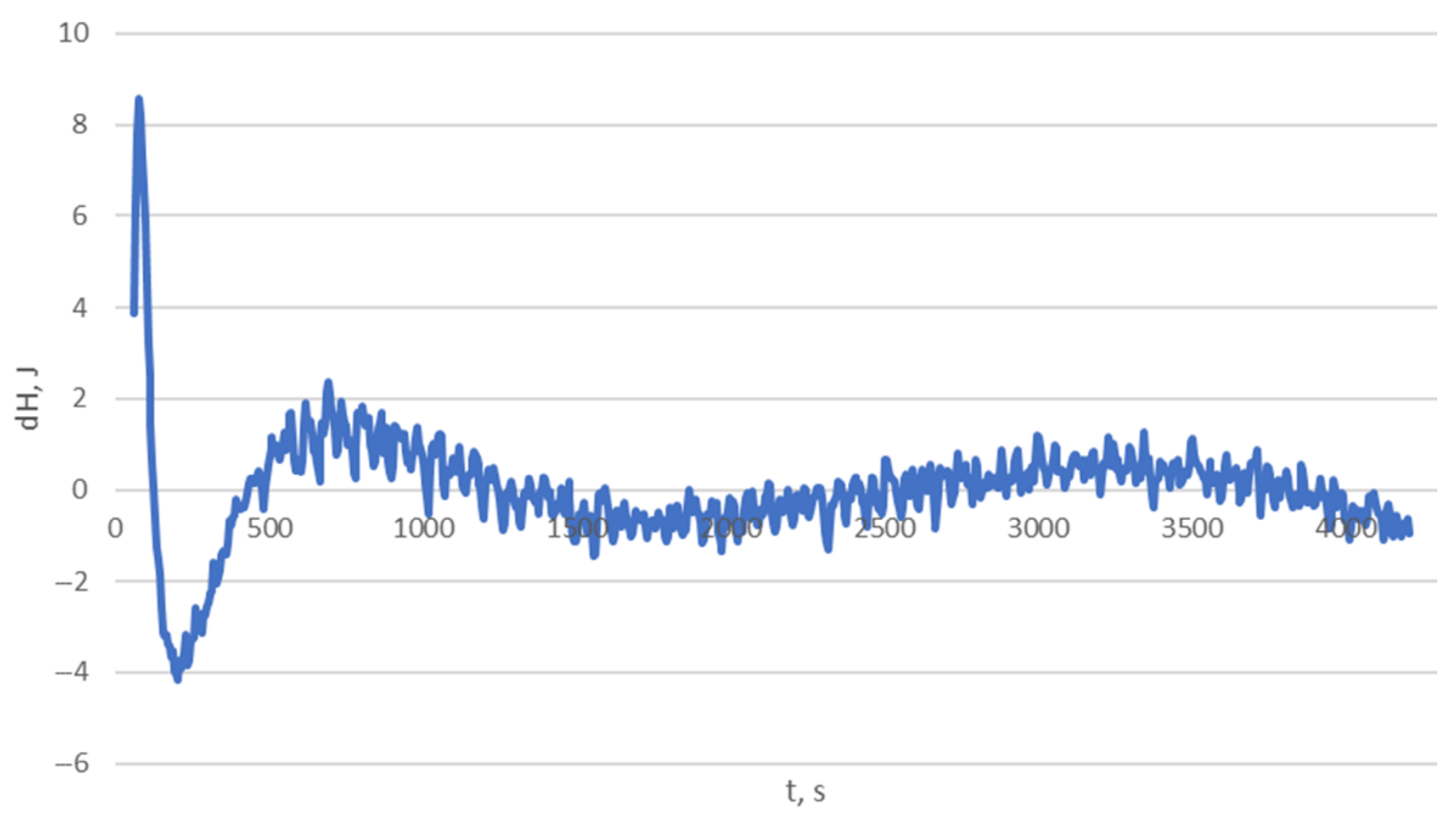
3.4. Computing Features
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nishiyama, E.; Tsukushi, I.; Fujimura, J.; Yokota, M. Construction of a top-loading adiabatic calorimeter equipped with a refrigerator. Thermochim. Acta 2020, 692, 178151. [Google Scholar] [CrossRef]
- Tan, Z.C.; Shi, Q.; Liu, X. Construction of High-Precision Adiabatic Calorimeter and Thermodynamic Study on Functional Materials. In Calorimetry—Design, Theory and Applications in Porous Solids; Piraján, J.C.M., Ed.; IntechOpen: London, UK, 2008. [Google Scholar]
- Kompan, T.A.; Kulagin, V.I.; Vlasova, V.V.; Kondratiev, S.V.; Lukin, A.Y.; Pukhov, N.F. State Primary Standard of Unit of Specific Heat Capacity of Solids (Get 60-2019). Meas. Tech. 2020, 63, 407–413. [Google Scholar] [CrossRef]
- Li, Y.; Ang, K.H.; Chong, G.C.Y. PID control system analysis and design. IEEE Control Syst. Mag. 2006, 26, 32–41. [Google Scholar]
- Barbieri, L.; Muzzupappa, M. Performance-Driven Engineering Design Approaches Based on Generative Design and Topology Optimization Tools: A Comparative Study. Appl. Sci. 2022, 12, 2106. [Google Scholar] [CrossRef]
- Bykov, N.Y.; Hvatov, A.A.; Kalyuzhnaya, A.; Boukhanovsky, A.V. A method for reconstructing models of heat and mass transfer from the spatio-temporal distribution of parameters. Pisma V Zhurnal Tekhnicheskoi Fiz. 2021, 47, 9–12. [Google Scholar]
- Maslyaev, M.; Hvatov, A.; Kalyuzhnaya, A.V. Partial differential equations discovery with EPDE framework: Application for real and synthetic data. J. Comp. Sci. 2021, 53, 101345. [Google Scholar] [CrossRef]
- Schaeffer, H.; Caflisch, R.; Hauck, C.D.; Osher, S. Learning partial differential equations via data discovery and sparse optimization. Proc. R. Soc. A Math. Phys. Eng. Sci. 2017, 473, 20160446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berg, J.; Nyström, K. Data-driven discovery of PDEs in complex datasets. J. Comput. Phys. 2019, 384, 239–252. [Google Scholar] [CrossRef] [Green Version]
- Rudy, S.H.; Alla, A.; Brunton, S.L.; Kutz, J.N. Data-driven identification of parametric partial differential equations. SIAM J. Appl. Dyn. Syst. 2019, 18, 643–660. [Google Scholar] [CrossRef]
- Qin, T.; Wu, K.; Xiu, D. Data driven governing equations approximation using deep neural networks. J. Comput. Phys. 2019, 395, 620–635. [Google Scholar] [CrossRef] [Green Version]
- Mangan, N.M.; Kutz, J.N.; Brunton, S.L.; Proctor, J.L. Model selection for dynamical systems via sparse regression and information criteria. Proc. R. Soc. A 2017, 473, 20170009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N.; Bialek, W. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
- Bongard, J.; Lipson, H. Automated reverse engineering of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2007, 104, 9943–9948. [Google Scholar] [CrossRef] [Green Version]
- Andreeva, T.A.; Bykov, N.Y.; Vlasova, V.V.; Kompan, T.A.; Kulagin, V.I.; Lukin, A.Y. Reference Adiabatic Calorimeter: Hardware Implementation and Control Algorithms. Meas. Tech. 2022, 64, 903–911. [Google Scholar] [CrossRef]
- Maslyaev, M.; Hvatov, A. Multi-Objective Discovery of PDE Systems Using Evolutionary Approach. In Proceedings of the 2021 IEEE Congress on Evolutionary Computation (CEC), Kraków, Poland, 28 June–1 July 2021; pp. 596–603. [Google Scholar]


| a01 | C0 | |
|---|---|---|
| −0.10711 | 271.87 | |
| SD | 0.00058 | 0.80 |
| A01 | a01 | b0 | C0 | |
|---|---|---|---|---|
| 4.518 × 10−11 | 0.08639 | 0.0463 | 271.79 | |
| SD | 0.075 × 10−11 | 0.00058 | 0.0031 | 0.84 |
| a01 | C0 | |
|---|---|---|
| 0.08206 | 267.7 | |
| SD | 0.00080 | 1.7 |
| a01 | C0 | a0–1 | C0–1 | |
|---|---|---|---|---|
| 0.08445 | 228.53 | 1.26 | 30.2 | |
| SD | 0.00030 | 0.62 | 0.07 | 0.6 |
| T0 | T02 | T03 | T1 | T12 | T13 | Const | |
|---|---|---|---|---|---|---|---|
| −147.0 | 4.36 | −0.038 | −2540 | 70.14 | −0.638 | 31,599 | |
| SD | 14.0 | 0.46 | 0.0060 | 215.95 | 6.50 | 0.058 | 2366 |
| T02 | T1 | T12 | Const | |
|---|---|---|---|---|
| 0.0968 | 208.7 | 3.011 | 3380 | |
| SD | 0.0010 | 2.4 | 0.035 | 37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreeva, T.A.; Bykov, N.Y.; Kompan, T.A.; Kulagin, V.I.; Lukin, A.Y.; Vlasova, V.V. Precision Calorimeter Model Development: Generative Design Approach. Processes 2023, 11, 152. https://doi.org/10.3390/pr11010152
Andreeva TA, Bykov NY, Kompan TA, Kulagin VI, Lukin AY, Vlasova VV. Precision Calorimeter Model Development: Generative Design Approach. Processes. 2023; 11(1):152. https://doi.org/10.3390/pr11010152
Chicago/Turabian StyleAndreeva, Tatiana A., Nikolay Yu. Bykov, Tatiana A. Kompan, Valentin I. Kulagin, Alexander Ya. Lukin, and Viktoriya V. Vlasova. 2023. "Precision Calorimeter Model Development: Generative Design Approach" Processes 11, no. 1: 152. https://doi.org/10.3390/pr11010152
APA StyleAndreeva, T. A., Bykov, N. Y., Kompan, T. A., Kulagin, V. I., Lukin, A. Y., & Vlasova, V. V. (2023). Precision Calorimeter Model Development: Generative Design Approach. Processes, 11(1), 152. https://doi.org/10.3390/pr11010152






