Strain Rate Effect on Mode I Debonding Characterization of Adhesively Bonded Aluminum Joints
Abstract
:1. Introduction
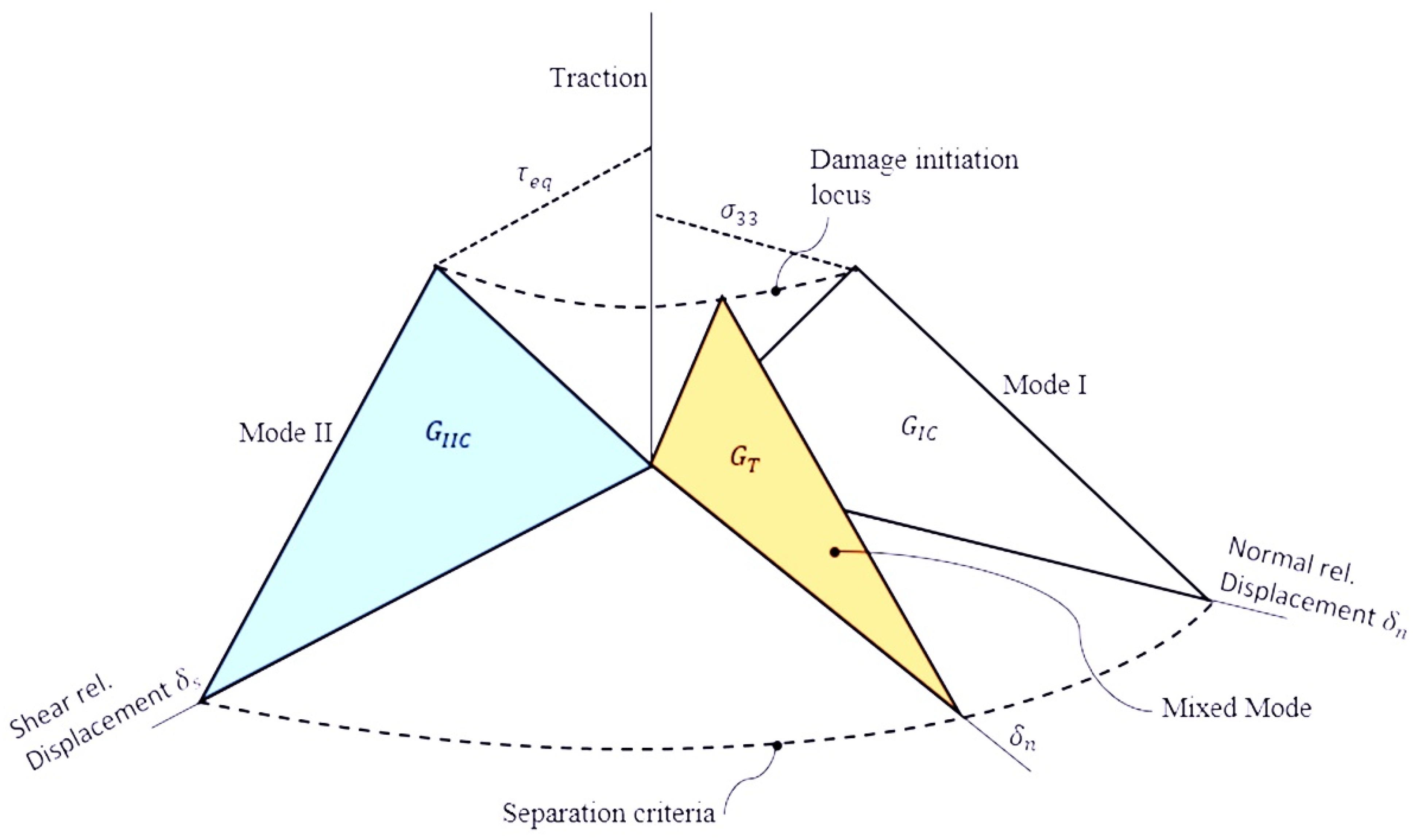
2. Cohesive Zone Model
Cohesive Zone Model Formulation
3. Materials and Methods
3.1. Mode I (Crack opening) Test
- (a)
- The Specimen Preparations
- (b)
- Mode I Test
- (c)
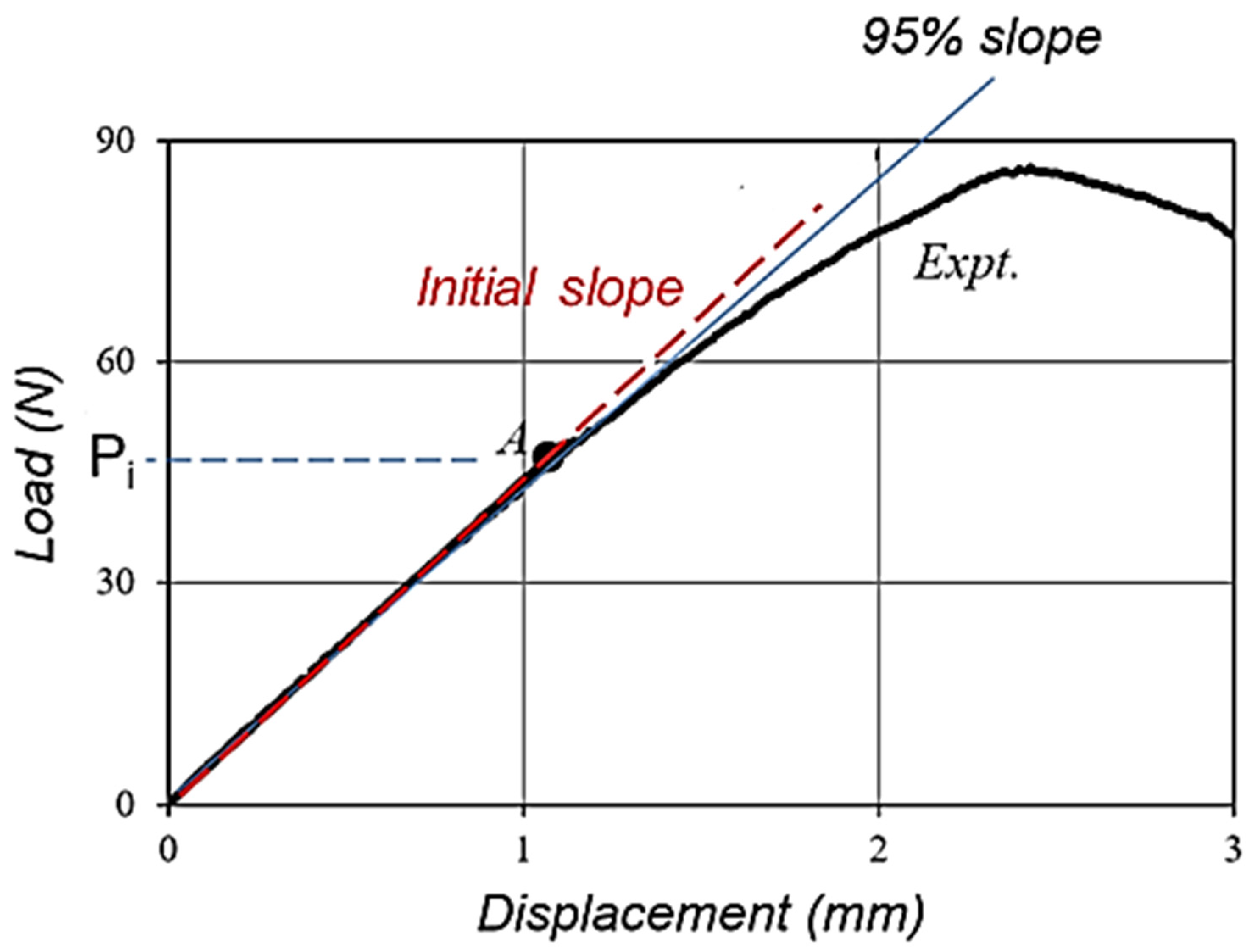
- Critical Strain Energy Release Rate
3.2. Finite Element Simulation
4. Results and Discussion
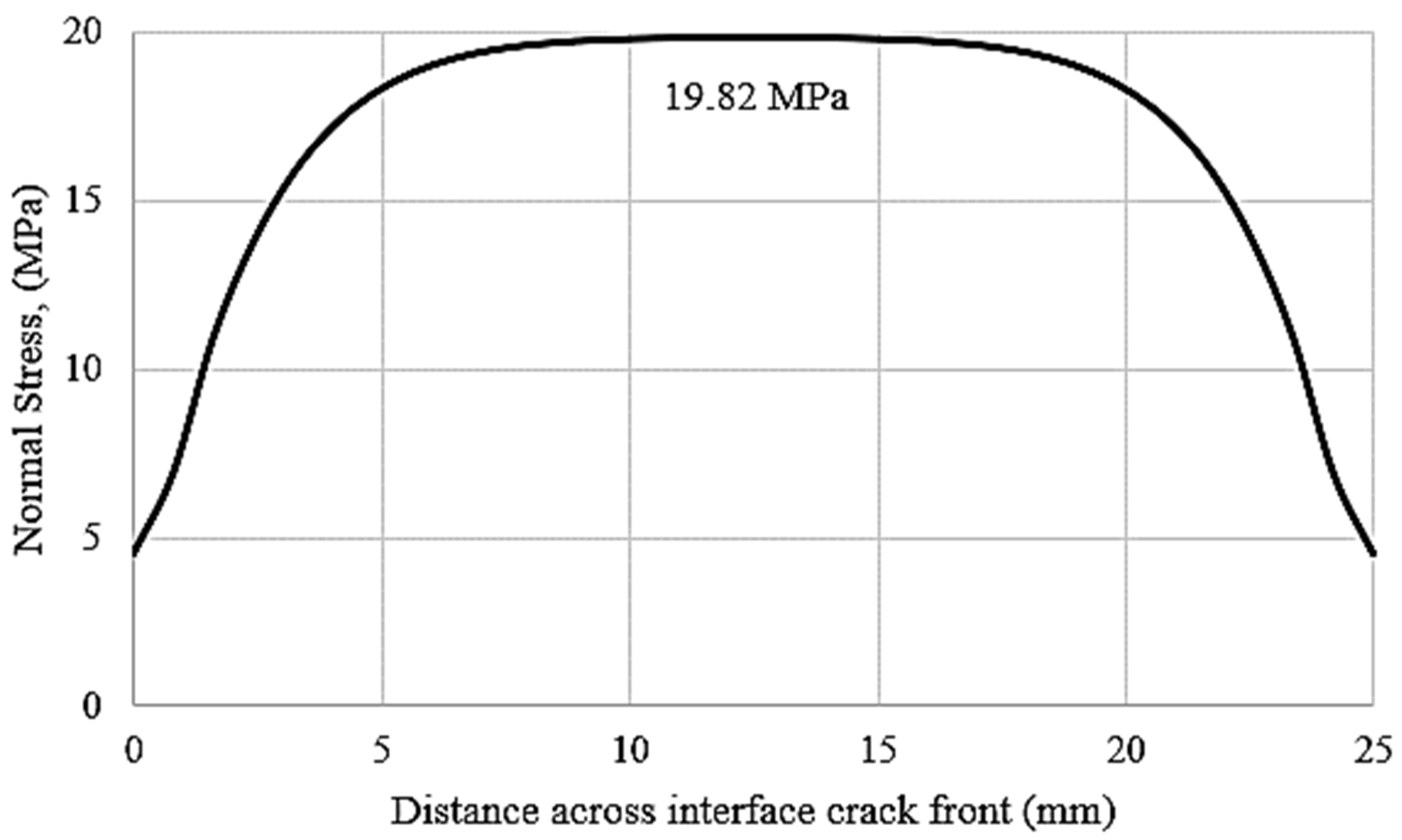
4.1. Interfacial Fracture Adhesive Joints under Mode I Debonding Loading
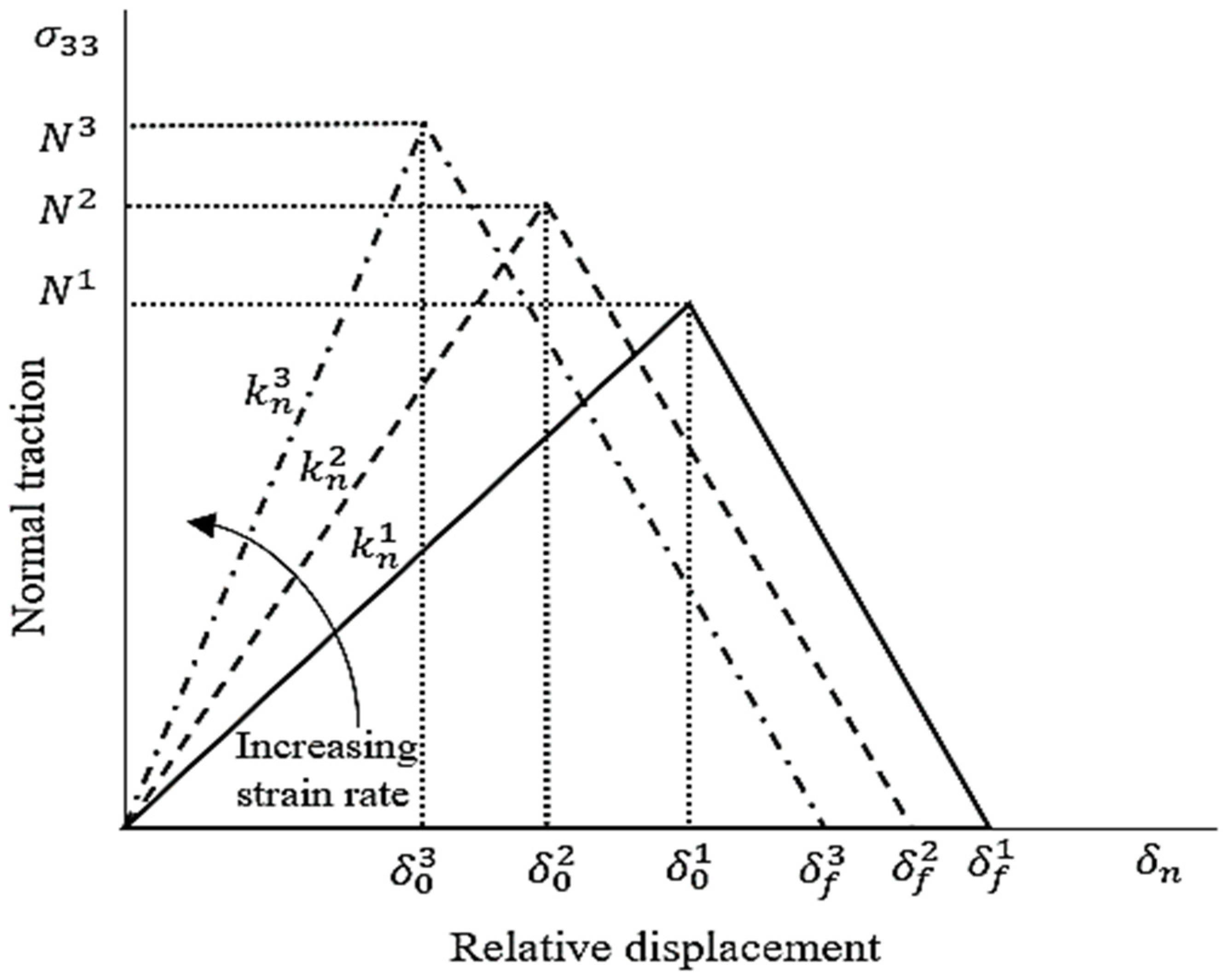
4.2. Loading Rate Effect on Adhesive joint Strain Energy Release Rate
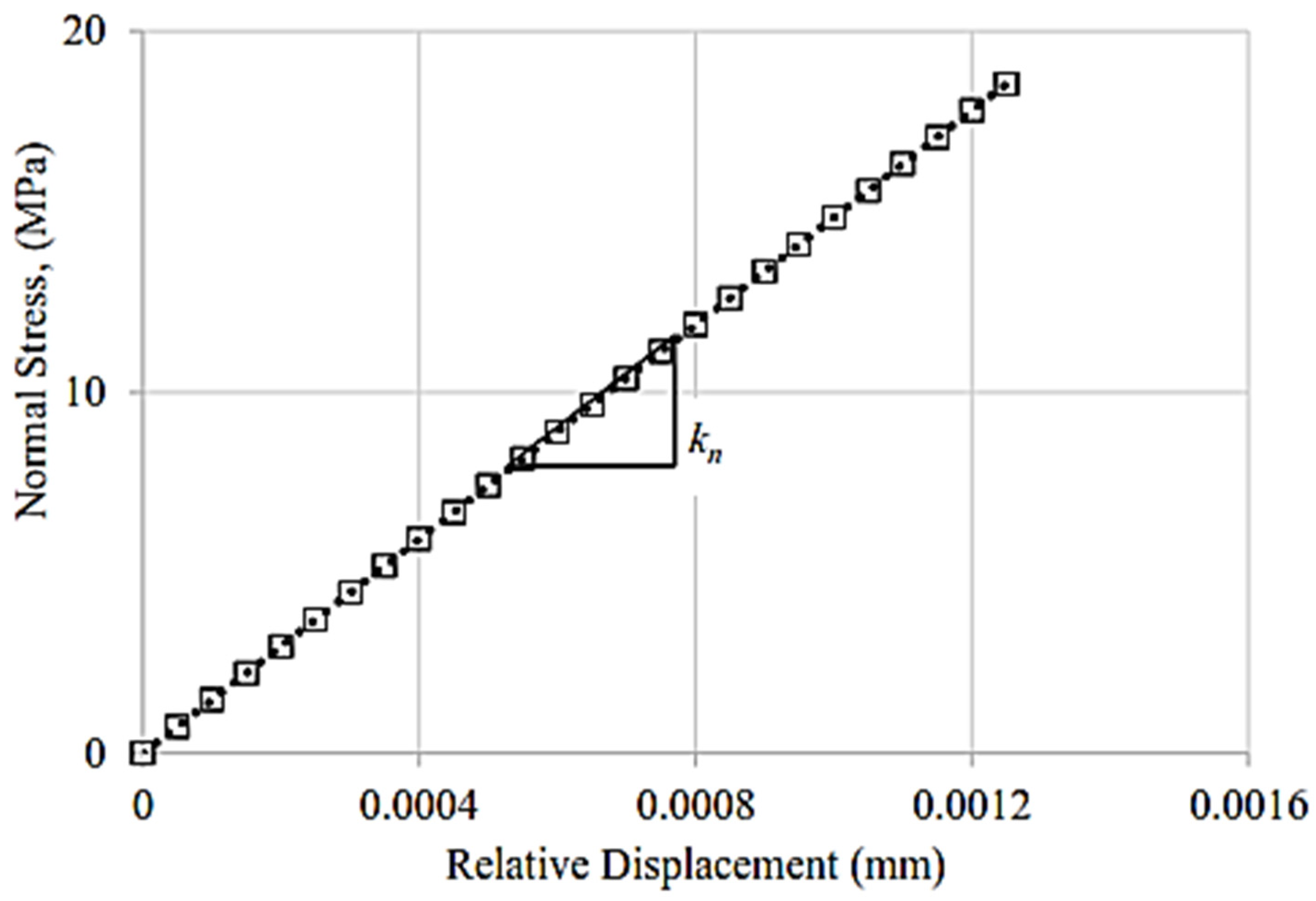
4.3. Extraction of CZM Parameters through an Experimental–FE Approach
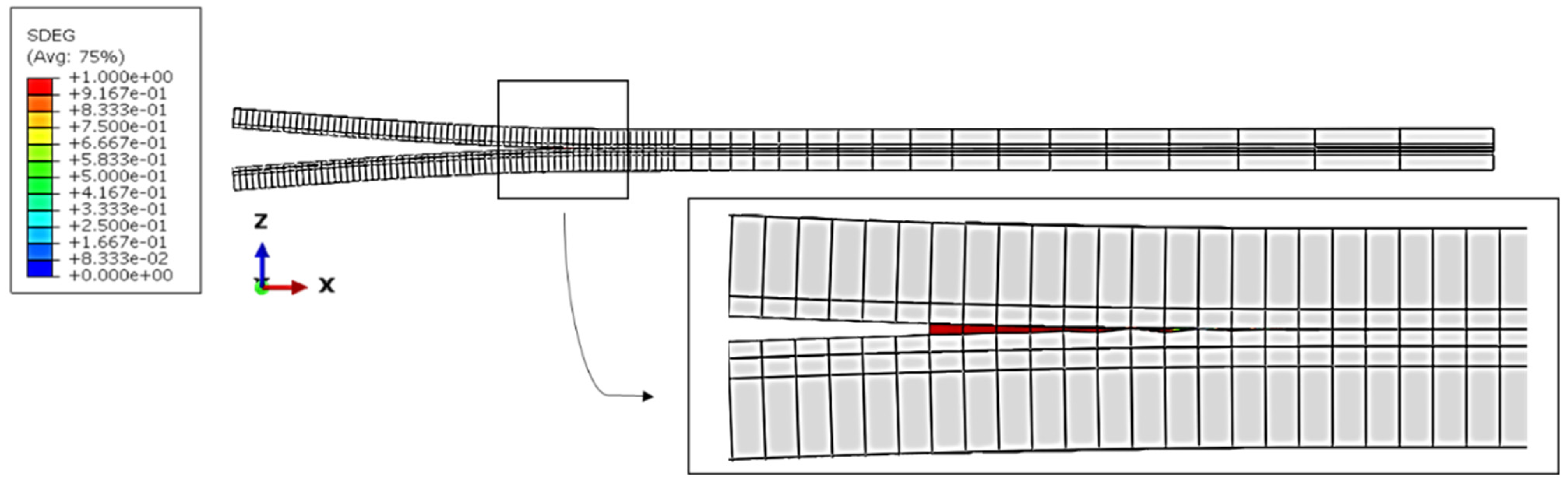
4.4. FE Model Validation for CZM
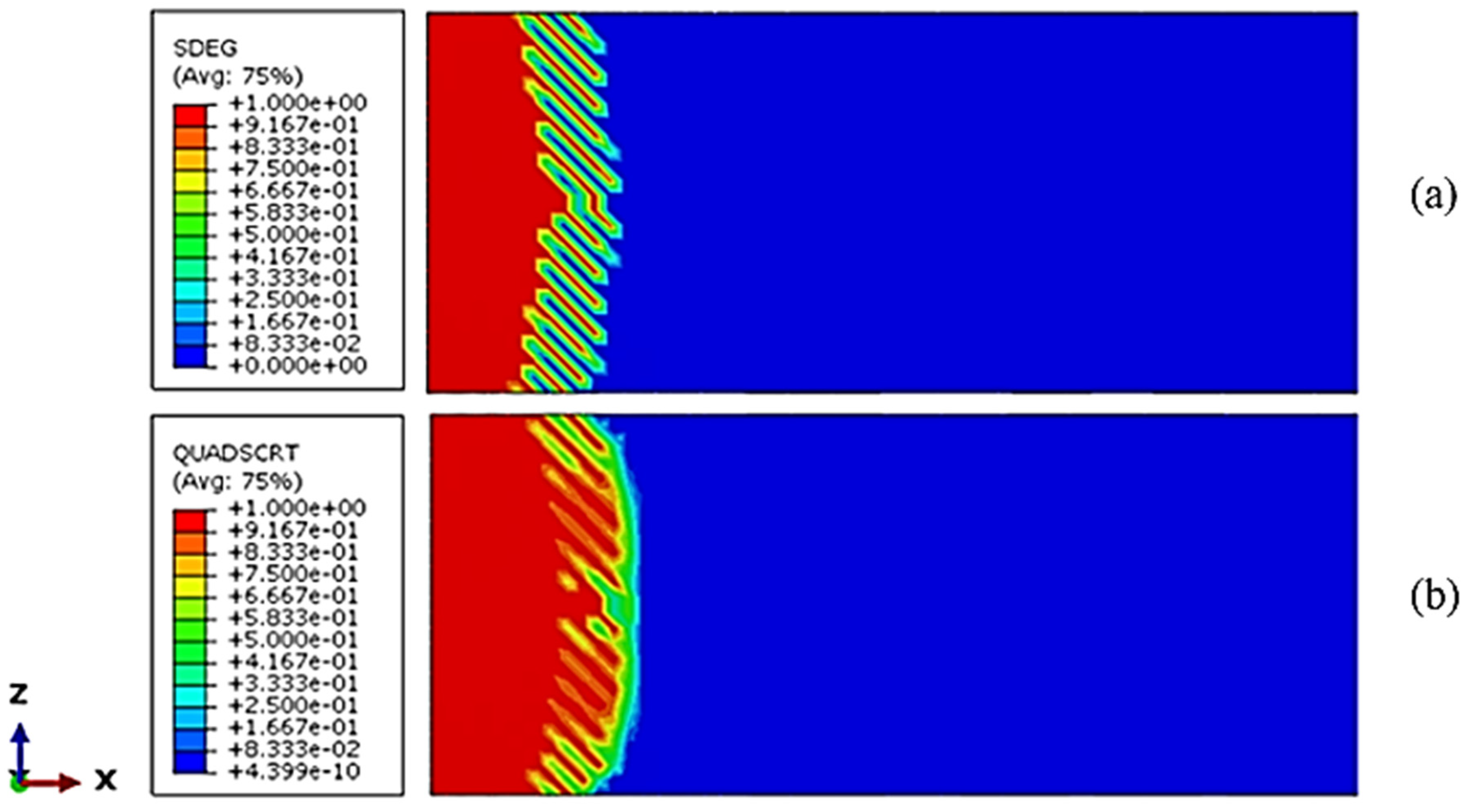
4.5. Fracture Process of Adhesively Bonded Joints
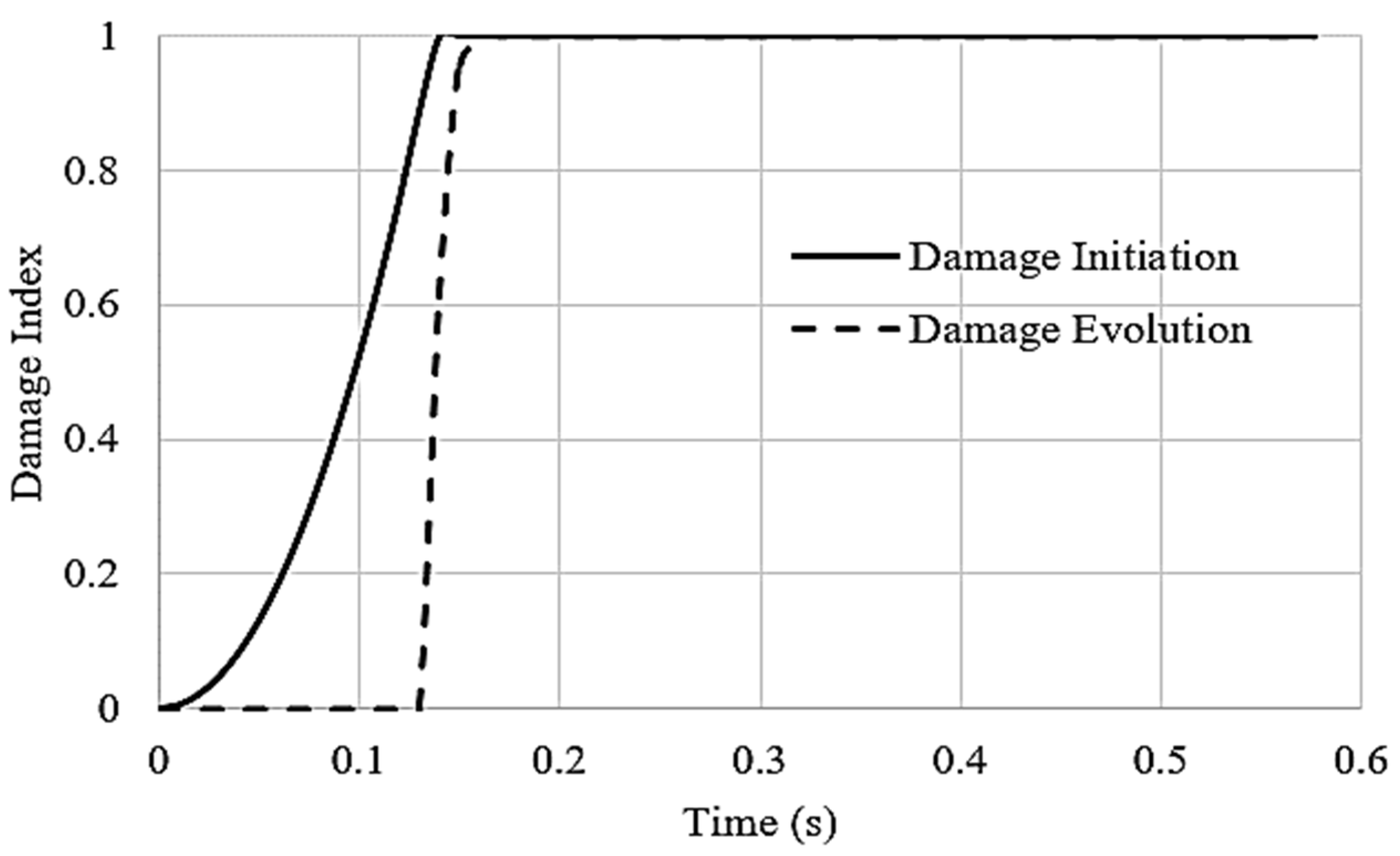
4.6. Interface Damage Accumulation
5. Conclusions
- ➢
- Adhesively bonded joints under Mode I loads have been studied experimentally and numerically to determine the damage and failure process.
- ➢
- For the DCB test, tensile strength, penalty stiffness, and fracture energy of the CZM interface properties were determined at various displacement rates of 5, 50, and 500 mm/min. It is observed that the tensile strength and penalty stiffness increase and fracture energy decreases with increasing displacement rate.
- ➢
- At displacement rates of 5, 50, and 500 mm/min, an extended CZM-based FE simulation approach for the strain rate of an adhesively bonded joint was evaluated.
- ➢
- The findings show that the interface fracture process is governed by an adhesive failure mechanism and that crack propagation is stable at the loading displacement rate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ebnesajjad, S.; Landrock, A.H. Adhesives Technology Handbook; William Andrew: Norwich, NY, USA, 2014; ISBN 0-323-35602-8. [Google Scholar]
- Johar, M.; Asasaari, S.F.M.; Tamin, M.N. Strain Rate-Dependent Deformation and Failure Process of Adhesive Joints. In Proceedings of the 36th International Electronics Manufacturing Technology Conference, Johor Bahru, Malaysia, 11–13 November 2014; pp. 1–5. [Google Scholar]
- Lall, P.; Islam, M.N.; Evans, J.; Suhling, J.C.; Shete, T. Damage Mechanics of Electronics on Metal-Backed Substrates in Harsh Environments. IEEE Trans. Comp. Packag. Technol. 2006, 29, 204–212. [Google Scholar] [CrossRef]
- Wang, J.; Kang, Y.L.; Qin, Q.H.; Fu, D.H.; Li, X.Q. Identification of Time-Dependent Interfacial Mechanical Properties of Adhesive by Hybrid/Inverse Method. Comput. Mater. Sci. 2008, 43, 1160–1164. [Google Scholar] [CrossRef]
- Campilho, R.D.S.G.; de Moura, M.F.S.F.; Domingues, J.J.M.S. Modelling Single and Double-Lap Repairs on Composite Materials. Compos. Sci. Technol. 2005, 65, 1948–1958. [Google Scholar] [CrossRef]
- Townsend, B.W.; Ohanehi, D.C.; Dillard, D.A.; Austin, S.R.; Salmon, F.; Gagnon, D.R. Characterizing Acrylic Foam Pressure Sensitive Adhesive Tapes for Structural Glazing Applications—Part I: DMA and Ramp-to-Fail Results. Int. J. Adhes. Adhes. 2011, 31, 639–649. [Google Scholar] [CrossRef]
- Khan, S.A.; Wong, K.J.; Sung, A.N.; Johar, M.; Tamin, M.N. Characterization of Interface Damage of Fiber-Reinforced Polymer Composite Laminates under Mode I Loading. AIP Conf. Proc. 2022, 2676, 050003. [Google Scholar]
- Koloor, S.S.R.; Abdul-Latif, A.; Tamin, M.N. Mechanics of Composite Delamination under Flexural Loading. KEM 2011, 462–463, 726–731. [Google Scholar] [CrossRef]
- Koloor, S.; Tamin, M. Mode-II Interlaminar Fracture and Crack-Jump Phenomenon in CFRP Composite Laminate Materials. Compos. Struct. 2018, 204, 594–606. [Google Scholar] [CrossRef]
- Wong, K.J.; Johar, M.; Koloor, S.S.R.; Petrů, M.; Tamin, M.N. Moisture Absorption Effects on Mode II Delamination of Carbon/Epoxy Composites. Polymers 2020, 12, 2162. [Google Scholar] [CrossRef]
- Borg, R.; Nilsson, L.; Simonsson, K. Simulating DCB, ENF and MMB Experiments Using Shell Elements and a Cohesive Zone Model. Compos. Sci. Technol. 2004, 64, 269–278. [Google Scholar] [CrossRef]
- Wosu, S.N.; Hui, D.; Dutta, P.K. Dynamic Mixed-Mode I/II Delamination Fracture and Energy Release Rate of Unidirectional Graphite/Epoxy Composites. Eng. Fract. Mech. 2005, 72, 1531–1558. [Google Scholar] [CrossRef]
- Marat-Mendes, R.; Freitas, M. DCB, ENF and ECT Tests for Interlaminar Fracture of Glass/Epoxy Unidirectional Laminates. In Proceedings of the 10th Portuguese Conference on Fracture, Guimarles, Portugal, 1 January 2006; pp. 22–24. [Google Scholar]
- Madhukar, M.S.; Drzal, L.T. Fiber-Matrix Adhesion and Its Effect on Composite Mechanical Properties: IV. Mode I and Mode II Fracture Toughness of Graphite/Epoxy Composites. J. Compos. Mater. 1992, 26, 936–968. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Abdullah, M.A.; Tamin, M.N.; Ayatollahi, M.R. Fatigue Damage of Cohesive Interfaces in Fiber-Reinforced Polymer Composite Laminates. Compos. Sci. Technol. 2019, 183, 107779. [Google Scholar] [CrossRef]
- Wong, K.J. Moisture Absorption Characteristics and Effects on Mechanical Behaviour of Carbon/Epoxy Composite: Application to Bonded Patch Repairs of Composite Structures. Ph.D. Thesis, Université de Bourgogne, Dijon, France, 2013. [Google Scholar]
- Na, J.; Fan, Y.; Tan, W.; Guo, S.; Mu, W. Mechanical Behavior of Polyurethane Adhesive Bonded Joints as a Function of Temperature and Humidity. J. Adhes. Sci. Technol. 2018, 32, 457–472. [Google Scholar] [CrossRef]
- Fernando, M.; Harjoprayitno, W.; Kinloch, A. A Fracture Mechanics Study of the Influence of Moisture on the Fatigue Behaviour of Adhesively Bonded Aluminium-Alloy Joints. Int. J. Adhes. Adhes. 1996, 16, 113–119. [Google Scholar] [CrossRef]
- Bordes, M.; Davies, P.; Cognard, J.-Y.; Sohier, L.; Sauvant-Moynot, V.; Galy, J. Prediction of Long Term Strength of Adhesively Bonded Steel/Epoxy Joints in Sea Water. Int. J. Adhes. Adhes. 2009, 29, 595–608. [Google Scholar] [CrossRef] [Green Version]
- Viana, G.; Costa, M.; Banea, M.; Da Silva, L. Moisture and Temperature Degradation of Double Cantilever Beam Adhesive Joints. J. Adhes. Sci. Technol. 2017, 31, 1824–1838. [Google Scholar] [CrossRef]
- Na, J.; Mu, W.; Qin, G.; Tan, W.; Pu, L. Effect of Temperature on the Mechanical Properties of Adhesively Bonded Basalt FRP-Aluminum Alloy Joints in the Automotive Industry. Int. J. Adhes. Adhes. 2018, 85, 138–148. [Google Scholar] [CrossRef]
- Hayashi, A.; Sekiguchi, Y.; Sato, C. Effect of temperature and loading rate on the mode I fracture energy of structural acrylic adhesives. J. Adv. Join. Process. 2022, 5, 100079. [Google Scholar] [CrossRef]
- Saleh, M.N.; Tomić, N.Z.; Marinković, A.; de Freitas, S.T. The effect of modified tannic acid (TA) eco-epoxy adhesives on mode I fracture toughness of bonded joints. Polym. Test. 2021, 96, 107122. [Google Scholar] [CrossRef]
- Khan, M.S.; Abdul-Latif, A.; Koloor, S.S.R.; Petrů, M.; Tamin, M.N. Representative Cell Analysis for Damage-Based Failure Model of Polymer Hexagonal Honeycomb Structure under the out-of-Plane Loadings. Polymers 2020, 13, 52. [Google Scholar] [CrossRef] [PubMed]
- Bang, H.; Lee, S.; Cho, C.; Cho, J.U. Study on Crack Propagation of Adhesively Bonded DCB for Aluminum Foam Using Energy Release Rate. J. Mech. Sci. Technol. 2015, 29, 45–50. [Google Scholar] [CrossRef]
- Geleta, T.N.; Woo, K.; Cairns, D.S.; Samborsky, D. Failure Behavior of Inclined Thick Adhesive Joints with Manufacturing Defect. J. Mech. Sci. Technol. 2018, 32, 2173–2182. [Google Scholar] [CrossRef]
- Campilho, R.D.S.G.; Banea, M.D.; Neto, J.A.B.P.; da Silva, L.F.M. Modelling Adhesive Joints with Cohesive Zone Models: Effect of the Cohesive Law Shape of the Adhesive Layer. Int. J. Adhes. Adhes. 2013, 44, 48–56. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Crocombe, A.; Anwar, S.; Hu, P. The Strength Prediction of Adhesive Single Lap Joints Exposed to Long Term Loading in a Hostile Environment. Int. J. Adhes. Adhes. 2014, 55, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Sugiman, S.; Crocombe, A.; Aschroft, I. Modelling the Static Response of Unaged Adhesively Bonded Structures. Eng. Fract. Mech. 2013, 98, 296–314. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, M.A.; Abdul-Latif, A.; Tamin, M.N. Methodology for Extracting Interface Damage Properties of FRP Composite Laminates under Cyclic Shear Loading Conditions. In Proceedings of the 2017 3rd International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Johor Bahru, Malaysia, 4–6 April 2017; pp. 197–201. [Google Scholar]
- Zou, Z.; Reid, S.R.; Li, S. A Continuum Damage Model for Delaminations in Laminated Composites. J. Mech. Phys. Solids 2003, 51, 333–356. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. In Advances in Applied Mechanics; Dryden, H.L., von Kármán, T.H., Kuerti, G., van den Dungen, F.H., Howarth, L., Eds.; Elsevier: Amsterdam, The Netherlands, 1962; Volume 7, pp. 55–129. ISBN 0065-2156. [Google Scholar]
- Davila, C.G.; Camanho, P.P. Decohesion Elements Using Two and Three-Parameter Mixed-Mode Criteria. In Proceedings of the American Helicopter Society Conferen, Williamsburg, VA, USA, 29 October–1 November 2001. [Google Scholar]
- Kenane, M.; Benzeggagh, M.L. Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites under Fatigue Loading. Compos. Sci. Technol. 1997, 57, 597–605. [Google Scholar] [CrossRef]
- Campilho, R.D.; Banea, M.; Neto, J.; Da Silva, L. Modelling of Single-Lap Joints Using Cohesive Zone Models: Effect of the Cohesive Parameters on the Output of the Simulations. J. Adhes. 2012, 88, 513–533. [Google Scholar] [CrossRef]
- Jogi, B.; Brahmankar, P.; Nanda, V.; Prasad, R. Some Studies on Fatigue Crack Growth Rate of Aluminum Alloy 6061. J. Mater. Process. Technol. 2008, 201, 380–384. [Google Scholar] [CrossRef]
- Azevedo, J.; Campilho, R.; Da Silva, F.; Faneco, T.; Lopes, R. Cohesive Law Estimation of Adhesive Joints in Mode II Condition. Theor. Appl. Fract. Mech. 2015, 80, 143–154. [Google Scholar] [CrossRef]
- Johar, M.; Wong, K.; Rashidi, S.; Tamin, M. Effect of Strain-Rate and Moisture Content on the Mechanical Properties of Adhesively Bonded Joints. J. Mech. Sci. Technol. 2020, 34, 1837–1845. [Google Scholar] [CrossRef]







| Property | Araldite 2015 | Al6061-T6 |
|---|---|---|
| Young’s modulus, E (GPa) | 1.85 | 69 |
| Poisson’s ratio, υ | 0.33 | 0.33 |
| Yield strength, (MPa) | 12.63 | 289 |
| Tensile strength, (MPa) | 21.63 | 328 |
| Curing temperature/time (°C/min) | 60/35 | - |
| Glass transition temperature/time (°C/min) | 67 | - |
| Displacement Rate (mm/min) | 5 | 50 | 500 | |
|---|---|---|---|---|
| Parameters | ||||
| Penalty stiffness, kn (N/mm3) | 1.4 × 105 | 1.7 × 105 | 2.0 × 106 | |
| Normal strength, N (MPa) | 19.82 | 28.02 | 36.76 | |
| Fracture energy, GIC (N/mm) | 0.092 | 0.082 | 0.081 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, S.A.; Rahimian Koloor, S.S.; King Jye, W.; Yidris, N.; Mohd Yusof, A.A.; Mohd Szali Januddi, M.A.F.; Tamin, M.N.; Johar, M. Strain Rate Effect on Mode I Debonding Characterization of Adhesively Bonded Aluminum Joints. Processes 2023, 11, 81. https://doi.org/10.3390/pr11010081
Khan SA, Rahimian Koloor SS, King Jye W, Yidris N, Mohd Yusof AA, Mohd Szali Januddi MAF, Tamin MN, Johar M. Strain Rate Effect on Mode I Debonding Characterization of Adhesively Bonded Aluminum Joints. Processes. 2023; 11(1):81. https://doi.org/10.3390/pr11010081
Chicago/Turabian StyleKhan, Safdar Ali, Seyed Saeid Rahimian Koloor, Wong King Jye, Noorfaizal Yidris, Ab Aziz Mohd Yusof, Mohd Al Fatihhi Mohd Szali Januddi, Mohd Nasir Tamin, and Mahzan Johar. 2023. "Strain Rate Effect on Mode I Debonding Characterization of Adhesively Bonded Aluminum Joints" Processes 11, no. 1: 81. https://doi.org/10.3390/pr11010081








