Thin-Film Carbon Nitride (C2N)-Based Solar Cell Optimization Considering Zn1−xMgxO as a Buffer Layer
Abstract
:1. Introduction
2. Numerical Modeling and Simulation Parameters
3. Results and Discussion
3.1. Energy Band Alignment
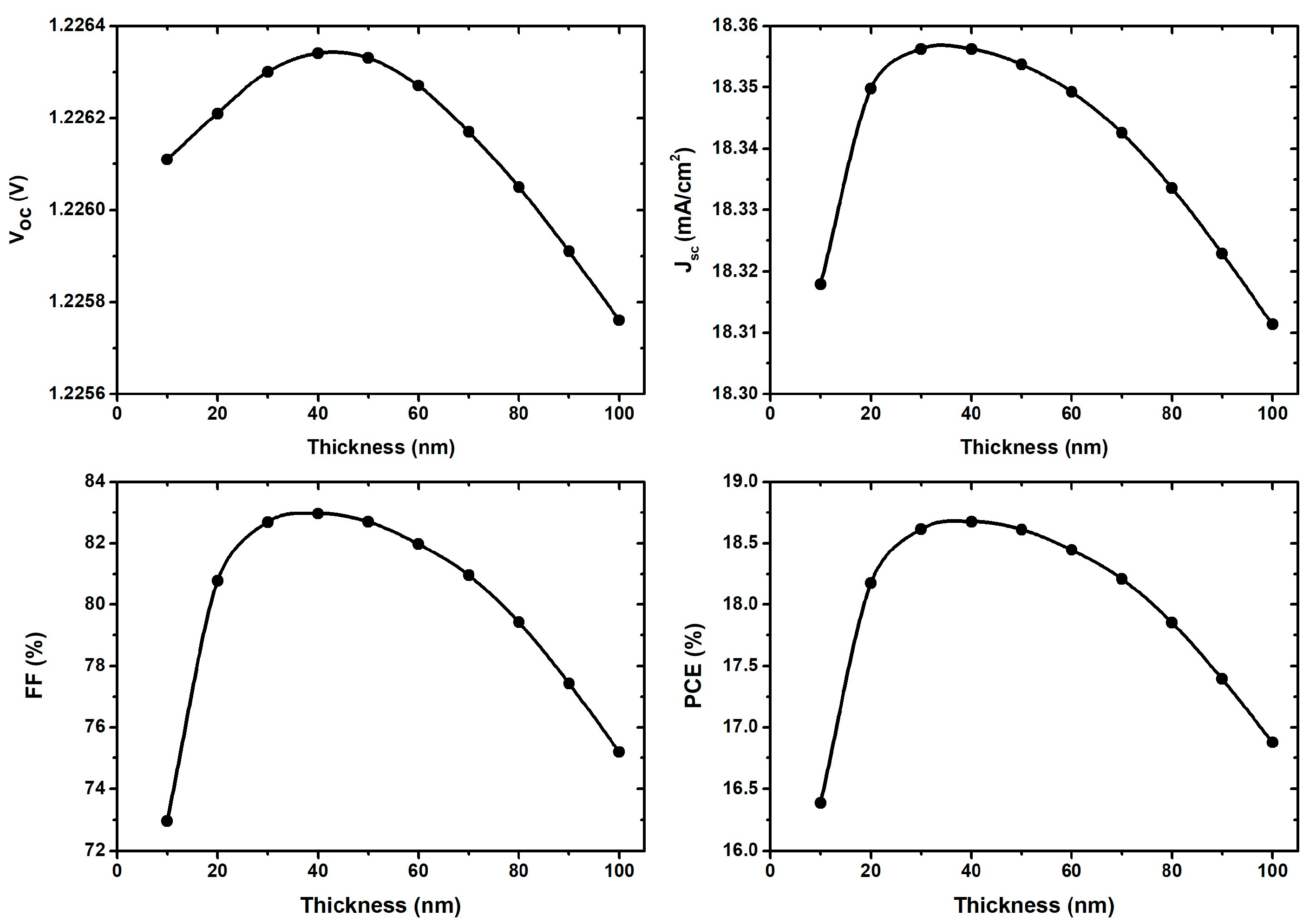
3.2. Thickness Optimization of the C2N Layer
3.3. Impact of C2N Defect Density
3.4. Influence of C2N-Doping Density
3.5. Thickness Optimization of the Buffer Layer
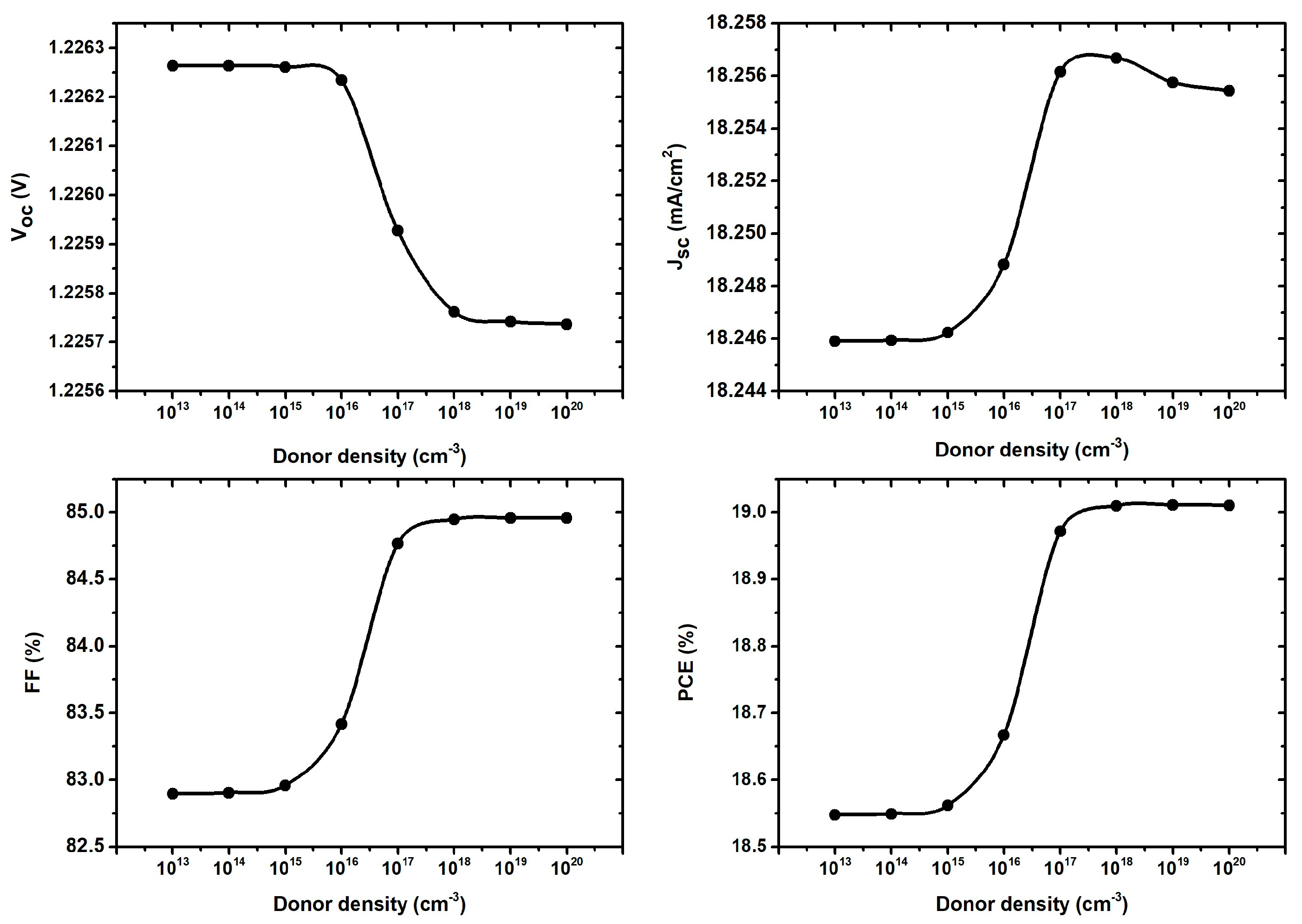
3.6. Optimization of the Buffer Layer Doping Density
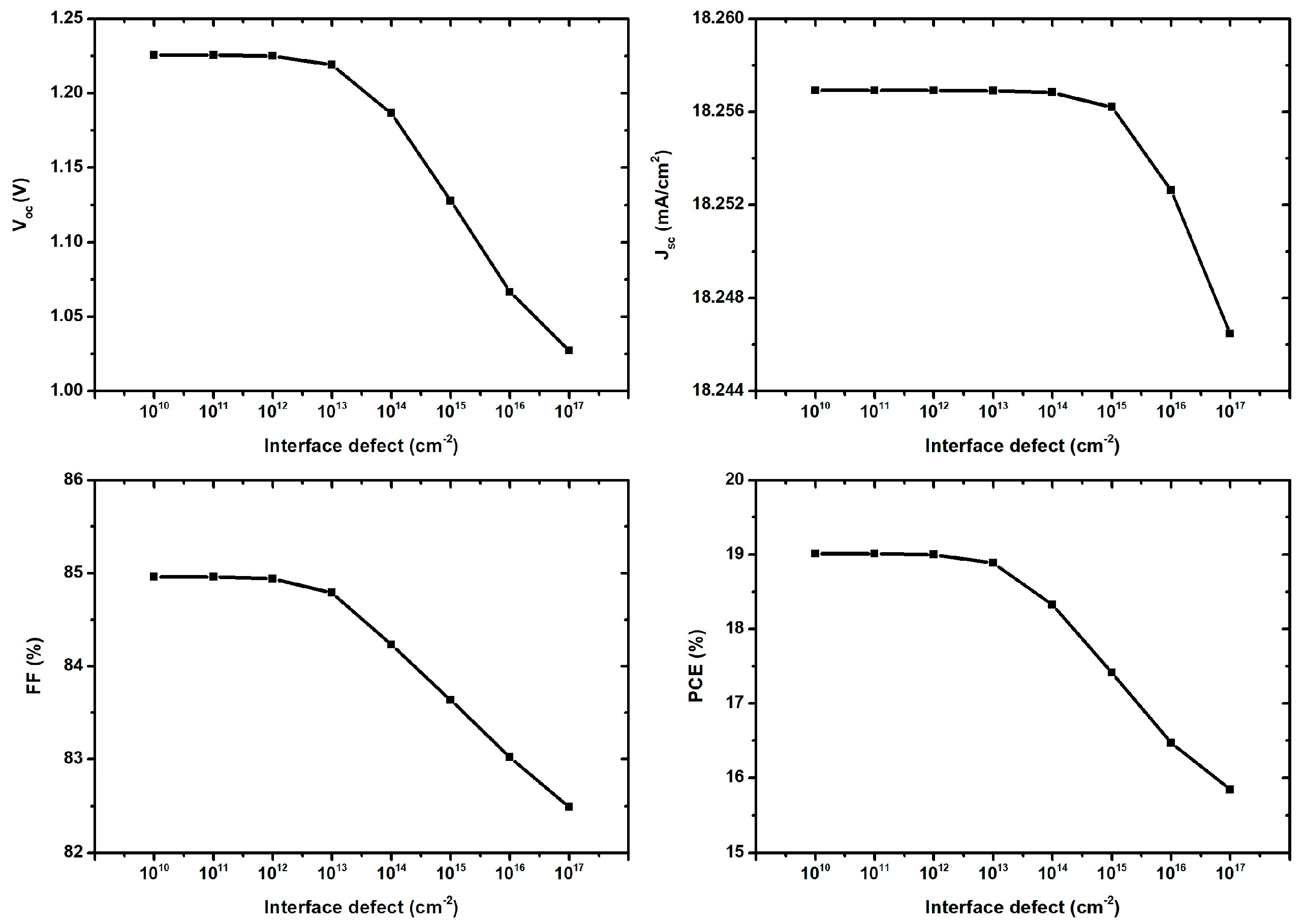
3.7. Effect of the Interface Defect of C2N/ZMO
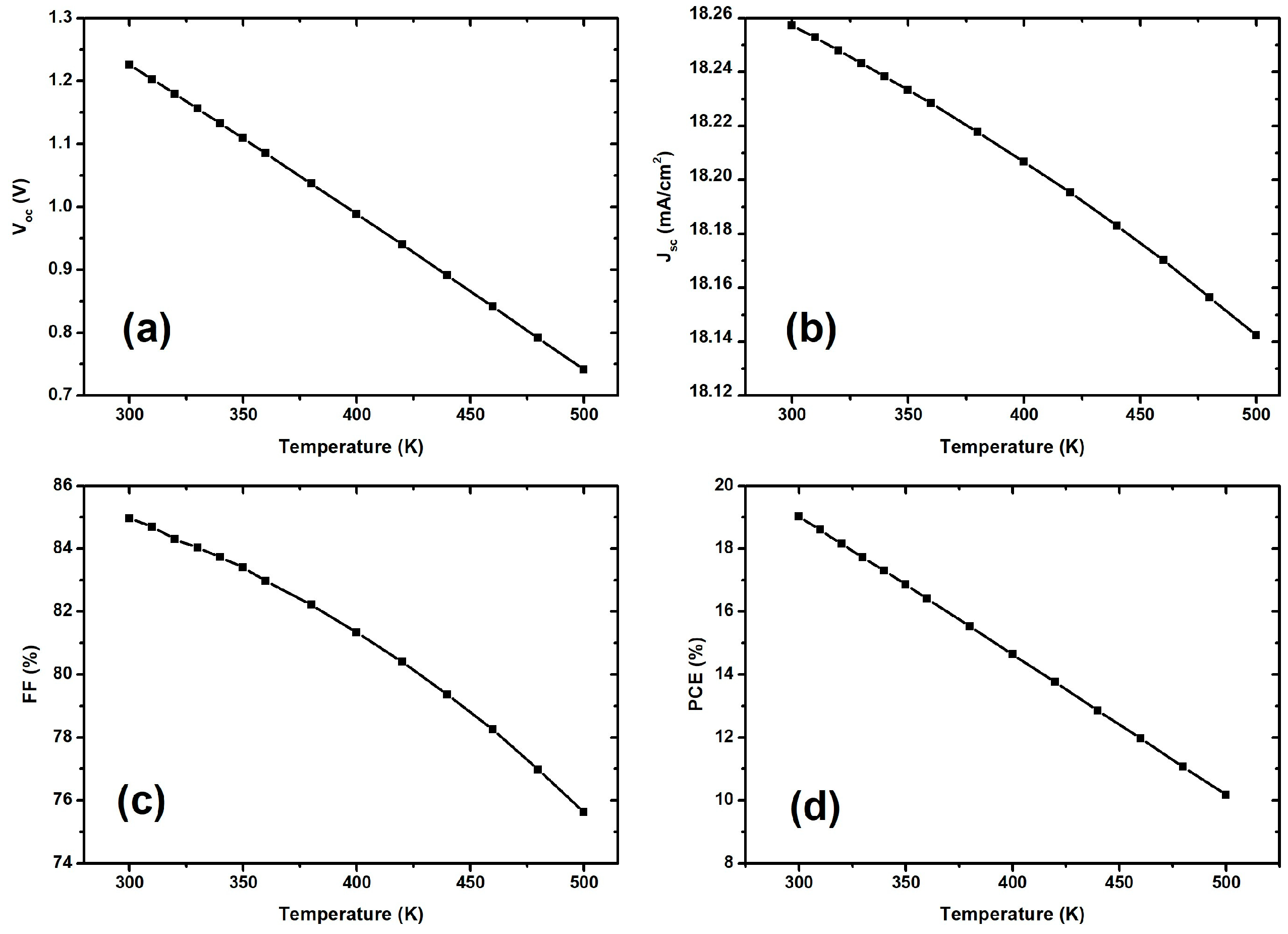
3.8. Impact of Temperature Variation on the Device Performance
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Raha, S.; Pal, S. A Study on the Present Environmental Scenario due to Pollution by Conventional Energy Sources—And Remedies: Solar Cell with Nanotechnology. Strat. Plan. Energy Environ. 2010, 30, 8–19. [Google Scholar] [CrossRef]
- Suri, M.; Betak, J.; Rosina, K.; Chrkavy, D.; Suriova, N.; Cebecauer, T.; Caltik, M.; Erdelyi, B. Global Photovoltaic Power Potential by Country; ESMAP: Washington, DC, USA, 2020. [Google Scholar]
- Soley, S.S.; Dwivedi, A.D.D. Advances in high efficiency crystalline silicon homo junction solar cell technology. AIP Conf. Proc. 2019, 2104, 030033. [Google Scholar] [CrossRef]
- Kuddus, A.; Ismail, A.B.M.; Hossain, J. Design of a highly efficient CdTe-based dual-heterojunction solar cell with 44% predicted efficiency. Sol. Energy 2021, 221, 488–501. [Google Scholar] [CrossRef]
- Zhang, W.-W.; Qi, H.; Ji, Y.-K.; He, M.-J.; Ren, Y.-T.; Li, Y. Boosting photoelectric performance of thin film GaAs solar cell based on multi-objective optimization for solar energy utilization. Sol. Energy 2021, 230, 1122–1132. [Google Scholar] [CrossRef]
- Farooq, W.; Alshahrani, T.; Kazmi, S.A.A.; Iqbal, J.; Khan, H.A.; Khan, M.; Raja, A.A.; Rehman, A.U. Materials Optimization for thin-film copper indium gallium selenide (CIGS) solar cell based on distributed braggs reflector. Optik 2021, 227, 165987. [Google Scholar] [CrossRef]
- Bangash, K.; Kazmi, S.; Farooq, W.; Ayub, S.; Musarat, M.; Alaloul, W.; Javed, M.; Mosavi, A. Thickness Optimization of Thin-Film Tandem Organic Solar Cell. Micromachines 2021, 12, 518. [Google Scholar] [CrossRef]
- Gusain, A.; Faria, R.M.; Miranda, P.B. Polymer Solar Cells—Interfacial Processes Related to Performance Issues. Front. Chem. 2019, 7, 61. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yasin, S.; Al Zoubi, T.; Moustafa, M. Design and simulation of high efficiency lead-free heterostructure perovskite solar cell using SCAPS-1D. Optik 2021, 229, 166258. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, R.; Li, X.; Yang, J. A many-body GW+ BSE investigation of electronic and optical properties of C2N. Appl. Phys. Lett. 2016, 13, 133108. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Mahmood, J.; Dou, Y.; Dou, S.; Li, F.; Dai, L.; Beak, J.B. 2D frameworks of C2N and C3N as new anode materials for lithium-ion batteries. Adv. Mater. 2017, 34, 1702007. [Google Scholar] [CrossRef]
- Tsoeu, S.E. First-Principles Design of Hybrid Carbon Nitride (C2n) with Gallium Sulphide and Gallium Selenide Two-Dimensional (2D) Materials as High-Performance Photovoltaic Cells; University of Johannesburg: Johannesburg, South Africa, 2021. [Google Scholar]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically thin MoS2: A new direct-gap semiconductor. Phys. Rev. Lett. 2010, 13, 136805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roy, S.; Bermel, P. Electronic and optical properties of ultra-thin 2D tungsten disulfide for photovoltaic applications. Sol. Energy Mater. Sol. Cells 2018, 174, 370–379. [Google Scholar] [CrossRef]
- Tiwari, S.K.; Sahoo, S.; Wang, N.; Huczko, A. Graphene research and their outputs: Status and prospect. J. Sci. Adv. Mater. Devices 2020, 5, 10–29. [Google Scholar] [CrossRef]
- Mahmood, J.; Lee, E.K.; Jung, M.; Shin, D.; Jeon, I.-Y.; Jung, S.-M.; Choi, H.-J.; Seo, J.-M.; Bae, S.-Y.; Sohn, S.-D.; et al. Nitrogenated holey two-dimensional structures. Nat. Commun. 2015, 6, 6486. [Google Scholar] [CrossRef] [Green Version]
- Sahin, H. Structural and phononic characteristics of nitrogenated holey graphene. Phys. Rev. B 2015, 92, 085421. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Han, J. Design and simulation of C2N based solar cell by SCAPS-1D software. Mater. Res. Express 2020, 7, 126303. [Google Scholar] [CrossRef]
- Yasin, S.; Abu Waar, Z.; Al Zoubi, T.; Moustafa, M. Optoelectronic simulation of a high efficiency C2N based solar cell via buffer layer optimization. Opt. Mater. 2021, 119, 111364. [Google Scholar] [CrossRef]
- Minemoto, T.; Murata, M. Theoretical analysis on effect of band offsets in perovskite solar cells. Sol. Energy Mater. Sol. Cells 2015, 133, 8–14. [Google Scholar] [CrossRef]
- Peelaers, H.; Kioupakis, E.; Van de Walle, C.G. Fundamental limits on optical transparency of transparent conducting oxides: Free-carrier absorption in SnO. Appl. Phys. Lett. 2012, 100, 011914. [Google Scholar] [CrossRef] [Green Version]
- Kephart, J.; McCamy, J.; Ma, Z.; Ganjoo, A.; Alamgir, F.; Sampath, W. Band alignment of front contact layers for high-efficiency CdTe solar cells. Sol. Energy Mater. Sol. Cells 2016, 157, 266–275. [Google Scholar] [CrossRef]
- Ke, Y.; Lany, S.; Berry, J.J.; Perkins, J.D.; Parilla, P.A.; Zakutayev, A.; Ohno, T.; O’Hayre, R.; Ginley, D.S. Enhanced Electron Mobility Due to Dopant-Defect Pairing in Conductive ZnMgO. Adv. Funct. Mater. 2014, 24, 2875–2882. [Google Scholar] [CrossRef]
- Bahfir, A.; Boumaour, M.; Kechouane, M. Prospects of potential ZnMgO front layer in CZTS solar cells. Optik 2018, 169, 196–202. [Google Scholar] [CrossRef]
- Ren, S.; Wang, H.; Li, Y.; Li, H.; He, R.; Wu, L.; Li, W.; Zhang, J.; Wang, W.; Feng, L. Rapid thermal annealing on ZnMgO window layer for improved performance of CdTe solar cells. Sol. Energy Mater. Sol. Cells 2018, 187, 97–103. [Google Scholar] [CrossRef]
- Ren, S.; Li, H.; Lei, C.; Li, C.; Yin, X.; Wu, L.; Li, W.; Zhang, J.; Wang, W.; Feng, L. Interface modification to enhance electron extraction by deposition of a ZnMgO buffer on SnO2-coated FTO in CdTe solar cells. Sol. Energy 2018, 177, 545–552. [Google Scholar] [CrossRef]
- Mohammadnejad, S.; Bahnamiri, Z.M.; Maklavani, S.E. Enhancement of the performance of kesterite thin-film solar cells using dual absorber and ZnMgO buffer layers. Superlattices Microstruct. 2020, 144, 106587. [Google Scholar] [CrossRef]
- Burgelman, M.M. Simulation Programme SCAPS-1D for Thin Film Solar Cells Developed at ELIS, University of Gent. Available online: https://scaps.elis.ugent.be/ (accessed on 2 February 2022).
- Anwar, F.; Mahbub, R.; Satter, S.S.; Ullah, S.M. Effect of Different HTM Layers and Electrical Parameters on ZnO Nanorod-Based Lead-Free Perovskite Solar Cell for High-Efficiency Performance. Int. J. Photoenergy 2017, 2017, 9846310. [Google Scholar] [CrossRef]
- Adewoyin, A.D.; Olopade, M.A.; Oyebola, O.O.; Chendo, M.A. Development of CZTGS/CZTS tandem thin film solar cell using SCAPS-1D. Optik 2018, 176, 132–142. [Google Scholar] [CrossRef]
- He, X.; Wu, L.; Hao, X.; Zhang, J.; Li, C.; Wang, W.; Feng, L.; Du, Z. The Band Structures of Zn1−xMgxO (In) and the simulation of CdTe solar cells with a Zn1−xMgxO (In) window layer by SCAPS. Energies 2019, 2, 291. [Google Scholar] [CrossRef] [Green Version]
- Gamal, N.; Sedky, S.H.; Shaker, A.; Fedawy, M. Design of lead-free perovskite solar cell using Zn1−xMgxO as ETL: SCAPS device simulation. Optik 2021, 242, 167306. [Google Scholar] [CrossRef]
- He, X.; Song, Y.; Wu, L.; Li, C.; Zhang, J.; Feng, L. Simulation of high-efficiency CdTe solar cells with Zn1−xMgxO window layer by SCAPS software. Mater. Res. Express 2018, 6, 065907. [Google Scholar] [CrossRef]
- Michaelson, H.B. The work function of the elements and its periodicity. J. Appl. Phys. 1977, 48, 4729–4733. [Google Scholar] [CrossRef] [Green Version]
- Fox, M. Optical Properties of Solids; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Araujo, P.T.; Terrones, M.; Dresselhaus, M.S. Defects and impurities in graphene-like materials. Mater. Today 2012, 15, 98–109. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, X.; Yang, G.; Zhou, X. Point Defect Effects on Photoelectronic Properties of the Potential Metal-Free C2N Photocatalysts: Insight from First-Principles Computations. J. Phys. Chem. 2018, 122, 5291–5302. [Google Scholar] [CrossRef]
- Zhong, J.-H.; Zhang, J.; Jin, X.; Liu, J.-Y.; Li, Q.; Li, M.-H.; Cai, W.; Wu, D.-Y.; Zhan, D.; Ren, B. Quantitative Correlation between Defect Density and Heterogeneous Electron Transfer Rate of Single Layer Graphene. J. Am. Chem. Soc. 2014, 136, 16609–16617. [Google Scholar] [CrossRef] [PubMed]
- Gawlik, G.; Ciepielewski, P.; Baranowski, J.M. Study of Implantation Defects in CVD Graphene by Optical and Electrical Methods. Appl. Sci. 2019, 9, 544. [Google Scholar] [CrossRef] [Green Version]
- Haider, S.Z.; Anwar, H.; Wang, M. A comprehensive device modelling of perovskite solar cell with inorganic copper iodide as hole transport material. Semicond. Sci. Technol. 2018, 33, 035001. [Google Scholar] [CrossRef] [Green Version]
- Ouslimane, T.; Et-Taya, L.; Elmaimouni, L.; Benami, A. Impact of absorber layer thickness, defect density, and operating temperature on the performance of MAPbI3 solar cells based on ZnO electron transporting material. Heliyon 2021, 7, e06379. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Bi, X.; Liu, Y.; Qin, B.; Li, Q.; Jiang, Q.; Mo, P. Numerical Investigation Energy Conversion Performance of Tin-Based Perovskite Solar Cells Using Cell Capacitance Simulator. Energies 2020, 13, 5907. [Google Scholar] [CrossRef]
- Sarilmaz, A.; Ozel, F.; Aljabour, A.; Khaskheli, A.R.; Kus, M. Effect of doping on thin film solar cell efficiency based on ZnMn2O4 nanocrystals. Mater. Today Proc. 2019, 18, 1861–1867. [Google Scholar] [CrossRef]
- Trukhanov, V.A.; Bruevich, V.V.; Paraschuk, D. Effect of doping on performance of organic solar cells. Phys. Rev. B 2011, 84, 205318. [Google Scholar] [CrossRef]
- Chowdhury, M.; Shahahmadi, S.; Chelvanathan, P.; Tiong, S.; Amin, N.; Techato, K.; Nuthammachot, N.; Chowdhury, T.; Suklueng, M. Effect of deep-level defect density of the absorber layer and n/i interface in perovskite solar cells by SCAPS-1D. Results Phys. 2020, 16, 102839. [Google Scholar] [CrossRef]
- Shockley, W.; Read, W., Jr. Statistics of the recombinations of holes and electrons. Phys. Rev. 1952, 5, 835. [Google Scholar] [CrossRef]
- Mandadapu, U.; Vedanayakam, S.V.; Thyagarajan, K.; Babu, B. Optimisation of high efficiency tin halide perovskite solar cells using SCAPS-1D. Int. J. Simul. Process Model. 2018, 3, 221–227. [Google Scholar] [CrossRef]
- Alzoubi, T.; Moustafa, M. Numerical optimization of absorber and CdS buffer layers in CIGS solar cells using SCAPS. Int. J. Smart Grid Clean Energy 2019, 8, 291–298. [Google Scholar] [CrossRef]
- Jhuma, F.A.; Shaily, M.Z.; Rashid, M.J. Towards high-efficiency CZTS solar cell through buffer layer optimization. Mater. Renew. Sustain. Energy 2019, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Zandi, S.; Seresht, M.J.; Khan, A.; Gorji, N.E. Simulation of heat loss in Cu2ZnSn4SxSe4−x thin film solar cells: A coupled optical-electrical-thermal modeling. Renew. Energy 2022, 181, 320–328. [Google Scholar] [CrossRef]

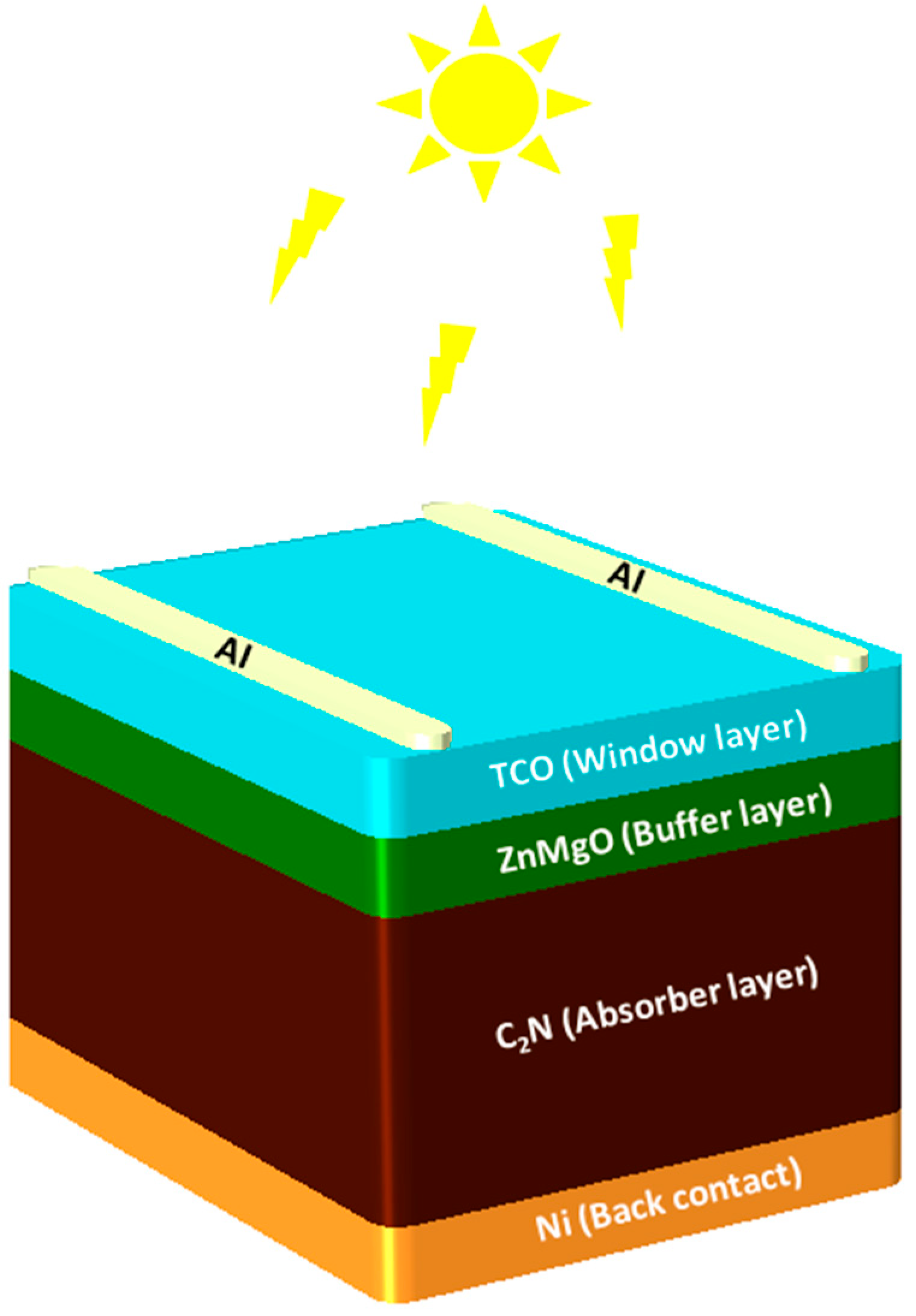

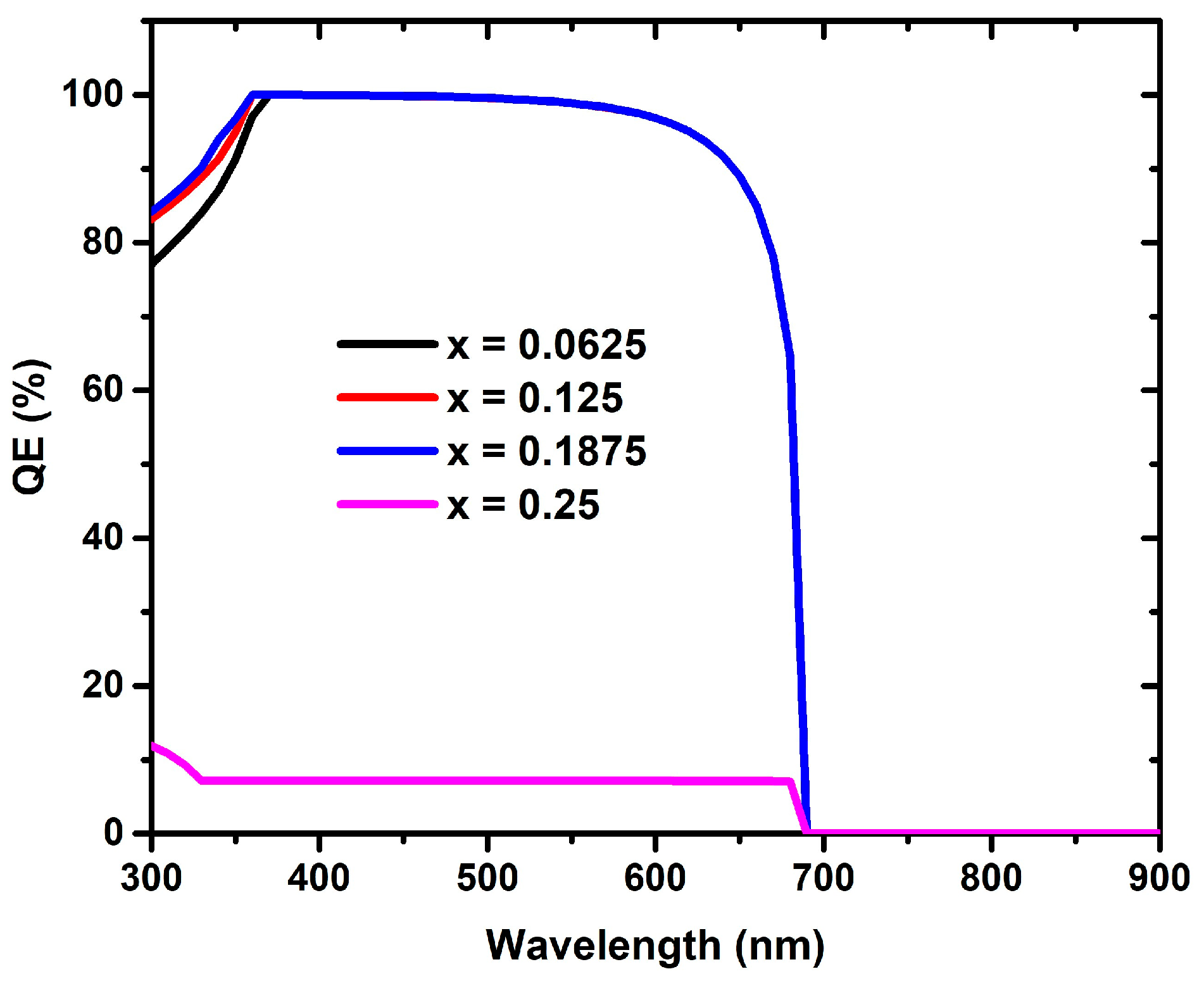
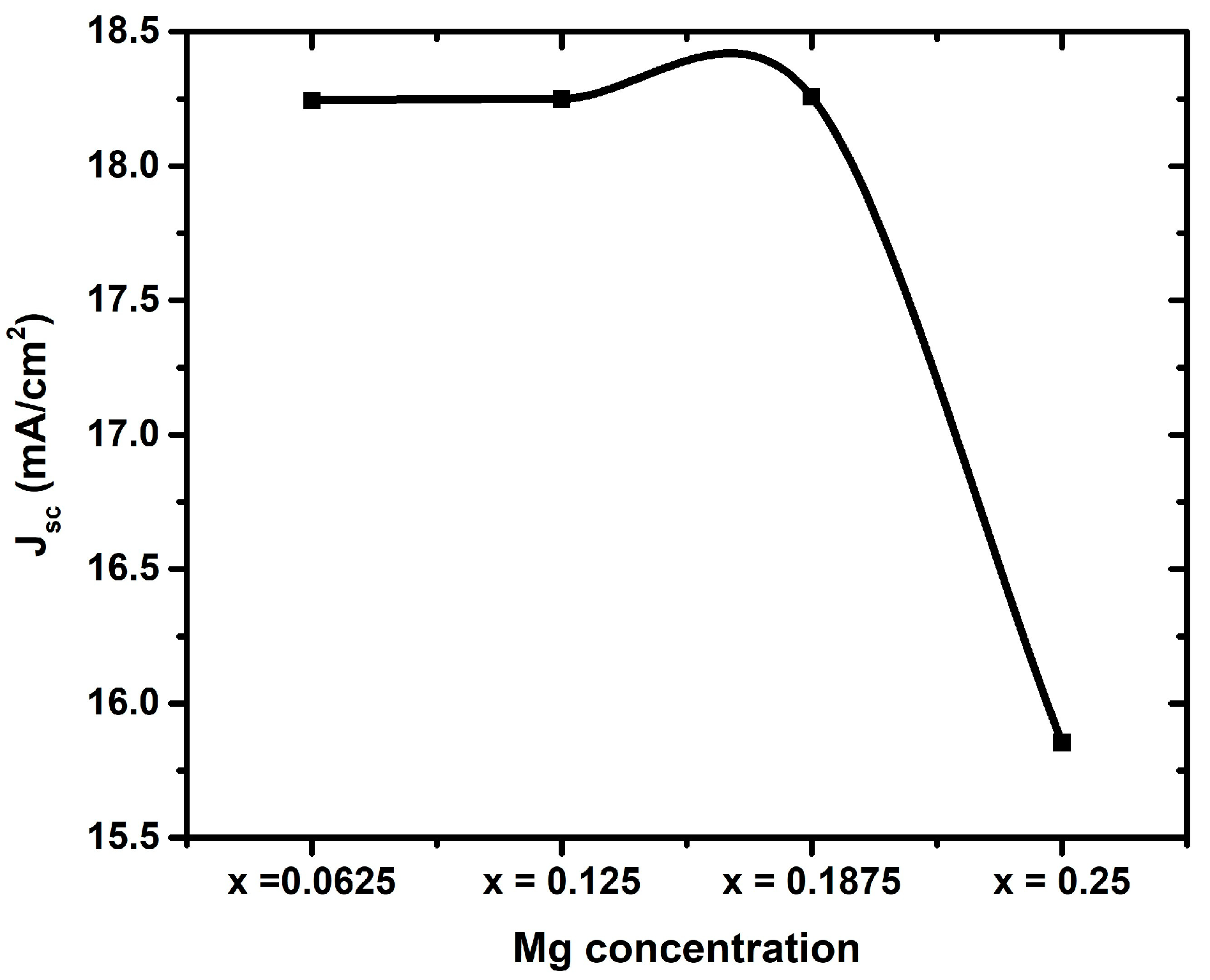

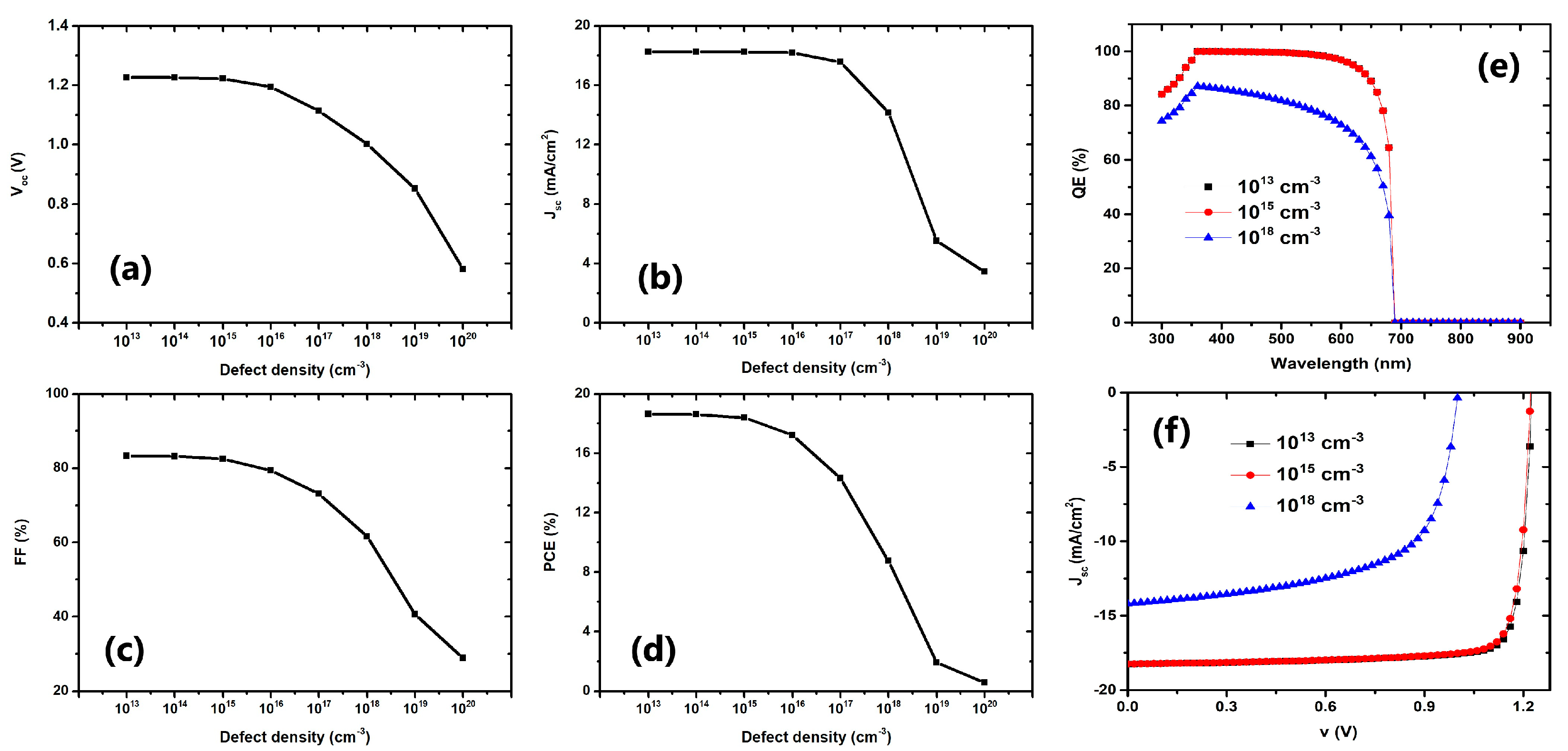

| Parameters | TCO [19,32] | Zn1−xMgxO [31,32,33] | C2N [18,19] | |||
|---|---|---|---|---|---|---|
| x = 0.0625 | x = 0.125 | x = 0.1875 | x = 0.25 | |||
| Thickness (nm) | 30 | 30 | 30 | 30 | 30 | 300 |
| Band gap (eV) | 3.5 | 3.41 | 3.48 | 3.65 | 3.82 | 1.8 |
| Electron affinity (eV) | 4 | 4.44 | 4.37 | 4.21 | 4.03 | 4.42 |
| Dielectric Permittivity | 9 | 9 | 9 | 9 | 9 | 4.5 |
| CB-effective density of states (cm−3) | 2.2 × 1018 | 1 × 1017 | 9 × 1016 | 1 × 1016 | 1 × 1015 | 1 × 1019 |
| VB-effective density of states (cm−3) | 1.8 × 1019 | 1 × 1018 | 9 × 1017 | 1 × 1017 | 1 × 1016 | 1 × 1015 |
| Electron thermal velocity (cm/s) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| Hole thermal velocity (cm/s) | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 | 1 × 107 |
| Electron mobility (cm2/(V·s)) | 20 | 50 | 50 | 50 | 50 | 13 |
| Hole mobility (cm2/(V·s)) | 10 | 20 | 20 | 20 | 20 | 20.6 |
| Donor doping concentration (cm−3) | 1 × 1014 | 1 × 1014 | 1 × 1014 | 1 × 1014 | 1 × 1014 | 0 |
| Acceptor doping concentration (cm−3) | 0 | 0 | 0 | 0 | 0 | 1 × 1014 |
| Defect density Nt (cm−3) | 1 × 1014 | 1 × 1014 | 1 × 1014 | 1 × 1014 | 1 × 1014 | 1 × 1014 |
| Defect type | Neutral | Neutral | Neutral | Neutral | Neutral | Neutral |
| Defect distribution | Single | Single | Single | Single | Single | Gaussian |
| Parameters | TCO/ZMO | ZMO/C2N |
|---|---|---|
| Defect type | Neutral | Neutral |
| Capture cross section of electrons (cm2) | 1 × 10−19 | 1 × 10−19 |
| Capture cross section of holes (cm2) | 1 × 10−19 | 1 × 10−19 |
| Energetic distribution | Single | Single |
| Energy level with respect to Ev (eV) | 0.6 | 0.6 |
| Major carrier barrier height relative to Ef (eV) | SCAPS | SCAPS |
| Major carrier barrier height relative to Ev (eV) | SCAPS | SCAPS |
| Parameters | Back-Contact Metal Electrode | Front-Contact Metal Electrode |
|---|---|---|
| Surface recombination velocity of electrons (cms−1) | 105 | 107 |
| Surface recombination velocity of holes (cms−1) | 107 | 105 |
| Work function (eV) | 5.35 Ni (111) [34] | 4.06 (AI) [34] |
| Working temperature (K) | 300 |
| Buffer Layer | CBO (eV) |
|---|---|
| C2N/Zn1−xMgxO (x = 0.0625) | −0.02 |
| C2N/Zn1−xMgxO (x = 0.125) | 0.05 |
| C2N/Zn1−xMgxO (x = 0.1875) | 0.21 |
| C2N/Zn1−xMgxO (x = 0.25) | 0.39 |
| Simulated Parameters | Zn1−xMgxO | |||
|---|---|---|---|---|
| x = 0.0652 | x = 0.125 | x = 0.1875 | x = 0.25 | |
| Voc (V) | 1.23 | 1.23 | 1.23 | 1.21 |
| Jsc (mA/cm2) | 18.24 | 18.25 | 18.26 | 18.23 |
| FF (%) | 84.89 | 84.94 | 84.96 | 79.25 |
| PCE (%) | 18.98 | 19 | 19.01 | 17.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, W.; Farooq, W.; Khan, A.D.; Jan, S.T.; Jasiński, M.; Leonowicz, Z.; Gono, R.; Petrov, J. Thin-Film Carbon Nitride (C2N)-Based Solar Cell Optimization Considering Zn1−xMgxO as a Buffer Layer. Processes 2023, 11, 91. https://doi.org/10.3390/pr11010091
Ahmad W, Farooq W, Khan AD, Jan ST, Jasiński M, Leonowicz Z, Gono R, Petrov J. Thin-Film Carbon Nitride (C2N)-Based Solar Cell Optimization Considering Zn1−xMgxO as a Buffer Layer. Processes. 2023; 11(1):91. https://doi.org/10.3390/pr11010091
Chicago/Turabian StyleAhmad, Waqas, Waqas Farooq, Adnan Daud Khan, Shayan Tariq Jan, Michał Jasiński, Zbigniew Leonowicz, Radomir Gono, and Jan Petrov. 2023. "Thin-Film Carbon Nitride (C2N)-Based Solar Cell Optimization Considering Zn1−xMgxO as a Buffer Layer" Processes 11, no. 1: 91. https://doi.org/10.3390/pr11010091
APA StyleAhmad, W., Farooq, W., Khan, A. D., Jan, S. T., Jasiński, M., Leonowicz, Z., Gono, R., & Petrov, J. (2023). Thin-Film Carbon Nitride (C2N)-Based Solar Cell Optimization Considering Zn1−xMgxO as a Buffer Layer. Processes, 11(1), 91. https://doi.org/10.3390/pr11010091











