Integration of Bayesian Adaptive Exponentially Weighted Moving Average Control Chart and Paired Ranked-Based Sampling for Enhanced Semiconductor Manufacturing Process Monitoring
Abstract
:1. Introduction
2. Bayesian Approach
2.1. Squared Error Loss Function
2.2. Linex Loss Function
3. Paired Ranked Set Sampling
3.1. Extreme Pair Ranked Set Sampling
3.2. Quartile Pair Ranked Set Sampling
4. Proposed AEWMA CC Utilizing Bayesian Approach with Different PRSS Schemes under LF
5. Simulation Study
- While determining the mean and variance of both the P distribution and PP distribution applying various LFs, we utilized the standard normal distribution as both the sampling and prior distribution. This entailed determining values such as and for various LFs;
- When employing a fixed smoothing constant (ψ) in a mathematical or statistical context, it is crucial to select a suitable value for another parameter referred to as “h”. This choice of ‘h’ can significantly impact the performance or behavior of the system or model being studied;
- Select a paired ranked set sample with a size of “n” from a population that follows a normal distribution, as a representation of an in-control process, i.e., ;
- Determine the plotting statistic as specified in Equation (22) and proceed with the process evaluation.
- If it is confirmed that the process is under control, proceed with the described steps iteratively until an out-of-control signal is identified, while maintaining a record of the consecutive in-control run lengths.
- Generate a random sample obtained from a normal distribution, where the mean has been intentionally adjusted or shifted from its usual position, i.e., ;
- Compute the value of Wt and evaluate the procedure by applying the proposed AEWMA CC within the Bayesian framework, utilizing different PRSS designs.
5.1. ARL Methods
5.1.1. Zero State ARL
5.1.2. Steady State ARL
6. Results, Discussions, and Findings
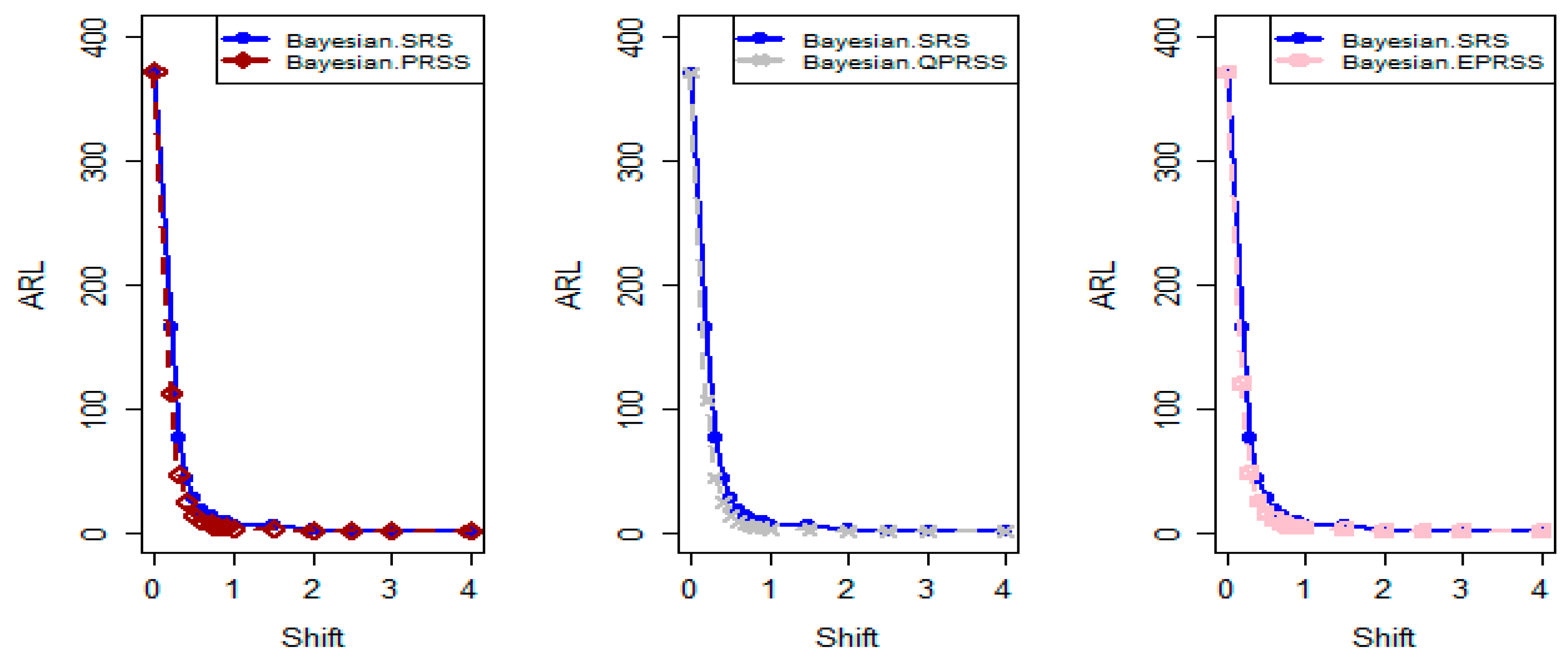
- The run length results of the provided Bayesian CC using the SELF across different PRSS schemes exhibit a rapid decrease as the mean shift increases. This observation suggests that the proposed method is unbiased, as evidenced in Table 1 and Table 2. For example, from Table 1 at and smoothing constant at various shifts, i.e., 𝛿 = 0.20 and 0.70. The ARL outcomes are 42.72 and 4.03 for PRSS, 42.35 and 4.55 for QPRSS, and the values of ARL for EPRSS are 41.79 and 4.48;
- From Table 3 and Table 4, it can be observed that the proposed technique can be affected with changes in the value of the smoothing constant, i.e., and . Under LLF, the results of ARL and SDRL for the proposed method with posterior distribution are displayed in Table 3 and Table 4, which indicate that the efficiency decreases with increase in the value of smoothing constant for the proposed method. For example, at , and shift 𝛿 = 0.20; however, the respective ARL values for the proposed method under PRSS, QPRSS, and EPRSS are 40.78, 38.42, and 40.47. For the same shift 𝛿 = 0.20 and , the value of ARL for PRSS is 66.76, under QPRSS is 64.23, and under EPRSS is 60.82;
- For the proposed method the results of ARL under PRSS are shown in Table 5 and Table 6. They show that the offered CC uses PRSS schemes under LLF for P and PP distribution at , 𝛿 = 0.50 and smoothing constant is 9.35 and the ARL value at is 11.28; in a similar case the ARL for QPRSS are 9.41 and 10.79. The ARL values using EPRSS are 9.32 and 10.91;
- From Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, we can see that the recommended Bayesian AEWMA CC is quite vulnerable in identifying out-of-control signals as compared with existing AEWMA CC applying SRS, according to the data (see Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7).
7. Real Data Applications
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shewhart, W.A. The application of statistics as an aid in maintaining quality of a manufactured product. J. Am. Stat. Assoc. 1925, 20, 546–548. [Google Scholar] [CrossRef]
- Page, E.S. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Roberts, S. CC tests based on geometric moving averages. Technometrics 1959, 42, 97–101. [Google Scholar] [CrossRef]
- Lu, C.-W.; Reynolds, M.R., Jr. EWMA CCs for monitoring the mean of autocorrelated processes. J. Qual. Technol. 1999, 31, 166–188. [Google Scholar] [CrossRef]
- Knoth, S. Accurate ARL computation for EWMA-S2 CCs. Stat. Comput. 2005, 15, 341–352. [Google Scholar] [CrossRef]
- Maravelakis, P.E.; Castagliola, P. An EWMA chart for monitoring the process standard deviation when parameters are estimated. Comput. Stat. Data Anal. 2015, 53, 2653–2664. [Google Scholar] [CrossRef]
- Chiu, J.-E.; Tsai, C.-H. Monitoring high-quality processes with one-sided conditional cumulative counts of conforming chart. J. Ind. Prod. Eng. 2015, 32, 559–565. [Google Scholar] [CrossRef]
- Noor-ul-Amin, M.; Tayyab, M. Enhancing the performance of exponential weighted moving average CC using paired double ranked set sampling. J. Stat. Comput. Simul. 2020, 90, 1118–1130. [Google Scholar] [CrossRef]
- Haq, A.; Woodall, W.H. A critique of the use of modified and moving average-based EWMA control charts. Qual. Reliab. Eng. Int. 2023, 39, 1269–1276. [Google Scholar] [CrossRef]
- Yeganeh, A.; Parvizi Amineh, M.; Shadman, A.; Shongwe, S.C.; Mohasel, S.M. Combination of Sequential Sampling Technique with GLR Control Charts for Monitoring Linear Profiles Based on the Random Explanatory Variables. Mathematics 2023, 11, 1683. [Google Scholar] [CrossRef]
- Riaz, M.; Zaman, B.; Raji, I.A.; Omar, M.H.; Mehmood, R.; Abbas, N. An Adaptive EWMA Control Chart Based on Principal Component Method to Monitor Process Mean Vector. Mathematics 2022, 10, 2025. [Google Scholar] [CrossRef]
- Woodall, W.H.; Haq, A.; Mahmoud, M.A.; Saleh, N.A. Reevaluating the performance of control charts based on ranked-set sampling. Qual. Eng. 2023, 1–6. [Google Scholar] [CrossRef]
- Haq, A.; Gulzar, R.; Khoo, M.B. An efficient adaptive EWMA CC for monitoring the process mean. Qual. Reliab. Eng. Int. 2018, 34, 563–571. [Google Scholar] [CrossRef]
- Sabahno, H.; Amiri, A.; Castagliola, P. A new adaptive control chart for the simultaneous monitoring of the mean and variability of multivariate normal processes. Comput. Ind. Eng. 2021, 151, 106524. [Google Scholar] [CrossRef]
- Santore, F.; Taconeli, C.A.; Rodrigues de Lara, I.A. An adaptive control chart for the process location based on ranked set sampling. Commun. Stat. Simul. Comput. 2021, 50, 3364–3382. [Google Scholar] [CrossRef]
- Capizzi, G.; Masarotto, G. An adaptive exponentially weighted moving average CC. Technometrics 2003, 45, 199–207. [Google Scholar] [CrossRef]
- Jiang, W.; Shu, L.; Apley, D.W. Adaptive CUSUM procedures with EWMA-based shift estimators. IIE Trans. 2008, 40, 992–1003. [Google Scholar] [CrossRef]
- Wu, Z.; Jiao, J.; Yang, M.; Liu, Y.; Wang, Z. An enhanced adaptive CUSUM CC. IIE Trans. 2009, 41, 642–653. [Google Scholar] [CrossRef]
- Huang, W.; Shu, L.; Su, Y. An accurate evaluation of adaptive exponentially weighted moving average schemes. IIE Trans. 2014, 46, 457–469. [Google Scholar] [CrossRef]
- Aly, A.A.; Saleh, N.A.; Mahmoud, M.A.; Woodall, W.H. A reevaluation of the adaptive exponentially weighted moving average CC when parameters are estimated. Qual. Reliab. Eng. Int. 2015, 31, 1611–1622. [Google Scholar] [CrossRef]
- Aly, A.A.; Hamed, R.M.; Mahmoud, M.A. Optimal design of the adaptive exponentially weighted moving average CC over a range of mean shifts. Commun. Stat. Simul. Comput. 2017, 46, 890–902. [Google Scholar] [CrossRef]
- Abbas, Z.; Nazir, H.Z.; Abid, M.; Akhtar, N.; Riaz, M. Enhanced nonparametric control charts under simple and ranked set sampling schemes. Trans. Inst. Meas. Control 2020, 42, 2744–2759. [Google Scholar] [CrossRef]
- Abbas, Z.; Nazir, H.Z.; Riaz, M.; Shi, J.; Abdisa, A.G. An unbiased function-based Poisson adaptive EWMA control chart for monitoring range of shifts. Qual. Reliab. Eng. Int. 2023, 39, 2185–2201. [Google Scholar] [CrossRef]
- Zaman, B.; Lee, M.H.; Riaz, M.; Abujiya, M.A.R. An adaptive approach to EWMA dispersion chart using Huber and Tukey functions. Qual. Reliab. Eng. Int. 2019, 35, 1542–1581. [Google Scholar] [CrossRef]
- Girshick, M.A.; Rubin, H. A Bayes approach to a quality control model. Ann. Math. Stat. 1952, 23, 114–125. [Google Scholar] [CrossRef]
- Riaz, S.; Riaz, M.; Nazeer, A.; Hussain, Z. On Bayesian EWMA CCs under different loss functions. Qual. Reliab. Eng. Int. 2017, 33, 2653–2665. [Google Scholar] [CrossRef]
- Aslam, M.; Anwar, S.M. An improved Bayesian Modified-EWMA location chart and its applications in mechanical and sport industry. PLoS ONE 2020, 15, e0229422. [Google Scholar] [CrossRef]
- Noor-ul-Amin, M.; Noor, S. An adaptive EWMA CC for monitoring the process mean in Bayesian theory under different loss functions. Qual. Reliab. Eng. Int. 2021, 37, 804–819. [Google Scholar] [CrossRef]
- Du, Y.; Duan, C.; Wu, T. Replacement scheme for lubricating oil based on Bayesian control chart. IEEE Trans. Instrum. Meas. 2020, 70, 1–10. [Google Scholar] [CrossRef]
- Ali, S. A predictive Bayesian approach to EWMA and CUSUM charts for time-between-events monitoring. J. Stat. Comput. Simul. 2020, 90, 3025–3050. [Google Scholar] [CrossRef]
- Lin, C.-H.; Lu, M.-C.; Yang, S.-F.; Lee, M.-Y. A Bayesian Control Chart for Monitoring Process Variance. Appl. Sci. 2021, 11, 2729. [Google Scholar] [CrossRef]
- Khan, I.; Khan, D.M.; Noor-ul-Amin, M.; Khalil, U.; Alshanbari, H.M.; Ahmad, Z. Hybrid EWMA Control Chart under Bayesian Approach Using Ranked Set Sampling Schemes with Applications to Hard-Bake Process. Appl. Sci. 2023, 13, 2837. [Google Scholar] [CrossRef]
- Wang, Y.; Khan, I.; Noor-ul-Amin, M.; Javaid, A.; Khan, D.M.; Alshanbari, H.M. Performance of Bayesian EWMA control chart with measurement error under ranked set sampling schemes with application in industrial engineering. Sci. Rep. 2023, 13, 14042. [Google Scholar] [CrossRef] [PubMed]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 186, 453–461. [Google Scholar]
- Gauss, C. Méthods Moindres Carrés: Memoire sur la Combination des Observations; Mallet-Bachelier: Paris, France, 1955. [Google Scholar]
- Varian, H.R. A Bayesian approach to real estate assessment. Stud. Bayesian Econom. Stat. Honor. Leonard J. Savage 1975, 195–208. Available online: https://cir.nii.ac.jp/crid/1572543024713332736 (accessed on 27 September 2023).
- Muttlak, H.A. Pair rank set sampling. Biom. J. 1996, 38, 879–885. [Google Scholar] [CrossRef]
- Balci, S.; Akkaya, A.D.; Ulgen, B.E. Modified maximum likelihood estimators using ranked set sampling. J. Comput. Appl. Math. 2013, 238, 171–179. [Google Scholar] [CrossRef]
- Tayyab, M.; Noor-ul-Amin, M.; Hanif, M. Exponential weighted moving average CCs for monitoring the process mean using pair ranked set sampling schemes. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 1941–1950. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]



| Shift | Bayes SRS | Bayes PRSS | Bayes QPRSS | Bayes EPRSS | ||||
|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | ARL | SDRL | ARL | SDRL | ARL | SDRL | |
| h = 0.0856 | h = 0.0475 | h = 0.0456 | h = 0.0448 | |||||
| 0.00 | 370.86 | 537.77 | 370.50 | 473.98 | 370.04 | 453.73 | 370.80 | 482.75 |
| 0.10 | 179.91 | 247.52 | 105.26 | 109.93 | 103.11 | 105.26 | 101.91 | 104.05 |
| 0.20 | 70.61 | 91.12 | 42.72 | 39.83 | 42.35 | 39.31 | 41.79 | 36.90 |
| 0.30 | 35.40 | 44.53 | 23.75 | 22.10 | 23.05 | 21.16 | 23.13 | 20.55 |
| 0.40 | 21.15 | 26.36 | 14.77 | 16.77 | 14.38 | 13.80 | 14.73 | 13.86 |
| 0.50 | 13.55 | 16.69 | 9.94 | 10.51 | 9.01 | 10.02 | 9.45 | 9.69 |
| 0.60 | 9.46 | 11.23 | 6.75 | 7.38 | 6.37 | 6.98 | 6.36 | 6.93 |
| 0.70 | 7.08 | 7.70 | 4.71 | 5.08 | 4.55 | 4.92 | 4.48 | 4.84 |
| 0.75 | 6.15 | 6.43 | 4.03 | 4.24 | 3.85 | 4.02 | 3.92 | 4.06 |
| 0.80 | 5.62 | 5.82 | 3.58 | 3.61 | 3.45 | 3.50 | 3.34 | 3.23 |
| 0.90 | 4.51 | 4.18 | 2.83 | 2.48 | 2.75 | 2.44 | 2.71 | 2.44 |
| 1.00 | 3.85 | 3.20 | 2.37 | 1.87 | 2.27 | 1.77 | 2.26 | 1.70 |
| 1.50 | 2.25 | 1.29 | 1.43 | 0.64 | 1.38 | 0.62 | 1.37 | 0.61 |
| 2.00 | 1.66 | 0.78 | 1.14 | 0.36 | 1.11 | 0.33 | 1.11 | 0.32 |
| 2.50 | 1.36 | 0.56 | 1.03 | 0.19 | 1.02 | 0.16 | 1.02 | 0.15 |
| 3.00 | 1.17 | 0.39 | 1 | 0 | 1 | 0 | 1 | 0 |
| 4.00 | 1.02 | 0.14 | 1 | 0 | 1 | 0 | 1 | 0 |
| Shift | Bayes SRS | Bayes PRSS | Bayes QPRSS | Bayes EPRSS | ||||
|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | ARL | SDRL | ARL | SDRL | ARL | SDRL | |
| h = 0.241 | h = 0.0869 | h = 0.0812 | h = 0.0734 | |||||
| 0.00 | 369.00 | 367.39 | 371.60 | 419.90 | 369.85 | 397.69 | 369.29 | 416.73 |
| 0.10 | 210.23 | 195.27 | 168.65 | 164.37 | 160.33 | 155.21 | 163.25 | 162.23 |
| 0.20 | 97.04 | 80.91 | 67.14 | 63.35 | 62.09 | 58.98 | 60.79 | 7.69 |
| 0.30 | 55.71 | 42.80 | 32.85 | 29.77 | 31.94 | 28.95 | 29.61 | 27.38 |
| 0.40 | 36.15 | 25.09 | 18.64 | 16.81 | 17.93 | 16.22 | 16.88 | 15.69 |
| 0.50 | 25.95 | 17.04 | 12.10 | 10.67 | 11.50 | 10.07 | 10.55 | 9.51 |
| 0.60 | 19.80 | 12.20 | 8.33 | 6.78 | 8.14 | 6.74 | 7.42 | 6.36 |
| 0.70 | 15.41 | 9.09 | 6.16 | 4.63 | 5.97 | 4.51 | 5.50 | 4.31 |
| 0.75 | 14.11 | 8.17 | 5.54 | 3.92 | 5.27 | 3.79 | 4.81 | 3.52 |
| 0.80 | 12.87 | 7.26 | 4.92 | 3.27 | 4.73 | 3.21 | 4.38 | 3.08 |
| 0.90 | 10.76 | 5.97 | 4.11 | 2.47 | 3.85 | 2.32 | 3.63 | 2.24 |
| 1.00 | 9.17 | 4.96 | 3.49 | 1.90 | 3.34 | 1.80 | 3.08 | 1.69 |
| 1.50 | 4.90 | 2.77 | 2.14 | 0.87 | 2.06 | 0.79 | 1.97 | 0.71 |
| 2.00 | 2.98 | 1.83 | 1.56 | 0.60 | 1.54 | 0.56 | 1.49 | 0.54 |
| 2.50 | 1.98 | 1.15 | 1.23 | 0.43 | 1.13 | 0.33 | 1.21 | 0.41 |
| 3.00 | 1.48 | 0.72 | 1.06 | 0.24 | 1 | 0 | 1 | 0 |
| 4.00 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| Shift | Bayes SRS | Bayes PRSS | Bayes QPRSS | Bayes EPRSS | ||||
|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | ARL | SDRL | ARL | SDRL | ARL | SDRL | |
| h = 0.086 | h = 0.0462 | h = 0.0479 | h = 0.0448 | |||||
| 0.00 | 370.98 | 539.06 | 370.94 | 416.25 | 370.09 | 451.21 | 369.57 | 489.53 |
| 0.10 | 184.38 | 254.91 | 100.40 | 107.66 | 98.76 | 105.55 | 100.94 | 107.63 |
| 0.20 | 71.98 | 92.48 | 40.78 | 38.36 | 38.42 | 35.78 | 40.47 | 36.40 |
| 0.30 | 36.26 | 45.49 | 23.14 | 21.42 | 22.30 | 20.25 | 22.78 | 20.45 |
| 0.40 | 21.09 | 26.30 | 14.33 | 14.21 | 13.50 | 14.05 | 14.55 | 13.83 |
| 0.50 | 13.71 | 16.73 | 9.48 | 10.15 | 9.56 | 9.99 | 9.35 | 9.73 |
| 0.60 | 9.53 | 11.25 | 6.53 | 7.19 | 6.48 | 7.05 | 6.27 | 6.82 |
| 0.70 | 7.09 | 7.86 | 4.59 | 5.05 | 4.56 | 4.92 | 4.52 | 4.93 |
| 0.75 | 6.20 | 6.50 | 4.01 | 4.18 | 3.88 | 4.02 | 3.88 | 4.09 |
| 0.80 | 5.54 | 5.54 | 3.45 | 3.46 | 3.92 | 4.11 | 3.39 | 3.40 |
| 0.90 | 4.52 | 4.17 | 2.76 | 2.51 | 3.43 | 3.44 | 2.72 | 2.46 |
| 1.00 | 3.83 | 3.20 | 2.33 | 1.81 | 2.28 | 1.77 | 2.25 | 1.71 |
| 1.50 | 2.26 | 1.27 | 1.41 | 0.65 | 1.40 | 0.62 | 1.37 | 0.62 |
| 2.00 | 1.66 | 0.78 | 1.13 | 0.35 | 1.11 | 0.33 | 1.10 | 0.32 |
| 2.50 | 1.34 | 0.55 | 1.02 | 0.16 | 1 | 0 | 1.02 | 0.15 |
| 3.00 | 1.16 | 0.39 | 1 | 0 | 1 | 0 | 1 | 0 |
| 4.00 | 1.02 | 0.15 | 1 | 0 | 1 | 0 | 1 | 0 |
| Shift | Bayes SRS | Bayes PRSS | Bayes QPRSS | Bayes EPRSS | ||||
|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | ARL | SDRL | ARL | SDRL | ARL | SDRL | |
| h = 0.242 | h = 0.0845 | h = 0.0789 | h = 0.0735 | |||||
| 0.00 | 370.14 | 434.88 | 371.13 | 456.32 | 371.39 | 394.59 | 370.44 | 447.97 |
| 0.10 | 212.09 | 198.42 | 167.63 | 165.47 | 161.83 | 158.98 | 157.34 | 162.61 |
| 0.20 | 86.77 | 83.25 | 66.32 | 61.82 | 64.73 | 61.05 | 60.20 | 57.76 |
| 0.30 | 55.44 | 42.26 | 31.80 | 29.41 | 28.51 | 26.37 | 28.48 | 26.35 |
| 0.40 | 36.76 | 25.98 | 18.68 | 16.80 | 17.30 | 15.61 | 16.85 | 15.50 |
| 0.50 | 25.86 | 16.88 | 12.04 | 10.38 | 11.55 | 10.18 | 10.68 | 9.59 |
| 0.60 | 19.65 | 12.16 | 8.27 | 6.84 | 7.81 | 6.50 | 7.30 | 6.19 |
| 0.70 | 15.62 | 9.17 | 6.15 | 4.60 | 5.79 | 4.38 | 5.48 | 4.26 |
| 0.75 | 14.23 | 8.29 | 5.54 | 3.97 | 5.20 | 3.72 | 4.87 | 3.61 |
| 0.80 | 12.83 | 7.30 | 4.93 | 3.36 | 4.53 | 3.01 | 4.30 | 3.03 |
| 0.90 | 10.79 | 5.90 | 4.07 | 2.48 | 3.80 | 2.33 | 3.66 | 2.24 |
| 1.00 | 9.25 | 5.00 | 3.49 | 1.93 | 3.25 | 1.80 | 3.11 | 1.70 |
| 1.50 | 4.95 | 2.80 | 2.12 | 0.85 | 2.04 | 0.77 | 1.96 | 0.71 |
| 2.00 | 2.97 | 1.81 | 1.55 | 0.59 | 1.55 | 0.56 | 1.49 | 0.54 |
| 2.50 | 1.97 | 1.13 | 1.23 | 0.43 | 1.23 | 0.42 | 1.20 | 0.40 |
| 3.00 | 1.48 | 0.73 | 1.06 | 0.25 | 1.03 | 0.17 | 1.05 | 0.23 |
| 4.00 | 1.09 | 0.30 | 1 | 0 | 1 | 0 | 1 | 0 |
| Shift | Bayes SRS | Bayes PRSS | Bayes QPRSS | Bayes EPRSS | ||||
|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | ARL | SDRL | ARL | SDRL | ARL | SDRL | |
| h = 0.0856 | h = 0.0464 | h = 0.0445 | h = 0.0449 | |||||
| 0.00 | 369.58 | 524.70 | 370.78 | 451.12 | 370.60 | 472.13 | 369.90 | 402.14 |
| 0.10 | 178.57 | 250.19 | 100.99 | 104.36 | 108.49 | 109.96 | 101.24 | 103.87 |
| 0.20 | 70.53 | 91.22 | 45.11 | 38.28 | 43.14 | 38.81 | 40.35 | 36.06 |
| 0.30 | 35.71 | 45.25 | 24.96 | 21.42 | 23.53 | 21.29 | 22.73 | 20.37 |
| 0.40 | 21.24 | 26.29 | 14.75 | 14.37 | 14.53 | 14.00 | 14.37 | 13.62 |
| 0.50 | 13.66 | 16.90 | 9.36 | 9.98 | 9.41 | 9.93 | 9.32 | 9.63 |
| 0.60 | 9.46 | 11.08 | 6.44 | 7.05 | 6.38 | 7.00 | 6.32 | 6.99 |
| 0.70 | 6.94 | 7.70 | 4.60 | 4.97 | 4.69 | 5.07 | 4.46 | 4.82 |
| 0.75 | 6.22 | 6.53 | 4.03 | 4.24 | 3.97 | 4.17 | 3.85 | 4.05 |
| 0.80 | 5.50 | 5.58 | 3.44 | 4.09 | 3.45 | 3.38 | 3.35 | 3.39 |
| 0.90 | 4.52 | 4.15 | 2.75 | 2.49 | 2.70 | 2.33 | 2.67 | 2.39 |
| 1.00 | 3.77 | 3.17 | 2.31 | 1.79 | 2.28 | 1.76 | 2.21 | 1.72 |
| 1.50 | 2.26 | 1.29 | 1.41 | 0.64 | 1.39 | 0.63 | 1.36 | 0.60 |
| 2.00 | 1.66 | 0.78 | 1.13 | 0.35 | 1.13 | 0.34 | 1.10 | 0.32 |
| 2.50 | 1.35 | 0.55 | 1.03 | 0.17 | 1.03 | 0.16 | 1.02 | 0.15 |
| 3.00 | 1.16 | 0.39 | 1 | 0 | 1 | 0 | 1 | 0 |
| 4.00 | 1.02 | 0.15 | 1 | 0 | 1 | 0 | 1 | 0 |
| Shift | Bayes SRS | Bayes PRSS | Bayes QPRSS | Bayes EPRSS | ||||
|---|---|---|---|---|---|---|---|---|
| ARL | SDRL | ARL | SDRL | ARL | SDRL | ARL | SDRL | |
| h = 0.2414 | h = 0.0547 | h = 0.0765 | h = 0.0764 | |||||
| 0.00 | 369.67 | 359.45 | 370.74 | 396.18 | 369.62 | 381.94 | 370.84 | 377.82 |
| 0.10 | 210.29 | 197.72 | 169.22 | 165.09 | 163.28 | 168.74 | 172.88 | 177.32 |
| 0.20 | 98.16 | 83.24 | 66.27 | 62.70 | 65.07 | 60.06 | 62.59 | 59.57 |
| 0.30 | 54.92 | 41.45 | 31.72 | 29.03 | 30.03 | 27.89 | 29.91 | 27.79 |
| 0.40 | 36.19 | 25.48 | 18.51 | 16.52 | 16.86 | 15.75 | 17.16 | 15.75 |
| 0.50 | 25.97 | 17.13 | 11.98 | 10.47 | 10.89 | 9.74 | 10.91 | 9.75 |
| 0.60 | 19.68 | 12.21 | 8.15 | 6.68 | 7.73 | 6.40 | 7.55 | 6.40 |
| 0.70 | 15.56 | 9.19 | 6.12 | 4.64 | 5.63 | 4.37 | 5.54 | 4.18 |
| 0.75 | 14.18 | 8.26 | 5.45 | 3.99 | 5.03 | 3.65 | 4.95 | 3.66 |
| 0.80 | 12.79 | 7.24 | 4.86 | 3.34 | 4.47 | 3.10 | 4.40 | 3.04 |
| 0.90 | 10.74 | 5.93 | 4.03 | 2.46 | 3.69 | 2.22 | 3.63 | 2.20 |
| 1.00 | 9.20 | 4.98 | 3.44 | 1.88 | 3.18 | 1.78 | 3.15 | 1.71 |
| 1.50 | 4.94 | 2.79 | 2.12 | 0.84 | 2.02 | 0.74 | 1.99 | 0.72 |
| 2.00 | 2.95 | 1.81 | 1.55 | 0.60 | 1.52 | 0.54 | 1.52 | 0.54 |
| 2.50 | 1.98 | 1.14 | 1.24 | 0.43 | 1.23 | 0.42 | 1.21 | 0.41 |
| 3.00 | 1.48 | 0.72 | 1.09 | 0.28 | 1.07 | 0.26 | 1.06 | 0.24 |
| 4.00 | 1.09 | 0.30 | 1 | 0 | 1 | 0 | 1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Noor-ul-Amin, M.; Khan, I.; Ismail, E.A.A.; Awwad, F.A. Integration of Bayesian Adaptive Exponentially Weighted Moving Average Control Chart and Paired Ranked-Based Sampling for Enhanced Semiconductor Manufacturing Process Monitoring. Processes 2023, 11, 2893. https://doi.org/10.3390/pr11102893
Liu B, Noor-ul-Amin M, Khan I, Ismail EAA, Awwad FA. Integration of Bayesian Adaptive Exponentially Weighted Moving Average Control Chart and Paired Ranked-Based Sampling for Enhanced Semiconductor Manufacturing Process Monitoring. Processes. 2023; 11(10):2893. https://doi.org/10.3390/pr11102893
Chicago/Turabian StyleLiu, Botao, Muhammad Noor-ul-Amin, Imad Khan, Emad A. A. Ismail, and Fuad A. Awwad. 2023. "Integration of Bayesian Adaptive Exponentially Weighted Moving Average Control Chart and Paired Ranked-Based Sampling for Enhanced Semiconductor Manufacturing Process Monitoring" Processes 11, no. 10: 2893. https://doi.org/10.3390/pr11102893
APA StyleLiu, B., Noor-ul-Amin, M., Khan, I., Ismail, E. A. A., & Awwad, F. A. (2023). Integration of Bayesian Adaptive Exponentially Weighted Moving Average Control Chart and Paired Ranked-Based Sampling for Enhanced Semiconductor Manufacturing Process Monitoring. Processes, 11(10), 2893. https://doi.org/10.3390/pr11102893








