Multiscale Fractal Characterization of Pore–Fracture Structure of Tectonically Deformed Coal Compared to Primary Undeformed Coal: Implications for CO2 Geological Sequestration in Coal Seams
Abstract
:1. Introduction
2. Experiments and Methods
2.1. Samples Information
2.2. Test Method
- Mercury intrusion porosimetry
- Low-temperature nitrogen adsorption
2.3. Calculation Method of Pore Fractal Dimension
2.3.1. Micropore
- Volume-Specific Surface Area model
- Polanyi adsorption potential theory
2.3.2. Mesopore
2.3.3. Macropore
2.3.4. Average Tortuosity
3. Experimental Results and Analyses
3.1. Experimental Results
3.1.1. Test Results of LNA
3.1.2. Test Results of MIP
3.2. Calculation Results of Multiscale Pore Fractal Dimensions
3.2.1. Fractal Results of Micropore
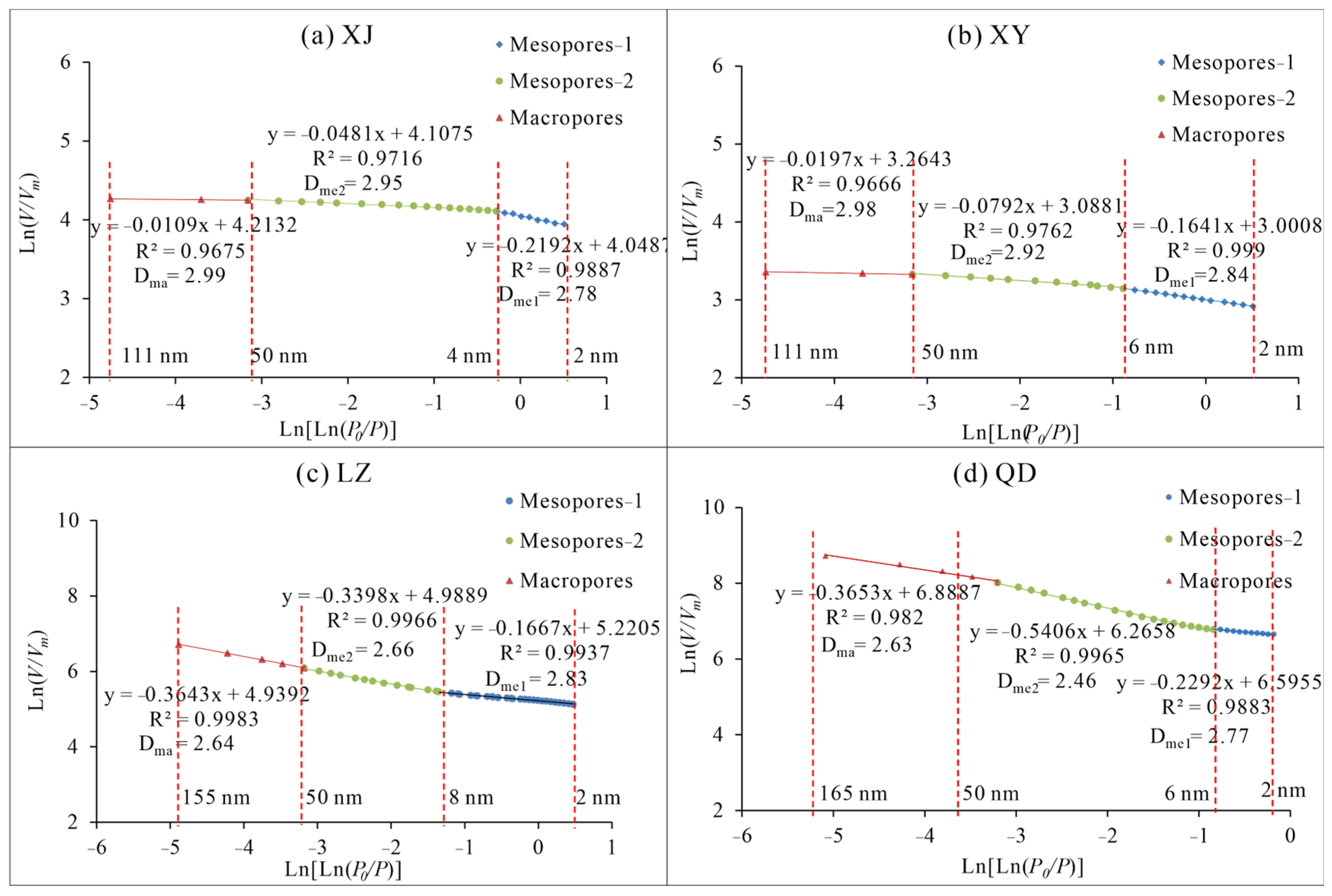
3.2.2. Mesopores and Part of Macropores
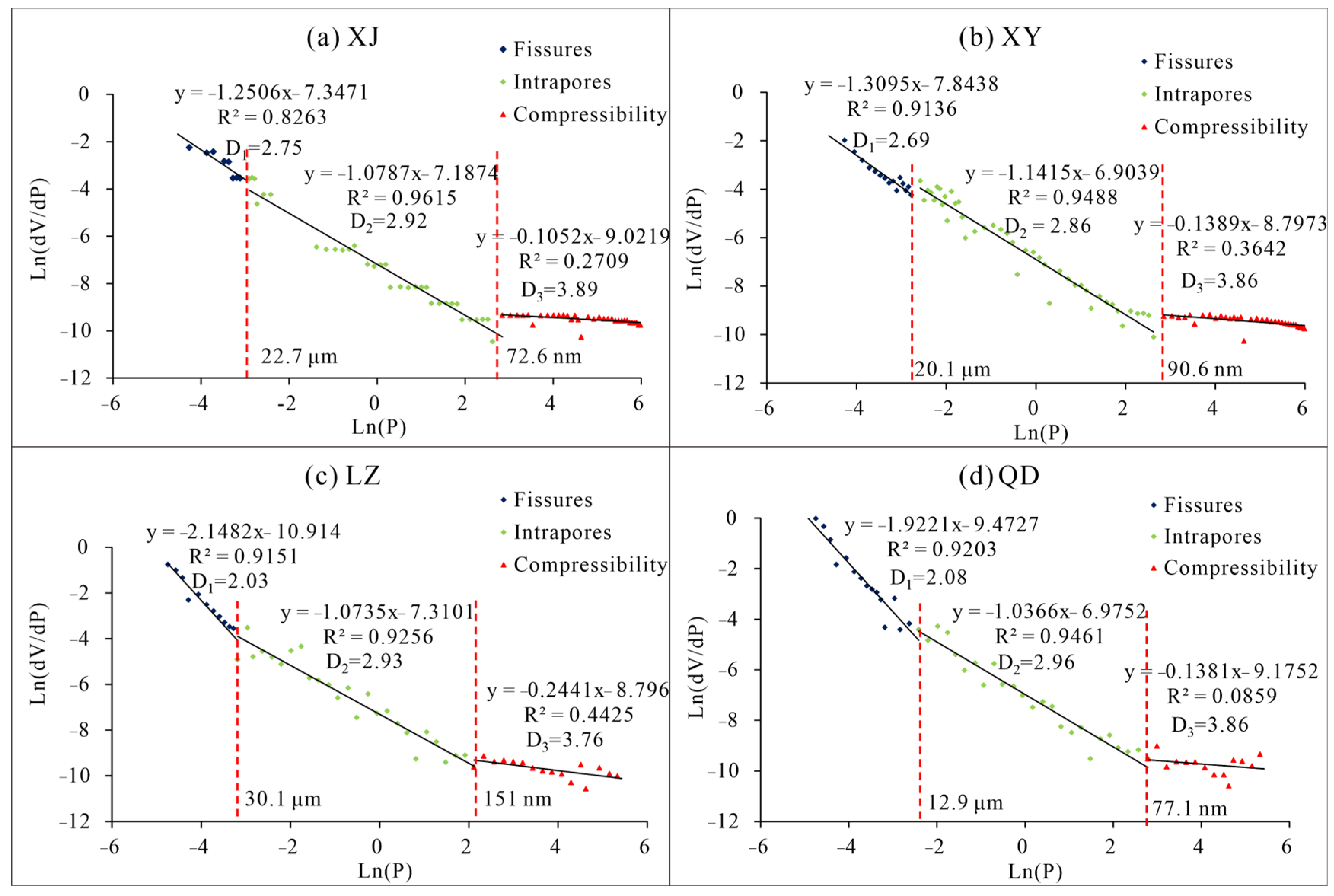
3.2.3. Macropores and Fractures
3.2.4. Fractal Characteristics of Average Tortuosity of Capillary
4. Discussion
4.1. Classification of Pore–Fractures Based on Fractal Results
4.1.1. The Accuracy of Fractal Results
4.1.2. Classification of Pore–Fractures
4.2. Implications for the CO2–ECBM
4.2.1. Injectivity of CO2 into Coal Seams
4.2.2. CO2 Storage Potential
5. Conclusions
- Based on the principles of different pore–fracture structure tests (MIP and LNA), different fractal methods were selected to quantitatively and uniformly characterize the development of multiscale pore–fracture structures in coal matrix. According to the fractal characteristics of the pore structure, a multiscale pore structure classification standard suitable for controlling the fluid migration process was formed, that is, filling pores (<2 nm), adsorption pores (2–8 nm), diffusion pores (8–150 nm), seepage pores (150 nm–30 μm), and fractures (>30 μm).
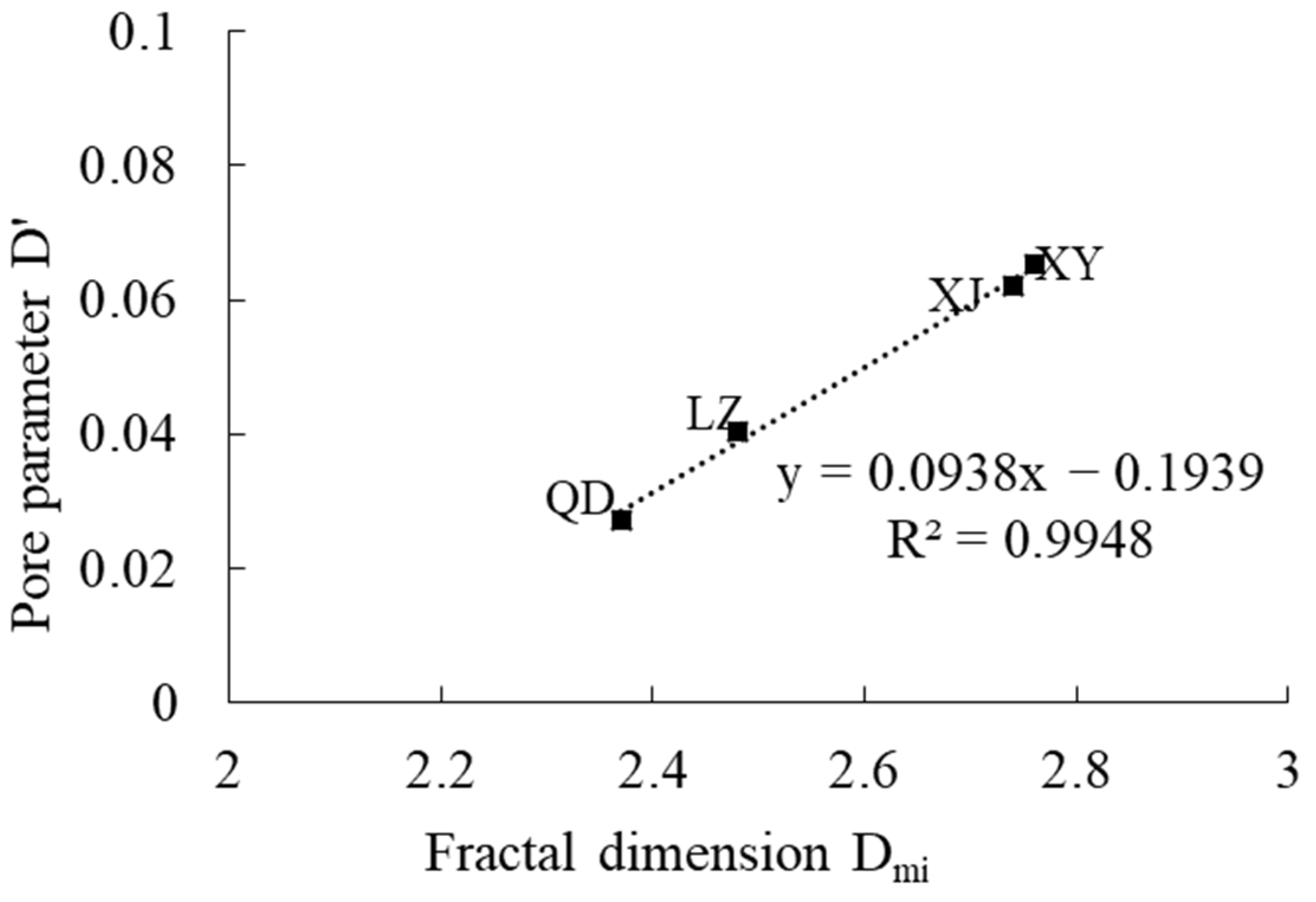
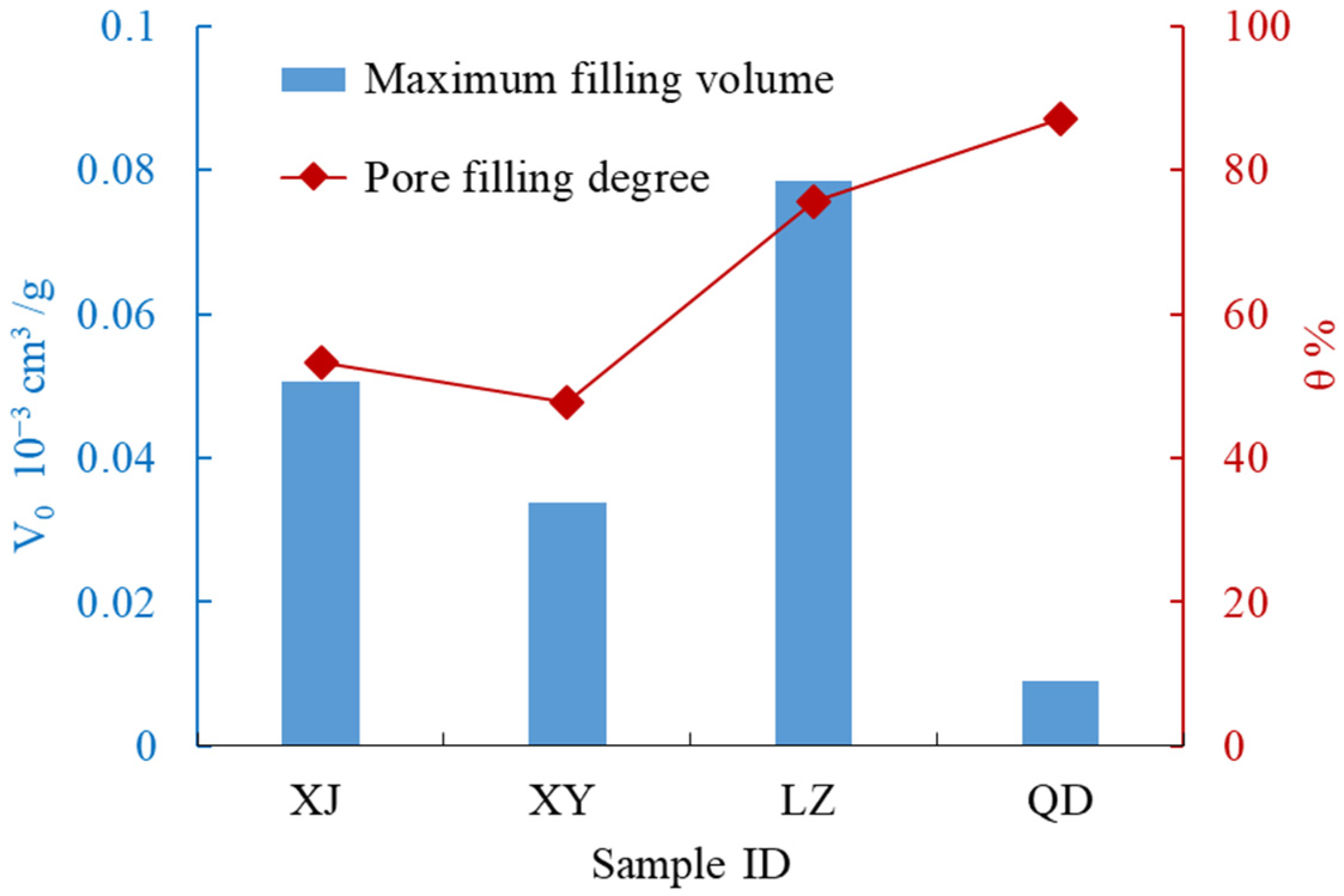
- The fractal analysis provides insights into the complexity and connectivity of the pore network, which is valuable in understanding the gas adsorption–diffusion–seepage process during CO2-ECBM. The larger pore volumes and smaller fractal dimensions of the migration pores (>8 nm) in TDC samples make it easier for CO2 to enter the micropores and displaces the adsorbed methane. As for the storage pores (<8 nm), TDC samples have the similar fractal dimension of the pores in 2–8 nm with PUC samples, while the fractal dimension of the filling pores (<2 nm) in TDC samples was relatively lower, nearly 2.4, which facilitates efficient gas volume filling and increases the pore-filling degree (θ).
- The pore–fracture structure of the TDC samples has more advantages for the CO2 injection and storage compared to PUC, meaning that TDC has the geological potential for CO2-ECBM. However, the engineering practice of CO2-ECBM in the coal seam is a complex process controlled by multi-factors except for pore–fracture structure; comprehensive investigations are essential to fully evaluate the feasibility and validity of CO2-ECBM in TDC reservoirs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Godec, M.; Koperna, G.; Gale, J. CO2-ECBM: A review of its status and global potential. Energy Procedia 2014, 63, 5858–5869. [Google Scholar] [CrossRef]
- Jafari, M.; Cao, S.C.; Jung, J. Geological CO2 sequestration in saline aquifers: Implication on potential solutions of China’s power sector. Resour. Conserv. Recycl. 2017, 121, 137–155. [Google Scholar] [CrossRef]
- Ross, H.E.; Hagin, P.; Zoback, M.D. CO2 storage and enhanced coalbed methane recovery: Reservoir characterization and fluid flow simulations of the Big George coal, Powder River Basin, Wyoming, USA. Int. J. Greenh. Gas. Con 2009, 3, 773–786. [Google Scholar] [CrossRef]
- Fitzgerald, J.E.; Pan, Z.; Sudibandriyo, M.; Robinson, J.R.L.; Gasem, K.A.M.; Reeves, S. Adsorption of methane, nitrogen, carbon dioxide and their mixtures on wet Tiffany coal. Fuel 2005, 84, 2351–2363. [Google Scholar] [CrossRef]
- Pini, R.; Marx, D.; Burlini, L.; Storti, G.; Mazzotti, M. Coal characterization for ECBM recovery: Gas sorption under dry and humid conditions, and its effect on displacement dynamics. Energy Procedia 2011, 4, 2157–2161. [Google Scholar] [CrossRef]
- Zhang, K.; Sang, S.; Zhou, X.; Liu, C.; Ma, M.; Niu, Q. Influence of supercritical CO2-H2O-caprock interactions on the sealing capability of deep coal seam caprocks related to CO2 geological storage: A case study of the silty mudstone caprock of coal seam no. 3 in the Qinshui Basin, China. Int. J. Greenh. Gas. Con 2021, 106, 103282. [Google Scholar] [CrossRef]
- Busch, A.; Gensterblum, Y. CBM and CO2-ECBM related sorption processes in coal: A review. Int. J. Coal Geol. 2011, 87, 49–71. [Google Scholar] [CrossRef]
- Jia, J.; Wang, D.; Li, B.; Wu, Y.; Zhao, D. Molecular simulation study on the effect of coal metamorphism on the competitive adsorption of CO2/CH4 in binary system. Fuel 2023, 335, 127046. [Google Scholar] [CrossRef]
- Rodosta, T.; Litynski, J.; Plasynski, S.; Spangler, L.; Finley, R.; Steadman, E.; Ball, D.; Hill, G.; McPherson, B.; Burton, E.; et al. US Department of Energy’s regional carbon sequestration partnership initiative: Update on validation and development phases. Energy Procedia 2011, 4, 3457–3464. [Google Scholar] [CrossRef]
- Wen, D.G.; Guo, J.Q.; Zhang, S.Q.; Xu, T.F.; Hu, Q.Y. The progress in the research on carbon dioxide geological storage in China. Geol. China 2014, 41, 1716–1723. [Google Scholar]
- Zhang, K.; Cheng, Y.; Li, W.; Wu, D.; Liu, Z. Influence of supercritical CO2 on pore structure and functional groups of coal: Implications for CO2 sequestration. J. Nat. Gas. Sci. Eng. 2017, 40, 288–298. [Google Scholar] [CrossRef]
- Zhang, K.; Sang, S.; Liu, C.; Ma, M.; Zhou, X. Experimental study the influences of geochemical reaction on coal structure during the CO2 geological storage in deep coal seam. J. Pet. Sci. Eng. 2019, 178, 1006–1017. [Google Scholar] [CrossRef]
- Malozyomov, B.V.; Golik, V.I.; Brigida, V.; Kukartsev, V.V.; Tynchenko, Y.A.; Boyko, A.A.; Tynchenko, S.V. Substantiation of drilling parameters for undermined drainage boreholes for increasing methane production from unconventional coal-gas collectors. Energies 2023, 16, 4276. [Google Scholar] [CrossRef]
- Bosikov, I.I.; Klyuev, R.V.; Mayer, A.V.; Stas, G.V. Development of a method for analyzing and evaluating the optimal state of aerogasodynamic processes in coal mines. Sustain. Dev. Mt. Territ. 2022, 14, 97–106. [Google Scholar] [CrossRef]
- Balovtsev, S.V.; Skopintseva, O.V.; Kulikova, E.Y. Hierarchical structure of aerological risks in coal mines. Sustain. Dev. Mt. Territ. 2022, 14, 276–285. [Google Scholar] [CrossRef]
- Pan, Z.; Ye, J.; Zhou, F.; Tan, Y.; Connell, L.D.; Fan, J. CO2 storage in coal to enhance coalbed methane recovery: A review of field experiments in China. Int. Geol. Rev. 2018, 60, 754–776. [Google Scholar] [CrossRef]
- Zhang, K.; Sang, S.X.; Ma, M.Y.; Zhou, X.Z.; Liu, C.J. Experimental Study on the Influence of Effective Stress on the Adsorption-Desorption Behavior of Tectonically Deformed Coal Compared with Primary Undeformed Coal in Huainan Coalfield, China. Energies 2022, 15, 6501. [Google Scholar] [CrossRef]
- Song, Y.; Jiang, B.; Qu, M. Macromolecular evolution and structural defects in tectonically deformed coals. Fuel 2019, 236, 1432–1445. [Google Scholar] [CrossRef]
- Xue, Y.; Ranjith, P.G.; Gao, F.; Zhang, D.; Cheng, H.; Chong, Z.; Hou, P. Mechanical behaviour and permeability evolution of gas-containing coal from unloading confining pressure tests. J. Nat. Gas. Sci. Eng. 2017, 40, 336–346. [Google Scholar] [CrossRef]
- Zhang, K.; Sang, S.X.; Ma, M.Y.; Zhou, X.Z.; Liu, C.J.; Shen, G.D. Permeability Response Characteristics of Primary Undeformed Coal and Tectonically Deformed Coal under Loading-Unloading Conditions in Huainan Coalfield, China. Acs Omega 2022, 7, 37485–37498. [Google Scholar] [CrossRef]
- Niu, Q.; Cao, L.; Sang, S.; Zhou, X.; Wang, Z. Anisotropic Adsorption Swelling and Permeability Characteristics with Injecting CO2 in Coal. Energy Fuel 2018, 32, 1979–1991. [Google Scholar] [CrossRef]
- Alexeev, A.D.; Vasilenko, T.A.; Ulyanova, E.V. Closed porosity in fossil coals. Fuel 1999, 78, 635–638. [Google Scholar] [CrossRef]
- Ju, Y.; Jiang, B.; Hou, Q.; Tan, Y.; Wang, G.; Xiao, W. Behavior and mechanism of the adsorption/desorption of tectonically deformed coals. Chin. Sci. Bull. 2009, 54, 88–94. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, D.; Pan, Z.; Yao, Y.; Li, J.; Qiu, Y. Pore structure and its impact on CH4 adsorption capacity and flow capability of bituminous and subbituminous coals from Northeast China. Fuel 2013, 103, 258–268. [Google Scholar] [CrossRef]
- Yao, Y.; Liu, D.; Tang, D.; Tang, S.; Huang, W. Fractal characterization of adsorption-pores of coals from North China: An investigation on CH4 adsorption capacity of coals. Int. J. Coal Geol. 2008, 73, 27–42. [Google Scholar] [CrossRef]
- Shao, X.; Pang, X.; Li, Q.; Wang, P.; Chen, D.; Shen, W.; Zhao, Z. Pore structure and fractal characteristics of organic-rich shales: A case study of the lower Silurian Longmaxi shales in the Sichuan Basin, SW China. Mar. Pet. Geol. 2017, 80, 192–202. [Google Scholar] [CrossRef]
- Yuan, W.; Pan, Z.; Li, X.; Yang, Y.; Zhao, C.; Connell, L.D.; Li, S.; He, J. Experimental study and modelling of methane adsorption and diffusion in shale. Fuel 2014, 117, 509–519. [Google Scholar] [CrossRef]
- Huang, T.; Du, P.; Peng, X.; Wang, P.; Zou, G. Pressure drop and fractal non-Darcy coefficient model for fluid flow through porous media. J. Pet. Sci. Eng. 2020, 184, 106579. [Google Scholar] [CrossRef]
- Yang, R.; He, S.; Yi, J.; Hu, Q. Nano-scale pore structure and fractal dimension of organic-rich Wufeng-Longmaxi shale from Jiaoshiba area, Sichuan Basin: Investigations using FE-SEM, gas adsorption and helium pycnometry. Mar. Pet. Geol. 2016, 70, 27–45. [Google Scholar] [CrossRef]
- Liu, C.J.; Wang, G.X.; Sang, S.X.; Gilani, W.; Rudolph, V. Fractal analysis in pore structure of coal under conditions of CO2 sequestration process. Fuel 2015, 139, 125–132. [Google Scholar] [CrossRef]
- Wu, J.; Yu, B. A fractal resistance model for flow through porous media. Int. J. Heat. Mass. Tran. 2007, 50, 3925–3932. [Google Scholar] [CrossRef]
- Liu, S.; Ma, J.; Sang, S.; Wang, T.; Du, Y.; Fang, H. The effects of supercritical CO2 on mesopore and macropore structure in bituminous and anthracite coal. Fuel 2018, 223, 32–43. [Google Scholar] [CrossRef]
- Zhang, G.; Ranjith, P.G.; Fu, X.; Li, X. Pore-fracture alteration of different rank coals: Implications for CO2 sequestration in coal. Fuel 2021, 289, 119801. [Google Scholar] [CrossRef]
- Meng, L.D.; Tao, L.Z.; Dong, C.Y. Study progress on pore-crack heterogeneity and geological influence factors of coal reservoir. Coal Sci. Technol. 2015, 43, 10–15. [Google Scholar] [CrossRef]
- Washburn, E.W. The Dynamics of Capillary Flow. Phys. Rev. 1921, 17, 273–283. [Google Scholar] [CrossRef]
- Zhang, J. Experimental study and modeling for co2 diffusion in coals with different particle sizes: Based on gas absorption (imbibition) and pore structure. Energy Fuel 2016, 30, 531–543. [Google Scholar] [CrossRef]
- Qi, L.; Tang, X.; Wang, Z.; Peng, X. Pore characterization of different types of coal from coal and gas outburst disaster sites using low temperature nitrogen adsorption approach. Int. J. Min. Sci. Technol. 2017, 27, 371–377. [Google Scholar] [CrossRef]
- Xie, W.; Wang, M.; Wang, X.; Wang, Y.; Hu, C. Nano-Pore structure and fractal characteristics of shale gas reservoirs: A case study of longmaxi formation in Southeastern Chongqing, China. J. Nanosci. Nanotechnol. 2021, 21, 343–353. [Google Scholar] [CrossRef]
- Hu, B.; Cheng, Y.; Pan, Z. Classification methods of pore structures in coal: A review and new insight. Gas. Sci. Eng. 2023, 110, 204876. [Google Scholar] [CrossRef]
- Dubinin, M.M.; Stoeckli, H.F. Homogeneous and heterogeneous micropore structures in carbonaceous adsorbents. J. Colloid. Interf. Sci. 1980, 75, 34–42. [Google Scholar] [CrossRef]
- Friesen, W.I.; Mikula, R.J. Mercury porosimetry of coals: Pore volume distribution and compressibility. Fuel 1988, 67, 1516–1520. [Google Scholar] [CrossRef]
- Krohn, C.E. Fractal measurements of sandstones, shales, and carbonates. J. Geophys. Res. Solid. Earth 1988, 93, 3297–3305. [Google Scholar] [CrossRef]
- Feng, Y.; Ning, Z.; Liu, H. Fractal characteristics of shales from a shale gas reservoir in the Sichuan Basin, China. Fuel 2014, 115, 378–384. [Google Scholar]
- Jaroniec, M. Evaluation of the fractal dimension from a single adsorption isotherm. Langmuir 1995, 11, 2316–2317. [Google Scholar] [CrossRef]
- Xie, H.P.; GAO, F.; Zhou, H.W.; Cheng, G.M.; Zhou, F.B. On theoretical and modeling approach to mining-enhanced permeability for simultaneous exploitation of coal and gas. J. China Coal Soc. 2013, 38, 1101–1108. [Google Scholar]
- Jaroniec, M.; Gilpin, R.K.; Choma, J. Correlation between microporosity and fractal dimension of active carbons. Carbon 1993, 31, 325–331. [Google Scholar] [CrossRef]
- Beekman, J.W.; Froment, G.F. Average lengthscale for tortuosity calculations. Ind. Eng. Chem. Fundam. 1982, 21, 243. [Google Scholar]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny–Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Wang, C.; Yang, S.; Li, X.; Li, J.; Jiang, C. Comparison of the initial gas desorption and gas-release energy characteristics from tectonically-deformed and primary-undeformed coal. Fuel 2019, 238, 66–74. [Google Scholar] [CrossRef]
- Dou, W.; Liu, L.; Jia, L.; Xu, Z.; Wang, M.; Du, C. Pore structure, fractal characteristics and permeability prediction of tight sandstones: A case study from Yanchang Formation, Ordos Basin, China. Mar. Pet. Geol. 2021, 123, 104737. [Google Scholar] [CrossRef]
- Hodot, B.B. Coal and Gas Outburst; China Industry Press: Beijing, China, 1966; (Chinese Translation). [Google Scholar]
- Gan, H.; Nandi, S.P.; Walker, P.L. Nature of the porosity in American coals. Fuel 1972, 51, 272–277. [Google Scholar] [CrossRef]
- Dubinin, M.M. On physical feasibility of Brunauer’s micropore analysis method. J. Colloid. Interf. Sci. 1974, 46, 351–356. [Google Scholar] [CrossRef]
- Wu, J.; Jin, K.; Tong, Y. Theory of coal pores and its application in evaluation of gas outburst proneness and gas drainage. J. China Coal Soc. 1991, 16, 86–95. [Google Scholar]
- Qin, Y.; Xu, Z.; Zhang, J. Natural classification of the high-rank coal pore structure and its application. J. China Coal Soc. 1995, 20, 266–271. [Google Scholar]
- Sang, S.; Zhu, Y.; Zhang, S.; Zhang, J.; Tang, J. Solid-gas interaction mechanism of coal-adsorbed gas (I)—Coal pore structure and solid-gas interaction. Nat. Gas. Ind. 2005, 25, 13–15. [Google Scholar]
- Dong, J.; Cheng, Y.; Liu, Q.; Zhang, H.; Zhang, K.; Hu, B. Apparent and True Diffusion Coefficients of Methane in Coal and Their Relationships with Methane Desorption Capacity. Energy Fuel 2017, 31, 2643–2651. [Google Scholar] [CrossRef]
- Smith, D.M.; Williams, F.L. Diffusion models for gas production from coal: Determination of diffusion parameters. Fuel 1984, 63, 256–261. [Google Scholar] [CrossRef]
- Niu, Q.; Cao, L.; Sang, S.; Wang, W.; Zhou, X.; Yuan, W.; Ji, Z.; Chang, J.; Li, M. Experimental study on the softening effect and mechanism of anthracite with CO2 injection. Int. J. Rock. Mech. Min. 2021, 138, 104614. [Google Scholar] [CrossRef]
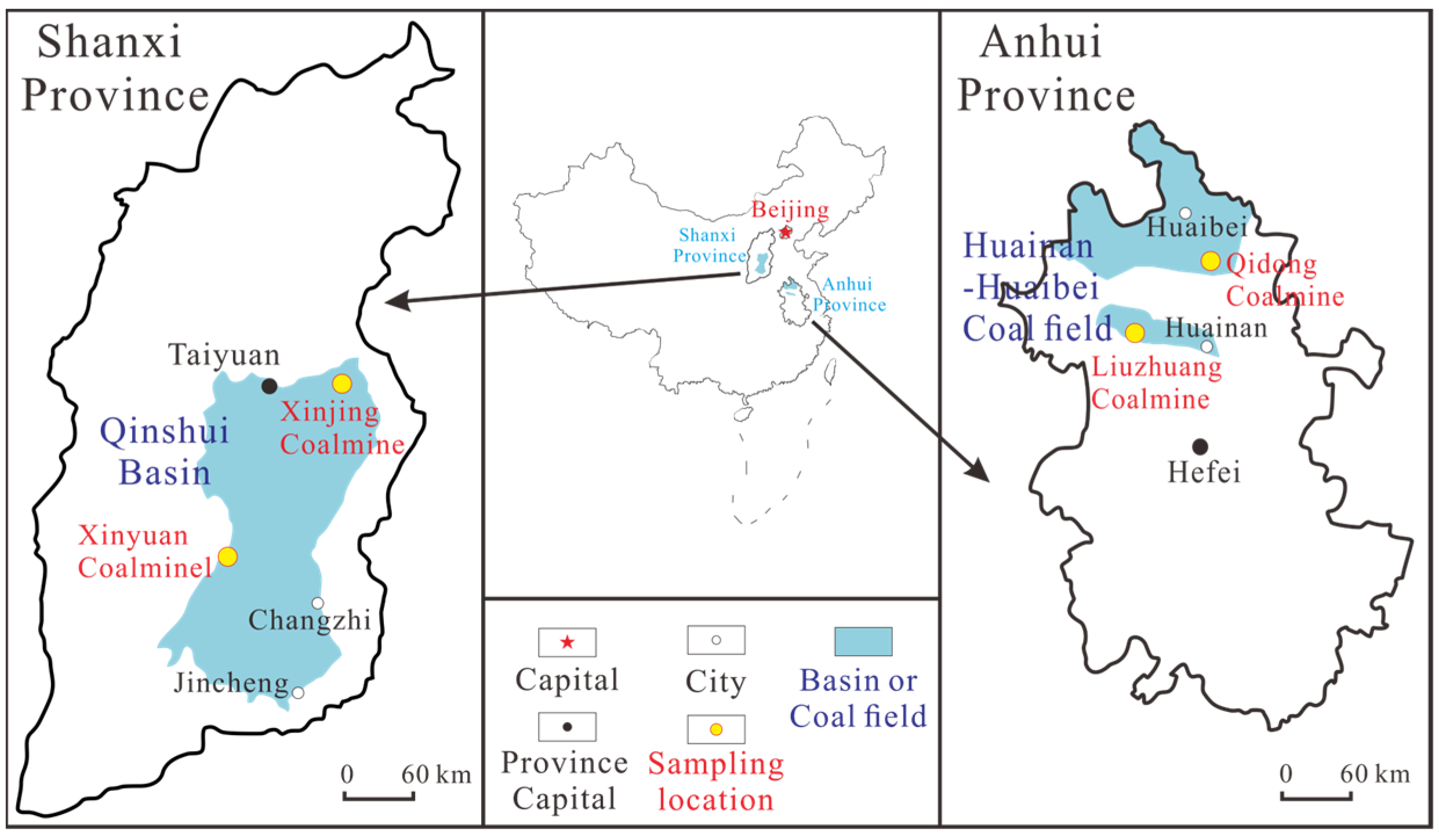




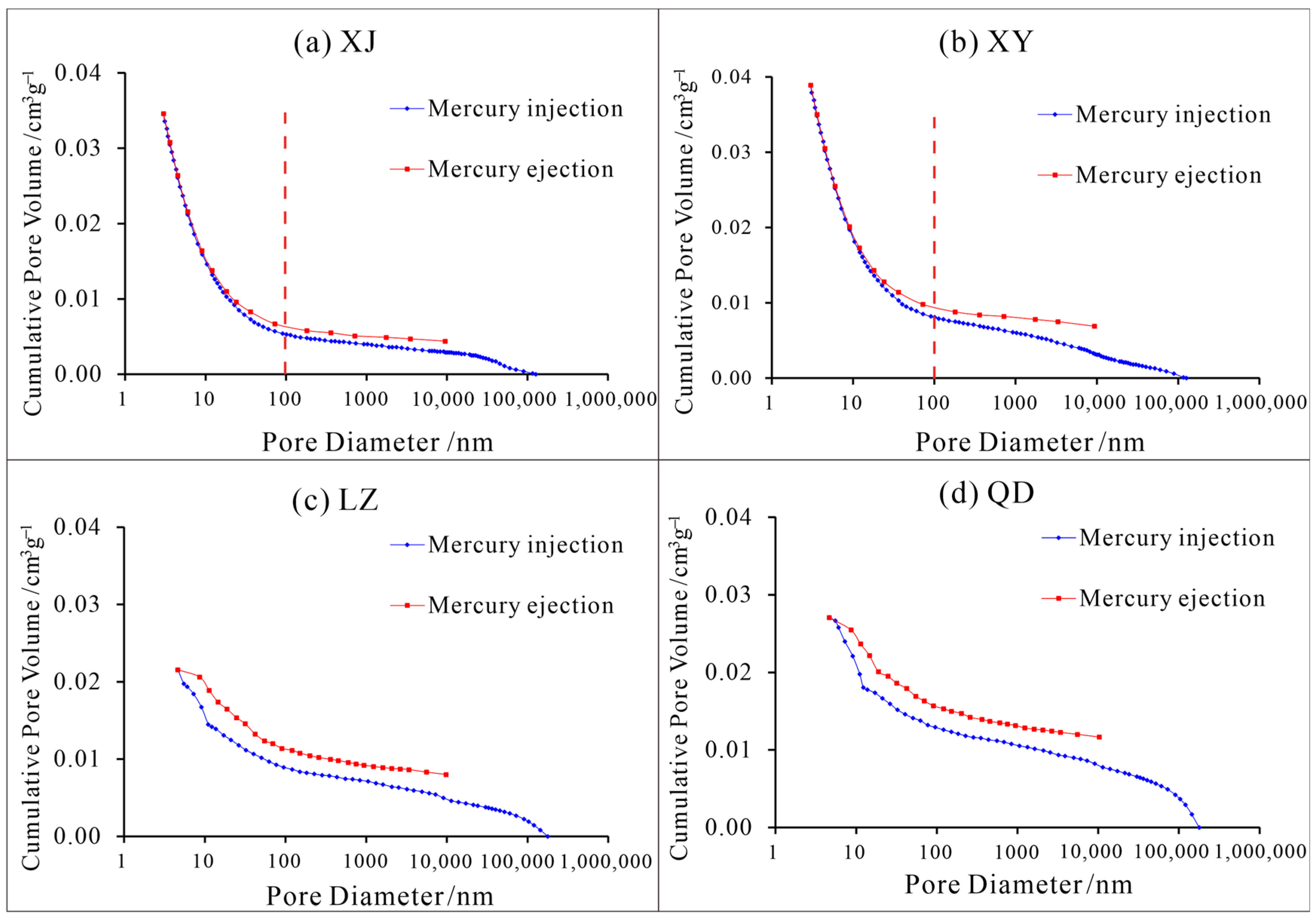
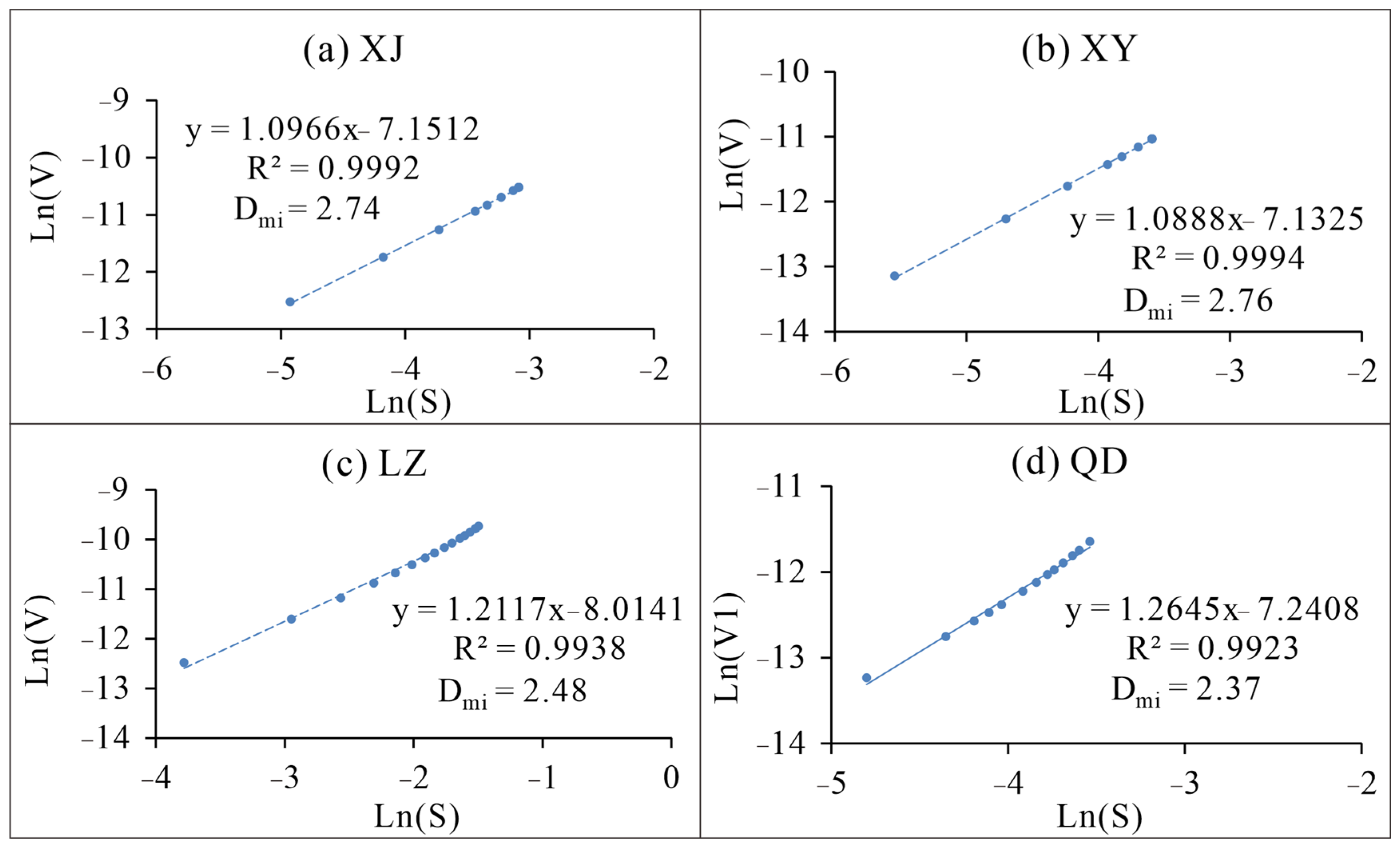
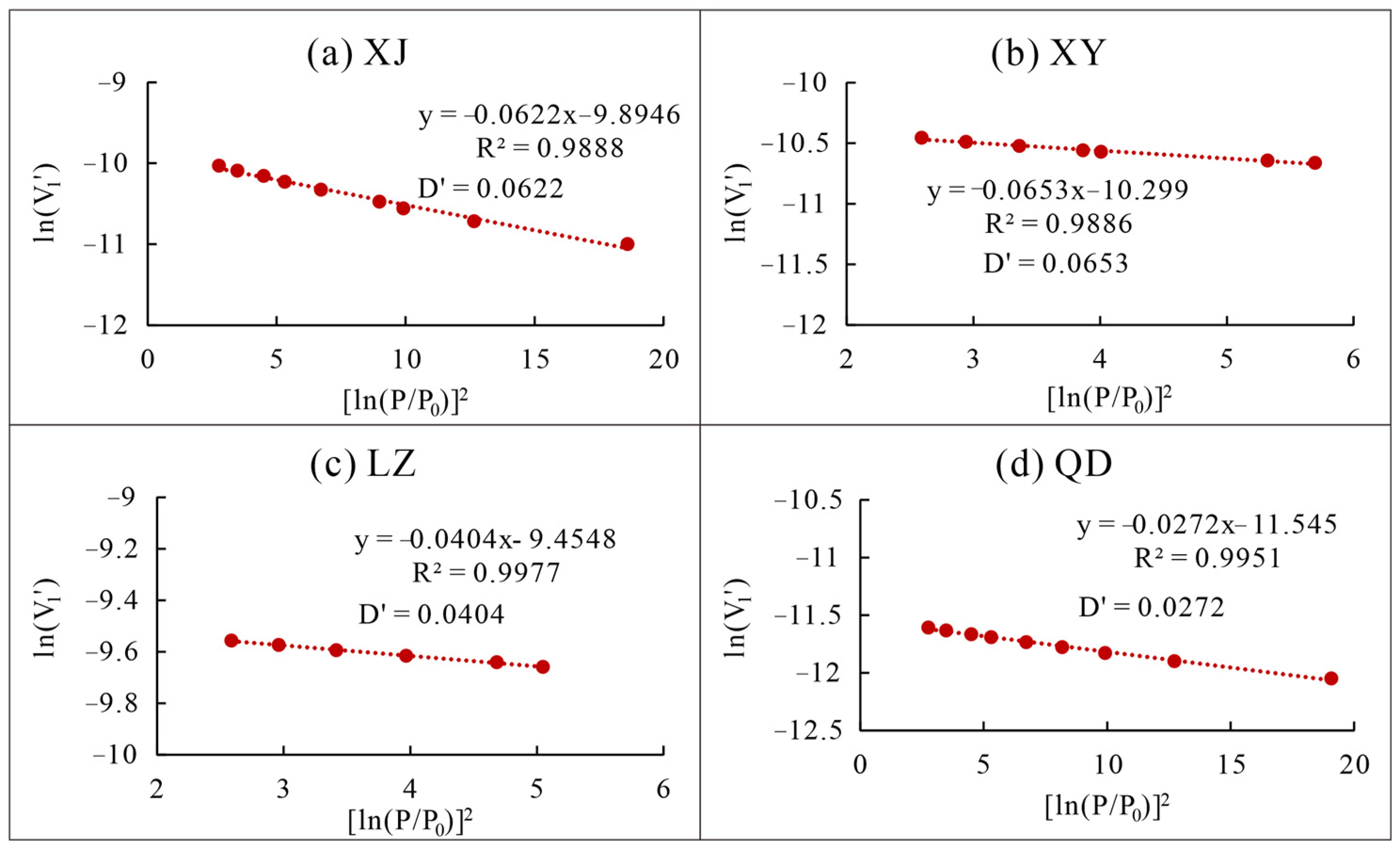
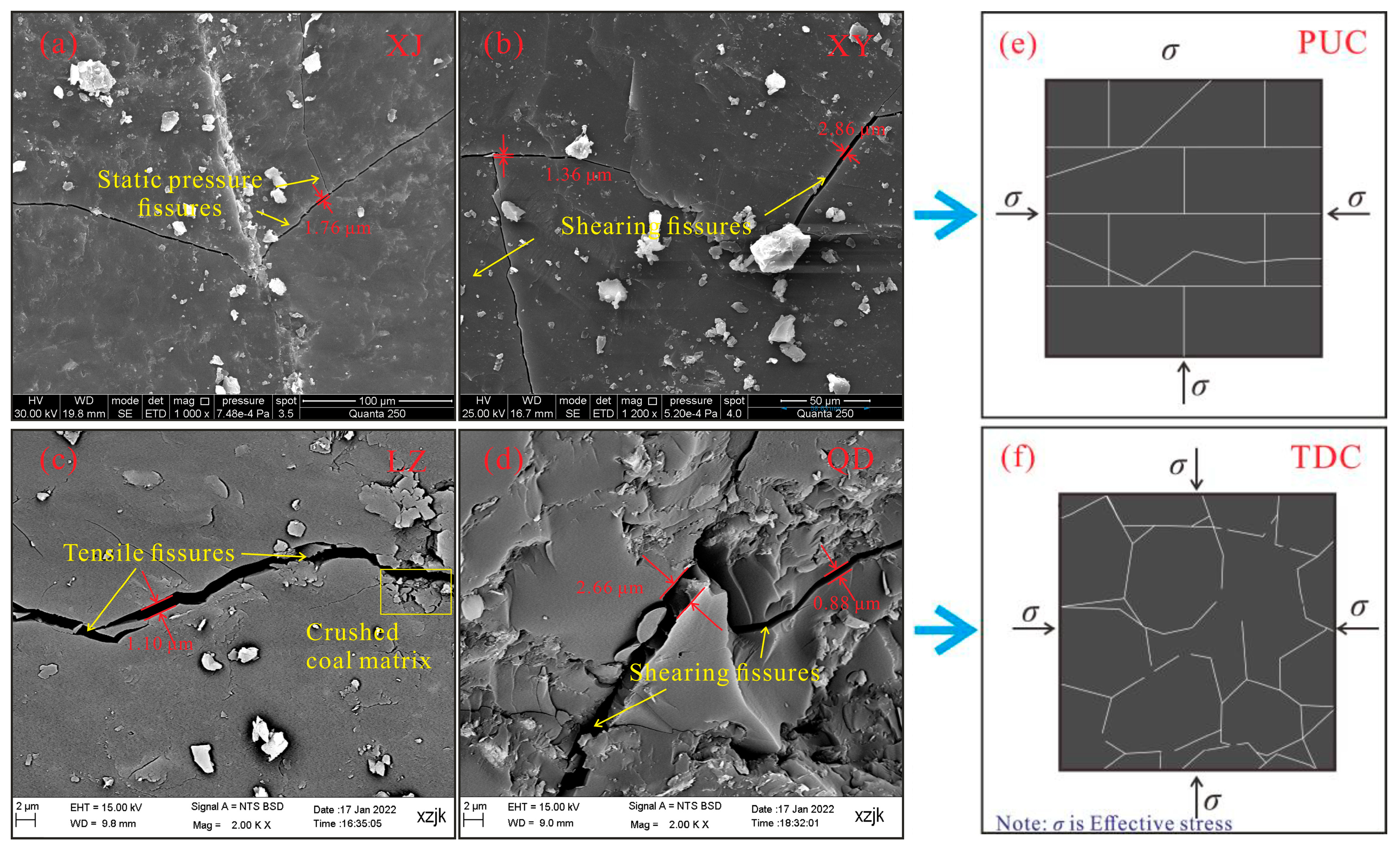

| Sample ID | Sampling Location | Depth /m | Coal Matrix Structure | Ro,max/% | Vdaf/ wt.% | Coal Rank | Porosity (%) | P (mD) |
|---|---|---|---|---|---|---|---|---|
| Xinjing (XJ) | Qinshui Basin | 585 | PUC | 2.63 | 10.02 | Semi-anthracite | 4.29 | 0.219 |
| Xinyuan (XY) | 833 | PUC | 1.81 | 15.26 | Low-volatile bituminous | 4.65 | 0.0537 | |
| Liuzhuang (LZ) | Huainan Coalfield | 820 | TDC | 0.93 | 39.34 | High-volatile bituminous | 2.80 | 0.0011 |
| Qidong (QD) | Huaibei Coalfield | 437 | TDC | 0.93 | 38.59 | High-volatile bituminous | 3.58 | 0.0093 |
| Pore Structure | Micropore | Mesopore | Macropore | Fracture |
|---|---|---|---|---|
| Pore diameter | <2 nm | 2–50 nm | 50 nm–1 μm | >1 μm |
| Testing methods | - | MIP (4.33 nm–226.41 μm) | ||
| LNA (0.85–150 nm) | - | |||
| Fractal methods | V-S model | FHH model | Menger sponge model | |
| Average tortuosity | ||||
| Sample ID | Mesopore-1 | Mesopore-2 | Macropore | ||||||
|---|---|---|---|---|---|---|---|---|---|
| d/nm | Dme1 | R2 | d/nm | Dme2 | R2 | d/nm | Dma1 | R2 | |
| XJ | 2~4 | 2.78 | 0.989 | 4~50 | 2.95 | 0.972 | 50~111 | 2.99 | 0.968 |
| XY | 2~6 | 2.84 | 0.999 | 6~50 | 2.92 | 0.976 | 50~111 | 2.98 | 0.967 |
| LZ | 2~8 | 2.83 | 0.994 | 8~50 | 2.66 | 0.997 | 50~155 | 2.64 | 0.998 |
| QD | 2~6 | 2.85 | 0.963 | 6~50 | 2.46 | 0.997 | 50~165 | 2.46 | 0.982 |
| Sample ID | Fractal Dimension | Pressure Classifications | |||||||
|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | P1 /MPa | d1 | P2 /MPa | d2 | P3 /MPa | d3 | |
| XJ | 2.75 | 2.92 | 3.89 | <0.055 | >22.7 μm | 0.055–17.19 | 72.6 nm–22.7 μm | >17.19 | <72.6 nm |
| XY | 2.69 | 2.86 | 3.86 | <0.062 | >20.1 μm | 0.062–13.76 | 90.6 nm–20.1 μm | >13.76 | <90.6 nm |
| LZ | 2.03 | 2.93 | 3.76 | <0.041 | >30.1 μm | 0.041–8.26 | 151.0 nm–30.1 μm | >8.26 | <151.0 nm |
| QD | 2.08 | 2.96 | 3.86 | <0.089 | >13.9 μm | 0.089–6.81 | 77.1 nm–13.9 μm | >6.81 | <77.1 nm |
| Sample ID | Porosity/% | Df | Tav | Lm/μm | Rav/μm | DT |
|---|---|---|---|---|---|---|
| XJ | 4.30 | 2.86 | 12.00 | 47.53 | 0.0075 | 1.31 |
| XY | 4.65 | 2.77 | 11.13 | 25.96 | 0.0081 | 1.32 |
| LZ | 2.80 | 2.85 | 18.23 | 25.94 | 0.0226 | 1.45 |
| QD | 3.58 | 2.89 | 14.35 | 9.03 | 0.0217 | 1.50 |
| Scholars | Time | Classification Standard of Pore | Data From |
|---|---|---|---|
| Hodot | 1966 | Micropore (<10 nm); Transitional pore (10–100 nm); Mesopore (100–1000 nm); Macropore (>1000 nm) | [51] |
| Gan et al. | 1972 | Micropore (0.4–1.2 nm); Transitional pore (1.2–30 nm); Macropore (>30 nm) | [52] |
| Dubinin | 1974 | Micropore (<1.3 nm); Sup-micropore (1.3–3.1 nm); Mesopore (3.1–300 nm); Macropore (>300 nm) | [53] |
| Wu et al. | 1991 | Micropore (<10 nm); Transitional pore (10–100 nm); Mesopore (100–1000 nm); Macropore (>1000 nm) | [54] |
| Qin et al. | 1995 | Micropore (<15 nm); Transitional pore (15–50 nm); Mesopore (50–400 nm); Macropore (>400 nm) | [55] |
| Sang et al. | 2005 | Absorption pore (<2 nm); adsorption pore (2–10 nm); Coagulation-adsorption pore (10–100 nm); Seepage pore (>100 nm) | [56] |
| Hu et al. | 2023 | Unreachable pore (<0.38 nm); Filling pore (0.38–1.50 nm); Diffusion pore (1.5–100 nm); Seepage pore (>100 nm) | [39] |
| Pore Classification | Filling Pore (<2 nm) | Adsorption Pores (2–8 nm) | Diffusion Pore (8–150 nm) | Seepage Pore (150 nm–30 μm) | Fracture (>30 μm) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sample ID | V | D | θ | V | D | V | D | V | D | V | D |
| XJ | 0.027 | 2.74 | 53.3 | 0.032 | 2.78 | 0.45 | 2.97 | 3.1 | 2.92 | 2 | 2.75 |
| XY | 0.016 | 2.76 | 47.8 | 0.012 | 2.84 | 0.42 | 2.95 | 5.9 | 2.86 | 1.7 | 2.69 |
| LZ | 0.059 | 2.48 | 75.5 | 0.12 | 2.83 | 1.26 | 2.65 | 4.68 | 2.93 | 3.69 | 2.03 |
| QD | 0.0079 | 2.37 | 87.2 | 0.052 | 2.85 | 0.72 | 2.46 | 5.76 | 2.96 | 6.56 | 2.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Liu, H.; Ma, M.; Xu, H.; Fang, H. Multiscale Fractal Characterization of Pore–Fracture Structure of Tectonically Deformed Coal Compared to Primary Undeformed Coal: Implications for CO2 Geological Sequestration in Coal Seams. Processes 2023, 11, 2934. https://doi.org/10.3390/pr11102934
Zhang K, Liu H, Ma M, Xu H, Fang H. Multiscale Fractal Characterization of Pore–Fracture Structure of Tectonically Deformed Coal Compared to Primary Undeformed Coal: Implications for CO2 Geological Sequestration in Coal Seams. Processes. 2023; 11(10):2934. https://doi.org/10.3390/pr11102934
Chicago/Turabian StyleZhang, Kun, Huihu Liu, Mengya Ma, Hongjie Xu, and Huihuang Fang. 2023. "Multiscale Fractal Characterization of Pore–Fracture Structure of Tectonically Deformed Coal Compared to Primary Undeformed Coal: Implications for CO2 Geological Sequestration in Coal Seams" Processes 11, no. 10: 2934. https://doi.org/10.3390/pr11102934
APA StyleZhang, K., Liu, H., Ma, M., Xu, H., & Fang, H. (2023). Multiscale Fractal Characterization of Pore–Fracture Structure of Tectonically Deformed Coal Compared to Primary Undeformed Coal: Implications for CO2 Geological Sequestration in Coal Seams. Processes, 11(10), 2934. https://doi.org/10.3390/pr11102934







