Numerical Simulation of Fluidization Behavior and Chemical Performance for Hydrochlorination of Silicon Tetrachloride in a Fluidized Bed Reactor
Abstract
:1. Introduction
2. Model Description
2.1. CFD Model
2.1.1. Eulerian-Granular Model
2.1.2. Turbulent Model
2.1.3. Drag Model
2.1.4. Heat Transfer Model
2.1.5. Species Transport Model
2.2. Chemical Reaction Kinetic Model
2.3. Numerical Solution Algorithms
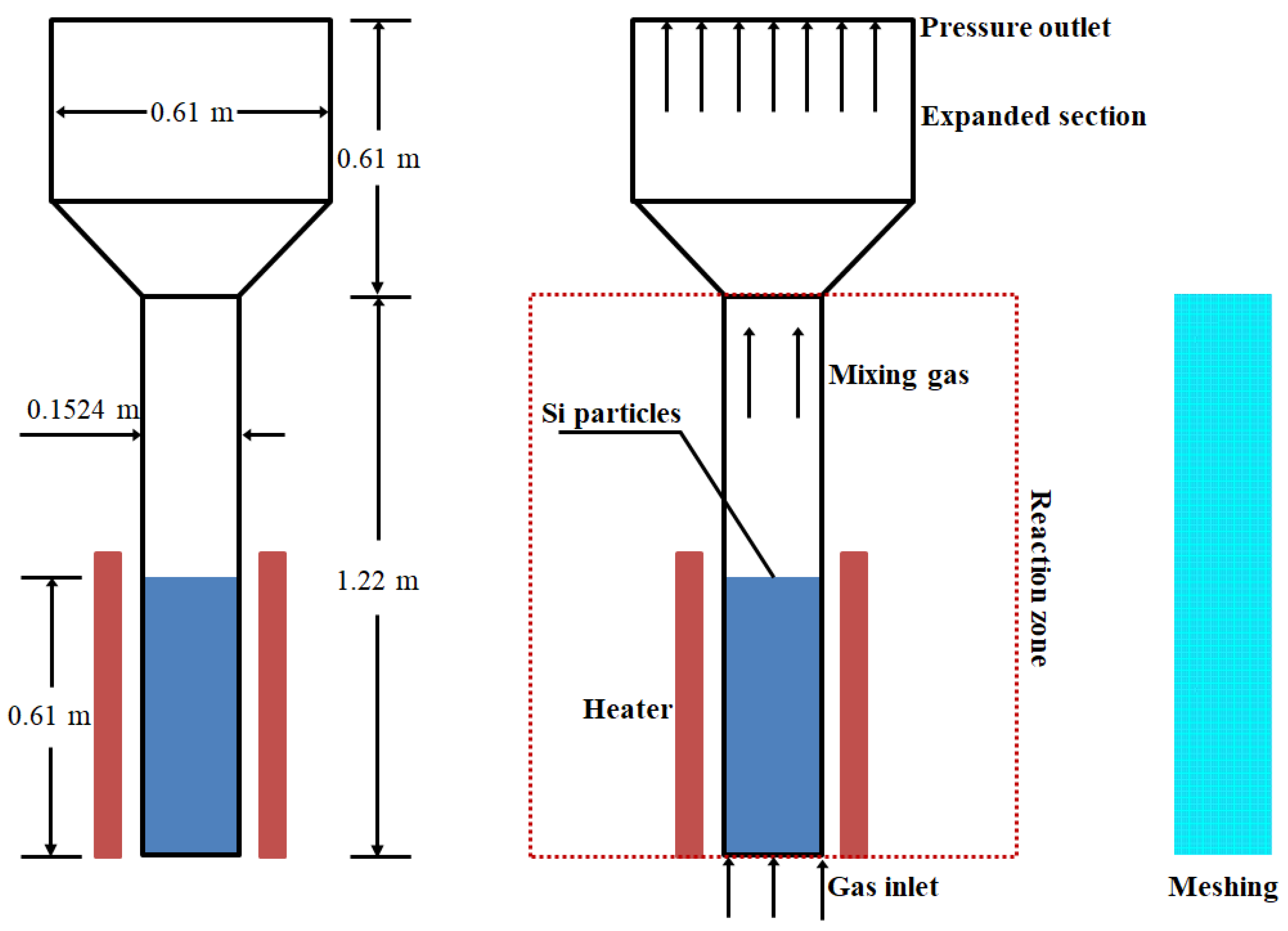
2.4. Geometrical Configuration
2.5. Grid Independence Verification
3. Results and Discussion
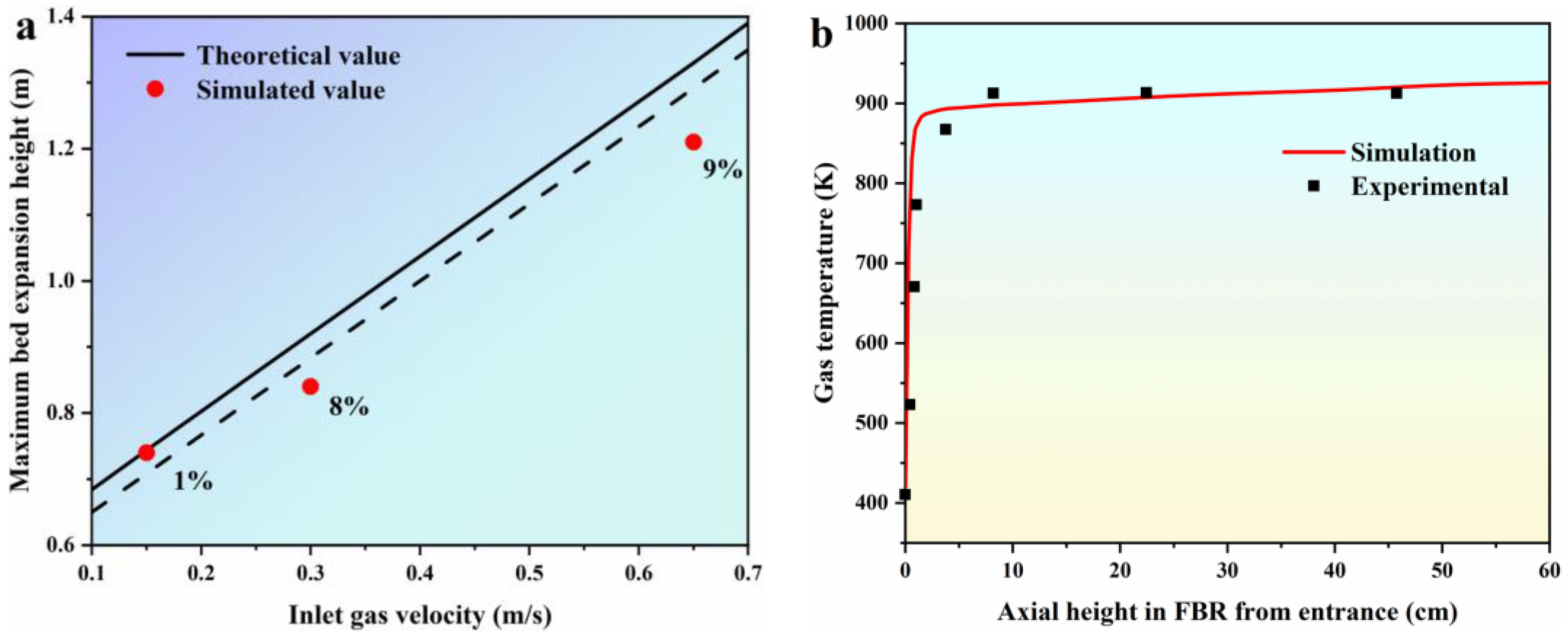
3.1. Model Validation
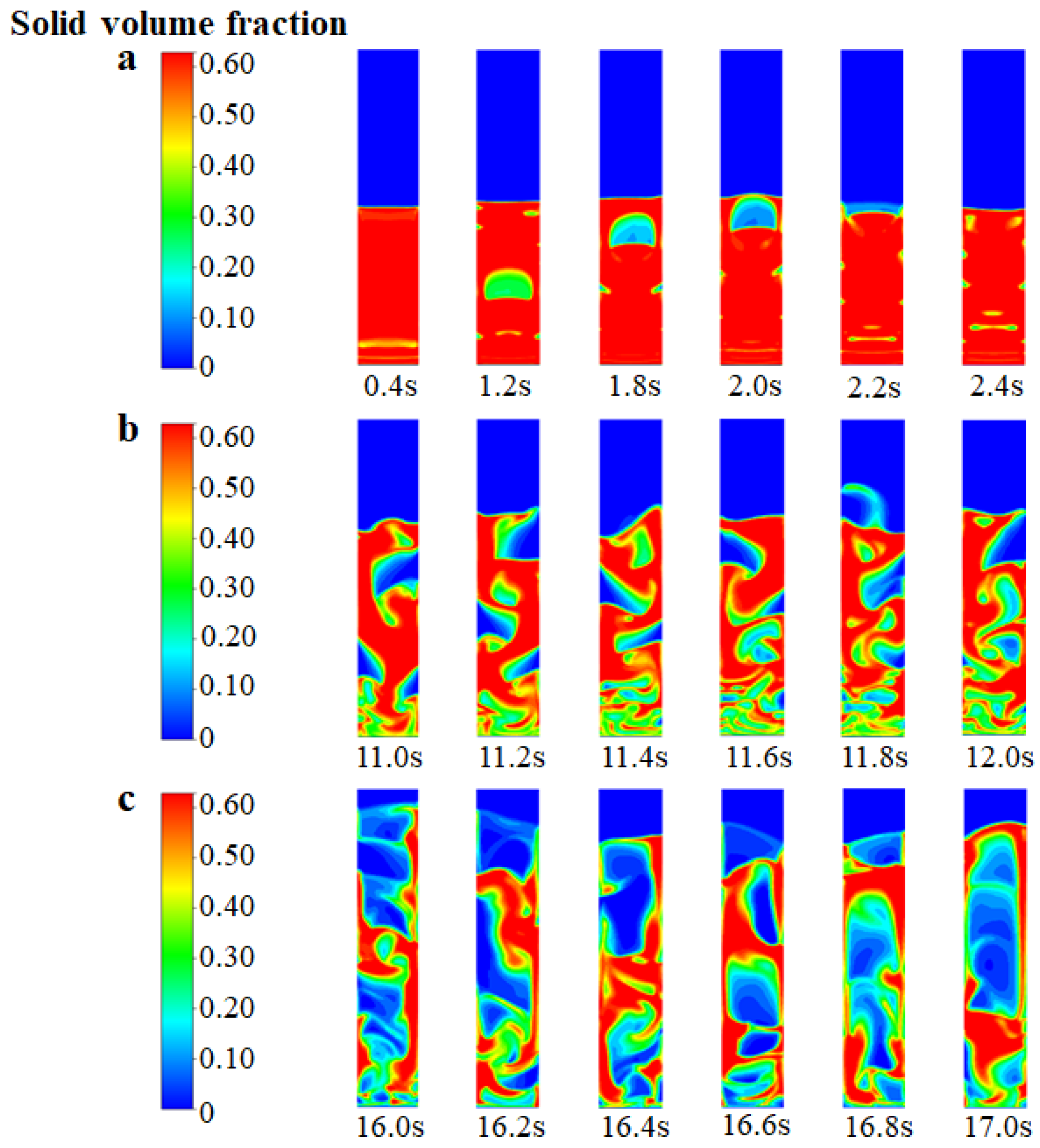
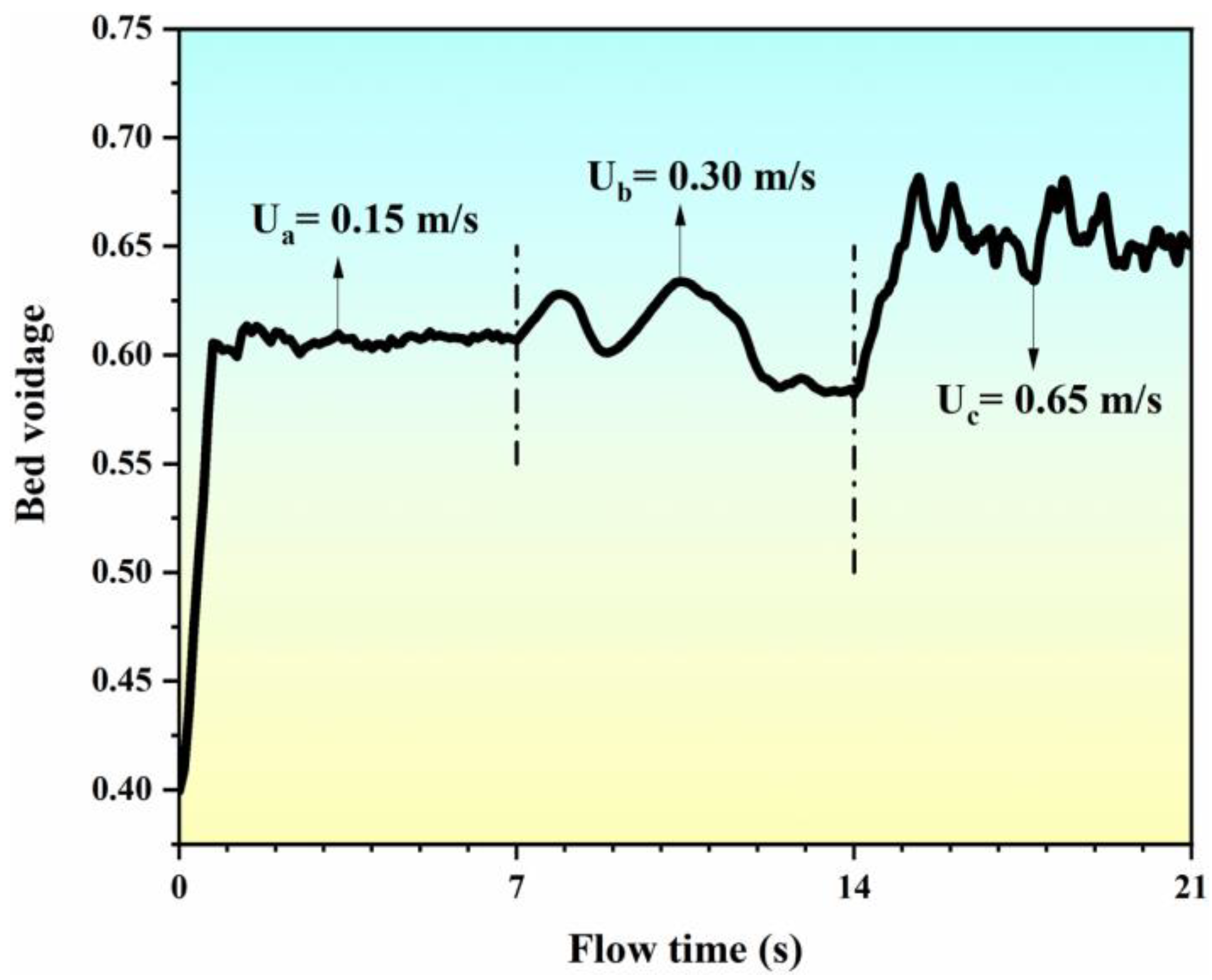
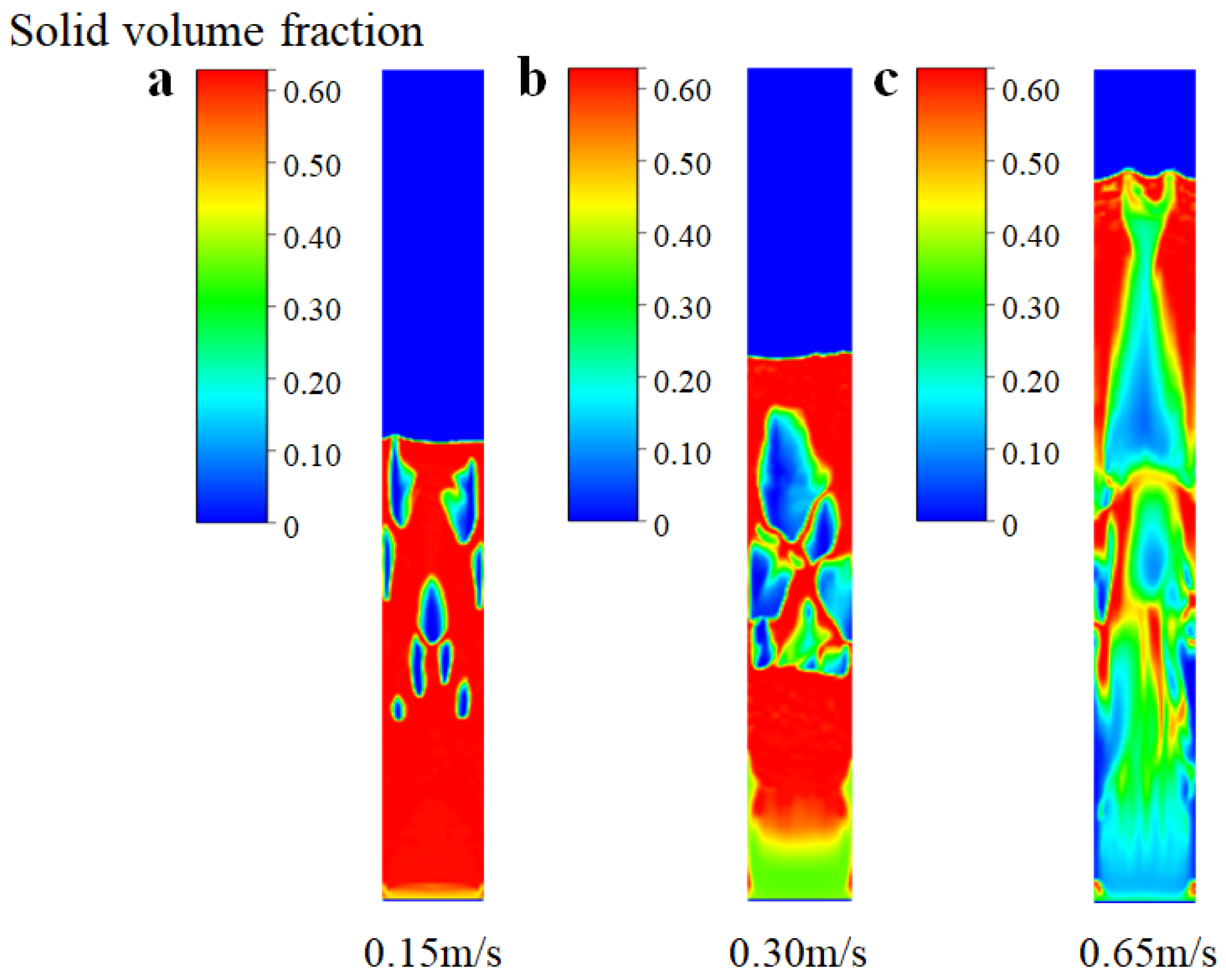
3.2. Flow Pattern and Regime
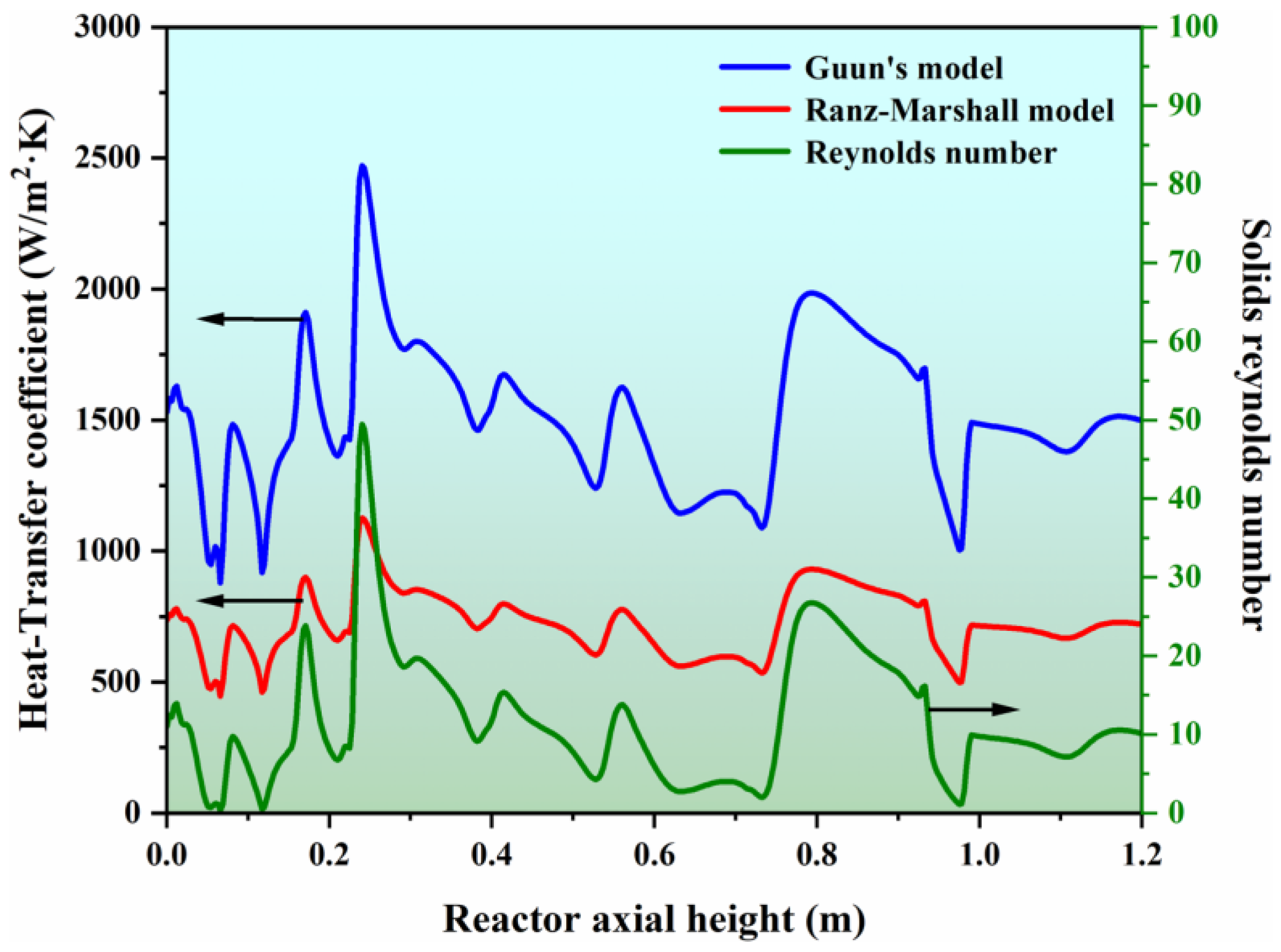
3.3. Heat Transfer Characteristics
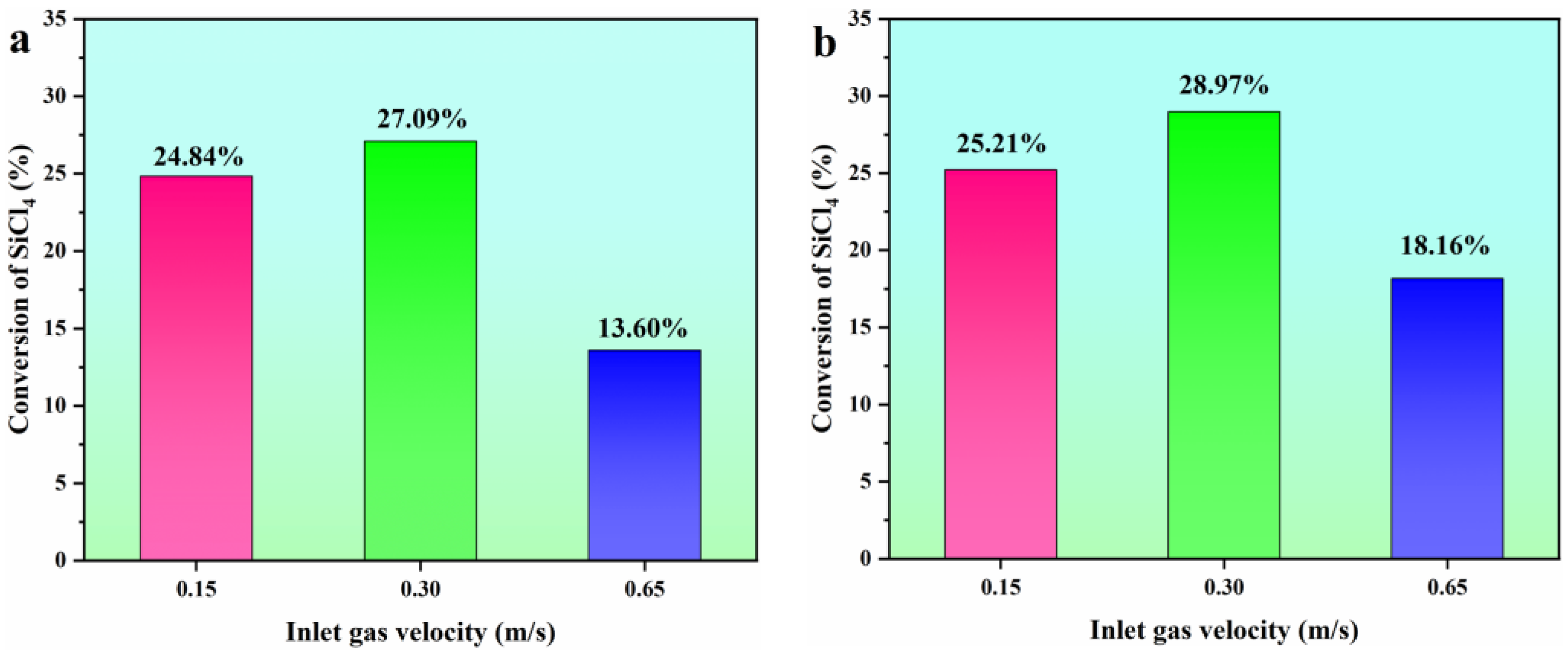
3.4. Chemical Reaction Performance
4. Conclusions
- The established EGM can reasonably describe the variation of the flow regime for the hydrochlorination of SiCl4 within the FBR. The effectiveness of the simulation method and the accuracy of the model were validated through comprehensive comparisons, encompassing a simulated Hmax in comparison to theoretical values obtained from empirical formulas and a comparison of the simulated gas temperature profile with data from Hsu’s experiments.
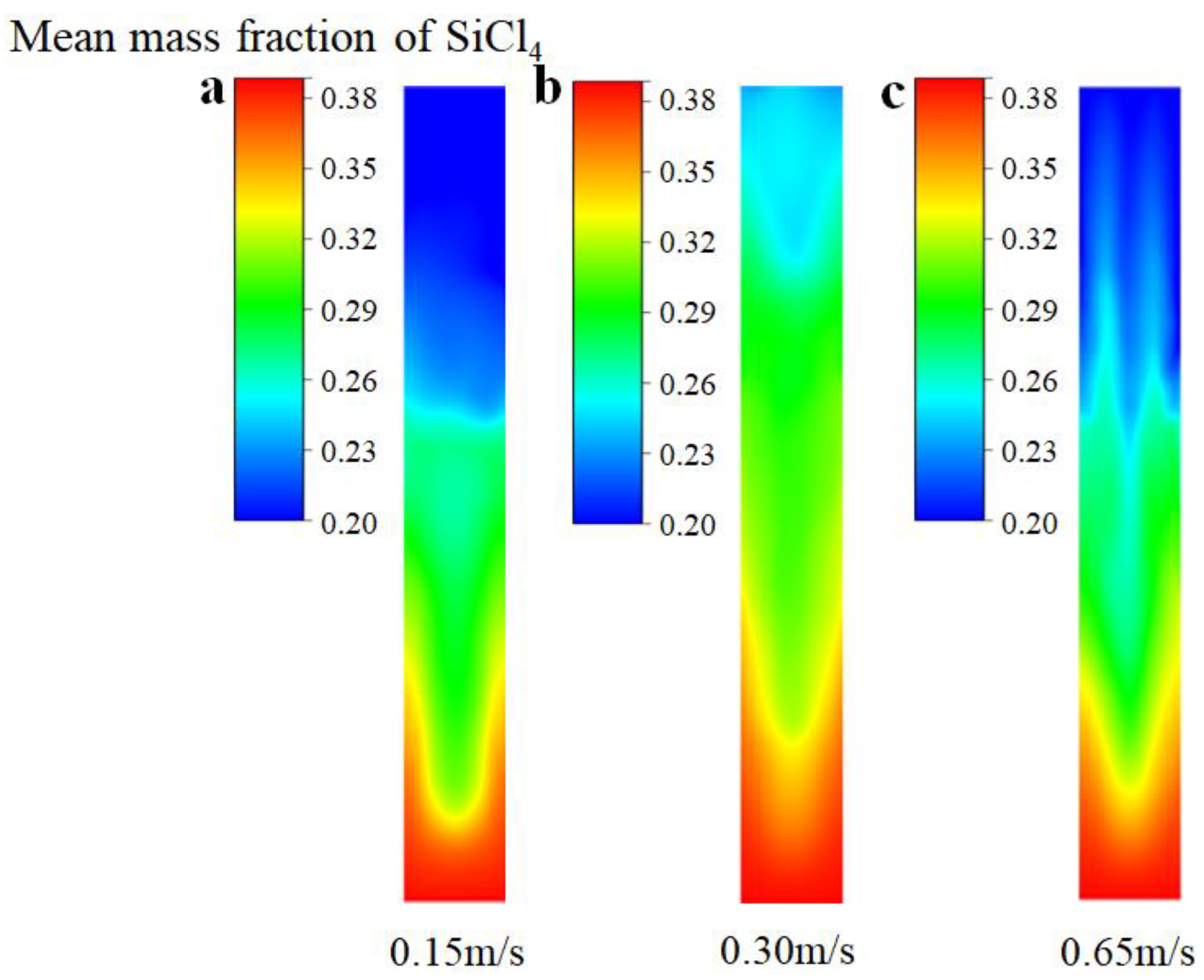
- The bed voidage increased with the flow time, coinciding with transitions in the flow regime within the FBR. Particularly noteworthy was the attainment of a more uniform distribution of SiCl4 under the bubbling fluidization state.
- The FBR exhibits remarkable heat transfer characteristics, as the reaction gas attains the preset bed temperature within a mere 10 mm from the entrance. Moreover, the presence of circulating bubbles within the FBR greatly enhances the uniform mixing of the SiCl4 reaction gas with silicon particles.
- When the FBR is in the bubbling stage, it promotes the effective mixing of the gas–solid phases, resulting in the highest conversion rate of SiCl4. Our predictions revealed a peak concentration of SiHCl3 at 13.08%, and a SiCl4 conversion rate of 28.97% was achieved under the conditions of bubbling fluidization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Pre-exponential factor, mol/(g∙s∙atm2) |
| CD | Drag coefficient |
| Cp | Heat capacity, J/(mol∙K) |
| D | Bed diameter, m |
| ds | Solid diameter, m |
| ess | Particle–particle restitution coefficient |
| Gk | Generation of turbulence kinetic energy |
| g | Gravitational acceleration, m/s2 |
| g0 | Radial distribution function |
| h | Specific enthalpy, J/(kg∙K) |
| hw | Wall–bed heat transfer coefficient, W/(m∙K) |
| hgs | Gas–solid heat transfer coefficient, W/(m∙K) |
| H | Specific enthalpy, J/(kg∙K) |
| ΔH | Enthalpy change, kJ |
| Hmax | Maximum bed expansion height, m |
| Hmf | Bed height at minimum fluidization, m |
| I | Identity matrix |
| Jn | Mass diffusion |
| k | Turbulence kinetic energy tensor |
| k0 | Apparent rate constant, mol/(g∙s∙atm2) |
| kg | Gas thermal conductivity, W/(m∙K) |
| ks | Solid thermal conductivity, W/(m∙K) |
| K1 | Adsorption equilibrium constants, atm−1 |
| K2 | Adsorption equilibrium constants, atm2/3 |
| Kp | Equilibrium rate constant, mol/(g∙s∙atm2) |
| Kgs | Interphase exchange coefficient, (kg∙m2)/s |
| mgs | Interphase mass transfer from gas to solid, kg/(m3∙s) |
| msg | Interphase mass transfer from solid to gas, kg/(m3∙s) |
| Nus | Nusselt number of solid phase |
| p | Pressure drop, Pa |
| Pr | Prandtl number |
| q | Heat flux, W/m2 |
| Rn | Net rate which chemical reaction produces a substance |
| Rc1 | Chemical reaction rate of the hydrogenation |
| Rc2 | Chemical reaction rate of the hydrochlorination |
| Res | Solid Reynolds number |
| Remf | Reynolds number at minimum fluidization |
| Sn | Source term |
| t | Flow time, s |
| T | Temperature, K |
| Tw | Wall temperature, K |
| Tf | Reference temperature, K |
| Umf | Minimum fluidizing velocity, m/s |
| Umb | Minimum bubbling velocity, m/s |
| Ums | Minimum slugging velocity, m/s |
| Z | FBR axial height, m |
| Greek symbols | |
| αg | Volume fraction of gas phase |
| αs | Volume fraction of solid phase |
| αmf | Bed void fraction at minimum fluidization |
| αs,max | Maximum volume fraction of solid phase |
| ε | Turbulence dissipation rate, m2/s3 |
| Θs | Granular temperature, m2/s2 |
| λs | Solid bulk viscosity, Pa∙s |
| μ | Gas viscosity, Pa∙s |
| μs | Solid shear viscosity, Pa∙s |
| μs,col | Solid collision viscosity, Pa∙s |
| μs,kin | Solid kinetic viscosity, Pa∙s |
| μs,fr | Solid fractional viscosity, Pa∙s |
| μs,eff | Effective solid viscosity, Pa∙s |
| Collisional dissipation of energy | |
| v | Velocity, m/s |
| ρ | Density, kg/m3 |
| τ | Shear stress, N/m2 |
| Exchange energy between gas and solid | |
| Subscripts | |
| g | Gas phase |
| s | Solid phase |
| m | Gas and solid phase, respectively |
| n | Species |
References
- Rabaia, M.K.H.; Semeraro, C.; Olabi, A.G. Recent progress towards photovoltaics’ circular economy. J. Clean. Prod. 2022, 373, 133864. [Google Scholar] [CrossRef]
- Deng, R.; Zhuo, Y.T.; Shen, Y.S. Recent progress in silicon photovoltaic module recycling processes. Resour. Conserv. Recycl. 2022, 187, 106612. [Google Scholar] [CrossRef]
- Yadav, S.; Chattopadhyay, K.; Singh, C.V. Solar grade silicon production: A review of kinetic, thermodynamic and fluid dynamics based continuum scale modeling. Renew. Sustain. Energy Rev. 2017, 78, 1288–1314. [Google Scholar] [CrossRef]
- Nie, Z.F.; Wang, Y.J.; Wang, C.; Guo, Q.J.; Hou, Y.Q.; Ramachandran, P.A.; Xie, G. Mathematical model and energy efficiency analysis of Siemens reactor with a quartz ceramic lining. Appl. Therm. Eng. 2021, 199, 117522. [Google Scholar] [CrossRef]
- Zhou, T.; Gong, L.L.; Cheng, X.D.; Pan, Y.L.; Li, C.C.; Zhang, H.P. Preparation and characterization of silica aerogels from by-product silicon tetrachloride under ambient pressure drying. J. Non-Cryst. Solids 2018, 499, 387–393. [Google Scholar] [CrossRef]
- Ding, W.J.; Yan, J.M.; Xiao, W.D. Hydrogenation of Silicon Tetrachloride in the Presence of Silicon: Thermodynamic and Experimental Investigation. Ind. Eng. Chem. Res. 2014, 53, 10943–10953. [Google Scholar] [CrossRef]
- Ding, W.J.; Wang, Z.B.; Yan, J.M.; Xiao, W.D. CuCl-Catalyzed Hydrogenation of Silicon Tetrachloride in the Presence of Silicon: Mechanism and Kinetic Modeling. Ind. Eng. Chem. Res. 2014, 53, 16725–16735. [Google Scholar] [CrossRef]
- Wu, J.; Chen, Z.; Ma, W.; Dai, Y. Thermodynamic estimation of silicon tetrachloride to trichlorosilane by a low temperature hydrogenation technique. Silicon 2017, 9, 69–75. [Google Scholar] [CrossRef]
- Wang, Y.; Nie, Z.; Guo, Q.; Song, Y.; Liu, L. Adsorption Behaviors of Chlorosilanes, HCl, and H2 on the Si(100) Surface: A First-Principles Study. ACS Omega 2022, 7, 42105–42114. [Google Scholar] [CrossRef] [PubMed]
- Ravasio, S.; Maso, M.; Cavalloti, C. Analysis of the Gas Phase Reactivity of Chlorosilanes. J. Phys. Chem. 2013, 117, 5221–5231. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Lee, W.H.; Park, Y.K.; Kim, H.Y.; Kang, N.Y.; Yoon, K.B.; Choi, W.C.; Yang, O.B. Catalytic conversion of silicon tetrachloride to trichlorosilane for a poly-Si process. Sol. Energy Mater. Sol. Cells 2012, 105, 142–147. [Google Scholar] [CrossRef]
- Jain, M.P.; Sathiyamoorthy, D.; Rao, V.G. Studies on Hydrochlorination of Silicon in a Fluidised Bed Reactor. Indian Chem. Eng. 2010, 53, 61–67. [Google Scholar] [CrossRef]
- Becker, F.; Buchholz, S.; Mleczko, L. Kinetic Modeling of the Hydrochlorination of Silicon with SiCl4 and H2. Chem. Ing. Tech. 2001, 73, 686. [Google Scholar] [CrossRef]
- Guan, G.Q.; Fushimi, C.; Tsutsumi, A. Prediction of flow behavior of the riser in a novel high solids flux circulating fluidized bed for steam gasification of coal or biomass. Chem. Eng. J. 2010, 164, 221–229. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, S.; Zhang, K.; Zhao, Y.H.; He, Y.R. Numerical studies of gas-solid flow behaviors and wall wear in a swirling fluidized bed. Powder Technol. 2021, 388, 233–240. [Google Scholar] [CrossRef]
- Shao, Y.J.; Li, Z.Z.; Zhong, W.Q.; Bian, Z.F.; Yu, A.B. Minimum fluidization velocity of particles with different size distributions at elevated pressures and temperatures. Chem. Eng. Sci. 2020, 216, 115555. [Google Scholar] [CrossRef]
- Chien, R.Y.; Tseng, W.F.; Wu, K.T. Numerical simulation of fuel reactor for a methanefueled chemical looping combustion using bubbling fluidized bed with internal particle circulation. Int. J. Hydrogen Energy 2021, 47, 37415–37428. [Google Scholar] [CrossRef]
- Pottimurthy, Y.; Wang, D.W.; Park, C.; Patil, S.; Tong, A.; Fan, L.S. Three-dimensional dynamic characterization of square-nosed slugging phenomena in a fluidized bed. Particuology. 2022, 67, 35–46. [Google Scholar] [CrossRef]
- Liu, S.S.; Xiao, W.D. Numerical simulations of particle growth in a silicon-CVD fluidized bed reactor via a CFD–PBM coupled model. Chem. Eng. Sci. 2014, 111, 112–125. [Google Scholar] [CrossRef]
- Liu, S.S.; Xiao, W.D. CFD–PBM coupled simulation of silicon CVD growth in a fluidized bed reactor: Effect of silane pyrolysis kinetic models. Chem. Eng. Sci. 2015, 127, 84–94. [Google Scholar] [CrossRef]
- Zhu, X.L.; Dong, P.F.; Zhu, Z.P.; Ocone, R.; Yang, W.Q.; Wang, H.G. Effects of pressure on flow regimes transition velocities and bubble properties in a pilot-scale pressurised circulating fluidised bed. Chem. Eng. J. 2021, 410, 128438. [Google Scholar] [CrossRef]
- Cho, Y.J.; Kim, S.J.; Nam, S.H.; Kang, Y.; Kim, S.D. Heat transfer and bubble properties in three-phase circulating fluidized beds. Chem. Eng. Sci. 2001, 56, 6107–6115. [Google Scholar] [CrossRef]
- Rashid, T.A.B.; Zhu, L.T.; Luo, Z.H. Comparative analysis of numerically derived drag models for development of bed expansion ratio correlation in a bubbling fluidized bed. Adv. Powder Technol. 2020, 31, 2723–2732. [Google Scholar] [CrossRef]
- Agu, C.E.; Torheim, L.A.; Eikeland, M.; Moldestad, B.M.E. Improved models for predicting bubble velocity, bubble frequency and bed expansion in a bubbling fluidized bed. Chem. Eng. Res. Des. 2019, 141, 361–371. [Google Scholar] [CrossRef]
- Yu, S.J.; Yang, X.X.; Zhou, H.; Li, Q.H.; Zhang, Y.G. Effects of bed size on the voidage in gas-solid bubbling fluidized beds. Powder. Technol. 2021, 387, 197–204. [Google Scholar] [CrossRef]
- Yu, S.J.; Yang, X.X.; Zhou, H.; Li, Q.H.; Zhang, Y.G. Statistical study of the distribution of voidage in a bubbling fluidized bed with a constant section. Chem. Eng. Res. Des. 2021, 171, 305–316. [Google Scholar] [CrossRef]
- Colomb, M.; Palanki, S.; Sylvester, N.D. Modeling the hydrochlorination reaction in a laboratory-scale fluidized bed reactor. Powder Technol. 2016, 292, 242–250. [Google Scholar] [CrossRef]
- Colomb, M.; Palanki, S.; Sylvester, N.D. Experimental verification of scalable model for the hydrochlorination reaction in a pilot-scale fluidized bed reactor. Powder Technol. 2016, 301, 989–998. [Google Scholar] [CrossRef]
- Liu, N.; Liu, X.P.; Wang, F.M.; Xin, F.; Sun, M.S.; Zhai, Y.; Zhang, X.B. CFD simulation study of the effect of baffles on the fluidized bed for hydrogenation of silicon tetrachloride. Chin. J. Chem. Eng. 2021, 45, 219–228. [Google Scholar] [CrossRef]
- Brennen, C.E. Fundamentals of Multiphase Flows; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Syamlal, M.; Rogers, W.; O’Brien, T.J. MFIX Documentation, Theory Guide; National Technical Information Service: Springfield, VA, USA, 1993. [Google Scholar]
- Lun, C.K.K.; Savage, S.B.; Jeffrey, D.J.; Chepurniy, N. Kinetic theories for granular flow inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J. Fluid Mech. 1984, 140, 223–256. [Google Scholar] [CrossRef]
- Schaeffer, D.G. Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 1987, 66, 19–50. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of Circulating Fluidized Beds: Kinetic Theory Approach; Illinois Institute of Technology: Chicago, IL, USA, 1991. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Gunn, D. Transfer of heat or mass to particles in fixed and fluidized beds. Int. J. Heat Mass Transfer. 1978, 21, 467–476. [Google Scholar] [CrossRef]
- Hsu, G.; Rohatgi, N.; Houseman, J. Silicon particle growth in a fluidized-bed reactor. AIChE J. 1987, 33, 784–791. [Google Scholar] [CrossRef]
- Matsen, J.M.; Hovmand, S.; Davidson, J.F. Expansion of fluidized beds in slug flow. Chem. Eng. Sci. 1969, 24, 1743–1754. [Google Scholar] [CrossRef]
- Cho, H.; Chung, C.; Han, G. Slugging bed height of polyethylene particles in a fluidized bed with an expanded section. Korean J. Chem. Eng. 2001, 18, 567–570. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Pre-exponential factor, A | 0.22 mol/(g∙s∙atm2) |
| Activation energy, E | 77.01 kJ/mol−1 |
| Reference temperature, Tr | 773 K |
| Equilibrium rate constant, Kp | 0.2645 atm−1/3 |
| Adsorption equilibrium constants, K1 | 0.2141 atm−1 |
| Adsorption equilibrium constants, K2 | 8.92 atm−1 |
| Enthalpy change, ΔH1 | 32.45 kJ/mol |
| Enthalpy change, ΔH2 | −12.85 kJ/mol |
| Enthalpy change, ΔHP | −36.73 kJ/mol |
| Parameters | Values |
|---|---|
| Bed height | 1.22 m |
| Bed width | 0.1524 m |
| Solid density | 2330 kg/m3 |
| Particle diameter | 235 μm |
| Solid–solid restitution coefficient | 0.9 |
| Gas density | 1.225 kg/m3 |
| Gas viscosity | 1.72 μPa·s |
| Initial bed height | 0.60 m |
| Initial solid volume fraction | 0.60 |
| Inlet gas velocity | 0.15/0.30/0.65 m/s |
| Wall temperature | 773 K |
| Inlet temperature | 300 K |
| Operating pressure | 2.0 MPa |
| SiCl4:H2:HCl | 1:4:1 |
| Parameters | Values |
|---|---|
| Inlet | Velocity-inlet |
| Outlet | Pressure-outlet |
| Drag model | Gidaspow et al. [35] |
| Heat transfer model | Guun [37] |
| Granular viscosity | Gidaspow et al. [35] |
| Granular bulk viscosity | Lun et al. [32] |
| Restitution | 0.9 |
| Wall-condition | No-slip |
| Friction viscosity | Schaeffer [33] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Dai, E.; Xu, S.; Yang, Y.; Yang, N.; Xie, G.; Nie, Z. Numerical Simulation of Fluidization Behavior and Chemical Performance for Hydrochlorination of Silicon Tetrachloride in a Fluidized Bed Reactor. Processes 2023, 11, 2979. https://doi.org/10.3390/pr11102979
Guo Q, Dai E, Xu S, Yang Y, Yang N, Xie G, Nie Z. Numerical Simulation of Fluidization Behavior and Chemical Performance for Hydrochlorination of Silicon Tetrachloride in a Fluidized Bed Reactor. Processes. 2023; 11(10):2979. https://doi.org/10.3390/pr11102979
Chicago/Turabian StyleGuo, Qijun, Enrui Dai, Shigang Xu, Yuehong Yang, Ni Yang, Gang Xie, and Zhifeng Nie. 2023. "Numerical Simulation of Fluidization Behavior and Chemical Performance for Hydrochlorination of Silicon Tetrachloride in a Fluidized Bed Reactor" Processes 11, no. 10: 2979. https://doi.org/10.3390/pr11102979
APA StyleGuo, Q., Dai, E., Xu, S., Yang, Y., Yang, N., Xie, G., & Nie, Z. (2023). Numerical Simulation of Fluidization Behavior and Chemical Performance for Hydrochlorination of Silicon Tetrachloride in a Fluidized Bed Reactor. Processes, 11(10), 2979. https://doi.org/10.3390/pr11102979






