Regenerative Braking of Electric Vehicles Based on Fuzzy Control Strategy
Abstract
:1. Introduction
2. Models and Problem Formulation
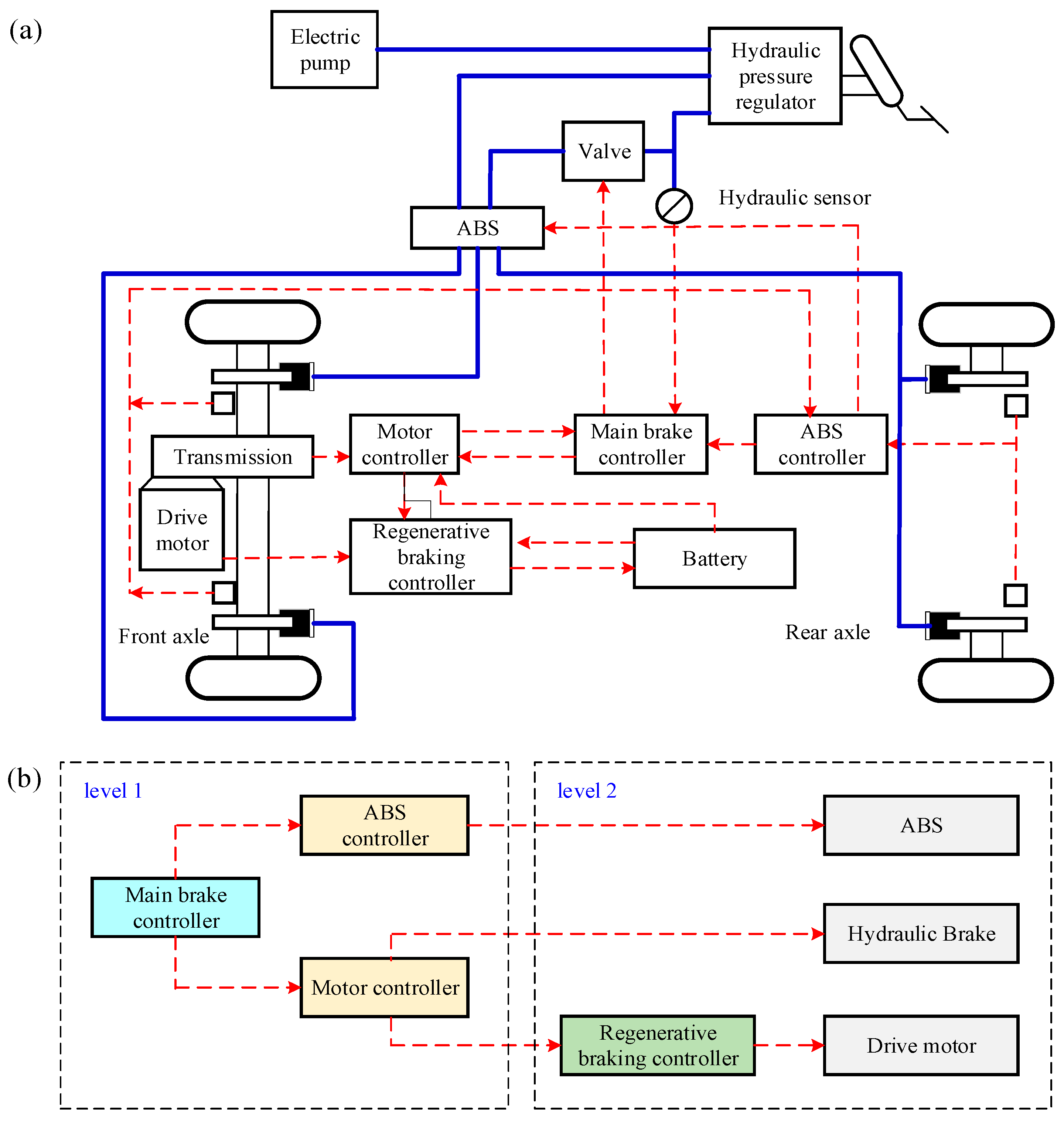
2.1. Design of Motor/Hydraulic Braking System
2.2. Dynamics Model of Electrical Vehicles
2.3. Parameters of the Drive Motor
2.4. SOC Calculation of Power Battery
2.5. Analysis of Energy Conversion
2.6. Six Driving Cycle Conditions
3. Methodology
3.1. Braking Force Distribution on the Front and Rear Axles
3.1.1. I Curve, f Curve, and r Curve
3.1.2. ECE Regulation Curve
3.1.3. Design of Braking Force Distribution for Front and Rear Axles
3.2. Fuzzy-Based Controller Design
3.2.1. Restrictions on Regenerative Braking
3.2.2. Fuzzy Control Rules
THEN k is i, i = 1, 2, …, n,
3.2.3. Structural Analysis of Fuzzy Controllers
3.3. Construction of Simulink Simulation
4. Results and Analysis
4.1. Variations in Regenerative Braking Coefficient
4.2. Energy Recovery Performance of Regenerative Braking
4.3. Energy Consumption Analysis
5. Comparison and Discussion
5.1. Performance of Regenerative Braking
5.2. Prospects for other Technologies to Improve Energy Saving Efficiency
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eckert, J.J.; Barbosa, T.P.; da Silva, S.F.; Silva, F.L.; Silva, L.C.A.; Dedini, F.G. Electric hydraulic hybrid vehicle powertrain design and optimization-based power distribution control to extend driving range and battery life cycle. Energy Convers. Manag. 2022, 252, 115094. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, W.; Li, W. Braking sense consistency strategy of electro-hydraulic composite braking system. Mech. Syst. Signal Process. 2018, 109, 196–219. [Google Scholar] [CrossRef]
- Ko, J.W.; Ko, S.Y.; Kim, I.S.; Hyun, D.Y.; Kim, H.-S. Co-operative control for regenerative braking and friction braking to increase energy recovery without wheel lock. Int. J. Automot. Technol. 2014, 15, 253262. [Google Scholar] [CrossRef]
- De Pinto, S.; Camocardi, P.; Chatzikomis, C.; Sorniotti, A.; Bottiglione, F.; Mantriota, G.; Perlo, P. On the comparison of 2- and 4-wheel-drive electric vehicle layouts with central motors and single- and 2-speed transmission systems. Energies 2020, 13, 3328. [Google Scholar] [CrossRef]
- Ju, J.; Li, W.; Liu, Y.; Zhang, C. Research on bifurcation and control of electromechanical coupling torsional vibration for wheel-side direct-driven transmission system. Proc. Inst. Mech. Eng. D 2021, 235, 93–104. [Google Scholar] [CrossRef]
- Li, W.; Zhu, X.; Ju, J. Hierarchical Braking Torque Control of In-Wheel-Motor-Driven Electric Vehicles over CAN. IEEE Access 2018, 6, 65189–65198. [Google Scholar] [CrossRef]
- Wang, F.; Lin, Z.; Xu, B.; Fiebig, W. An Electric-Hydrostatic Energy Storage System for Hydraulic Hybrid Wheel Loader. IEEE Trans. Veh. Technol. 2022, 71, 7044–7056. [Google Scholar] [CrossRef]
- Strohmaier, K.G.; Cronk, P.M.; Van De Ven, J.D. Design optimization of a hydraulic flywheel accumulator for a hydraulic hybrid vehicle. Int. J. Fluid Power 2015, 16, 149–161. [Google Scholar] [CrossRef]
- Raman, S.R.; Cheng, K.W.; Xue, X.D.; Fong, Y.C.; Cheung, S. Hybrid energy storage system with vehicle body integrated super-capacitor and li-ion battery: Model, design and implementation, for distributed energy storage. Energies 2021, 14, 6553. [Google Scholar] [CrossRef]
- He, Q.; Yang, Y.; Luo, C.; Zhai, J.; Luo, R.; Fu, C. Energy recovery strategy optimization of dual-motor drive electric vehicle based on braking safety and efficient recovery. Energy 2022, 248, 123543. [Google Scholar] [CrossRef]
- He, Q.; Chen, Y.; Fu, C. Efficiency optimization and control strategy of regenerative braking system with dual motor. Energies 2020, 13, 711. [Google Scholar]
- Suyanto, S.; Darwito, P.; Wahyuono, R.A.; Arifin, M.S.; Sudarmanta, B. Design of Regenerative Braking System for Electric Motorcycle Based on Supercapacitor with Fuzzy PID. Int. J. Automot. Technol. 2023, 24, 187–194. [Google Scholar] [CrossRef]
- Rizzo, G.; Tiano, F.A.; Mariani, V.; Marino, M. Optimal Modulation of Regenerative Braking in Through-The-Road Hybridized Vehicles. Energies 2021, 14, 6835. [Google Scholar] [CrossRef]
- Chen, X.; Wei, L.; Wang, X.; Li, L.; Wu, Q.; Xiao, L. Hierarchical cooperative control of anti-lock braking and energy regeneration for electromechanical brake-by-wire system. Mech. Syst. Signal Process. 2021, 159, 107796. [Google Scholar] [CrossRef]
- Li, W.; Du, H.; Li, W. Four-Wheel Electric Braking System Configuration with New Braking Torque Distribution Strategy for Improving Energy Recovery Efficiency. IEEE Trans. Intell. Transp. Syst. 2020, 21, 87–103. [Google Scholar] [CrossRef]
- Vodovozov, V.; Aksjonov, A.; Petlenkov, E.; Raud, Z. Neural Network-Based Model Reference Control of Braking Electric Vehicles. Energies 2021, 14, 2373. [Google Scholar] [CrossRef]
- Vodovozov, V.; Raud, Z.; Petlenkov, E. Review on Braking Energy Management in Electric Vehicles. Energies 2021, 14, 4477. [Google Scholar] [CrossRef]
- Verma, S.; Mishra, S.; Gaur, A.; Chowdhury, S.; Mohapatra, S.; Dwivedi, G.; Verma, P. A comprehensive review on energy storage in hybrid electric vehicle. J. Traffic Transp. Eng. 2021, 8, 621–637. [Google Scholar] [CrossRef]
- Li, X.J.; Zhang, X.W.; Wang, Y.X. Regenerative Braking Control Strategies with Fixed Ratio and Variable Ratio Braking Forces Optimization Distribution for Electric Vehicles during Downhill Process. Int. J. Automot. Technol. 2022, 23, 667–681. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, X.W.; Wang, Y.X.; Hu, W.C. Regenerative Braking Control Strategy of Electric Vehicles Based on Braking Stability Requirements. Int. J. Automot. Technol. 2021, 22, 465–473. [Google Scholar]
- Jiang, Y.; Zheng, Y.P.; Guo, Y.; Cong, M. Regenerative Braking Control Strategy to Improve Braking Energy Recovery of Pure Electric Bus. SAE Int. J. Veh. Dyn. Stab. NVH 2020, 4, 221–232. [Google Scholar] [CrossRef]
- Bian, J.D.; Qiu, B. Effect of road gradient on regenerative braking energy in a pure electric vehicle. Int. J. Automot. Technol. 2018, 232, 1736–1746. [Google Scholar] [CrossRef]
- Liu, F. A PMSM fuzzy logic regenerative braking control strategy for electric vehicles. J. Intell. Fuzzy Syst. 2021, 41, 4873–4881. [Google Scholar] [CrossRef]
- Qiu, C.Q.; Wang, G.L.; Meng, M.Y.; Shen, Y.J. A novel control strategy of regenerative braking system for electric vehicles under safety critical driving situations. Energy 2018, 149, 329–340. [Google Scholar] [CrossRef]
- Zhang, H.J.; Zhang, F.; Yang, L.; Gao, Y.; Jin, B.Q. Multi-Parameter Collaborative Power Prediction to Improve the Efficiency of Supercapacitor-Based Regenerative Braking System. IEEE Trans. Energy Convers. 2021, 36, 2612–2622. [Google Scholar] [CrossRef]
- Geng, C.; Ning, D.W.; Guo, L.F.; Xue, Q.C.; Mei, S.J. Simulation Research on Regenerative Braking Control Strategy of Hybrid Electric Vehicle. Energies 2021, 14, 2202. [Google Scholar] [CrossRef]
- Ning, X.B.; Wang, J.Z.; Yin, Y.M.; Shangguan, J.R.; Bao, N.X.; Li, N. Regenerative Braking Algorithm for Parallel Hydraulic Hybrid Vehicles Based on Fuzzy Q-Learning. Energies 2023, 16, 1895. [Google Scholar] [CrossRef]
- Zhao, Q.H.; Zhang, H.X.; Xin, Y.F. Research on Control Strategy of Hydraulic Regenerative Braking of Electrohydraulic Hybrid Electric Vehicles. Math. Probl. Eng. 2021, 2021, 5391351. [Google Scholar] [CrossRef]
- Chai, W.S.; bin Romli, M.I.F.; Yaakob, S.B.; Fang, L.H.; Aihsan, M.Z. Regenerative Braking Optimization Using Particle Swarm Algorithm for Electric Vehicle. J. Adv. Comput. Intell. 2022, 26, 1022–1030. [Google Scholar] [CrossRef]
- Cui, D.; Xiang, Z.R. Nonsingular Fixed-Time Fault-Tolerant Fuzzy Control for Switched Uncertain Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2023, 31, 174–183. [Google Scholar] [CrossRef]
- Tong, S.C.; Li, Y.M.; Sui, S. Adaptive Fuzzy Tracking Control Design for SISO Uncertain Nonstrict Feedback Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2016, 24, 1441–1454. [Google Scholar] [CrossRef]
- Xiang, X.B.; Yu, C.Y.; Lapierre, L.; Zhang, J.L.; Zhang, Q. Survey on Fuzzy-Logic-Based Guidance and Control of Marine Surface Vehicles and Underwater Vehicles. IEEE Trans. Fuzzy Syst. 2018, 20, 572–586. [Google Scholar] [CrossRef]
- Qiu, J.B.; Sun, K.K.; Wang, T.; Gao, H.J. Observer-Based Fuzzy Adaptive Event-Triggered Control for Pure-Feedback Nonlinear Systems with Prescribed Performance. IEEE Trans. Fuzzy Syst. 2019, 27, 2152–2162. [Google Scholar] [CrossRef]
- Cordon, O. A historical review of evolutionary learning methods for Mamdani-type fuzzy rule-based systems: Designing interpretable genetic fuzzy systems. Int. J. Approx. Reason. 2011, 52, 894–913. [Google Scholar] [CrossRef]
- Ojha, V.; Abraham, A.; Snasel, V. Heuristic design of fuzzy inference systems: A review of three decades of research. Eng. Appl. Artif. Intel. 2019, 85, 845–864. [Google Scholar] [CrossRef]
- Yorukoglu, A.; Altug, E. Estimation of Unbalanced Loads in Washing Machines Using Fuzzy Neural Networks. IEEE/ASME Trans. Mechatron. 2013, 18, 1182–1190. [Google Scholar] [CrossRef]
- Chiou, C.B.; Chiou, C.H.; Chu, C.M.; Lin, S.L. The application of fuzzy control on energy saving for multi-unit room air-conditioners. Appl. Therm. Eng. 2009, 29, 310–316. [Google Scholar] [CrossRef]
- Morioka, K.; Kovacs, S.; Lee, J.H.; Korondi, P. A Cooperative Object Tracking System with Fuzzy-Based Adaptive Camera Selection. Int. J. Smart Sens. Intell. Syst. 2010, 3, 338–358. [Google Scholar] [CrossRef]
- Safeer, S.; Pandey, R.P.; Rehman, B.; Safdar, T.; Ahmad, I.; Hasan, S.W.; Ullah, A. A review of artificial intelligence in water purification and wastewater treatment: Recent advancements. J. Water Process Eng. 2022, 49, 102974. [Google Scholar] [CrossRef]
- Wang, Y.C.; Chien, C.J.; Chi, R.H.; Hou, Z.S. A Fuzzy-Neural Adaptive Terminal Iterative Learning Control for Fed-Batch Fermentation Processes. IEEE Trans. Fuzzy Syst. 2015, 17, 423–433. [Google Scholar] [CrossRef]
- Sadeghian, M.; Fatehi, A. Identification, prediction and detection of the process fault in a cement rotary kiln by locally linear neuro-fuzzy technique. J. Process Control 2011, 21, 302–308. [Google Scholar] [CrossRef]
- Fayaz, M.; Ullah, I.; Park, D.H.; Kim, K.; Kim, D. An Integrated Risk Index Model Based on Hierarchical Fuzzy Logic for Underground Risk Assessment. Appl. Sci. 2017, 7, 1037. [Google Scholar] [CrossRef]
- Jia, T.H.; Pan, Y.N.; Liang, H.J.; Lam, H.K. Event-Based Adaptive Fixed-Time Fuzzy Control for Active Vehicle Suspension Systems with Time-Varying Displacement Constraint. IEEE Trans. Fuzzy Syst. 2022, 30, 2813–2821. [Google Scholar] [CrossRef]
- Ahmadi, S.; Bathaee, S.M.T.; Hosseinpour, A.H. Improving fuel economy and performance of a fuel-cell hybrid electric vehicle (fuel-cell, battery, and ultra-capacitor) using optimized energy management strategy. Energy Convers. Manag. 2018, 160, 74–84. [Google Scholar] [CrossRef]
- Sulaiman, N.; Hannan, M.A.; Mohamed, A.; Ker, P.J.; Majlan, E.H.; Daud, W.R.W. Optimization of energy management system for fuel-cell hybrid electric vehicles: Issues and recommendations. Appl. Energy 2018, 228, 2061–2079. [Google Scholar] [CrossRef]
- Park, Y.; Park, S.; Ahn, C. Performance Potential of Regenerative Braking Energy Recovery of Autonomous Electric Vehicles. Int. J. Control Autom. 2023, 21, 1442–1454. [Google Scholar] [CrossRef]
- Huang, A.R.W.; Chen, C.S. A low-cost driving simulator for full vehicle dynamics simulation. IEEE Trans. Veh. Technol. 2003, 52, 162–172. [Google Scholar] [CrossRef]
- Ghike, C.; Shim, T.; Asgari, I. Integrated control of wheel drive-brake torque for vehicle-handling enhancement. Proc. Inst. Mech. Eng. D 2009, 223, 439–457. [Google Scholar] [CrossRef]
- He, Z.J.; Shi, Q.; Wei, Y.J.; Zheng, J.X.; Gao, B.Z.; He, L. A Torque Demand Model Predictive Control Approach for Driving Energy Optimization of Battery Electric Vehicle. IEEE Trans. Veh. Technol. 2021, 70, 3232–3242. [Google Scholar] [CrossRef]
- Huang, C.X.; Lei, F.; Han, X.; Zhang, Z.Y. Determination of modeling parameters for a brushless DC motor that satisfies the power performance of an electric vehicle. Meas. Control 2019, 52, 765–774. [Google Scholar] [CrossRef]
- Zheng, P.; Wu, Q.; Bai, J.G.; Tong, C.D.; Song, Z.Y. Analysis and Experiment of a Novel Brushless Double Rotor Machine for Power-Split Hybrid Electrical Vehicle Applications. Energies 2013, 6, 3209–3223. [Google Scholar] [CrossRef]
- Aouadj, N.; Hartani, K.; Fatiha, M. New Integrated Vehicle Dynamics Control System Based on the Coordination of Active Front Steering, Direct Yaw Control, and Electric Differential for Improvements in Vehicle Handling and Stability. SAE Int. J. Veh. Dyn. Stab. NVH 2020, 2, 119–133. [Google Scholar] [CrossRef]
- Ukil, A.; Bloch, R.; Andenna, A. Estimation of Induction Motor Operating Power Factor from Measured Current and Manufacturer Data. IEEE Trans. Energy Convers. 2011, 2, 699–706. [Google Scholar] [CrossRef]
- Hu, J.J.; Yang, Y.; Jia, M.X.; Guan, Y.J.; Fu, C.Y.; Liao, S.P. Research on Harmonic Torque Reduction Strategy for Integrated Electric Drive System in Pure Electric Vehicle. Electronics 2020, 9, 1241. [Google Scholar] [CrossRef]
- Ahssan, M.R.; Ektesabi, M.M.; Gorji, S.A. Electric Vehicle with Multi-Speed Transmission: A Review on Performances and Complexities. SAE Int. J. Altern. Powertrains 2018, 7, 169–181. [Google Scholar] [CrossRef]
- Li, Z.H.; Jiang, S.; Dong, J.; Wang, S.F.; Ming, Z.N.; Li, L. Battery capacity design for electric vehicles considering the diversity of daily vehicles miles traveled. Transport. Res. C-Emer. 2016, 72, 272–282. [Google Scholar] [CrossRef]
- Zhang, C.P.; Wang, L.Y.; Li, X.; Chen, W.; Yin, G.G.; Jiang, J.C. Robust and Adaptive Estimation of State of Charge for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2015, 62, 4948–4957. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Fan, X.B. Design of battery management system based on improved ampere-hour integration method. Int. J. Electr. Hybrid. 2022, 14, 1–29. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Guo, T.Z.; Gao, M.Y.; He, Z.W.; Dong, Z.K. Review of SoC Estimation Methods for Electric Vehicle Li-ion Batteries. J. Electron. Inf. Techn. 2021, 43, 1803–1815. [Google Scholar]
- Noelle, D.J.; Wang, M.; Le, A.V.; Shi, Y.; Qiao, Y. Internal resistance and polarization dynamics of lithium-ion batteries upon internal shorting. Appl. Energy 2018, 212, 796–808. [Google Scholar] [CrossRef]
- Qiu, C.S.; He, G.; Shi, W.K.; Zou, M.J.; Liu, C. The polarization characteristics of lithium-ion batteries under cyclic charge and discharge. J. Solid State Electrochem. 2019, 23, 1887–1902. [Google Scholar] [CrossRef]
- Meng, Z.W.; Zhang, T.Z.; Zhang, H.X.; Zhao, Q.H.; Yang, J. Energy Management Strategy for an Electromechanical-Hydraulic Coupled Power Electric Vehicle Considering the Optimal Speed Threshold. Energies 2021, 14, 5300. [Google Scholar] [CrossRef]
- Itani, K.; De Bernardinis, A.; Khatir, Z.; Jammal, A. Comparison between two braking control methods integrating energy recovery for a two-wheel front driven electric vehicle. Energy Convers. Manag. 2016, 122, 330–343. [Google Scholar] [CrossRef]
- Xie, Y.K.; Li, Y.Y.; Zhao, Z.C.; Dong, H.; Wang, S.Q.; Liu, J.P.; Guan, J.H.; Duan, X.B. Microsimulation of electric vehicle energy consumption and driving range. Appl. Energy 2020, 267, 115081. [Google Scholar] [CrossRef]
- Wang, K.L.; Ding, K.W.; Yang, T. Experimental Study on the Seismic Performance of New Energy Dissipation Connectors in an Autoclaved Aerated Concrete Panel with Assembled Steel Frame. Appl. Sci. 2023, 12, 13035. [Google Scholar] [CrossRef]
- Giakoumis, E.G.; Zachiotis, A.T. Investigation of a Diesel-Engined Vehicle’s Performance and Emissions during the WLTC Driving CycleComparison with the NEDC. Energies 2017, 10, 240. [Google Scholar] [CrossRef]
- Oh, C.; Cha, G. Impact of fuel, injection type and after-treatment system on particulate emissions of light-duty vehicles using different fuels on FTP-75 and HWFET test cycles. Int. J. Automot. Technol. 2015, 16, 895–901. [Google Scholar] [CrossRef]
- Duan, Z.J.; Mei, N.; Feng, L.L.; Yu, S.G.; Jiang, Z.Y.; Chen, D.F.; Xu, X.M.; Hong, J.C. Research on Hydrogen Consumption and Driving Range of Hydrogen Fuel Cell Vehicle under the CLTC-P Condition. World Electr. Veh. J. 2022, 13, 9. [Google Scholar] [CrossRef]
- Hwang, H.Y.; Lan, T.S.; Chen, J.S. Optimization and Application for Hydraulic Electric Hybrid Vehicle. Energies 2020, 13, 322. [Google Scholar] [CrossRef]
- Li, S.Q.; Yu, B.; Feng, X.Y. Research on braking energy recovery strategy of electric vehicle based on ECE regulation and I curve. Sci. Progress 2020, 103, 0036850419877762. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yu, L.Y.; Wang, Z.Z.; Zuo, L.; Song, J. All-Wheel Braking Force Allocation During a Braking-in-Turn Maneuver for Vehicles with the Brake-by-Wire System Considering Braking Efficiency and Stability. IEEE Trans. Veh. Technol. 2016, 65, 4752–4767. [Google Scholar] [CrossRef]
- Ma, Z.W.; Sun, D.X. Energy Recovery Strategy Based on Ideal Braking Force Distribution for Regenerative Braking System of a Four-Wheel Drive Electric Vehicle. IEEE Access 2020, 8, 136234–136242. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Dong, Y.Y.; Han, Y.W. Dynamic and Control of Electric Vehicle in Regenerative Braking for Driving Safety and Energy Conservation. J. Vib. Eng. Technol. 2020, 8, 179–197. [Google Scholar] [CrossRef]
- Song, J.; Kim, H.; Boo, K. A study on an anti-lock braking system controller and rear-wheel controller to enhance vehicle lateral stability. Proc. Inst. Mech. Eng. D 2007, 221, 777–787. [Google Scholar] [CrossRef]
- Xiao, B.Y.; Lu, H.Z.; Wang, H.L.; Ruan, J.G.; Zhang, N. Enhanced Regenerative Braking Strategies for Electric Vehicles: Dynamic Performance and Potential Analysis. Energies 2017, 10, 1875. [Google Scholar] [CrossRef]
- Zhou, Z.; Huang, M.H. Regenerative braking algorithm for the electric vehicle with a seamless two-speed transmission. Proc. Inst. Mech. Eng. D 2019, 233, 905–916. [Google Scholar] [CrossRef]
- Xu, G.Q.; Xu, K.; Zheng, C.H.; Zhang, X.Y.; Zahid, T. Fully Electrified Regenerative Braking Control for Deep Energy Recovery and Maintaining Safety of Electric Vehicles. IEEE Trans. Veh. Technol. 2016, 65, 1186–1198. [Google Scholar] [CrossRef]
- Xu, G.Q.; Li, W.M.; Xu, K.; Song, Z.B. An Intelligent Regenerative Braking Strategy for Electric Vehicles. Energies 2011, 4, 1461–1477. [Google Scholar] [CrossRef]
- Mendes, J.; Araujo, R.; Sousa, P.; Apostolo, F.; Alves, L. An architecture for adaptive fuzzy control in industrial environments. Comput. Ind. 2011, 62, 364–373. [Google Scholar] [CrossRef]
- Novak, V. Reasoning about mathematical fuzzy logic and its future. Fuzzy Sets Syst. 2012, 192, 25–44. [Google Scholar] [CrossRef]
- Papageorgiou, E.I.; Salmeron, J.L. A Review of Fuzzy Cognitive Maps Research During the Last Decade. IEEE Trans. Fuzzy Syst. 2013, 21, 66–79. [Google Scholar] [CrossRef]
- Zhang, J.C.; Yang, X.Y. Some properties of fuzzy reasoning in propositional fuzzy logic systems. Inform. Sci. 2010, 180, 4661–4671. [Google Scholar] [CrossRef]
- Yun, Y.S. A Zadeh’s max-min composition operator for 3-dimensional triangular fuzzy number. J. Intell. Fuzzy Syst. 2020, 39, 3783–3793. [Google Scholar] [CrossRef]
- Van Broekhoven, E.; De Baets, B. Fast and accurate center of gravity defuzzification of fuzzy system outputs defined on trapezoidal fuzzy partitions. Fuzzy Sets Syst. 2006, 157, 904–918. [Google Scholar] [CrossRef]
- Cao, S.G.; Rees, N.W.; Feng, G. Mamdani-type fuzzy controllers are universal fuzzy controllers. Fuzzy Sets Syst. 2001, 123, 359–367. [Google Scholar] [CrossRef]
- Feng, G. A survey on analysis and design of model-based fuzzy control systems. IEEE Trans. Fuzzy Syst. 2006, 14, 676–697. [Google Scholar] [CrossRef]
- Yildiz, A.; Özel, M.A. A Comparative Study of Energy Consumption and Recovery of Autonomous Fuel-Cell Hydrogen–Electric Vehicles Using Different Powertrains Based on Regenerative Braking and Electronic Stability Control System. Appl. Sci. 2021, 11, 2515. [Google Scholar] [CrossRef]
- Jamadar, N.M.; Jadhav, H.T. A review on braking control and optimization techniques for electric vehicle. Proc. Inst. Mech. Eng. D 2021, 235, 2371–2382. [Google Scholar] [CrossRef]
- Saiteja, P.; Ashok, B.; Wagh, A.S.; Farrag, M.E. Critical review on optimal regenerative braking control system architecture, calibration parameters and development challenges for EVs. Int. J. Energy Res. 2022, 46, 20146–20179. [Google Scholar] [CrossRef]
- Hamada, A.T.; Orhan, M.F. An overview of regenerative braking systems. J. Energy Storage 2022, 52, 105033. [Google Scholar] [CrossRef]
- Martyushev, N.V.; Malozyomov, B.V.; Sorokova, S.N.; Efremenkov, E.A.; Qi, M.X. Mathematical Modeling of the State of the Battery of Cargo Electric Vehicles. Mathematics 2023, 11, 536. [Google Scholar] [CrossRef]
- Wu, T.L.; Wang, F.; Ye, P. Regenerative Braking Strategy of Dual-Motor EV Considering Energy Recovery and Brake Stability. World Electr. Veh. J. 2023, 14, 19. [Google Scholar] [CrossRef]
- Yin, Y.L.; Zhang, X.X.; Zhan, S.; Ma, S.P.; Huang, X.J.; Wang, F.Z. DQN regenerative braking control strategy based on adaptive weight coefficients. Proc. Inst. Mech. Eng. D 2023, 09544070231186200. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Xiong, R.; Cai, X.; Wang, Z.; Yang, R.X. Regenerative Braking Control Strategy for Distributed Drive Electric Vehicles Based on Slope and Mass Co-Estimation. IEEE T. Intell. Transp. 2023, 24, 1. [Google Scholar] [CrossRef]
- Ashok, B.; Kannan, C.; Deepak, C.; Ramesh, R.; Narendhra, T.M.; Farrag, M.E.; Ashok, S.D.; Vignesh, R.; Saiteja, P.; Kavitha, C. Model based integrated control strategy for effective brake energy recovery to extend battery longevity in electric two wheelers. Proc. Inst. Mech. Eng. D 2023, 09544070231167616. [Google Scholar] [CrossRef]
- Liu, J.A.; Bu, L.; Fu, B.; Zheng, J.Y.; Wang, G.S.; He, L.H.; Hu, Y.L. Research on Adaptive Distribution Control Strategy of Braking Force for Pure Electric Vehicles. Processes 2023, 11, 1152. [Google Scholar] [CrossRef]
- Sandrini, G.; Chindamo, D.; Gadola, M. Regenerative Braking Logic That Maximizes Energy Recovery Ensuring the Vehicle Stability. Energies 2022, 15, 5846. [Google Scholar] [CrossRef]
- Shang, Y.; Ma, C.; Yang, K.; Tan, D. Regenerative Braking Control Strategy Based on Multi-source Information Fusion under Environment Perception. Int. J. Automot. Technol. 2022, 23, 805–815. [Google Scholar] [CrossRef]
- Chang, J.J.; Zhang, Y.F. Research on Optimization Control Strategy for Braking Energy Recovery of a Battery Electric Vehicle Based on EMB System. Automot. Eng. 2022, 44, 64–72. [Google Scholar]
- Chu, L.; Chang, C.; Zhao, D.; Xu, Y.W. Research on Cooperative Braking Control Algorithm Based on Nonlinear Model Prediction. World Electr. Veh. J. 2021, 12, 173. [Google Scholar] [CrossRef]
- Liu, H.W.; Lei, Y.L.; Fu, Y.; Li, X.Z. An Optimal Slip Ratio-Based Revised Regenerative Braking Control Strategy of Range-Extended Electric Vehicle. Energies 2020, 13, 1526. [Google Scholar] [CrossRef]
- Heydari, S.; Fajri, P.; Sabzehgar, R.; Asrari, A. Optimal Brake Allocation in Electric Vehicles for Maximizing Energy Harvesting During Braking. IEEE Trans. Energy Convers. 2020, 35, 1806. [Google Scholar] [CrossRef]
- Ji, F.Z.; Pan, Y.; Zhou, Y.; Du, F.R.; Zhang, Q.; Li, G. Energy recovery based on pedal situation for regenerative braking system of electric vehicle. Vehicle Syst. Dyn. 2020, 58, 144. [Google Scholar] [CrossRef]
- He, H.W.; Wang, C.; Jia, H.; Cui, X. An intelligent braking system composed single-pedal and multi-objective optimization neural network braking control strategies for electric vehicle. Appl. Energy 2020, 259, 114172. [Google Scholar] [CrossRef]
- Gang, L.; Zhi, Y. Energy saving control based on motor efficiency map for electric vehicles with four-wheel independently driven in-wheel motors. Adv. Mech. Eng. 2018, 10, 1687814018793064. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, G.; Li, W.; Zheng, L. Regenerative Braking for Electric Vehicle Based on Fuzzy Logic Control Strategy. In Proceedings of the International Conference on Mechanical and Electronics Engineering, Kyoto, Japan, 1–3 August 2010. [Google Scholar]
- Tao, Y.; Xie, X.; Zhao, H.; Xu, W.; Chen, H. A Regenerative Braking System for Electric Vehicle with Four In-Wheel Motors Based on Fuzzy Control. In Proceedings of the Chinese Control Conference, Dalian, China, 26–28 July 2017. [Google Scholar]
- Cao, X.; Ishikawa, T. Optimum design of a regenerative braking system for electric vehicles based on fuzzy control strategy. IEEJ Trans. Electr. Electron. Eng. 2016, 11, S186–S187. [Google Scholar] [CrossRef]
- Zhu, G.H.; Lin, J.B.; Liu, Q.W.; He, H.W. Research on the Energy-Saving Strategy of Path Planning for Electric Vehicles Considering Traffic Information. Energies 2019, 12, 3601. [Google Scholar] [CrossRef]
- Martyushev, N.V.; Malozyomov, B.V.; Khalikov, I.H.; Kukartsev, V.A.; Kukartsev, V.V.; Tynchenko, V.S.; Tynchenko, Y.A.; Qi, M.X. Review of Methods for Improving the Energy Efficiency of Electrified Ground Transport by Optimizing Battery Consumption. Energies 2023, 16, 729. [Google Scholar] [CrossRef]
- Liu, X.Y.; Reddi, K.; Elgowainy, A.; Lohse-Busch, H.; Wang, M.; Rustagi, N. Comparison of well-to-wheels energy use and emissions of a hydrogen fuel cell electric vehicle relative to a conventional gasoline-powered internal combustion engine vehicle. Int. J. Hydrogen Energy 2020, 45, 972–983. [Google Scholar] [CrossRef]
- Fotouhi, A.; Yusof, R.; Rahmani, R.; Mekhilef, S.; Shateri, N. A review on the applications of driving data and traffic information for vehicles’ energy conservation. Renew. Sustain. Energy Rev. 2014, 37, 822–833. [Google Scholar] [CrossRef]
- Inci, M.; Savrun, M.M.; Celik, O. Integrating electric vehicles as virtual power plants: A comprehensive review on vehicle-to-grid (V2G) concepts, interface topologies, marketing and future prospects. J. Energy Storage 2022, 55, 105579. [Google Scholar] [CrossRef]













| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Unloaded weight mu/kg | 1650 | Air resistance coefficient Cd | 0.45 |
| Fully loaded weight mf/kg | 1920 | Position of COM hg | 0.58 |
| Wheelbase L/m | 2.670 | Rolling resistance coefficient f | 0.02 |
| Distance from the front axle to COM a/m | 1.340 | Driving range S/km | 400 |
| Distance from the rear axle to COM b/m | 1.430 | Maximum speed umax/km·h−1 | 150 |
| Windward area A/m2 | 2.5 | Tire rolling radius r/m | 0.33 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power Pe/kW | 36 | Peek speed nmax/r·min−1 | 9000 |
| Peak power Pmax/kW | 95 | Rated torque Te/N·m | 96 |
| Rated speed ne/r·min−1 | 3600 | Peak torque Tmax/N·m | 255 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated voltage Ue/V | 336 | Maximum charging power PBmax/kW | 110 |
| Battery capacity Qcap/Ah | 270 | Specific energy E/Wh/kg | 120 |
| Input | Output | Input | Output | ||||
|---|---|---|---|---|---|---|---|
| z | SOC | u | k | z | SOC | u | k |
| L | L | L | SH | M | L | L | SH |
| M | SH | M | H | ||||
| H | H | H | M | ||||
| SH | M | SH | L | ||||
| M | L | SH | M | L | SH | ||
| M | SH | M | M | ||||
| H | M | H | L | ||||
| SH | L | SH | L | ||||
| H | L | SH | H | L | H | ||
| M | H | M | H | ||||
| H | H | H | M | ||||
| SH | L | SH | M | ||||
| SH | L | H | SH | L | H | ||
| M | M | M | M | ||||
| H | L | H | L | ||||
| SH | SL | SH | SL | ||||
| H | L | L | H | SH | L | L | H |
| M | M | M | M | ||||
| H | M | H | M | ||||
| SH | L | SH | L | ||||
| M | L | M | M | L | M | ||
| M | M | M | L | ||||
| H | L | H | L | ||||
| SH | L | SH | SL | ||||
| H | L | M | H | L | L | ||
| M | L | M | L | ||||
| H | L | H | SL | ||||
| SH | SL | SH | SL | ||||
| SH | L | M | SH | L | L | ||
| M | L | M | SL | ||||
| H | SL | H | SL | ||||
| SH | SL | SH | SL | ||||
| Input | Output | Input | Output | ||||
|---|---|---|---|---|---|---|---|
| z | SOC | u | k | z | SOC | u | k |
| L | M | M | SH | M | M | M | H |
| H | H | H | M | ||||
| SH | M | SH | L | ||||
| H | M | SH | H | M | M | ||
| H | M | H | L | ||||
| SH | L | SH | L | ||||
| Driving Cycle | No Regenerative Braking | Regenerative Braking | ε/% | ||||
|---|---|---|---|---|---|---|---|
| SOCint/% | SOCend/% | ΔSOCn/% | SOCint/% | SOCend/% | ΔSOCy/% | ||
| NEDC | 90 | 87.63 | 2.37 | 90 | 87.98 | 2.02 | 15.01 |
| WHTC | 90 | 85.70 | 4.30 | 90 | 86.70 | 3.30 | 23.20 |
| FTP-72 | 90 | 87.99 | 2.01 | 90 | 88.60 | 1.40 | 30.51 |
| FTP-75 | 90 | 86.96 | 3.04 | 90 | 87.86 | 2.14 | 29.59 |
| CLTC-P | 90 | 87.58 | 2.42 | 90 | 88.28 | 1.72 | 29.16 |
| NYCC | 90 | 89.57 | 0.43 | 90 | 89.74 | 0.26 | 40.13 |
| Work | Vehicle Category | Control Algorithm | Drive Cycle | Recovery Efficiency |
|---|---|---|---|---|
| He et al. [10] | pure electric vehicles | electro-hydraulic coordinated | WLTC | 3.35% |
| Yang et al. [11] | electric vehicles | minimum loss | NYCC | 1.18% |
| Jiang et al. [21] | pure electric bus | parallel regenerative braking | NEDC | 17.4% |
| Geng et al. [26] | hybrid electric vehicles | multi parameters fuzzy | NEDC WLTC | 15.55% 11.71% |
| Ning et al. [27] | electric vehicles | fuzzy Q-learning | UDDS | 8.91% |
| Zhao et al. [28] | hybrid electric vehicles | fuzzy optimization | NEDC | 1.22% |
| Li et al. [70] | electric vehicles | fuzzy control method | NEDC | 9.12% |
| Wu et al. [92] | dual-motor EVs | genetic algorithm | self-defined braking | 22.8% |
| Yin et al. [93] | hybrid electric vehicles | Q-learning network | self-defined braking | 7.4% |
| Chen et al. [94] | distributed drive electric vehicles | neural network and least square algorithm | US06 EUDC REP05 | 9.62% 5.04% 3.13%, |
| Ashok et al. [95] | electric two wheelers | fuzzy PID | WLTP Class 2 NYCC | 17% 44% |
| Liu et al. [96] | electric vehicles | adaptive distribution control | NEDC NYCC | 52.62% 47.45% |
| Sandrini et al. [97] | electric vehicle | RB logic | WLTC US06 | 29.5–30.3% 23.9–24.4% |
| Shang et al. [98] | electric vehicles | multi-source information fusion | self-defined braking | 16.1% |
| Chang et al. [99] | electric vehicles | PSO fuzzy | NEDC CLTC-P | 2.5% 1.56% |
| Chun et al. [100] | electric vehicles | nonlinear model predictive control | WLTC | 30.4% |
| Liu et al. [101] | range-extended electric vehicles | revised regenerative braking control strategy | WLTP | 16.6% |
| Heydari et al. [102] | electric vehicles | optimal brake allocation | UDDS | 8.09% |
| Ji et al. [103] | electric vehicles | energy recovery mode A | FTP-75 | 20.39% |
| He et al. [104] | electric vehicles | optimization neural network | NEDC | 26.15% |
| Gang et al. [105] | electric vehicles | energy saving control | NEDC UDDS J1015 | 6% 5.17% 4.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Ma, X.; Su, R.; Huang, Z.; Zhang, C. Regenerative Braking of Electric Vehicles Based on Fuzzy Control Strategy. Processes 2023, 11, 2985. https://doi.org/10.3390/pr11102985
Yin Z, Ma X, Su R, Huang Z, Zhang C. Regenerative Braking of Electric Vehicles Based on Fuzzy Control Strategy. Processes. 2023; 11(10):2985. https://doi.org/10.3390/pr11102985
Chicago/Turabian StyleYin, Zongjun, Xuegang Ma, Rong Su, Zicheng Huang, and Chunying Zhang. 2023. "Regenerative Braking of Electric Vehicles Based on Fuzzy Control Strategy" Processes 11, no. 10: 2985. https://doi.org/10.3390/pr11102985
APA StyleYin, Z., Ma, X., Su, R., Huang, Z., & Zhang, C. (2023). Regenerative Braking of Electric Vehicles Based on Fuzzy Control Strategy. Processes, 11(10), 2985. https://doi.org/10.3390/pr11102985






