Competitive Equilibrium Analysis of Power Generation Transaction Subjects Considering Tradable Green Certificates
Abstract
:1. Introduction
- (1)
- By studying the cost difference between thermal power generation and renewable energy power generation, the power generation cost of the two power generation modes is analyzed in detail. In order to maximize the revenue of the thermal power producers alliance and renewable energy power producers alliance, a market equilibrium model including the green certificate trading market and electricity market is constructed.
- (2)
- The model was solved by combining nondominated sorting genetic algorithm II (NSGA-II) with grey relational projection (GRP). In the first stage, the NSGA-II algorithm was used to find a well-distributed Pareto solution set. In the second stage, the GRP method is used to calculate the priority membership of the solution set to select the best compromise solution.
- (3)
- The changes in power generation and clearance results of different types of power producers under different quota ratios were compared, and the market power behavior of each power producer based on the market equilibrium results was analyzed. By introducing the market power index, this study quantifies the influence of renewable energy forecasting errors on the market power of power generators.
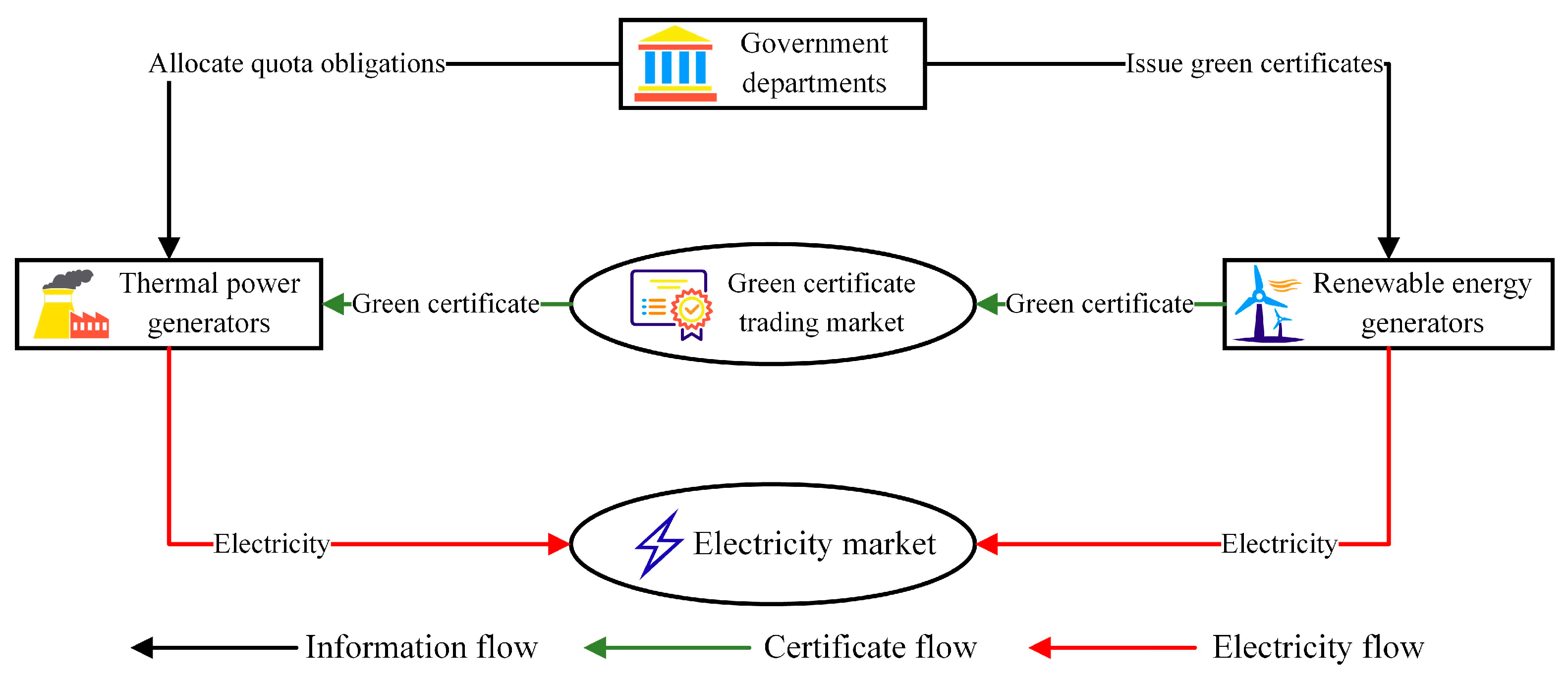
2. Equilibrium Model of Electricity Market under Renewable Portfolio Standard
2.1. Model Building Ideas
2.2. Model Assumptions
2.3. Green Certificate Transaction Mode
2.4. Renewable Energy Uncertainty
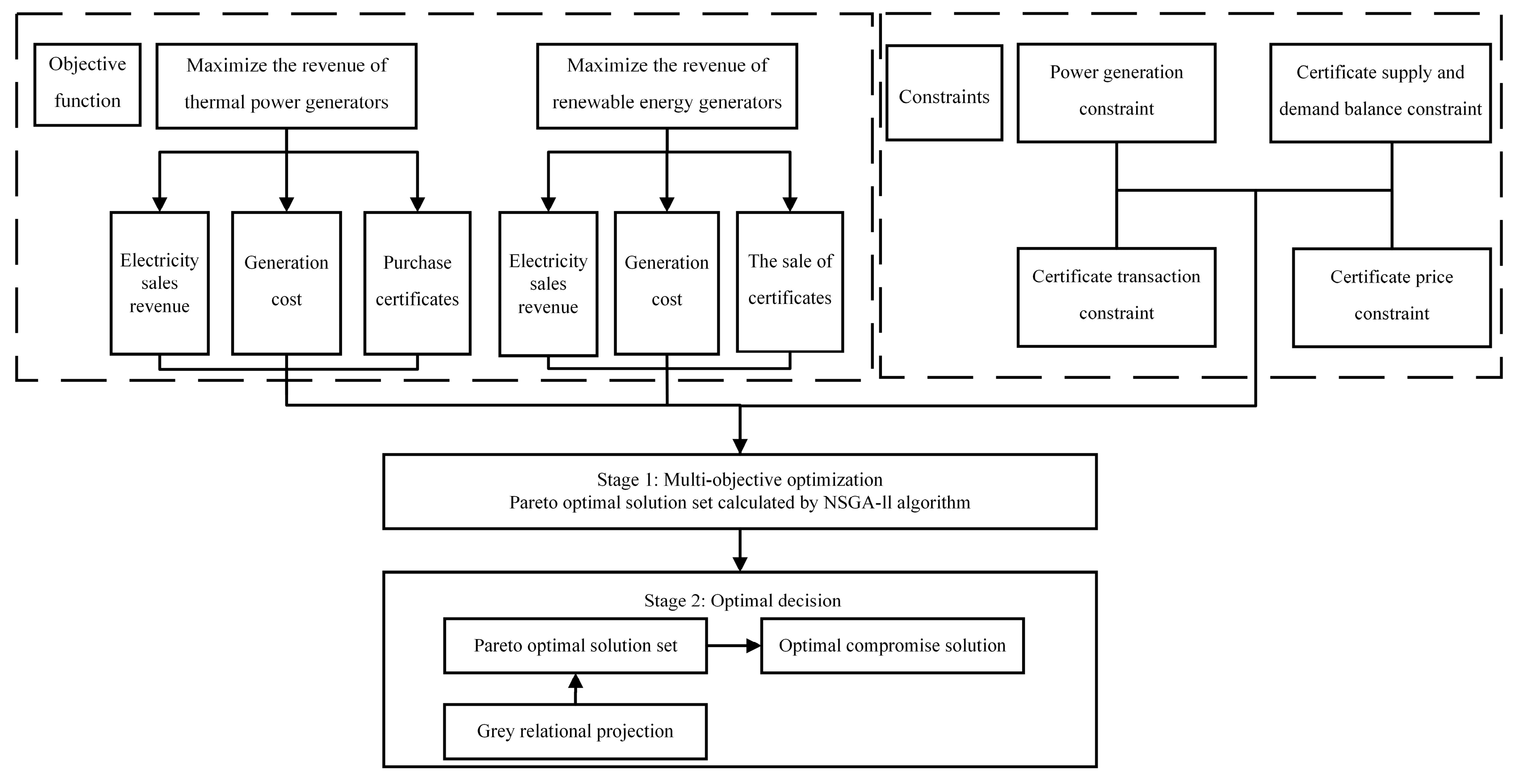
2.5. Objective Function
2.5.1. Maximize the Revenue of Thermal Power Generators
2.5.2. Maximize the Revenue of Renewable Energy Generators
2.6. Constraints
3. Model Solving
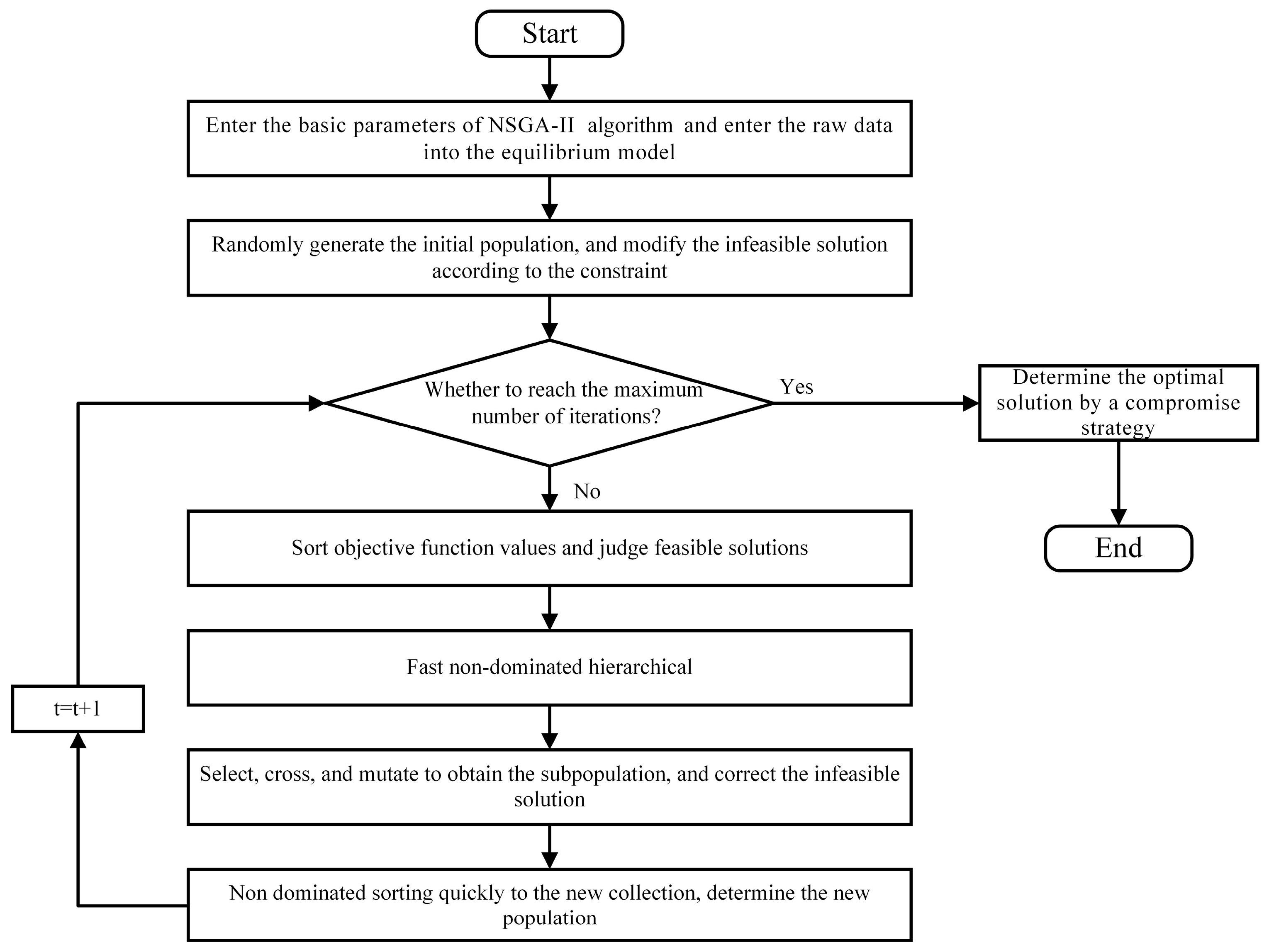
3.1. Solving Framework
3.2. NSGA-II Solving Algorithm
3.3. Grey Relation Projection
4. Case Study
4.1. Parameter Setting
4.2. Pareto Optimal Solution Set
4.3. Analysis on the Equilibrium Results under Renewable Portfolio Standard
4.3.1. The Impact of Quota Changes on the Power Generation of Power Generators
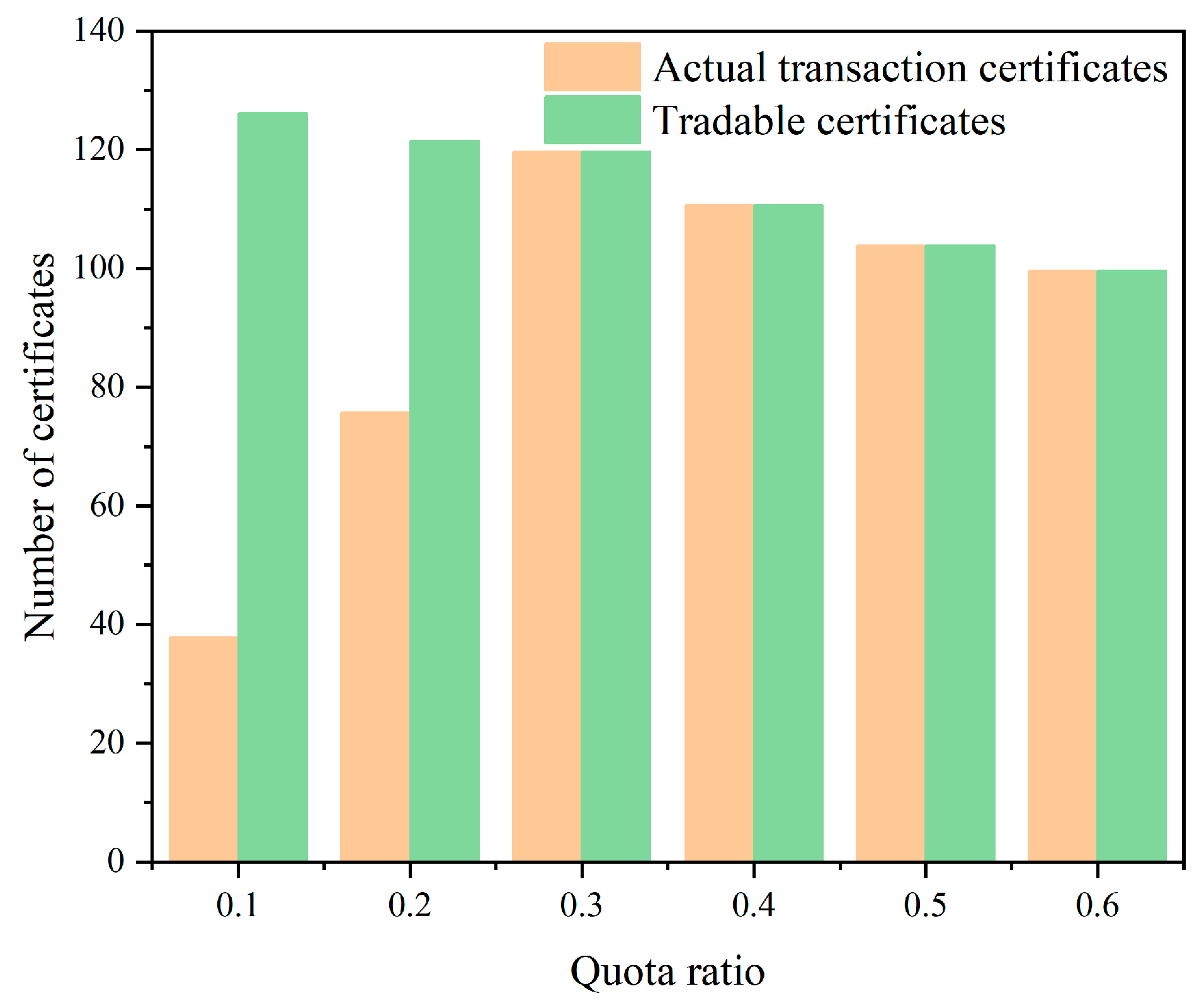
4.3.2. The Impact of Quota Changes on the Number of Market Transaction Certificates
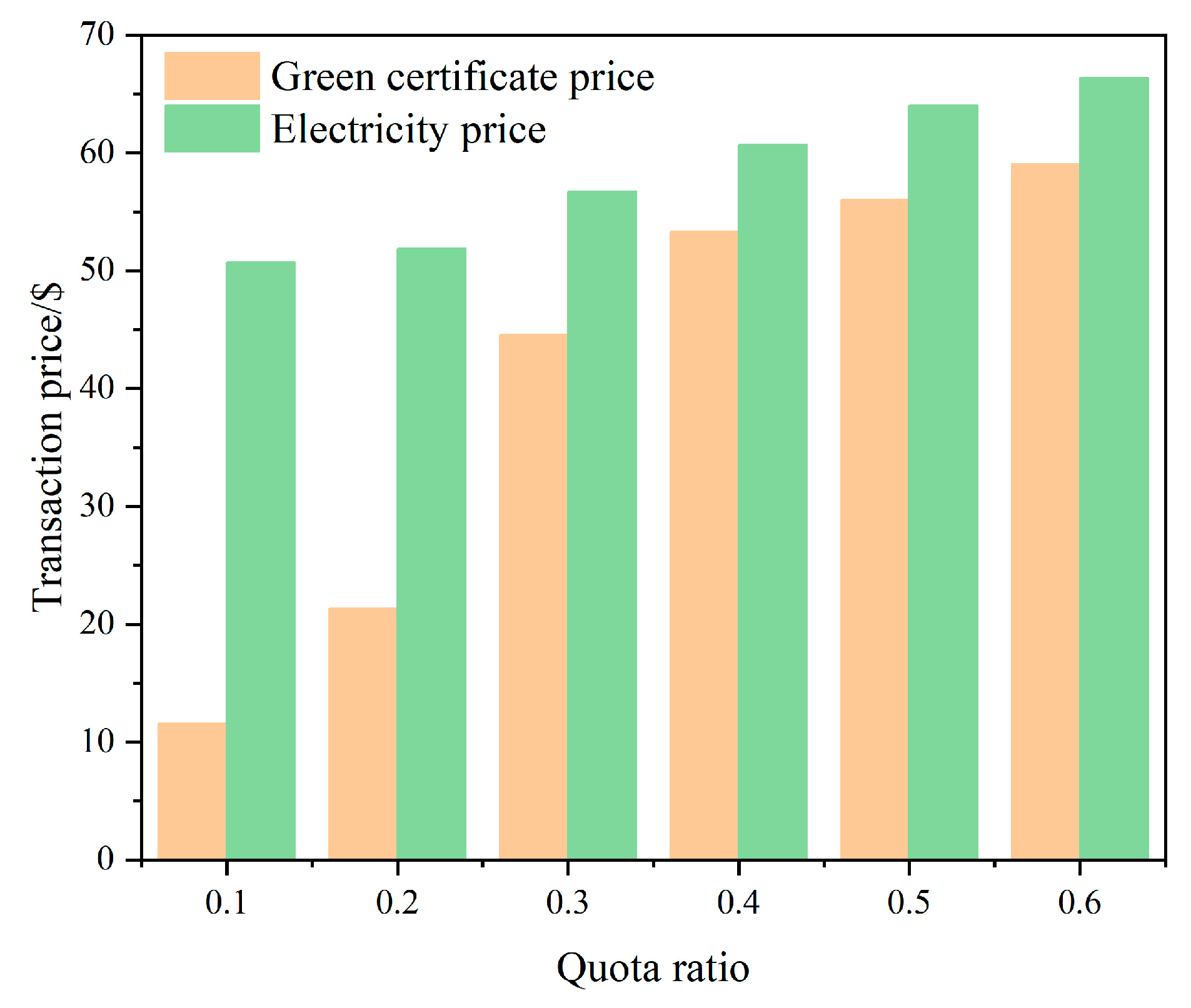
4.3.3. The Impact of Quota Changes on Electricity Market Transaction Prices and Green Certificate Prices
4.3.4. The Impact of Quota Changes on the Market Power of Generators
4.4. Sensitivity Analysis of Model Parameters
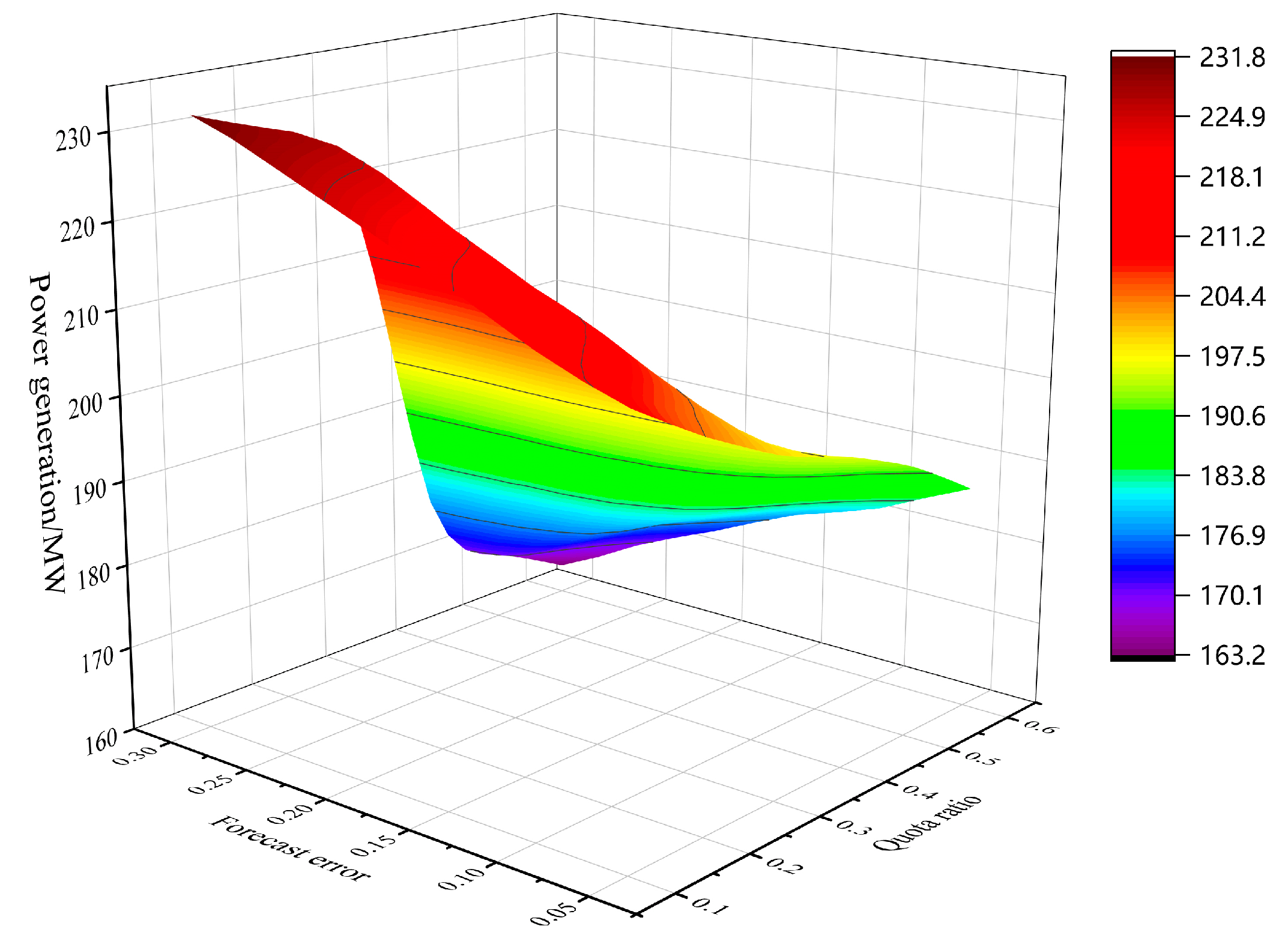
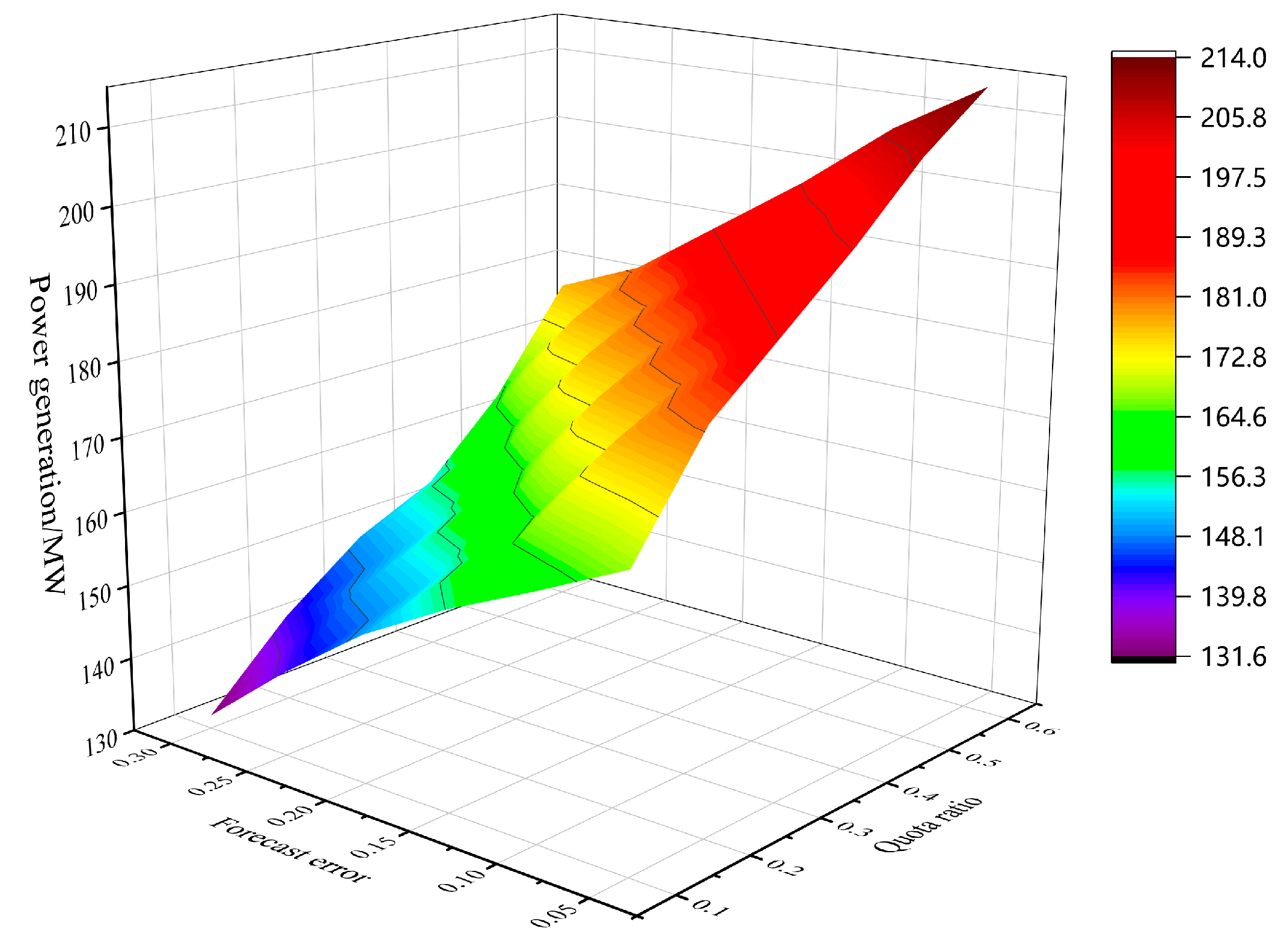
4.4.1. The Impact of Renewable Energy Forecast Errors on the Power Generation of Power Generators
4.4.2. The Impact of Renewable Energy Forecast Errors on the Market Power of Generators
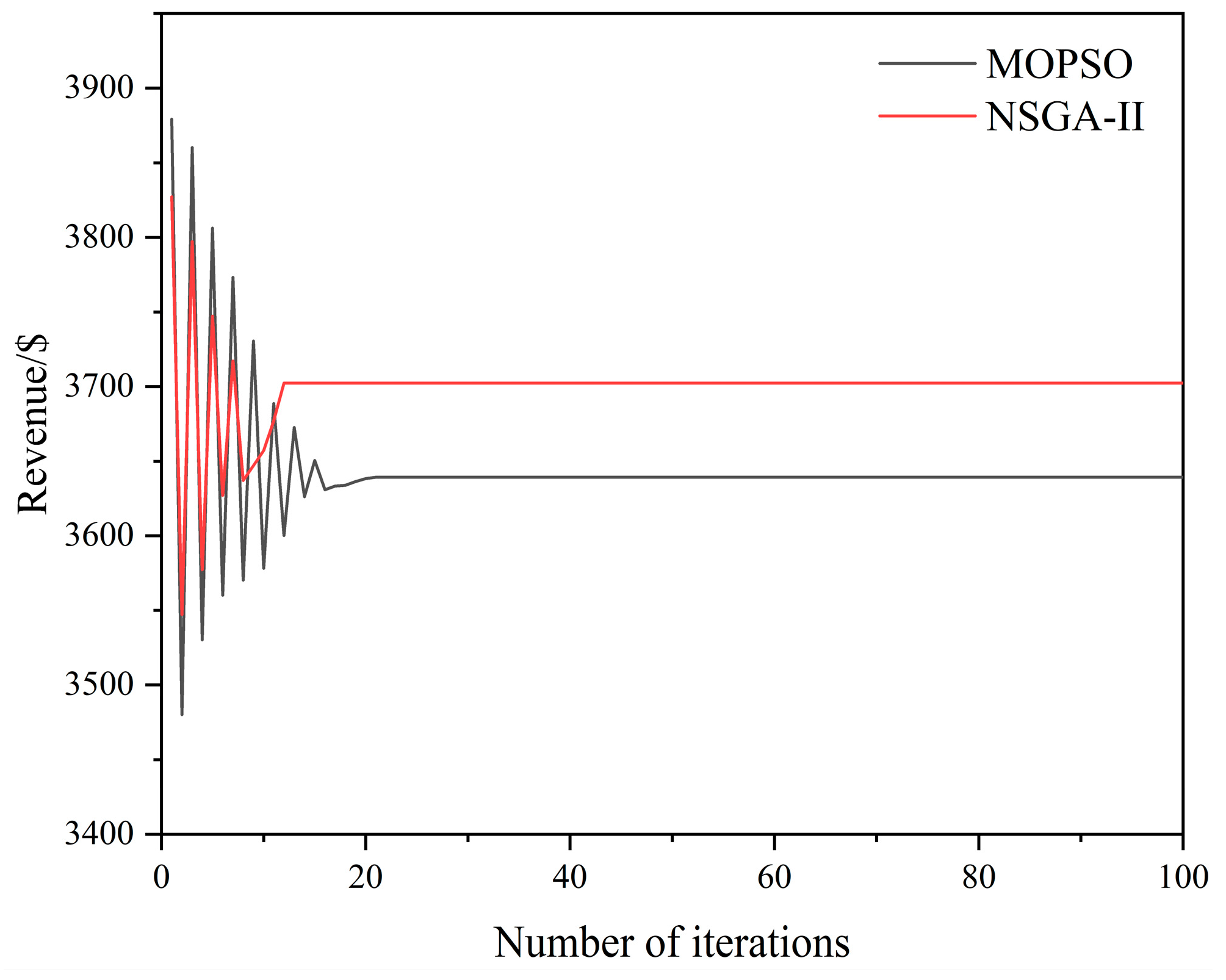
4.5. Comparison with Multi-Objective Particle Swarm Optimization Algorithm
5. Conclusions
- (1)
- In the process of electricity market transactions, renewable energy generators will exercise market power in two markets, and under different quota requirements, renewable energy generators will choose to exercise market power in different markets. When the quota is relatively low, renewable energy generators will choose to exercise market power by holding certificates in the green certificate market; when the quota is relatively high, renewable energy generators will exercise market power by reducing power generation in the electricity market. These strategic actions will lead to the rise of certificate prices and electricity market transaction prices. The higher the quota, the greater the market power of renewable energy generators.
- (2)
- For thermal power generators the increase in the price of green certificates increases the cost of power generation for thermal power generators. In response to the higher price of green certificates, thermal power generators choose to reduce their demand for certificates by reducing the electricity market generation, thereby reducing the cost of purchasing green certificates. At the same time, a reduction in electricity generation in the power market will further increase the market trading price.
- (3)
- The improvement of the prediction accuracy of renewable energy means a reduction in the power generation cost of renewable energy generators, which can effectively reduce the transaction price of the two markets and ease the market power behavior of power generators. Renewable energy generators with relatively low power generation costs are more inclined to earn higher returns by selling more electricity in the power market, which has a positive effect on easing the market power of renewable energy generators. By introducing the Lerner index, we can intuitively quantify and verify the market power decision-making behavior of each power producer in the two markets.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| RPS | Renewable portfolio standard |
| TGC | Tradable green certificates |
| NSGA-II | Nondominated sorting genetic algorithm II |
| GRP | Grey relational projection |
| Electricity market transaction price | |
| , | Constants greater than 0 |
| Total demand in the electricity market | |
| , | Intercept and slope of the supply function, respectively |
| Number of green certificates sold by the j-th renewable energy generator | |
| Price of green certificates | |
| Standard deviation of the load forecast error | |
| Load reserve of the system | |
| Load prediction error | |
| Renewable energy generation forecast error | |
| Standard deviation of the renewable energy generation forecast error | |
| Scale parameter | |
| , | Proportional coefficient |
| Kurtosis | |
| Probability density function of the normal distribution | |
| Reserve capacity that the renewable energy generator needs to configure | |
| , | i-th thermal power generator and the j-th renewable energy generator |
| , | the power generation cost of the i-th thermal power generator and the j-th renewable energy generator |
| Fuel cost of the i-th thermal power generator | |
| , | Power generation of the i-th thermal power generator and the j-th renewable energy generator |
| , , | Fuel cost coefficients of the i-th thermal power generator |
| , | Maintenance cost of the i-th thermal power generator and the j-th renewable energy generator |
| , | Equipment maintenance coefficient of the i-th thermal power generator and the j-th renewable energy generator |
| , | Equipment depreciation cost of the i-th thermal power generator and the j-th renewable energy generator |
| , | Installation cost of the i-th thermal power generator and the j-th renewable energy generator |
| , | Installation volume coefficient of the i-th thermal power generator and the j-th renewable energy generator |
| , | Operating life period of the device of the i-th thermal power generator and the j-th renewable energy generator |
| Annual interest rate | |
| Reserve cost of the j-th renewable energy generator | |
| , | Reserve capacity coefficient |
| Projection value | |
| Number of indicators | |
| Gray correlation coefficient | |
| Weight of each indicator | |
| Priority membership |
References
- Zhang, J.H.; Gao, R.; Xu, N.H.; Xie, C.P. How Can China Achieve Its Non-fossil Energy Target? An Effective Allocation of China’s Renewable Electricity Consumption Obligation. Front. Energy Res. 2020, 8, 103. [Google Scholar] [CrossRef]
- Jiang, Y.C.; Cao, H.X.; Yang, L.; Fei, F.; Li, J.; Lin, Z.M. Mechanism Design and Impact Analysis of Renewable Portfolio Standard. Autom. Electr. Power Syst. 2020, 44, 187–199. [Google Scholar]
- Xiao, Y.P.; Wang, X.F.; Wang, X.L.; Bie, Z.H. Review on Electricity Market Towards High Proportion of Renewable Energy. Proc. CSEE 2018, 38, 663–674. [Google Scholar]
- Zhao, X.G.; Zuo, Y.; Wang, H.; Wang, Z. How can the cost and effectiveness of renewable portfolio standards be coordinated? Incentive mechanism design from the coevolution perspective. Renew. Sustain. Energy Rev. 2022, 158, 112096. [Google Scholar]
- Tan, Q.L.; Ding, Y.H.; Zheng, J.; Dai, M.; Zhang, Y.M. The effects of carbon emissions trading and renewable portfolio standards on the integrated wind-photovoltaic-thermal power-dispatching system: Real case studies in China. Energy 2021, 222, 119927. [Google Scholar] [CrossRef]
- Jordaan, S.M.; Park, J.Y.; Rangarajan, S. Innovation in intermittent electricity and stationary energy storage in the United States and Canada: A review. Renew. Sustain. Energy Rev. 2022, 158, 112149. [Google Scholar] [CrossRef]
- Zhao, X.G.; Liang, J.; Ren, L.Z.; Zhang, Y.Z.; Xu, J.Y. Top-Level Institutional Design for Energy Low-Carbon Transition: Renewable Portfolio Standards. Power Syst. Technol. 2018, 42, 1164–1169. [Google Scholar]
- Zhang, L.B.; Chen, C.Q.; Wang, Q.W.; Zhou, D.Q. The impact of feed-in tariff reduction and renewable portfolio standard on the development of distributed photovoltaic generation in China. Energy 2021, 232, 120933. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, Y.; Zeng, X.T.; Huang, G.H.; Li, Y.P. Analyzing the carbon mitigation potential of tradable green certificates based on a TGC-FFSRO model: A case study in the Beijing-Tianjin-Hebei region, China. Sci. Total Environ. 2018, 630, 469–486. [Google Scholar] [CrossRef]
- Chen, X.L.; Wang, X.L.; Lyu, J.H.; Zhang, H.; Zhu, Z.Y.; Wang, Y.F. Optimal Operation Model of Two-level Electricity Market Under the Responsibility of Renewable Energy Consumption. J. Glob. Energy Interconnect. 2020, 3, 430–440. [Google Scholar]
- Dai, T.; Qiao, W. Finding Equilibria in the Pool-Based Electricity Market with Strategic Wind Power Producers and Network Constraints. IEEE Trans. Power Syst. 2017, 32, 389–399. [Google Scholar] [CrossRef]
- Song, X.H.; Han, J.J.; Zhang, L.; Zhao, C.P.; Wang, P.; Liu, X.Y.; Li, Q.C. Impacts of renewable portfolio standards on multi-market coupling trading of renewable energy in China: A scenario-based system dynamics model. Energy Policy 2021, 159, 112647. [Google Scholar] [CrossRef]
- Guo, H.Y.; Chen, Q.X.; Xia, Q.; Kang, C.Q. Modeling Strategic Behaviors of Renewable Energy with Joint Consideration on Energy and Tradable Green Certificate Markets. IEEE Trans. Power. Syst. 2020, 35, 1898–1910. [Google Scholar] [CrossRef]
- Fang, Y.J.; Wei, W.; Mei, S.W. How dynamic renewable portfolio standards impact the diffusion of renewable energy in China? A networked evolutionary game analysis. Renew Energy. 2022, 193, 778–788. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.N.; Sun, G.Q.; Zhou, Y.Z. Strategic Investment in Power and Heat Markets: A Nash-Cournot Equilibrium Model. IEEE Trans. Industr. Inform. 2022, 18, 6057–6067. [Google Scholar] [CrossRef]
- Xiao, Y.P.; Wang, X.F.; Wang, X.L.; Dang, C.; Lu, M. Behavior analysis of wind power producer in electricity market. Appl. Energy 2016, 171, 325–335. [Google Scholar] [CrossRef]
- Xiao, Y.P.; Wang, X.F.; Wang, X.L.; Dang, C.; Lu, M. The Effect of Prosumer Duality on Power Market: Evidence from the Cournot Model. IEEE Trans. Power. Syst. 2023, 38, 692–701. [Google Scholar]
- Sun, G.Q.; Wang, R.; Chen, S.; Wu, C.; Wei, Z.N.; Zang, H.X. Nash-Cournot power market model with a high penetration of prosumers: A distributionally robust optimization approach. J. Clean. Prod. 2022, 353, 131565. [Google Scholar] [CrossRef]
- Yuan, G.L.; Liu, P.D.; Jia, X.C.; Dong, J.F.; Fang, F. Economic optimal scheduling considering tradable green certificate system. Acta Energiae Solaris Sinica. 2021, 42, 139–146. [Google Scholar]
- Li, L.; Tan, Z.F.; Zhang, E.Y. Research on market power in the implementation of renewable portfolio standard. Power Syst. Prot. Control 2014, 42, 106–112. [Google Scholar]
- Lu, Z.L.; Sun, S.J.; Tang, Z.Q.; Wei, Q. Optimal scheduling of plus and minus spinning reserve in microgrid based on sequence operation theory. Power Syst. Prot. Control 2017, 45, 100–109. [Google Scholar]
- Shao, L.Z.; Liu, R.H.; Wang, H.B.; Liu, Y.F.; Ye, L.; Yao, J.G. A method for cost allocation of reserve based on conditional value at risk. Power Syst. Prot. Control 2018, 46, 23–30. [Google Scholar]
- Xiao, Y.; Xie, J.; Liu, R.P.; Li, Y.H. A new calculation method of reserve capacity considering wind power forecasting error. Power Syst. Prot. Control 2019, 47, 78–85. [Google Scholar]
- Zhou, Y.J.; Hua, Q.S.; Liu, P.; Sun, L. Multi-objective optimal droop control of solid oxide fuel cell based integrated energy system. Int. J. Hydrog. Energy 2023, 48, 11382–11389. [Google Scholar] [CrossRef]
- Li, C.T.; Xu, C.B.; Li, X.M. A multi-criteria decision-making framework for site selection of distributed PV power stations along high-speed railway. J. Clean. Prod. 2020, 277, 124086. [Google Scholar] [CrossRef]
- Li, Z.M.; Xu, Y.; Fang, S.D.; Wang, Y.; Zheng, X.D. Multiobjective Coordinated Energy Dispatch and Voyage Scheduling for a Multienergy Ship Microgrid. IEEE Trans. Appl. Ind. 2020, 56, 989–999. [Google Scholar] [CrossRef]



| Parameter | G1 | G2 | G3 | G4 | G5 | G6 |
|---|---|---|---|---|---|---|
| qmax | 280 MW | 310 MW | 320 MW | 330 MW | 300 MW | 350 MW |
| qmin | 30 MW | 30 MW | 30 MW | 30 MW | 100 MW | 100 MW |
| a | 0.082 | 0.076 | 0.073 | 0.061 | - | - |
| b | 25.265 | 23.588 | 23.097 | 23.971 | - | - |
| c | 96.3 | 95.1 | 95.3 | 94.9 | - | - |
| Quota Ratio | Thermal Power Generators Alliance Revenue/$ | Renewable Energy Generators Alliance Revenue/$ | Priority Membership |
|---|---|---|---|
| 10% | 29,932.92 | 7927.11 | 0.835 |
| 20% | 25,822.22 | 13,092.61 | 0.865 |
| 30% | 18,942.55 | 20,016.52 | 0.834 |
| 40% | 10,682.59 | 30,898.27 | 0.872 |
| 50% | 8779.87 | 34,858.33 | 0.872 |
| 60% | 7957.80 | 36,142.83 | 0.828 |
| Quota Ratio | 10% | 20% | 30% | 40% | 50% | 60% |
|---|---|---|---|---|---|---|
| G1 | 0.492 | 0.529 | 0.551 | 0.599 | 0.610 | 0.673 |
| G5 | 0.293 | 0.528 | 0.679 | 0.764 | 0.813 | 0.866 |
| Quota Ratio | 10% | 20% | 30% | 40% | 50% | 60% | |
|---|---|---|---|---|---|---|---|
| G1 | 0.1 | 0.462 | 0.504 | 0.521 | 0.539 | 0.550 | 0.586 |
| 0.15 | 0.489 | 0.512 | 0.532 | 0.565 | 0.582 | 0.604 | |
| 0.2 | 0.492 | 0.529 | 0.551 | 0.599 | 0.610 | 0.673 | |
| G5 | 0.1 | 0.245 | 0.421 | 0.596 | 0.633 | 0.635 | 0.709 |
| 0.15 | 0.262 | 0.444 | 0.631 | 0.699 | 0.710 | 0.795 | |
| 0.2 | 0.293 | 0.528 | 0.679 | 0.764 | 0.813 | 0.866 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, J.; Jia, R.; Gao, X.; Cao, G.; Dang, J.; Li, W.; Li, P. Competitive Equilibrium Analysis of Power Generation Transaction Subjects Considering Tradable Green Certificates. Processes 2023, 11, 3008. https://doi.org/10.3390/pr11103008
Wen J, Jia R, Gao X, Cao G, Dang J, Li W, Li P. Competitive Equilibrium Analysis of Power Generation Transaction Subjects Considering Tradable Green Certificates. Processes. 2023; 11(10):3008. https://doi.org/10.3390/pr11103008
Chicago/Turabian StyleWen, Jiaxing, Rong Jia, Xin Gao, Ge Cao, Jian Dang, Wei Li, and Peihang Li. 2023. "Competitive Equilibrium Analysis of Power Generation Transaction Subjects Considering Tradable Green Certificates" Processes 11, no. 10: 3008. https://doi.org/10.3390/pr11103008
APA StyleWen, J., Jia, R., Gao, X., Cao, G., Dang, J., Li, W., & Li, P. (2023). Competitive Equilibrium Analysis of Power Generation Transaction Subjects Considering Tradable Green Certificates. Processes, 11(10), 3008. https://doi.org/10.3390/pr11103008







