Analysis of Controllability in Cyber–Physical Power Systems under a Novel Load-Capacity Model
Abstract
:1. Introduction
- By combining the network topology and functional characteristics of the system, a load-capacity model is developed to address the research gap in cascading failure of CPPS. The validity of the results is verified through the modeling of realistic networks, enhancing the persuasiveness of our findings.
- By considering the real-time node loads and the distribution of power flow and information flow in CPPS, a novel load redistribution strategy is introduced. Compared to other strategies, this strategy can quickly terminate failures and prevent system collapse.
- This paper comprehensively analyzes different information network topologies and network parameters, and it investigates the controllability of the system after cascading failures under different coupling strategies and capacity parameters. Guidelines for future smart grid planning are provided.
2. Methods
2.1. Cyber–Physical Power System Model
2.2. Controllability of Cyber–Physical Power System
3. Fault Propagation of CPPS under Cascading Failure
3.1. Initial Load and Capacity Model
3.1.1. Load Capacity Model in Power Networks
- Generation Nodes: These nodes feed power into the grid.
- Load Nodes: These nodes consume power from the grid.
- Transmission Nodes: These nodes neither consume nor contribute power to the grid.
3.1.2. Load Capacity Model in Information Networks
3.2. The Process of Cascading Failure
- Underloading Node: The node’s load is within its rated range.
- Heavy-Loading Node: The load on the node exceeds the rated range but does not exceed the capacity of the node. Therefore, the node is still in a normal operating state, but it cannot remain in this state for a long time or it will cause the node to fail.
- Overloading Node: The node load exceeds the capacity of the node and the node fails.
4. Case Study and Discussion
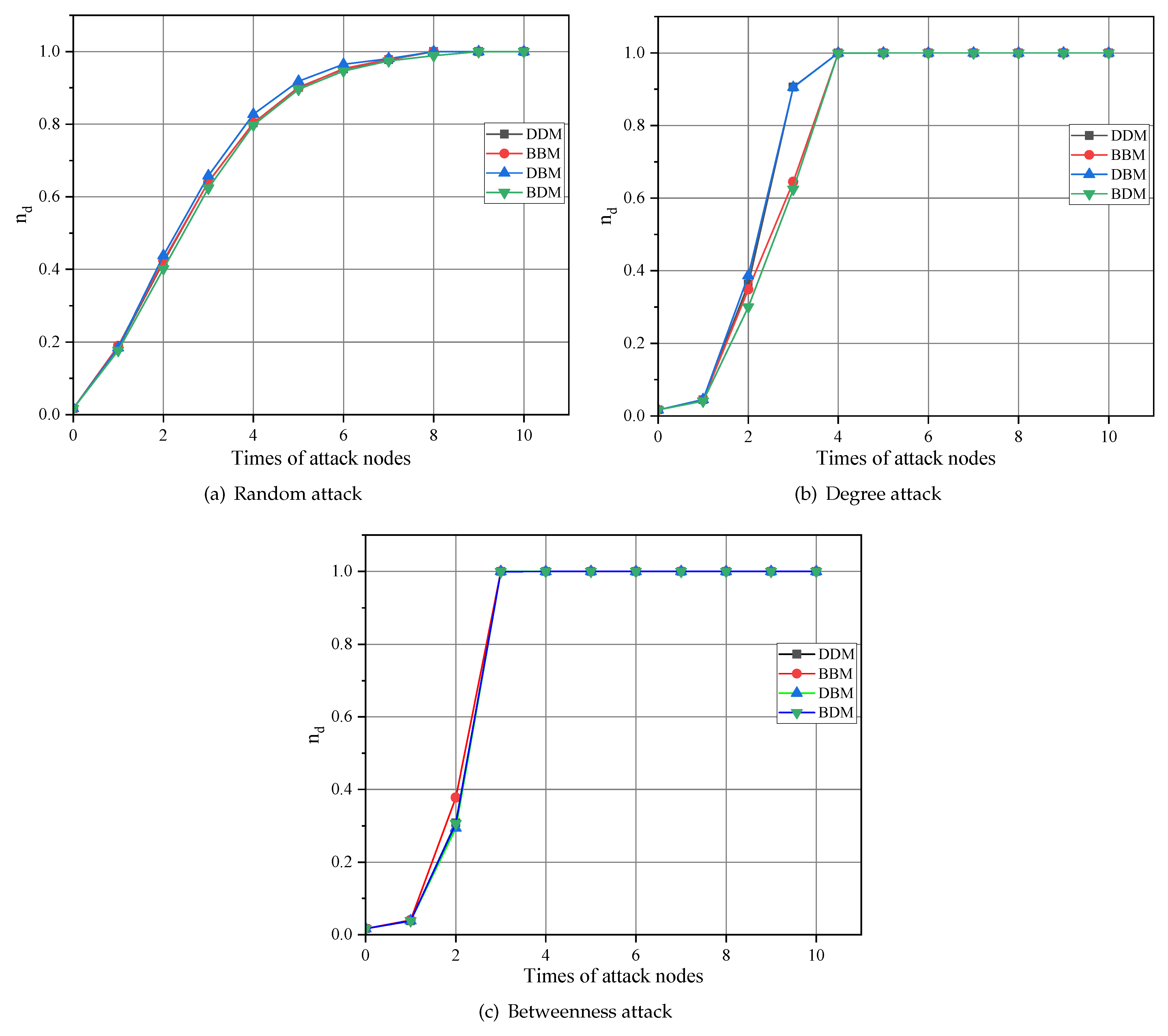
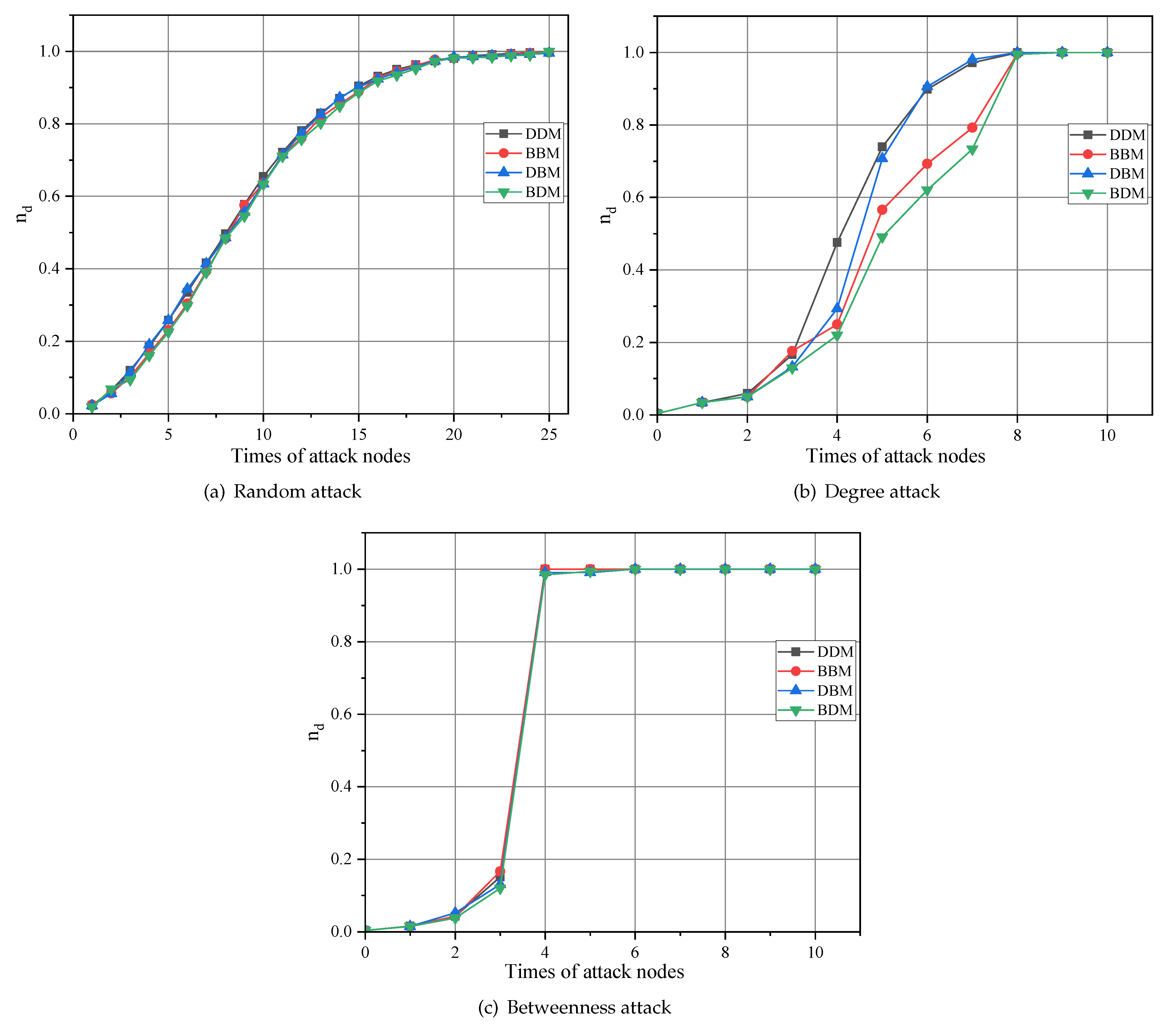
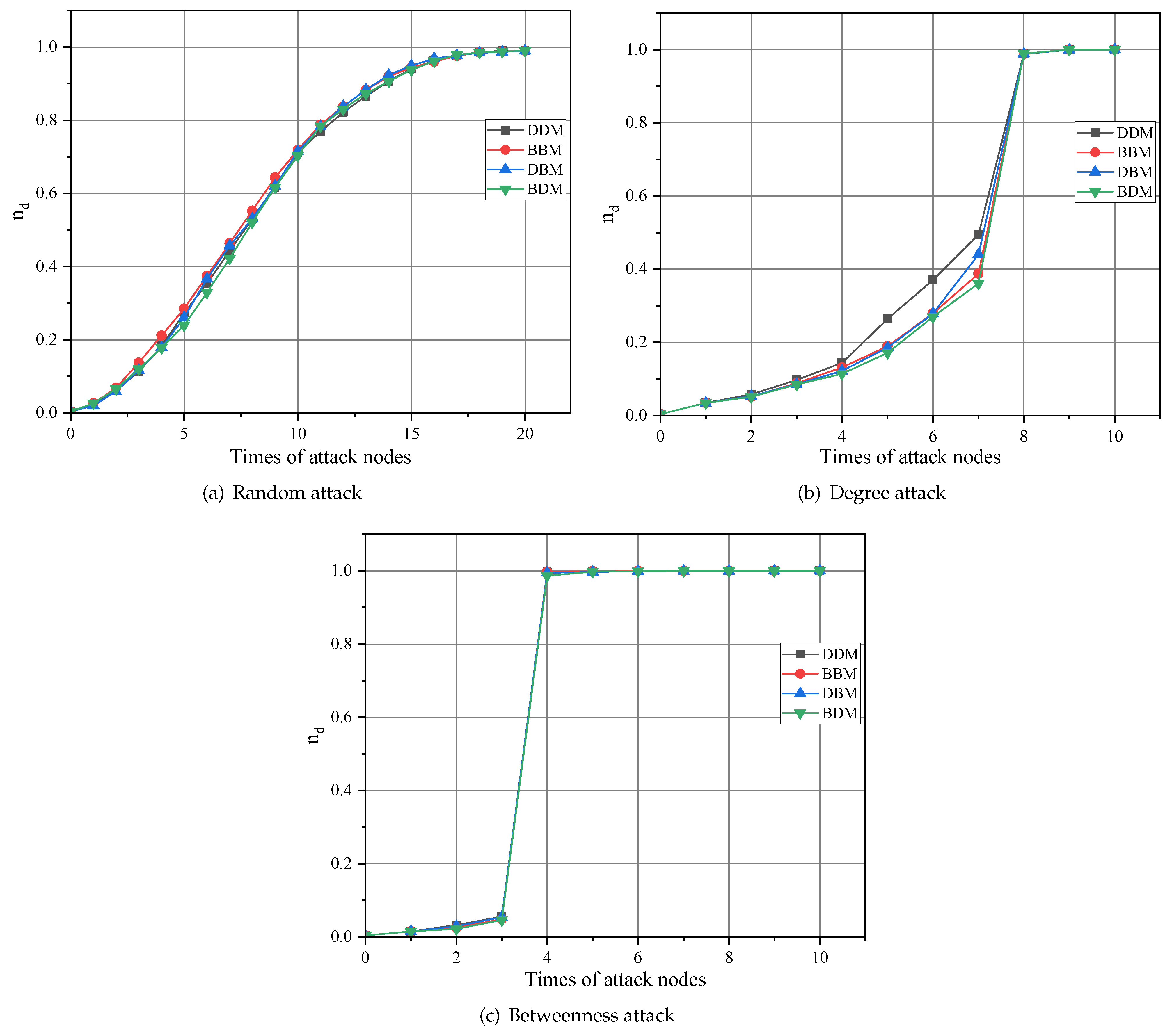
- DDM: High-degree nodes in the power network are connected to high-degree nodes in the information network.
- BBM: High-betweenness nodes in the power network are connected to high betweenness nodes in the information network.
- DBM: High-degree nodes in the power network are connected to high betweenness nodes in the information network.
- BDM: High-betweenness nodes in the power network are connected to high-degree nodes in the information network.
4.1. Initial Network Topology
4.2. The Controllability of CPPS in Different Network Types
4.2.1. Case A: IEEE 39-Node System
4.2.2. Case B: Chinese 132-Node System
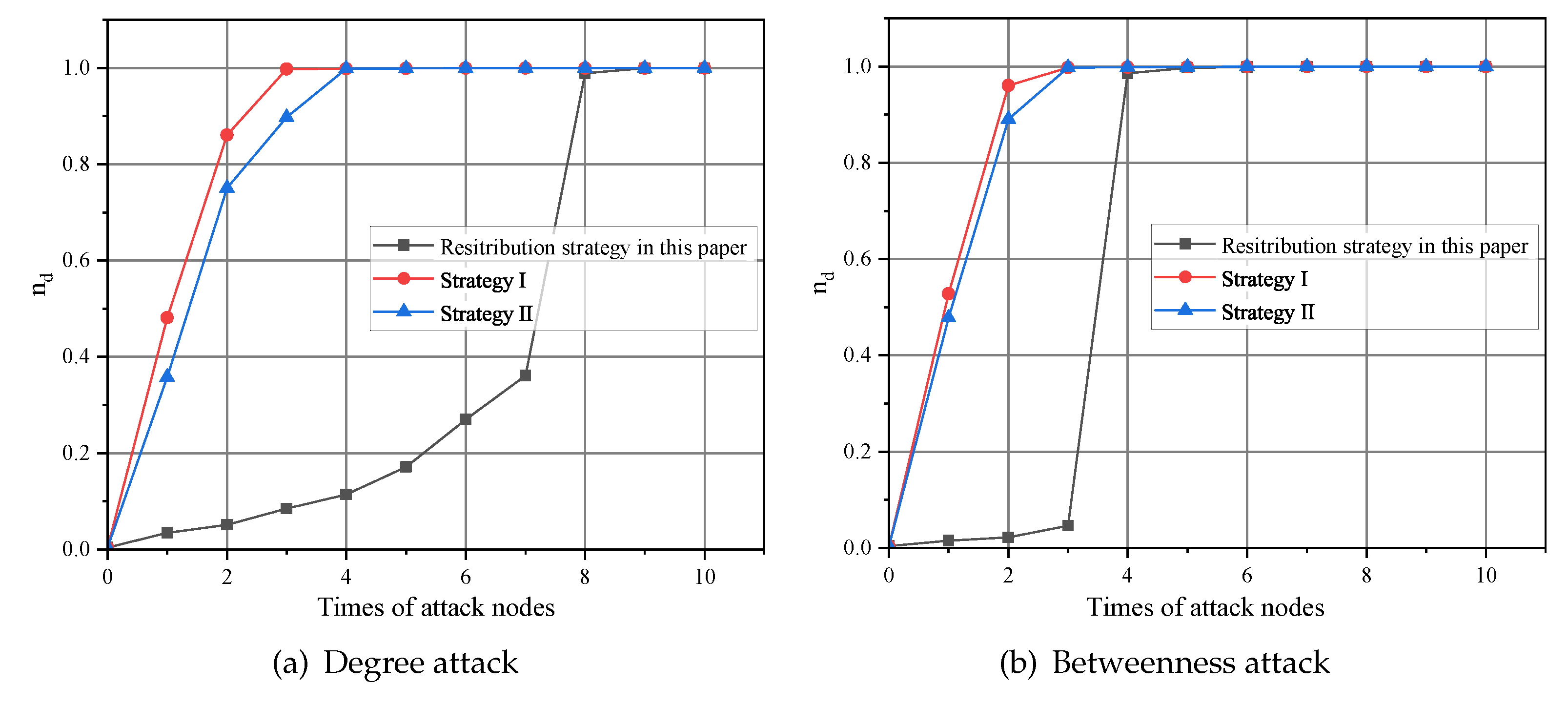
4.3. CPPS Controllability under Different Redistribution Strategies
4.3.1. Case A: IEEE 39-Node System
4.3.2. Case B: Chinese 132-Node System
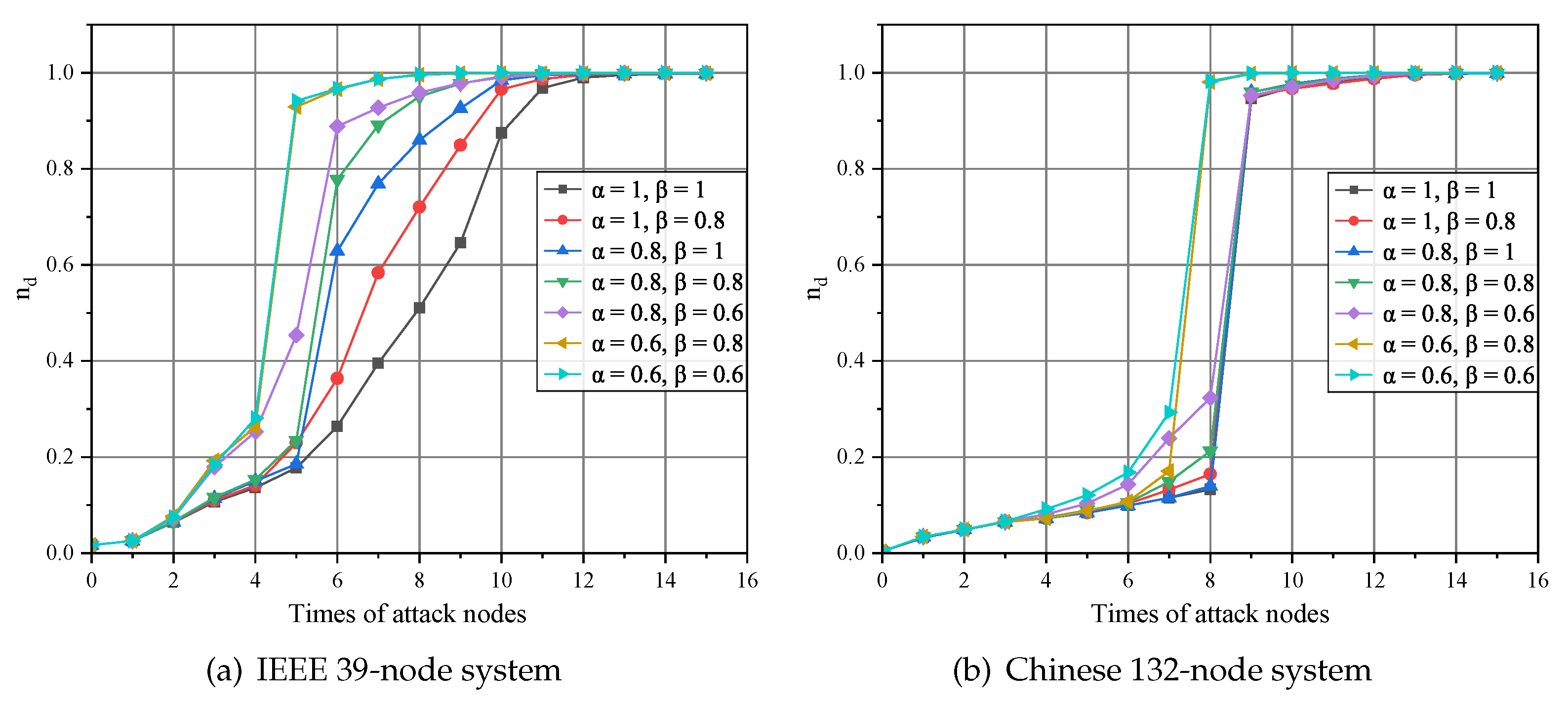
4.4. Effect of Various Parameters on the Controllability of CPPS Cascading Failures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faheem, M.; Shah, S.B.H.; Butt, R.A.; Raza, B.; Anwar, M.; Ashraf, M.W.; Ngadi, M.A.; Gungor, V.C. Smart grid communication and information technologies in the perspective of Industry 4.0: Opportunities and challenges. Comput. Sci. Rev. 2018, 30, 1–30. [Google Scholar] [CrossRef]
- Salkuti, S.R. Challenges, issues and opportunities for the development of smart grid. Int. J. Electr. Comput. Eng. 2020, 10, 1179–1186. [Google Scholar] [CrossRef]
- Qu, Z.; Shi, H.; Wang, Y.; Yin, G.; Abu-Siada, A. Active and Passive Defense Strategies of Cyber-Physical Power System against Cyber Attacks Considering Node Vulnerability. Processes 2022, 10, 1351. [Google Scholar] [CrossRef]
- Yohanandhan, R.V.; Elavarasan, R.M.; Manoharan, P.; Mihet-Popa, L. Cyber-physical power system (CPPS): A review on modeling, simulation, and analysis with cyber security applications. IEEE Access 2020, 8, 151019–151064. [Google Scholar] [CrossRef]
- Sturaro, A.; Silvestri, S.; Conti, M.; Das, S.K. A realistic model for failure propagation in interdependent cyber-physical systems. IEEE Trans. Netw. Sci. Eng. 2018, 7, 817–831. [Google Scholar] [CrossRef]
- Wang, Q.; Cai, X.; Tang, Y.; Ni, M. Methods of cyber-attack identification for power systems based on bilateral cyber-physical information. Int. J. Electr. Power Energy Syst. 2021, 125, 106515. [Google Scholar] [CrossRef]
- Khan, M.M.S.; Giraldo, J.A.; Parvania, M. Attack detection in power distribution systems using a cyber-physical real-time reference model. IEEE Trans. Smart Grid 2021, 13, 1490–1499. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, W.; Liu, F.; Shafie-khah, M.; Mei, S.; Catalão, J.P. Optimal contracts of energy mix in a retail market under asymmetric information. Energy 2018, 165, 634–650. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef]
- Wang, X.; Du, J.; Zou, R.; Zhou, Z. Key node identification of wireless sensor networks based on cascade failure. Mod. Phys. Lett. B 2020, 34, 2050394. [Google Scholar] [CrossRef]
- Motter, A.E.; Lai, Y.C. Cascade-based attacks on complex networks. Phys. Rev. E 2002, 66, 065102. [Google Scholar] [CrossRef]
- Jin, Z.; Duan, D.; Wang, N. Cascading failure of complex networks based on load redistribution and epidemic process. Phys. A Stat. Mech. Its Appl. 2022, 606, 128041. [Google Scholar] [CrossRef]
- Lang, M.; Shkolnikov, M. Harmonic dynamics of the abelian sandpile. Proc. Natl. Acad. Sci. USA 2019, 116, 2821–2830. [Google Scholar] [CrossRef] [PubMed]
- Li, M.J.; Tse, C.K.; Liu, D.; Zhang, X. Cascading Failure Propagation and Mitigation Strategies in Power Systems. IEEE Syst. J. 2023, 17, 3282–3293. [Google Scholar] [CrossRef]
- Wang, W.X.; Chen, G. Universal robustness characteristic of weighted networks against cascading failure. Phys. Rev. E 2008, 77, 026101. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.N.; Liu, B.H.; Nguyen, N.P.; Dumba, B.; Chou, J.T. Smart grid vulnerability and defense analysis under cascading failure attacks. IEEE Trans. Power Deliv. 2021, 36, 2264–2273. [Google Scholar] [CrossRef]
- Cai, Y.; Cao, Y.; Li, Y.; Huang, T.; Zhou, B. Cascading failure analysis considering interaction between power grids and communication networks. IEEE Trans. Smart Grid 2015, 7, 530–538. [Google Scholar] [CrossRef]
- Artime, O.; De Domenico, M. Abrupt transition due to non-local cascade propagation in multiplex systems. New J. Phys. 2020, 22, 093035. [Google Scholar] [CrossRef]
- Zhou, D.; Elmokashfi, A. Overload-based cascades on multiplex networks and effects of inter-similarity. PLoS ONE 2017, 12, e0189624. [Google Scholar] [CrossRef]
- Artime, O.; Benigni, B.; Bertagnolli, G.; d’Andrea, V.; Gallotti, R.; Ghavasieh, A.; Raimondo, S.; De Domenico, M. Multilayer Network Science: From Cells to Societies; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Lo, C.H.; Ansari, N. Decentralized controls and communications for autonomous distribution networks in smart grid. IEEE Trans. Smart Grid 2012, 4, 66–77. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Slotine, J.J.; Barabási, A.L. Controllability of complex networks. Nature 2011, 473, 167–173. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Zhao, C.; Di, Z.; Wang, W.X.; Lai, Y.C. Exact controllability of complex networks. Nat. Commun. 2013, 4, 2447. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, G.; Wang, X.; Tang, W.K. Controllability of networked MIMO systems. Automatica 2016, 69, 405–409. [Google Scholar] [CrossRef]
- Jiang, L.; Tang, L.; Lü, J. Controllability of multilayer networks. Asian J. Control. 2022, 24, 1517–1527. [Google Scholar] [CrossRef]
- Miao, S.; Su, H.; Liu, B. Controllability of Discrete-Time Multi-agent Systems with Matrix-Weighted Networks. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2984–2988. [Google Scholar] [CrossRef]
- Kalman, R.E. Mathematical description of linear dynamical systems. J. Soc. Ind. Appl. Math. Ser. A Control. 1963, 1, 152–192. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, B.h.; Zhang, Z.; Yin, X.g.; Wang, B. An electrical betweenness approach for vulnerability assessment of power grids considering the capacity of generators and load. Phys. A Stat. Mech. Its Appl. 2011, 390, 4692–4701. [Google Scholar] [CrossRef]
- Feng, O.; Zhang, H.; Liu, H.; Zhong, G. Enhancing the Robustness of Scale-Free Networks: The Simulation of Cascade Failures with Adjustable Initial Load Parameters. Processes 2023, 11, 2118. [Google Scholar] [CrossRef]
- Balasis, G.; Balikhin, M.A.; Chapman, S.C.; Consolini, G.; Daglis, I.A.; Donner, R.V.; Kurths, J.; Paluš, M.; Runge, J.; Tsurutani, B.T.; et al. Complex systems methods characterizing nonlinear processes in the near-earth electromagnetic environment: Recent advances and open challenges. Space Sci. Rev. 2023, 219, 38. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Von Meier, A. Electric Power Systems: A Conceptual Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Hamilton, W.L. Graph Representation Learning; Morgan & Claypool Publishers: Williston, VT, USA, 2020. [Google Scholar]
- Wang, Y.; Dong, J.; Zhao, J.; Qu, Z.; Huang, J. Dynamic Load Redistribution of Power CPS Based on Comprehensive Index of Coupling Node Pairs. Processes 2022, 10, 1937. [Google Scholar] [CrossRef]
- Ozel, O.; Sinopoli, B.; Yağan, O. Uniform redundancy allocation maximizes the robustness of flow networks against cascading failures. Phys. Rev. E 2018, 98, 042306. [Google Scholar] [CrossRef]
- Fu, X.; Yao, H.; Yang, Y. Cascading failures in wireless sensor networks with load redistribution of links and nodes. Ad Hoc Netw. 2019, 93, 101900. [Google Scholar] [CrossRef]
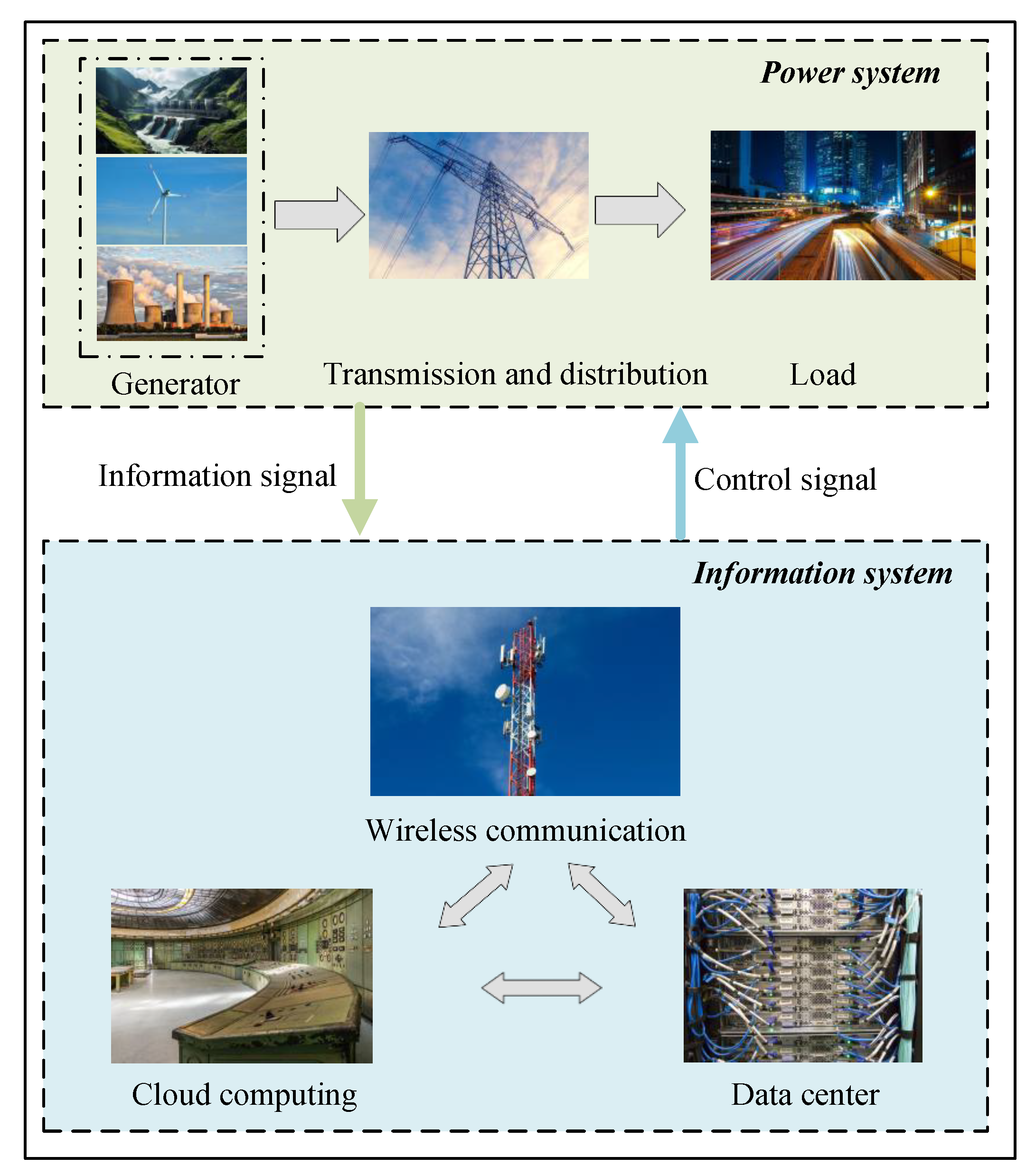
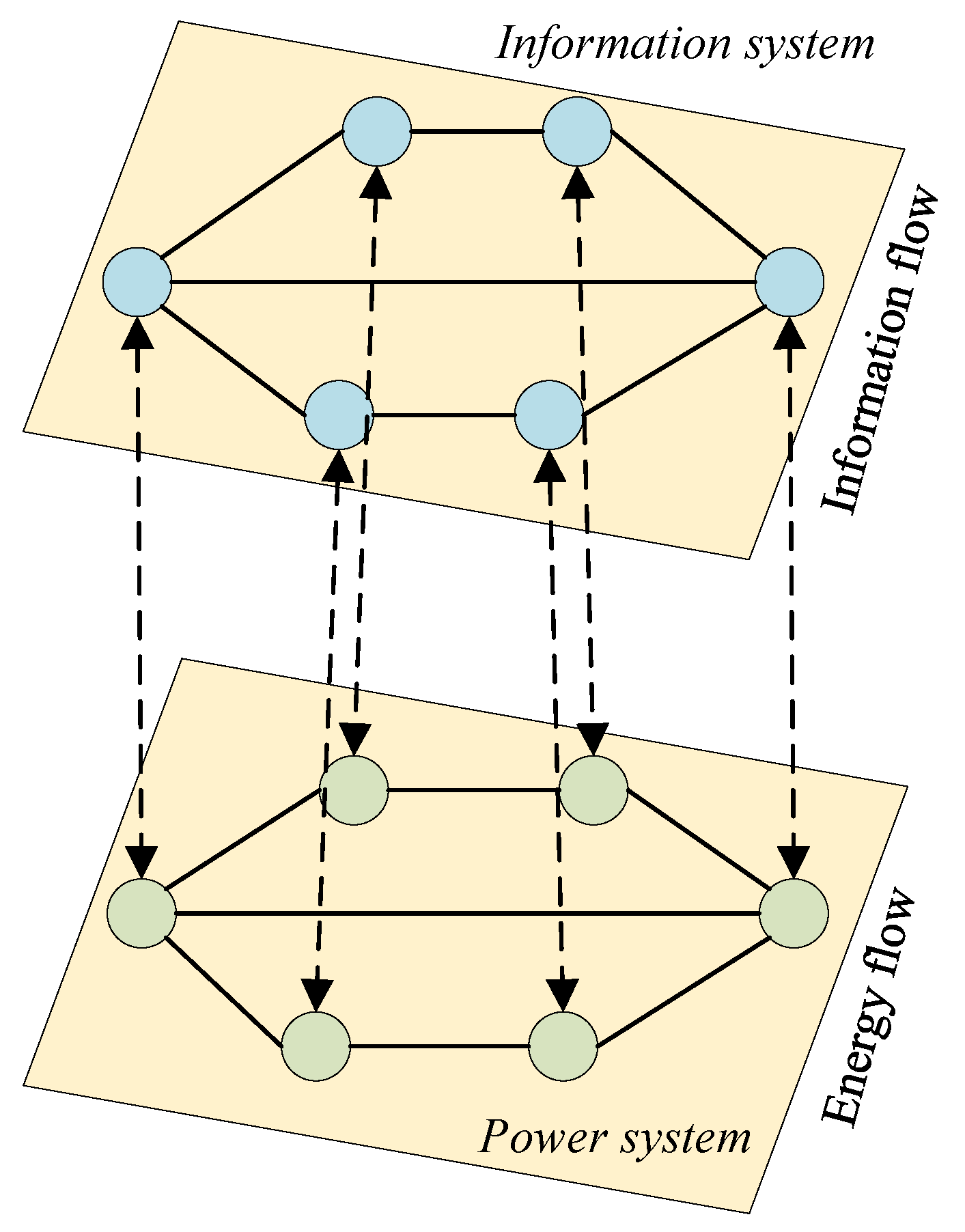



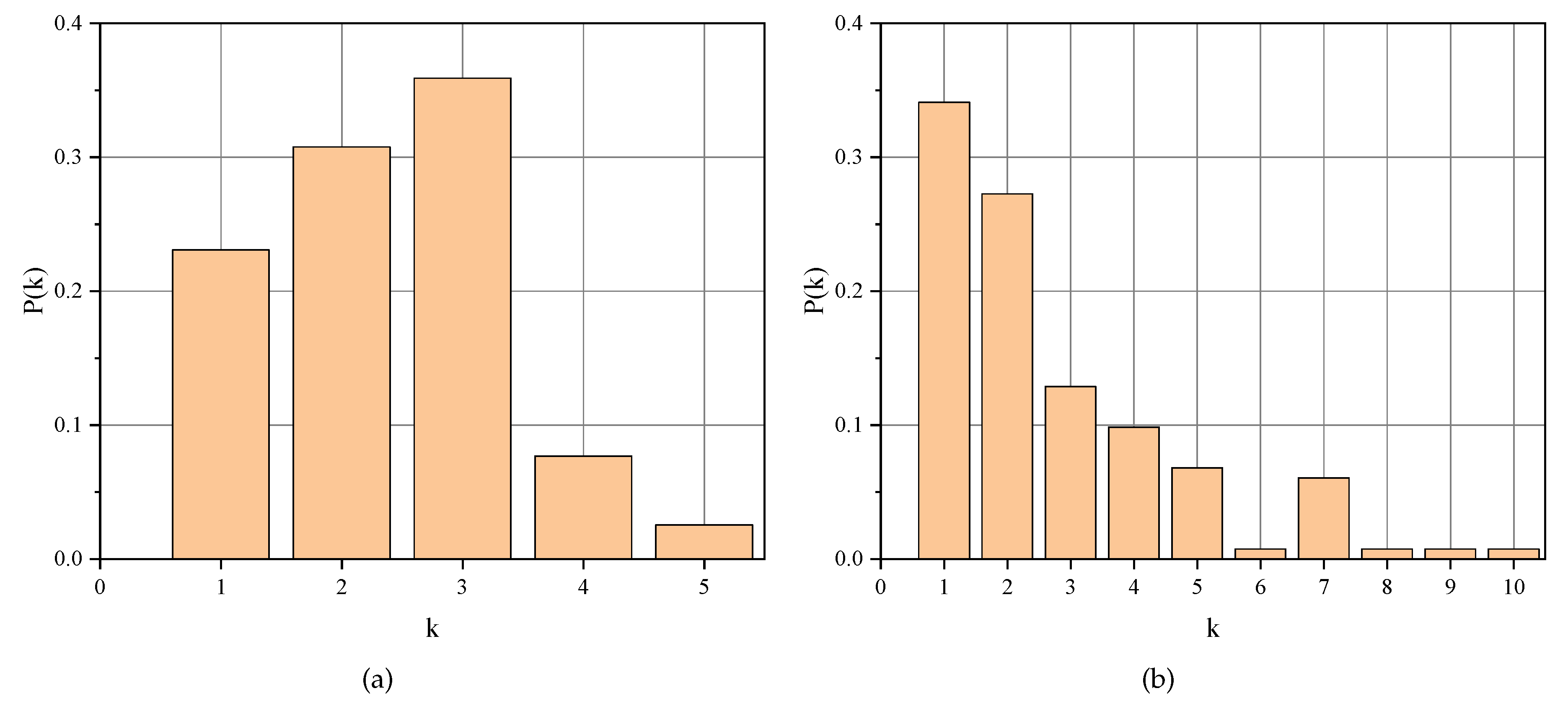


| Network Type | N | L | Clustering Coefficient | |
|---|---|---|---|---|
| IEEE 39-Node System | 39 | 39 | 0.0769 | 0.0385 |
| Chinese 132-Node System | 132 | 180 | 0.2273 | 0.0880 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, Y.; Li, Y.; Xu, T.; He, Z.; Zhu, Q. Analysis of Controllability in Cyber–Physical Power Systems under a Novel Load-Capacity Model. Processes 2023, 11, 3046. https://doi.org/10.3390/pr11103046
Ge Y, Li Y, Xu T, He Z, Zhu Q. Analysis of Controllability in Cyber–Physical Power Systems under a Novel Load-Capacity Model. Processes. 2023; 11(10):3046. https://doi.org/10.3390/pr11103046
Chicago/Turabian StyleGe, Yaodong, Yan Li, Tianqi Xu, Zhaolei He, and Quancong Zhu. 2023. "Analysis of Controllability in Cyber–Physical Power Systems under a Novel Load-Capacity Model" Processes 11, no. 10: 3046. https://doi.org/10.3390/pr11103046
APA StyleGe, Y., Li, Y., Xu, T., He, Z., & Zhu, Q. (2023). Analysis of Controllability in Cyber–Physical Power Systems under a Novel Load-Capacity Model. Processes, 11(10), 3046. https://doi.org/10.3390/pr11103046










