Simulation and Experiment on Elimination for the Bottom-Sitting Adsorption Effect of a Submersible Based on a Submerged Jet
Abstract
:1. Introduction
2. Methods
2.1. Analysis of the Bottom-Sitting Adsorption Effect
2.2. Turbulent Flow Calculation Model and Jet Pattern
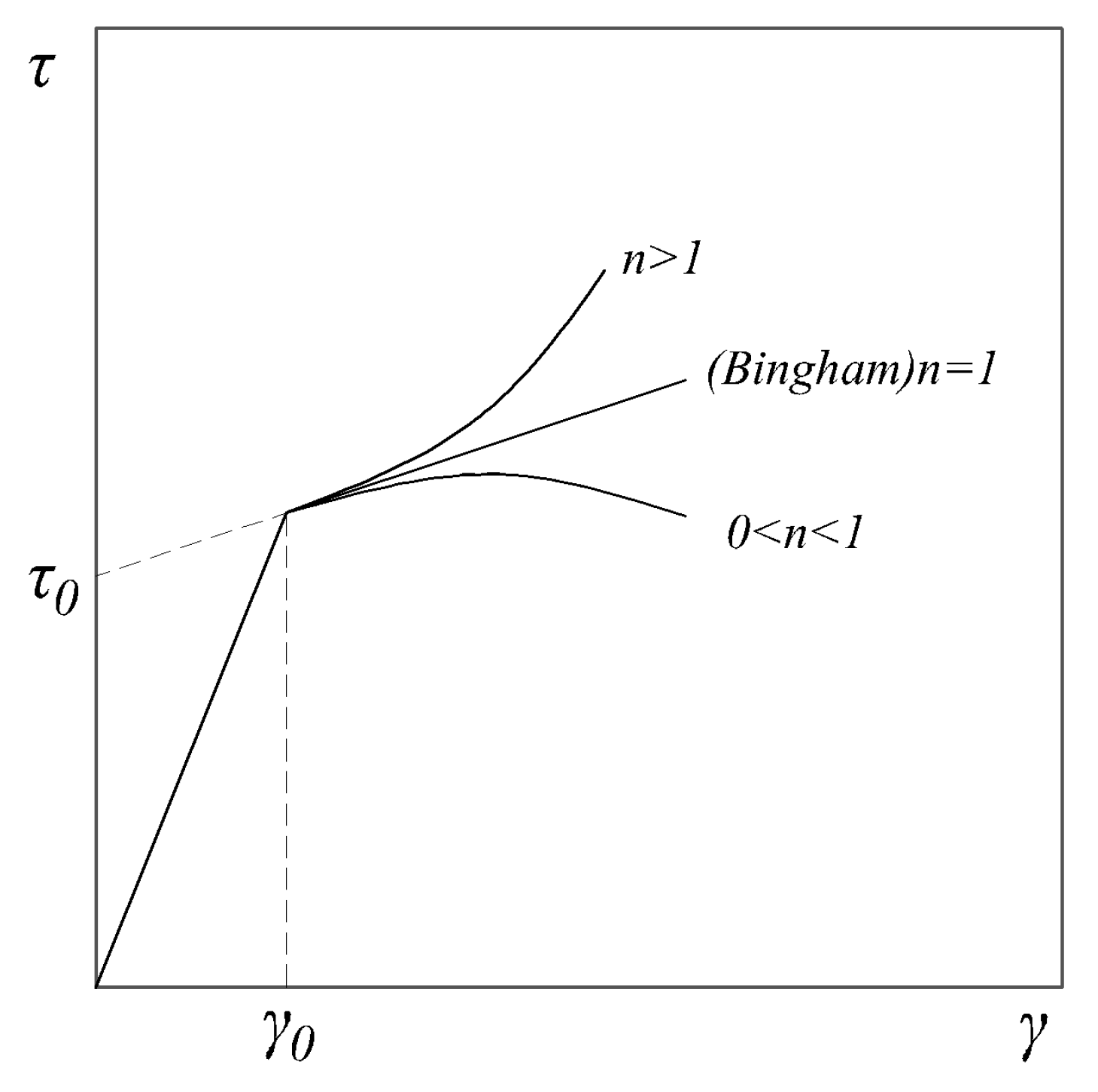
2.3. Soil Liquefaction Law and Soil Rheology Calculation Model
3. Calculation and Analysis
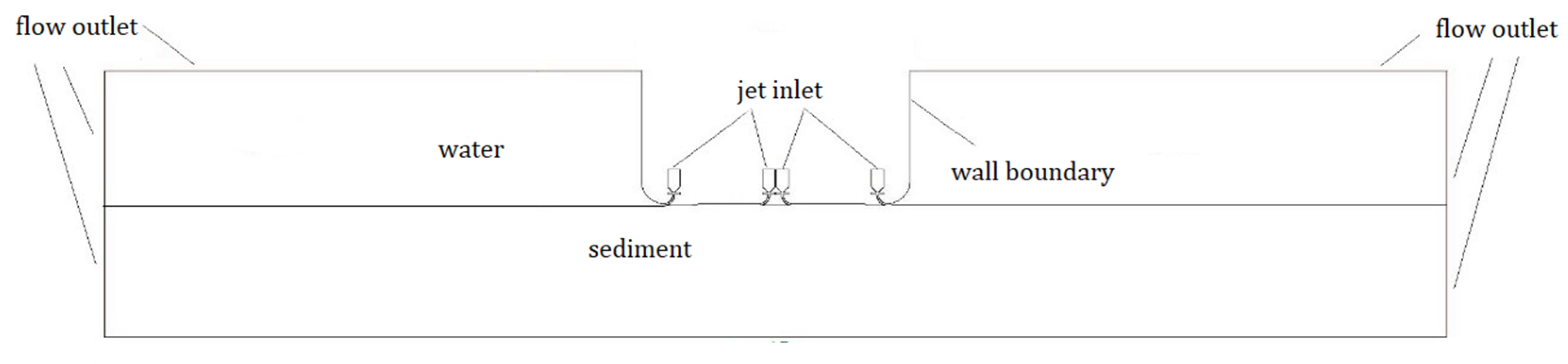
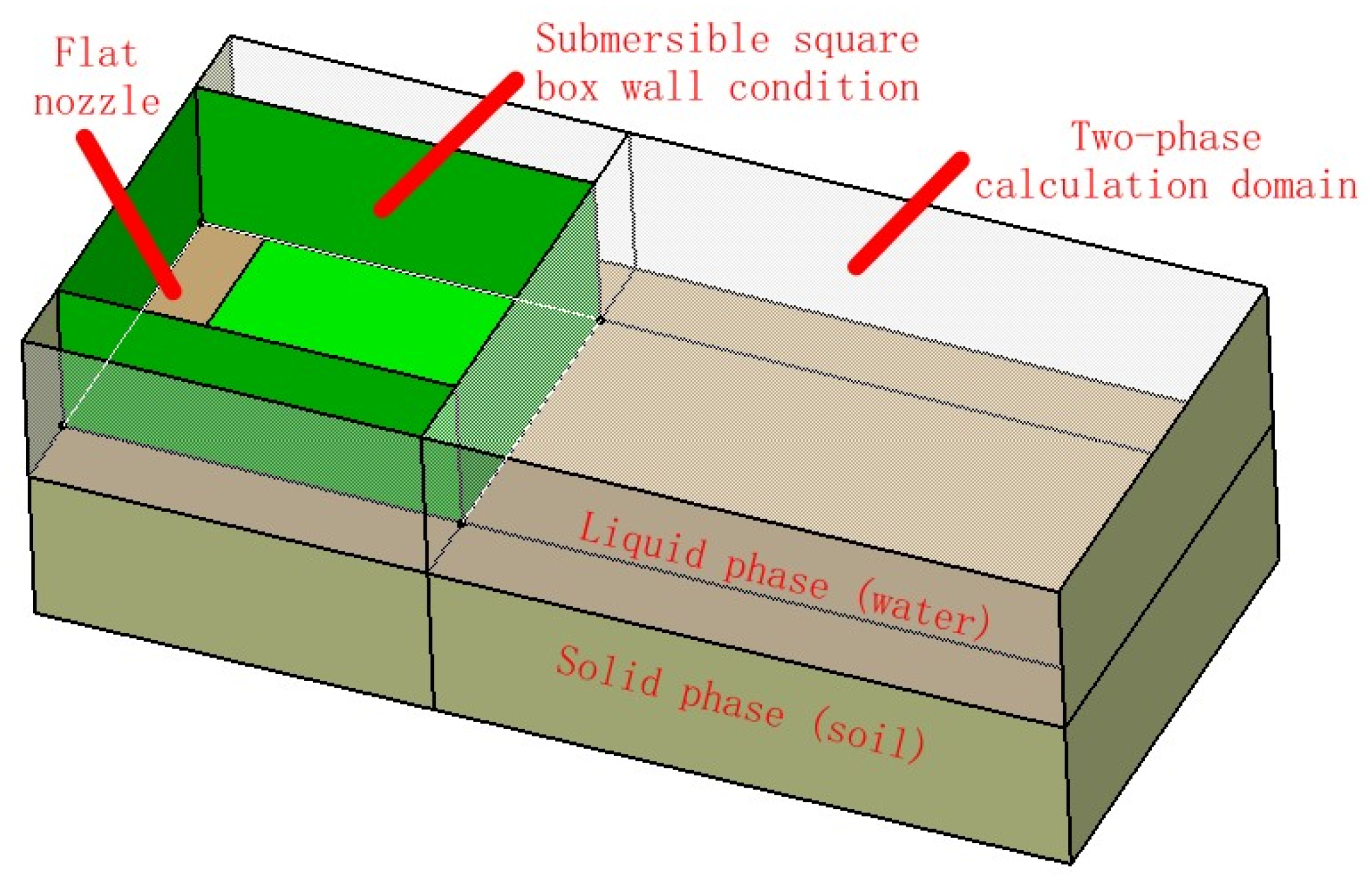
3.1. Two-Dimensional Water Jet Calculation Model
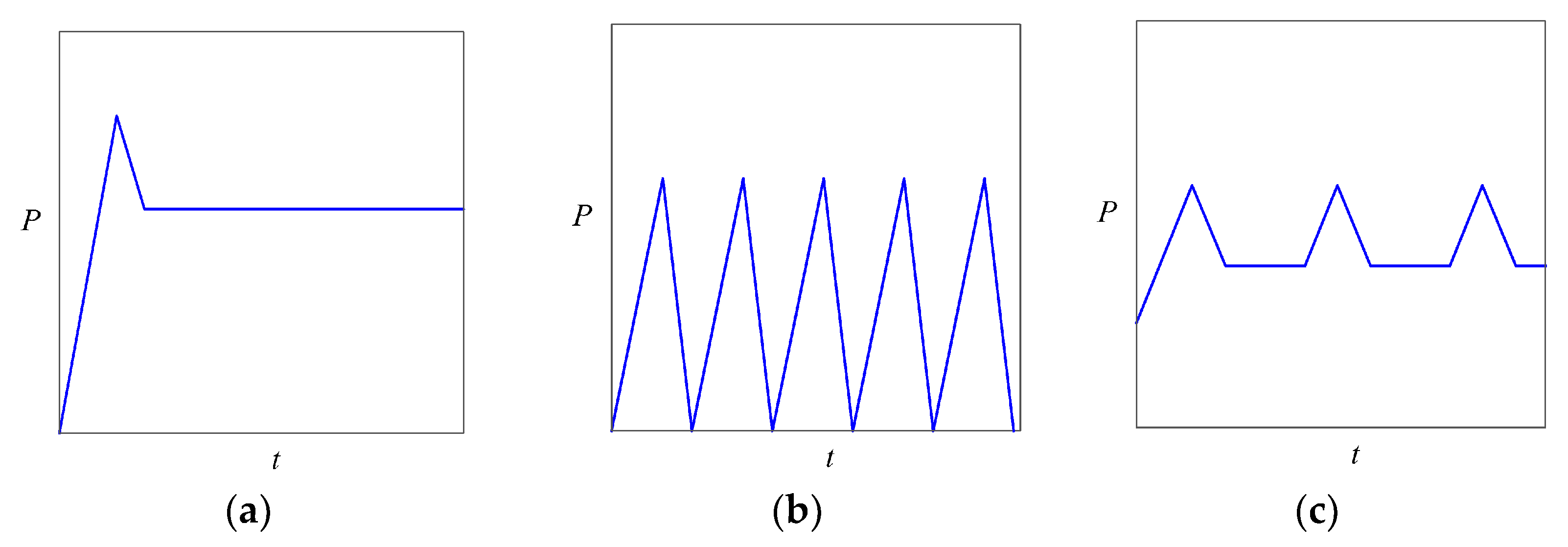
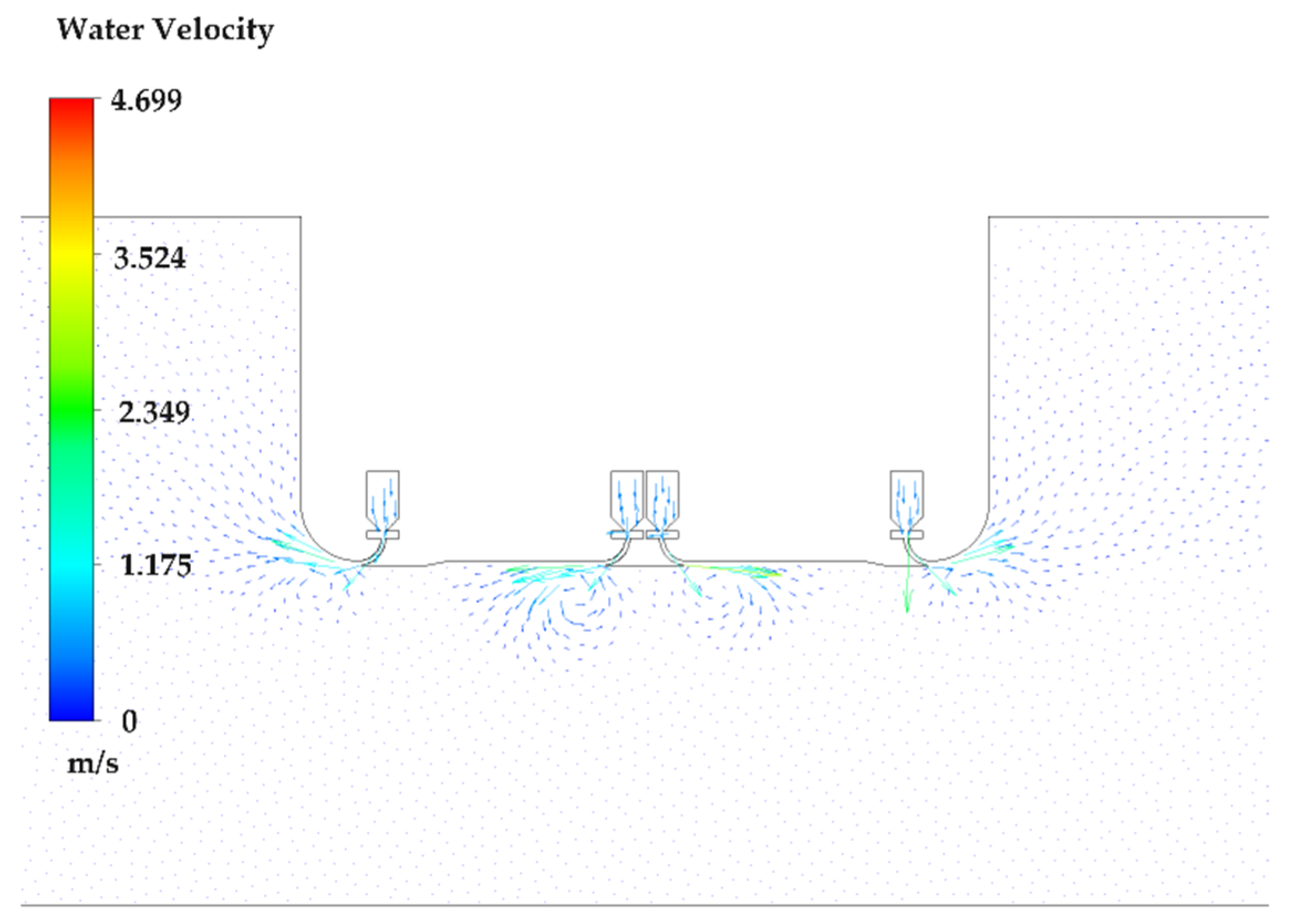
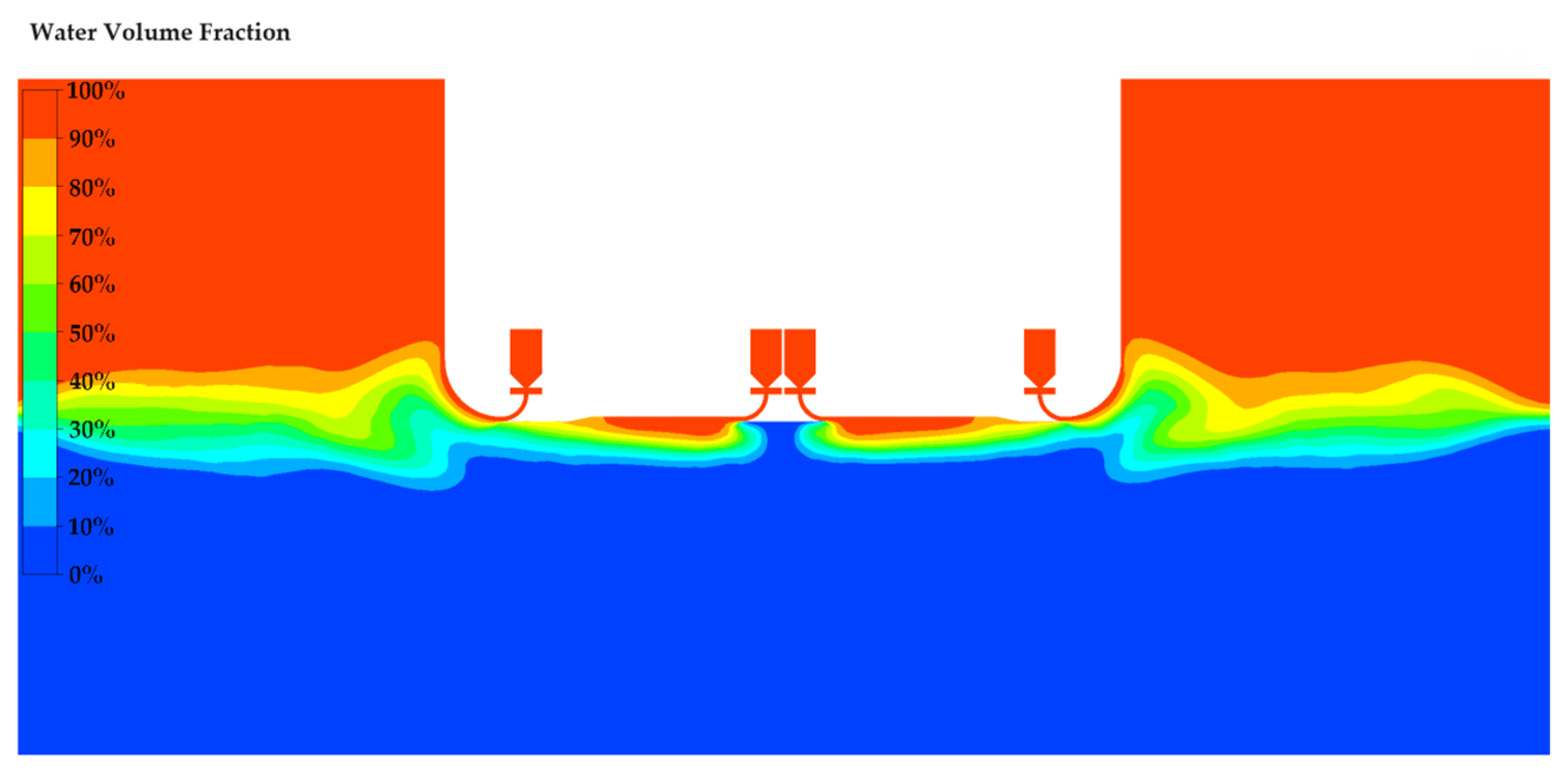
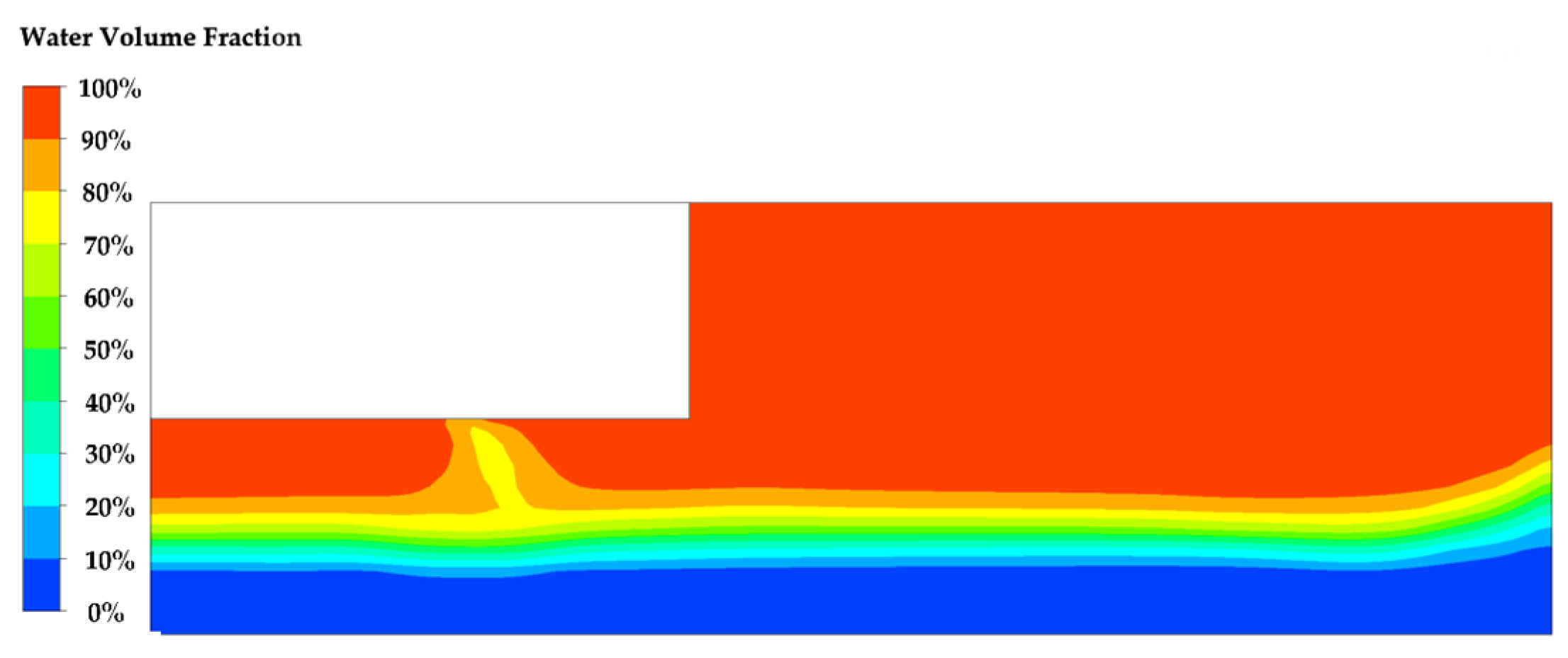
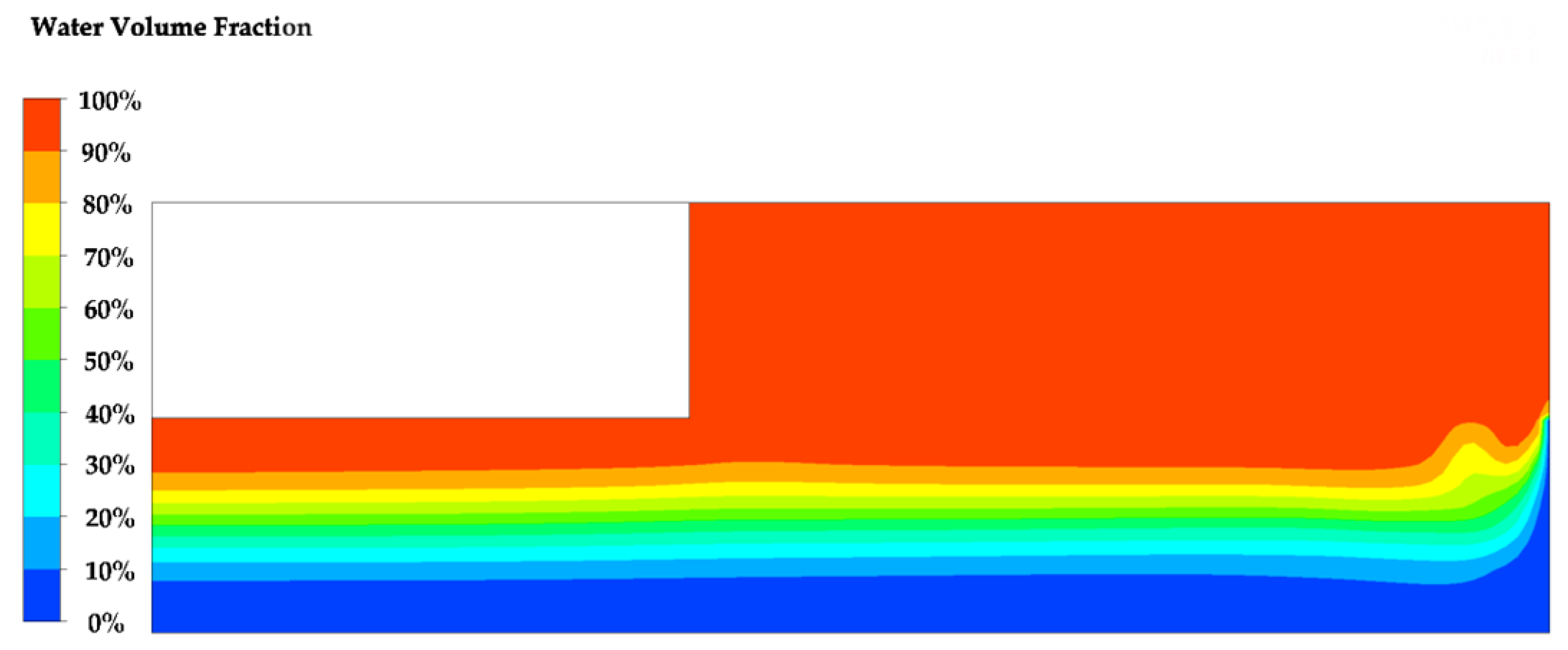
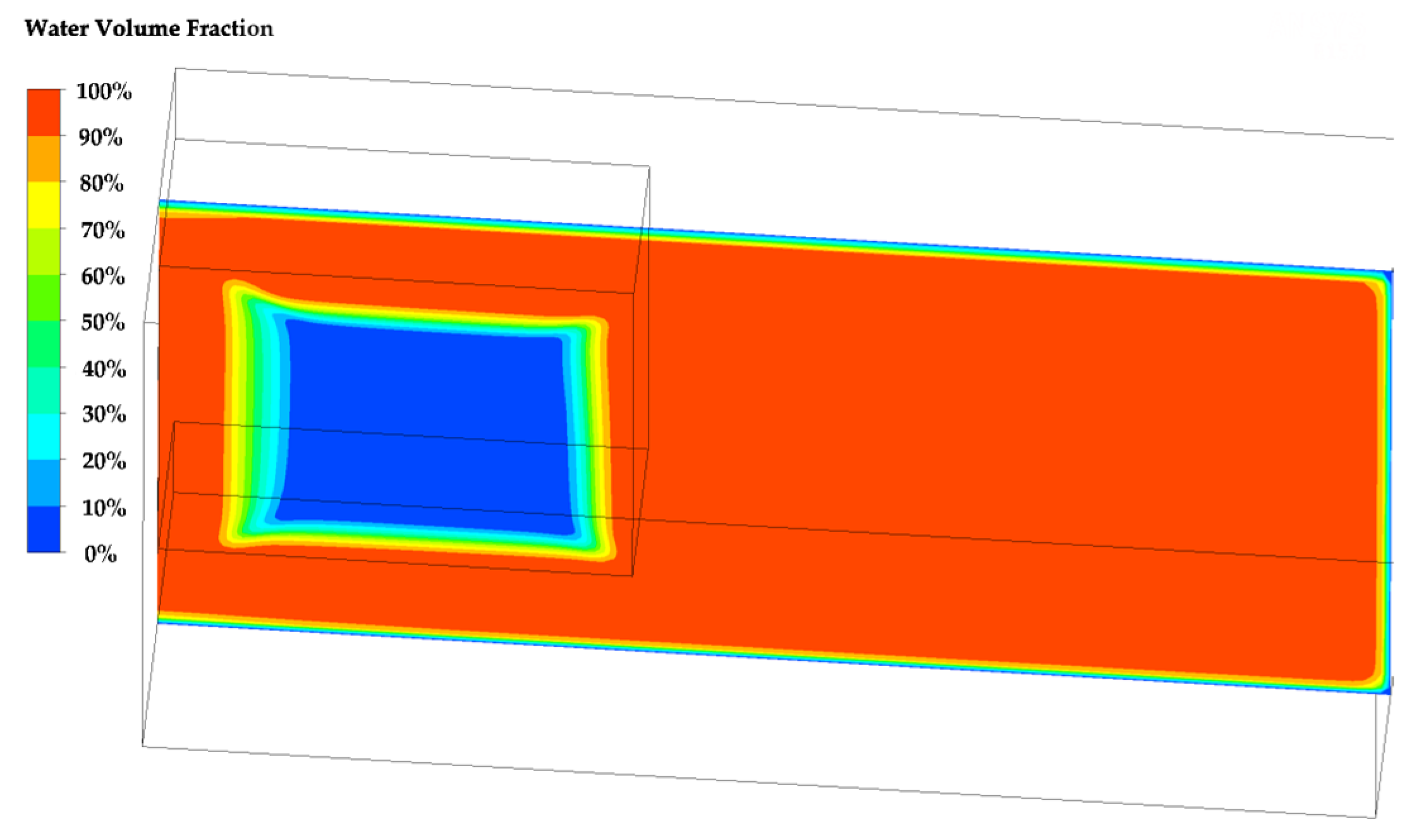
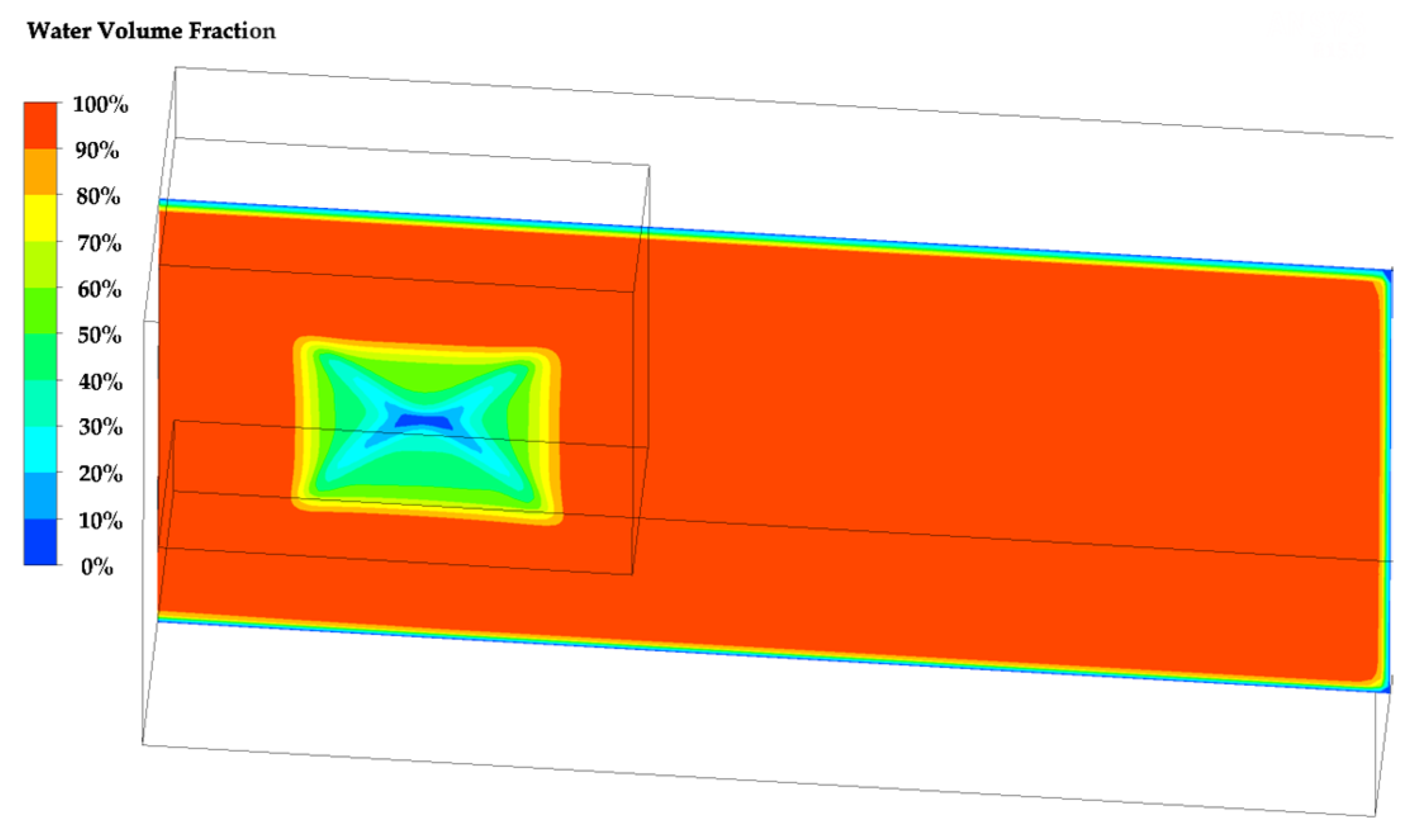
3.2. Continuous Jet Calculation of a Two-Dimensional Water Jet
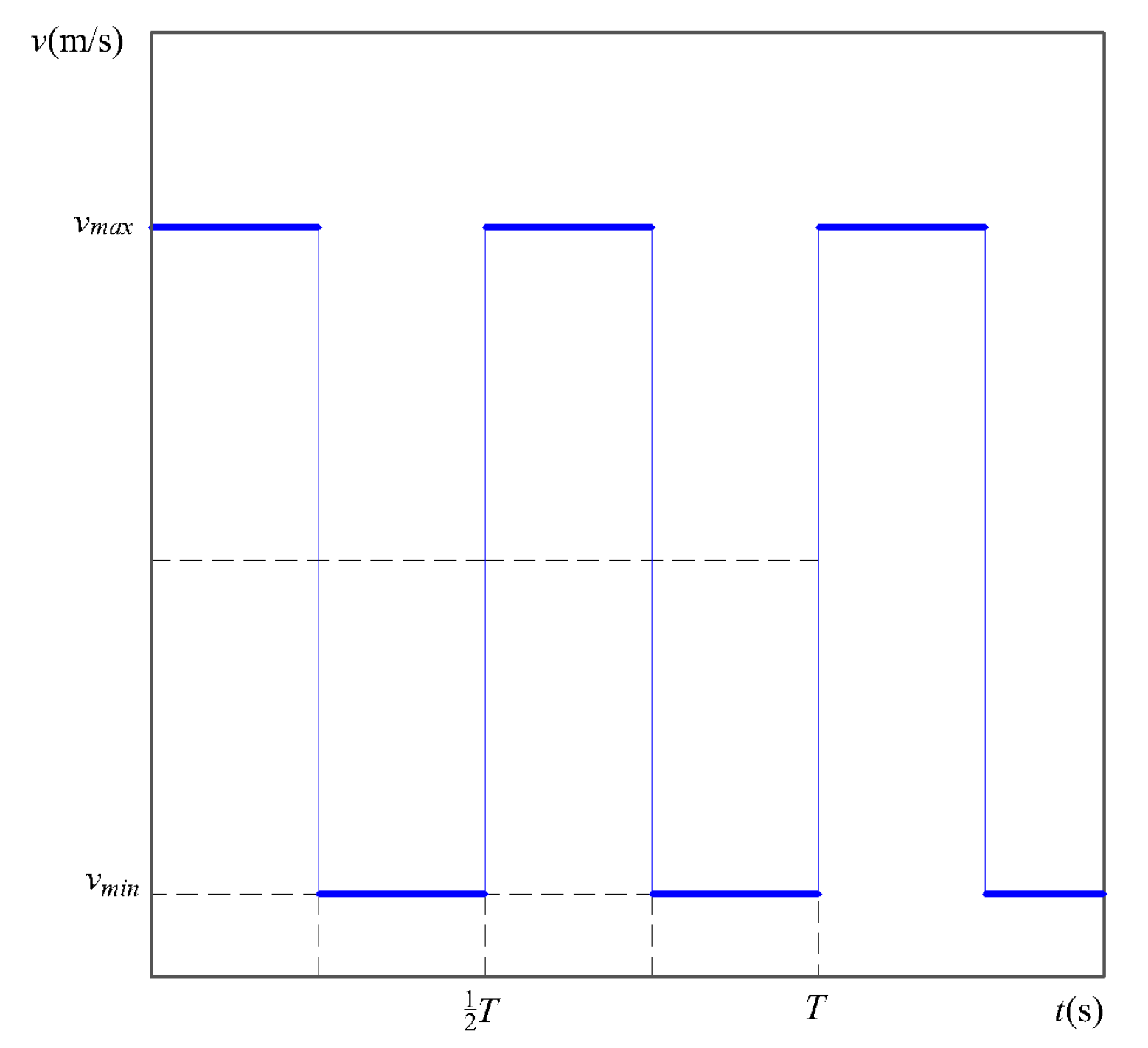
3.3. Pulsed Jet Calculation of a Two-Dimensional Water Jet
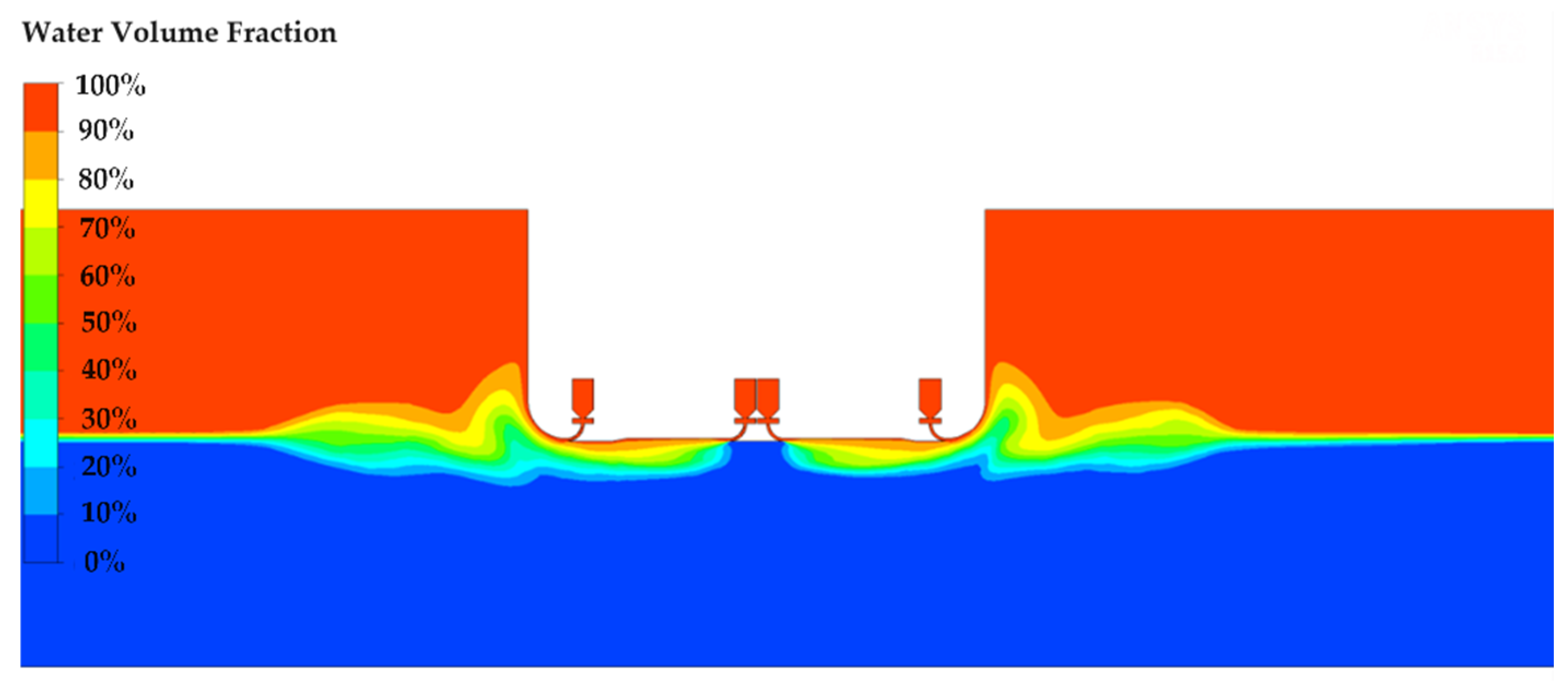
3.4. Calculation and Analysis of a Three-Dimensional Water Jet
4. Experiment
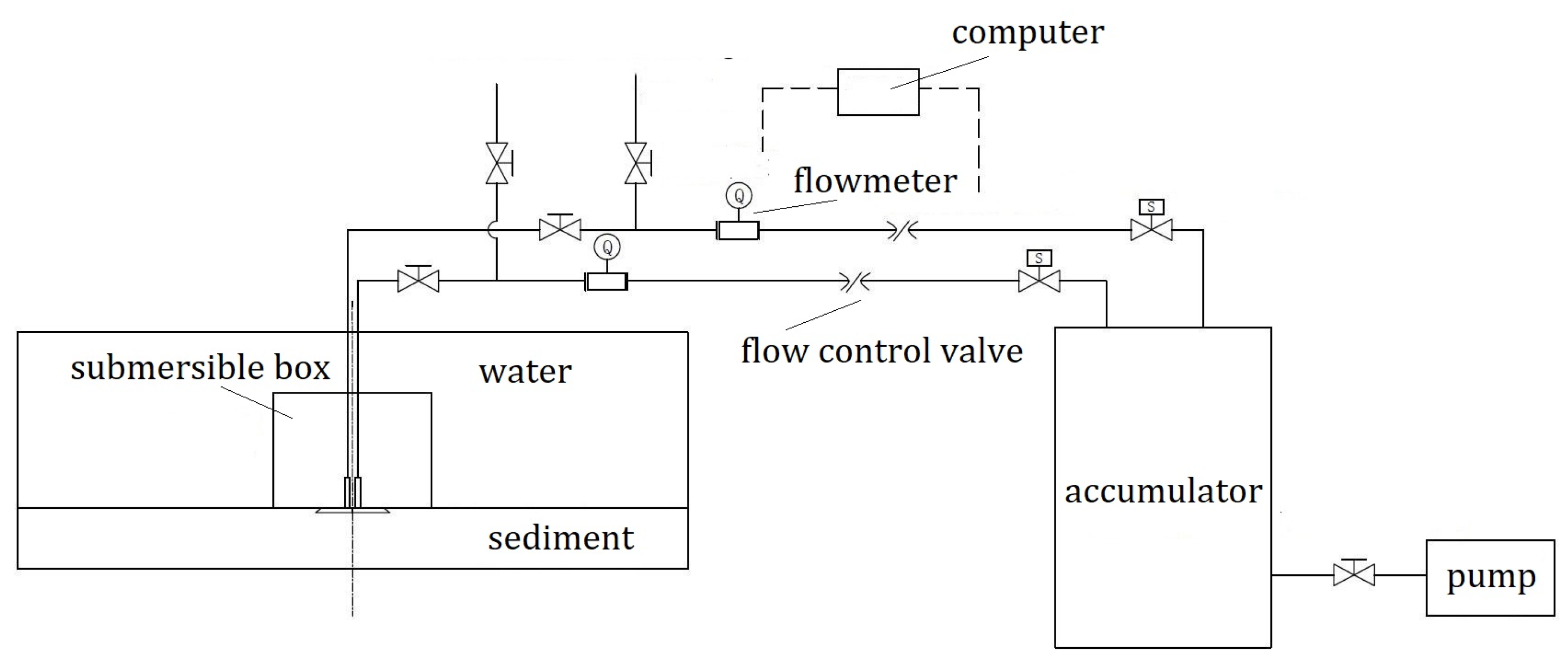
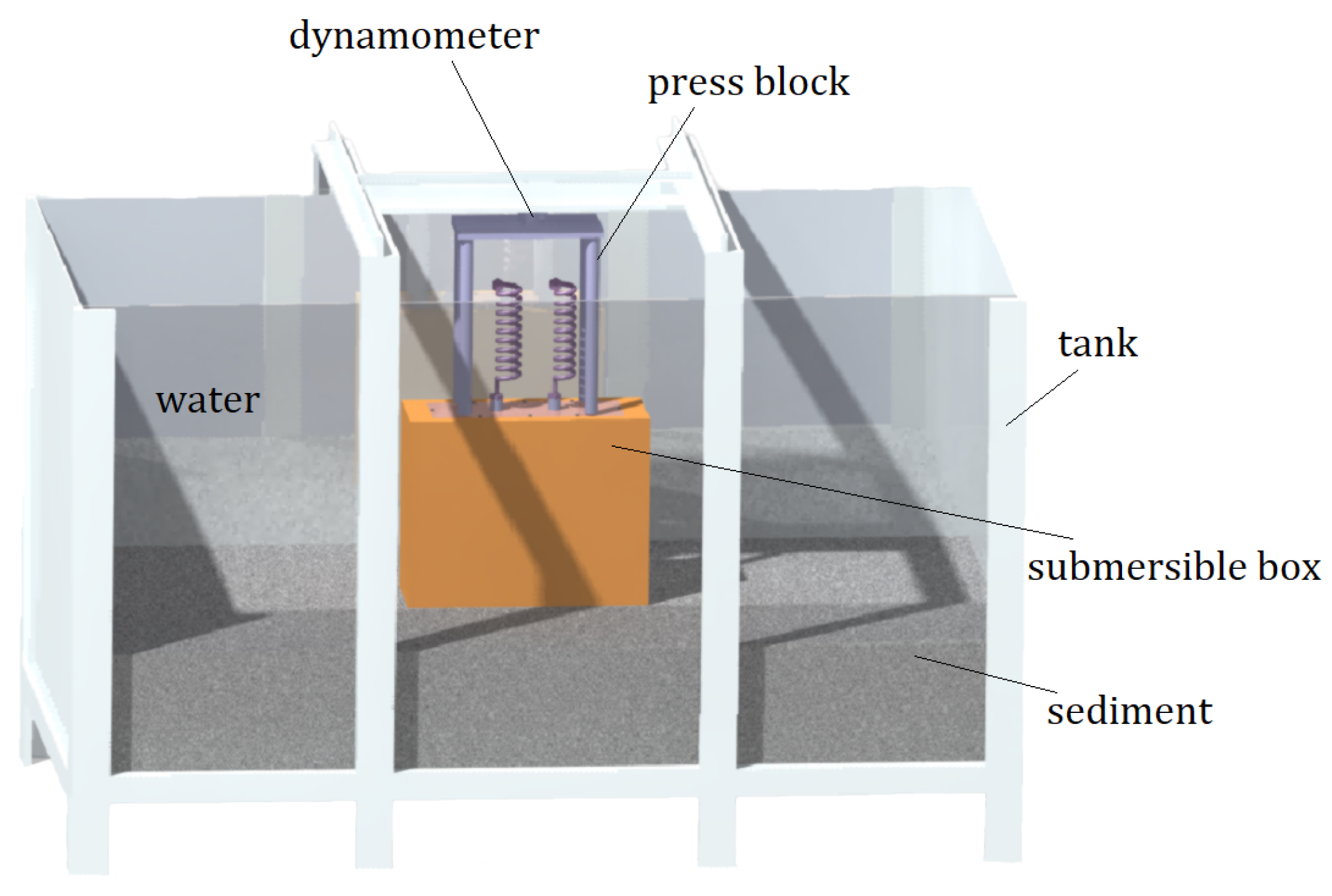
4.1. Experiment Design and Test Preparation
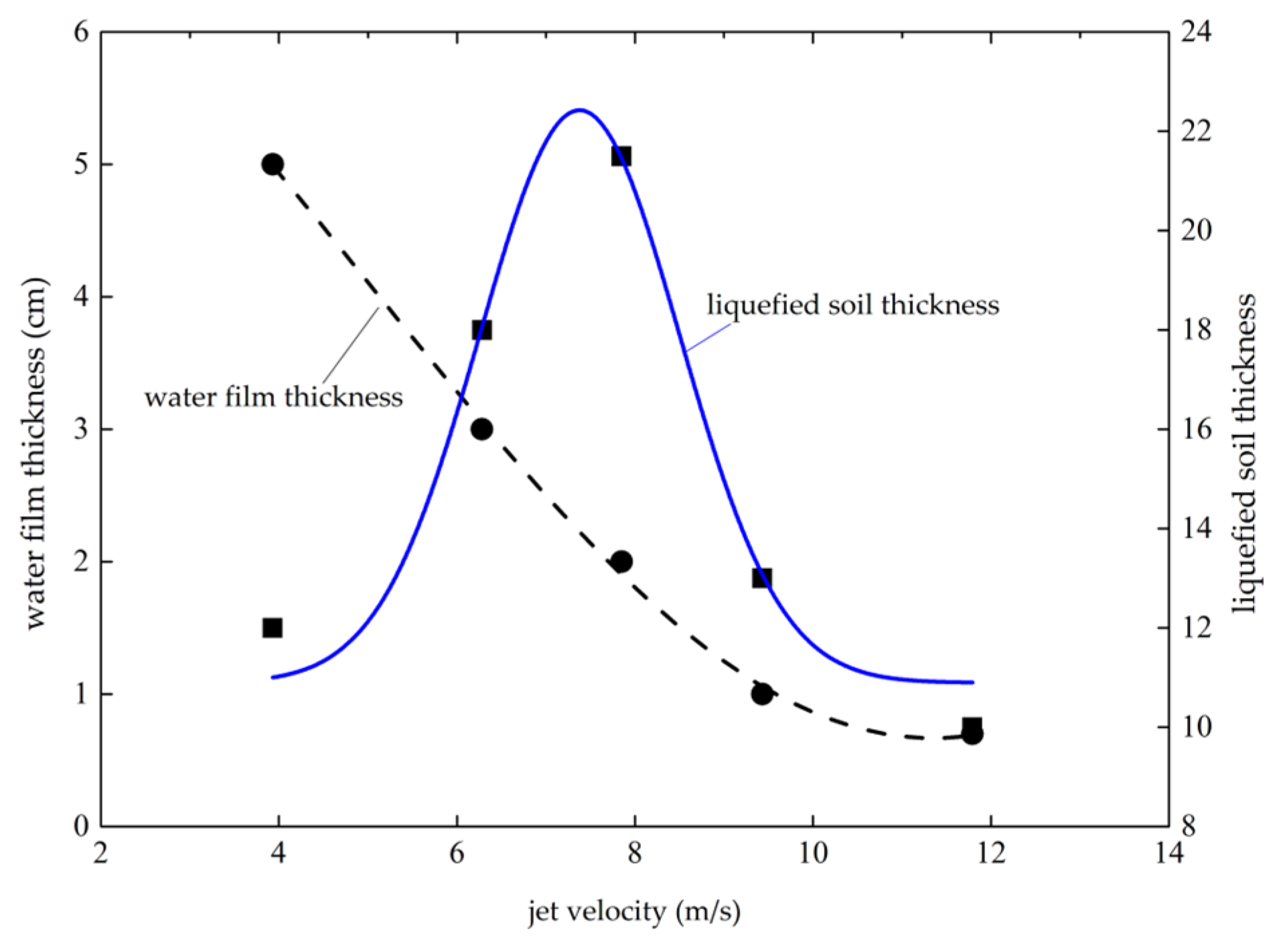
4.2. Experimental Results
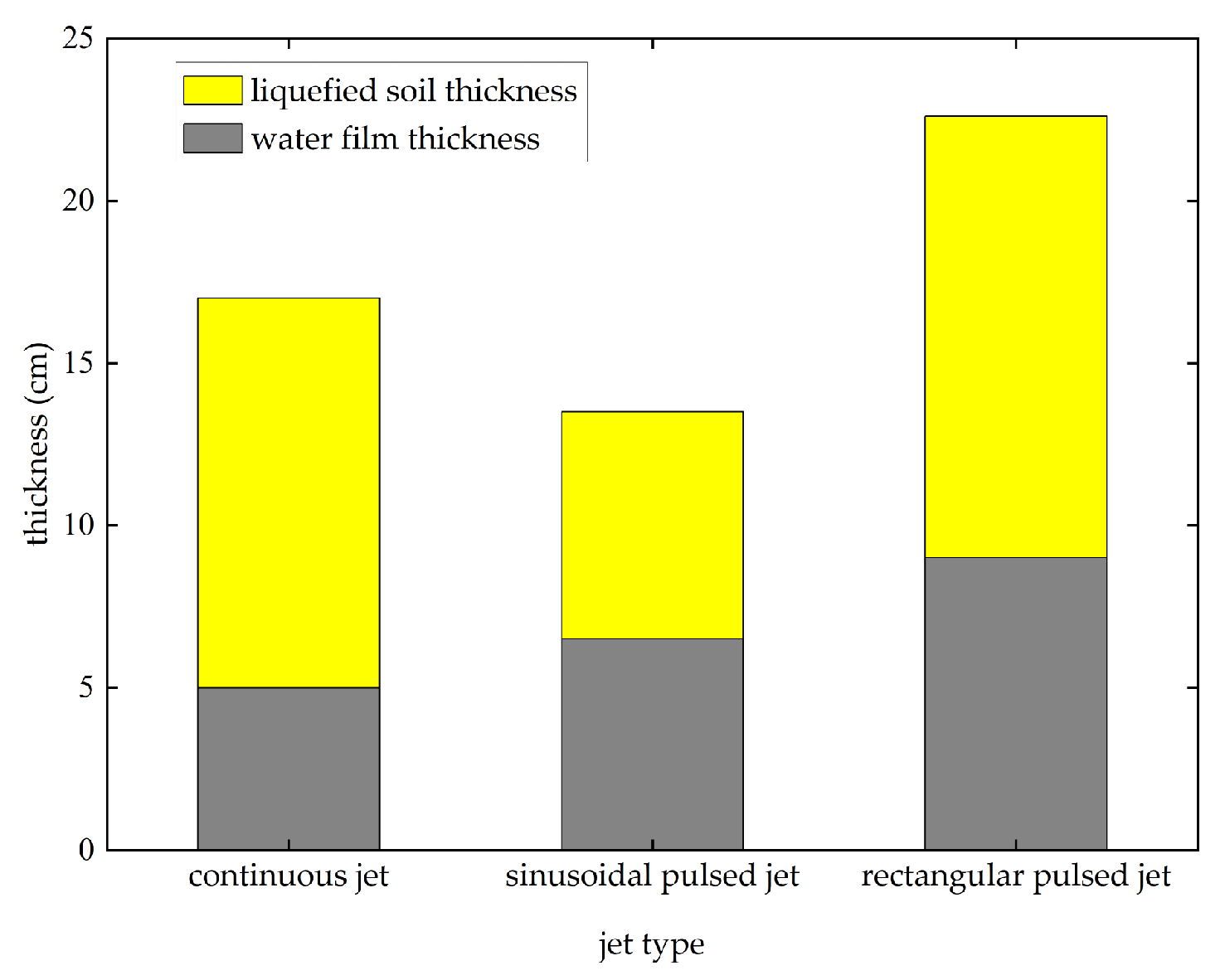
5. Result and Discussion
- (1)
- The water film thickness was 5 cm, and the liquefied soil thickness was 12 cm, which was based on the continuous jet.
- (2)
- The water film thickness was 6.5 cm, and the liquefied soil thickness was 7 cm, which was based on the sinusoidal pulsed jet.
- (3)
- The water film thickness was 9 cm, and the liquefied soil thickness was 13.6 cm, which was based on the rectangular pulsed jet.
6. Conclusions
- (1)
- The analysis method and experimental scheme for eliminating the bottom-sitting adsorption effect of under-sea equipment were established.
- (2)
- The calculation shows that the pulsed jet had a stronger ability to liquefy soil to eliminate the adsorption effect than the continuous jet. And a rectangular pulsed jet may be the best way.
- (3)
- By carrying out the water jet experiment of the bottom sitting adsorption effect of the submersible box, it was verified that the horizontal line jet could restore the buoyancy of the submersible box. And the jet velocity and weight–floating ratio were key control parameters. This physical phenomenon could further guide future research work on the self-rescue of under-sea equipment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Y.; Shen, Y.; Xie, J.; Cui, W. Landing research on deep-sea human occupied vehicle. J. Ship Mech. 2008, 12, 642–648. [Google Scholar]
- Momber, A.W. An SEM-study of high-speed hydrodynamic erosion of cementitious composites. Compos. Part B-Eng. 2003, 34, 135–142. [Google Scholar] [CrossRef]
- Yahiro, T.; Yoshida, H. On the characteristics of high speed water jet in the liquid and its utilization on induction grouting method. In Proceedings of the Second International Symposium on Jet Cutting Technology, Cambridge, UK, 2–4 April 1974; pp. G4/41–G4/63. [Google Scholar]
- Zhang, F.; Li, J.; Deng, Y.; Xu, C. Numerical investigation of mixing process of high-pressure jet-cutting clay by water-air coaxial nozzle considering soil rheological properties. Comput. Geotech. 2023, 165, 105878. [Google Scholar] [CrossRef]
- Shen, Z. Water Jet Theory and Technology; China University of Petroleum Press: Dongying, China, 1988. [Google Scholar]
- Bienen, B.; Gaudin, C.; Cassidy, M. The influence of pull-out load on the efficiency of jetting during spudcan extraction. Appl. Ocean. Res. 2009, 31, 202–211. [Google Scholar] [CrossRef]
- Karamigolbaghi, M.; Ghaneeizad, S.; Atkinson, J.; Bennett, S.; Wells, R. Critical assessment of jet erosion test methodologies for cohesive soil and sediment. Geomorphology 2017, 295, 529–536. [Google Scholar] [CrossRef]
- Passini, L.; Schnaid, F.; Rocha, M.; Moller, S. Mechanism of model pile installation by water jet fluidization in sand. Ocean. Eng. 2018, 170, 160–170. [Google Scholar] [CrossRef]
- Mazurek, K.; Rajaratnam, N.; Sego, D. Scour of cohesive soil by submerged circular turbulent impinging jets. J. Hydraul. Eng. 2001, 127, 598–606. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Mazurek, K. An experimental study of sand deposition from sediment laden water jets. J. Hydraul. Res. 2006, 44, 560–566. [Google Scholar] [CrossRef]
- Clark, L.; Wynn, T. Methods for determining streambank critical shear stress and soil erodibility: Implications for erosion rate predictions. Am. Soc. Agric. Biol. Eng. 2007, 50, 95–106. [Google Scholar]
- Raie, M.; Tassoulas, J. Installation of Torpedo Anchors: Numerical Modeling. J. Geotech. Geoenviron. Eng. 2009, 135, 1805–1813. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Zhang, Z. Measures for improving the leg-pull-out efficiency of offshore jack-up drilling platforms in West Africa. China Offshore Oil Gas 2016, 28, 132–137. [Google Scholar]
- Wang, T.; Song, B. Study on jet excavation mechanism in cohesive soil. Chin. J. Hydrodyn. 2018, 33, 337–343. [Google Scholar]
- Wang, T.; Song, B. Study on deepwater conductor jet excavation mechanism in cohesive soil. Appl. Ocean. Res. 2019, 82, 225–235. [Google Scholar] [CrossRef]
- Chen, Q.; Tan, B. Study on problems in pulling up legs of offshore jack-up drilling platform-shengli NO.6. Ocean. Eng. 1993, 11, 84–92. [Google Scholar]
- Chee, M.W.L.; Ghasemi, G.; Rashid, M.A.; Fernandes, R.R.; Wilson, D.I. Cleaning of thick viscoplastic soil layer by impinging water jets. J. Food Eng. 2023, 340, 111290. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, G.; Chen, C. The rate characteristics of the wave-induced liquefaction process of the silty soil in the seabed. Period. Ocean. Univ. China 2018, 48, 115–122. [Google Scholar]
- Ibrahim, A.; Meguid, M. Continuum-Based Approach to Model Particulate Soil-Water Interaction: Model Validation and Insight into Internal Erosion. Processes 2021, 9, 785. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, Q.; Liu, H.; Yang, Q.; Zhang, H. Experimental study umbrella suction anchor in seabed soil bearing characteristics of wave-induced liquefaction. Period. Ocean. Univ. China 2018, 48, 131–136. [Google Scholar]
- Zen, K.; Yamazaki, H. Mechanism of wave-induced liquefaction and densification in seabed. Soils Found. 1990, 30, 90–104. [Google Scholar] [CrossRef]
- Zen, K.; Yamazaki, H. Field observation and analysis of wave-induced liquefaction in seabed. Soils Found. 1991, 31, 161–179. [Google Scholar] [CrossRef]
- Sassa, S.; Yakayama, T.; Mizutani, M.; Tsujio, D. Field observations of the build-up and dissipation of residual pore pressures in seabed sands under the passage of storm waves. J. Geotech. Geoenviron. Eng. 2006, 39, 410–414. [Google Scholar]
- Chang, W.; Rathje, E.; Stokoe, K.; Hazirbaba, K. In situ pore-pressure generation behavior of liquefiable sand. J. Geotech. Geoenviron. Eng. 2007, 133, 921–931. [Google Scholar] [CrossRef]
- Besses, B.; Magnin, A.; Jay, P. Viscoplastic flow around a cylinder in an infinite medium. J. Non-Newton. Fluid Mech. 2003, 115, 27–49. [Google Scholar] [CrossRef]
- Zhu, H.; Randolph, M.F. Numerical analysis of a cylinder moving through rate-dependent undrained soil. Ocean Eng. 2011, 38, 943–953. [Google Scholar] [CrossRef]









| (Pa·s) | n | (Pa) | (s−1) |
|---|---|---|---|
| 612 | 0.1 | 1300 | 0.001 |
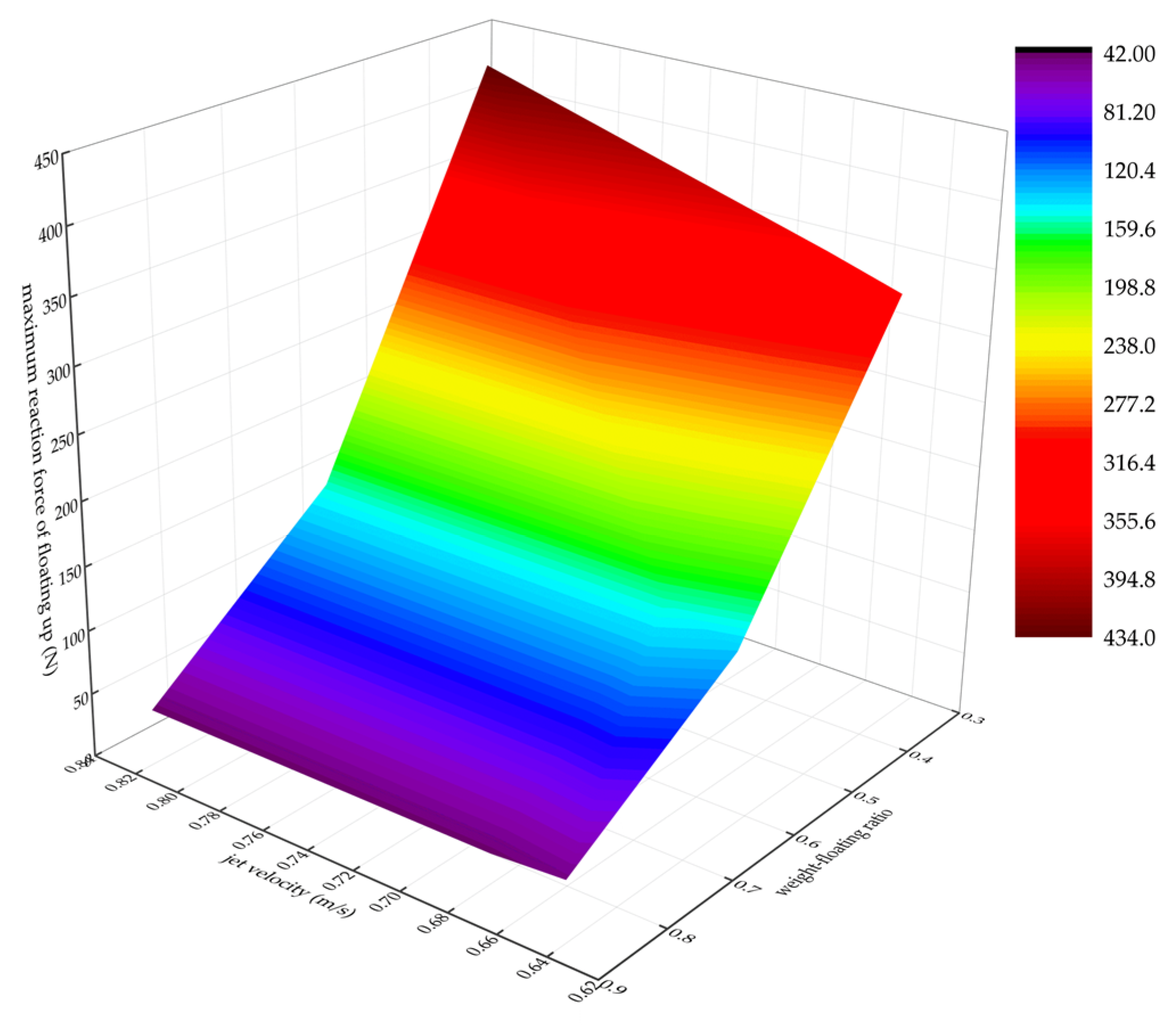
| Weight–Floating Ratio | Jet Velocity (m/s) | Average Maximum Reaction Force (N) | Standard Deviation |
|---|---|---|---|
| 0.375 | 0.65 | 355.07 | ±23.94 |
| 0.375 | 0.67 | 318.02 | ±25.44 |
| 0.375 | 0.82 | 433.35 | ±23.87 |
| 0.625 | 0.65 | 135.73 | ±7.73 |
| 0.625 | 0.67 | 154.75 | ±10.59 |
| 0.625 | 0.82 | 153.53 | ±8.89 |
| 0.875 | 0.65 | 48.02 | ±1.61 |
| 0.875 | 0.67 | 43.84 | ±2.31 |
| 0.875 | 0.82 | 43.27 | ±1.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Ye, C.; Gong, P.; Xu, F.; Zhang, D.; Cong, S.; Liu, S. Simulation and Experiment on Elimination for the Bottom-Sitting Adsorption Effect of a Submersible Based on a Submerged Jet. Processes 2023, 11, 3452. https://doi.org/10.3390/pr11123452
Zhang H, Ye C, Gong P, Xu F, Zhang D, Cong S, Liu S. Simulation and Experiment on Elimination for the Bottom-Sitting Adsorption Effect of a Submersible Based on a Submerged Jet. Processes. 2023; 11(12):3452. https://doi.org/10.3390/pr11123452
Chicago/Turabian StyleZhang, Hao, Cong Ye, Peng Gong, Fengwei Xu, Dongjing Zhang, Shuguang Cong, and Shuai Liu. 2023. "Simulation and Experiment on Elimination for the Bottom-Sitting Adsorption Effect of a Submersible Based on a Submerged Jet" Processes 11, no. 12: 3452. https://doi.org/10.3390/pr11123452
APA StyleZhang, H., Ye, C., Gong, P., Xu, F., Zhang, D., Cong, S., & Liu, S. (2023). Simulation and Experiment on Elimination for the Bottom-Sitting Adsorption Effect of a Submersible Based on a Submerged Jet. Processes, 11(12), 3452. https://doi.org/10.3390/pr11123452








