Research on Assembly Sequence Optimization Classification Method of Remanufacturing Parts Based on Different Precision Levels
Abstract
:1. Introduction
2. Optimization Model of Remanufactured Part Grading Selection with Different Precision Levels
2.1. Remanufactured Part Grading Matching Constraints
2.2. Comprehensive Model of Remanufactured Part Classification and Selection
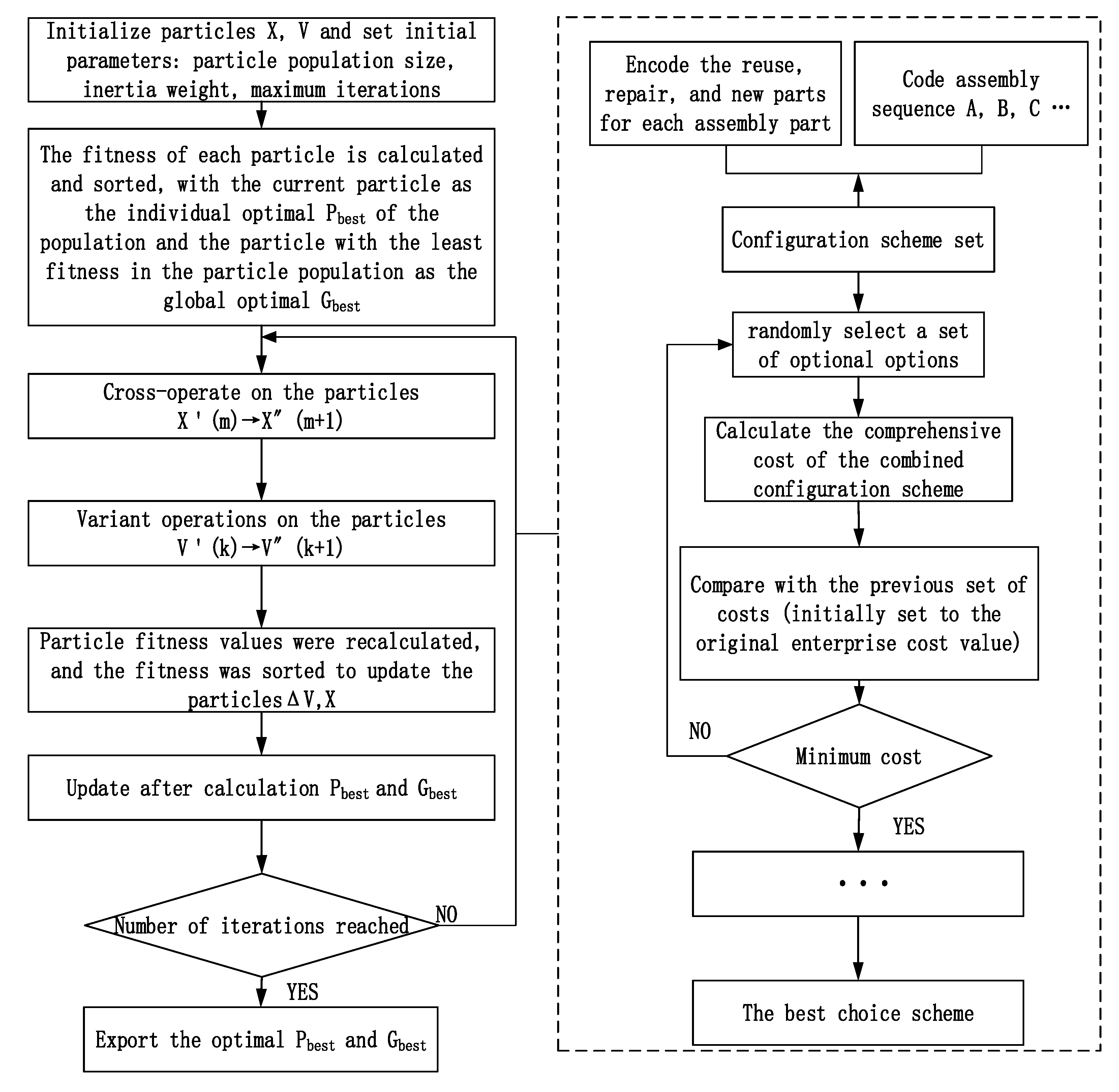
3. Model Solution
4. Example Verification
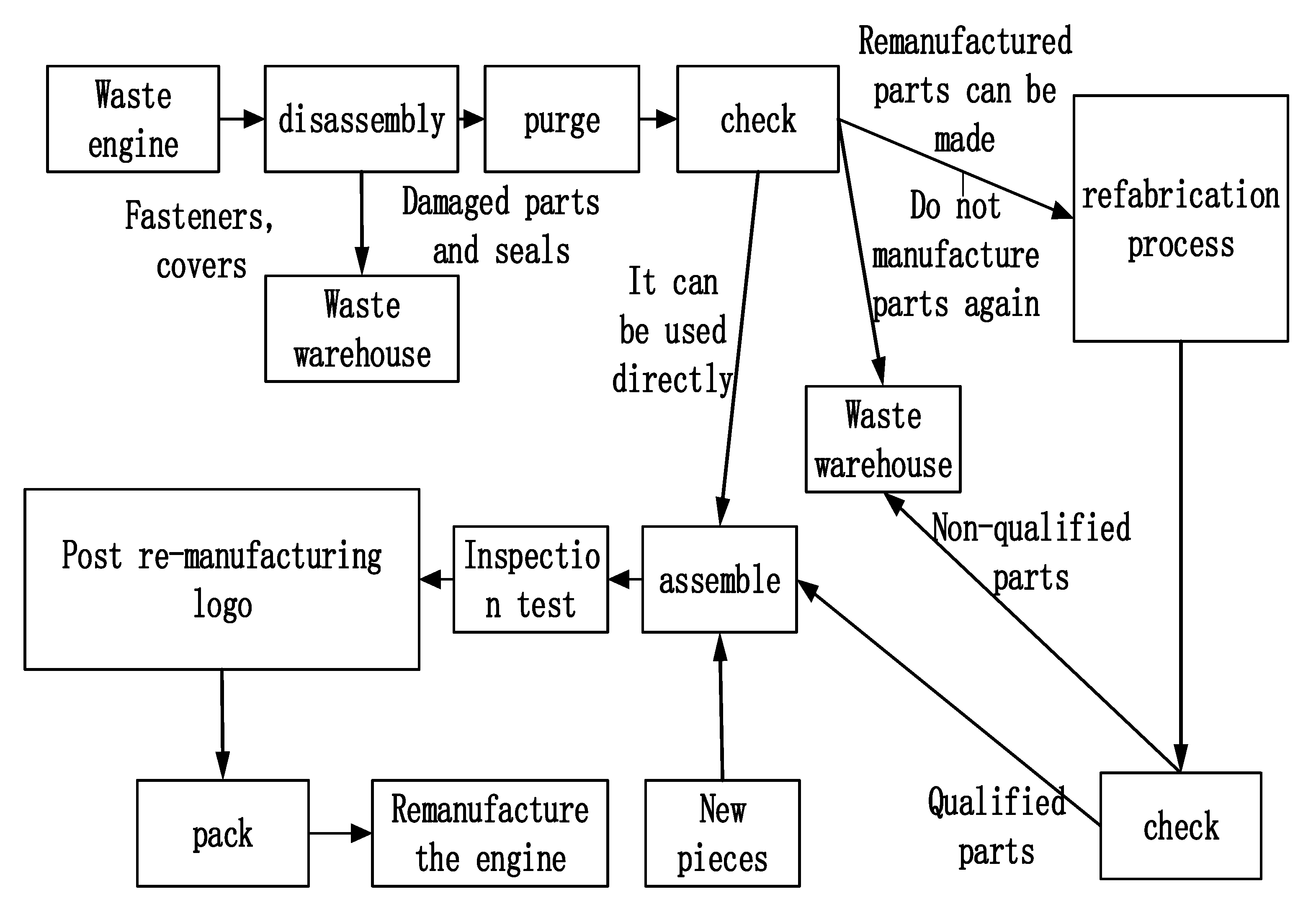
4.1. Method Implementation
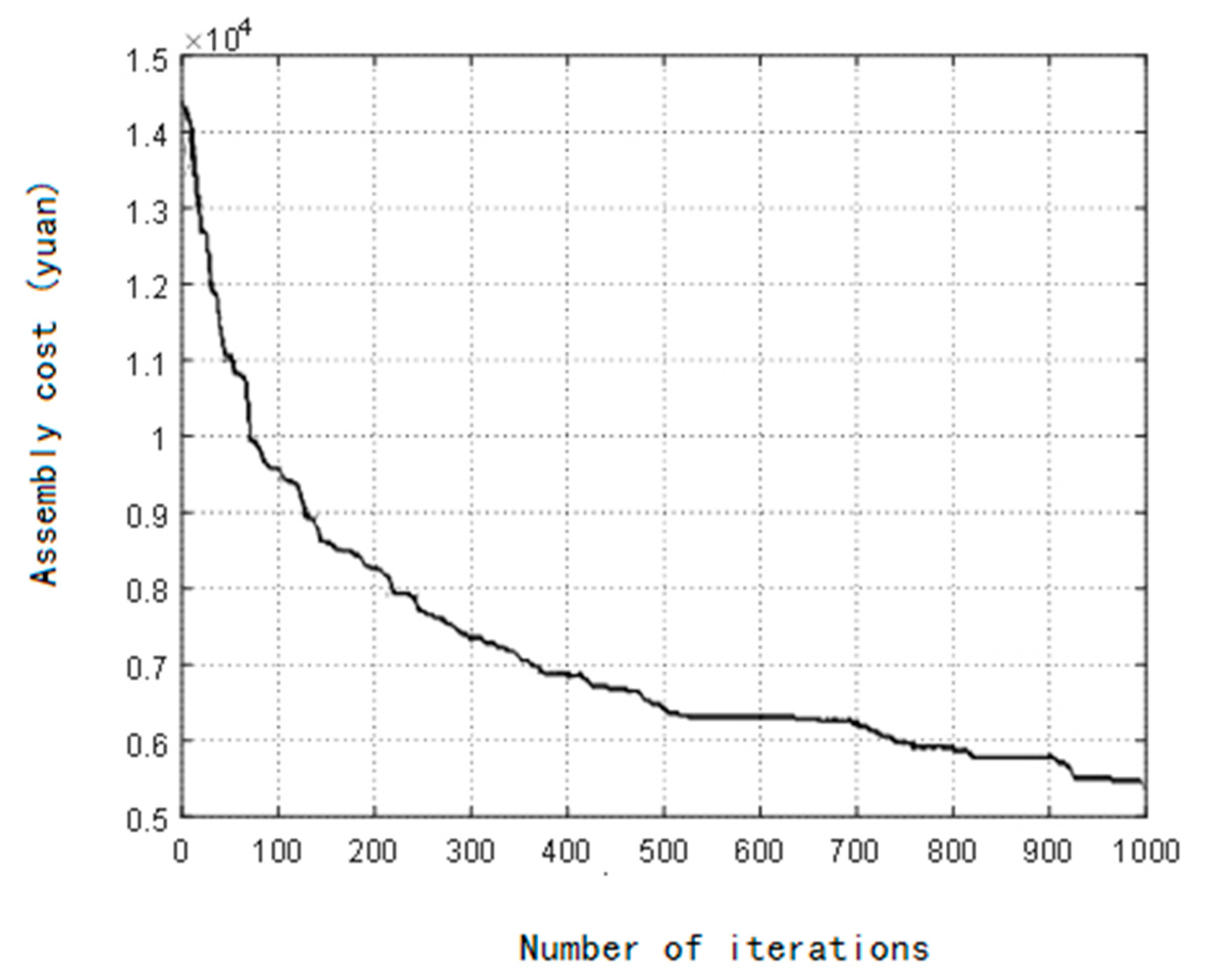
4.2. Results Comparison
4.3. Comparison with the Previous Literature
5. Conclusions
- Remanufactured assembly control is difficult to standardize. Under the condition that the assembly accuracy of remanufactured parts not be lower than that of new products, the classification accuracy standard of remanufactured parts was calculated through mathematical formulas, the optimization model of classification selection under different accuracy conditions was established, and a combinatorial optimization algorithm to solve the model was proposed;
- This article took the remanufacturing assembly of an engine crank-connecting rod mechanism as an example. The data comparison showed that the optimal assembly sequence obtained by the hierarchical matching model proposed in this study can effectively ensure different remanufacturing assembly accuracy requirements and improve remanufacturing. The success rate guarantees an improvement in assembly quality and a reduction in after-sale claim costs. The best assembly sequence provides the best assembly quality and the lowest claim cost. The concept of optimality refers to the best assembly time and quality of remanufactured parts with different precisions. The success rate of assembly and the reduction in after-sale claim costs provided new theories and methods for remanufacturing enterprises, which should adopt hierarchical assembly.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; Guo, Y.; Zhang, Z.; Xia, X. Extensive Concept, State-of-the Art Developing Trends of Remanufacturing Service. J. Mech. Eng. 2021, 57, 138–153. [Google Scholar]
- Yin, L.; Yang, F. Study on selective assembly of remanufacturing parts to be assembled based on NSGA-Ⅲ. J. Mach. Des. 2022, 39, 53–60. [Google Scholar]
- Yang, W.; Meng, C.; Cao, W.; Xie, K.; Yu, P. Assembly Sequence Optimization based on Improved Genetic Algorithm. J. Mech. Transm. 2016, 40, 67–70. [Google Scholar]
- Su, B.; Huang, X.; Ren, Y.; Wang, F.; Xiao, H.; Zheng, B. Research on Selective Assembly Method Optimization for Construction Machinery Remanufacturing Based on Ant Colony Algorithm. J. Mech. Eng. 2017, 53, 60–68. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, H.; Jiang, Z. An approach for blank dimension design considering energy consumption. Int. J. Adv. Manuf. Technol. 2016, 87, 1229–1235. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, Z.; Zhang, H.; Cheng, H. Optimization Study of Remanufacturing Reconditioning Scheme for Used Parts Based on Failure Features—Research on optimization of waste parts based on failure feature. Mach. Tool Hydraul. Press. 2016, 44, 168–172. [Google Scholar]
- Geda, M.W.; Kwong, C.K.; Jiang, H.M. Fastening method selection with simultaneous consideration of product assembly and disassembly from a remanufacturing perspective. Int. J. Adv. Manuf. Technol. 2019, 101, 1481–1493. [Google Scholar] [CrossRef]
- Xiao, Y.; Yan, W.; Wang, R. Research on Blank Optimization Design Based on Low-Carbon and Low-Cost Blank Process Route Optimization Mode. Sustainability 2021, 13, 1929. [Google Scholar] [CrossRef]
- Zhu, H.; Ding, Z.; Chen, B.; Jiang, Z. Cost Prediction of End-of-life Products Remanufacturing Based on Improved BP Neural Network. Mach. Tool Hydraul. 2020, 48, 34–38. [Google Scholar]
- Suszyński, M.; Peta, K. Assembly Sequence Planning Using Artificial Neural Networks for Mechanical Parts Based on Selected Criteria. Appl. Sci. 2021, 11, 10414. [Google Scholar] [CrossRef]
- Suszyński, M.; Peta, K.; Černohlávek, V.; Svoboda, M. Mechanical Assembly Sequence Determination Using Artificial Neural Networks Based on Selected DFA Rating Factors. Symmetry 2022, 14, 1013. [Google Scholar] [CrossRef]
- Liu, M.; Liu, C. The invention relates to an assembly size classification method for remanufactured parts. U.S. Patent CN103413024B, 8 February 2017. [Google Scholar]
- Oh, Y.; Behdad, S. Simultaneous reassembly and procurement planning in assemble-to-order remanufacturing systems. Int. J. Prod. Econ. 2017, 184, 168–178. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Jiang, X.; Liu, W.; Shi, M.; Yang, S.; Yang, G. Precision prediction and error propagation model of remanufacturing machine tool assembly process. Comput. Integr. Manuf. Syst. 2021, 27, 1300–1308. [Google Scholar]
- Yenipazarli, A. Managing new and remanufactured products to mitigate environmental damage under emissions regulation. Eur. J. Oper. Res. 2016, 249, 117–130. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Pulkkinen, J.; Gabbouj, M. Particle Swarm Optimization. Expert Syst. Appl. 2014, 38, 2212–2223. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Khan, I.A.; Alkhammash, H.I.; Sajjad, I.A.; Hussain, B. An Improved Particle Swarm Optimization with Chaotic Inertia Weight and Acceleration Coefficients for Optimal Extraction of PV Models Parameters. Energies 2021, 14, 2980. [Google Scholar] [CrossRef]
- Xian, X.; Zhou, Z.; Huang, G.; Nong, J.; Liu, B.; Xie, L. Optimal Sensor Placement for Estimation of Center of Plantar Pressure Based on the Improved Genetic Algorithms. IEEE Sens. J. 2021, 21, 28077–28086. [Google Scholar] [CrossRef]
- Kang, M.; Li, Y.; Jiao, L.; Wang, M. Differential Analysis of ARX Block Ciphers Based on an Improved Genetic Algorithm. Chin. J. Electron. 2022, 32, 225–236. [Google Scholar]
- Vanderstar, G.; Musilek, P. Optimal Design of Distribution Overhead Powerlines using Genetic Algorithms. IEEE Trans. Power Deliv. 2021, 37, 1803–1812. [Google Scholar] [CrossRef]
- Fernandes, J.; Arsenio, A.J.; Arnaud, J. Optimization of a Horizontal Axis HTS ZFC Levitation Bearing Using Genetic Decision Algorithms Over Finite Element Results. IEEE Trans. Appl. Supercond. 2020, 30, 3601308. [Google Scholar] [CrossRef]
- Chen, J. The Research on Critical Assembly Process Quality Control Method and Supporting System for Remanufacturing Engine. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2016. [Google Scholar]
- Xiao, Y.M.; Zhang, H. Multiobjective optimization of machining center process route: Tradeoffs between energy and cost. J. Clean. Prod. 2021, 28, 21–26. [Google Scholar] [CrossRef]
- Zhang, Y. Method and Key Technology of Assembly Quality Control for Remanufactured Engine. Ph.D. Thesis, Hefei University of Technology, Hefei, China, 2017. [Google Scholar]
- Zhang, J.; Li, Y. Motor Rolling Bearing Compound Fault Diagnosis Based on Particle Swarm Optimization & Blind Source Separation. Mach. Tool Hydraul. 2019, 47, 167–172. [Google Scholar]
- Xiao, Y.; Wang, R.; Yan, W.; Ma, L. Optimum Design of Blank Dimensions Guided by a Business Compass in the Machining Process. Processes 2021, 9, 1286. [Google Scholar] [CrossRef]
- Xing, Z.; Jiang, A.L.; Xie, J.J.; Feng, Y.C. Benefit analysis and Surface Engineering Application of Automobile Engine Remanufacturing. China Surf. Eng. 2004, 9, 1–5. [Google Scholar]
- Chang, X.; Zhong, Y.; Wang, Y.; Chen, Z. Research of low-carbon policy to promote automotive parts remanufacturing in China:A case study of auto engine remanufacturing. Syst. Eng. Theory Pract. 2013, 33, 2811–2821. [Google Scholar]
- Zhang, Y.F.; Li, M.; Liu, S.C. IoT-based production process optimization method for automobile engine remanufacturing. In Proceedings of the ICRA 2014—IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–5 June 2014. [Google Scholar]
- Shi, J.; Hu, J.; Jin, Z.; Ma, Y.; Ma, M.; Wang, H.; Ma, Q. Recycling Mode and Remanufacturing Cost Analysis of Used Automobile Engine Based on System Dynamics. J. Phys. Conf. Ser. 2021, 1986, 012041. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, S.; Liu, Y.; Yang, H.; Li, M.; Huisingh, D.; Wang, L. The ‘Internet of Things’ enabled real-time scheduling for remanufacturing of automobile engines. J. Clean. Prod. 2018, 185, 562–575. [Google Scholar] [CrossRef]
- Yu, X.; Jiang, N.; Wang, L.P. Characteristics and Approaches to the Information System of Automobile Engine Remanufacturing. J. Cent. South Univ. For. Technol. 2009, 29, 176–179. [Google Scholar]
- Ju, J.; Li, W.; Wang, Y.; Fan, M.; Liu, Y. Optimization Design of Vibration Control Parameters of Flexible Manipulators Based on Multi-Population Genetic Algorithm. Mach. Tool Hydraul. 2016, 44, 94–97. [Google Scholar]
- Liu, L. Research on assembling method of remanufacturing engine. Ph.D. Thesis, Tianjin University of Science and Technology, Tianjin, China, 2017. [Google Scholar]
- Wen, H.; Meng, X.; Zeng, A.; Guo, X.; Xu, X. Fatigue life prediction of neural network remanufactured based on second-order particle swarm optimization. Sci. Technol. Eng. 2019, 19, 21–26. [Google Scholar]
- Yuan, S.; Li, T.; Wang, B.; Liu, Q. Co-evolutionary iterated greedy algorithm for the two-stage flow shop group scheduling problem. Syst. Eng. Theory Pract. 2020, 40, 2707–2716. [Google Scholar]

| Classification | Variance Wide Scaling Coefficient | Tolerance Width Casting Coefficient |
|---|---|---|
| 2 | 1.8 | 1.3 |
| 3 | 2.1 | 1.4 |
| 4 | 2.4 | 1.5 |
| Cylinder Code | 1 Neck | 2 Neck | 3 Neck | 4 Neck | 5 Neck |
|---|---|---|---|---|---|
| 1-01 | 48.013 | 48.005 | 48.009 | 48.012 | 48.006 |
| 1-02 | 48.014 | 48.012 | 48.012 | 48.013 | 48.013 |
| 1-03 | 48.019 | 48.014 | 48.013 | 48.012 | 48.002 |
| 1-04 | 48.012 | 48.012 | 48.005 | 48.013 | 48.005 |
| 1-05 | 48.007 | 48.011 | 48.004 | 48.002 | 48.013 |
| Crankshaft Code | 1 Neck | 2 Neck | 3 Neck | 4 Neck | 5 Neck |
|---|---|---|---|---|---|
| 2-01 | 43.987 | 43.992 | 43.995 | 43.986 | 43.992 |
| 2-02 | 43.982 | 43.904 | 43.994 | 43.987 | 43.996 |
| 2-03 | 43.986 | 43.981 | 43.984 | 43.985 | 43.997 |
| 2-04 | 43.988 | 43.992 | 43.988 | 43.986 | 43.988 |
| 2-05 | 43.996 | 43.996 | 43.992 | 43.989 | 43.986 |
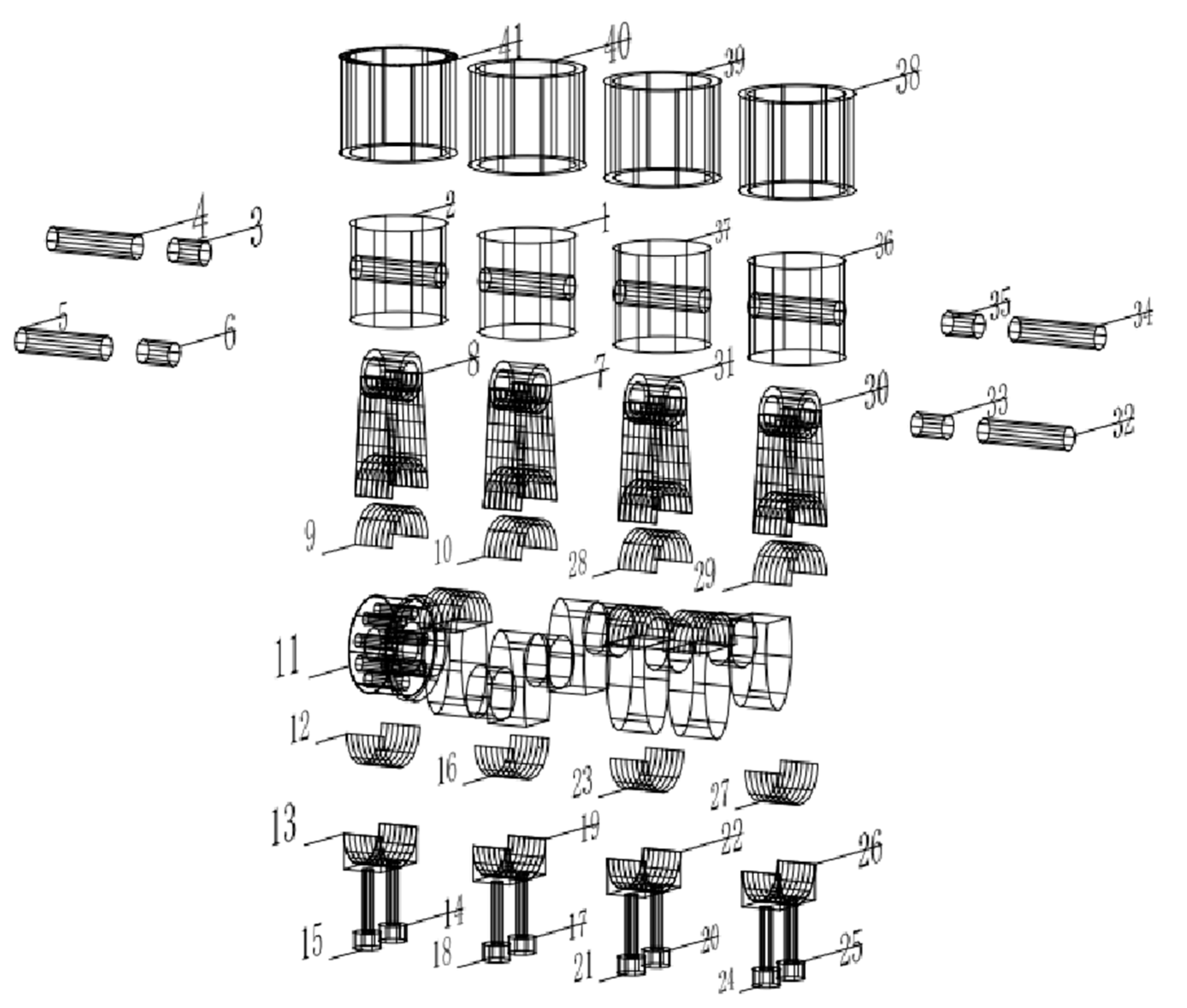
| Serial Number | Part Name | Installation Direction | Assembling Tool |
|---|---|---|---|
| 1,2,36,37 | plunger | -Z | handwork |
| 3,6,33,35 | bush | +X −X | handwork |
| 4,5,32,34 | gudgeon pin | +X −X | hacksaw, chassis, heavy hammer |
| 7,8,30,31 | shank of connecting rod | −Z | handwork |
| 9,10,28,29 | upper half bearing | −Z | handwork |
| 11 | bent axle | — | — |
| 12,16,23,27 | lower half bearing | +Z | handwork |
| 13,19,22,26 | connecting rod cap | +Z | handwork |
| 14,15,17,18,20,21,24,15 | screw bolt | +Z | screwdriver, wrench |
| 38,39,40,41 | Air cylinder | −Z | workbench, pistol, pliers |
| Rank | Crank Linkage Assembly Sequence |
|---|---|
| 1 | 11→9→8→3→2→4→10→7→6→1→5→28→31→35→37→34→29→30→33→36→32→12→16→23→27→13→14→15 19→17→18→22→20→21→26→24→25→38→39→40→41 |
| 2 | 11→10→7→6→1→5→28→31→35→37→34→9→8→3→2→4→29→30→33→36→32→16→19→17→18→23→22→20 21→12→13→14→15→27→26→24→25→38→39→40→41 |
| Project | January | February | March | April | May | June | July | August | September | October | November | December |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Success rate in 2019/% | 83.27 | 83.67 | 84.56 | 85.23 | 83.49 | 84.53 | 86.19 | 85.27 | 84.13 | 82.94 | 84.52 | 85.17 |
| Success rate in 2020/% | 89.52 | 90.34 | 90.73 | 88.78 | 90.36 | 89.95 | 88.57 | 92.31 | 90.47 | 90.28 | 90.32 | 90.46 |
| Compensation expenses in 2019 (10,000) | 84.21 | 83.46 | 84.53 | 78.46 | 78.42 | 80.31 | 9.85 | 98.34 | 97.18 | 88.43 | 89.56 | 84.59 |
| Compensation expenses in 2020 (10,000) | 62.34 | 48.57 | 46.82 | 47.32 | 59.15 | 52.34 | 58.29 | 48.73 | 58.49 | 46.54 | 59.48 | 48.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Zhou, J.; Xing, S.; Zhu, X. Research on Assembly Sequence Optimization Classification Method of Remanufacturing Parts Based on Different Precision Levels. Processes 2023, 11, 383. https://doi.org/10.3390/pr11020383
Xiao Y, Zhou J, Xing S, Zhu X. Research on Assembly Sequence Optimization Classification Method of Remanufacturing Parts Based on Different Precision Levels. Processes. 2023; 11(2):383. https://doi.org/10.3390/pr11020383
Chicago/Turabian StyleXiao, Yongmao, Jincheng Zhou, Shixiong Xing, and Xiaoyong Zhu. 2023. "Research on Assembly Sequence Optimization Classification Method of Remanufacturing Parts Based on Different Precision Levels" Processes 11, no. 2: 383. https://doi.org/10.3390/pr11020383
APA StyleXiao, Y., Zhou, J., Xing, S., & Zhu, X. (2023). Research on Assembly Sequence Optimization Classification Method of Remanufacturing Parts Based on Different Precision Levels. Processes, 11(2), 383. https://doi.org/10.3390/pr11020383






