Multi-Sensor Data Fusion for Real-Time Multi-Object Tracking
Abstract
:1. Introduction
- The sensor fusion framework has large flexibility regarding the types and number of sensors.
- The framework reacts robustly in case of individual sensor failures.
- The framework is real-time capable.
- The fusion framework is generic, and thus it can be also used for static sensor applications such as roadside units (RSU). In this case, the movement compensation module is removed (i.e., the velocity is set to zero).
2. Related Work
3. Sensor Fusion Framework
3.1. Kalman Filter
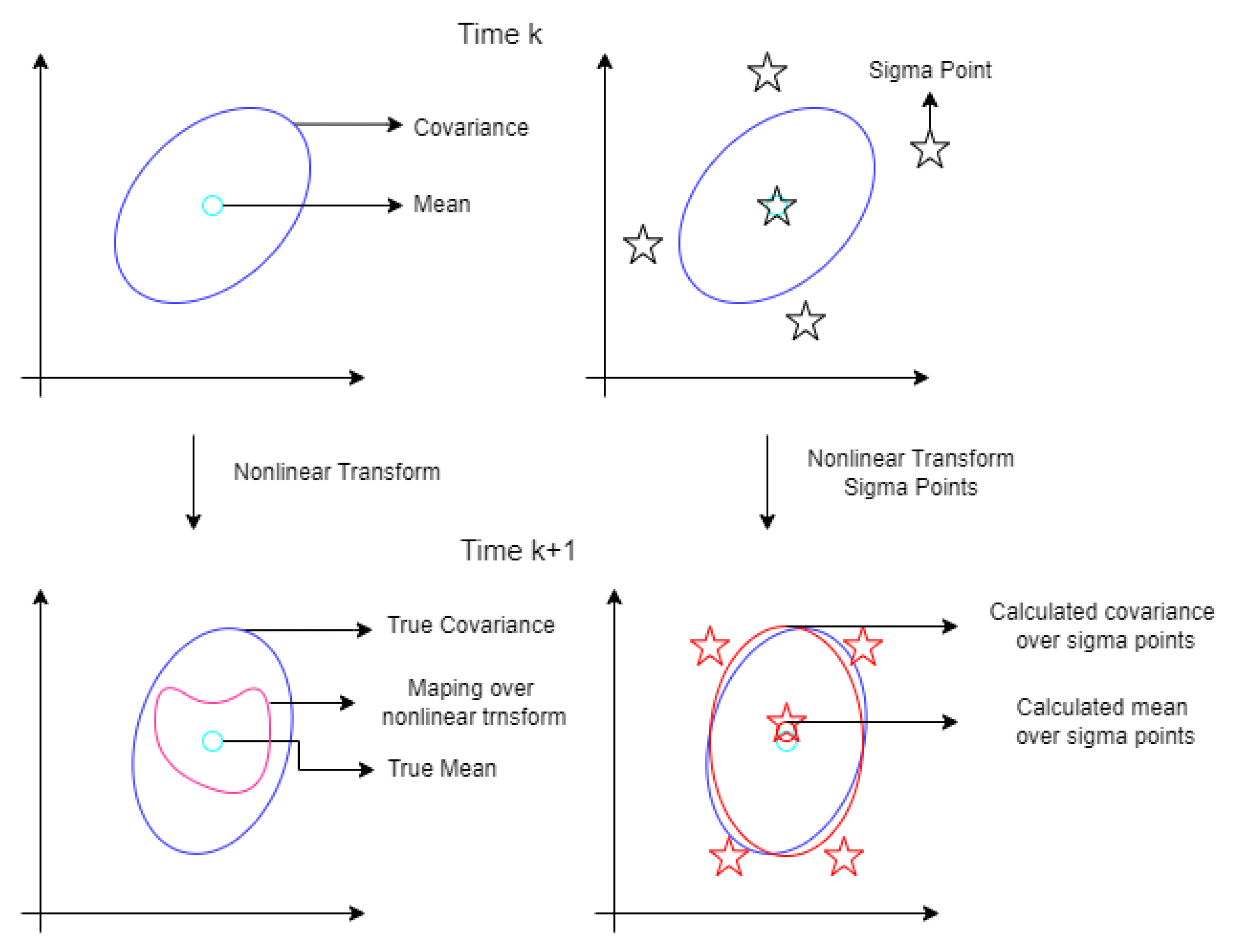
3.2. Unscented Kalman Filter (UKF)
3.3. Motion Model
3.4. Motion Compensation and Object Association
4. Sensor Perception Models
4.1. Camera
4.2. LiDAR
4.3. Radar
5. Simulation and Experiment Results
5.1. Simulation Results
5.2. Possible Inaccuracies of the Detection Algorithms
5.3. nuScenes Results
6. Sensor Fault Detection
7. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Galvao, L.G.; Abbod, M.; Kalganova, T.; Palade, V.; Huda, M.N. Pedestrian and Vehicle Detection in Autonomous Vehicle Perception Systems—A Review. Sensors 2021, 21, 7267. [Google Scholar] [CrossRef] [PubMed]
- Llinas, J.; Hall, D.L. An introduction to multisensor data fusion. Proc. IEEE 1997, 85, 6–23. [Google Scholar]
- Chen, X.; Ma, H.; Wan, J.; Li, B.; Xia, T. Multi-View 3D Object Detection Network for Autonomous Driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Kaempchen, N.; Buehler, M.; Dietmayer, K. Feature-level fusion for free-form object tracking using laserscanner and video. In Proceedings of the IEEE Intelligent Vehicles Symposium, Las Vegas, NV, USA, 6–8 June 2005. [Google Scholar]
- Floudas, N.; Polychronopoulos, A.; Aycard, O.; Burlet, J.; Ahrholdt, M. High Level Sensor Data Fusion Approaches For Object Recognition. In Proceedings of the IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 13–15 June 2007. [Google Scholar]
- Michaelm, A.; Nico, K. High-Level Sensor Data Fusion Architecture for Vehicle Surround Environment Perception. In Proceedings of the 8th International Workshop on Intelligent Transportation, Hamburg, Germany, 22–23 March 2011. [Google Scholar]
- Li, W.; Wang, Z.; Wei, G.; Ma, L.; Hu, J.; Ding, D. A Survey on Multisensor Fusion and Consensus Filtering for Sensor Networks. Discret. Dyn. Nat. Soc. 2015, 2015, 683701. [Google Scholar] [CrossRef]
- Chen, H.; Kirubarajan, T.; Bar-shalom, Y. Performance limits of track-to-track fusion versus centralized estimation: Theory and application. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 386–400. [Google Scholar] [CrossRef]
- Premebida, C.; Monteiro, G.; Nunes, U.; Peixoto, P. A Lidar and Vision-based Approach for Pedestrian and Vehicle Detection and Tracking. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Seattle, WA, USA, 30 September–3 October 2007. [Google Scholar]
- Zhang, F.; Clarke, D.; Knoll, A. Vehicle Detection Based on LiDAR and Camera Fusion. In Proceedings of the International IEEE Conference on Intelligent Transportation Systems (ITSC), Qingdao, China, 8–11 October 2014. [Google Scholar]
- Wang, X.; Xu, L.; Sun, H.; Xin, J.; Zheng, N. On-Road Vehicle Detection and Tracking Using MMW Radar and Monovision Fusion. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2075–2084. [Google Scholar] [CrossRef]
- Gohring, D.; Wang, M.; Schnurmacher, M.; Ganjineh, T. Radar/Lidar Sensor Fusion for Car-Following on Highways. In Proceedings of the International Conference on Automation, Robotics and Applications, Wellington, New Zealand, 6–8 December 2011. [Google Scholar]
- Shahian Jahromi, B.; Tulabandhula, T.; Cetin, S. Real-Time Hybrid Multi-Sensor Fusion Framework for Perception in Autonomous Vehicles. Sensors 2019, 19, 4357. [Google Scholar] [CrossRef] [PubMed]
- Luiten, J.; Fischer, T.; Leibe, B. Track to Reconstruct and Reconstruct to Track. IEEE Robot. Autom. Lett. 2020, 5, 1803–1810. [Google Scholar] [CrossRef]
- Yeong, D.J.; Velasco-Hernandez, G.; Barry, J.; Walsh, J. Sensor and Sensor Fusion Technology in Autonomous Vehicles: A Review. Sensors 2021, 21, 2140. [Google Scholar] [CrossRef] [PubMed]
- Kocić, J.; Jovičić, N.; Drndarević, V. Sensors and Sensor Fusion in Autonomous Vehicles. In Proceedings of the Telecommunications Forum (TELFOR), Belgrade, Serbia, 20–21 November 2018; pp. 420–425. [Google Scholar]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Fluids Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Li, Q.; Li, R.; Ji, K.; Dai, W. Kalman Filter and Its Application. In Proceedings of the International Conference on Intelligent Networks and Intelligent Systems (ICINIS), Tianjin, China, 1–3 November 2015. [Google Scholar]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter. Available online: https://www.cs.unc.edu/~welch/media/pdf/kalman_intro.pdf (accessed on 16 January 2023).
- Fujii, K. Extended Kalman Filter. Tech. rep. The ACFA-Sim-J Group. 2003. Available online: https://www-jlc.kek.jp/2004sep/subg/offl/kaltest/doc/ReferenceManual.pdf (accessed on 16 January 2023).
- Julier, S.J.; Uhlmann, J.K. New extension of the kalman filter to nonlinear systems. In Proceedings of the Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 21–24 April 1997; pp. 182–193. [Google Scholar]
- Wan, E.A.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000. [Google Scholar]
- Sakai, A.; Tamura, Y.; Kuroda, Y. An Efficient Solution to 6DOF Localization Using Unscented Kalman Filter for Planetary Rovers. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009. [Google Scholar]
- Julier, S.J. The spherical simplex unscented transformation. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003. [Google Scholar]
- Jeon, D.; Choi, H.; Kim, J. UKF data fusion of odometry and magnetic sensor for a precise indoor localization system of an autonomous vehicle. In Proceedings of the 13th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Xian, China, 19–22 August 2016. [Google Scholar]
- Anjum, M.L.; Park, J.; Hwang, W.; Kwon, H.I.; Kim, J.H.; Lee, C.; Kim, K.S. Sensor data fusion using Unscented Kalman Filter for accurate localization of mobile robots. In Proceedings of the ICCAS 2010, Gyeonggi-do, Republic of Korea, 27–30 October 2010. [Google Scholar]
- Kokkala, J.; Solin, A.; Särkkä, S. Sigma-Point Filtering Based Parameter Estimation in Nonlinear Dynamic Systems. J. Adv. Inf. Fusion 2015, 11, 15–30. [Google Scholar]
- Cholesky, A.-L. Note sur une méthode de résolution des équations normales provenant de l’application de la méthode des moindres carrés à un système d’équations linéaires en nombre inférieur à celui des inconnues (Procédé du Commandant Cholesky). Bull. Géod. 1924, 2, 67–77. [Google Scholar]
- Schubert, R.; Richter, E.; Wanielik, G. Comparison and evaluation of advanced motion models for vehicle tracking. In Proceedings of the 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008. [Google Scholar]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated Vehicle Sideslip Angle Estimation Considering Signal Measurement Characteristic. IEEE Sens. J. 2021, 21, 21675–21687. [Google Scholar] [CrossRef]
- Liu, W.; Xiong, L.; Xia, X.; Lu, Y.; Gao, L.; Song, S. Vision-aided intelligent vehicle sideslip angle estimation based on a dynamic model. IET Intell. Transp. Syst. 2020, 14, 1183–1189. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Sahbani, B.; Adiprawita, W. Kalman filter and Iterative-Hungarian Algorithm implementation for low complexity point tracking as part of fast multiple object tracking system. In Proceedings of the 6th International Conference on System Engineering and Technology (ICSET), Bandung, Indonesia, 3–4 October 2016. [Google Scholar]
- Rong, G.; Shin, B.H.; Tabatabaee, H.; Lu, Q.; Lemke, S.; Boise, E.; Uhm, G.; Gerow, M.; Mehta, S.; Agafonov, E.; et al. LGSVL Simulator: A High Fidelity Simulator for Autonomous Driving. arXiv 2020, arXiv:2005.03778. [Google Scholar]
- Fridman, L. Human-Centered Autonomous Vehicle Systems: Principles of Effective Shared Autonomy. arXiv 2018, arXiv:1810.01835. [Google Scholar]
- Li, Y.; Ma, L.; Zhong, Z.; Liu, F.; Chapman, M.A.; Cao, D.; Li, J. Deep Learning for LiDAR Point Clouds in Autonomous Driving: A Review. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 3412–3432. [Google Scholar] [CrossRef]
- Bhoi, A. Monocular Depth Estimation: A Survey. arXiv 2019, arXiv:1901.09402. [Google Scholar]
- Kumar, G.A.; Lee, J.H.; Hwang, J.; Park, J.; Youn, S.H.; Kwon, S. LiDAR and Camera Fusion Approach for Object Distance Estimation in Self-Driving Vehicles. Symmetry 2020, 12, 324. [Google Scholar] [CrossRef] [Green Version]
- Bochkovskiy, A.; Wang, C.Y.; Liao, H.Y.M. YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Wu, B.; Wan, A.; Yue, X.; Keutzer, K. SqueezeSeg: Convolutional Neural Nets with Recurrent CRF for Real-Time Road-Object Segmentation from 3D LiDAR Point Cloud. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 1887–1893. [Google Scholar]
- Shi, S.; Wang, X.; Li, H. PointRCNN: 3D Object Proposal Generation and Detection From Point Cloud. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Autoware. AI. Autoware: Open-Source Software for Urban Autonomous Driving; The Autoware Foundation: Nagoya, Japan, 2019. [Google Scholar]
- Kellner, D.; Klappstein, J.; Dietmayer, K. Grid-based DBSCAN for clustering extended objects in radar data. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012. [Google Scholar]
- Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuScenes: A multimodal dataset for autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Kettelgerdes, M.; Böhm, L.; Elger, G. Correlating Intrinsic Parameters and Sharpness for Condition Monitoring of Automotive Imaging Sensors. In Proceedings of the 5th International Conference on System Reliability and Safety (ICSRS), Palermo, Italy, 24–26 November 2021. [Google Scholar]





| Scenario One (All Sensors) | Target Car 3 (Different Sensor Combinations) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Target Car Name | TC2 | TC3 | TC4 | L + R | L + C | R + C | L | R | C |
| RMSE in Longitudinal Distance (cm) | 6.7 | 7.0 | 7.4 | 6.9 | 8.9 | 12.6 | 8.1 | 10.8 | 43 |
| RMSE in Lateral Distance (cm) | 6.1 | 4.8 | 7.3 | 7.0 | 4.7 | 5.4 | 7.2 | 19.7 | 5.2 |
| RMSE in Velocity (m/s) | 0.27 | 0.21 | 0.53 | 0.21 | 0.68 | 0.25 | 0.67 | 0.18 | 0.99 |
| Missing Detection | Error in the Detection | |||||
|---|---|---|---|---|---|---|
| Target Car Name | TC2 | TC3 | TC4 | TC2 | TC3 | TC4 |
| RMSE in Longitudinal distance (cm) | 11.4 | 12.7 | 10.5 | 10.7 | 14.2 | 13.4 |
| RMSE in Lateral distance (cm) | 8.3 | 7.2 | 8.1 | 15.4 | 15.1 | 19.0 |
| RMSE in Velocity (m/s) | 0.44 | 0.31 | 0.42 | 0.33 | 0.29 | 0.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Senel, N.; Kefferpütz, K.; Doycheva, K.; Elger, G. Multi-Sensor Data Fusion for Real-Time Multi-Object Tracking. Processes 2023, 11, 501. https://doi.org/10.3390/pr11020501
Senel N, Kefferpütz K, Doycheva K, Elger G. Multi-Sensor Data Fusion for Real-Time Multi-Object Tracking. Processes. 2023; 11(2):501. https://doi.org/10.3390/pr11020501
Chicago/Turabian StyleSenel, Numan, Klaus Kefferpütz, Kristina Doycheva, and Gordon Elger. 2023. "Multi-Sensor Data Fusion for Real-Time Multi-Object Tracking" Processes 11, no. 2: 501. https://doi.org/10.3390/pr11020501
APA StyleSenel, N., Kefferpütz, K., Doycheva, K., & Elger, G. (2023). Multi-Sensor Data Fusion for Real-Time Multi-Object Tracking. Processes, 11(2), 501. https://doi.org/10.3390/pr11020501





