Alternative to Detecting Changes in the Mean of an Autoregressive Fractionally Integrated Process with Exponential White Noise Running on the Modified EWMA Control Chart
Abstract
:1. Introduction
2. Preliminaries
2.1. The ARFI(p, d) Model
2.2. The Modified EWMA Control Chart
2.3. The Design of the Modified EWMA Scheme
3. Derivation of Analytical and Approximate ARLs for Process with Exponential White Noise on a Modified EWMA Control Chart
3.1. The Analytical ARL Using the Exact Formula
3.2. The Approximate ARL Based on the Numerical IE
3.3. The Algorithm for Computing the Exact ARL
| Algorithm 1. The exact formula of ARL for a long-memory ARFI (p, d) process on a modified EWMA control chart |
| The algorithmic description of the exact formula for a long-memory ARFI(p, d) process running on a modified EWMA control chart is as follows. |
| Input: |
| Set the values of the model coefficients: |
| Set the values of the model coefficients: |
| Set the parameters for the modified EWMA control chart: = 0.05, 0.10, 0.20; k = 0.0, 0.2, 0.5, 1.0, 2.0 |
| Set the mean: for the in-control ARL0 |
| Set the mean shifts: |
| Output: |
| In-control ARL |
| 1: Solve the ARFI model defined as for a generalized long-memory ARFI(p, d) process with exponential white noise. |
| 2: Determine the values of the process coefficients and the initial values of . |
| 3: Specify for the in-control exponential white noise; i.e., |
| 4: Compute modified EWMA statistic for the long-memory ARFI(p, d) process given in Equation (7). |
| 5: Determine the values of the control chart coefficient for various combinations of and |
| 6: Calculate UCL (H) corresponding to the desired ARL0 by using Equation (15). |
| 7: Execute Steps 2–6 while in control and then calculate the value of corresponding to each combination. |
| Out-of-control ARL |
| 8: Compute ARL1 for shifts in the process mean as given in Equation (16), where H is attained as per steps 6 and 7. |
| 9: Record the computational time for the first out-of-control ARL1 signal. |
| 10: Repeat steps 6–9 and calculate ARL1 corresponding to the specific shift size |
4. Performance Evaluation and Comparison
4.1. Construction of the Control Limits
4.2. Performance of the Control Charts
- The ARL1 values tended to decline rapidly and monotonically as was increased.
- The ARL1 values created by the exact formula were comparable to those approximated by using the numerical IE technique. The percentage accuracy results were around 99% in all cases, meaning that they are in good agreement.
- The computational time to calculate ARL1 using the exact formula (less than 0.001 s) was substantially less than that required by the numerical IE technique (3–4 s) in all cases.
4.3. Evaluation of the Modified EWMA Control Chart
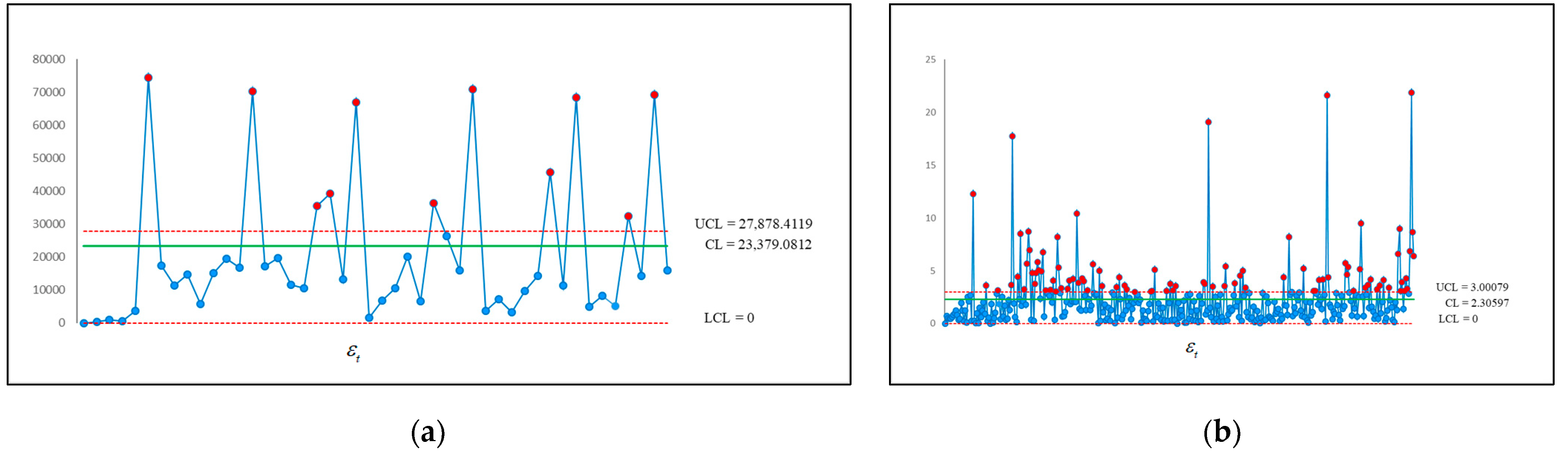
5. Application of the Proposed Exact Formula for the ARL
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Montgomery, D.C. Introduction to Statistical Quality Control Case Study; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Roberts, S.W. Control Chart Tests Based on Geometric Moving Averages. Technometrics 1959, 42, 239–250. [Google Scholar] [CrossRef]
- Crowder, S. Design of Exponentially Weighted Moving Average Schemes. Int. J. Qual. Eng. Tech. 1989, 21, 155–162. [Google Scholar] [CrossRef]
- Hsoon, N.G.C.; Case, K.E. Development and evaluation of control charts using exponentially weighted moving averages. J. Qual. Technol. 1989, 21, 242–250. [Google Scholar]
- Lucas, J.M.; Saccucci, M.S. The exponentially weighted moving average control schemes: Properties and enhancements (with discussion). Technimetrics 1990, 32, 23–26. [Google Scholar] [CrossRef]
- Riaz, M.; Ahmad, S.; Mahmood, T.; Abbas, N. On Reassessment of the HWMA Chart for Process Monitoring. Processes 2022, 10, 1129. [Google Scholar] [CrossRef]
- Patel, A.K.; Divecha, J. Modified exponentially weighted moving average (EWMA) control chart for an analytical process data. J. Chem. Eng. Mater. Sci. 2011, 2, 12–20. [Google Scholar]
- Khan, N.; Aslam, M.; Jun, C.H. Design of a control chart using a modified EWMA statistic. Qual. Reliab. Eng. Int. 2017, 33, 1095–1104. [Google Scholar] [CrossRef]
- Gan, F.F. Monitoring Poisson observations using modified exponentially weighted moving average control charts. Commun. Stat.-Simul. Comput. 1993, 19, 103–124. [Google Scholar] [CrossRef]
- Khan, N.; Yasmin, T.; Aslam, M.; Jun, C.H. On the performance of modified EWMA charts using resampling schemes. Oper. Res. Decis. 2018, 28, 29–43. [Google Scholar]
- Schmid, W. On EWMA charts for time series. Front. Stat. Qual. Control. 1997, 5, 115–137. [Google Scholar]
- Herdiani, E.T.; Fandrilla, G.; Sunusi, N. Modified Exponential Weighted Moving Average (EWMA) Control Chart on Autocorrelation Data. J. Phys. Conf. Ser. 2018, 979, 012097. [Google Scholar] [CrossRef]
- Lampreia, S.P.G.F.S.; Requeijo, J.F.G.; Dias, J.A.M.; Vairinhos, V.M.; Barbosa, P.I.S. Condition monitoring based on modified CUSUM and EWMA control charts. J. Qual. Maint. Eng. 2018, 24, 119–132. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Joyeux, R. An introduction to long-range time series models and fractional differencing. J. Time Ser. Anal. 1980, 1, 15–30. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Palma, W. Long-Memory Time Series: Theory and Methods; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Beran, J.; Feng, Y.; Ghosh, S.; Kulik, R. Long-Memory Processes—Probabilistic Properties and Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ramjee, R.; Crato, N.; Ray, B.K. A note on moving average forecasts of long memory processes with an application to quality control. Int. J. Forecast. 2002, 18, 291–297. [Google Scholar] [CrossRef]
- Rabyk, L.; Schmid, W. EWMA control charts for detecting changes in the mean of a long-memory process. Metrika 2016, 79, 267–301. [Google Scholar] [CrossRef]
- Okhrin, Y.; Schmid, W. Stochastic inequalities for the run length of the EWMA chart for long-memory processes. Revstat. Stat. J. 2019, 17, 67–90. [Google Scholar]
- Jacobs, P.A.; Lewis, P.A.W. A mixed autoregressive-moving average exponential sequence and point process (EARMA 1,1). Adv. Appl. Probab. 1977, 9, 87–104. [Google Scholar] [CrossRef]
- Ibazizen, M.; Fellag, H. Bayesian estimation of an AR(1) process with exponential white noise. J. Theor. Appl. Stat. 2003, 37, 365–372. [Google Scholar] [CrossRef]
- Pereira, I.M.S.; Turkman, M.A.A. Bayesian prediction in threshold autoregressive models with exponential white noise. Soc. Estad. Investig. Oper. Test 2004, 13, 45–64. [Google Scholar] [CrossRef]
- Suparman, S. A new estimation procedure using a reversible jump MCMC algorithm for AR models of exponential white noise. Int. J. GEOMATE 2018, 15, 85–91. [Google Scholar]
- Paichit, P.; Peerajit, W. The average run length for continuous distribution process mean shift detection on a modified EWMA control chart. Asia-Pac. J. Sci. Technol. 2022, 27, 109–118. [Google Scholar]
- Peerajit, W. Cumulative Sum Control Chart Applied to Monitor Shifts in the Mean of a Long-memory ARFIMAX(p, d*, q, r) Process with Exponential White Noise. Thail. Stat. 2022, 20, 144–161. [Google Scholar]
- Crowder, S. A simple method for studying run length distributions of exponentially weighted moving average charts. Technometrics 1987, 29, 401–407. [Google Scholar]
- Champ, C.W.; Rigdon, S.E. A comparison of the markov chain and the integral equation approaches for evaluating the run length distribution of quality control charts. Commun. Stat.-Simul. Comput. 1991, 20, 191–204. [Google Scholar] [CrossRef]
- Phanyaem, S.; Areepong, Y.; Sukparungsee, S. Explicit formulas of average run length for ARMA(1, 1) process of CUSUM control chart. Far East J. Appl. Math. 2014, 90, 211–224. [Google Scholar]
- Sunthornwat, R.; Areepong, Y. Average run length on CUSUM control chart for seasonal and non-seasonal moving average processes with exogenous variables. Symmetry 2020, 12, 173\. [Google Scholar] [CrossRef]
- Phanthuna, P.; Areepong, Y.; Sukparungsee, S. Run length distribution for a modified EWMA scheme fitted with a stationary AR(p) model. Commun. Stat.-Simul. Comput. 2021. [Google Scholar] [CrossRef]
- Areepong, Y.; Peerajit, W. Integral equation solutions for the average run length for monitoring shifts in the mean of a generalized seasonal ARFIMAX(P, D, Q, r)s process running on a CUSUM control chart. PLoS ONE 2022, 17, e0264283. [Google Scholar] [CrossRef]
- Phanthuna, P.; Areepong, Y. Detection Sensitivity of a Modified EWMA Control Chart with a Time Series Model with Fractionality and Integration. Emerg. Sci. J. 2022, 6, 1134–1152. [Google Scholar] [CrossRef]
- Silpakob, K.; Areepong, Y.; Sukparungsee, S.; Sunthornwat, R. A New Modified EWMA Control Chart for Monitoring Processes Involving Autocorrelated Data. Intell. Autom. Soft Comput. 2023, 36, 218–298. [Google Scholar] [CrossRef]
- Mcleod, I.; Hipel, K.W. Simulation Procedures for Box-Jenkins Models. Water Resour. Res. 1978, 14, 969–975. [Google Scholar] [CrossRef]
- Aning, R.O.; Abbasi, S.A.; Riaz, M. Monitoring of serially correlated processes using residual control charts. Sci. Iran. 2017, 24, 1603–1614. [Google Scholar]
- Fonseca, A.; Ferreira, P.H.; Nascimento, D.C.; Fiaccone, R.; Correa, C.U.; Piña, A.G.; Louzada, F. Water Particles Monitoring in the Atacama Desert: SPC Approach Based on Proportional Data. Axioms 2021, 10, 154. [Google Scholar] [CrossRef]
- Supharakonsakun, Y.; Areepong, Y.; Sukparungsee, S. The Performance of a Modified EWMA Control Chart for Monitoring Autocorrelated PM2.5 and Carbon Monoxide Air Pollution Data. PeerJ 2020, 8, e10467. [Google Scholar]
- Sofonea, M.; Han, W.; Shillor, M. Analysis and Approximation of Contact Problems with Adhesion or Damage; Chapman and Hall/CRC: New York, NY, USA, 2005. [Google Scholar]
| λ | k | Long-Memory Models | |||||
|---|---|---|---|---|---|---|---|
| d = 0.15 | d = 0.30 | d = 0.45 | d = 0.15 | d = 0.30 | d = 0.45 | ||
| 0.05 | 0.0 | 1.847423905 | 1.514830700 | 1.288933760 | 1.580654300 | 1.355604580 | 1.196054520 |
| 0.2 | 2.067005240 | 1.730856440 | 1.502560820 | 1.797381280 | 1.569938430 | 1.408698370 | |
| 0.5 | 2.396440000 | 2.054914850 | 1.822998020 | 2.122499230 | 1.891442100 | 1.727652800 | |
| 1.0 | 2.945884130 | 2.595259160 | 2.357225970 | 2.664635220 | 2.427470164 | 2.259379681 | |
| 2.0 | 4.047244550 | 3.677779121 | 3.427118068 | 3.750859956 | 3.501075556 | 3.324117363 | |
| 0.10 | 0.0 | 1.935118820 | 1.573871550 | 1.331945360 | 1.644881290 | 1.403065300 | 1.233255050 |
| 0.2 | 2.175098680 | 1.805922530 | 1.558817820 | 1.878471920 | 1.631449530 | 1.458043980 | |
| 0.5 | 2.536442520 | 2.155034800 | 1.899957280 | 2.229957090 | 1.974915150 | 1.795979350 | |
| 1.0 | 3.142676800 | 2.739911780 | 2.470956350 | 2.818971162 | 2.549959640 | 2.361411141 | |
| 2.0 | 4.372174930 | 3.922586520 | 3.623381301 | 4.010690557 | 3.711187907 | 3.501740791 | |
| 0.>20 | 0.0 | 2.132823260 | 1.704069900 | 1.425806400 | 1.787056760 | 1.506908620 | 1.314198020 |
| 0.2 | 2.421379540 | 1.972166200 | 1.681405890 | 2.058996510 | 1.766089380 | 1.564949260 | |
| 0.5 | 2.862318560 | 2.380051070 | 2.069247950 | 2.473067910 | 2.159663890 | 1.945045230 | |
| 1.0 | 3.621426280 | 3.076799520 | 2.728667740 | 3.181411710 | 2.829723170 | 2.590134860 | |
| 2.0 | 5.252565020 | 4.547212732 | 4.105681310 | 4.681259070 | 4.233149313 | 3.931832113 | |
| Coefficients of Model | q | δ | 0.01 | 0.05 | 0.10 | 0.50 | 1.00 | 3.00 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ||||
| 1.00 | 0.10 | 0.15 | 0.00 | Exact | 159.452 | <0.001 | 48.227 | <0.001 | 25.576 | <0.001 | 5.516 | <0.001 | 3.094 | <0.001 | 1.633 | <0.001 |
| NIE | 159.452 | 3.64 | 48.227 | 3.59 | 25.576 | 3.47 | 5.517 | 3.72 | 3.094 | 3.45 | 1.633 | 3.56 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 99.98 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 145.165 | <0.001 | 42.237 | <0.001 | 22.410 | <0.001 | 5.064 | <0.001 | 2.937 | <0.001 | 1.611 | <0.001 | |||
| NIE | 145.165 | 3.53 | 42.237 | 3.77 | 22.410 | 3.64 | 5.064 | 3.50 | 2.937 | 3.53 | 1.612 | 3.50 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 99.94 | ||||||||||
| 0.50 | Exact | 124.713 | <0.001 | 34.504 | <0.001 | 18.373 | <0.001 | 4.469 | <0.001 | 2.724 | <0.001 | 1.581 | <0.001 | |||
| NIE | 124.713 | 3.47 | 34.504 | 3.47 | 18.373 | 3.56 | 4.469 | 3.55 | 2.724 | 3.45 | 1.581 | 3.61 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 94.321 | <0.001 | 24.505 | <0.001 | 13.219 | <0.001 | 3.663 | <0.001 | 2.419 | <0.001 | 1.533 | <0.001 | |||
| NIE | 94.321 | 3.58 | 24.505 | 3.50 | 13.219 | 3.47 | 3.663 | 3.64 | 2.419 | 3.50 | 1.533 | 3.80 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 50.243 | <0.001 | 12.391 | <0.001 | 7.018 | <0.001 | 2.572 | <0.001 | 1.962 | <0.001 | 1.448 | <0.001 | |||
| NIE | 50.243 | 3.63 | 12.391 | 3.64 | 7.018 | 3.55 | 2.572 | 3.45 | 1.962 | 3.63 | 1.448 | 3.59 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.30 | 0.00 | Exact | 136.014 | <0.001 | 38.555 | <0.001 | 20.139 | <0.001 | 4.635 | <0.001 | 2.706 | <0.001 | 1.520 | <0.001 | ||
| NIE | 136.014 | 3.52 | 38.555 | 3.44 | 20.139 | 3.48 | 4.635 | 3.67 | 2.706 | 3.78 | 1.520 | 3.59 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 122.063 | <0.001 | 33.480 | <0.001 | 17.777 | <0.001 | 4.260 | <0.001 | 2.576 | <0.001 | 1.502 | <0.001 | |||
| NIE | 122.063 | 3.58 | 33.480 | 3.70 | 17.777 | 3.84 | 4.260 | 3.55 | 2.576 | 3.45 | 1.502 | 3.94 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 102.606 | <0.001 | 27.019 | <0.001 | 14.463 | <0.001 | 3.768 | <0.001 | 2.398 | <0.001 | 1.477 | <0.001 | |||
| NIE | 102.606 | 3.45 | 27.019 | 3.49 | 14.463 | 3.48 | 3.768 | 3.47 | 2.398 | 3.61 | 1.477 | 3.45 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 74.838 | <0.001 | 18.831 | <0.001 | 10.292 | <0.001 | 3.106 | <0.001 | 2.144 | <0.001 | 1.436 | <0.001 | |||
| NIE | 74.838 | 3.47 | 18.831 | 3.55 | 10.292 | 3.49 | 3.106 | 3.64 | 2.144 | 3.66 | 1.436 | 3.72 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 37.181 | <0.001 | 9.226 | <0.001 | 5.392 | <0.001 | 2.218 | <0.001 | 1.767 | <0.001 | 1.366 | <0.001 | |||
| NIE | 37.181 | 3.44 | 9.226 | 3.61 | 5.392 | 3.52 | 2.219 | 3.64 | 1.767 | 3.56 | 1.366 | 3.63 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 99.95 | 100.00 | 100.00 | ||||||||||
| 0.45 | 0.00 | Exact | 123.548 | <0.001 | 33.849 | <0.001 | 17.866 | <0.001 | 4.148 | <0.001 | 2.475 | <0.001 | 1.447 | <0.001 | ||
| NIE | 123.548 | 3.47 | 33.849 | 3.45 | 17.866 | 3.59 | 4.148 | 3.56 | 2.475 | 3.52 | 1.447 | 3.66 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 110.073 | <0.001 | 29.289 | <0.001 | 15.538 | <0.001 | 3.819 | <0.001 | 2.361 | <0.001 | 1.432 | <0.001 | |||
| NIE | 110.073 | 3.58 | 29.289 | 3.70 | 15.538 | 3.50 | 3.819 | 3.47 | 2.361 | 3.48 | 1.432 | 3.86 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 91.547 | <0.001 | 23.521 | <0.001 | 12.611 | <0.001 | 3.388 | <0.001 | 2.205 | <0.001 | 1.409 | <0.001 | |||
| NIE | 91.547 | 3.48 | 23.522 | 3.53 | 12.611 | 3.45 | 3.388 | 3.47 | 2.205 | 3.48 | 1.409 | 3.51 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 65.666 | <0.001 | 16.282 | <0.001 | 8.950 | <0.001 | 2.809 | <0.001 | 1.984 | <0.001 | 1.374 | <0.001 | |||
| NIE | 65.666 | 3.45 | 16.282 | 3.83 | 8.950 | 3.48 | 2.809 | 3.44 | 1.984 | 3.48 | 1.374 | 3.53 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 31.708 | <0.001 | 7.914 | <0.001 | 4.697 | <0.001 | 2.037 | <0.001 | 1.656 | <0.001 | 1.313 | <0.001 | |||
| NIE | 31.708 | 3.69 | 7.914 | 3.56 | 4.697 | 3.44 | 2.037 | 3.69 | 1.656 | 3.64 | 1.313 | 3.55 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| Coefficients of Model | q | δ | 0.01 | 0.05 | 0.10 | 0.50 | 1.00 | 3.00 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ||||
| 1.00 | 0.10 | 0.15 | 0.00 | Exact | 155.369 | <0.001 | 46.464 | <0.001 | 24.643 | <0.001 | 5.385 | <0.001 | 3.048 | <0.001 | 1.626 | <0.001 |
| NIE | 155.369 | 3.45 | 46.464 | 3.67 | 24.643 | 3.63 | 5.385 | 3.48 | 3.048 | 3.61 | 1.626 | 3.56 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 144.283 | <0.001 | 41.887 | <0.001 | 22.229 | <0.001 | 5.044 | <0.001 | 2.934 | <0.001 | 1.614 | <0.001 | |||
| NIE | 144.283 | 3.56 | 41.887 | 3.47 | 22.229 | 3.47 | 5.044 | 3.67 | 2.934 | 3.56 | 1.614 | 3.69 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 128.546 | <0.001 | 35.880 | <0.001 | 19.088 | <0.001 | 4.586 | <0.001 | 2.775 | <0.001 | 1.596 | <0.001 | |||
| NIE | 128.546 | 3.47 | 35.880 | 3.52 | 19.088 | 3.50 | 4.586 | 3.53 | 2.775 | 3.44 | 1.596 | 3.56 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 105.241 | <0.001 | 27.885 | <0.001 | 14.941 | <0.001 | 3.948 | <0.001 | 2.543 | <0.001 | 1.568 | <0.001 | |||
| NIE | 105.241 | 3.59 | 27.885 | 3.63 | 14.941 | 3.47 | 3.948 | 3.66 | 2.543 | 3.70 | 1.568 | 3.55 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 71.247 | <0.001 | 17.719 | <0.001 | 9.674 | <0.001 | 3.038 | <0.001 | 2.181 | <0.001 | 1.518 | <0.001 | |||
| NIE | 71.247 | 3.53 | 17.719 | 3.61 | 9.674 | 3.63 | 3.038 | 3.44 | 2.181 | 3.72 | 1.518 | 3.72 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.30 | 0.00 | Exact | 130.888 | <0.001 | 36.635 | <0.001 | 19.399 | <0.001 | 4.485 | <0.001 | 2.649 | <0.001 | 1.509 | <0.001 | ||
| NIE | 130.888 | 3.48 | 36.635 | 3.52 | 19.399 | 3.49 | 4.485 | 3.53 | 2.649 | 3.49 | 1.509 | 3.64 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 119.429 | <0.001 | 32.567 | <0.001 | 17.307 | <0.001 | 4.192 | <0.001 | 2.551 | <0.001 | 1.499 | <0.001 | |||
| NIE | 119.429 | 3.53 | 32.567 | 3.45 | 17.307 | 3.52 | 4.192 | 3.44 | 2.551 | 3.47 | 1.499 | 3.86 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 103.389 | <0.001 | 27.276 | <0.001 | 14.603 | <0.001 | 3.799 | <0.001 | 2.415 | <0.001 | 1.483 | <0.001 | |||
| NIE | 103.389 | 3.44 | 27.278 | 3.56 | 14.603 | 3.56 | 3.799 | 3.55 | 2.415 | 3.53 | 1.483 | 3.73 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 80.092 | <0.001 | 20.317 | <0.001 | 11.061 | <0.001 | 3.253 | <0.001 | 2.214 | <0.001 | 1.458 | <0.001 | |||
| NIE | 80.092 | 3.53 | 20.317 | 3.63 | 11.061 | 3.48 | 3.253 | 3.64 | 2.214 | 3.56 | 1.458 | 3.84 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 46.549 | <0.001 | 11.496 | <0.001 | 6.567 | <0.001 | 2.473 | <0.001 | 1.900 | <0.001 | 1.413 | <0.001 | |||
| NIE | 46.549 | 3.70 | 11.496 | 3.55 | 6.567 | 3.59 | 2.473 | 3.58 | 1.900 | 3.56 | 1.413 | 3.84 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.45 | 0.00 | Exact | 118.103 | <0.001 | 31.950 | <0.001 | 16.885 | <0.001 | 3.998 | <0.001 | 2.417 | <0.001 | 1.435 | <0.001 | ||
| NIE | 118.103 | 3.56 | 31.950 | 3.61 | 16.885 | 3.61 | 3.998 | 3.45 | 2.417 | 3.52 | 1.435 | 3.48 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 106.848 | <0.001 | 28.240 | <0.001 | 15.002 | <0.001 | 3.738 | <0.001 | 2.330 | <0.001 | 1.426 | <0.001 | |||
| NIE | 106.848 | 3.47 | 28.240 | 3.62 | 15.002 | 3.53 | 3.738 | 3.67 | 2.330 | 3.53 | 1.426 | 3.50 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 91.271 | <0.001 | 23.447 | <0.001 | 12.578 | <0.001 | 3.389 | <0.001 | 2.208 | <0.001 | 1.412 | <0.001 | |||
| NIE | 91.271 | 3.56 | 23.447 | 3.67 | 12.578 | 3.48 | 3.389 | 3.45 | 2.208 | 3.67 | 1.412 | 3.70 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 69.046 | <0.001 | 17.198 | <0.001 | 9.425 | <0.001 | 2.904 | <0.001 | 2.031 | <0.001 | 1.389 | <0.001 | |||
| NIE | 69.046 | 3.48 | 17.198 | 3.55 | 9.425 | 3.44 | 2.904 | 3.87 | 2.031 | 3.55 | 1.390 | 3.53 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 37.989 | <0.001 | 9.404 | <0.001 | 5.474 | <0.001 | 2.216 | <0.001 | 1.753 | <0.001 | 1.349 | <0.001 | |||
| NIE | 37.989 | 3.61 | 9.404 | 3.56 | 5.474 | 3.47 | 2.216 | 3.44 | 1.753 | 3.45 | 1.349 | 3.64 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| Coefficients of Model | q | δ | 0.01 | 0.05 | 0.10 | 0.50 | 1.00 | 3.00 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ||||
| 1.00 | 0.10 | 0.15 | 0.00 | Exact | 150.313 | <0.001 | 44.356 | <0.001 | 23.539 | <0.001 | 5.238 | <0.001 | 3.001 | <0.001 | 1.622 | <0.001 |
| NIE | 150.313 | 3.77 | 44.356 | 3.67 | 23.539 | 3.56 | 5.238 | 3.44 | 3.001 | 3.44 | 1.622 | 3.67 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 145.627 | <0.001 | 42.436 | <0.001 | 22.527 | <0.001 | 5.107 | <0.001 | 2.968 | <0.001 | 1.628 | <0.001 | |||
| NIE | 145.627 | 3.72 | 42.436 | 3.66 | 22.527 | 3.59 | 5.107 | 3.55 | 2.968 | 3.44 | 1.628 | 3.66 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 140.469 | <0.001 | 40.340 | <0.001 | 21.404 | <0.001 | 4.950 | <0.001 | 2.929 | <0.001 | 1.639 | <0.001 | |||
| NIE | 140.469 | 3.45 | 40.340 | 3.81 | 21.404 | 3.58 | 4.950 | 3.42 | 2.929 | 3.53 | 1.639 | 3.53 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 139.377 | <0.001 | 39.600 | <0.001 | 20.858 | <0.001 | 4.815 | <0.001 | 2.898 | <0.001 | 1.661 | <0.001 | |||
| NIE | 139.377 | 3.63 | 39.600 | 3.45 | 20.858 | 3.56 | 4.815 | 3.61 | 2.898 | 3.70 | 1.661 | 3.75 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 286.635 | <0.001 | 100.019 | <0.001 | 42.036 | <0.001 | 5.463 | <0.001 | 3.046 | <0.001 | 1.732 | <0.001 | |||
| NIE | 286.618 | 3.55 | 100.018 | 3.56 | 42.036 | 3.42 | 5.463 | 3.42 | 3.046 | 3.48 | 1.732 | 3.55 | ||||
| %Acc | 99.99 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.30 | 0.00 | Exact | 123.119 | <0.001 | 33.837 | <0.001 | 17.950 | <0.001 | 4.270 | <0.001 | 2.571 | <0.001 | 1.495 | <0.001 | ||
| NIE | 123.119 | 3.66 | 33.837 | 3.69 | 17.950 | 3.47 | 4.270 | 3.55 | 2.571 | 3.52 | 1.495 | 3.58 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 116.176 | <0.001 | 31.466 | <0.001 | 16.749 | <0.001 | 4.119 | <0.001 | 2.529 | <0.001 | 1.498 | <0.001 | |||
| NIE | 116.176 | 3.59 | 31.466 | 3.72 | 16.749 | 3.52 | 4.119 | 3.52 | 2.529 | 3.48 | 1.498 | 3.64 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 106.702 | <0.001 | 28.367 | <0.001 | 15.180 | <0.001 | 3.915 | <0.001 | 2.472 | <0.001 | 1.503 | <0.001 | |||
| NIE | 106.702 | 3.67 | 28.367 | 3.48 | 15.180 | 3.59 | 3.915 | 3.45 | 2.472 | 3.80 | 1.503 | 3.55 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 93.710 | <0.001 | 24.337 | <0.001 | 13.139 | <0.001 | 3.636 | <0.001 | 2.393 | <0.001 | 1.512 | <0.001 | |||
| NIE | 93.710 | 3.45 | 24.337 | 3.56 | 13.139 | 3.53 | 3.636 | 3.56 | 2.393 | 3.63 | 1.512 | 3.69 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 81.662 | <0.001 | 20.667 | <0.001 | 11.203 | <0.001 | 3.322 | <0.001 | 2.304 | <0.001 | 1.542 | <0.001 | |||
| NIE | 81.662 | 3.52 | 20.667 | 3.88 | 11.203 | 3.59 | 3.322 | 3.48 | 2.304 | 3.61 | 1.542 | 3.83 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.45 | 0.00 | Exact | 109.513 | <0.001 | 29.072 | <0.001 | 15.405 | <0.001 | 3.772 | <0.001 | 2.330 | <0.001 | 1.418 | <0.001 | ||
| NIE | 109.513 | 3.61 | 29.072 | 3.55 | 15.405 | 3.47 | 3.772 | 3.52 | 2.330 | 3.48 | 1.418 | 3.63 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.20 | Exact | 102.125 | <0.001 | 26.742 | <0.001 | 14.239 | <0.001 | 3.625 | <0.001 | 2.288 | <0.001 | 1.419 | <0.001 | |||
| NIE | 102.125 | 3.66 | 26.742 | 3.76 | 14.239 | 3.50 | 3.625 | 3.47 | 2.288 | 3.52 | 1.419 | 3.55 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 0.50 | Exact | 91.894 | <0.001 | 23.653 | <0.001 | 12.695 | <0.001 | 3.423 | <0.001 | 2.230 | <0.001 | 1.421 | <0.001 | |||
| NIE | 91.894 | 3.44 | 23.653 | 3.48 | 12.695 | 3.58 | 3.423 | 3.58 | 2.230 | 3.52 | 1.421 | 3.53 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 1.00 | Exact | 77.186 | <0.001 | 19.463 | <0.001 | 10.601 | <0.001 | 3.136 | <0.001 | 2.144 | <0.001 | 1.425 | <0.001 | |||
| NIE | 77.186 | 3.41 | 19.464 | 3.53 | 10.601 | 3.48 | 3.136 | 3.48 | 2.144 | 3.64 | 1.425 | 3.53 | ||||
| %Acc | 100.00 | 99.99 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| 2.00 | Exact | 56.629 | <0.001 | 14.028 | <0.001 | 7.867 | <0.001 | 2.725 | <0.001 | 2.015 | <0.001 | 1.439 | <0.001 | |||
| NIE | 56.629 | 3.55 | 14.028 | 3.62 | 7.867 | 3.42 | 2.725 | 3.84 | 2.015 | 3.66 | 1.439 | 3.59 | ||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | ||||||||||
| Coefficients of Model | q | δ | 0.01 | 0.05 | 0.10 | 0.50 | 1.00 | 3.00 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | |||||
| 1.00 | 0.10 | 0.20 | 0.15 | 0.00 | Exact | 140.082 | <0.001 | 40.153 | <0.001 | 21.258 | <0.001 | 4.791 | <0.001 | 2.778 | <0.001 | 1.542 | <0.001 |
| NIE | 140.082 | 4.37 | 40.153 | 4.51 | 21.258 | 4.75 | 4.791 | 4.59 | 2.778 | 4.53 | 1.542 | 4.56 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 126.021 | <0.001 | 34.914 | <0.001 | 18.539 | <0.001 | 4.402 | <0.001 | 2.642 | <0.001 | 1.523 | <0.001 | ||||
| NIE | 126.021 | 4.59 | 34.914 | 4.53 | 18.539 | 4.62 | 4.402 | 4.70 | 2.642 | 4.56 | 1.523 | 4.70 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 106.318 | <0.001 | 28.228 | <0.001 | 15.099 | <0.001 | 3.891 | <0.001 | 2.458 | <0.001 | 1.497 | <0.001 | ||||
| NIE | 106.318 | 4.62 | 28.228 | 4.50 | 15.100 | 4.65 | 3.891 | 4.45 | 2.458 | 4.45 | 1.497 | 4.69 | |||||
| %Acc | 100.00 | 100.00 | 99.99 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 78.001 | <0.001 | 19.727 | <0.001 | 10.759 | <0.001 | 3.203 | <0.001 | 2.194 | <0.001 | 1.455 | <0.001 | ||||
| NIE | 78.001 | 4.75 | 19.727 | 4.58 | 10.760 | 4.55 | 3.203 | 4.48 | 2.194 | 4.61 | 1.455 | 4.62 | |||||
| %Acc | 100.00 | 100.00 | 99.99 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 39.163 | <0.001 | 9.703 | <0.001 | 5.642 | <0.001 | 2.279 | <0.001 | 1.802 | <0.001 | 1.382 | <0.001 | ||||
| NIE | 39.163 | 4.45 | 9.703 | 4.55 | 5.642 | 4.69 | 2.279 | 4.50 | 1.802 | 4.53 | 1.382 | 4.58 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.30 | 0.00 | Exact | 127.019 | <0.001 | 35.132 | <0.001 | 18.559 | <0.001 | 4.285 | <0.001 | 2.541 | <0.001 | 1.468 | <0.001 | |||
| NIE | 127.019 | 4.55 | 35.132 | 4.45 | 18.559 | 4.52 | 4.285 | 4.52 | 2.541 | 4.59 | 1.468 | 4.76 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 113.392 | <0.001 | 30.427 | <0.001 | 16.148 | <0.001 | 3.943 | <0.001 | 2.422 | <0.001 | 1.452 | <0.001 | ||||
| NIE | 113.392 | 4.48 | 30.427 | 4.61 | 16.148 | 4.44 | 3.943 | 4.44 | 2.422 | 4.52 | 1.452 | 4.73 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 94.580 | <0.001 | 24.466 | <0.001 | 13.113 | <0.001 | 3.494 | <0.001 | 2.260 | <0.001 | 1.429 | <0.001 | ||||
| NIE | 94.580 | 4.42 | 24.466 | 4.50 | 13.113 | 4.45 | 3.494 | 4.52 | 2.260 | 4.47 | 1.429 | 4.64 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 68.145 | <0.001 | 16.964 | <0.001 | 9.311 | <0.001 | 2.892 | <0.001 | 2.030 | <0.001 | 1.392 | <0.001 | ||||
| NIE | 68.145 | 4.42 | 16.964 | 4.67 | 9.311 | 4.70 | 2.892 | 4.55 | 2.030 | 4.53 | 1.392 | 4.55 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 33.149 | <0.001 | 8.259 | <0.001 | 4.881 | <0.001 | 2.087 | <0.001 | 1.687 | <0.001 | 1.328 | <0.001 | ||||
| NIE | 33.149 | 4.72 | 8.259 | 4.39 | 4.881 | 4.58 | 2.087 | 4.64 | 1.687 | 4.62 | 1.328 | 4.55 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.45 | 0.00 | Exact | 118.941 | <0.001 | 32.178 | <0.001 | 16.963 | <0.001 | 3.964 | <0.001 | 2.385 | <0.001 | 1.417 | <0.001 | |||
| NIE | 118.941 | 4.66 | 32.178 | 4.53 | 16.963 | 4.50 | 3.964 | 4.56 | 2.385 | 4.58 | 1.417 | 4.56 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 105.693 | <0.001 | 27.811 | <0.001 | 14.745 | <0.001 | 3.653 | <0.001 | 2.277 | <0.001 | 1.403 | <0.001 | ||||
| NIE | 105.693 | 4.67 | 27.811 | 4.48 | 14.745 | 4.47 | 3.653 | 4.59 | 2.277 | 4.50 | 1.403 | 4.56 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 87.576 | <0.001 | 22.301 | <0.001 | 11.960 | <0.001 | 3.246 | <0.001 | 2.130 | <0.001 | 1.382 | <0.001 | ||||
| NIE | 87.576 | 4.50 | 22.301 | 4.56 | 11.960 | 4.55 | 3.246 | 4.48 | 2.130 | 4.52 | 1.382 | 4.73 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 62.460 | <0.001 | 15.407 | <0.001 | 8.485 | <0.001 | 2.699 | <0.001 | 1.922 | <0.001 | 1.349 | <0.001 | ||||
| NIE | 62.460 | 4.42 | 15.407 | 4.44 | 8.485 | 4.41 | 2.699 | 4.44 | 1.922 | 4.50 | 1.349 | 4.56 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 29.888 | <0.001 | 7.478 | <0.001 | 4.462 | <0.001 | 1.971 | <0.001 | 1.613 | <0.001 | 1.292 | <0.001 | ||||
| NIE | 29.888 | 4.47 | 7.478 | 4.56 | 4.462 | 4.42 | 1.971 | 4.45 | 1.613 | 4.44 | 1.292 | 4.58 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| Coefficients of model | q | δ | 0.01 | 0.05 | 0.10 | 0.50 | 1.00 | 3.00 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | |||||
| 1.00 | 0.10 | 0.20 | 0.15 | 0.00 | Exact | 135.095 | <0.001 | 38.239 | <0.001 | 20.257 | <0.001 | 4.642 | <0.001 | 2.723 | <0.001 | 1.532 | <0.001 |
| NIE | 135.095 | 4.81 | 38.239 | 4.89 | 20.257 | 4.91 | 4.642 | 4.55 | 2.723 | 4.62 | 1.532 | 4.78 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 123.629 | <0.001 | 34.066 | <0.001 | 18.102 | <0.001 | 4.340 | <0.001 | 2.621 | <0.001 | 1.521 | <0.001 | ||||
| NIE | 123.629 | 4.50 | 34.066 | 4.41 | 18.102 | 4.50 | 4.340 | 4.58 | 2.621 | 4.45 | 1.521 | 4.58 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 107.523 | <0.001 | 28.628 | <0.001 | 15.312 | <0.001 | 3.935 | <0.001 | 2.480 | <0.001 | 1.505 | <0.001 | ||||
| NIE | 107.523 | 4.47 | 28.628 | 4.66 | 15.312 | 4.53 | 3.935 | 4.53 | 2.480 | 4.58 | 1.505 | 4.58 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 84.014 | <0.001 | 21.453 | <0.001 | 11.651 | <0.001 | 3.370 | <0.001 | 2.273 | <0.001 | 1.479 | <0.001 | ||||
| NIE | 84.014 | 4.56 | 21.453 | 4.47 | 11.651 | 4.66 | 3.370 | 4.62 | 2.273 | 4.62 | 1.479 | 4.62 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 49.881 | <0.001 | 12.319 | <0.001 | 6.989 | <0.001 | 2.563 | <0.001 | 1.949 | <0.001 | 1.433 | <0.001 | ||||
| NIE | 49.881 | 4.77 | 12.319 | 4.50 | 6.989 | 4.47 | 2.563 | 4.47 | 1.949 | 4.58 | 1.433 | 4.76 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.30 | 0.00 | Exact | 121.649 | <0.001 | 33.222 | <0.001 | 17.568 | <0.001 | 4.134 | <0.001 | 2.483 | <0.001 | 1.457 | <0.001 | |||
| NIE | 121.649 | 4.65 | 33.222 | 4.67 | 17.568 | 4.47 | 4.134 | 4.59 | 2.483 | 4.48 | 1.457 | 4.77 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 110.311 | <0.001 | 29.407 | <0.001 | 15.625 | <0.001 | 3.864 | <0.001 | 2.393 | <0.001 | 1.447 | <0.001 | ||||
| NIE | 110.311 | 4.53 | 29.407 | 4.92 | 15.625 | 4.72 | 3.864 | 4.55 | 2.393 | 4.48 | 1.447 | 4.62 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 94.565 | <0.001 | 24.470 | <0.001 | 13.121 | <0.001 | 3.503 | <0.001 | 2.267 | <0.001 | 1.432 | <0.001 | ||||
| NIE | 94.565 | 4.47 | 24.470 | 4.58 | 13.121 | 4.64 | 3.503 | 4.67 | 2.267 | 4.67 | 1.432 | 4.61 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 71.985 | <0.001 | 18.017 | <0.001 | 9.857 | <0.001 | 3.000 | <0.001 | 2.083 | <0.001 | 1.409 | <0.001 | ||||
| NIE | 71.985 | 4.55 | 18.017 | 4.48 | 9.857 | 4.50 | 3.000 | 4.48 | 2.083 | 4.61 | 1.409 | 4.58 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 40.155 | <0.001 | 9.931 | <0.001 | 5.752 | <0.001 | 2.285 | <0.001 | 1.794 | <0.001 | 1.368 | <0.001 | ||||
| NIE | 40.155 | 4.66 | 9.931 | 4.51 | 5.752 | 4.55 | 2.285 | 4.69 | 1.794 | 4.48 | 1.368 | 4.73 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.45 | 0.00 | Exact | 113.414 | <0.001 | 30.300 | <0.001 | 15.996 | <0.001 | 3.816 | <0.001 | 2.327 | <0.001 | 1.405 | <0.001 | |||
| NIE | 113.414 | 4.62 | 30.300 | 4.45 | 15.996 | 4.37 | 3.816 | 4.47 | 2.327 | 4.45 | 1.405 | 4.56 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 102.301 | <0.001 | 26.734 | <0.001 | 14.195 | <0.001 | 3.569 | <0.001 | 2.244 | <0.001 | 1.396 | <0.001 | ||||
| NIE | 102.301 | 4.44 | 26.734 | 4.69 | 14.195 | 4.44 | 3.569 | 4.47 | 2.244 | 4.44 | 1.396 | 4.39 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 86.990 | <0.001 | 22.136 | <0.001 | 11.880 | <0.001 | 3.238 | <0.001 | 2.130 | <0.001 | 1.383 | <0.001 | ||||
| NIE | 86.990 | 4.48 | 22.136 | 4.50 | 11.880 | 4.42 | 3.238 | 4.41 | 2.130 | 4.44 | 1.383 | 4.52 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 65.297 | <0.001 | 16.165 | <0.001 | 8.878 | <0.001 | 2.779 | <0.001 | 1.962 | <0.001 | 1.362 | <0.001 | ||||
| NIE | 65.297 | 4.44 | 16.165 | 4.44 | 8.878 | 4.47 | 2.779 | 4.55 | 1.962 | 4.49 | 1.362 | 4.52 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 35.335 | <0.001 | 8.761 | <0.001 | 5.133 | <0.001 | 2.128 | <0.001 | 1.699 | <0.001 | 1.324 | <0.001 | ||||
| NIE | 35.335 | 4.47 | 8.761 | 4.41 | 5.133 | 4.48 | 2.128 | 4.62 | 1.699 | 4.83 | 1.324 | 4.66 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| Coefficients of model | q | δ | 0.01 | 0.05 | 0.10 | 0.50 | 1.00 | 3.00 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | ARL1 | Time | |||||
| 1.00 | 0.10 | 0.20 | 0.15 | 0.00 | Exact | 127.681 | <0.001 | 35.503 | <0.001 | 18.838 | <0.001 | 4.435 | <0.001 | 2.647 | <0.001 | 1.519 | <0.001 |
| NIE | 127.681 | 4.58 | 35.503 | 4.73 | 18.838 | 4.52 | 4.435 | 4.55 | 2.647 | 4.70 | 1.519 | 4.62 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 120.986 | <0.001 | 33.154 | <0.001 | 17.642 | <0.001 | 4.284 | <0.001 | 2.606 | <0.001 | 1.522 | <0.001 | ||||
| NIE | 120.986 | 4.70 | 33.154 | 4.55 | 17.642 | 4.58 | 4.284 | 4.66 | 2.606 | 4.91 | 1.522 | 4.59 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 111.957 | <0.001 | 30.112 | <0.001 | 16.094 | <0.001 | 4.083 | <0.001 | 2.551 | <0.001 | 1.528 | <0.001 | ||||
| NIE | 111.957 | 4.59 | 30.112 | 5.03 | 16.094 | 4.51 | 4.083 | 4.67 | 2.551 | 4.95 | 1.528 | 4.53 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 100.036 | <0.001 | 26.286 | <0.001 | 14.142 | <0.001 | 3.816 | <0.001 | 2.477 | <0.001 | 1.539 | <0.001 | ||||
| NIE | 100.036 | 4.61 | 26.286 | 4.72 | 14.142 | 4.52 | 3.816 | 4.66 | 2.477 | 4.51 | 1.539 | 4.81 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 94.358 | <0.001 | 24.213 | <0.001 | 12.923 | <0.001 | 3.570 | <0.001 | 2.411 | <0.001 | 1.575 | <0.001 | ||||
| NIE | 94.357 | 4.53 | 24.213 | 4.53 | 12.923 | 4.42 | 3.570 | 4.62 | 2.411 | 4.56 | 1.575 | 4.62 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.30 | 0.00 | Exact | 113.249 | <0.001 | 30.351 | <0.001 | 16.089 | <0.001 | 3.910 | <0.001 | 2.398 | <0.001 | 1.440 | <0.001 | |||
| NIE | 113.250 | 4.73 | 30.351 | 4.47 | 16.089 | 4.66 | 3.910 | 4.47 | 2.398 | 4.50 | 1.440 | 4.73 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 105.939 | <0.001 | 27.996 | <0.001 | 14.907 | <0.001 | 3.760 | <0.001 | 2.356 | <0.001 | 1.442 | <0.001 | ||||
| NIE | 105.939 | 4.50 | 27.996 | 4.48 | 14.907 | 4.64 | 3.760 | 4.67 | 2.356 | 4.50 | 1.442 | 4.52 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 95.836 | <0.001 | 24.879 | <0.001 | 13.344 | <0.001 | 3.557 | <0.001 | 2.297 | <0.001 | 1.444 | <0.001 | ||||
| NIE | 95.836 | 4.53 | 24.879 | 4.67 | 13.344 | 4.62 | 3.557 | 4.51 | 2.297 | 4.56 | 1.444 | 4.73 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 81.408 | <0.001 | 20.681 | <0.001 | 11.239 | <0.001 | 3.269 | <0.001 | 2.212 | <0.001 | 1.450 | <0.001 | ||||
| NIE | 81.408 | 4.56 | 20.681 | 4.41 | 11.239 | 4.58 | 3.269 | 4.50 | 2.212 | 4.48 | 1.450 | 4.58 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 62.135 | <0.001 | 15.450 | <0.001 | 8.595 | <0.001 | 2.871 | <0.001 | 2.090 | <0.001 | 1.468 | <0.001 | ||||
| NIE | 62.135 | 4.55 | 15.450 | 4.73 | 8.595 | 4.52 | 2.871 | 4.59 | 2.090 | 4.59 | 1.468 | 4.56 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.45 | 0.00 | Exact | 104.612 | <0.001 | 27.427 | <0.001 | 14.524 | <0.001 | 3.590 | <0.001 | 2.239 | <0.001 | 1.387 | <0.001 | |||
| NIE | 104.612 | 4.56 | 27.427 | 4.52 | 14.524 | 4.66 | 3.590 | 4.44 | 2.239 | 4.47 | 1.387 | 4.50 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.20 | Exact | 97.172 | <0.001 | 25.145 | <0.001 | 13.388 | <0.001 | 3.447 | <0.001 | 2.198 | <0.001 | 1.388 | <0.001 | ||||
| NIE | 97.172 | 4.52 | 25.145 | 4.45 | 13.388 | 4.47 | 3.447 | 4.44 | 2.198 | 4.51 | 1.388 | 4.50 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 0.50 | Exact | 86.859 | <0.001 | 22.115 | <0.001 | 11.879 | <0.001 | 3.250 | <0.001 | 2.141 | <0.001 | 1.389 | <0.001 | ||||
| NIE | 86.859 | 4.50 | 22.115 | 4.45 | 11.879 | 4.47 | 3.250 | 4.44 | 2.141 | 4.45 | 1.389 | 4.59 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 1.00 | Exact | 71.970 | <0.001 | 17.985 | <0.001 | 9.823 | <0.001 | 2.968 | <0.001 | 2.055 | <0.001 | 1.392 | <0.001 | ||||
| NIE | 71.970 | 4.41 | 17.985 | 5.37 | 9.823 | 4.50 | 2.968 | 4.41 | 2.055 | 4.47 | 1.392 | 4.67 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| 2.00 | Exact | 50.490 | <0.001 | 12.465 | <0.001 | 7.057 | <0.001 | 2.550 | <0.001 | 1.921 | <0.001 | 1.402 | <0.001 | ||||
| NIE | 50.490 | 4.45 | 12.465 | 4.44 | 7.057 | 4.34 | 2.550 | 4.45 | 1.921 | 4.42 | 1.402 | 4.53 | |||||
| %Acc | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||
| Long-Memory ARFI(1, d) Model | Long-Memory ARFI(2, d) Model | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | 0.15 | 0.30 | 0.45 | 0.15 | 0.30 | 0.45 | |||||||
| Control Chart | EWMA (k = 0) | MEWMA (k = 2) | EWMA (k = 0) | MEWMA (k = 2) | EWMA (k = 0) | MEWMA (k = 2) | EWMA (k = 0) | MEWMA (k = 2) | EWMA (k = 0) | MEWMA (k = 2) | EWMA (k = 0) | MEWMA (k = 2) | |
| 0.01 | ARL1 | 159.4520 | 50.2430 | 136.0140 | 37.1810 | 123.5480 | 31.7080 | 140.0820 | 39.1630 | 127.0190 | 33.1490 | 118.9410 | 29.8880 |
| SDRL1 | 158.9512 | 49.7405 | 135.5131 | 36.6776 | 123.0470 | 31.2040 | 139.5811 | 38.6598 | 126.5180 | 32.6452 | 118.4399 | 29.3837 | |
| MRL1 | 110.1768 | 34.4781 | 93.9307 | 25.4238 | 85.2899 | 21.6299 | 96.7505 | 26.7977 | 87.6958 | 22.6288 | 82.0966 | 20.3682 | |
| 0.05 | ARL1 | 48.2270 | 12.3910 | 38.5550 | 9.2260 | 33.8490 | 7.9140 | 40.1530 | 9.7030 | 35.1320 | 8.2590 | 32.1780 | 7.4780 |
| SDRL1 | 47.7244 | 11.8805 | 38.0517 | 8.7117 | 33.3453 | 7.3971 | 39.6498 | 9.1894 | 34.6284 | 7.7429 | 31.6741 | 6.9601 | |
| MRL1 | 33.0806 | 8.2374 | 26.3762 | 6.0418 | 23.1140 | 5.1312 | 27.4839 | 6.3728 | 24.0034 | 5.3707 | 21.9557 | 4.8285 | |
| 0.10 | ARL1 | 25.5760 | 7.0180 | 20.1390 | 5.3920 | 17.8660 | 4.6970 | 21.2580 | 5.6420 | 18.5590 | 4.8810 | 16.9630 | 4.4620 |
| SDRL1 | 25.0710 | 6.4988 | 19.6326 | 4.8664 | 17.3588 | 4.1671 | 20.7520 | 5.1176 | 18.0521 | 4.3524 | 16.4554 | 3.9303 | |
| MRL1 | 17.3791 | 4.5091 | 13.6098 | 3.3790 | 12.0339 | 2.8953 | 14.3856 | 3.5529 | 12.5143 | 3.0234 | 11.4078 | 2.7316 | |
| 0.50 | ARL1 | 5.5160 | 2.5720 | 4.6350 | 2.2180 | 4.1480 | 2.0370 | 4.7910 | 2.2790 | 4.2850 | 2.0870 | 3.9640 | 1.9710 |
| SDRL1 | 4.9910 | 2.0108 | 4.1047 | 1.6436 | 3.6136 | 1.4534 | 4.2618 | 1.7073 | 3.7518 | 1.5062 | 3.4277 | 1.3834 | |
| MRL1 | 3.4653 | 1.4079 | 2.8521 | 1.1564 | 2.5127 | 1.0267 | 2.9608 | 1.1999 | 2.6082 | 1.0626 | 2.3843 | 0.9791 | |
| 1.00 | ARL1 | 3.0940 | 1.9620 | 2.7060 | 1.7670 | 2.4750 | 1.6560 | 2.7780 | 1.8020 | 2.5410 | 1.6870 | 2.3850 | 1.6130 |
| SDRL1 | 2.5454 | 1.3738 | 2.1486 | 1.1642 | 1.9107 | 1.0423 | 2.2224 | 1.2022 | 1.9788 | 1.0766 | 1.8175 | 0.9944 | |
| MRL1 | 1.7755 | 0.9726 | 1.5025 | 0.8306 | 1.3392 | 0.7485 | 1.5533 | 0.8562 | 1.3859 | 0.7716 | 1.2753 | 0.7164 | |
| 3.00 | ARL1 | 1.6330 | 1.4480 | 1.5200 | 1.3660 | 1.4470 | 1.3130 | 1.5420 | 1.3820 | 1.4680 | 1.3280 | 1.4170 | 1.2920 |
| SDRL1 | 1.0167 | 0.8054 | 0.8890 | 0.7071 | 0.8042 | 0.6411 | 0.9142 | 0.7266 | 0.8289 | 0.6600 | 0.7687 | 0.6142 | |
| MRL1 | 0.7314 | 0.5908 | 0.6462 | 0.5263 | 0.5901 | 0.4834 | 0.6629 | 0.5391 | 0.6063 | 0.4957 | 0.5667 | 0.4661 | |
| δ | Applications 1 | Applications 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| ARL1 | SDRL1 | MRL1 | ARL1 | SDRL1 | MRL1 | |||
| Exact | NIE | Exact | NIE | |||||
| 0.01 | 60.4034 | 60.4034 | 59.9013 | 41.5209 | 28.556 | 28.5556 | 28.0515 | 19.4449 |
| (<0.001) | (9.063) | (<0.001) | (11.015) | |||||
| 0.05 | 14.8503 | 14.8503 | 14.3416 | 9.9428 | 6.9413 | 6.9413 | 6.4219 | 4.4558 |
| (<0.001) | (8.640) | (<0.001) | (11.485) | |||||
| 0.10 | 8.1881 | 8.18812 | 14.3416 | 5.3215 | 4.0418 | 4.0418 | 4.0418 | 2.4386 |
| (<0.001) | (8.891) | (<0.001) | (11.078) | |||||
| 0.50 | 2.6265 | 2.6265 | 2.0669 | 1.4464 | 1.6670 | 1.6670 | 1.0545 | 0.7567 |
| (<0.001) | (9.375) | (<0.001) | (10.984) | |||||
| 1.00 | 1.8810 | 1.8810 | 1.8810 | 0.9138 | 1.3532 | 1.3532 | 0.6913 | 0.5160 |
| (<0.001) | (9.063) | (<0.001) | (11.001) | |||||
| 3.00 | 1.3324 | 1.3324 | 1.3324 | 0.4992 | 1.1277 | 1.1277 | 0.3795 | 0.3182 |
| (<0.001) | (8.750) | (<0.001) | (10.969) | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peerajit, W.; Areepong, Y. Alternative to Detecting Changes in the Mean of an Autoregressive Fractionally Integrated Process with Exponential White Noise Running on the Modified EWMA Control Chart. Processes 2023, 11, 503. https://doi.org/10.3390/pr11020503
Peerajit W, Areepong Y. Alternative to Detecting Changes in the Mean of an Autoregressive Fractionally Integrated Process with Exponential White Noise Running on the Modified EWMA Control Chart. Processes. 2023; 11(2):503. https://doi.org/10.3390/pr11020503
Chicago/Turabian StylePeerajit, Wilasinee, and Yupaporn Areepong. 2023. "Alternative to Detecting Changes in the Mean of an Autoregressive Fractionally Integrated Process with Exponential White Noise Running on the Modified EWMA Control Chart" Processes 11, no. 2: 503. https://doi.org/10.3390/pr11020503






