Optimization of the Automated Production Process Using Software Simulation Tools
Abstract
:1. Introduction
2. Materials and Methods
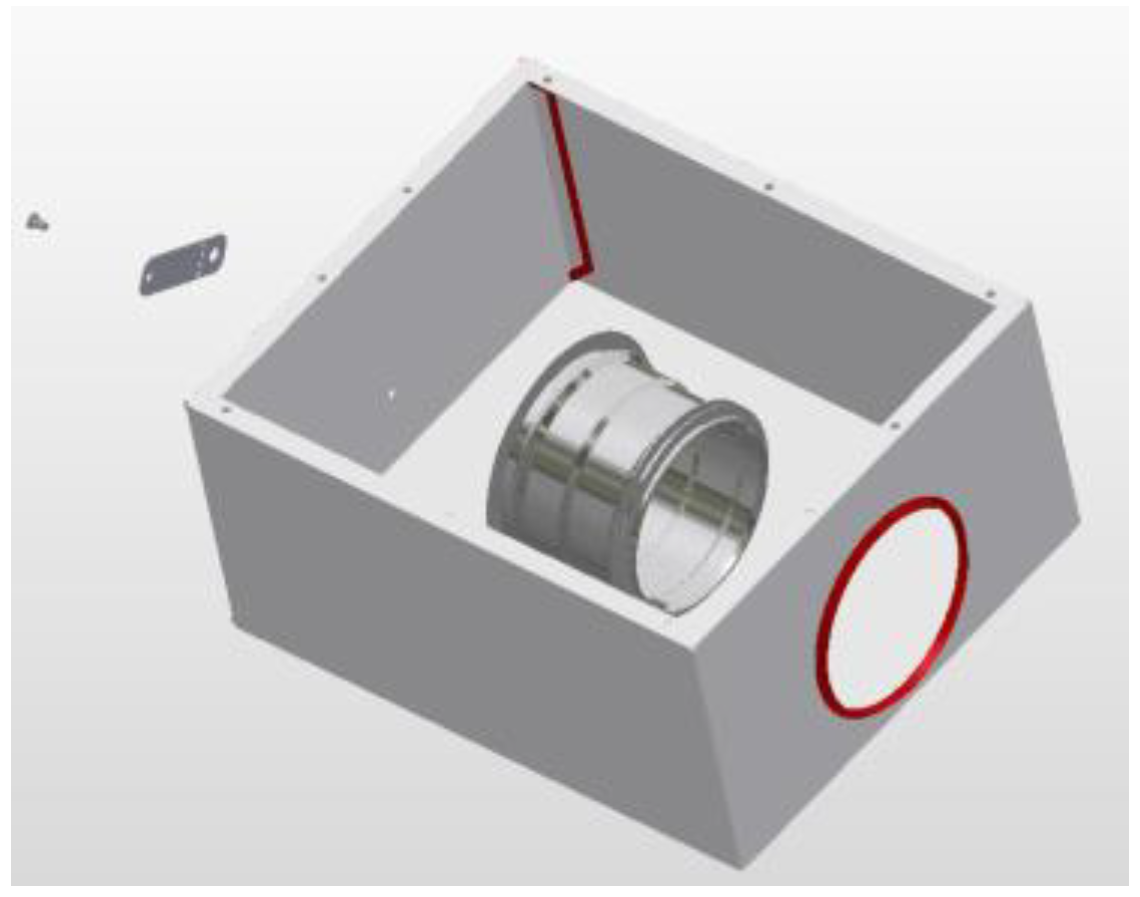
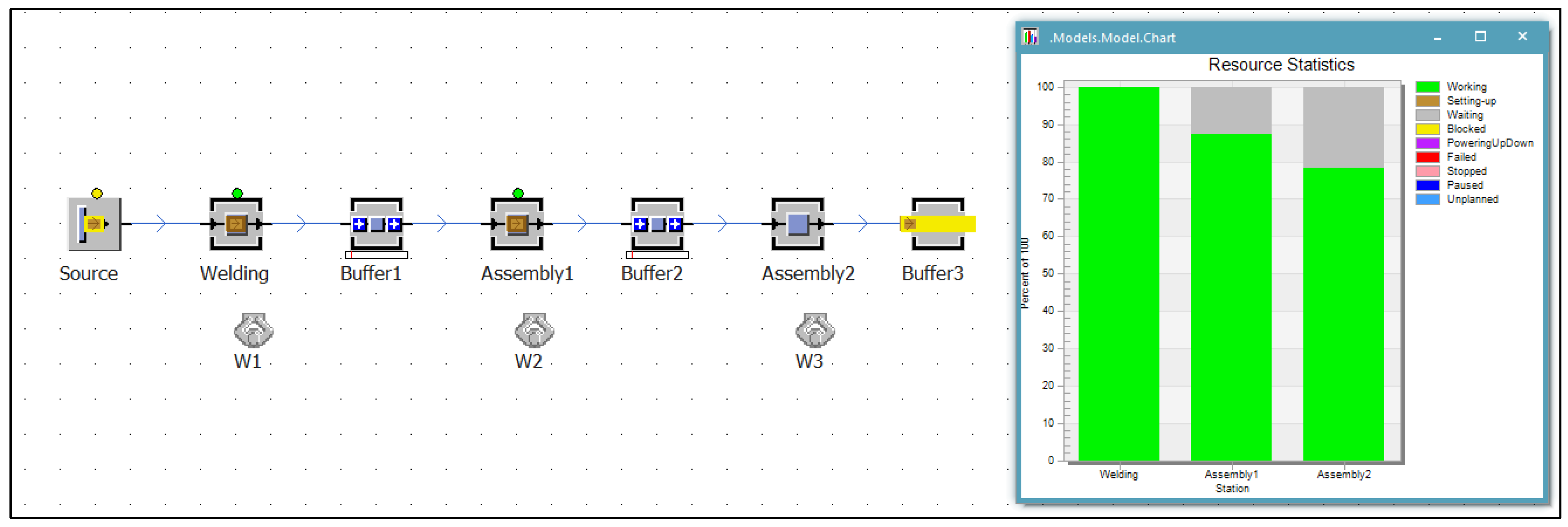
2.1. Current State of Production
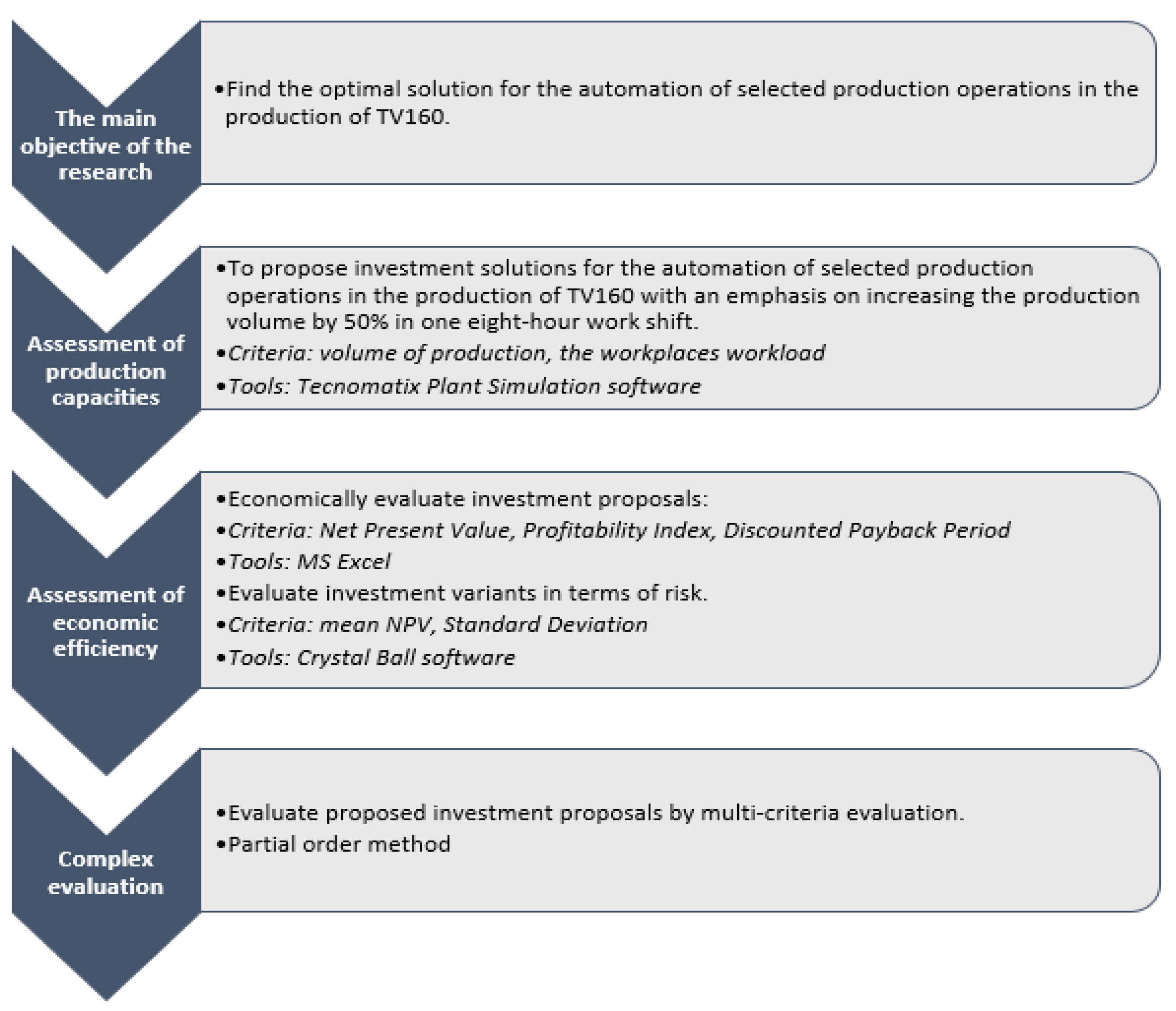
2.2. Methodical Procedure of Solution
3. Results and Discussion
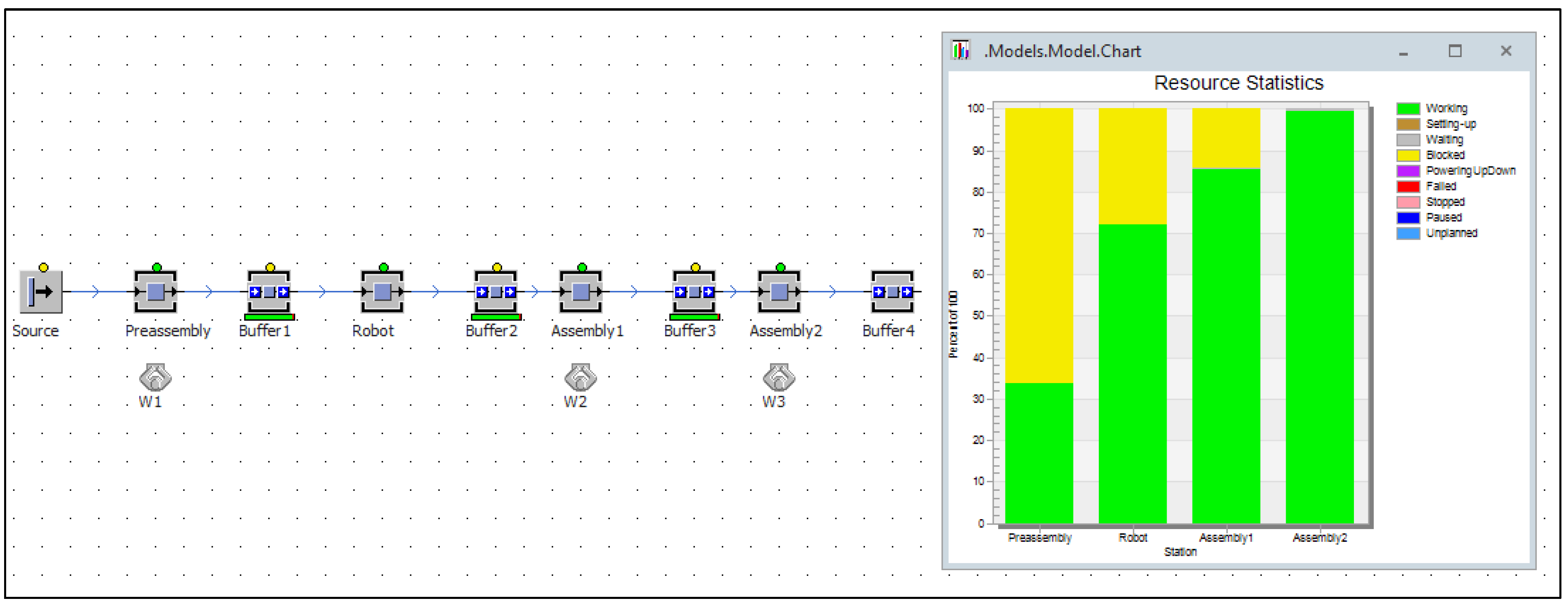
3.1. Proposals for Investment Variants of Production Line Automation
3.2. Economic Evaluation of Investment Variants of the Production Line
3.3. Complex Evaluation of Investment Variants
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Freiberg, F.; Scholz, P. Evaluation of Investment in Modern Manufacturing Equipment Using Discrete Event Simulation. Procedia Econ. Financ. 2015, 34, 217–224. [Google Scholar]
- Aguilar, H.; García-Villoria, A.; Pastor, R. A survey of the parallel assembly lines balancing problem. Comput. Oper. Res. 2020, 124, 105061. [Google Scholar] [CrossRef]
- Van Hop, N. A heuristic solution for fuzzy mixed-model line balancing problem. Eur. J. Oper. Res. 2006, 168, 798–810. [Google Scholar]
- Lin, Y.-C.; Yeh, C.-C.; Chen, W.-H.; Hsu, K.-Y. Implementation Criteria for Intelligent Systems in Motor Production Line Process Management. Processes 2020, 8, 537. [Google Scholar]
- Zhao, R.; Zou, G.; Su, Q.; Zou, S.; Deng, W.; Yu, A.; Zhang, H. Digital Twins-Based Production Line Design and Simulation Optimization of Large-Scale Mobile Phone Assembly Workshop. Machines 2022, 10, 367. [Google Scholar] [CrossRef]
- Daneshjo, N.; Malega, P. Improvement project of production line using automation. TEM J. 2020, 9, 1003–1010. [Google Scholar] [CrossRef]
- Takai, S. An approach to integrate product and process design using augmented liaison diagram, assembly sequencing, and assembly line balancing. J. Mech. Des. Trans. 2021, 143, 1–17. [Google Scholar] [CrossRef]
- Lu, C.; Yang, Z. Integrated assembly sequence planning and assembly line balancing with ant colony optimization approach. Int. J. Adv. Manuf. Technol. 2015, 83, 243–256. [Google Scholar]
- Liu, X.; Yang, X.; Lei, M. Optimisation of mixed-model assembly line balancing problem under uncertain demand. J. Manuf. Syst. 2021, 59, 214–227. [Google Scholar]
- Kalayci, C.B.; Hancilar, A.; Gungor, A.; Gupta, S.M. Multi-objective fuzzy disassembly line balancing using a hybrid discrete artificial bee colony algorithm. J. Manuf. Syst. 2015, 37, 672–682. [Google Scholar] [CrossRef]
- Yilmaz, H.; Yilmaz, M. A multi-manned assembly line balancing problem with classified teams: A new approach. Assem. Autom. 2016, 36, 51–59. [Google Scholar] [CrossRef]
- Hu, X.; Wu, C. Workload smoothing in two-sided assembly lines. Assem. Autom. 2018, 38, 51–56. [Google Scholar] [CrossRef]
- Niroomand, S.; Vizvari, B. Straight assembly line balancing by workload smoothing: New results. IMA J. Manag. Math. 2022, 1–26. [Google Scholar] [CrossRef]
- Fathi, M.; Fontes, D.B.; Urenda Moris, M.; Ghobakhloo, M. Assembly line balancing problem: A comparative evaluation of heuristics and a computational assessment of objectives. J. Model Manag. 2018, 13, 455–474. [Google Scholar] [CrossRef]
- Azizoğlu, M.; İmat, S. Workload smoothing in simple assembly line balancing. Comput. Oper. Res. 2018, 89, 51–57. [Google Scholar]
- Chai, J.-F.; Hu, X.-M.; Qu, H.-W.; Li, M.-H.; Xu, H.-J.; Liu, Y.; Yu, T. Production line 3D visualization monitoring system design based on OpenGL. Adv. Manuf. 2018, 6, 126–135. [Google Scholar]
- Kayar, M.; Akalin, M. Comparing Heuristic and Simulation Methods Applied to the Apparel Assembly Line Balancing Problem. Fibres Text East Eur. 2016, 24, 131–137. [Google Scholar]
- Wang, Y.; Yang, O. Research on industrial assembly line balancing optimization based on genetic algorithm and witness simulation. Int. J. Simul. Model 2017, 16, 334–342. [Google Scholar] [CrossRef]
- Bongomin, O.; Mwasiagi, J.I.; Nganyi, E.O.; Nibikora, I. A complex garment assembly line balancing using simulation-based optimization. Eng. Rep. 2020, 2, e12258. [Google Scholar]
- Mihály, Z.; Lelkes, Z. Improving Flow Lines by Unbalancing. Informatica 2019, 43, 39–44. [Google Scholar] [CrossRef]
- Yang, B.; Chen, W.; Lin, C. The algorithm and simulation of multi-objective sequence and balancing problem for mixed mode assembly line. Int. J. Simul. Model 2017, 16, 357–367. [Google Scholar]
- Song, L.; Jin, S.; Tang, P. Simulation and optimization of logistics distribution for an engine production line. J. Ind. Eng. Manag. 2016, 9, 59–72. [Google Scholar]
- Longo, C.S.; Fantuzzi, C. Simulation and optimization of industrial production lines. At-Automatisierungstechnik 2018, 66, 320–330. [Google Scholar] [CrossRef]
- Pekarcikova, M.; Trebuna, P.; Kliment, M.; Dic, M. Solution of Bottlenecks in the Logistics Flow by Applying the Kanban Module in the Tecnomatix Plant Simulation Software. Sustainability 2021, 13, 7989. [Google Scholar]
- Malega, P.; Gazda, V.; Rudy, V. Optimization of production system in plant simulation. Simulation 2021, 98, 295–306. [Google Scholar]
- Sujová, E.; Vysloužilová, D.; Čierna, H.; Bambura, R. Simulation Models of Production Plants as a Tool for Implementation of the Digital Twin Concept into Production. Manuf. Technol. 2020, 20, 527–533. [Google Scholar] [CrossRef]
- Grabowik, C.; Ćwikła, G.; Kalinowski, K.; Kuc, M. A Comparison Analysis of the Computer Simulation Results of a Real Production System: Production System Modelling with FlexSim and Plant Simulation Software. Adv. Intell. Syst. Comput. 2020, 950, 344–354. [Google Scholar]
- Suhanyiova, A.; Suhanyi, L. Analysis of depreciation of intangible and tangible fixed assets and the impact of depreciation on the profit or loss and on the tax base of the enterprise. In Proceedings of the 18th International Scientific Conference on International Relations—Current Issues of World Economy and Politics, Smolenice, Slovakia, 30 November–1 December 2017; pp. 939–950. [Google Scholar]
- Zhao, J. Risk Assessment Method of Agricultural Management Investment Based on Genetic Neural Network. Secur. Commun. Networks 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Ilbahar, E.; Kahraman, C.; Cebi, S. Risk assessment of renewable energy investments: A modified failure mode and effect analysis based on prospect theory and intuitionistic fuzzy AHP. Energy 2022, 239, 121907. [Google Scholar]
- Khalfi, L.; Ourbih-Tari, M. Stochastic risk analysis in Monte Carlo simulation: A case study. Commun. Stat. Simul. Comput. 2019, 49, 3041–3053. [Google Scholar]
- Huo, Y.; Xu, C.; Shiina, T. Period value at risk and its estimation by Monte Carlo simulation. Appl. Econ. Lett. 2021, 29, 1675–1679. [Google Scholar] [CrossRef]
- Tobisova, A.; Senova, A.; Rozenberg, R. Model for Sustainable Financial Planning and Investment Financing Using Monte Carlo Method. Sustainability 2022, 14, 8785. [Google Scholar]
- Abba, Z.Y.I.; Balta-Ozkan, N.; Hart, P. A holistic risk management framework for renewable energy investments. Renew Sustain. Energy Rev. 2022, 160, 112305. [Google Scholar]
- Zhu, L. A simulation based real options approach for the investment evaluation of nuclear power. Comput. Ind. Eng. 2012, 63, 585–593. [Google Scholar] [CrossRef]
- Edjossan-Sossou, A.M.; Galvez, D.; Deck, O.; Al Heib, M.; Verdel, T.; Dupont, L.; Chery, O.; Camargo, M.; Morel, L. Sustainable risk management strategy selection using a fuzzy multi-criteria decision approach. Int. J. Disaster Risk Reduct. 2020, 45, 101474. [Google Scholar] [CrossRef]
- Ristanović, V.; Primorac, D.; Kozina, G. Operational Risk Management Using Multi-Criteria Assessment (AHP Model). The. Vjesn. 2021, 28, 678–683. [Google Scholar]
- Derradji, R.; Hamzi, R. Multi-criterion analysis based on integrated process-risk optimization. J. Eng. Des. Technol. 2020, 18, 1015–1035. [Google Scholar]
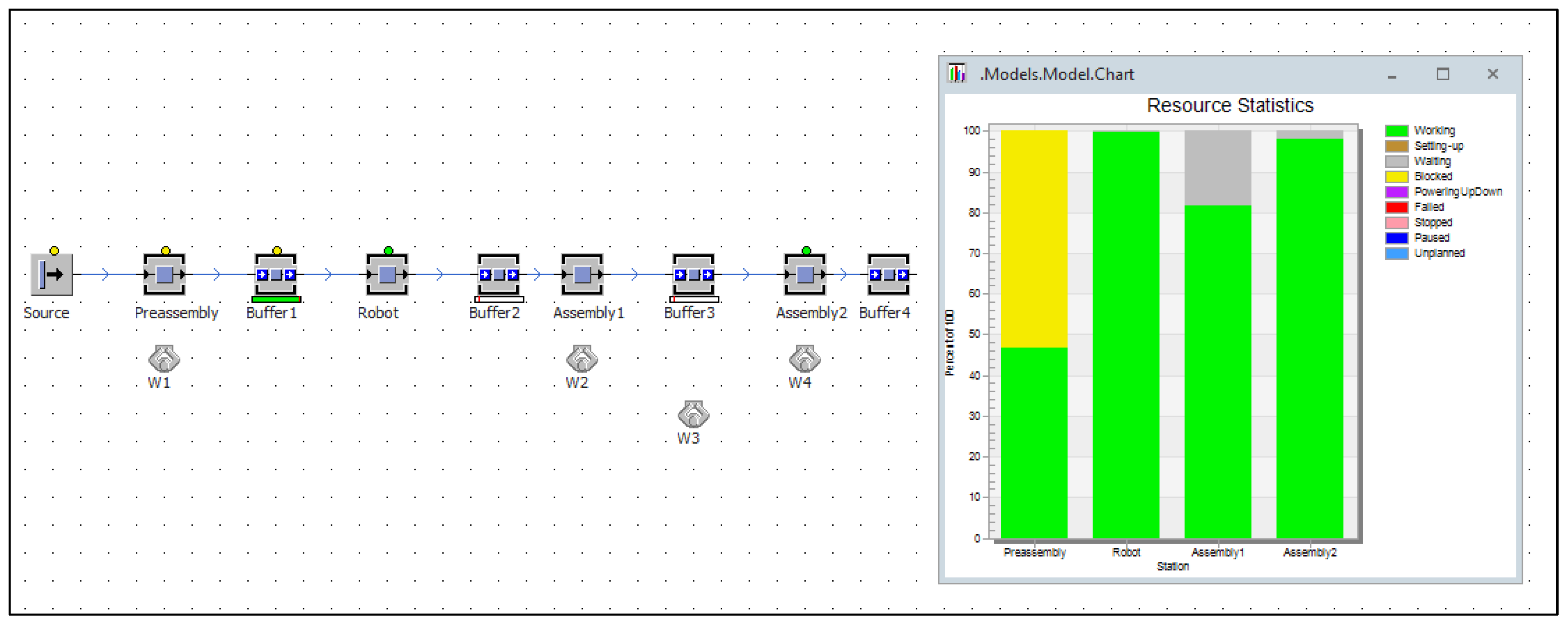
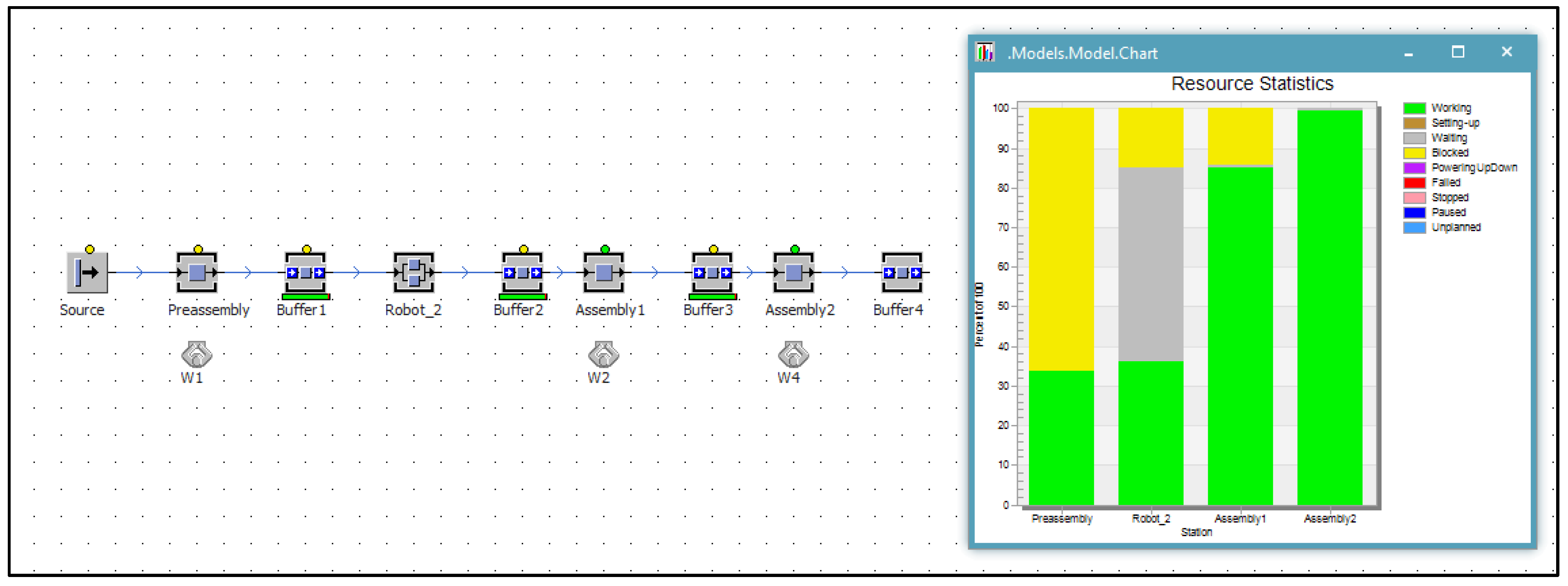
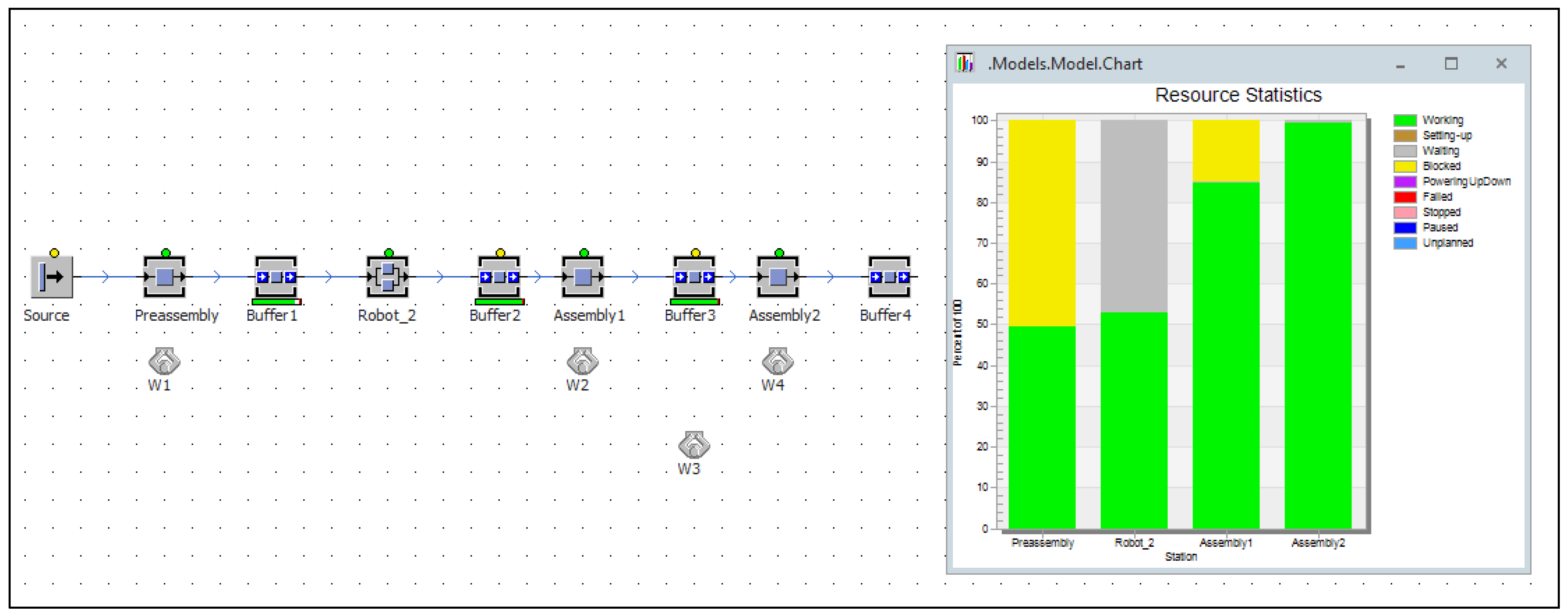


| Workplace | Production Operations/Operation Times (s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Welding | Chimney installation | Chimney welding | Sidewall riveting | Sidewall welding | Tip cleaning 19.92 s Assistance from Assembly1 workplace at “Sidewall riveting” operation 15 s | ||||
| 137.70 | 15.21 | 24.43 | 43.07 | 50.07 | |||||
| Assembly1 | Stickers incl. submissions | Chimney and interior sealing | Insert the seal | Flap installation | Cover sealing | Assistance on Welding workplace at “Sidewall riveting” operation 15 s | |||
| 120.07 | 13.43 | 35.71 | 17.29 | 20.50 | 18.14 | ||||
| Assembly2 | Closing by cover | Riveting the lid | Knocking the lid | Labeling | Flap inspection | Inserting accessories | Closing by 2 lids | Labeling QA | Transfer to the box |
| 108.07 | 10.93 | 33.86 | 12.20 | 12.93 | 19.79 | 3.86 | 15.00 | 3.43 | 9.00 |
| Operation “Labeling” transferred to an off-line worker (operator) | |||||||||
| Workplace 1 | Pre-Assembly | Workplace 2 | Robot | |||||
|---|---|---|---|---|---|---|---|---|
| Production Operations | Chimney Installation | Installation into the Jig | Production Operations | Welding | Chimney Sealing | |||
| TV160 | 15.2 | 24.4 | TV160 | 110.0 | 19.7 | |||
| Variant 1a | 30 | Variant 1a | 66 | |||||
| Variant 1b | 30 | Variant 1b | 66 | |||||
| Variant 2a | 30 | Variant 2a | 33 | |||||
| Variant 2b | 30 | Variant 2b | 33 | |||||
| Workplace 3 | Assembly1 | |||||||
| Production operations | Stickers incl. submissions | Chimney sealing | Insert the seal | Flap installation | Sealing the cover | Closing the lid | ||
| TV160 | 13.4 | 35.7 | 17.3 | 20.5 | 18.1 | 10.9 | ||
| Variant 1a | 81 | |||||||
| Variant 1b | 54 | |||||||
| Variant 2a | 81 | |||||||
| Variant 2b | 54 | |||||||
| Workplace 4 | Assembly2 | |||||||
| Production operations | Lid riveting | Knocking of rivets | Labelling | Flap inspection | Inserting accessories | Closing with two covers | Gluing the QA label | Transfer to the box |
| TV160 | 33.9 | 12.2 | 12.9 | 19.8 | 3.9 | 15.0 | 3.4 | 9.0 |
| Variant 1a | 98 | |||||||
| Variant 1b | 66 | |||||||
| Variant 2a | 98 | |||||||
| Variant 2b | 66 | |||||||
| Indicator | Unit | Value |
|---|---|---|
| Number of welds on the chimney | pcs | 7 |
| Number of welds on the product body | pcs | 30 |
| Welding time for 1 weld | s | 3 |
| Length of sealant of the chimney | m | 0.5 |
| Length of sealant of the body | m | 1.76 |
| Length of sealant for sealing the top lid | m | 3.93 |
| Application time of sealant with a length of 12 m | min | 1 |
| Number of Robots | Number of Workers | Operation Time (s/pcs) | Production (pcs/8 h) | Increase in Production Compared to the Current State | |||||
|---|---|---|---|---|---|---|---|---|---|
| Pre-Assembly | Robot | Assembly1 | Assembly2 | (pcs/8 h) | (%) | ||||
| Currant state | 0 | 3 | 138 | - | 121 | 109 | 207 | - | |
| V1a | 1 | 3 | 30 | 66 | 81 | 98 | 291 | +40 | 40.6 |
| V1b | 1 | 4 | 30 | 66 | 54 | 66 | 434 | +109 | 109.7 |
| V2a | 2 | 3 | 30 | 33 | 81 | 98 | 291 | +40 | 40.6 |
| V2b | 2 | 4 | 30 | 33 | 54 | 66 | 440 | +112 | 112.6 |
| Indicator | Unit | Value | |
|---|---|---|---|
| 1 Robot | 2 Robots Parallel | ||
| Investment costs | EUR | 138,000 | 276,000 |
| Nominal time fund | days/year | 265 | |
| Efficient time fund of the robot | h/year, 1robot | 2014 | |
| Utilization of robots | % | 85.00 | |
| Depreciation period of the robot | years | 6 | |
| Product price | EUR/pc | 9.50 | |
| Labor costs | EUR/h | 10.50 | |
| Material consumption | EUR/2pcs | 10.00 | |
| Financial Criterion | Unit | Acceptable Value | Expected Value | |||
|---|---|---|---|---|---|---|
| V1a | V1b | V2a | V2b | |||
| NPV | EUR | NPV > 0 | 4380 | 456,786 | −136,571 | 315,835 |
| PI | coeff. | PI > 1 | 1.03 | 4.31 | 0.51 | 2.14 |
| DPP | years | DPB < 6 | 5.79 | 1.22 | 10.88 | 2.55 |
| Risk Factor | Unit | Statistical Characteristic | Distribution |
|---|---|---|---|
| Nominal time fund | days/year | Likeliest 265; Min. 258; Max. 270 | BetaPERT |
| Investment costs | EUR/1robot | Mean 138,000; Std. Dev. 13,800 | Normal |
| Planned downtime for repair and maintenance of robots | % | Likeliest 5.00; Min. 4.00; Max. 5.50 | BetaPERT |
| Material consumption | EUR/2pcs | Likeliest 10; Min. 10; Max. 12 | Triangular |
| Labor costs | EUR/h | Likeliest 10.00; Min. 10.50; Max. 12.00 | Triangular |
| Electricity price | EUR/kWh | Likeliest 2.4; Min. 3; Max. 4 | Triangular |
| Electricity consumption | kWh/month | Likeliest 20; Min. 18; Max. 22 | BetaPERT |
| Product price | EUR/pc | Likeliest 9.50; Min. 9.00; Max. 10.50 | Triangular |
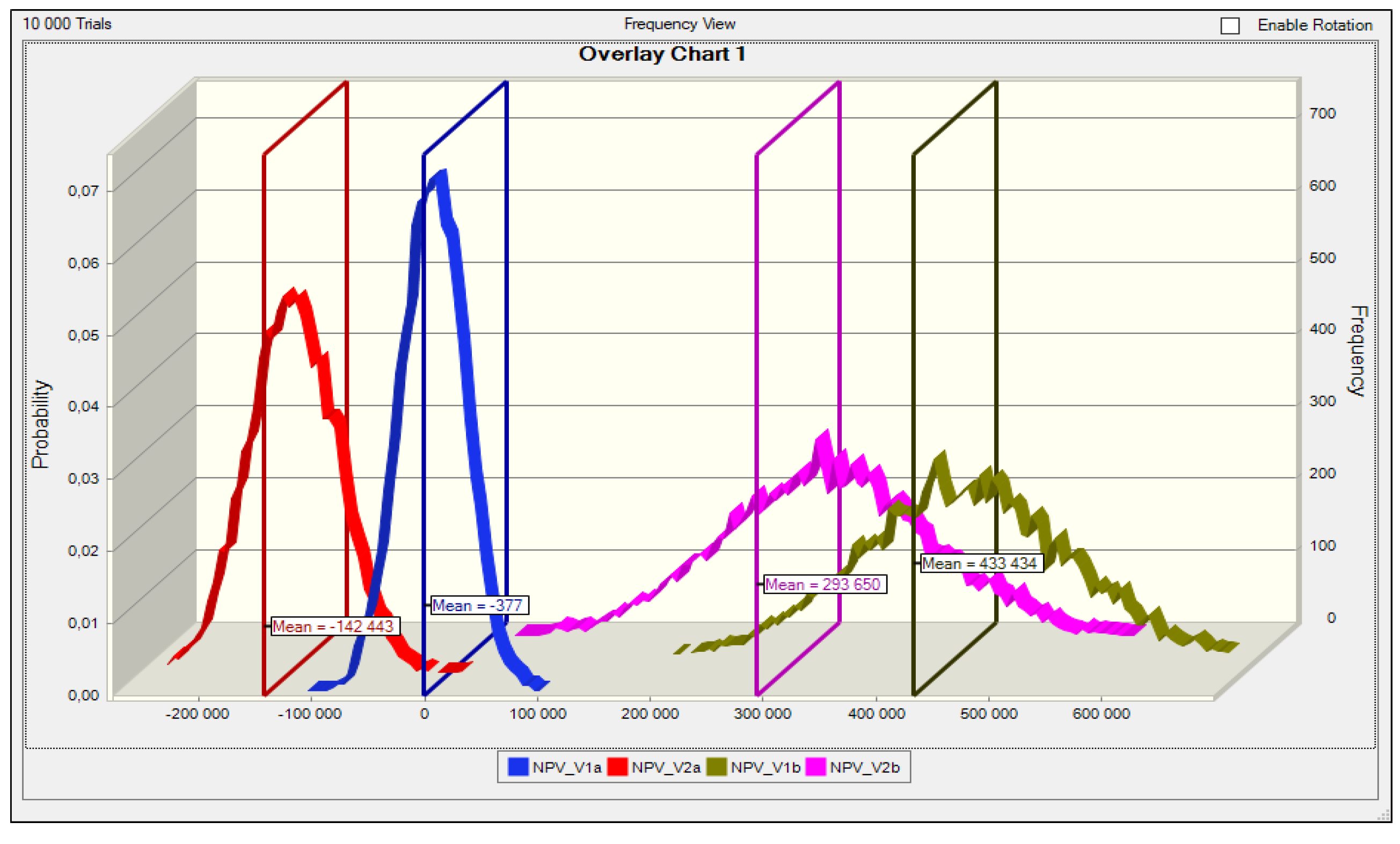
| Statistical Characteristics | V1a | V1b | V2a | V2b |
|---|---|---|---|---|
| Trials | 10,000 | 10,000 | 10,000 | 10,000 |
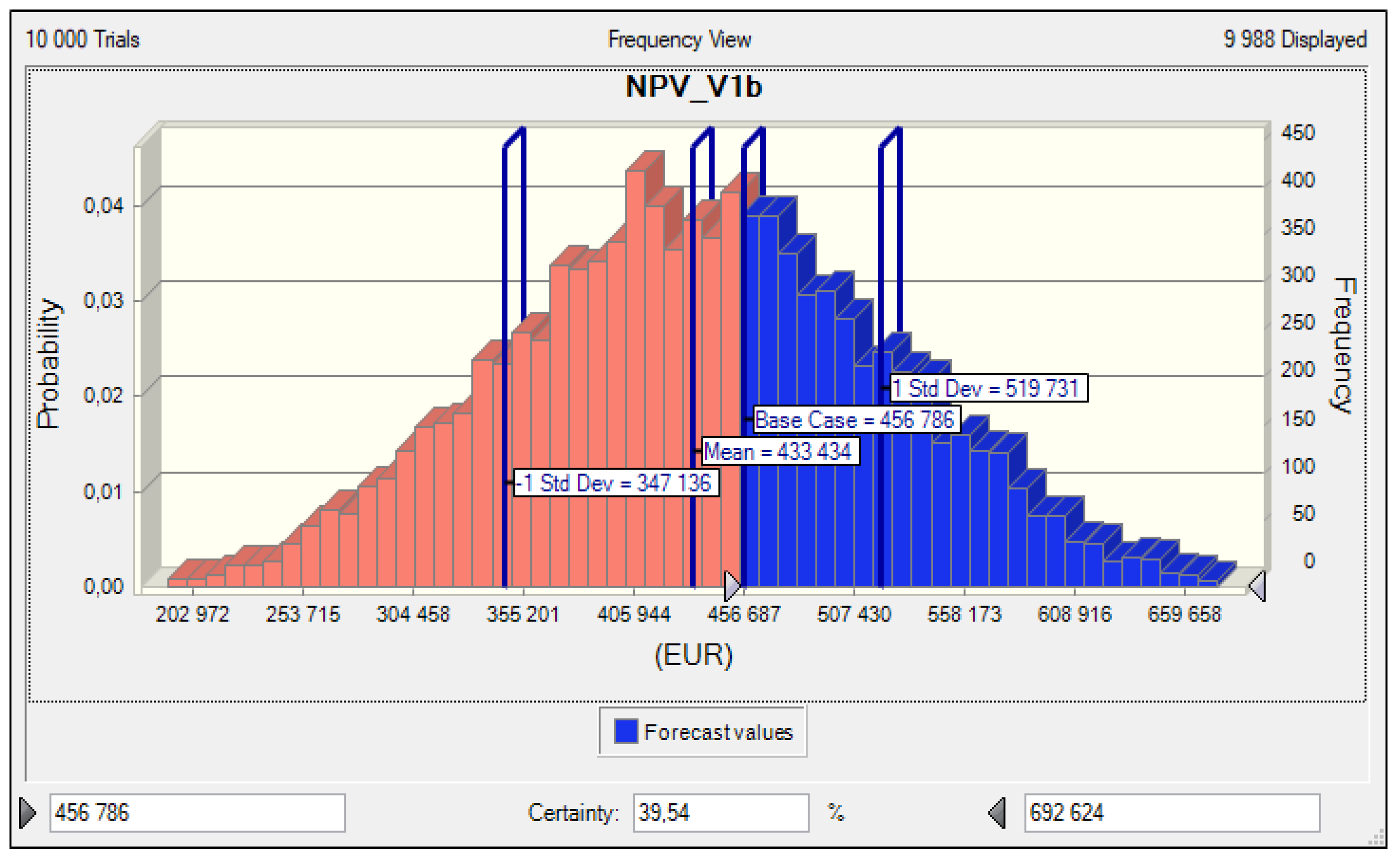
| Base Case | 4380 | 456,786 | −136,571 | 315,835 |
| Mean | −377 | 433,434 | −142,443 | 293,650 |
| Median | −236 | 433,376 | −142,678 | 292,926 |
| Standard Deviation | 28,253 | 86,298 | 39,503 | 89,483 |
| Variance | 798,234,864 | 7,447,266,993 | 1,560,457,568 | 8,007,283,349 |
| Skewness | 0.0011 | 0.0186 | 0.0262 | 0.0266 |
| Kurtosis | 2.92 | 2.69 | 2.99 | 2.8 |
| Coeff. of Variation | −74.88 | 0.1991 | −0.2773 | 0.3047 |
| Minimum | −115,446 | 156,810 | −281,807 | −18,798 |
| Maximum | 98,432 | 692,624 | 11,474 | 651,255 |
| Indicator | Value (EUR) | Deviation from NPV_V1b | |
|---|---|---|---|
| (EUR) | (%) | ||
| NPV_V1b | 456,786 | - | - |
| mean NPV_V1b | 433,434 | −23,352 | −5.1 |
| Indicator | Unit | V1b | V2b | ||
|---|---|---|---|---|---|
| Value | Partial Orders | Value | Partial Orders | ||
| Number of robots | pc | 1 | 1. | 2 | 2. |
| Number of workers | person | 4 | 1. | 4 | 1. |
| Production volume | pcs/8 h | 434 | 2. | 440 | 1. |
| NPV | EUR | 456,786 | 1. | 315,835 | 2. |
| PI | coeff. | 4.31 | 1. | 2.14 | 2. |
| DPP | years | 1.22 | 1. | 2.55 | 2. |
| Mean NPV | EUR | 433,434 | 1. | 293,650 | 2. |
| Coeff. of Variation | coeff. | 0.1991 | 1. | 0.3047 | 2. |
| The sum of the partial orders | 9 | 14 | |||
| Overall order | 1. | 2. | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Janeková, J.; Fabianová, J.; Kádárová, J. Optimization of the Automated Production Process Using Software Simulation Tools. Processes 2023, 11, 509. https://doi.org/10.3390/pr11020509
Janeková J, Fabianová J, Kádárová J. Optimization of the Automated Production Process Using Software Simulation Tools. Processes. 2023; 11(2):509. https://doi.org/10.3390/pr11020509
Chicago/Turabian StyleJaneková, Jaroslava, Jana Fabianová, and Jaroslava Kádárová. 2023. "Optimization of the Automated Production Process Using Software Simulation Tools" Processes 11, no. 2: 509. https://doi.org/10.3390/pr11020509
APA StyleJaneková, J., Fabianová, J., & Kádárová, J. (2023). Optimization of the Automated Production Process Using Software Simulation Tools. Processes, 11(2), 509. https://doi.org/10.3390/pr11020509






