Optimum Design for Inserted Tooth Slips Setting Process Based on the Furrow Effect
Abstract
:1. Introduction
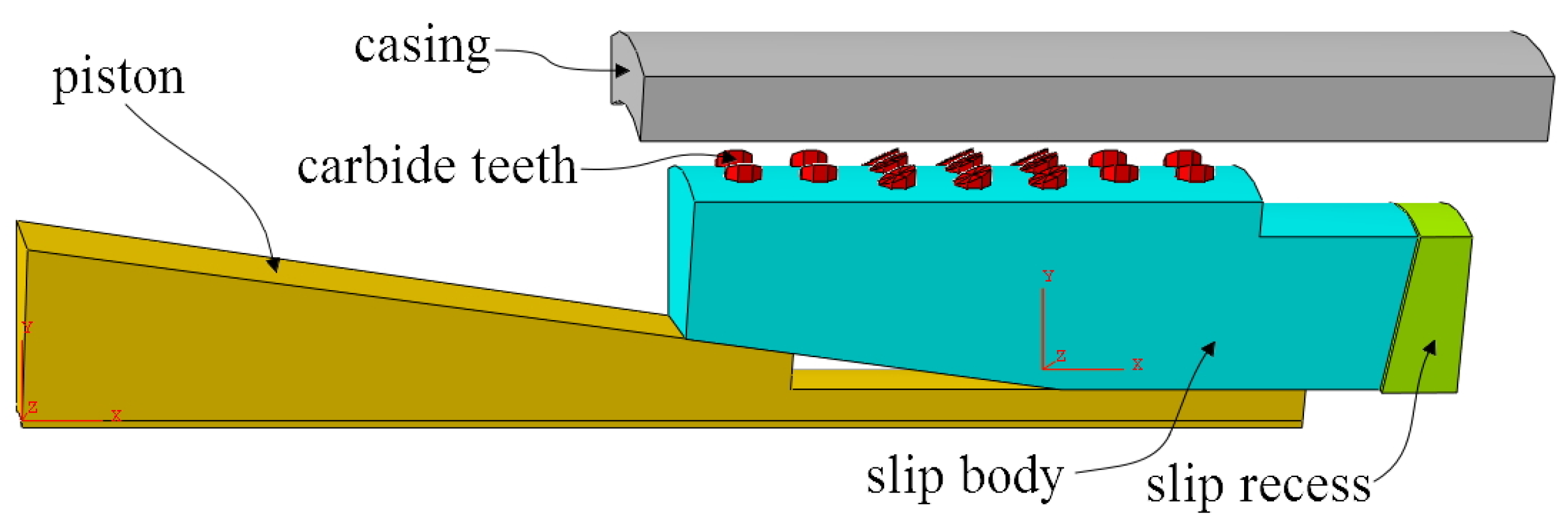
2. The Structure and Working Principle of the Inserted Tooth Slip Sidetracking Packer
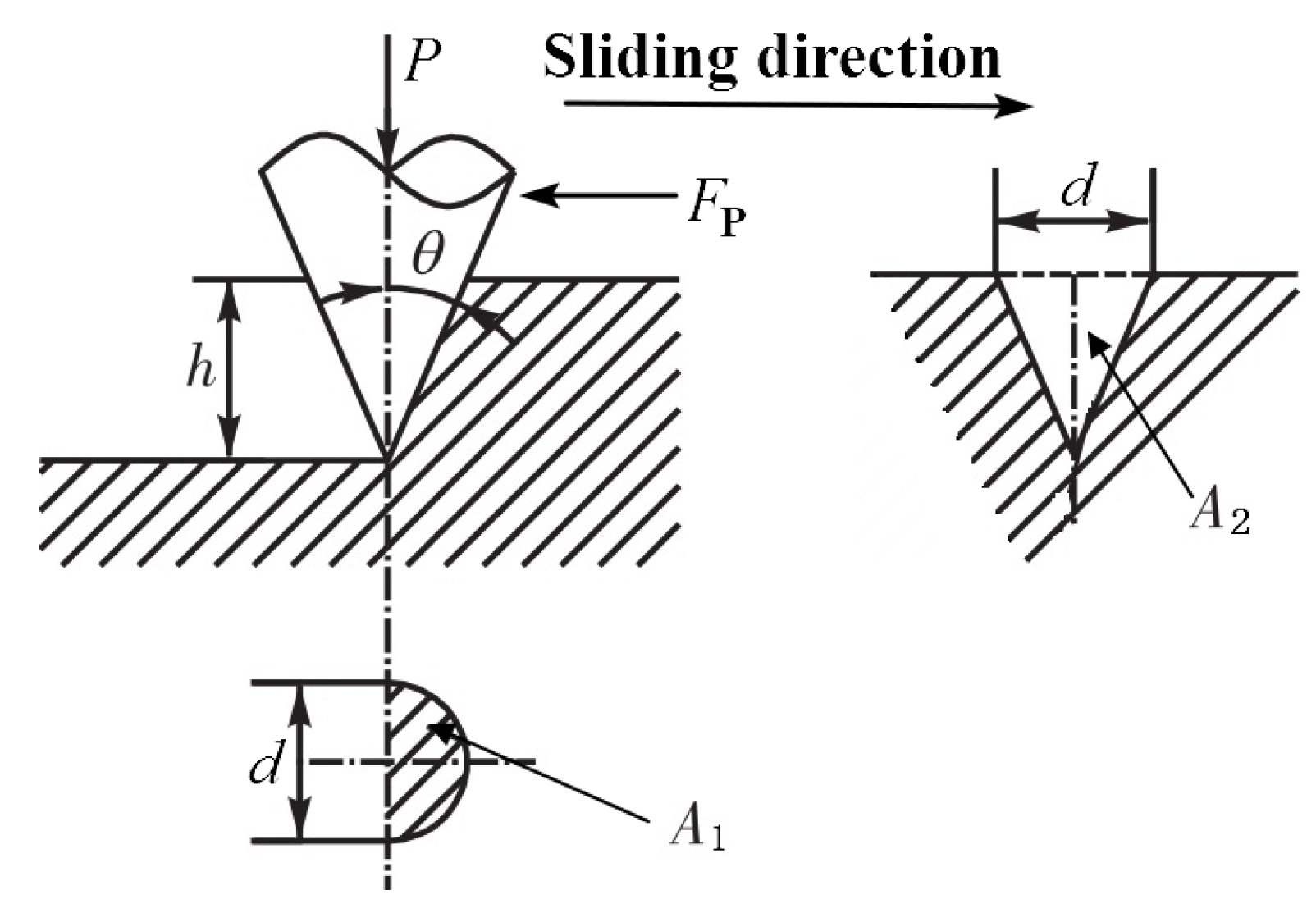
3. The Effect of Furrow Action
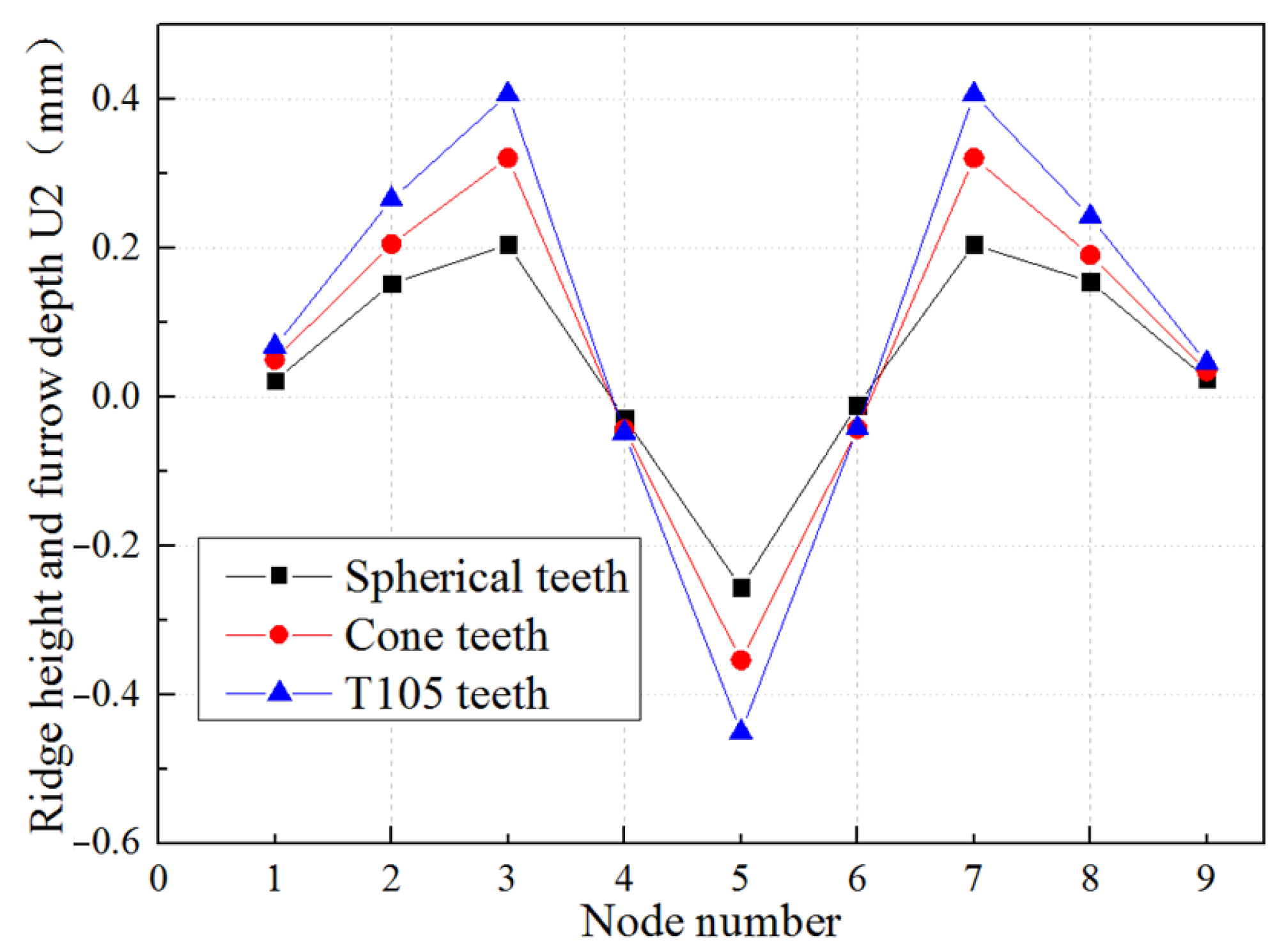
4. Numerical Simulation Analysis Based on Furrow Effect
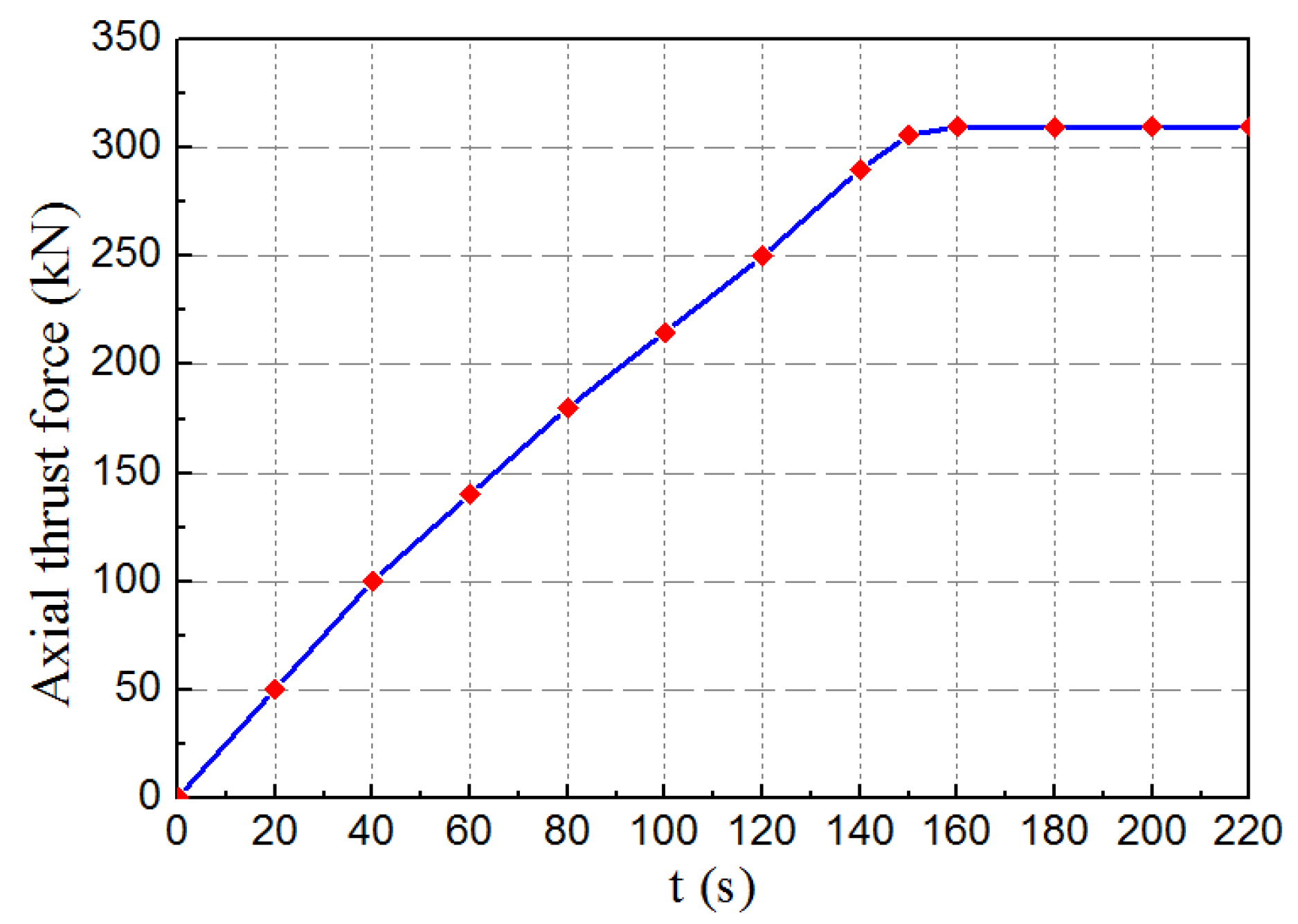
4.1. Finite Element Simulation Model
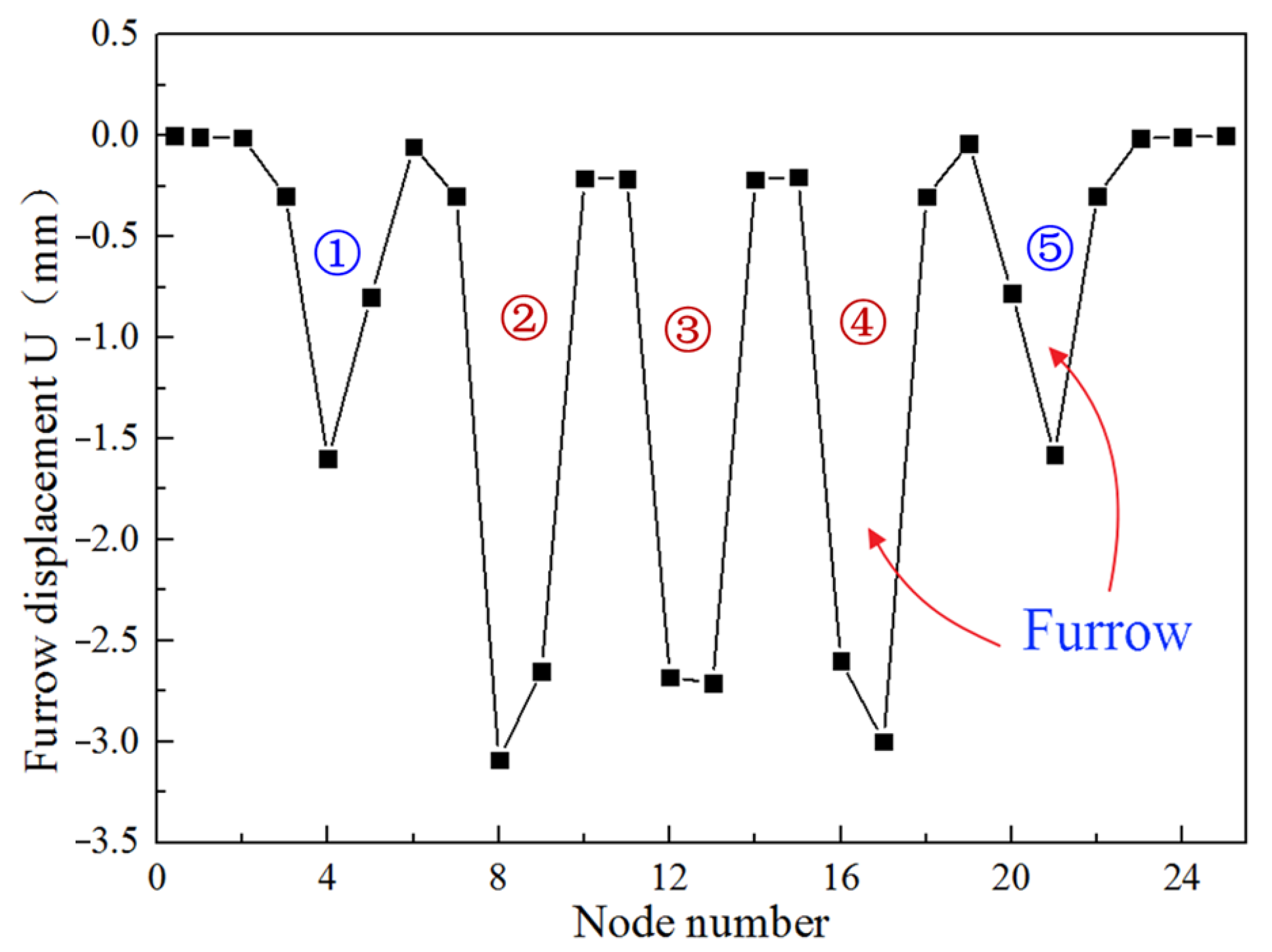
4.2. Taking No Account of the Furrow Effect
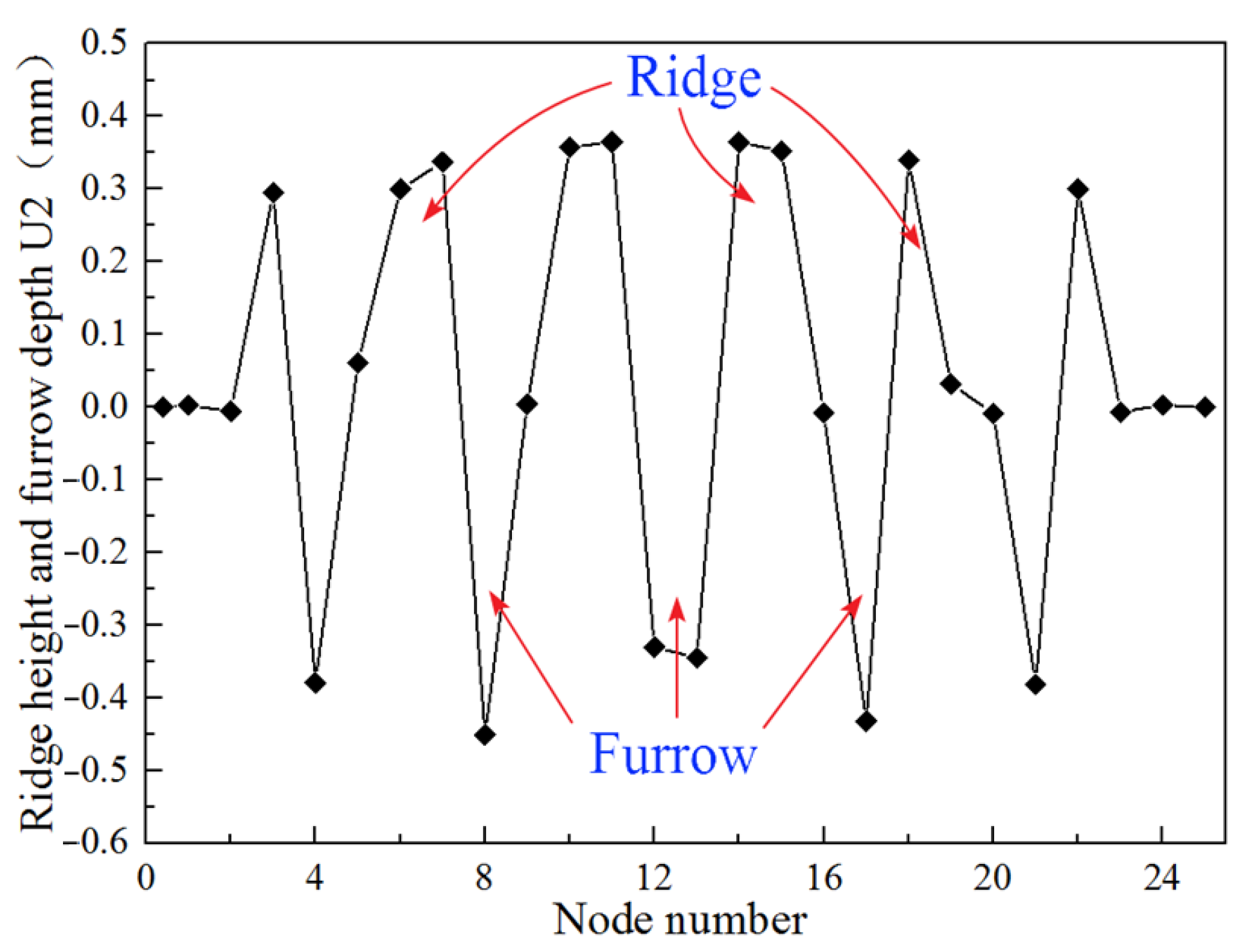
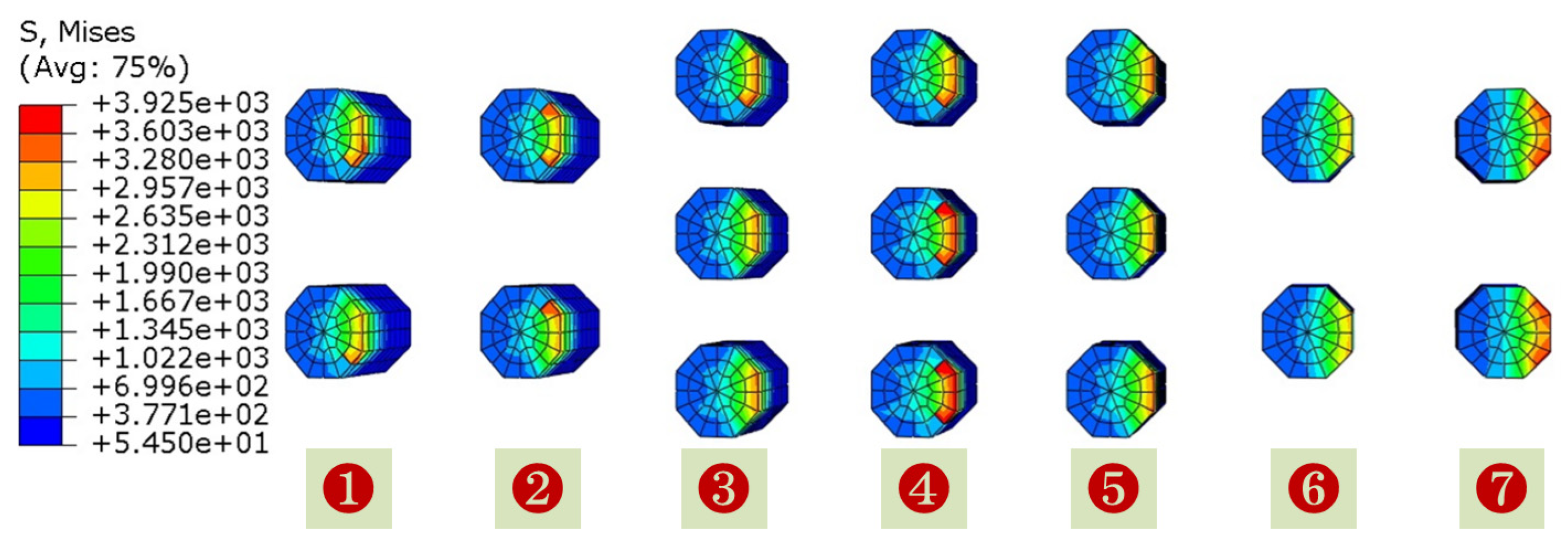
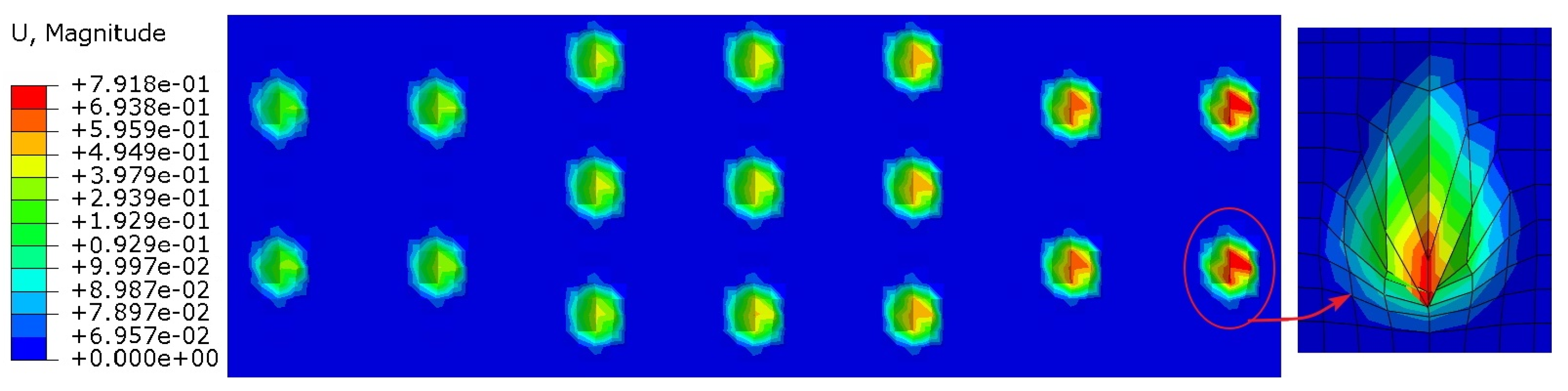
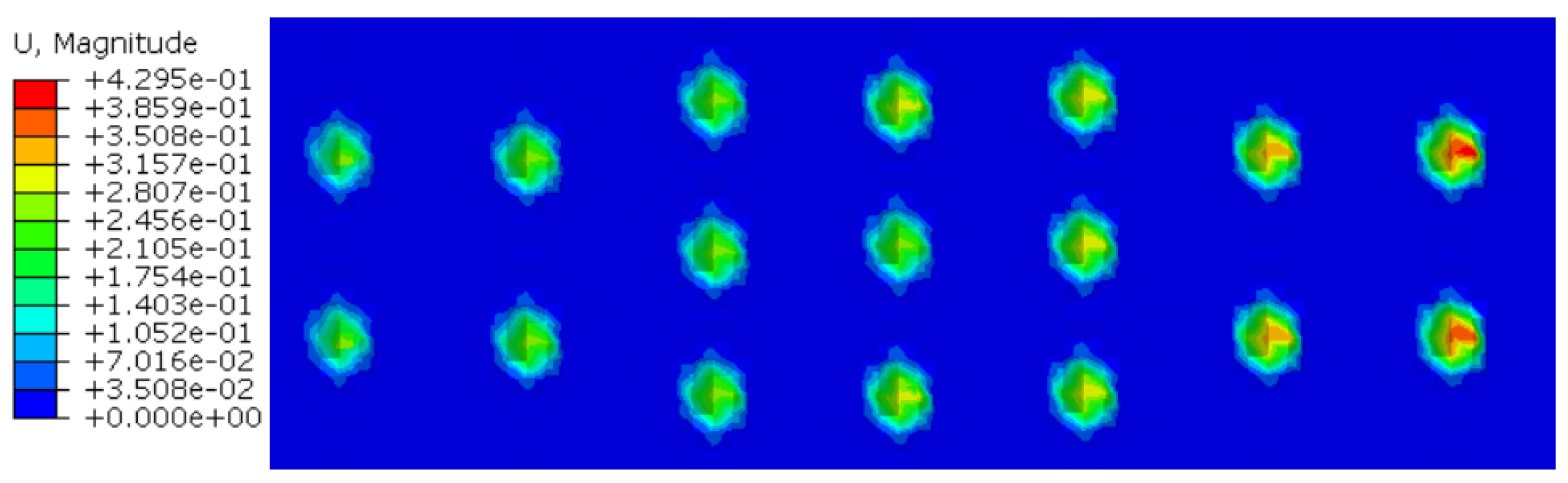
4.3. Considering the Furrow Effect and Adhesion Effect
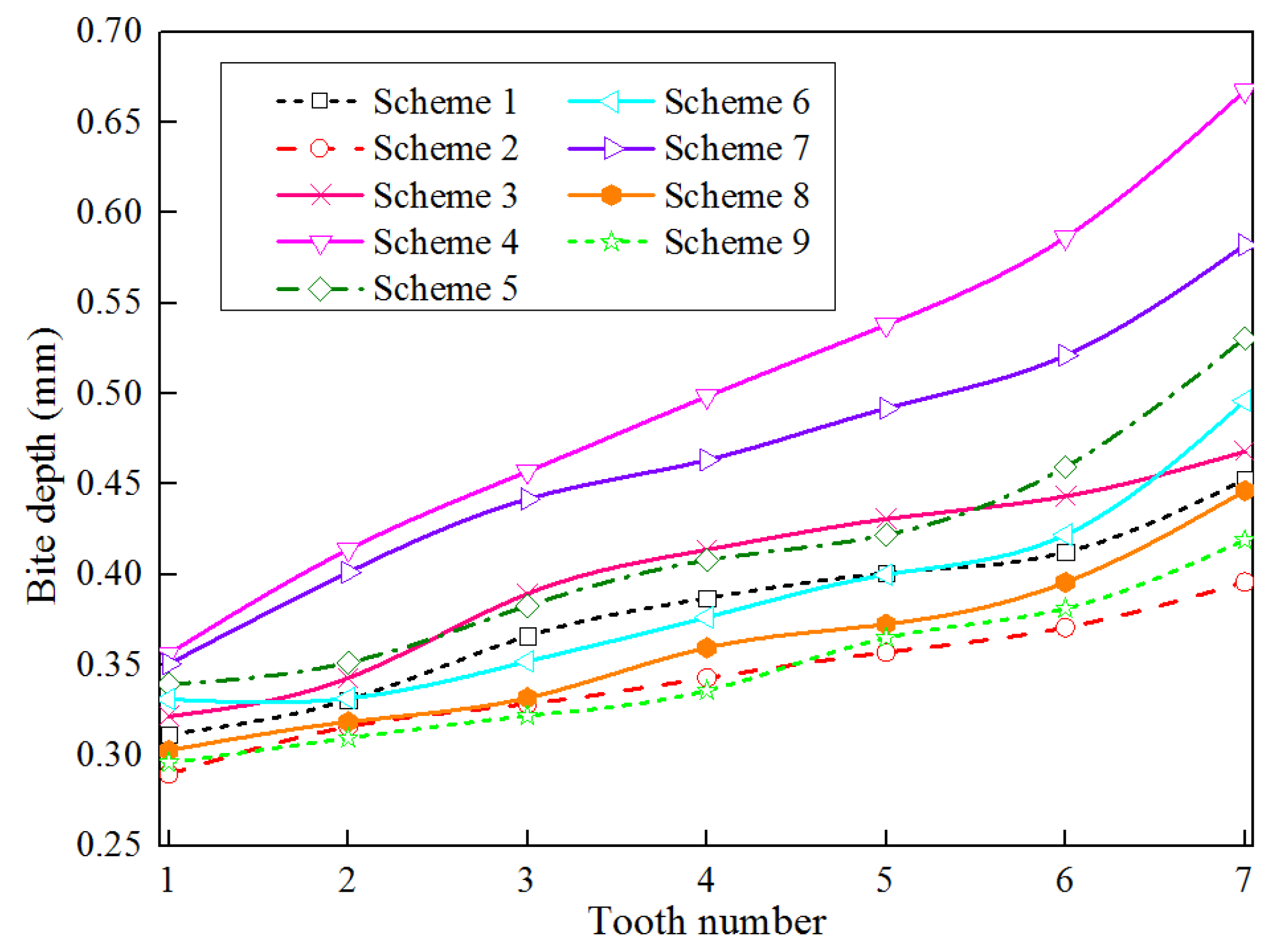
5. Orthogonal Optimization Analysis of Slip Structure and Experiment Study
5.1. Orthogonal Optimization Analysis of Slip Structure
5.2. Experiment Study
6. Conclusions
- (1)
- In the FEA and calculation of the setting process of inserted tooth-type slip, it is not only necessary to consider the furrow friction coefficient fp, but also the effect of the ridge on the furrow friction coefficient fp, which requires the introduction of correction factor kp.
- (2)
- The corresponding furrow friction coefficient fp varies according to the different furrow effects occurring on the casing surface caused by the various types of teeth inserted on the packer slips. The furrow effect is related to the sharpness of the tooth tips of the slips. The sharper the tooth tips are, the more obvious the furrow effect is.
- (3)
- Under the dual effects of the furrow effect and the adhesion effect, the teeth of the slip feed into the casing wall to produce a uniform and distinct indentation, and the disconnection of the maximum stress area of each indentation, as well as the safety and reliability of all carbide teeth, realize the reliable setting of the packer.
- (4)
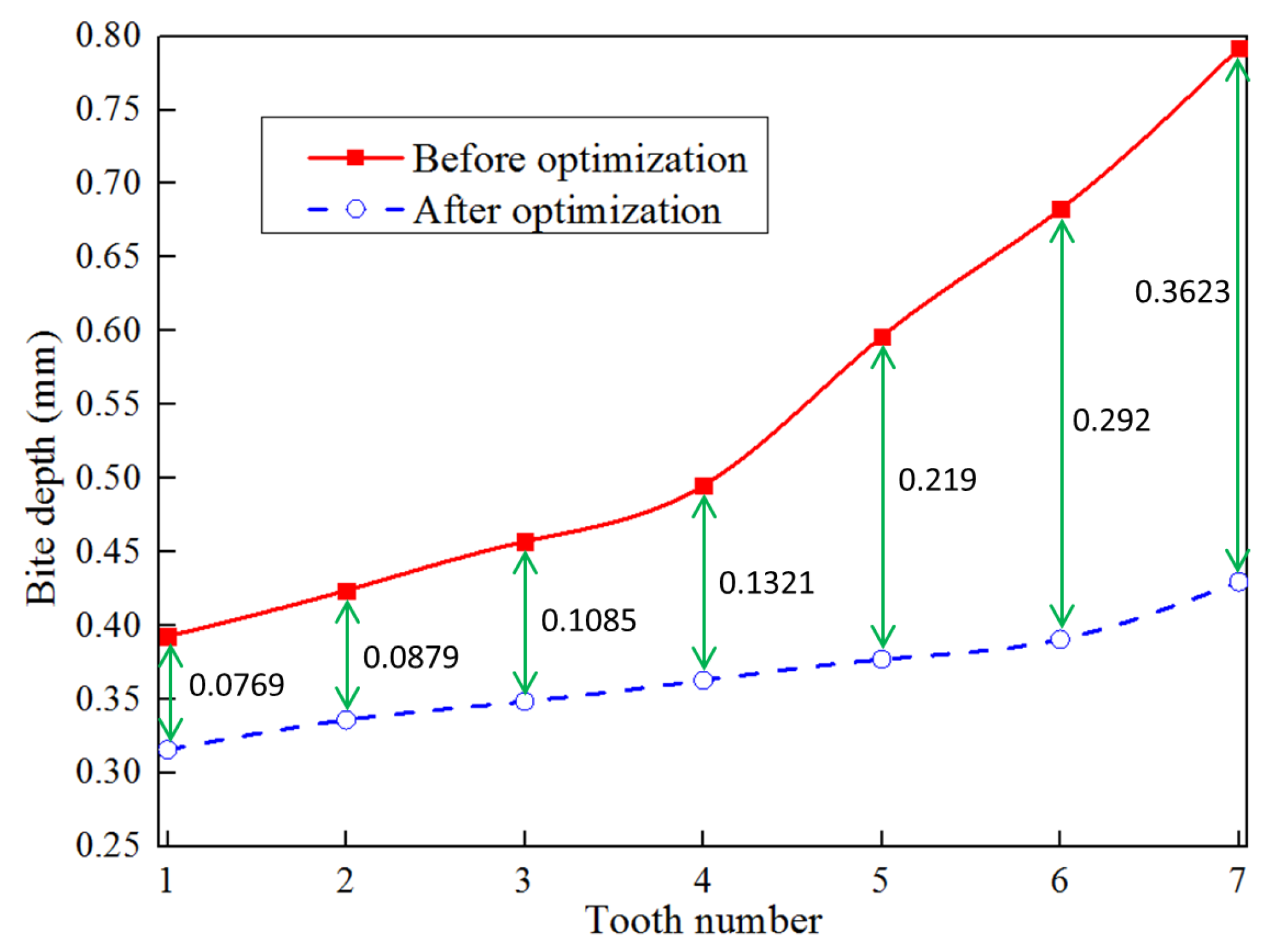
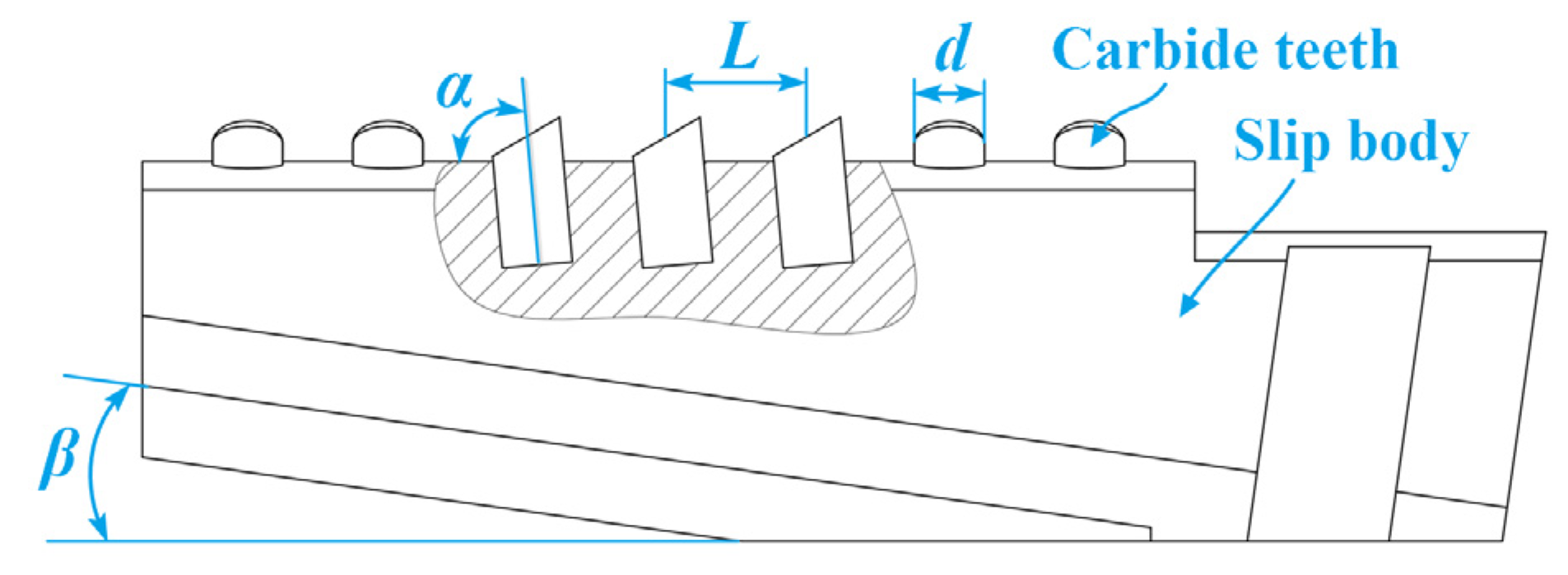
- Through orthogonal experiments, the optimal combination parameters of the slips were obtained by taking the optimal bite depth uniformity as the objective function: slip tooth installation spacing L = 10 mm, slip tooth installation angle α = 80°, slip tooth diameter d = 10 mm, and slip wedge angle β = 6°. The standard deviation of bite depth uniformity of the optimized slip teeth is 74.45% lower than that before optimization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A1 | is the projected area of the normal setting load support surface |
| A2 | is the projected area of the furrow groove, as shown in Figure 3 |
| P | is the normal setting load |
| FP | is the furrow friction resistance |
| σs | is the yield strength |
| fp | is the furrow friction coefficient |
| θ | is the half-cone angle |
| kp | is the correction factor |
| fa | is the adhesive friction coefficient |
| T | is the setting load of each slip |
| F | is the axial load borne by each slip |
| f | is the total friction coefficient |
| L | is slip tooth installation spacing, as shown in Figure 16 |
| α | is the slip tooth installation angle |
| d | is the slip tooth diameter |
| β | is the slip wedge angle |
References
- Kong, C.; Zhang, D.; Liang, Z.; Cai, R. Mechanical analysis of drill bit during dual-casing sidetracking. J. Pet. Sci. Eng. 2017, 159, 970–976. [Google Scholar] [CrossRef]
- Campbell, J.M.; Gregurek, P.; Swadi, S.N.; Dewey, C.; Desai, P. New tools and procedures increase reliability of openhole sidetrack operations. In Proceedings of the SPE Eastern Regional Meeting, Columbus, OH, USA, 17–19 August 2011. [Google Scholar]
- Orodu, O.D.; Tang, Z.; Anawe, P.A. Sidetrack and recompletion risk evaluation—Waterflooded reservoir. J. Pet. Sci. Eng. 2011, 78, 705–718. [Google Scholar] [CrossRef]
- Okogbe, B.; Orimoloye, S.; Adewale, O.; Avanoma, E.; Alikor, E.O.; Papuc, V. Cased Hole Section Milling And Under Reaming Operation In Converting Oil Well Into A Water Disposal Well, Onshore Amukpe Oil Field. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 5–7 August 2013. [Google Scholar] [CrossRef]
- Chen, Y. Development and application of a new double-slip hpht liner hanger. Nat. Gas Ind. 2010, 30, 48–50. [Google Scholar]
- Zhang, D.R.; Li, D.; Kong, C.Y. Design of new-pattern sidetracking setting tool and finite element analysis for slips. Oil Field Equip. 2012, 41, 69–71. (In Chinese) [Google Scholar]
- Wu, K.S.; Xie, B.; Yang, X.K. 3-D fea of contact for slip system of packer systems. Oil Field Equip. 2005, 34, 47–49. (In Chinese) [Google Scholar]
- Wang, Z.J.; Deng, W.D.; Lin, Z.C.; Shang, X.; Wang, Y. Finite element analysis and structure improvements of packer slip in horizontal wells. Oil Drill. Prod. Technol. 2013, 35, 78–81. [Google Scholar]
- Wu, E.C. Mechanical Analysis & Experimental Research on Valvular Slip; Daqing Petroleum Institute: Daqing, China, 2007. (In Chinese) [Google Scholar]
- Wang, D.; He, S.P.; Zhang, X. A study on contact stress of packer slip. J. Exp. Mech. 2006, 21, 351–356. [Google Scholar]
- Chen, Y.; Tan, J.; Xiao, G. Investigation on the Depth of Slip Hanger Teeth Bite into Casing and the Mechanical Properties of Casing under Different Suspension Loads in Ultra-Deep Wells. Stroj. Vestn. J. Mech. Eng. 2021, 67, 516–524. [Google Scholar] [CrossRef]
- Persson, B. Influence of frozen capillary waves on contact mechanics. Wear 2008, 264, 746–749. [Google Scholar] [CrossRef]
- Bharat, B.; Jacob, N.I.; Uzi, L. Nanotribology: Friction, wear and lubrication at the atomic scale. Nature 1995, 374, 607–616. [Google Scholar]
- Xie, Z.F.; Yu, J.X.; Qian, L.M. Load effect on the translation of friction mechanism of four materials. J. Shanghai Jiaotong Univ. 2009, 43, 1930–1935. (In Chinese) [Google Scholar]
- Gao, S.Z.; Xu, G.B. Sliding-friction coefficient calculation method of plane-gate walk supporting. J. Tianjin Univ. 2014, 47, 383–388. (In Chinese) [Google Scholar]
- Zhou, X.R.; Yang, Q.M. Friction, Wear and Lubrication; Petroleum Industry Press: Beijing, China, 1997. (In Chinese) [Google Scholar]
- Wen, S.Z.; Huang, P. Tribological Principles; Tsinghua University Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Bikerman, J.J. Ploughing and Adhesion of Sliding Metals. J. Appl. Phys. 1943, 14, 436. [Google Scholar] [CrossRef]
- Huynh, N.T.; Nguyen, T.V.T.; Nguyen, Q.M. Optimum Design for the Magnification Mechanisms Employing Fuzzy Logic–ANFIS. Comput. Mater. Contin. 2022, 73, 5961–5983. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.M. CFD Analysis and Optimum Design for a Centrifugal Pump Using an Effectively Artificial Intelligent Algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef]
- Pal, M.; Mandal, N.K.; Aggarwal, M.L. A-optimal designs for optimum mixture in an additive quadratic mixture model. Statistics 2017, 51, 265–276. [Google Scholar] [CrossRef]
- Sun, Y.; Li, C.; You, J.; Bu, C.; Yu, L.; Yan, Z.; Liu, X.; Zhang, Y.; Chen, X. An Investigation of the Properties of Expanded Polystyrene Concrete with Fibers Based on an Orthogonal Experimental Design. Materials 2022, 15, 1228. [Google Scholar] [CrossRef]
- Chen, S.; Jin, E.; Xu, G.; Zhuo, S.; Chen, X. Factors Influencing the Low-Temperature Properties of Styrene-Butadiene-Styrene Modified Asphalt Based on Orthogonal Tests. Polymers 2023, 15, 52. [Google Scholar] [CrossRef]
- Li, J.; Su, W.; Zhang, Z.; Guan, Z.; Li, J.; Wang, J. Design and Numerical Study of Argon Gas Diversion System Using Orthogonal Experiment to Reduce Impurities in Large-Sized Casting Silicon. Crystals 2022, 12, 562. [Google Scholar] [CrossRef]
- Liu, K.-P.; Niu, X.-B.; Zhang, Y.-D.; Ji, Z.-C.; Feng, J.-Y.; Li, W.-Q. Key design parameters and optimum method of medium- and high-velocity synchronous induction coilgun based on orthogonal experimental design. Chin. Phys. B 2019, 28, 024102. [Google Scholar] [CrossRef]
- Cai, C.; Kang, Y.; Wang, X.; Hu, Y.; Chen, H.; Yuan, X.; Cai, Y. Mechanism of supercritical carbon dioxide (SC-CO2) hydro-jet fracturing. J. CO2 Util. 2018, 26, 575–587. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, J.; Zhang, W.; Liu, B. Multiparameter and Multiobjective Optimization Design Based on Orthogonal Method for Mixed Flow Fan. Energies 2020, 13, 2819. [Google Scholar] [CrossRef]
- Xu, C.; Nie, W.; Yang, S.; Peng, H.; Liu, Z.; Ma, Q.; Guo, C.; Liu, Q. Numerical simulation of the multi-index orthogonal experiments on the spray dust-settling devices. Powder Technol. 2020, 371, 217–230. [Google Scholar] [CrossRef]
- Quan, H.; Guo, Y.; Li, R.; Su, Q.; Chai, Y. Optimization design and experimental study of vortex pump based on orthogonal test. Sci. Prog. 2020, 103, 0036850419881883. [Google Scholar] [CrossRef]
- Han, X.; Zhao, S.; Liu, C.; Chen, C.; Xu, F. Optimization of geometrical design of clinching tools in clinching process with extensible dies. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 3889–3897. [Google Scholar] [CrossRef]
- Shu, Q.-Y.; Wang, X.-P. Orthogonal complements and extending orthogonal subsets of semimodules. Linear Multilinear Algebra 2021, 1–19. [Google Scholar] [CrossRef]
- Yang, X.; Liu, G.; Li, Y.; Gao, S. Structural Optimization of Reciprocating Seal with Magnetic Fluid Based on Orthogonal Test Design. J. Magn. 2021, 26, 229–237. [Google Scholar] [CrossRef]
- Sun, M.; Liu, W.; Liu, J.; Tang, P.; Hao, C. Adaptive Subspace Detection Based on Gradient Test for Orthogonal Interference. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1868–1877. [Google Scholar] [CrossRef]









| Material | Tungsten | Steel | Copper | Tin | Iron | Lead |
|---|---|---|---|---|---|---|
| kp | 1.55 | 1.35–1.70 | 1.55 | 2.40 | 1.90 | 2.90 |
| Tooth Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Bending stress/MPa | 2192 | 1933 | 2056 | 2073 | 2173 | 1963 | 1996 | 1992 | 2473 |
| Tooth number | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | — |
| Bending stress/MPa | 2578 | 2067 | 2108 | 2050 | 1915 | 1925 | 2364 | 2347 | — |
| Test Number | Test Factor | |||
|---|---|---|---|---|
| L/mm | α/° | d/mm | β/° | |
| 1 | 10 | 75 | 7 | 6 |
| 2 | 10 | 80 | 10 | 8 |
| 3 | 10 | 85 | 12 | 10 |
| 4 | 15 | 75 | 10 | 10 |
| 5 | 15 | 80 | 12 | 6 |
| 6 | 15 | 85 | 7 | 8 |
| 7 | 20 | 75 | 12 | 8 |
| 8 | 20 | 80 | 7 | 10 |
| 9 | 20 | 85 | 10 | 6 |
| Test Number | Test Criteria | ||
|---|---|---|---|
| Maximum Stress of Slip Tooth /MPa | Maximum Bite Depth /mm | Bite Depth Uniformity of Each Tooth | |
| 1 | 3263 | 0.4523 | 0.0444 |
| 2 | 3138 | 0.3881 | 0.0308 |
| 3 | 3462 | 0.4602 | 0.0476 |
| 4 | 3876 | 0.6673 | 0.0738 |
| 5 | 3356 | 0.5196 | 0.0580 |
| 6 | 3637 | 0.4959 | 0.0540 |
| 7 | 3789 | 0.5821 | 0.0665 |
| 8 | 3532 | 0.4463 | 0.0453 |
| 9 | 3208 | 0.4137 | 0.0381 |
| Parameters | Maximum Stress of Slip Tooth/MPa | |||
|---|---|---|---|---|
| A | B | C | D | |
| K1 | 3287.7 | 3642.7 | 3477.3 | 3275.7 |
| K2 | 3623.0 | 3342.0 | 3407.3 | 3521.3 |
| K3 | 3509.7 | 3435.7 | 3535.7 | 3623.3 |
| Range R | 335.3 | 300.7 | 128.4 | 347.6 |
| Parameters | Maximum Bite Depth/mm | |||
|---|---|---|---|---|
| A | B | C | D | |
| K1 | 0.4335 | 0.5672 | 0.4648 | 0.4619 |
| K2 | 0.5609 | 0.4513 | 0.4897 | 0.4887 |
| K3 | 0.4807 | 0.4566 | 0.5206 | 0.5246 |
| Range R | 0.1274 | 0.1159 | 0.0558 | 0.0627 |
| Parameters | Bite Depth Uniformity | |||
|---|---|---|---|---|
| A | B | C | D | |
| K1 | 0.04093 | 0.06157 | 0.0479 | 0.04683 |
| K2 | 0.06193 | 0.0447 | 0.04757 | 0.05043 |
| K3 | 0.04997 | 0.04657 | 0.05737 | 0.05557 |
| Range R | 0.021 | 0.01687 | 0.0098 | 0.00873 |
| Optimization Objective | Parameters | |||
|---|---|---|---|---|
| A | B | C | D | |
| Optimal stress of slip tooth | 1 | 2 | 2 | 1 |
| Optimal bite depth | 2 | 1 | 3 | 3 |
| Optimal uniformity of bite depth | 1 | 2 | 2 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Kong, C.; Tang, R.; Feng, W.; Li, Y.; Yang, M. Optimum Design for Inserted Tooth Slips Setting Process Based on the Furrow Effect. Processes 2023, 11, 573. https://doi.org/10.3390/pr11020573
Wang Q, Kong C, Tang R, Feng W, Li Y, Yang M. Optimum Design for Inserted Tooth Slips Setting Process Based on the Furrow Effect. Processes. 2023; 11(2):573. https://doi.org/10.3390/pr11020573
Chicago/Turabian StyleWang, Qixin, Chunyan Kong, Ruihuan Tang, Wenrong Feng, Yang Li, and Mingkun Yang. 2023. "Optimum Design for Inserted Tooth Slips Setting Process Based on the Furrow Effect" Processes 11, no. 2: 573. https://doi.org/10.3390/pr11020573
APA StyleWang, Q., Kong, C., Tang, R., Feng, W., Li, Y., & Yang, M. (2023). Optimum Design for Inserted Tooth Slips Setting Process Based on the Furrow Effect. Processes, 11(2), 573. https://doi.org/10.3390/pr11020573










