B-LIME: An Improvement of LIME for Interpretable Deep Learning Classification of Cardiac Arrhythmia from ECG Signals
Abstract
:1. Introduction
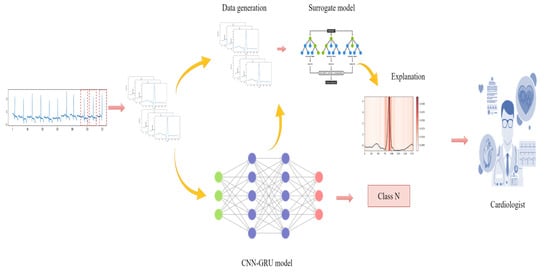
- Proposing B-LIME as an improvement of the LIME method for generating a credible and meaningful explanation of ECG signal data, taking into account the signals’ temporal dependency, and comparing performance to LIME.
- Proposing a data-generation technique that is locally faithful to the neighborhood of the prediction being explained to generate credible explanations.
- Proposing an explanation method that simulates the reasonable accuracy of the original ML model and generates meaningful explanations.
- Proposing a visual representation of LIME on the ECG dataset by applying a heatmap to highlight important areas on the heartbeat signal that the CNN-GRU mode uses for prediction.
- Developing a hybrid 1D CNN-GRU model combining two powerful deep learning algorithms to classify four types of arrhythmias from ECG lead II.
2. Related Work
3. Materials and Methods
3.1. LIME Explanation Technique
3.2. The Proposed B-LIME Technique
| Algorithm 1: B-LIME pseudocode | |
| Output: Explanations | |
| Start Algorithm (B-LIME) | |
| Phase 1, Split ECG record into heartbeats | |
| 1 | | |
| 2 | | |
| 3 | | |
| 4 | | |
| 5 | | |
| 6 | | |
| 7 | | |
| 8 | | |
| Phase 2, Bootstrapping resampling | |
| 9 | | |
| 10 | | |
| 11 | | |
| 12 | |random integer between 0 and |
| 13 | | |
| 14 | | |
| 15 | | |
| Phase 3, Generate explanations | |
| 16 | | Function RandomForest (data, p): |
| 17 | | |
| 18 | | |
| 19 | | |
| 20 | | |
| 21 | | |
| 22 | | |
| 23 | | |
| 24 | | |
| 25 | | |
| 26 | | |
| 27 | | |
| 28 | |, p) |
| 29 | End;//Algorithm |
3.2.1. Data Generation
3.2.2. Explanations Generation
3.2.3. Heatmap
- Identifying feature importance: Heatmaps can be used to visualize the importance of different features in a model. This can help you understand which features are most influential in the model’s predictions and can inform feature selection or feature engineering efforts.
- Explaining model predictions: Heatmaps can be used to visualize the relationships between different features and the model’s predictions. This can help to understand how the model uses different features to make predictions and can provide insight into the model’s decision-making process.
4. Case Study
4.1. Data Preparation
4.2. Training Classification Model
4.3. Experiments Setup
5. Results and Discussion
5.1. CNN-GRU Model
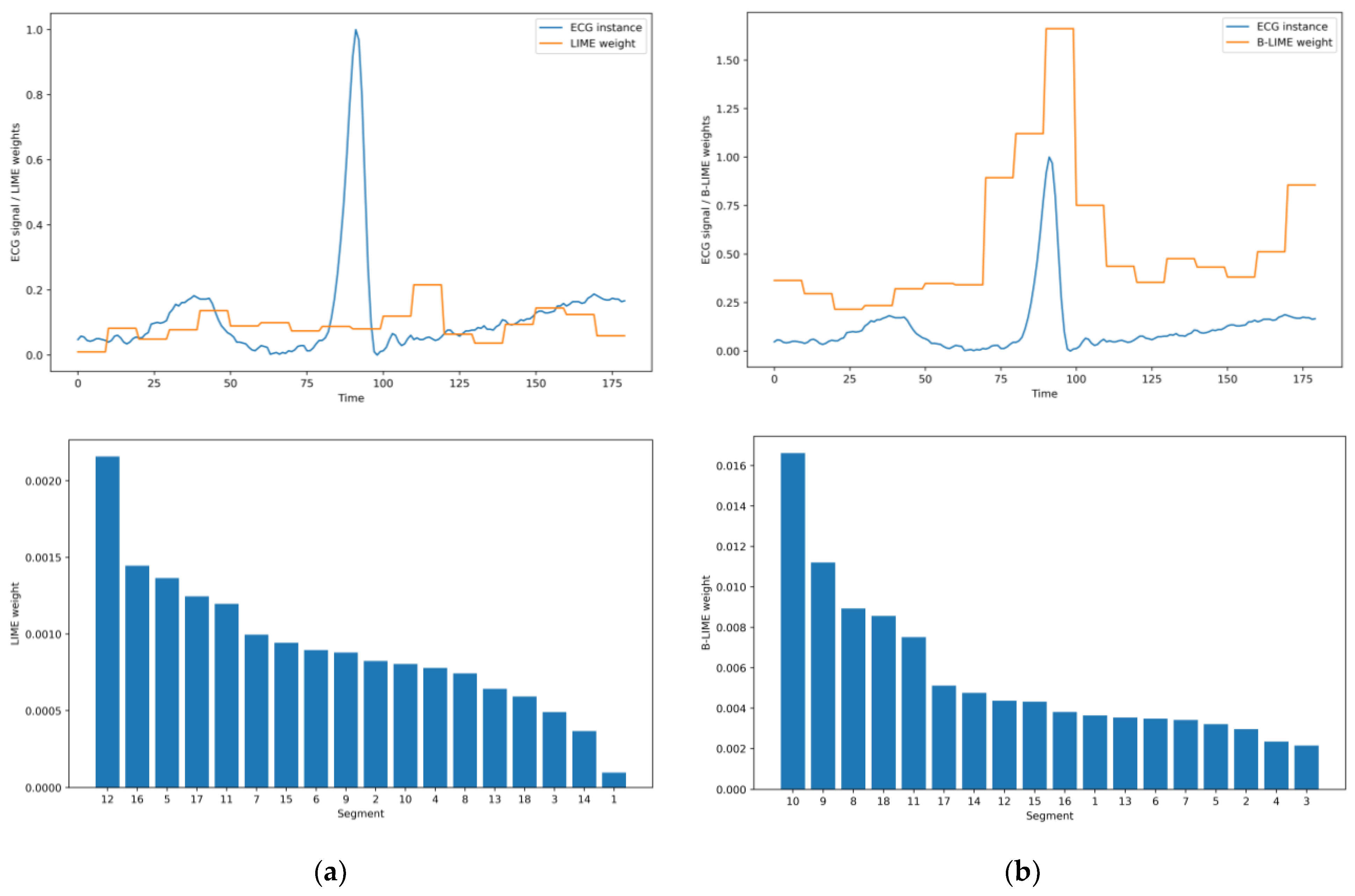
5.2. B-LIME Technique
5.3. Significance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, H.; Zhang, Z.; Xie, Z.; Lin, S. Local Relation Networks for Image Recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019. [Google Scholar]
- Abdel-Hamid, O.; Mohamed, A.-R.; Jiang, H.; Deng, L.; Penn, G.; Yu, D. Convolutional Neural Networks for Speech Recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2014, 22, 1533–1545. [Google Scholar] [CrossRef] [Green Version]
- Chowdhary, K.R. Natural Language Processing. In Fundamentals of Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2020; pp. 603–649. [Google Scholar]
- Abdullah, T.A.; Ali, W.; Malebary, S.; Ahmed, A.A. A Review of Cyber Security Challenges Attacks and Solutions for Internet of Things Based Smart Home. Int. J. Comput. Sci. Netw. Secur 2019, 19, 139. [Google Scholar]
- Abdullah, T.A.A.; Ali, W.; Abdulghafor, R. Empirical Study on Intelligent Android Malware Detection Based on Supervised Machine Learning. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 215–225. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Gabbouj, M. Real-Time Patient-Specific Ecg Classification by 1-D Convolutional Neural Networks. IEEE Trans. Biomed. Eng. 2016, 63, 664–675. [Google Scholar] [CrossRef] [PubMed]
- Alkhodari, M.; Fraiwan, L. Convolutional and Recurrent Neural Networks for the Detection of Valvular Heart Diseases in Phonocardiogram Recordings. Comput. Methods Programs Biomed. 2021, 200, 105940. [Google Scholar] [CrossRef] [PubMed]
- London, A.J. Artificial Intelligence and Black-Box Medical Decisions: Accuracy Versus Explainability. Hastings Cent. Rep. 2019, 49, 15–21. [Google Scholar] [CrossRef]
- Abdullah, T.A.A.; Zahid, M.S.M.; Ali, W. A Review of Interpretable Ml in Healthcare: Taxonomy, Applications, Challenges, and Future Directions. Symmetry 2021, 13, 2439. [Google Scholar] [CrossRef]
- Haunschmid, V.; Manilow, E.; Widmer, G. Audiolime: Listenable Explanations Using Source Separation. Expert Rev. Cardiovasc. Ther. 2020, 18, 77–84. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Why Should I Trust You? Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Neves, I.; Folgado, D.; Santos, S.; Barandas, M.; Campagner, A.; Ronzio, L.; Cabitza, F.; Gamboa, H. Interpretable Heartbeat Classification Using Local Model-Agnostic Explanations on Ecgs. Comput. Biol. Med. 2021, 133, 104393. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Ali, W.; Abdullah, T.A.; Malebar, S.Y. Classifying Cardiac Arrhythmia from Ecg Signal Using 1d Cnn Deep Learning Model. Mathematics 2023, 11, 562. [Google Scholar] [CrossRef]
- Ul Hassan, S.; Zahid, M.S.M.; Abdullah, T.A.A.; Husain, K. Classification of Cardiac Arrhythmia Using a Convolutional Neural Network and Bi-Directional Long Short-Term Memory. Digital Health 2022, 8, 20552076221102766. [Google Scholar] [CrossRef] [PubMed]
- Ayano, Y.M.; Schwenker, F.; Dufera, B.D.; Debelee, T.G. Interpretable Machine Learning Techniques in Ecg-Based Heart Disease Classification: A Systematic Review. Diagnostics 2022, 13, 111. [Google Scholar] [CrossRef] [PubMed]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. Anchors: High-Precision Model-Agnostic Explanations. In Proceedings of the AAAI, Palo Alto, CA, USA, 26–28 March 2018. [Google Scholar]
- Zhou, B.K.; Lapedriza, A.; Oliva, A.; Torralba, A. Learning Deep Features for Discriminative Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-Cam: Visual Explanations from Deep Networks Via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.-R.; Samek, W. On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sangroya, A.; Rastogi, M.; Anantaram, C.; Vig, L. Guided-Lime: Structured Sampling Based Hybrid Approach Towards Explaining Blackbox Machine Learning Models. In Proceedings of the CIKM (Workshops), Galway, UK, 19–23 October 2020. [Google Scholar]
- Visani, G.; Bagli, E.; Chesani, F. Optilime: Optimized Lime Explanations for Diagnostic Computer Algorithms. arXiv 2020, arXiv:2006.05714. [Google Scholar]
- Shankaranarayana, S.M.; Runje, D. Alime: Autoencoder Based Approach for Local Interpretability. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Guimaraes, Portugal, 4–6 November 2020. [Google Scholar]
- Botari, T.; Hvilshøj, F.; Izbicki, R.; de Carvalho, A.C.P.L.F. Melime: Meaningful Local Explanation for Machine Learning Models. arXiv 2020, arXiv:2009.05818. [Google Scholar]
- Hall, P.; Gill, N.; Kurka, M.; Phan, W. Machine Learning Interpretability with H2O Driverless AI. 2017. Available online: https://docs.h2o.ai/driverless-ai/latest-stable/docs/booklets/MLIBooklet.pdf (accessed on 13 February 2023).
- Hu, L.; Chen, J.; Nair, V.N.; Sudjianto, A. Locally Interpretable Models and Effects Based on Supervised Partitioning (Lime-Sup). arXiv 2018, arXiv:1806.00663. [Google Scholar]
- Ahern, I.; Noack, A.; Guzman-Nateras, L.; Dou, D.; Li, B.; Huan, J. Normlime: A New Feature Importance Metric for Explaining Deep Neural Networks. arXiv 2019, arXiv:1909.04200. [Google Scholar]
- Zafar, M.R.; Khan, N.M. Dlime: A Deterministic Local Interpretable Model-Agnostic Explanations Approach for Computer-Aided Diagnosis Systems. arXiv 2019, arXiv:1906.10263. [Google Scholar]
- Rabold, J.; Siebers, M.; Schmid, U. Explaining Black-Box Classifiers with Ilp–Empowering Lime with Aleph to Approximate Non-Linear Decisions with Relational Rules. In Proceedings of the International Conference on Inductive Logic Programming, Ferrara, Italy, 2–4 September 2018. [Google Scholar]
- Li, X.; Xiong, H.; Li, X.; Zhang, X.; Liu, J.; Jiang, H.; Chen, Z.; Dou, D. G-Lime: Statistical Learning for Local Interpretations of Deep Neural Networks Using Global Priors. Artif. Intell. 2023, 314, 103823. [Google Scholar] [CrossRef]
- Zhou, Z.; Hooker, G.; Wang, F. S-Lime: Stabilized-Lime for Model Explanation. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021. [Google Scholar]
- Kovalev, M.S.; Utkin, L.V.; Kasimov, E.M. Survlime: A Method for Explaining Machine Learning Survival Models. Knowl.-Based Syst. 2020, 203, 106164. [Google Scholar] [CrossRef]
- Utkin, L.V.; Kovalev, M.S.; Kasimov, E.M. Survlime-Inf: A Simplified Modification of Survlime for Explanation of Machine Learning Survival Models. arXiv 2020, arXiv:2005.02387. [Google Scholar]
- Nogueira, S.; Sechidis, K.; Brown, G. On the Stability of Feature Selection Algorithms. J. Mach. Learn. Res. 2017, 18, 6345–6398. [Google Scholar]
- Khaire, U.M.; Dhanalakshmi, R. Stability of Feature Selection Algorithm: A Review. J. King Saud Univ. Comput. Inf. Sci. 2019, 34, 1060–1073. [Google Scholar] [CrossRef]
- Sagheer, A.; Zidan, M.; Abdelsamea, M.M. A Novel Autonomous Perceptron Model for Pattern Classification Applications. Entropy 2019, 21, 763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ou, G.; Murphey, Y.L. Multi-Class Pattern Classification Using Neural Networks. Pattern Recognit. 2007, 40, 4–18. [Google Scholar] [CrossRef]
- Biau, G. Analysis of a Random Forests Model. J. Mach. Learn. Res. 2012, 13, 1063–1095. [Google Scholar]
- Bertolini, R.; Finch, S.J.; Nehm, R.H. Quantifying Variability in Predictions of Student Performance: Examining the Impact of Bootstrap Resampling in Data Pipelines. Comput. Educ. Artif. Intell. 2022, 3, 00067. [Google Scholar] [CrossRef]
- Tibshirani, R.J.; Efron, B. An Introduction to the Bootstrap; Monographs on Statistics and Applied Probability; Imprint Chapman and Hall/CRC: New York, NY, USA, 1993; Volume 57. [Google Scholar]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Dixon, P.M. Bootstrap Resampling. In Encyclopedia of Environmetrics; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Abdulkareem, N.M.; Abdulazeez, A.M. Machine Learning Classification Based on Radom Forest Algorithm: A Review. Int. J. Sci. Bus. 2021, 5, 128–142. [Google Scholar]
- Abdullah, T.A.A.; Zahid, M.S.B.M.; Tang, T.B.; Ali, W.; Nasser, M. Explainable Deep Learning Model for Cardiac Arrhythmia Classification. In Proceedings of the International Conference on Future Trends in Smart Communities (ICFTSC), Kuching, Sarawak, Malaysia, 1–2 December 2022; pp. 87–92. [Google Scholar] [CrossRef]
- Denisko, D.; Hoffman, M.M. Classification and Interaction in Random Forests. Proc. Natl. Acad. Sci. USA 2018, 115, 1690–1692. [Google Scholar] [CrossRef] [Green Version]
- Utkin, L.V.; Kovalev, M.S.; Coolen, F.P.A. Imprecise Weighted Extensions of Random Forests for Classification and Regression. Appl. Soft Comput. 2020, 92, 106324. [Google Scholar] [CrossRef]
- Liu, B.; Wei, Y. Interpreting Random Forests. J. Chem. Inf. Model. 2015, 55, 1362–1372. [Google Scholar]
- Zhang, J.; Wang, J. A Comprehensive Survey on Interpretability of Machine Learning Models. ACM Comput. Surv. CSUR 2018, 51, 93. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Moody, G.B.; Mark, R.G. Mit-Bih Arrhythmia Database. 1992. Available online: physionet.org (accessed on 9 January 2023).
- Gai, N.D. Ecg Beat Classification Using Machine Learning and Pre-Trained Convolutional Neural Networks. arXiv 2022, arXiv:2207.06408. [Google Scholar]
- Ege, H. How to Handle Imbalance Data and Small Training Sets in Ml. 2020. Available online: towardsdatascience.com (accessed on 9 January 2023).
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef] [Green Version]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Graves, A.; Graves, A. Long Short-Term Memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Chen, Y. Convolutional Neural Network for Sentence Classification. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Chan, W.; Park, D.; Lee, C.; Zhang, Y.; Le, Q.; Norouzi, M. Speechstew: Simply Mix All Available Speech Recognition Data to Train One Large Neural Network. arXiv 2021, arXiv:2104.02133. [Google Scholar]
- Nweke, H.F.; Teh, Y.W.; Al-Garadi, M.A.; Alo, U.R. Deep Learning Algorithms for Human Activity Recognition Using Mobile and Wearable Sensor Networks: State of the Art and Research Challenges. Expert Syst. Appl. 2018, 105, 233–261. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1d Convolutional Neural Networks and Applications: A Survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Dey, R.; Salem, F.M. Gate-Variants of Gated Recurrent Unit (Gru) Neural Networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017. [Google Scholar]
- Zhao, R.; Wang, D.; Yan, R.; Mao, K.; Shen, F.; Wang, J. Machine Health Monitoring Using Local Feature-Based Gated Recurrent Unit Networks. IEEE Trans. Ind. Electron. 2018, 65, 1539–1548. [Google Scholar] [CrossRef]
- Andersen, R.S.; Peimankar, A.; Puthusserypady, S. A Deep Learning Approach for Real-Time Detection of Atrial Fibrillation. Expert Syst. Appl. 2019, 115, 465–473. [Google Scholar] [CrossRef]
- Guo, L.; Sim, G.; Matuszewski, B. Inter-Patient Ecg Classification with Convolutional and Recurrent Neural Networks. Biocybern. Biomed. Eng. 2019, 39, 868–879. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Brownlee, J. A Gentle Introduction to Batch Normalization for Deep Neural Networks. 2019. Available online: https://machinelearningmastery.com/batch-normalization-for-training-of-deep-neural-networks/#:~:text=Batch%20normalization%20is%20a%20technique,required%20to%20train%20deep%20networks (accessed on 13 February 2023).
- Curtin, A.E.; Burns, K.V.; Bank, A.J.; Netoff, T.I. Qrs Complex Detection and Measurement Algorithms for Multichannel Ecgs in Cardiac Resynchronization Therapy Patients. IEEE J. Transl. Eng. Health Med. 2018, 6, 1900211. [Google Scholar] [CrossRef]
- Shutari, H.; Saad, N.; Nor, N.B.M.; Tajuddin, M.F.N.; Alqushaibi, A.; Magzoub, M.A. Towards Enhancing the Performance of Grid-Tied Vswt Via Adopting Sine Cosine Algorithm-Based Optimal Control Scheme. IEEE Access 2021, 9, 139074–139088. [Google Scholar] [CrossRef]








| Parameter Value | Parameter Value |
|---|---|
| Filter | 64 |
| Kernel size | 5 |
| No. of GRU units | 64 |
| Dropout | 0.2 |
| Learning rate | 0.001 |
| Decay | 1 × 10−6 |
| Batch size | 512 |
| Epoch | 100 |
| Matrix | Training Data | Testing Data | ||||||
|---|---|---|---|---|---|---|---|---|
| F | N | S | V | F | N | S | V | |
| Precision | 1.00 | 1.00 | 1.00 | 1.00 | 0.72 | 0.99 | 0.84 | 0.97 |
| Recall | 1.00 | 1.00 | 1.00 | 0.99 | 0.86 | 0.99 | 0.92 | 0.96 |
| F1-score | 1.00 | 1.00 | 1.00 | 1.00 | 0.78 | 0.99 | 0.88 | 0.97 |
| AUC | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 0.99 | 0.99 | 1.00 |
| Specificity | 1.00 | 1.00 | 1.00 | 1.00 | 0.90 | 0.99 | 0.93 | 0.97 |
| Loss | 0.02 | 0.11 | ||||||
| Accuracy | 1.00 | 0.99 | ||||||
| Jaccard Index | 1.00 | 1.00 | ||||||
| Sum of Squares (SS) | Degree of Freedom (DF) | F Value | p Value | |
|---|---|---|---|---|
| Method | 0.001938 | 1.0 | 188.767973 | 8.544500 × 10−35 |
| Residual | 0.003676 | 358.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, T.A.A.; Zahid, M.S.M.; Ali, W.; Hassan, S.U. B-LIME: An Improvement of LIME for Interpretable Deep Learning Classification of Cardiac Arrhythmia from ECG Signals. Processes 2023, 11, 595. https://doi.org/10.3390/pr11020595
Abdullah TAA, Zahid MSM, Ali W, Hassan SU. B-LIME: An Improvement of LIME for Interpretable Deep Learning Classification of Cardiac Arrhythmia from ECG Signals. Processes. 2023; 11(2):595. https://doi.org/10.3390/pr11020595
Chicago/Turabian StyleAbdullah, Talal A. A., Mohd Soperi Mohd Zahid, Waleed Ali, and Shahab Ul Hassan. 2023. "B-LIME: An Improvement of LIME for Interpretable Deep Learning Classification of Cardiac Arrhythmia from ECG Signals" Processes 11, no. 2: 595. https://doi.org/10.3390/pr11020595
APA StyleAbdullah, T. A. A., Zahid, M. S. M., Ali, W., & Hassan, S. U. (2023). B-LIME: An Improvement of LIME for Interpretable Deep Learning Classification of Cardiac Arrhythmia from ECG Signals. Processes, 11(2), 595. https://doi.org/10.3390/pr11020595