Efficient Non-Destructive Detection of Interface Adhesion State by Interfacial Thermal Conductance: A Molecular Dynamics Study
Abstract
:1. Introduction
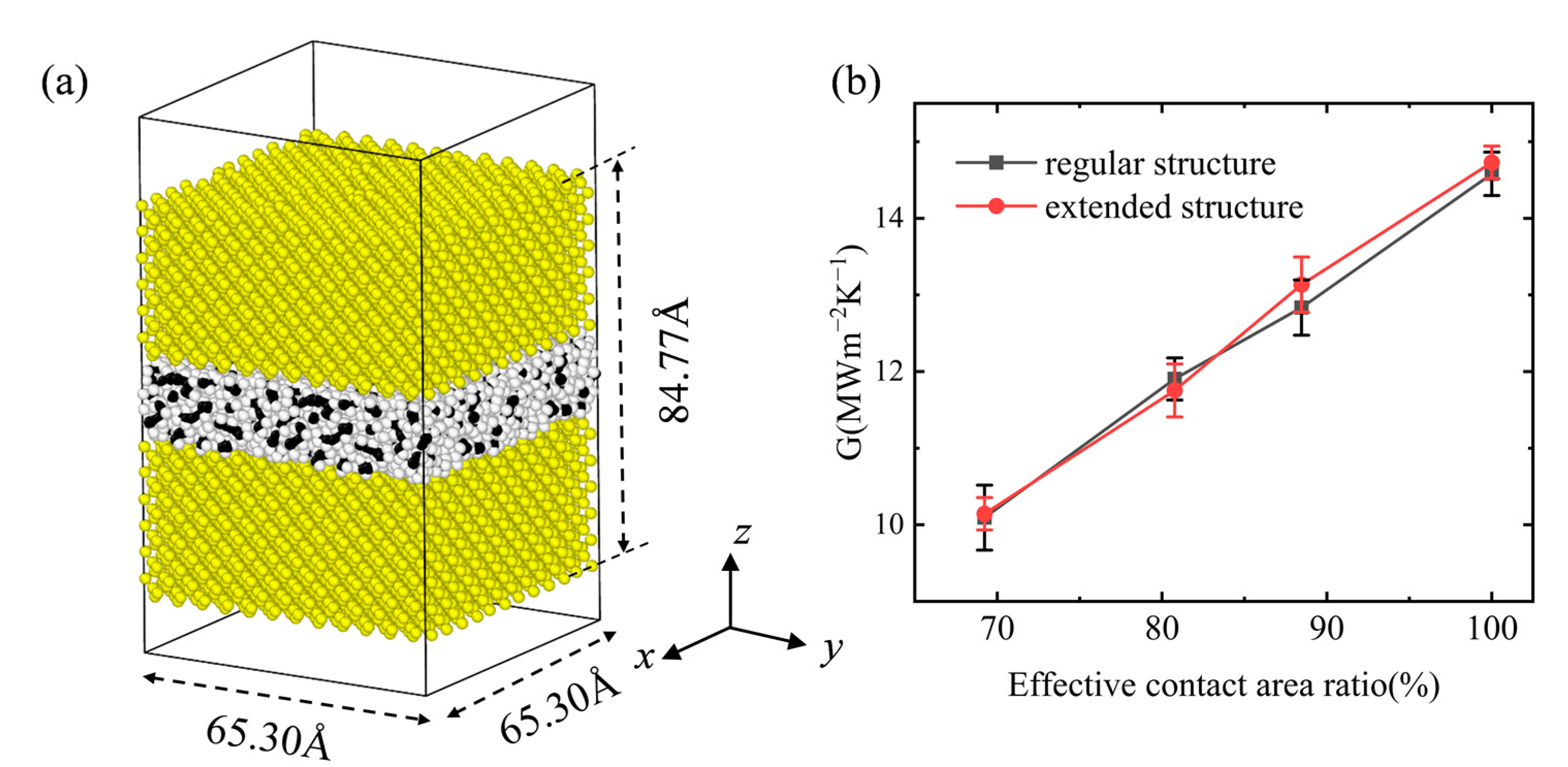
2. Model and Simulation Method
3. Results and Discussion
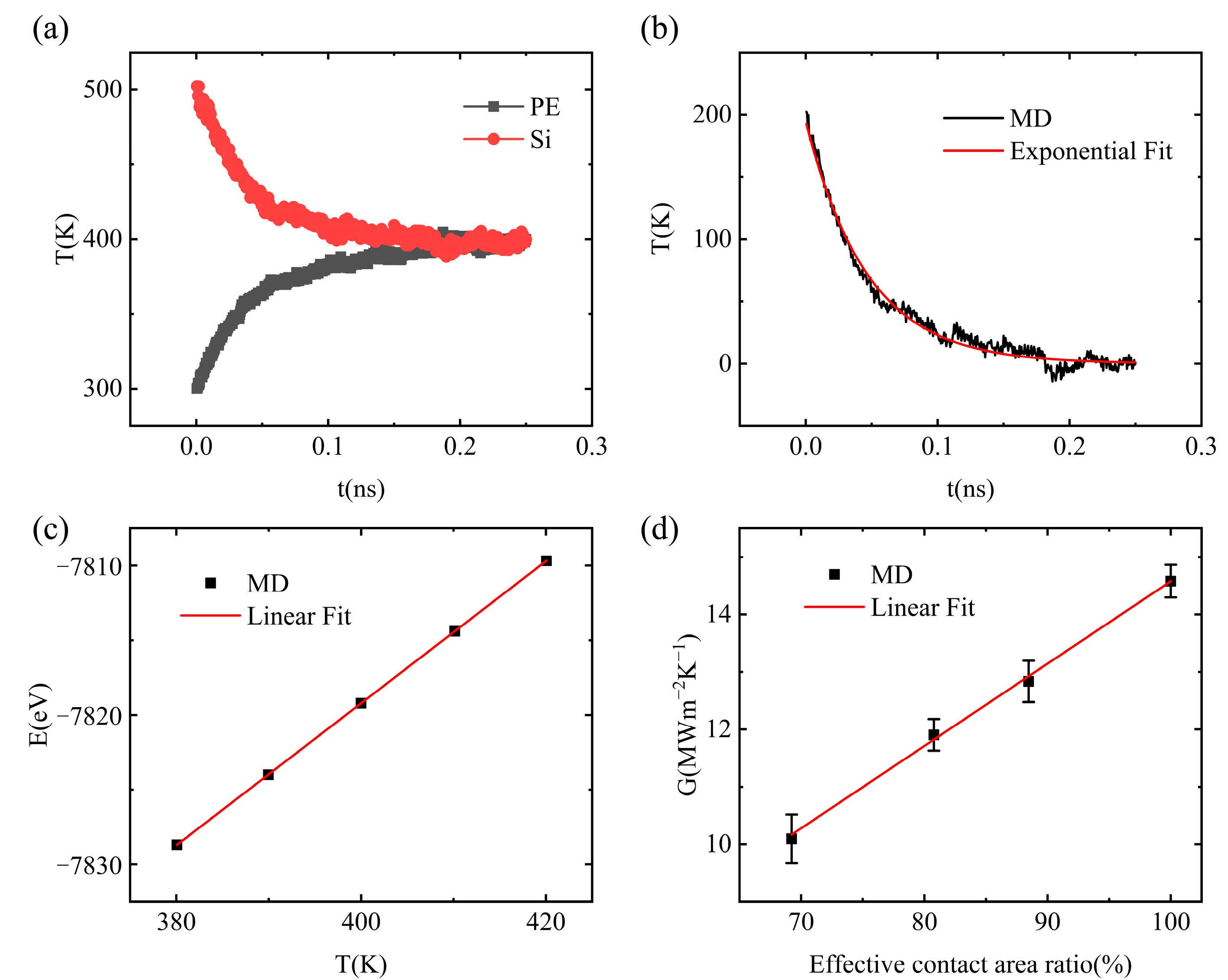
3.1. Interfacial Thermal Conductance of a Single Vacuole Model at 500 K
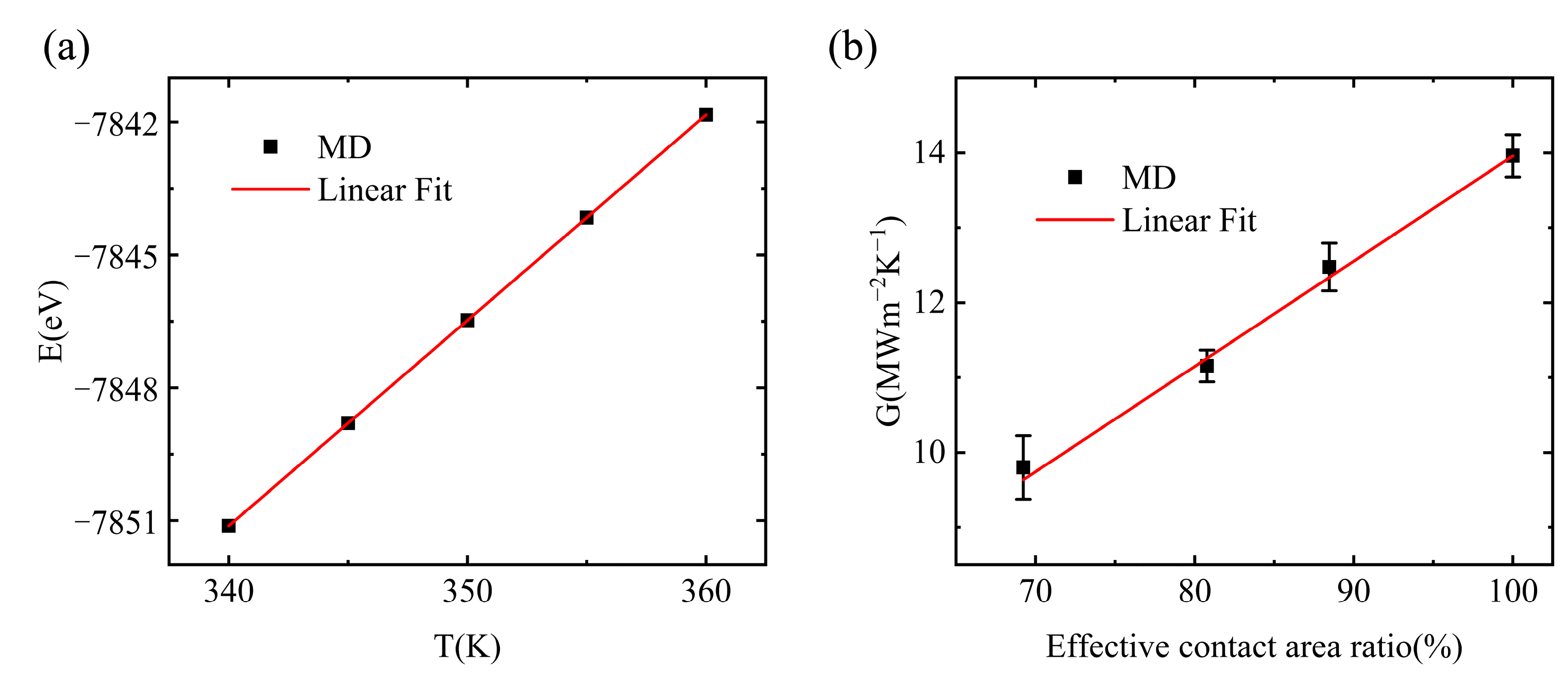
3.2. Interfacial Thermal Conductance of a Single Vacuole Model at 400 K
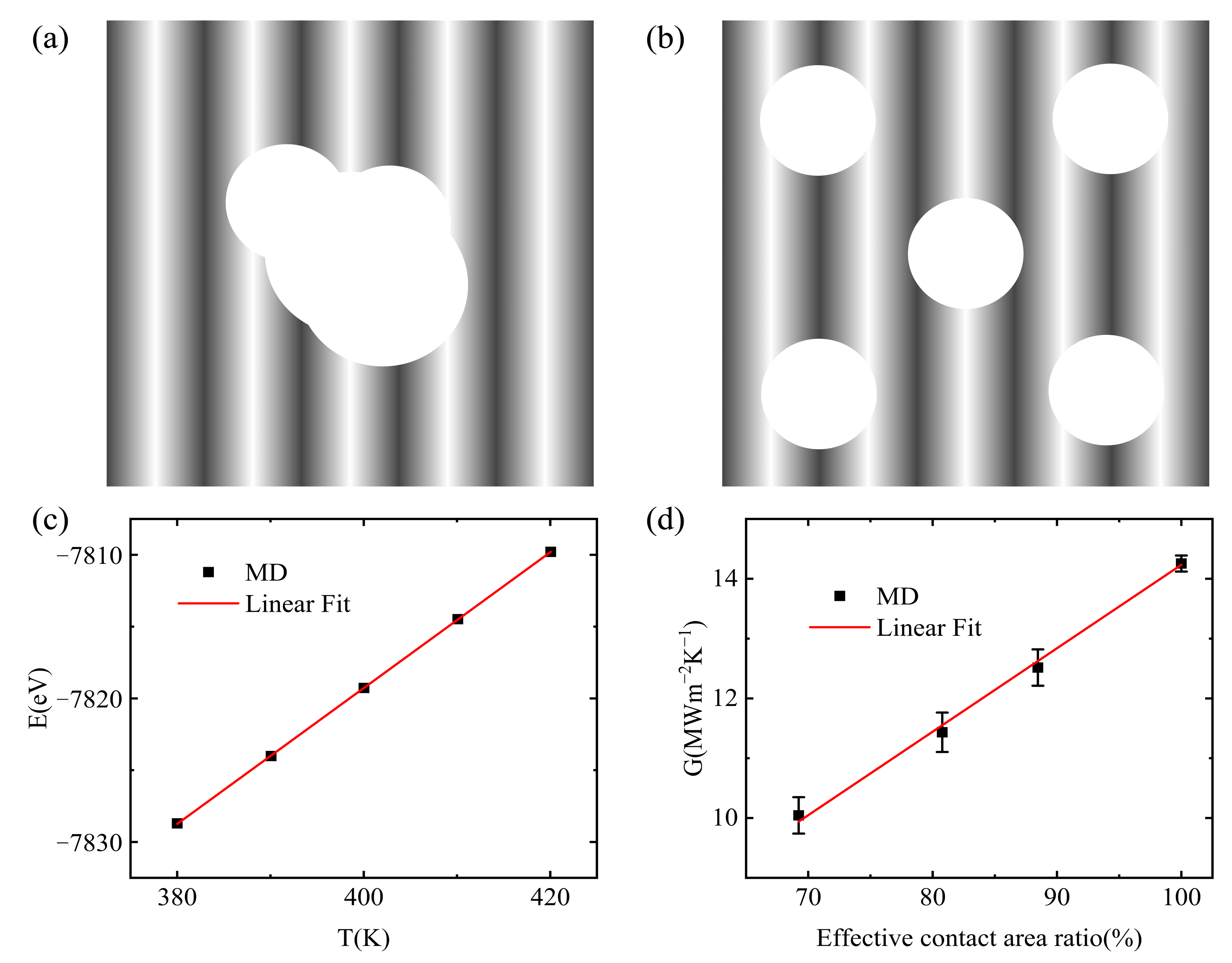
3.3. Interfacial Thermal Conductance of a Multiple Vacuole Model at 500 K
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, R.; Lin, J.; Wang, P.-C.; Zhu, C.; Wu, Y. Effect of adhesive characteristics on static strength of adhesive-bonded aluminum alloys. Int. J. Adhes. Adhes. 2015, 57, 85–94. [Google Scholar] [CrossRef]
- Heinzmann, C.; Weder, C.; de Espinosa, L.M. Supramolecular polymer adhesives: Advanced materials inspired by nature. Chem. Soc. Rev. 2016, 45, 342–358. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, S.; Li, M.; Liu, A. A review on mechanical properties of pressure sensitive adhesives. Int. J. Adhes. Adhes. 2013, 41, 98–106. [Google Scholar] [CrossRef]
- Pethrick, R.A. Design and ageing of adhesives for structural adhesive bonding—A review. J. Mater. Des. Appl. 2014, 229, 349–379. [Google Scholar] [CrossRef]
- Kadioglu, F.; Adams, R.D. Flexible adhesives for automotive application under impact loading. Int. J. Adhes. Adhes. 2015, 56, 73–78. [Google Scholar] [CrossRef]
- Ghobril, C.; Grinstaff, M.W. The chemistry and engineering of polymeric hydrogel adhesives for wound closure: A tutorial. Chem. Soc. Rev. 2015, 44, 1820–1835. [Google Scholar] [CrossRef]
- Saboori, A.; Aversa, A.; Marchese, G.; Biamino, S.; Lombardi, M.; Fino, P. Application of Directed Energy Deposition-Based Additive Manufacturing in Repair. Appl. Sci. 2019, 9, 3316. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Rosentrater, K.A. Life Cycle Assessment of Urea-Formaldehyde Adhesive and Phenol-Formaldehyde Adhesives. Environ. Processes 2020, 7, 553–561. [Google Scholar] [CrossRef]
- Shi, C.Y.; Zhang, Q.; Tian, H.; Qu, D.H. Supramolecular adhesive materials from small-molecule self-assembly. SmartMat 2020, 1, e1012. [Google Scholar] [CrossRef]
- Bao, Z.; Gao, M.; Sun, Y.; Nian, R.; Xian, M. The recent progress of tissue adhesives in design strategies, adhesive mechanism and applications. Mater. Sci. Eng. C Mater. Biol. Appl. 2020, 111, 110796. [Google Scholar] [CrossRef]
- Martinsen, K.; Hu, S.J.; Carlson, B.E. Joining of dissimilar materials. CIRP Ann. Manuf. Technol. 2015, 64, 679–699. [Google Scholar] [CrossRef] [Green Version]
- Szabelski, J.; Karpinski, R.; Machrowska, A. Application of an Artificial Neural Network in the Modelling of Heat Curing Effects on the Strength of Adhesive Joints at Elevated Temperature with Imprecise Adhesive Mix Ratios. Materials 2022, 15, 721. [Google Scholar] [CrossRef] [PubMed]
- Vassilopoulos, A.P. The history of fiber-reinforced polymer composite laminate fatigue. Int. J. Fatigue 2020, 134, 105512. [Google Scholar] [CrossRef]
- Bahraminasab, M.; Sahari, B.B.; Edwards, K.L.; Farahmand, F.; Hong, T.S.; Arumugam, M.; Jahan, A. Multi-objective design optimization of functionally graded material for the femoral component of a total knee replacement. Mater. Des. 2014, 53, 159–173. [Google Scholar] [CrossRef]
- Kulisz, M.; Rudawska, A.; Maziarz, M.; Miturska, I.; Szala, M.; Badurowicz, M.; Cel, W.; Chmielewska, M.; Czyż, Z.; Falkowicz, K.; et al. Impact of Selected Structural, Material and Exploitation Factors on Adhesive Joints Strength. MATEC Web Conf. 2019, 252, 01006. [Google Scholar] [CrossRef] [Green Version]
- Zuo, P.; Vassilopoulos, A.P. Review of fatigue of bulk structural adhesives and thick adhesive joints. Int. Mater. Rev. 2020, 66, 313–338. [Google Scholar] [CrossRef]
- Back, J.-H.; Hwang, J.-U.; Lee, Y.-H.; Baek, D.; Park, J.-W.; Kim, H.-J.; Kim, J.-H.; Song, H.-K.; Yoo, M.-J. Morphological study and mechanical property of epoxy-foam adhesives based on epoxy composites for automotive applications. Int. J. Adhes. Adhes. 2018, 87, 124–129. [Google Scholar] [CrossRef]
- Sun, P.; Qin, B.; Xu, J.F.; Zhang, X. High-Performance Supramolecular Adhesives. Macromol. Chem. Phys. 2022, 224, 2200332. [Google Scholar] [CrossRef]
- Back, J.H.; Baek, D.; Shin, J.H.; Jang, S.W.; Kim, H.J.; Kim, J.H.; Song, H.K.; Hwang, J.W.; Yoo, M.J. Resistance to Cleavage of Core(-)Shell Rubber/Epoxy Composite Foam Adhesive under Impact Wedge(-)Peel Condition for Automobile Structural Adhesive. Polymers 2019, 11, 152. [Google Scholar] [CrossRef] [Green Version]
- Miturska-Baranska, I.; Rudawska, A.; Doluk, E. Influence of Physical Modification of the Adhesive Composition on the Strength Properties of Aerospace Aluminum Alloy Sheet Adhesive Joints. Materials 2022, 15, 7799. [Google Scholar] [CrossRef]
- Teng, X.; Jin, M.; Ding, C.; Lu, C. A rapid screening method for thermal conductivity properties of thermal insulation materials by a thermochemiluminescence probe. Chem. Commun. 2020, 56, 12781–12784. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z.; Shi, R.; Chandrashekar, B.N.; Shen, N.; Song, H.; Wang, N.; Chen, J.; Cheng, C. Impact of Nanoscale Roughness on Heat Transport across the Solid–Solid Interface. Adv. Mater. Interfaces 2019, 7, 1901582. [Google Scholar] [CrossRef]
- Li, S.; Chen, Y.; Zhao, J.; Wang, C.; Wei, N. Atomic structure causing an obvious difference in thermal conductance at the Pd-H2O interface: A molecular dynamics simulation. Nanoscale 2020, 12, 17870–17879. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Hu, M.; Keblinski, P.; Li, B. Thermal rectification at silicon-amorphous polyethylene interface. Appl. Phys. Lett. 2008, 92, 211908. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3D computer graphics. Comp. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Hu, M.; Keblinski, P.; Schelling, P.K. Kapitza conductance of silicon–amorphous polyethylene interfaces by molecular dynamics simulations. Phys. Rev. B 2009, 79, 104305. [Google Scholar] [CrossRef]
- Wei, N.; Xu, L.; Wang, H.Q.; Zheng, J.C. Strain engineering of thermal conductivity in graphene sheets and nanoribbons: A demonstration of magic flexibility. Nanotechnology 2011, 22, 105705. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, Y.; Cai, K.; Jiang, J.; Zheng, J.-C.; Zhao, J.; Wei, N. Interfacial thermal conductance in graphene/black phosphorus heterogeneous structures. Carbon 2017, 117, 399–410. [Google Scholar] [CrossRef] [Green Version]
- Jund, P.; Jullien, R. Molecular-dynamics calculation of the thermal conductivity of vitreous silica. Phys. Rev. B 1999, 59, 13707–13711. [Google Scholar] [CrossRef] [Green Version]
- Lampin, E.; Palla, P.L.; Francioso, P.A.; Cleri, F. Thermal conductivity from approach-to-equilibrium molecular dynamics. J. Appl. Phys. 2013, 114, 033525. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotechnol. 2014, 9, 372–377. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Melis, C.; Colombo, L. Lattice thermal conductivity of Si1−xGex nanocomposites. Phys. Rev. Lett. 2014, 112, 065901. [Google Scholar] [CrossRef] [PubMed]



| Atom 1 | Atom 2 | σ(Å) | ϵ(eV) |
|---|---|---|---|
| C | C | 3.5000 | 0.00286 |
| C | H | 2.9580 | 0.00193 |
| Si | Si | 2.4799 | 0.00173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Ma, N.; Chen, J.; Wei, N. Efficient Non-Destructive Detection of Interface Adhesion State by Interfacial Thermal Conductance: A Molecular Dynamics Study. Processes 2023, 11, 1032. https://doi.org/10.3390/pr11041032
Guo J, Ma N, Chen J, Wei N. Efficient Non-Destructive Detection of Interface Adhesion State by Interfacial Thermal Conductance: A Molecular Dynamics Study. Processes. 2023; 11(4):1032. https://doi.org/10.3390/pr11041032
Chicago/Turabian StyleGuo, Jianhua, Niping Ma, Jiale Chen, and Ning Wei. 2023. "Efficient Non-Destructive Detection of Interface Adhesion State by Interfacial Thermal Conductance: A Molecular Dynamics Study" Processes 11, no. 4: 1032. https://doi.org/10.3390/pr11041032
APA StyleGuo, J., Ma, N., Chen, J., & Wei, N. (2023). Efficient Non-Destructive Detection of Interface Adhesion State by Interfacial Thermal Conductance: A Molecular Dynamics Study. Processes, 11(4), 1032. https://doi.org/10.3390/pr11041032





