Physical and Mechanical Behaviors of Compacted Soils under Hydraulic Loading of Wetting–Drying Cycles

Abstract

Exposed geo−infrastructures filled with compacted soils experience cyclic wetting–drying effects due to environment and underground water fluctuations. Soil physical and mechanical behaviors are prone to deterioration to a great extent, e.g., swelling, collapse, or even slope failure, resulting in huge losses to human life, safety, and engineering construction. In this paper, hydraulic loading tests of wetting–drying cycles were carried out on compacted fine soil via a one−dimensional pressure plate apparatus equipped with bender elements. The influences of wetting–drying paths on the soil characteristics of moisture content, void ratio and shear modulus were obtained and analyzed. Results showed that cyclic wetting–drying effects weakened the soil’s water retention capacity. It was observed that it was harder for pore water to approach saturation at a lower matric suction level and to be expelled at a higher matric suction level. Typical swelling and shrinkage deformations occurred during the hydraulic loading processes, and volume expansion was generated after the drying–wetting cycles at a given value of matric suction, which deteriorated the densely compacted soils to a relatively looser state. Then, a unified soil–water characteristic surface was proposed to describe the unique relationships of moisture content, void ratio, and matric suction. Moreover, the small−strain shear modulus of the soil, in terms of shear wave velocity, was reduced by 32.2–35.5% and 13.8–25.8% at the same degree of saturation during the first and second wetting paths, respectively. Therefore, the volume expansion and modulus degradation resulting from the wetting–drying cycles should attract particular attention to avoid further distresses in the practical engineering.

1. Introduction

Compacted fine soils are widely used as fillings in transportation and hydraulic infrastructure, such as embankments in highways, high−speed railways, and earth dams in water conservancy facilities. Although soils are usually compacted to a compactness of up to 93–97% at their optimum moisture contents, they are exposed to cyclic wetting and drying effects due to environment and underground water fluctuations. In contrast to saturated soils, the behaviors of unsaturated soils are more complicated, and include swelling−shrinking, softening−hardening under the hydraulic loading of wetting–drying processes [1,2,3]. Therefore, changes in physical properties, e.g., moisture content, void ratio, permeability, and supporting modulus may be harmful to the stability of earth structures and durability of superstructures, which need to be taken into account in engineering design.

Due to the interaction of pore water and the atmosphere in unsaturated soils, suction plays a vital role on soil water and volume characteristics. The soil–water retention curve (SWRC) is commonly adopted in predicting the soil properties with different function forms. Numerous studies have been undertaken to study the changes of water contents and the void ratio caused by variations of matric suction, especially for expansive soils [4,5,6,7,8]. The moisture content increased, and suction decreased with the infiltration of rainfall or underground water, resulting in volumetric swelling of highly compacted soils. Due to the thermal evaporation, volumetric shrinkage occurred during the decrease in moisture contents and increase in suction. To evaluate the influences of volumetric changes on the SWRC, Pasha et al. [9,10,11,12,13,14] proposed a hysteretic model to predict water retention curve with the void ratio effectively. Most importantly, suction paths in compacted embankments and earth dams are far from simply monotonic, where cyclic suction changes give rise to accumulative swelling or shrinkage deformation. Chen et al. [4] obtained a single dry−wet cycle in laboratory test, the SWRCs illustrated that saturated water content is more than 40%, and an inflection point occurs when the water content is about 25%. Khan et al. [15] found the void ratio increases with the increasing number of wet−dry cycles. Louati et al. [16] found that between 4 and 6 wetting–drying cycles, the permeability decreased in low compacted clay (generally by less than 2) and increased in highly compacted clay (between 10 and 200 times), and all samples with different initial densities converged to the similar permeability values after 7 cycles. Liang et al. [17] showed that with increasing wet−dry cycles, the cohesion tended to decrease, but the angle of internal friction decreased relatively little. Moreover, the accumulative swelling and shrinkage deformation due to wetting–drying cycles is strongly dependent on specimen’s compactness and applied net stresses [6]. Nowamooz and Masrouri [18] showed that the cyclic wetting and drying process promotes a net accumulation of swelling strains on densely compacted specimens and a net accumulation of shrinking strains on loosely compacted specimens. Eventually, the final asymptotic strain is unique for a given compacted soil and is independent from the as−compacted density. The difference between swelling and shrinkage deformations reaches its maximum values in the first cycle and decreases to approach zero after experiencing three to four wetting–drying cycles.

The cyclic wetting–drying can alter soil hydraulic behavior to a great extent and cause deformation, so as to exacerbate the performance of soil in various practical engineering, e.g., surface cracking, surface or shallow failure of unsaturated soil slope [15,17,19,20]. Previous studies were mainly focused on the volumetric behavior of compacted expansive soils. However, most human earthworks are compacted with non−expansive soils. Therefore, it is more practical to study the wetting–drying induced behaviors of these ordinary fine soils. In addition to the changes of water content and volume, the influences of wetting–drying cycles are worthy particular emphasis on soil modulus. In this study, cyclic wetting–drying tests were carried out on densely compacted non−expansive fine soil at its optimum moisture content. Influences of wetting–drying paths on the characteristics of soil water, void ratio and shear modulus were analyzed. Based on these, a unified soil–water characteristic surface of moisture content, void ratio and matric suction was proposed, as well as a modified expression to describe the relationship between shear modulus and matric suction.

2. Materials and Methods

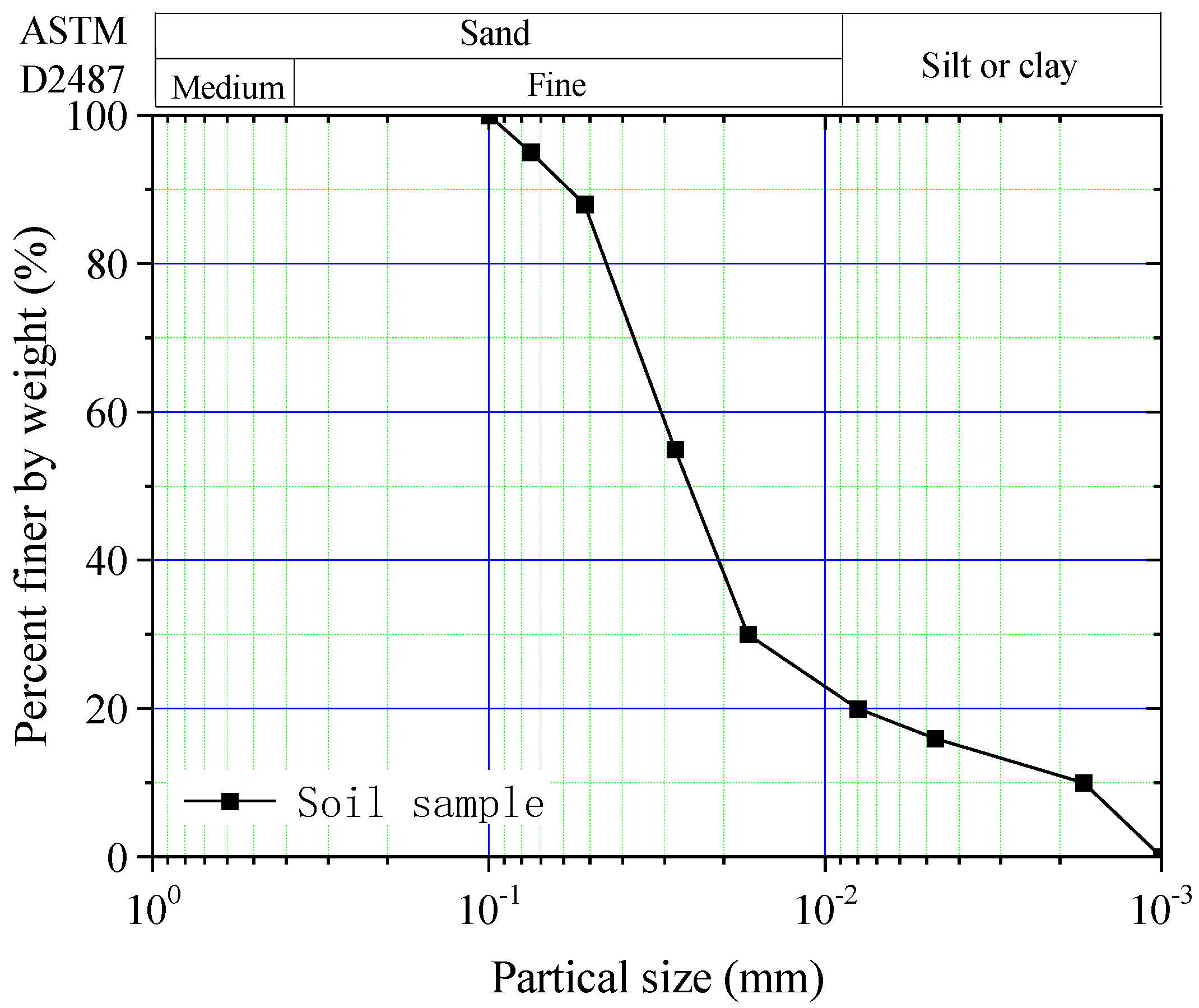
2.1. Soil Properties

The testing soils were sampled around the flooded areas of Yellow River in Shandong Province, China, which were used as the main subgrade fillings in the construction of transportation infrastructure, as shown in Figure 1. Figure 2 shows the soil particle size distribution curve, composed of 85.9% silt and 11.1% clay. The soil liquid limit and plastic index were 31.2% and 11.2%, which was classified as low liquid limit clay (CL). The optimum moisture content (OMC) and maximum dry density were 12% and 1.91 g/cm³ obtained from the standard Proctor compaction tests.

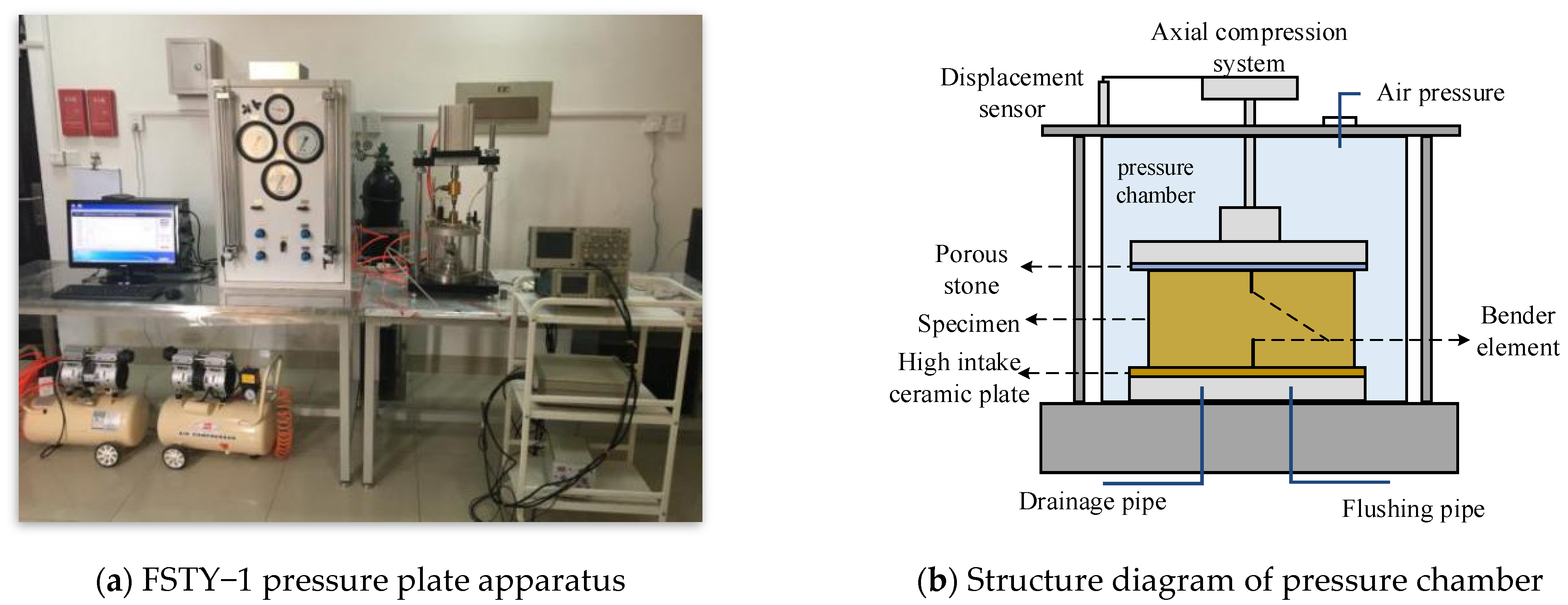
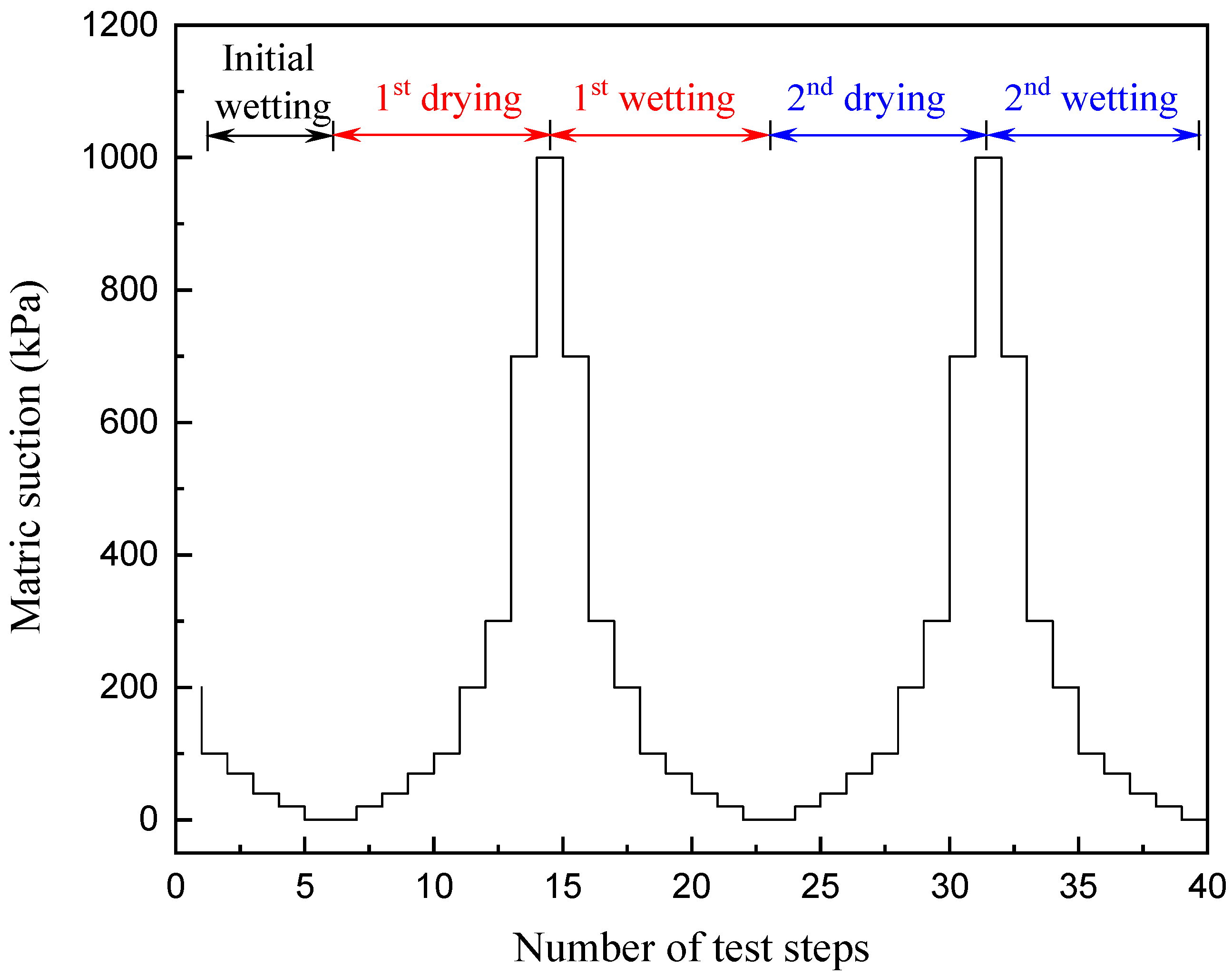
2.2. Experimental Program

The soil cyclic wetting–drying test was conducted using the FSTY−1 pressure plate apparatus with the help of axis translation technique as shown in Figure 3. Ceramic plate with the air entry value was equipped at the bottom of the pressure chamber, which could apply matric suction up to 1.5 MPa to the soil sample with the dimensions of 90 mm in diameter and 26.2 mm in height. Drainage pipe, connected to the bottom of the ceramic plate, was used to record the volume of water absorbed and drained by the soil sample. Meanwhile, due to the lateral restriction in the pressure plate apparatus, the displacement sensor was only installed at the top of the soil sample to record the swelling or compression deformation. Besides, a pair of bender elements was installed at the top and bottom of the pressure chamber, which could generate and receive the shear wave through the soil sample. The small−strain shear modulus (G₀) could be calculated based on the shear wave velocity using the following equation:

$$G_0=\rho v_s^2$$

(1)

where $\rho$ and $v_s^{}$ are soil density and shear wave velocity, respectively. Therefore, the soil void ratio (e), moisture content (w) and small−strain shear modulus (G₀) could be determined during the cyclic wetting–drying test.

Soil specimen was prepared by static compaction method to the compactness of 95.6% at moisture content of 12.2%, compared to the desired compactness of 96% at moisture content of 12%. At the beginning of the tests, the residual bubbles at the bottom of the ceramic plate were flushed with the flushing pipe to reduce the testing error. The axial pressure of 1 kPa was applied on the top of the soil specimen to ensure the tight contact between the displacement sensor and soil. Since the initial matric suction of compacted soils in situ was around 200 kPa, the soil specimen was applied with the same matric suction until the water infiltration was stable in the pressure plate apparatus. Therefore, the initial soil compactness stabilized at 96.0% with the moisture content of 11.3%, corresponding to the void ratio of 0.51. Then, the wetting and drying cycles were imposed on the soil specimen. As illustrated in Figure 4, the specimen was subjected to decreasing matric suction in a series of steps from 200 kPa to 0 kPa to simulate the initial wetting process in the field, which was termed as initial wetting path. As the matric suction decreased, water was absorbed from the drainage pipe to the soil specimen. The movement of water and axial deformation were continuously monitored until the equilibrium condition was reached. Typically, 5–7 days are required to achieve equilibrium at a given suction, and the shear wave velocity was measured simultaneously. After reaching the saturation condition, the first drying process was then initiated by increasing the value of matric suction in a series of steps from 0 kPa to 1000 kPa. Water in the soil specimen was expelled into the drainage pipe. A 120−day period with three wetting and two drying paths was undertaken to investigate the moisture content, void ratio, and shear modulus of the CL soil.

3. Test Results and Analysis

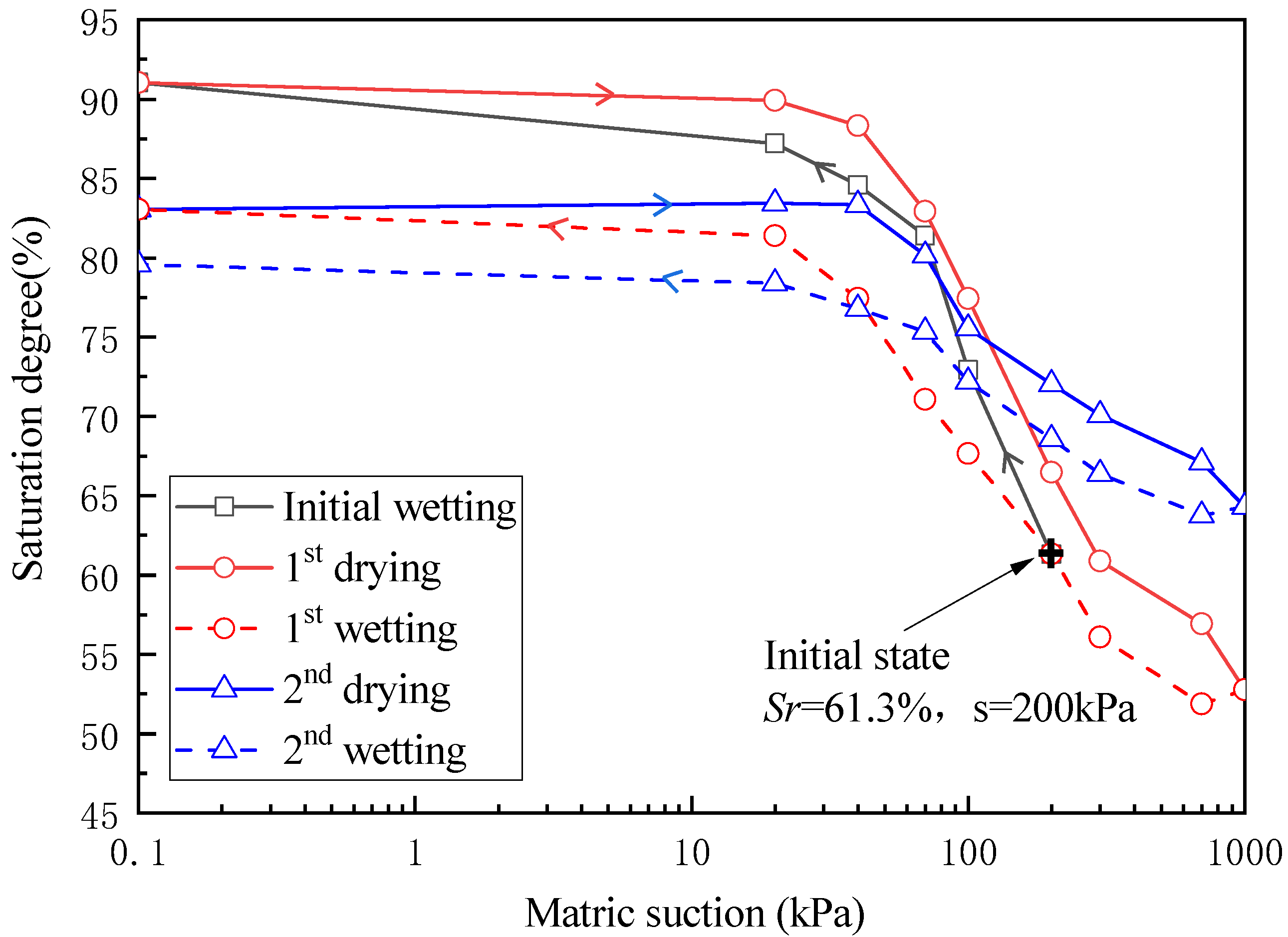
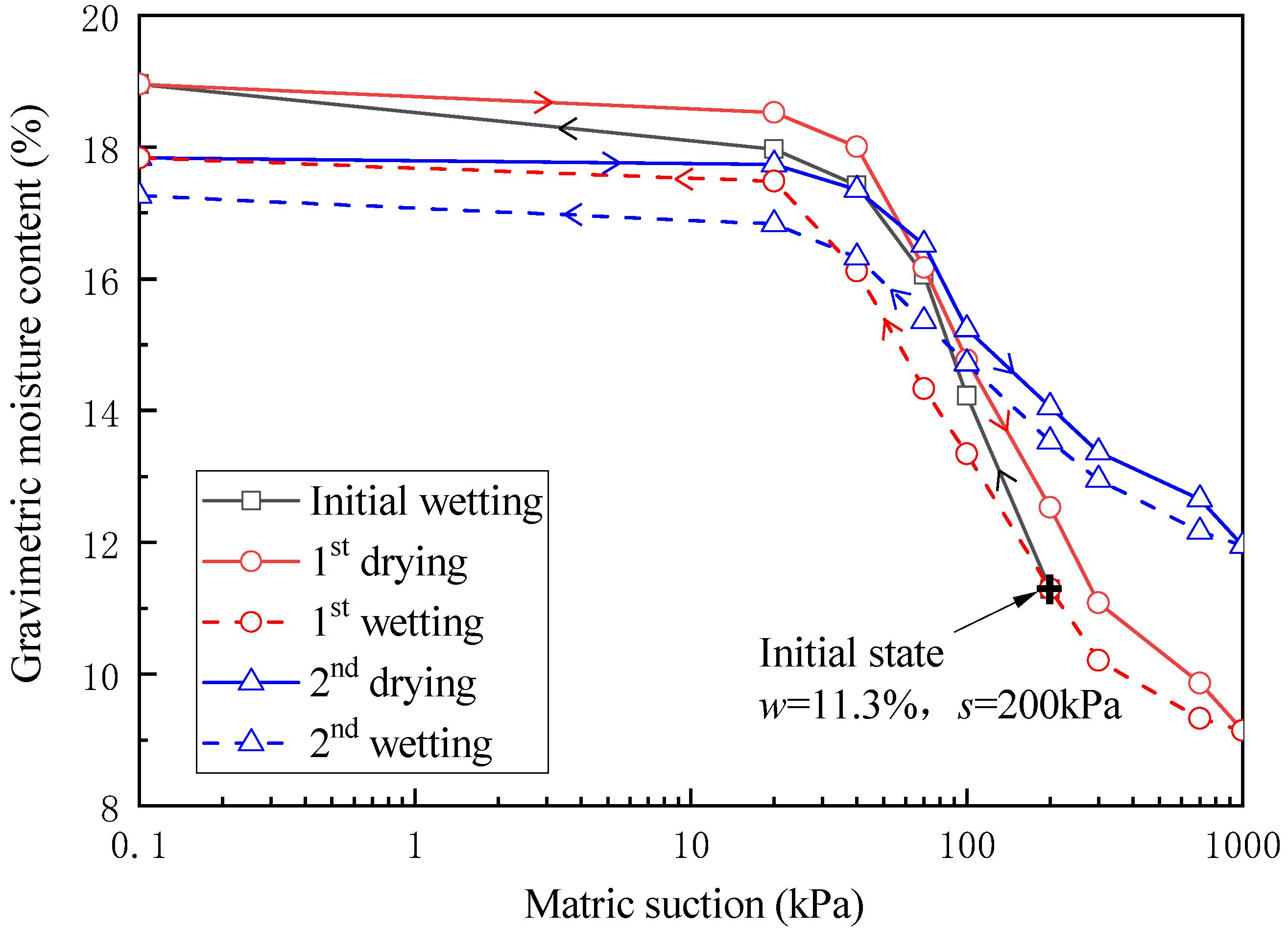
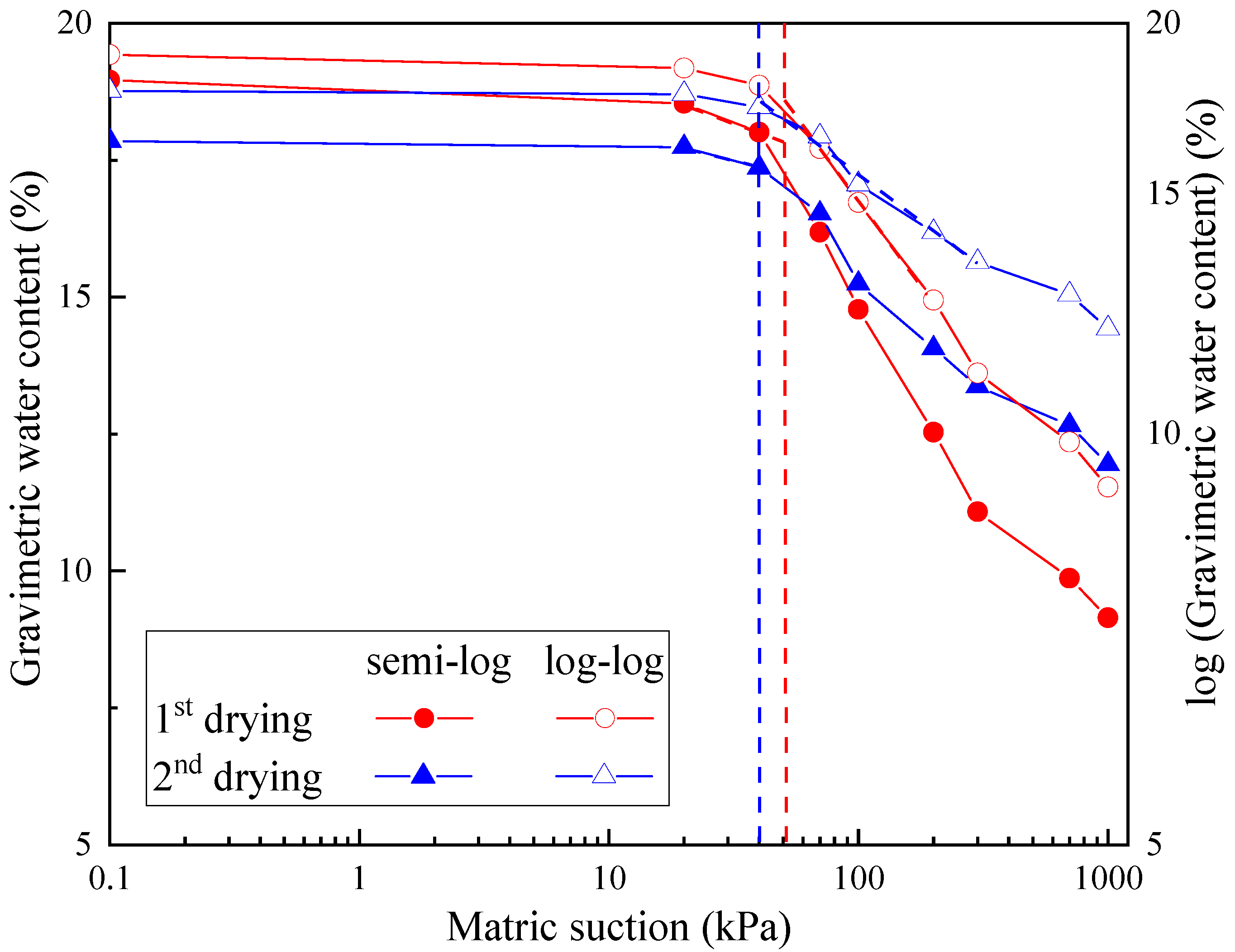
3.1. Soil–Water Characteristic

Typical unimodal soil–water retention curves (SWRC) are plotted in Figure 5, with the relationship of degree of saturation (Sr) and matric suction under three wetting and two drying cycles. Hysteresis loops were observed between the drying and wetting paths, where the degree of saturation at the drying path was higher than that at the wetting path. Meanwhile, the size of the hysteresis loop was the largest in the first cycle, and the varying ranges of Sr decreased from 52.8–91.1% in the first cycle to 64.3–83.1% in the second cycle. Dane and Lenhard [21] attributed the hysteresis in SWRC to four reasons: (1) the ‘ink bottle’ effect, (2) the contact angle effect, (3) air entrapment, and (4) deformation of the solid phase. As matric suction decreased from 200 to 0 kPa in the initial wetting path, the degree of saturation increased from the original value of 61.3% to 91.1%, corresponding to the gravimetric moisture content (GMC) of 11.3% to 19.0% as shown in Figure 6. It was hard to saturate the soil specimen to Sr = 100% due to the entrapped air in the soil void. After that, the drying process was activated with the increase of matric suction, which presented a typical sigmoidal shape. The degree of saturation decreased slowly until reaching the air entry value (AEV) of matric suction, which represented the starting point of suction hardening. According to Pasha et al. [22], the SWRC drying path data were suggested to be plotted on both semi−log and log–log scales on the same graph to determine AEV. Therefore, as shown in Figure 7, the AEV of the first drying path was estimated to be about 54.1 kPa, which decreased to 41.5 kPa of the second drying path. It seems that soil water is more easily expelled due to the wetting–drying cycles. When the matric suction increased to 1000 kPa, the values of Sr decreased to 52.8% and 64.3% at the end of the first and second drying paths, corresponding to the GMCs of 9.1% and 11.9%. Moreover, as the matric suction decreased during the wetting paths, the SWRC did not return to the original degree of saturation, where the values of Sr decreased to 83.1% and 79.6% at the end of second and third wetting paths, but at a reduced rate. However, the GMCs decreased only from 19.0% to 17.8% and 17.3%, respectively. This indicates that the soil volume might change during the wetting–drying cycles. According to Bell [23], drying initiated cementation by aggregation formation, leading to some relatively large interpores formed between the aggregated soil lumps. These large interpores reduced the specimen’s rate of absorption along a certain range of the wetting paths, which could be observed in Figure 5 that both the desorption and absorption rates were much higher during the first drying–wetting path than the subsequent cycles. Consequently, the drying and wetting history weakens the movement ability of water in the void, and the degree of saturation tends to become smaller at low suction and higher at larger suction rates.

The Fredlund and Xing (FX) water retention model [24] was used to describe the cyclic drying–wetting data.

$$\theta =C\left(\psi \right)\cdot \frac{{\theta }_S}{{\left\{\ln \left[\exp \left(1\right)+{\left(\frac{\psi }{a}\right)}^b\right]\right\}}^c}$$

(2)

$$C\left(\psi \right)=1-\frac{\ln \left(1+\frac{\psi }{{\psi }_r}\right)}{\ln \left(1+\frac{{10}^6}{{\psi }_r}\right)}$$

(3)

where a, b, c, and Ψ_r are four model parameters; θ is the volumetric water content; θ_s is the saturated volumetric water content, which is 0.65 for the used CL soil; Ψ is the matric suction; Ψ_r is the matric suction corresponding to the residual volumetric water content. The corresponding fitting parameters and the entire fitting curves of the wetting–drying cycles are presented in

Table 1. Fitting SWRC parameters by using Fredlund & Xing model.

Parameters	Initial Wetting	First Drying	First Wetting	Second Drying	Second Wetting
a	137.75	54.07	33.02	41.55	28.26
b	1.30	2.17	1.85	1.83	1.34
c	1.25	0.36	0.35	0.21	0.23
Ψr	3.23 × 106	7.59 × 107	2.56 × 107	1.39 × 107	2.92 × 107
R2	0.988	0.998	0.997	0.989	0.995

and Figure 8, respectively. The results show that the unimodal wetting–drying curves could be well fitted by the FX model, and the fitting goodness R² of all fitting curves are more than 0.98.

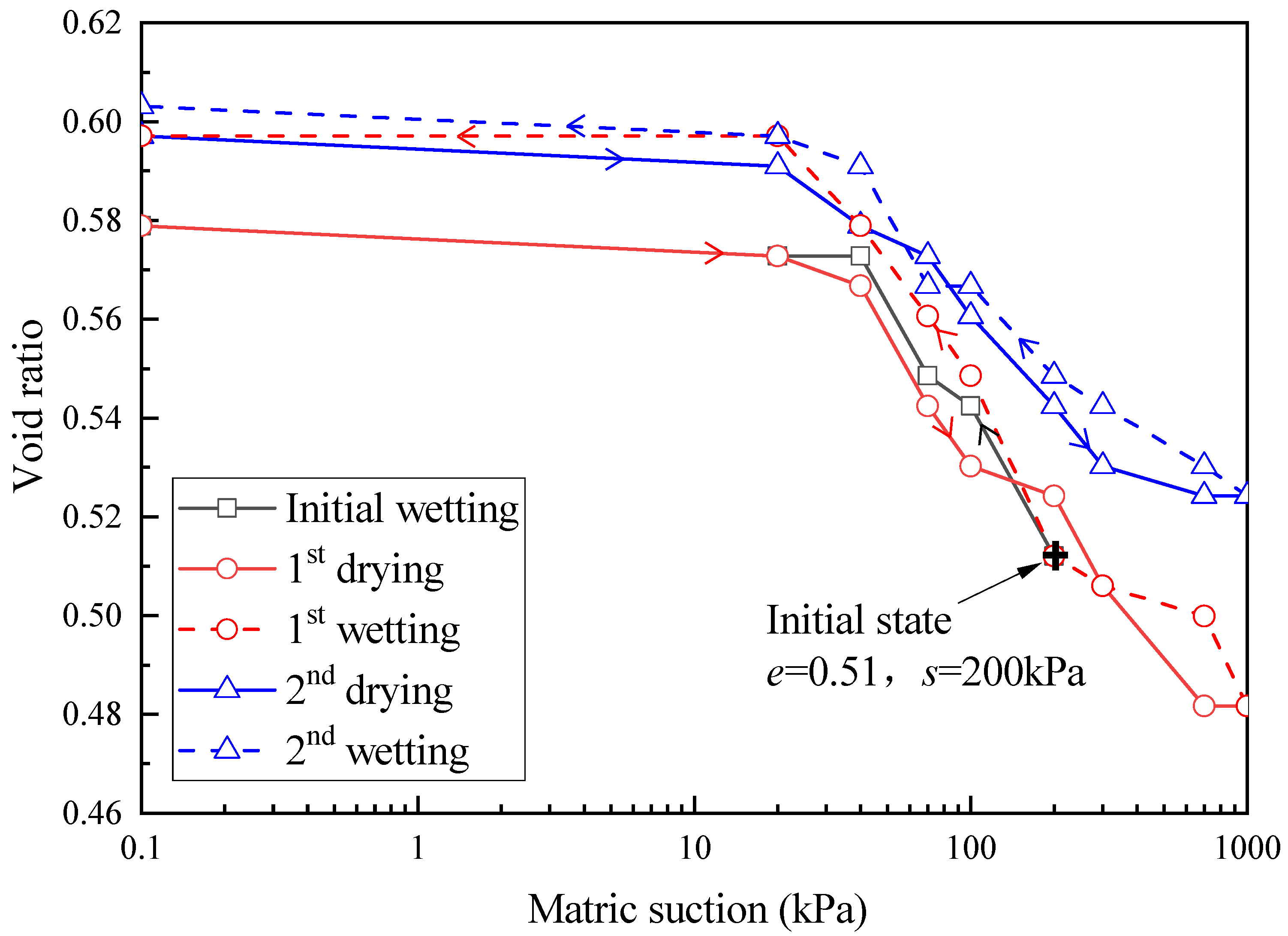
3.2. Soil Void Ratio Characteristics

Figure 9 depicts the changes in the void ratio versus controlled suction during the drying–wetting cycles, which was also considered as the hydraulic loading process represented in the form of shrinkage and swelling curves. Generally, the CL soil swelled with the decrease of matric suction and shrank with the increase of matric suction, and the drying–wetting cycles resulted in the soil volume expansion. As matric suction decreased from 200 to 40 kPa in the initial wetting path, the void ratio increased from 0.51 to 0.57 with the swelling index of 0.087. The void ratio showed minimal changes with the matric suction decreasing from 40 kPa to 0 kPa, because little water was found to enter the soil void as shown in Figure 9. The void ratio presented similar variations during the hydraulic loading in the subsequent drying–wetting cycles, where obvious volume changes were expected to develop as the matric suction exceeded the AEVs. In the first drying–wetting path, the soil void ratio first shrank from 0.58 to 0.48 with the compressibility index of 0.061 with the increasing matric suction, and then expanded from 0.48 to 0.60 with the swelling index of 0.096. It can be found that the void ratio increased by 1.1–4.2% due to the first drying–wetting cycle at the same matric suction. In the second drying–wetting path, the void ratio first decreased from 0.60 to 0.52, and then returned to about 0.60 at the end of wetting path, where the plastic volume changes could be ignored. The corresponding compressibility and swelling indexes reduced to 0.052 and 0.061, respectively. The differences between the compressibility and swelling indexes were much larger for the first drying–wetting cycle than the second cycle, explaining that the volume change in the first cycle was significantly larger than the second one. It should be noted that the compressibility index reduced during drying–wetting cycles, which is not consistent with the assumption commonly used in constitutive models of unsaturated soils regarding the independence of the elastic compressibility index and the hydraulic and mechanical loadings [25]. However, the phenomenon of soil swelling in the wetting path and declining after a few drying–wetting cycles is in accordance with the literature [25]. Accordingly, an elastic–plastic volume increase happens during the suction reduction.

The soil shrinkage characteristic curve (SSCC) is always presented as a plot of moisture ratio ϑ versus the void ratio as shown in Figure 10, where ϑ is the product of gravimetric moisture content $w$ and specific gravity G_s. Cornelis et al. [26] proposed an exponential function to describe the SSCC:

$$e=e_0+\alpha \exp \left(-\beta {\vartheta }^{-\gamma }\right)$$

(4)

where e₀ is the void ratio at oven−dryness and a, β, γ are model parameters. Based on the measured data of CL soil, the fitting curves, and parameters of SSCC are presented in Figure 10 and

Table 2. Fitting parameters of SSCC.

Test Conditions	Parameters				R2
	e0	a	β	γ
first drying cycle	0.44	2.98	2.10	−1.50	0.97
second drying cycle	0.48	0.86	0.23	−2.59	0.98

, where the fitting degree R² of all fitting curves are greater than 0.97. It can be obviously observed that the CL soil shrank with the water discharge, and the two drying paths are moving away from the saturation line, which denotes the volume change (shrinkage) is the same as the amount of water lost from the soil. In fact, the measured decrement in the soil void ratio is less than the volume of water lost from the soil around the matric suction of 0–1000 kPa used in the tests, which is termed as the proportional shrinkage zone. The reason is that when water is removed from the large soil pores with increasing matric suction, the soil becomes unsaturated, and air enters the pores [27].

The volume swelling curve of the wetting paths could be fitted with the e−w curve model proposed by Peng et al. [28]. The model is applicable to a wide range of soils, and the expression is as follows:

$$e=e_r+\frac{e_s-e_r}{{\left[1+{\left(\chi w{G}_s\right)}^{-p}\right]}^q}$$

(5)

where χ, p and q are model parameters; e_r is residual void ratio; e_s is void ratio at saturation; G_s is specific gravity of soil, equal to 2.78 for the CL soil; w_sat is gravimetric moisture content at saturation. When the soil is saturated, the void ratio e can be expressed as the gravimetric moisture content w multiplied by specific gravity G_s. Therefore, the complete relationship between void ratio and gravimetric moisture content can be further expressed as follows:

$$\left\{\begin{array}{c}e=e_r+\frac{e_s-e_r}{{\left[1+{\left(\chi w{G}_s\right)}^{-p}\right]}^q} \left(w\le w_{sat}\right)\\ e=w{G}_s \left(w=w_{sat}\right)\end{array}\right.$$

(6)

The fitting results of the soil volume swelling curves are listed in

Table 3. Fitting parameters of soil volume swelling curve.

Test Conditions	Parameters				R2
	χ	p	q	er
first wetting cycle	0.024	8.61	0.51	0.47	0.98
second wetting cycle	0.022	26.26	0.14	0.50	0.98

and Figure 11, which are in good agreement with the measured wetting data for the two cycles. Compared with the relatively larger differences of the void ratio versus matric suction between the two wetting paths in Figure 9, the values of the void ratio are quite close when expressed in terms of gravimetric moisture content. It indicates that the void ratio or soil volume is more sensitive to the gravimetric moisture content. The void ratio increases obviously from 0.48 to 0.60 as the gravimetric moisture content grows from 9.1% to 17.8%. The volume expansion caused by the water absorption results in significant reduction of the soil compactness degree from the initial value of 96.0% to 90.6% at the end of second wetting cycle. Therefore, the detriment of soil wetting not only lies in the strength reduction caused by increased moisture content, but also loosens the CL soil to a restively lower compaction degree.

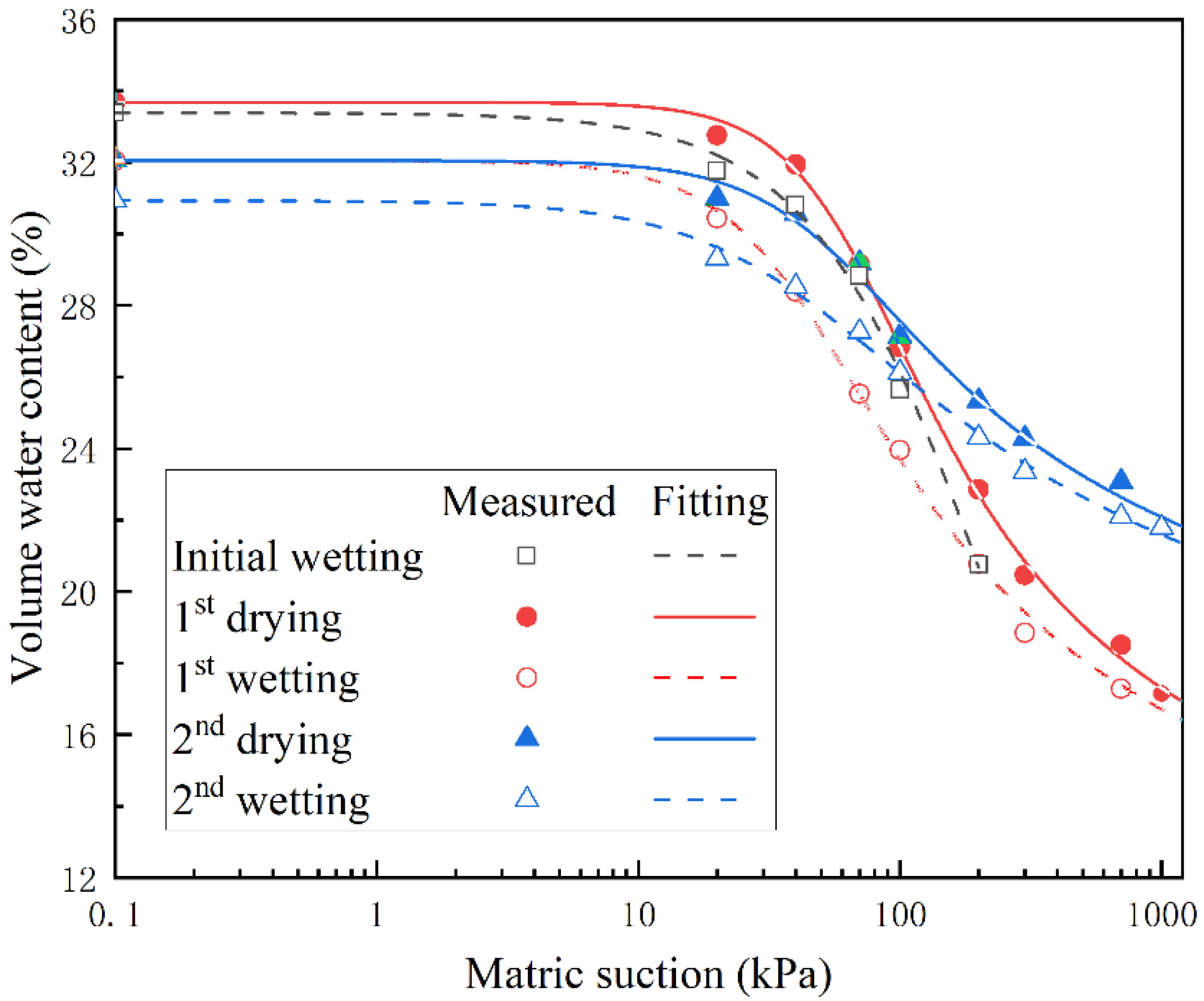
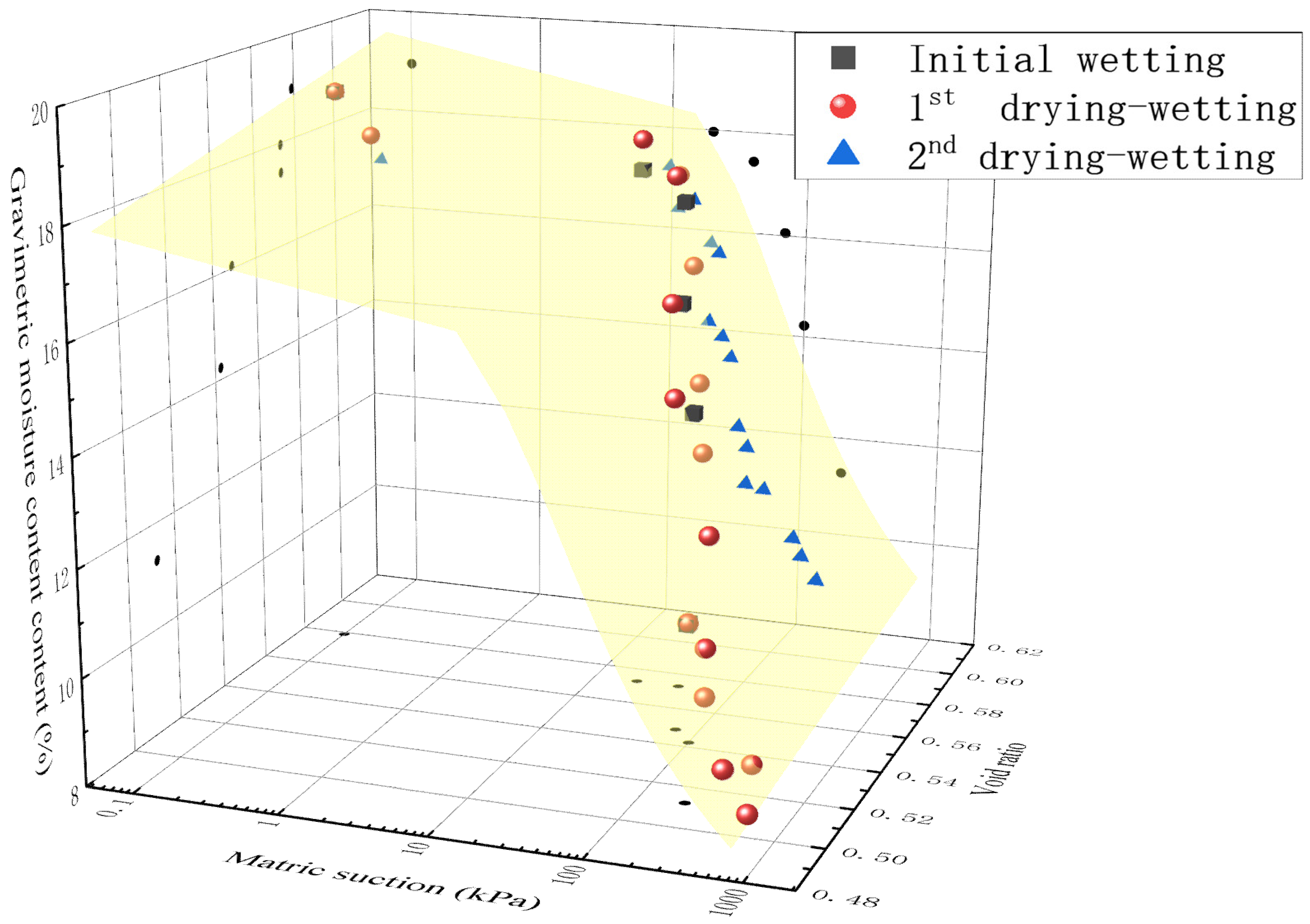
3.3. Unified Soil–Water Characteristic Surface of Moisture Content, Void Ratio and Matric Suction

Both the water content and volume of CL soils vary with the matric suction during the wetting–drying paths. Therefore, the gravimetric moisture content, void ratio and matric suction are inherently coupled, but they are always described in two partial expressions. The volumetric water content θ is dependent on the gravimetric moisture and void ratio, and the θ−w−e relationship can be expressed as:

$$\theta =\frac{w\cdot G_s}{1+e}$$

(7)

Substituting Equation (7) into the θ−ψ model of Equation (3) yields the w−e−ψ model as follows:

$$w=\left[1-\frac{\ln \left(1+\frac{\psi }{{\psi }_r}\right)}{\ln \left(1+\frac{{10}^6}{{\psi }_r}\right)}\right]\cdot \frac{1}{{\left\{\ln \left[\exp \left(1\right)+{\left(\frac{\psi }{a}\right)}^b\right]\right\}}^c}\cdot \frac{\left(1+e\right)w_S}{\left(1+e_S\right)}$$

(8)

where w_s and e_s are the gravimetric moisture content and void ratio at saturation. Equation (8) could be used to describe the unified soil–water characteristic surface (SWCS) of gravimetric moisture content, void ratio, and matric suction. Instead of fitting the soil–water characteristics at the individual wetting or drying path, an attempt was made to fit the entire wetting–drying cycles using Equation (8). The fitting parameters are summarized in

Table 4. Fitting parameters of soil–water characteristic surface.

Parameter	a	b	c	Ψr	R2
Value	40.36	1.67	0.41	5.25 × 106	0.94

, and the fitting degree R² reaches up to 0.94. Figure 12 plots the fitted soil–water characteristic surface for all the wetting–drying cycles that agrees well with the measured data. Results suggest that all the w−e−ψ relationships at different wetting–drying paths may be located on the same surface. Therefore, any one of gravimetric moisture content, void ratio and matric suction could be determined once the other two are provided, based on the unified w−e−ψ model of Equation (8). Moreover, the mutual relationships between w−e, w−ψ and e−ψ could also obtained as shown in Figure 12, via the projections at each coordinate plane, respectively.

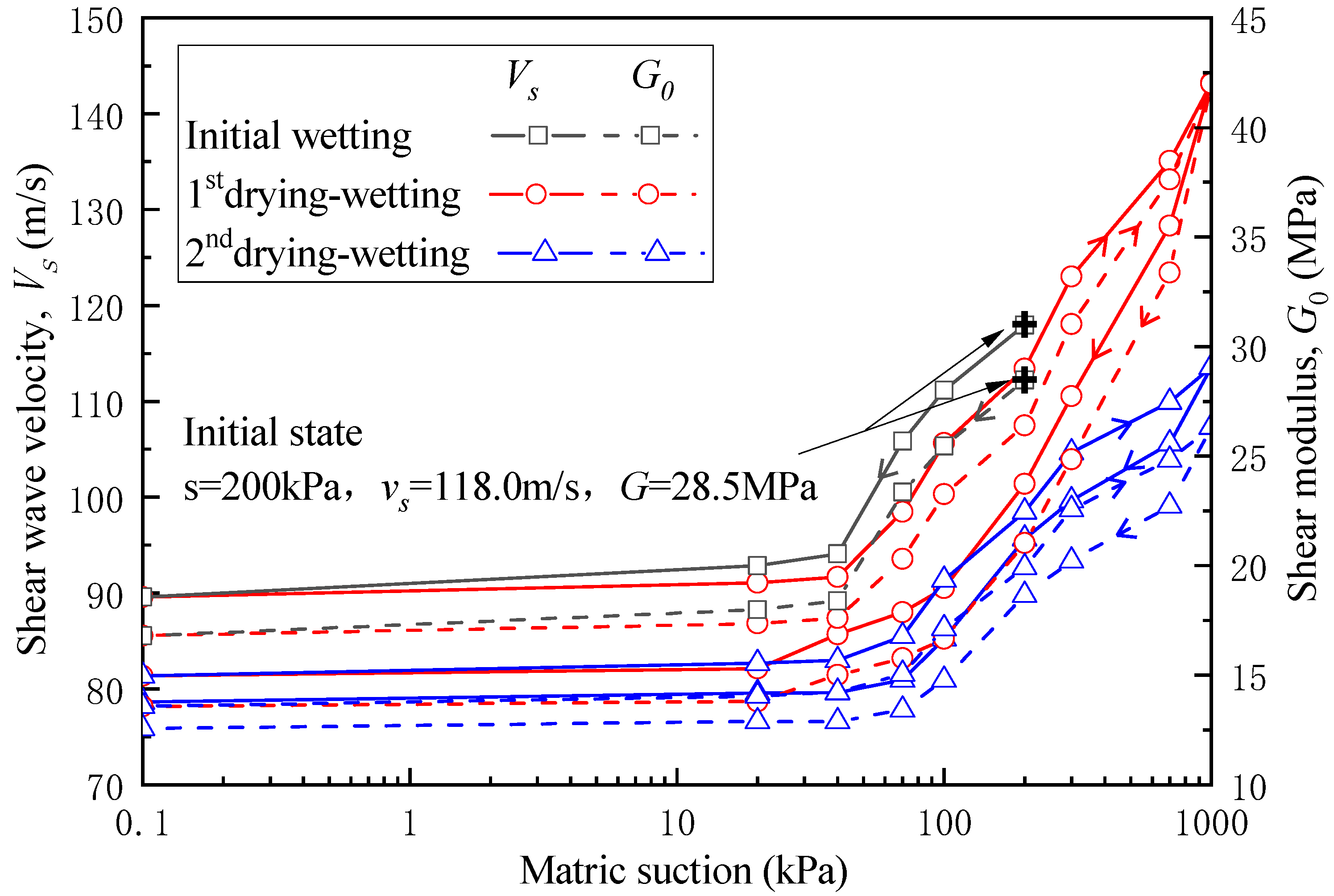
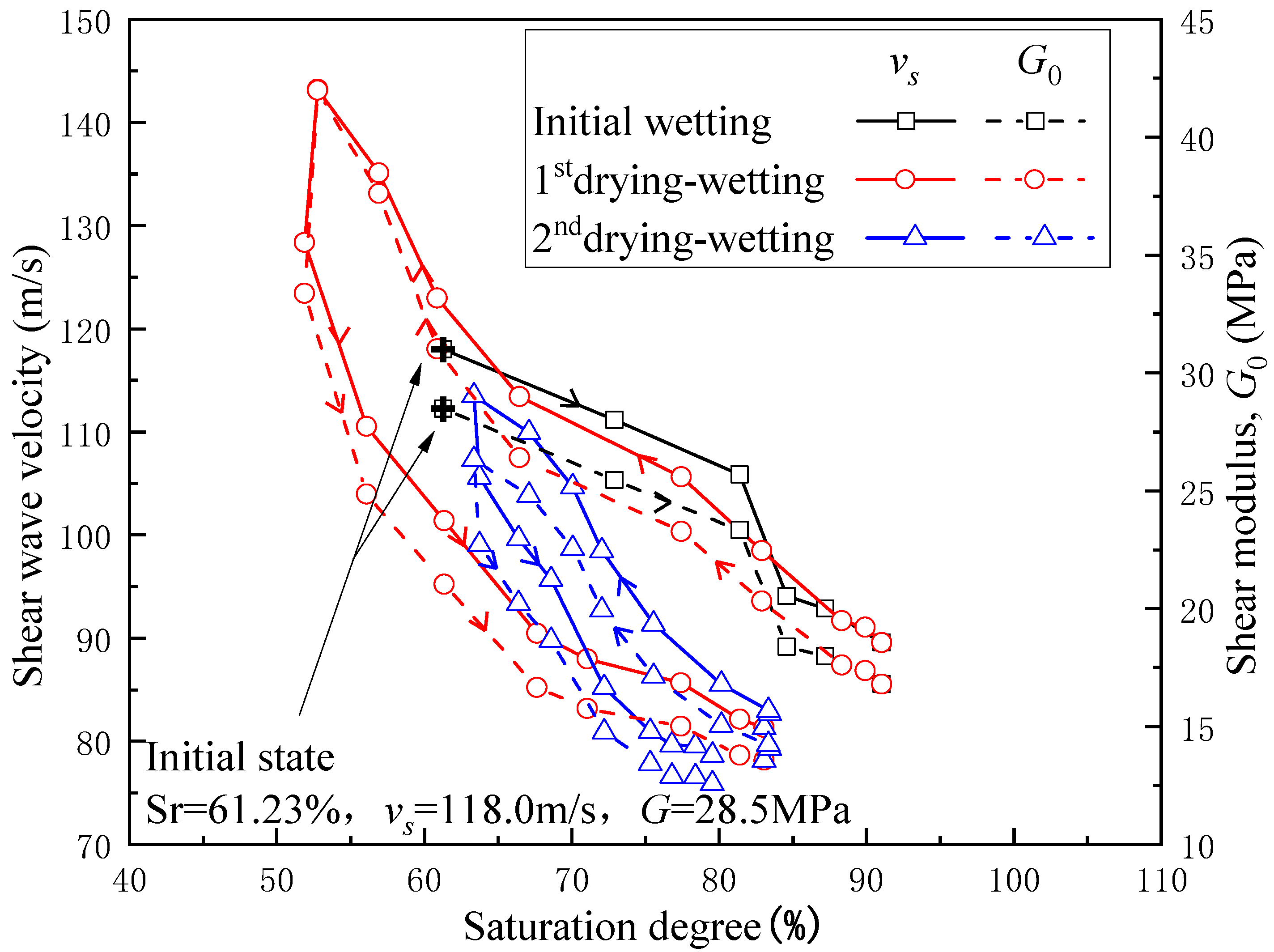
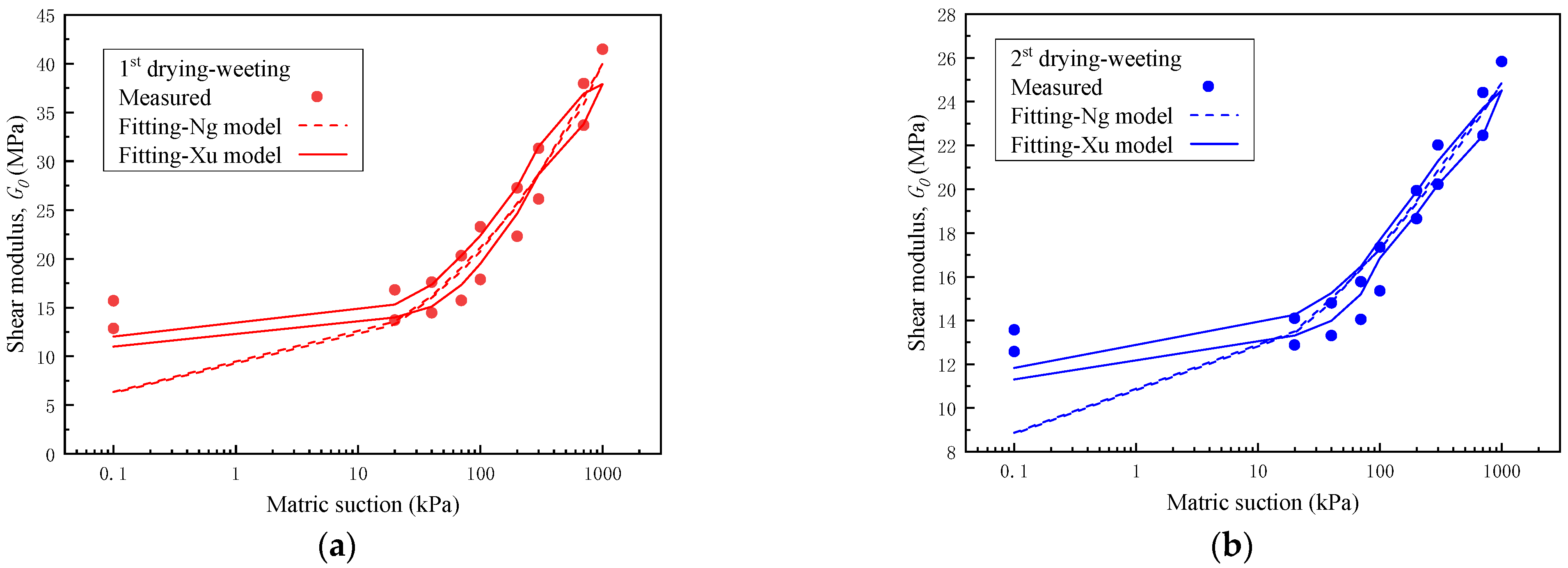
3.4. Shear Wave Velocity and Modulus

Shear wave velocity was measured until the water equilibrium condition was reached at individual matric suction, and the small−strain shear modulus was computed using Equation (1) to represent the performance of soil stiffness. Figure 13 shows the relationships between shear wave velocity, shear modulus and matric suction at all wetting–drying paths. It can be found that the shear modulus is largely dependent on both the matric suction and drying–wetting cycles. A decrease in matric suction weakens the contact stresses acting on the soil skeleton; thus, G₀ is expected to decrease [29]. The initial G₀ was about 28.5 MPa for the CL soil with compactness of 96.0% at moisture content of 11.3%, which decreased sharply to 18.4 MPa as the matric suction decreased to 40 kPa. Then, a small degradation of G₀ was observed as the matric suction further reduced to 0 kPa. Similar relationships also appeared in other drying and wetting paths, and a turning point of matric suction close to the air entry value indeed existed, above which G₀ was significantly influenced by soil suction. For the first drying–wetting cycle, the values of G₀ increased to 42.0 MPa at matric suction of 1000 kPa, and reduced to only 13.6 MPa at matric suction of 0 kPa. In the second drying–wetting cycle, the values of G₀ were 26.3 MPa and 12.6 MPa at the end of drying and wetting paths, respectively. A large reduction in G₀ occurred in the first drying–wetting cycle, similar to the variations of saturation, water contents and void ratio hysteresis illustrated in Figure 4, Figure 5, Figure 6 and Figure 7. It indicates that drying–wetting cycles could result in irreversible degradation of G₀. Consequently, the noticeable influences of drying–wetting cycles on the performance degradation of soil capacity should arouse more attention in practical engineering applications.

Since the soil water content and void ratio are both affected by matric suction, shear modulus is generally represented by the soil degree of saturation S_r, as shown in Figure 14. It can be recognized that G₀ appeared to have a monotonic relationship with S_r for each wetting or drying path. Similar to the variations of water content and void ratio versus matric suction, larger hysteresis also occurred in the first drying–wetting cycle than the second cycle. Compared to the shear modulus during the two drying paths, the values of G₀ were relatively reduced by 32.2–35.5% and 13.8–25.8% at the same Sr during the first and second wetting paths, respectively. In fact, higher matric suction was required to achieve the similar values of Sr in the second drying–wetting cycle as shown in Figure 5. However, most of the values of G₀ in the second drying–wetting cycle seemed lower than those of the first cycle, except for S_r ≤ 72% in the wetting paths. It indicates that significant degradation in shear modulus has been aggravated contributed to the drying–wetting cycles. Meanwhile, the values of G₀ are also affected by the matric suction beside the degree of saturation. Payan et al. [30,31,32,33,34] established the small−strain shear modulus models considering particle shape, stress anisotropy, and the amount of silt particles for sandy soils. For fine soils, Ng [35] introduced an empirical formula to describe the relationship between G₀ and matric suction in Equation (9).

$$G_0=C^2\cdot F\left(e\right)\cdot {\left(\frac{{\sigma }_i-u_a}{p_r}\times \frac{{\sigma }_j-u_a}{p_r}\right)}^{\delta }\cdot {\left(1+\frac{\psi }{p_r}\right)}^{2\lambda }$$

(9)

where $G_0$ is the shear modulus at very small strain; C is an inherent material constant; p_r is a reference stress, equal to 1 kPa; σ_i−u_a and σ_j−u_a are the principal effective stresses in the plane; ψ is the matric suction; δ, λ are fitting parameters. F(e) is considered as a void ratio function, which could be expressed as:

$$F\left(e\right)=\frac{1}{0.3+0.7e^2}$$

(10)

Xu [36] further introduced the degree of saturation into Equation (9) as:

$$G_0=C^2\cdot F\left(e\right)\cdot {\left(\frac{{\sigma }_i-u_a}{p_r}\times \frac{{\sigma }_j-u_a}{p_r}\right)}^{\delta }\cdot {\left(1+\frac{\psi }{p_r}\right)}^{2\lambda }\cdot S_r^{\gamma }$$

(11)

Since one−dimensional tests were conducted in this paper with a constant axial load of 1 kPa, Equation (11) could be improved as:

$$G_0=C^2\cdot F\left(e\right)\cdot {\left(1+\frac{\psi }{p_r}\right)}^{2\lambda }\cdot S_r^{\gamma }$$

(12)

The values of fitting parameters were listed in

Table 5. The values of fitting parameters.

Test Conditions	Parameters (Xu Model)				Parameters (Ng Model)
	a	b	C	R2	a	C	R2
first cycle	0.037	−1.15	37.62	0.82	0.13	2.09	0.83
second cycle	0.028	−1.20	40.15	0.86	0.070	2.51	0.82

and the fitting curves of the drying–wetting cycles are presented in Figure 15. The results show that the G₀ curves could be better fitted by the Xu model.

4. Conclusions

Based on the one−dimensional cyclic wetting–drying test of the densely compacted fine soil, the variations of soil physical properties in terms of saturation, moisture content and void ratio related to matric suction were revealed at different wetting–drying cycles. The corresponding small−strain shear modulus was evaluated using the bender elements. Accordingly, the following conclusions can be drawn:

(1)

The water retention capacity of soil showed a decreasing tendency in degrees of saturation and moisture contents when the number of wetting–drying cycles increased. Both the desorption and absorption rates were much higher during the first drying–wetting path than the subsequent cycles, and the degree of saturation tended to become smaller at low suction and higher at larger suction;

(2)

The compacted CL soil exhibited typical swelling and shrinkage deformations during the hydraulic loading processes, and the differences between the compressibility and swelling indexes were much larger for the first drying–wetting cycle than the second cycle. Accumulative deformation in terms of volume expansion was generated after the drying–wetting cycles, which deteriorated the densely compacted soils to a relatively looser state;

(3)

A unified formula was proposed to describe the soil–water characteristic surface of gravimetric moisture content, void ratio, and matric suction for the entire wetting–drying cycles. All the w−e−ψ relationships at different wetting–drying paths were approximately located on the same surface, indicating that the relationship within w, e and ψ was unique;

(4)

Shear modulus was found to be dependent on matric suction and the degree of saturation. Wetting–drying cycles gave rise to significant degradation in shear modulus, especially in the first cycle. Consequently, these noticeable influences of the wetting–drying cycles on the performance degradation of the soil−supporting modulus should arouse more attention in practical engineering applications, as these are caused not only by the increase in moisture content, but can also be attributed to the increase in void ratio.