Research on Adaptive Distribution Control Strategy of Braking Force for Pure Electric Vehicles
Abstract
:1. Introduction
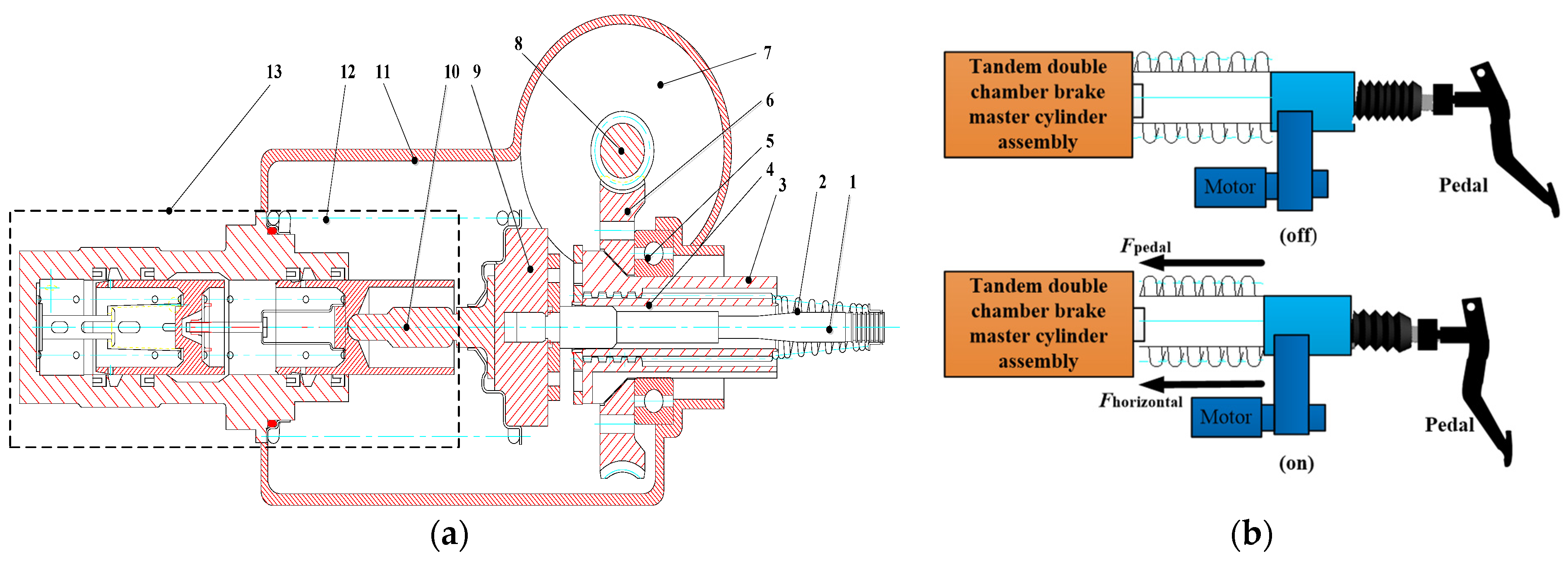
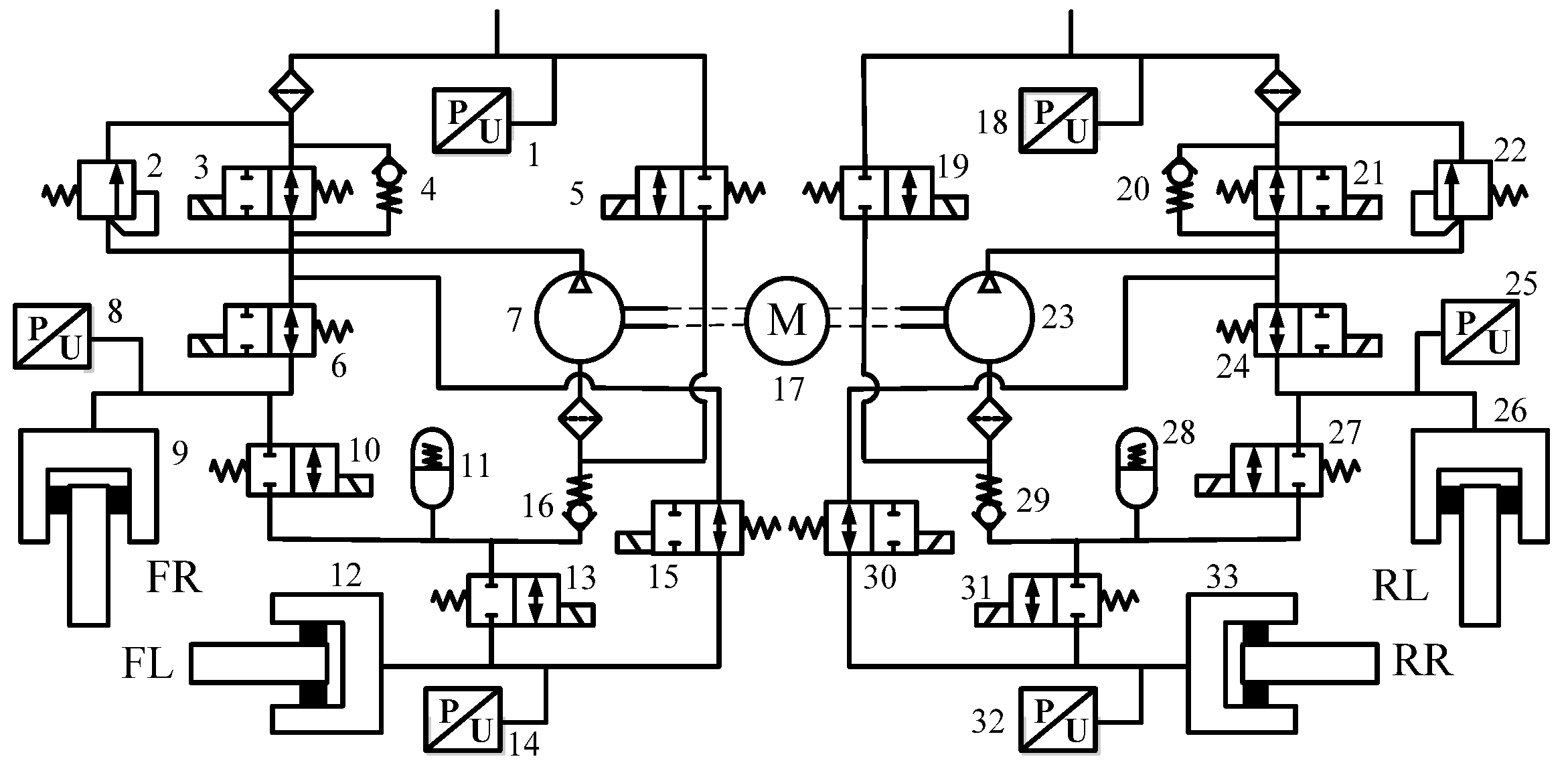
2. Vehicle Configuration and Braking System
3. Vehicle Dynamics Modeling
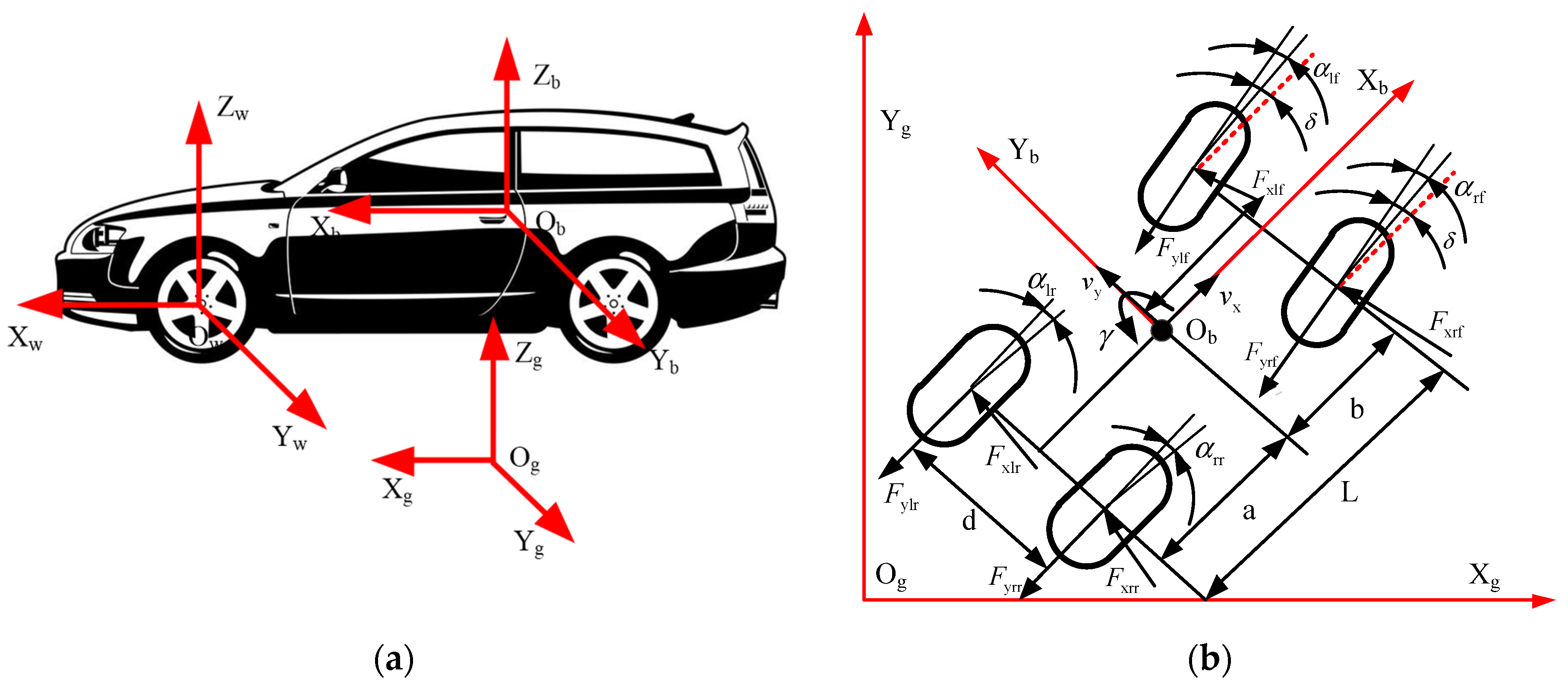
3.1. Vehicle 7-DOF Model
3.2. Tire Model
3.3. Battery Model
3.4. Powertrain Model
3.5. Braking System Model
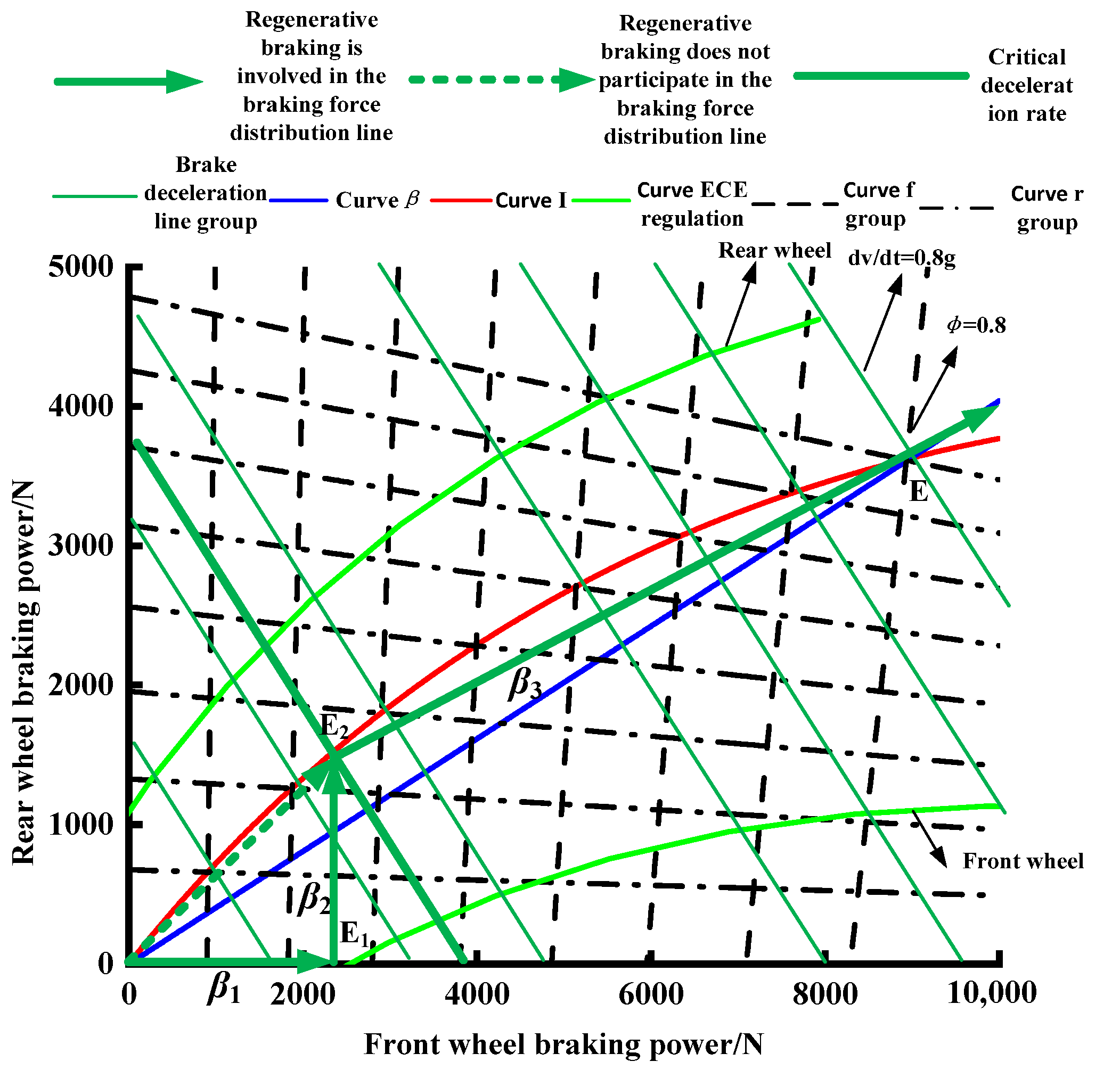
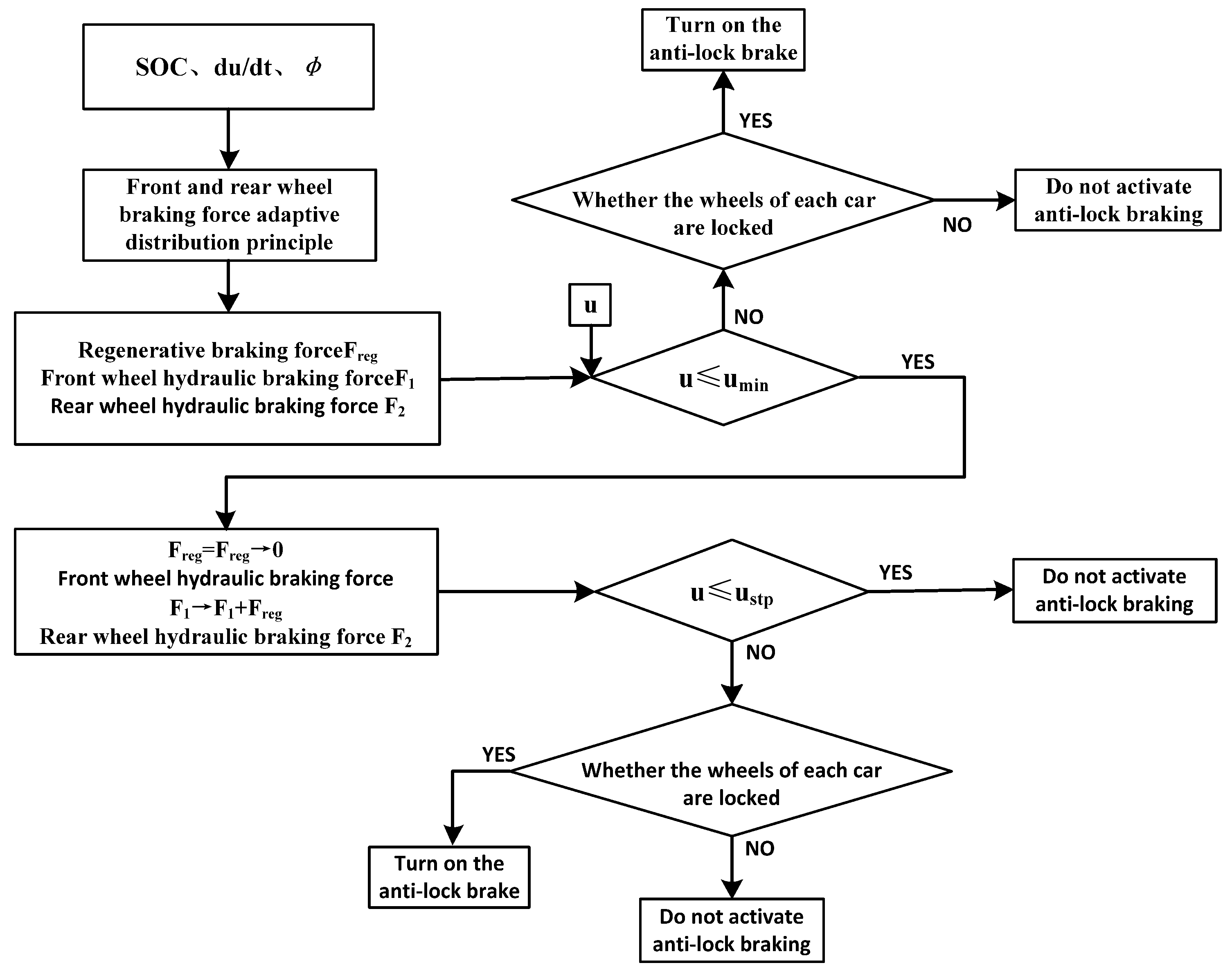
4. Adaptive Distribution Control Strategy of Braking Force
5. Simulation Analysis
5.1. Vehicle Parameters
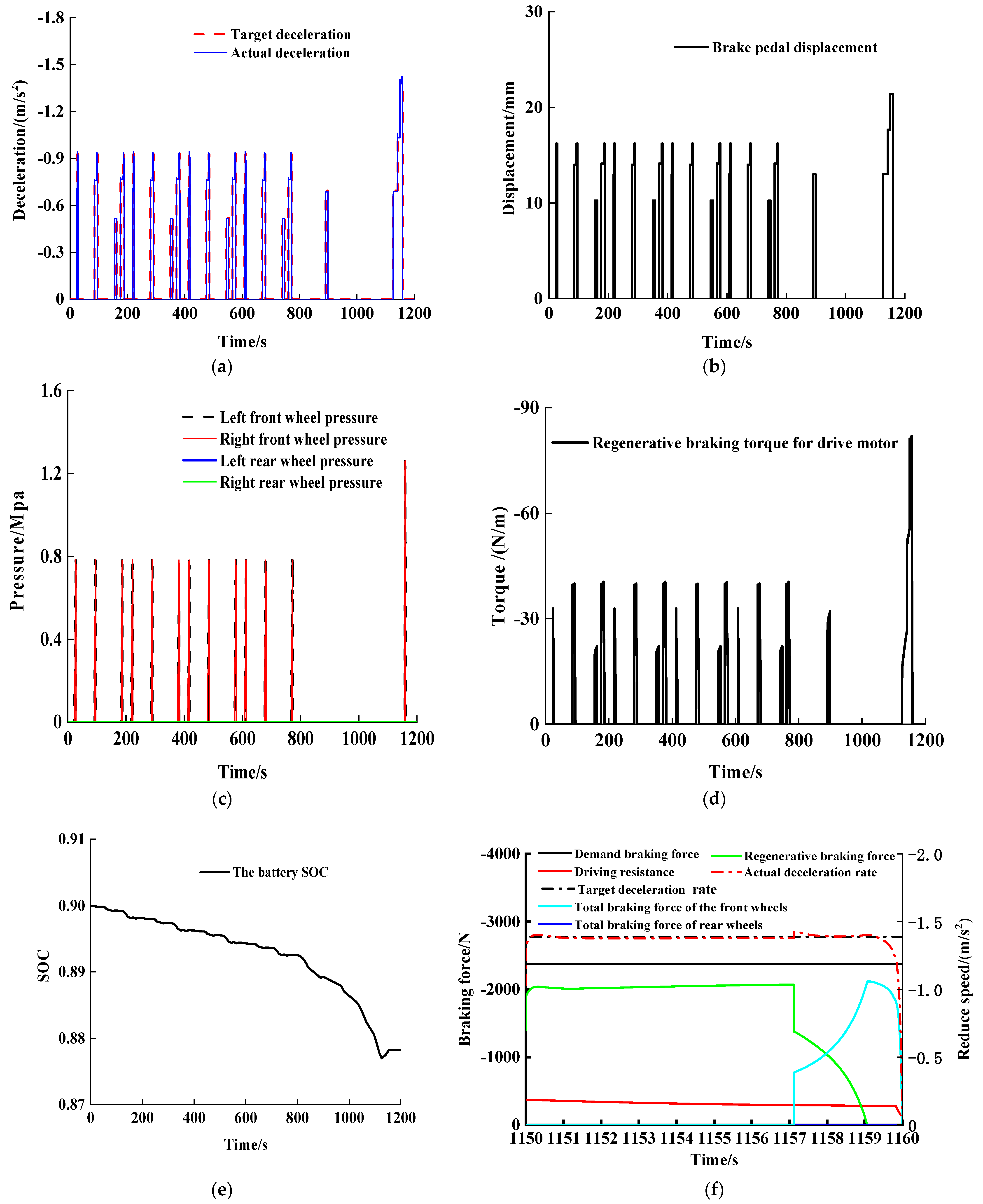
5.2. Simulation Results of NEDC and NYCC Cycle Conditions with High Attachment
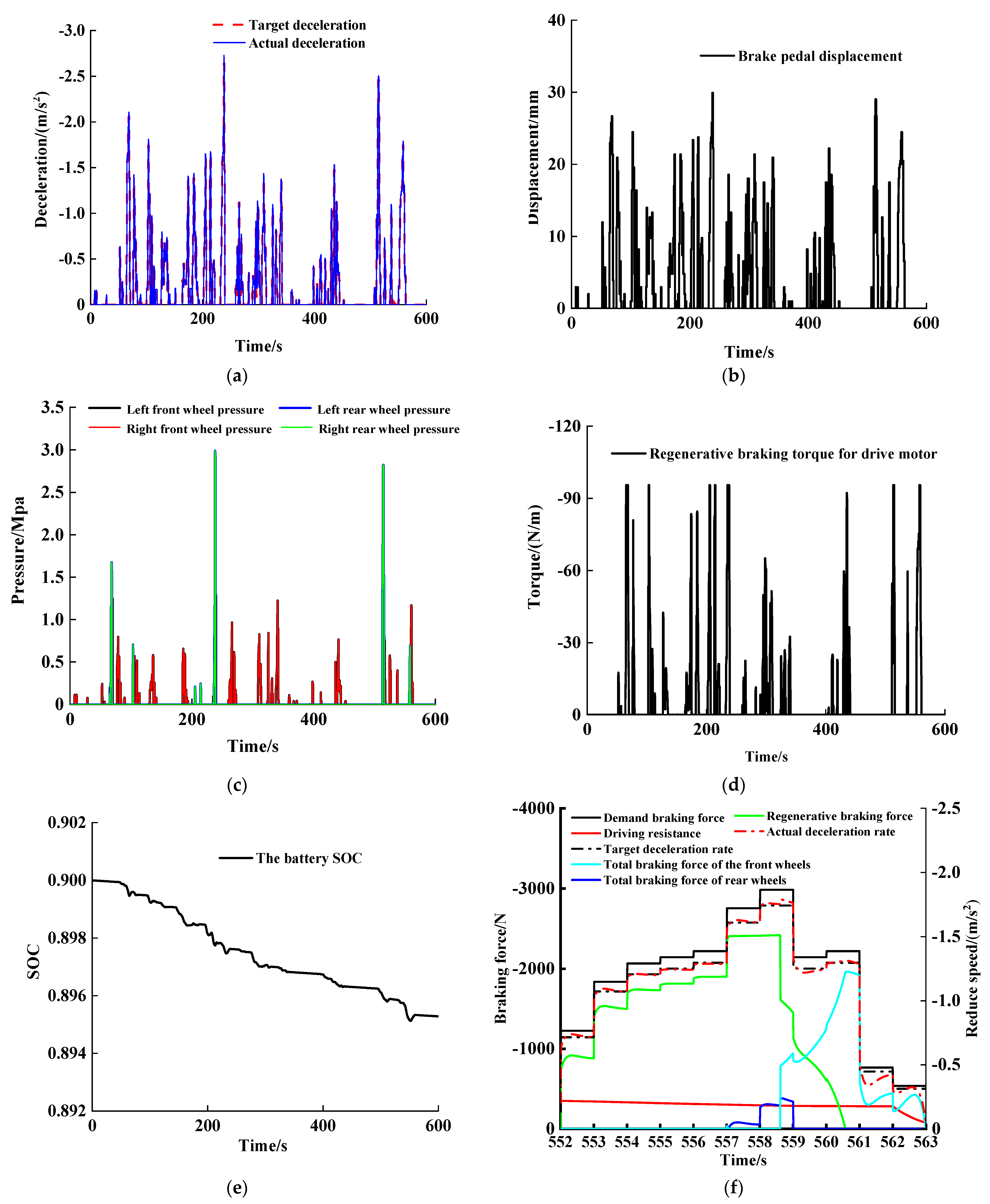
5.3. Simulation Results of Extremely Low Adhesion Road Surface
5.4. Braking Force Distribution Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kwon, K.; Minsik, S.; Seungjae, M. Efficient multi-objective optimization of gear ratios and motor torque distribution for electric vehicles with two-motor and two-speed powertrain system. Appl. Energy 2020, 259, 114190. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, J.; Xu, X.; Cai, Y.; Zhou, Z.; Sun, X. A comprehensive dynamic efficiency-enhanced energy management strategy for plug-in hybrid electric vehicles. Appl. Energy 2019, 247, 657–669. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, J.; Zhao, J.; Shi, K.; Dong, P.; Wang, S.; Liu, Y.; Guo, W.; Liu, X. Comparative study on fuel saving potential of series-parallel hybrid transmission and series hybrid transmission. Energy Convers. Manag. 2022, 252, 114970. [Google Scholar] [CrossRef]
- Xiao, B.; Lu, H.; Wang, H.; Ruan, J.; Zhang, N. Enhanced Regenerative Braking Strategies for Electric Vehicles: Dynamic Performance and Potential Analysis. Energies 2017, 10, 1875. [Google Scholar] [CrossRef] [Green Version]
- Ruan, J.; Walker, P.; Watterson, P.; Zhang, N. The dynamic performance and economic benefit of a blended braking system in a multi-speed battery electric vehicle. Appl. Energy 2016, 183, 1240–1258. [Google Scholar] [CrossRef]
- Geraee, S.; Mohammadbagherpoor, M.; Shafiei, M.; Valizadeh, M.; Montazeri, F.; Feyzi, M.R. Regenerative braking of electric vehicle using a modified direct torque control and adaptive control theory. Comput. Electr. Eng. 2018, 69, 85–97. [Google Scholar] [CrossRef]
- Qin, Y.; Tang, X.; Jia, T.; Duan, Z.; Zhang, J.; Li, Y.; Zheng, L. Noise and vibration suppression in hybrid electric vehicles: State of the art and challenges. Renew. Sustain. Energy Rev. 2020, 124, 109782. [Google Scholar] [CrossRef]
- Yu, Z. Automobile Theory; Mechanical Industry Press: Beijing, China, 2018; pp. 134–142. [Google Scholar]
- Lian, Y.; Zhao, Y.; Hu, L.; Tian, Y. Longitudinal collision avoidance control of electric vehicles based on a new safety distance model and constrained-regenerative-braking-strength-continuity braking force distribution strategy. IEEE Trans. Veh. Technol. 2015, 65, 4079–4094. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, W.; Li, W. Braking sense consistency strategy of electro-hydraulic composite braking system. Mech. Syst. Signal Process. 2018, 109, 196–219. [Google Scholar] [CrossRef]
- Xu, G.; Li, W.; Xu, K.; Song, Z. An Intelligent Regenerative Braking Strategy for Electric Vehicles. Energies 2011, 4, 1461–1477. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Sun, D. Energy recovery strategy based on ideal braking force distribution for regenerative braking system of a four-wheel drive electric vehicle. IEEE Access 2020, 8, 136234–136242. [Google Scholar] [CrossRef]
- Kumar, C.N.; Subramanian, S.C. Cooperative control of regenerative braking and friction braking for a hybrid electric vehicle. Proceedings of the Institution of Mechanical Engineers. J. Automob. Eng. 2016, 230, 103–116. [Google Scholar] [CrossRef]
- Li, S.; Yu, B.; Feng, X. Research on braking energy recovery strategy of electric vehicle based on ECE regulation and I curve. Sci. Prog. 2020, 103, 0036850419877762. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Ouyang, M.; Gu, J. Optimal Regenerative Braking Control for Permanent Magnet Synchronous Motors in Electric Vehicles. Proc. CSEE 2013, 33, 83–91. [Google Scholar]
- Ko, J.; Ko, S.; Son, H.; Yoo, B.; Cheon, J.; Kim, H. Development of brake system and regenerative braking cooperative control algorithm for automatic-transmission-based hybrid electric vehicles. IEEE Trans. Veh. Technol. 2014, 64, 431–440. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, J.; Halim, D. Braking force control strategy for electric vehicles with load variation and wheel slip considerations. IET Electr. Syst. Transp. 2017, 7, 41–47. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, X. Control strategy of regenerative braking system in electric vehicles. Energy Procedia 2018, 152, 496–501. [Google Scholar] [CrossRef]
- Liang, L.I.; Gang, J.I.A.; Jian, S.O.N.G. Progress on Vehicle Dynamics Stability Control System. J. Mech. Eng. 2013, 49, 95–107. [Google Scholar]
- Johnson, V.H. Battery performance models in ADVISOR. J. Power Sources 2022, 110, 321–329. [Google Scholar] [CrossRef]
- Li, G.; Lin, Y.; He, H. Regenerative Braking Control Strategy for Electric Vehicle. Trans. Beijing Inst. Technol. 2009, 29, 520–524. [Google Scholar]
- Yong, J.; Gao, F.; Ding, N. Design and Validation of an Electro-Hydraulic Brake System Using Hardware-in-the-loop Real-time Simulation. Int. J. Automot. Technol. 2017, 18, 603–612. [Google Scholar] [CrossRef]
- Zhao, Z.; Peng, Y. Simulation on Series Electro-hydraulic Combined Braking for 4WD Hybrid Electric Car. J. Syst. Simul. 2012, 24, 208–215. [Google Scholar]
- Ma, Y.; Zhao, J.; Zhao, H.; Lu, C.; Chen, H. MPC-based slip ratio control for electric vehicle considering road roughness. IEEE Access 2019, 7, 52405–52413. [Google Scholar] [CrossRef]




| Parameter | The Numerical | Parameter | The Numerical |
|---|---|---|---|
| 1/(Ce1Re1) | 37.5342 | 1/(Ce2Re2) | 38.3128 |
| k1 | 0.589 | k2 | 0.936 |
| The Basic Parameters | The Numerical | The Basic Parameters | The Numerical |
|---|---|---|---|
| Curb weight | 1600 kg | Maximum motor power | 135 Kw |
| Windward area | 2.58 m2 | Maximum motor speed | 12,000 rpm |
| Total battery capacity | 259 Ah | Maximum motor torque | 300 N·m |
| Speed ratio of reducer | 8.55 | The wheel radius | 0.307 m |
| Front/rear wheel radius | 0.307 m | Effective radius of rear wheel action | 0.11 m |
| Effective radius of front wheel action | 0.122 m | Height of vehicle center of mass above ground | 0.52 m |
| Distance from center of mass to front axle | 1.208 m | Distance from center of mass to rear axle | 1.542 m |
| Comparing the Results | Driving Cycles | |
|---|---|---|
| NEDC | NYCC | |
| Total braking energy/kj | 1962.72 | 936.99 |
| Recoverable energy/kj | 1032.75 | 444.56 |
| Recovery of energy/% | 52.62 | 47.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Bu, L.; Fu, B.; Zheng, J.; Wang, G.; He, L.; Hu, Y. Research on Adaptive Distribution Control Strategy of Braking Force for Pure Electric Vehicles. Processes 2023, 11, 1152. https://doi.org/10.3390/pr11041152
Liu J, Bu L, Fu B, Zheng J, Wang G, He L, Hu Y. Research on Adaptive Distribution Control Strategy of Braking Force for Pure Electric Vehicles. Processes. 2023; 11(4):1152. https://doi.org/10.3390/pr11041152
Chicago/Turabian StyleLiu, Jingang, Lei Bu, Bing Fu, Jianyun Zheng, Gaosheng Wang, Lihong He, and Yuliang Hu. 2023. "Research on Adaptive Distribution Control Strategy of Braking Force for Pure Electric Vehicles" Processes 11, no. 4: 1152. https://doi.org/10.3390/pr11041152
APA StyleLiu, J., Bu, L., Fu, B., Zheng, J., Wang, G., He, L., & Hu, Y. (2023). Research on Adaptive Distribution Control Strategy of Braking Force for Pure Electric Vehicles. Processes, 11(4), 1152. https://doi.org/10.3390/pr11041152






