Bifurcation Analysis of a Rotor-Casing Coupling System with Bolted Flange Connection under the Effect of Rotor-Casing Rubbing Fault
Abstract
:1. Introduction
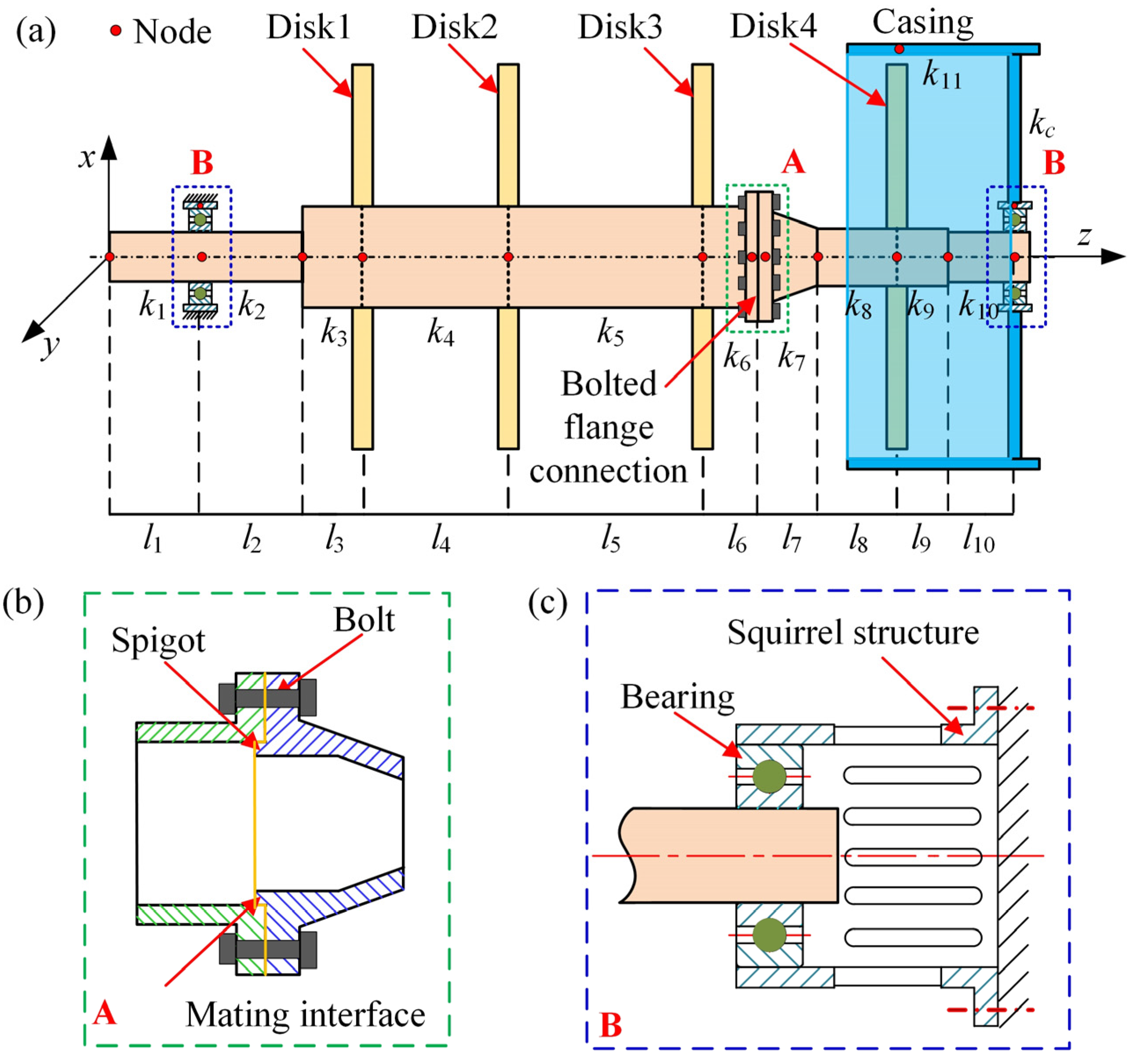
2. Dynamic Modeling of a Rotor-Casing Coupling System with Bolted Connection
- (a)
- The rotor and casing are supposed to be rigid, and the central axis of the shaft and casing are parallel; thus, only the lateral vibration of the coupling system is considered;
- (b)
- The shaft segments shown in Figure 2a are massless; thus, the effect of the gyroscopic and polar moment of inertia can be neglected;
- (c)
- The vibration of the coupling system transmits through direct contact during the rubbing fault and through the squirrel structure;
- (d)
- The nonlinearities due to frictional contacts at the mating interface of the bolted flange connection during vibrations is ignored in the present work.
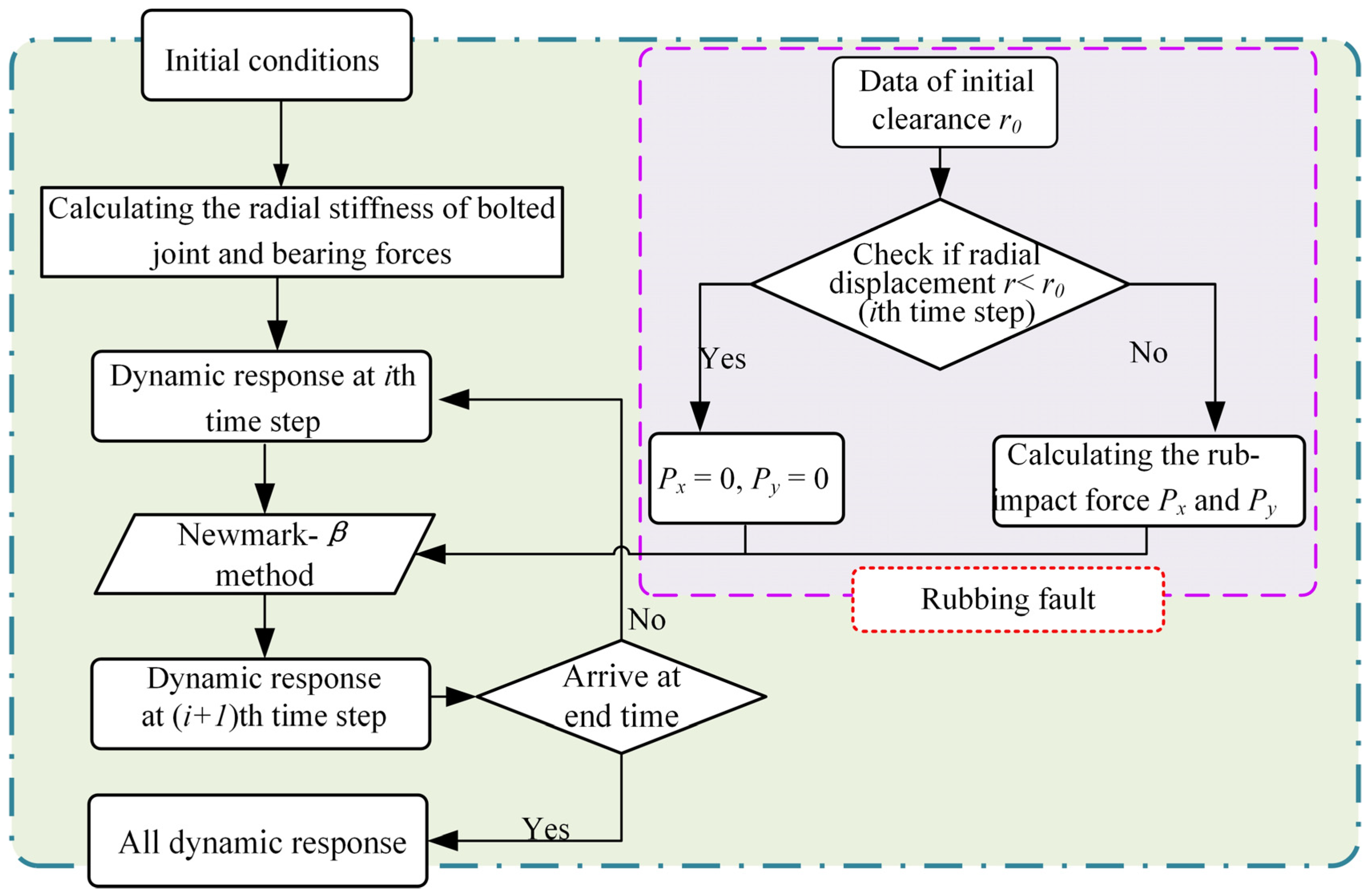
2.1. Rotor-Casing Rubbing Force Model
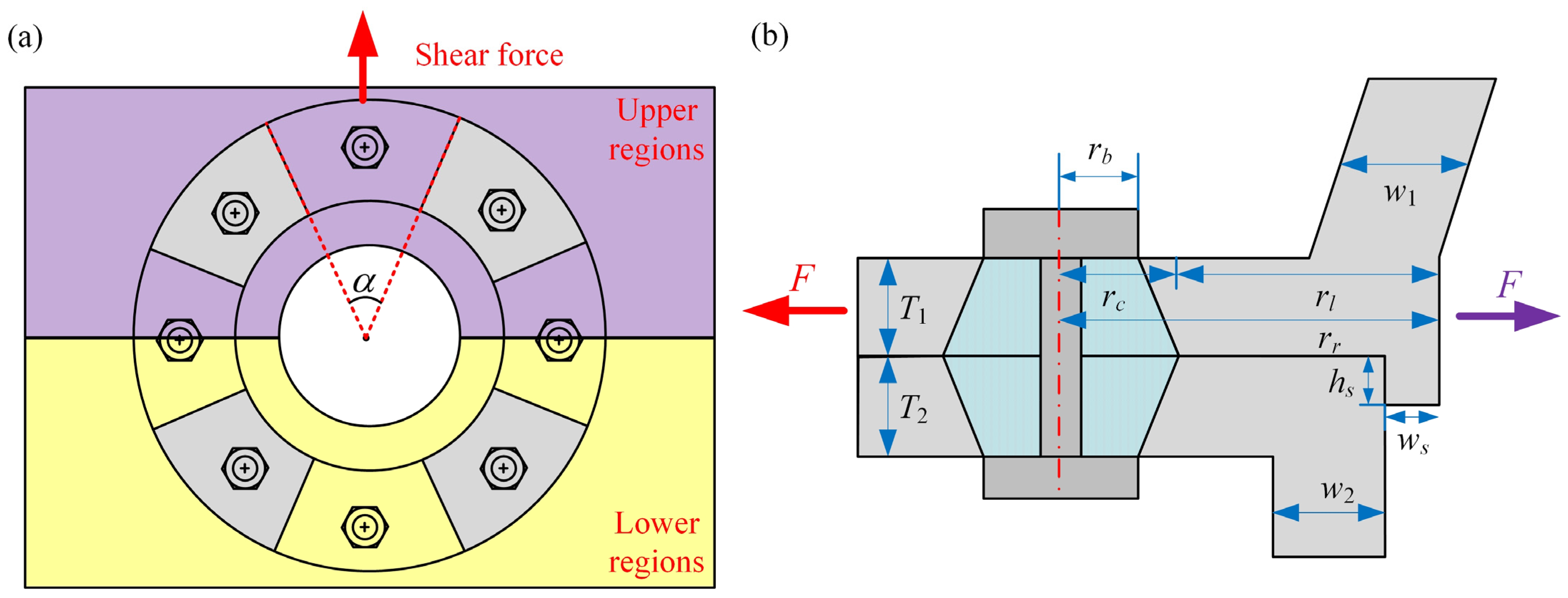
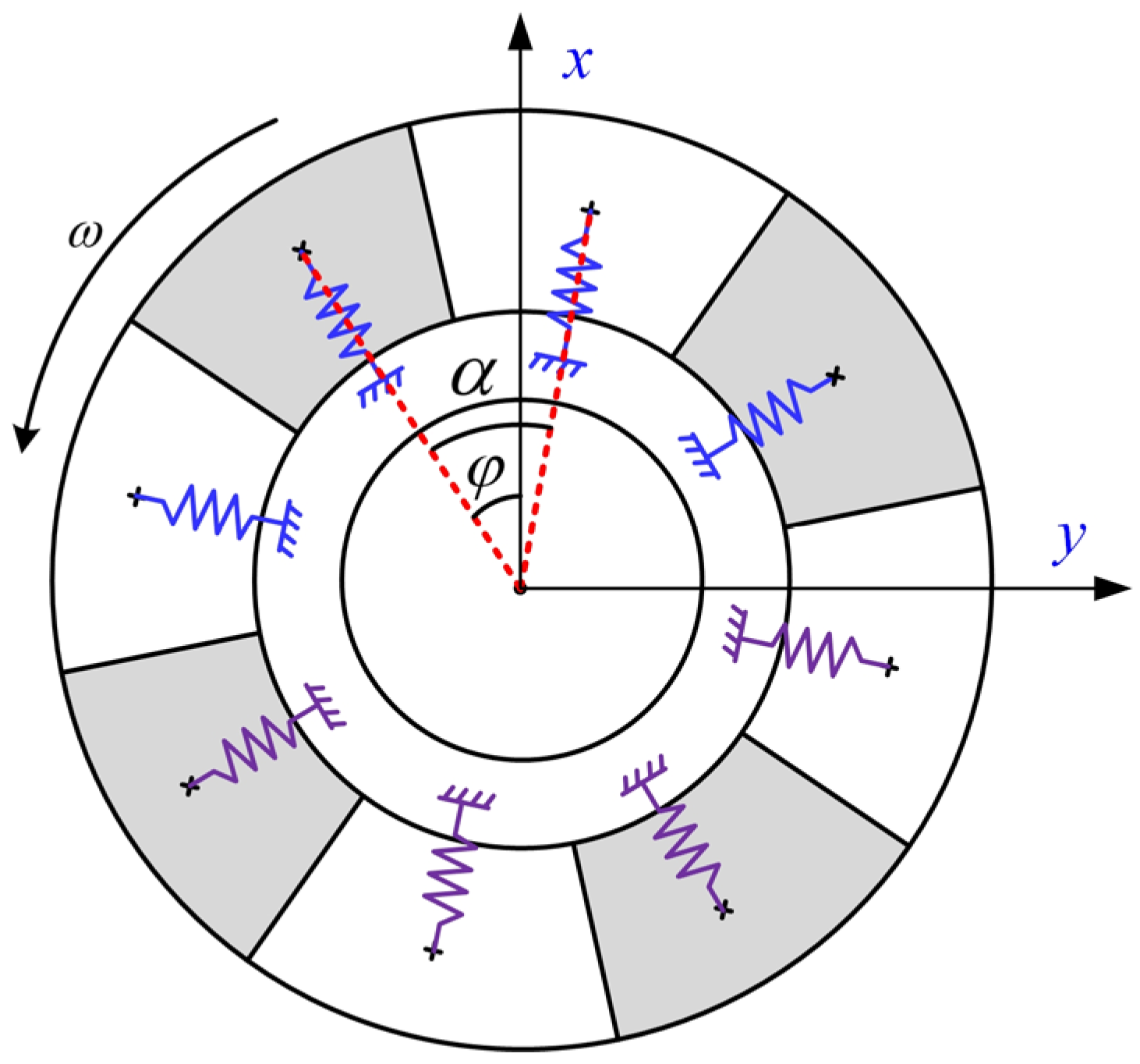
2.2. Modeling of the Bolted Flange Connection with a Spigot
2.3. Motion Equations of the Rotor System
2.4. Non-Dimensional Model
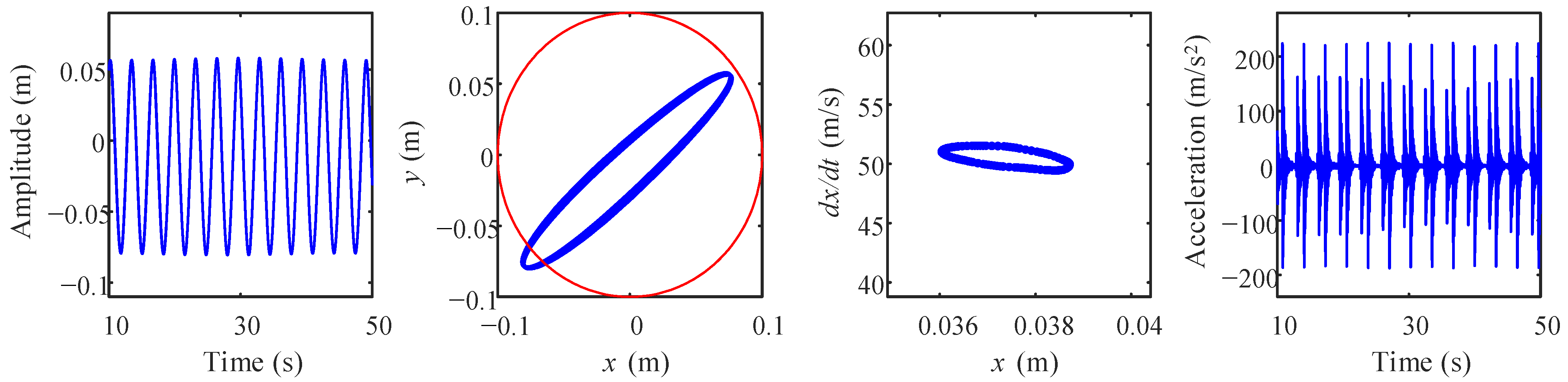
3. Numerical Simulation on the Effect of Rotor-Casing Rubbing Fault
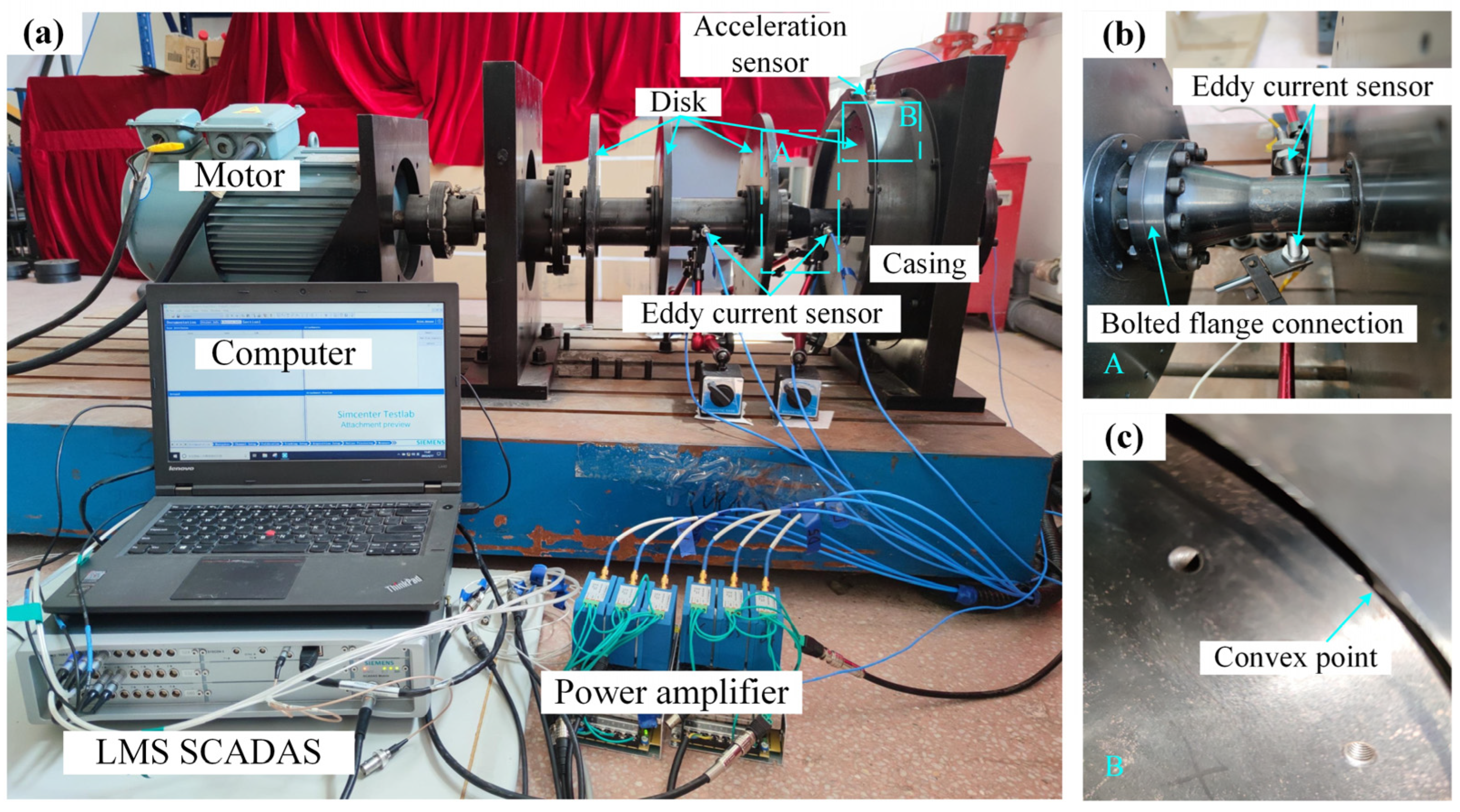
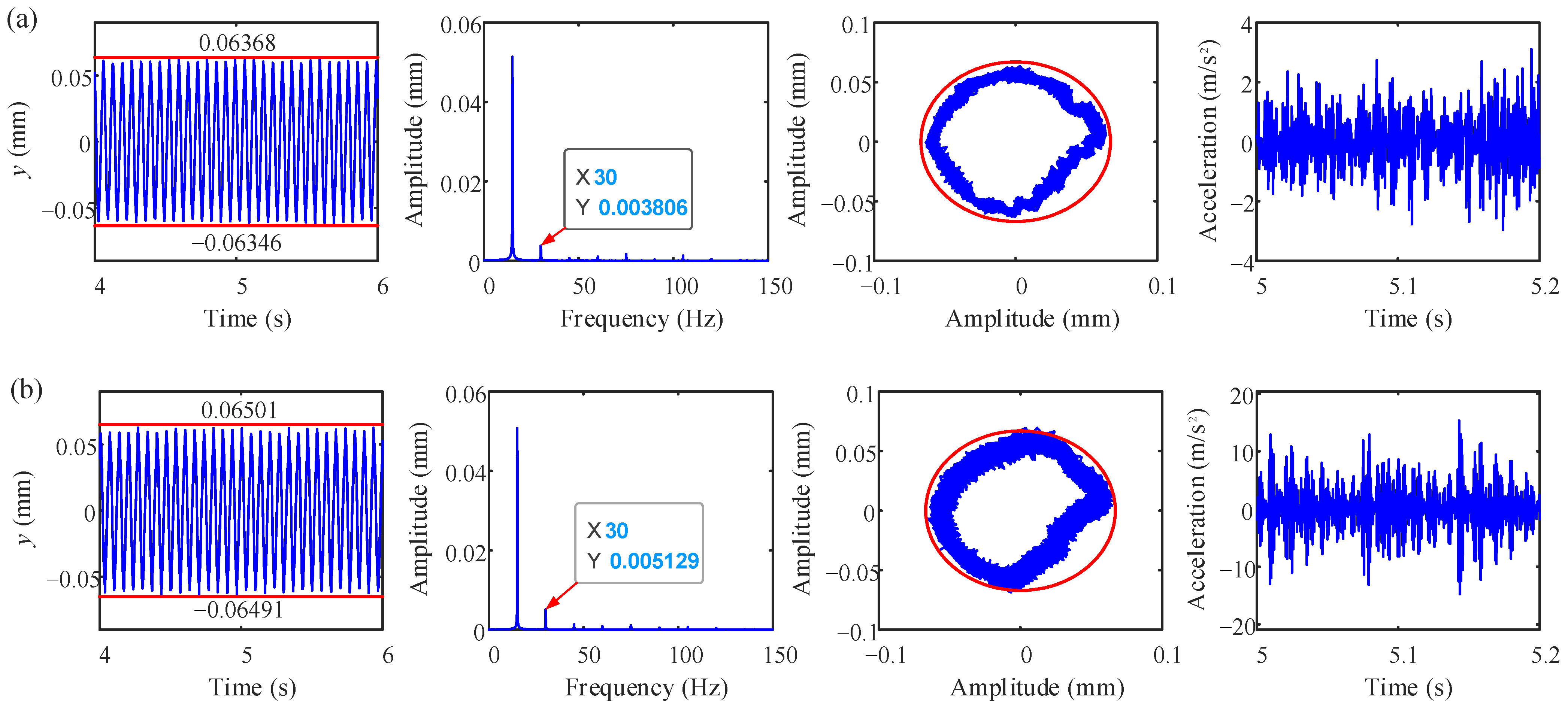
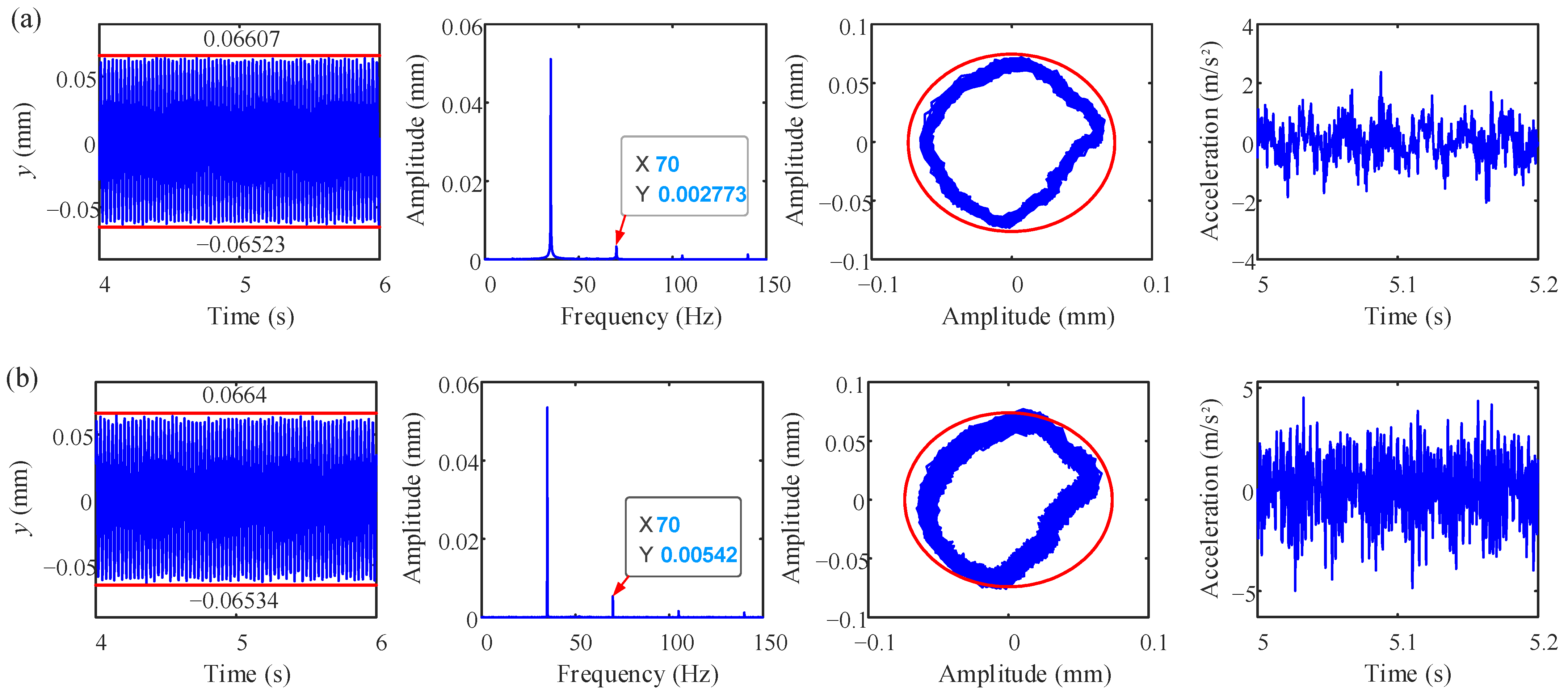
4. Experimental Study
5. Conclusions
- The coupling system produces rich forms of motion, which are described as changing from quasi-periodic motion to 1T-periodic motion, quasi-periodic motion, 1T-periodic motion, 2T-periodic motion, and quasi-periodic motion. The rubbing fault significantly affects the state of the system’s motion; for example, weakening the periodic motion to a certain extent or expanding the rotational speed range of the quasi-periodic motion would reduce the system stability.
- When the rubbing fault occurs, the amplitudes of the harmonic 2fr significantly increase, which is attributed to the additional nonlinear effect introduced by the impact forces acting on the rotor system. Moreover, the maximum value of the casing acceleration is also increased in the case with rotor-casing rubbing fault; for example, the maximum value of casing acceleration at 9480 rev/min increases from about 25 m/s2 to about 210 m/s2 under the rubbing fault. The above phenomenon can be considered as the most distinguishable characteristic for diagnosing the aggravation of rubbing fault in the rotor-casing coupling system.
- The experiments were conducted for four cases (with and without rubbing fault at ω = 1800 rev/min and ω = 2100 rev/min); the results show that the amplitudes of the harmonic 2fr and casing acceleration are obviously increased, which agree with the simulation results.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Srivastava, A.K.; Tiwari, M.; Singh, A. Identification of rotor-stator rub and dependence of dry whip boundary on rotor parameters. Mech. Syst. Signal Process. 2021, 159, 107845. [Google Scholar] [CrossRef]
- Jiang, M.; Zheng, Z.; Xie, Y.; Zhang, D. Local Sensitivity Analysis of Steady-State Response of Rotors with Rub-Impact to Parameters of Rubbing Interfaces. Appl. Sci. 2021, 11, 1307. [Google Scholar] [CrossRef]
- Koten, H. Recent Researches in Engineering Sciences, 1st ed.; Livre de Lyon: Lyon, France, 2021. [Google Scholar]
- Jamia, N.; Jalali, H.; Taghipour, J.; Friswell, M.; Khodaparast, H.H. An equivalent model of a nonlinear bolted flange joint. Mech. Syst. Signal Process. 2020, 153, 107507. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Z.; Liu, J.; Ma, H.; Yang, D. Dynamic modeling and stability analysis of a rotor-bearing system with bolted-disk joint. Mech. Syst. Signal Process. 2021, 158, 107778. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Z.; Wang, J.; Ma, H.; Yang, D. Numerical and experimental analysis of the effect of eccentric phase difference in a rotor-bearing system with bolted-disk joint. Nonlinear Dyn. 2021, 105, 2105–2132. [Google Scholar] [CrossRef]
- Pan, W.; Li, X.; Ling, L.; Qu, H. Dynamic modeling and response analysis of rub-impact rotor system with squeeze film damper under maneuvering load. Appl. Math. Model. 2023, 114, 544–582. [Google Scholar] [CrossRef]
- Behzad, M.; Alvandi, M. Unbalance-induced rub between rotor and compliant-segmented stator. J. Sound Vib. 2018, 429, 96–129. [Google Scholar] [CrossRef]
- Behzad, M.; Alvandi, M. Friction-induced backward rub of rotors in non-annular clearances: Experimental observations and numerical analysis. Tribol. Int. 2020, 152, 106430. [Google Scholar] [CrossRef]
- Briend, Y.; Chatelet, E.; Dufour, R.; Andrianoely, M.-A.; Legrand, F.; Sousa, M.S.; Steffen, V.; Baudin, S. Dry-whip phenomenon in on-board rotordynamics: Modeling and experimentation. J. Sound Vib. 2021, 513, 116398. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Ma, Z.; Wang, X.; Wu, Q.; Fan, Z. Coupled bending-torsional vibration analysis for rotor-bearing system with rub-impact of hydraulic generating set under both dynamic and static eccentric electromagnetic excitation. Chaos Solitons Fractals 2021, 147, 110960. [Google Scholar] [CrossRef]
- Gao, T.; Cao, S.; Hou, L.; Hou, Y. An experimental study on the nonlinear vibration phenomenon of a rotor system subjected to barrel roll flight and coupled rub-impact faults. Measurement 2019, 153, 107406. [Google Scholar] [CrossRef]
- Kandil, A. Investigation of the whirling motion and rub/impact occurrence in a 16-pole rotor active magnetic bearings system with constant stiffness. Nonlinear Dyn. 2020, 102, 2247–2265. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, D.; Yu, T.; Wang, D.; Li, C. Prediction of dynamic characteristics of a dual-rotor system with fixed point rubbing—Theoretical analysis and experimental study. Int. J. Mech. Sci. 2016, 115–116, 253–261. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, Y.; Cao, D.; Chen, G.; Jin, Y. Response evaluation of imbalance-rub-pedestal looseness coupling fault on a geometrically nonlinear rotor system. Mech. Syst. Signal Process. 2018, 118, 423–442. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, L.; Hu, A.; Chen, K. Nonlinear dynamic response on multi-fault rod fastening rotor with variable parameters. Appl. Math. Model. 2023, 114, 147–161. [Google Scholar] [CrossRef]
- Mokhtar, A.; Darpe, A.K.; Gupta, K. Investigations of Rubbing Phenomenon during Coast-up Operation of a Cryogenic Engine Turbopump. J. Vib. Eng. Technol. 2019, 8, 737–749. [Google Scholar] [CrossRef]
- Zeng, J.; Ma, H.; Yu, K.; Guo, X.; Wen, B. Rubbing response comparisons between single blade and flexible ring using different rubbing force models. Int. J. Mech. Sci. 2019, 164, 105164. [Google Scholar] [CrossRef]
- Kang, Y.; Cao, S.; Hou, Y.; Chen, N.; Li, B. Dynamics research on the rubbing process and rubbing forms of rotor-blade-casing systems. Int. J. Non-Linear Mech. 2022, 147, 104242. [Google Scholar] [CrossRef]
- Wang, N.; Jiang, D.; Xu, H. Effects of Rub-Impact on Vibration Response of a Dual-Rotor System-Theoretical and Experimental Investigation. Exp. Tech. 2019, 44, 299–311. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Wang, S.; Yan, H.; Liao, P. Bifurcation analysis of a magnetically supported rigid rotor in auxiliary bearings. Chaos Solitons Fractals 2018, 118, 328–336. [Google Scholar] [CrossRef]
- Prabith, K.; Krishna, I.R.P. The numerical modeling of rotor–stator rubbing in rotating machinery: A comprehensive review. Nonlinear Dyn. 2020, 101, 1317–1363. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, L.; Su, H.; Hu, A.; Yang, X. Dynamic analysis of composite rod fastening rotor system considering multiple parameter influence. Appl. Math. Model. 2022, 105, 615–630. [Google Scholar] [CrossRef]
- Hong, J.; Yang, Z.; Wang, Y.; Cheng, R.; Ma, Y. Combination resonances of rotor systems with asymmetric residual preloads in bolted joints. Mech. Syst. Signal Process. 2023, 183, 109626. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Zhang, F.; Feng, Y. Nonlinear Analysis of Rod Fastened Rotor under Nonuniform Contact Stiffness. Shock Vib. 2020, 2020, 8851996. [Google Scholar] [CrossRef]
- Li, J.; Yang, Z.; Ren, Q.; Mo, G.; Zhong, W.; Feng, Y.; Li, G. Study on the bistable vibration behaviour of a rod-fastened rotor-bearing system. Nonlinear Dyn. 2022, 109, 609–629. [Google Scholar] [CrossRef]
- Qin, Z.Y.; Han, Q.K.; Chu, F.L. Analytical model of bolted disk–drum joints and its application to dynamic analysis of jointed rotor. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2013, 228, 646–663. [Google Scholar] [CrossRef]
- Qin, Z.; Han, Q.; Chu, F. Bolt loosening at rotating joint interface and its influence on rotor dynamics. Eng. Fail. Anal. 2016, 59, 456–466. [Google Scholar] [CrossRef]
- Li, C.; Qiao, R.; Tang, Q.; Miao, X. Investigation on the vibration and interface state of a thin-walled cylindrical shell with bolted joints considering its bilinear stiffness. Appl. Acoust. 2020, 172, 107580. [Google Scholar] [CrossRef]
- Wu, X.; Jiao, Y.; Chen, Z.; Ma, W. Establishment of a contact stiffness matrix and its effect on the dynamic behavior of rod-fastening rotor bearing system. Arch. Appl. Mech. 2021, 91, 3247–3271. [Google Scholar] [CrossRef]
- Wang, L.; Wang, A.; Jin, M.; Huang, Q.; Yin, Y. Nonlinear effects of induced unbalance in the rod fastening rotor-bearing system considering nonlinear contact. Arch. Appl. Mech. 2019, 90, 917–943. [Google Scholar] [CrossRef]
- Wang, L.; Wang, A.; Jin, M.; Yin, Y.; Heng, X.; Ma, P. Nonlinear dynamic response and stability of a rod fastening rotor with internal damping effect. Arch. Appl. Mech. 2021, 91, 3851–3867. [Google Scholar] [CrossRef]
- Mokhtar, A.; Darpe, A.K.; Gupta, K. Analysis of stator vibration response for the diagnosis of rub in a coupled rotor-stator system. Int. J. Mech. Sci. 2018, 144, 392–406. [Google Scholar] [CrossRef]
- Wang, N.; Liu, C.; Jiang, D.; Behdinan, K. Casing vibration response prediction of dual-rotor-blade-casing system with blade-casing rubbing. Mech. Syst. Signal Process. 2018, 118, 61–77. [Google Scholar] [CrossRef]
- Yang, Y.; Ouyang, H.; Yang, Y.; Cao, D.; Wang, K. Vibration analysis of a dual-rotor-bearing-double casing system with pedestal looseness and multi-stage turbine blade-casing rub. Mech. Syst. Signal Process. 2020, 143, 106845. [Google Scholar] [CrossRef]
- Li, Y.; Wen, C.; Luo, Z.; Jin, L. Vibration analysis of a multi-disk bolted joint rotor-bearing system subjected to fixed-point rubbing fault. Int. J. Non-Linear Mech. 2022, 146, 104165. [Google Scholar] [CrossRef]
- Li, Y.; Wen, C.; Luo, Z.; Jin, L. Bifurcation studies of a bolted-joint rotor system subjected to fixed-point rubbing fault. Nonlinear Dyn. 2022, 110, 3045–3073. [Google Scholar] [CrossRef]
- Chipato, E.T.; Shaw, A.D.; Friswell, M. Nonlinear rotordynamics of a MDOF rotor–stator contact system subjected to frictional and gravitational effects. Mech. Syst. Signal Process. 2021, 159, 107776. [Google Scholar] [CrossRef]
- Wen, C.; Li, Y.; Jin, L.; Yang, D. Bifurcation and Stability Analysis of a Bolted Joint Rotor System Contains Multi-Discs Subjected to Rub-Impact Effect. Processes 2022, 10, 1763. [Google Scholar] [CrossRef]
- Yu, P.; Wang, C.; Hou, L.; Chen, G. Dynamic characteristics of an aeroengine dual-rotor system with inter-shaft rub-impact. Mech. Syst. Signal Process. 2021, 166, 108475. [Google Scholar] [CrossRef]
- Xiang, L.; Zhang, Y.; Hu, A.; Ye, F. Dynamic analysis and experiment investigation of a cracked dual-disc bearing-rotor system based on orbit morphological characteristics. Appl. Math. Model. 2019, 80, 17–32. [Google Scholar] [CrossRef]
- Cao, J.; Ma, C.; Jiang, Z.; Liu, S. Nonlinear dynamic analysis of fractional order rub-impact rotor system. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1443–1463. [Google Scholar] [CrossRef]
- Gao, T.; Cao, S. Paroxysmal impulse vibration phenomena and mechanism of a dual–rotor system with an outer raceway defect of the inter-shaft bearing. Mech. Syst. Signal Process. 2021, 157, 107730. [Google Scholar] [CrossRef]
- Mir-Haidari, S.-E.; Behdinan, K. Nonlinear effects of bolted flange connections in aeroengine casing assemblies. Mech. Syst. Signal Process. 2021, 166, 108433. [Google Scholar] [CrossRef]
- Yu, P.; Li, L.; Chen, G.; Yang, M. Dynamic modelling and vibration characteristics analysis for the bolted joint with spigot in the rotor system. Appl. Math. Model. 2021, 94, 306–331. [Google Scholar] [CrossRef]
- Haslam, A.H.; Schwingshackl, C.W.; Rix, A.I.J. A parametric study of an unbalanced Jeffcott rotor supported by a rolling-element bearing. Nonlinear Dyn. 2020, 99, 2571–2604. [Google Scholar] [CrossRef]
- Jin, Y.; Liu, Z.; Yang, Y.; Li, F.; Chen, Y. Nonlinear vibrations of a dual-rotor-bearing-coupling misalignment system with blade-casing rubbing. J. Sound Vib. 2021, 497, 115948. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Y.; Ma, H.; Shi, M.; Wang, P. A novel diagnosis indicator for rub-impact of rotor system via energy method. Mech. Syst. Signal Process. 2023, 185, 109825. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, Y.-P.; Lin, J.; Han, Q.; Liu, Y. Analysis of nonlinear vibrations and health assessment of a bearing-rotor with rub-impact based on a data-driven approach. J. Sound Vib. 2022, 534, 117068. [Google Scholar] [CrossRef]





| Physical Parameters | Values | Physical Parameters | Values |
|---|---|---|---|
| Length of the shaft section l1 (m) | 0.08 | Radius of the shaft section r1 (m) | 0.04 |
| Length of the shaft section l2 (m) | 0.08 | Radius of the shaft section r2 (m) | 0.04 |
| Length of the shaft section l3 (m) | 0.05 | Radius of the shaft section r3 (m) | 0.08 |
| Length of the shaft section l4 (m) | 0.11 | Radius of the shaft section r4 (m) | 0.08 |
| Length of the shaft section l5 (m) | 0.14 | Radius of the shaft section r5 (m) | 0.08 |
| Length of the shaft section l6 (m) | 0.07 | Radius of the shaft section r6 (m) | 0.08 |
| Length of the shaft section l7 (m) | 0.07 | Radius of the shaft section r7 (m) | 0.07 |
| Length of the shaft section l8 (m) | 0.08 | Radius of the shaft section r8 (m) | 0.05 |
| Length of the shaft section l9 (m) | 0.07 | Radius of the shaft section r9 (m) | 0.05 |
| Length of the shaft section l10 (m) | 0.09 | Radius of the shaft section r10 (m) | 0.04 |
| Stiffness of squirrel ks (N/m) | 1 × 108 | Coupling stiffness kc (N/m) | 1 × 103 |
| Mass of disk 1, 2, 3 (kg) | 17.16 | Eccentricity of disk 1,2,3,4 (m) | 0.05 × 10−3 |
| Mass of disk 4 (kg) | 16.4 | Outer radius of the spigot ro (m) | 0.05 |
| Friction coefficient at rubbing position η | 0.1 | Radius of the bolt head rb (m) | 0.012 |
| Width of each region of bolted flange W (m) | 0.06 | Radius of spigot R (m) | 0.06 |
| Thicknesses of upper flange T1 (m) | 0.01 | Poisson ratio of upper flange v1 | 0.28 |
| Thicknesses of lower flange T2 (m) | 0.01 | Poisson ratio of lower flange v2 | 0.28 |
| Elastic modulus of upper flange E1 (Pa) | 1.96 × 1011 | Inner radius of the spigot ri (m) | 0.06 |
| Elastic modulus of lower flange E2 (Pa) | 1.96 × 1011 | Clearance between rotor and casing r0 (m) | 1 × 10−4 |
| Radius of Outer Race R (mm) | Radius of Inner Race r (mm) | Numbers of Ball Elements Nb | Contact Stiffness (N/m3/2) | Bearing Clearance r0 (µm) |
|---|---|---|---|---|
| 63.9 | 40.1 | 8 | 13.4 × 109 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Wen, C.; Long, T.; Jin, L.; Li, Y. Bifurcation Analysis of a Rotor-Casing Coupling System with Bolted Flange Connection under the Effect of Rotor-Casing Rubbing Fault. Processes 2023, 11, 1301. https://doi.org/10.3390/pr11051301
Zhu Z, Wen C, Long T, Jin L, Li Y. Bifurcation Analysis of a Rotor-Casing Coupling System with Bolted Flange Connection under the Effect of Rotor-Casing Rubbing Fault. Processes. 2023; 11(5):1301. https://doi.org/10.3390/pr11051301
Chicago/Turabian StyleZhu, Zhimin, Chuanmei Wen, Tianliang Long, Long Jin, and Yuqi Li. 2023. "Bifurcation Analysis of a Rotor-Casing Coupling System with Bolted Flange Connection under the Effect of Rotor-Casing Rubbing Fault" Processes 11, no. 5: 1301. https://doi.org/10.3390/pr11051301






