A Dynamic Partition Model for Multi-Energy Power Grid Energy Balance Considering Electric Vehicle Response Willingness
Abstract
:1. Introduction
2. Source, Load, and Storage Uncertainty Model
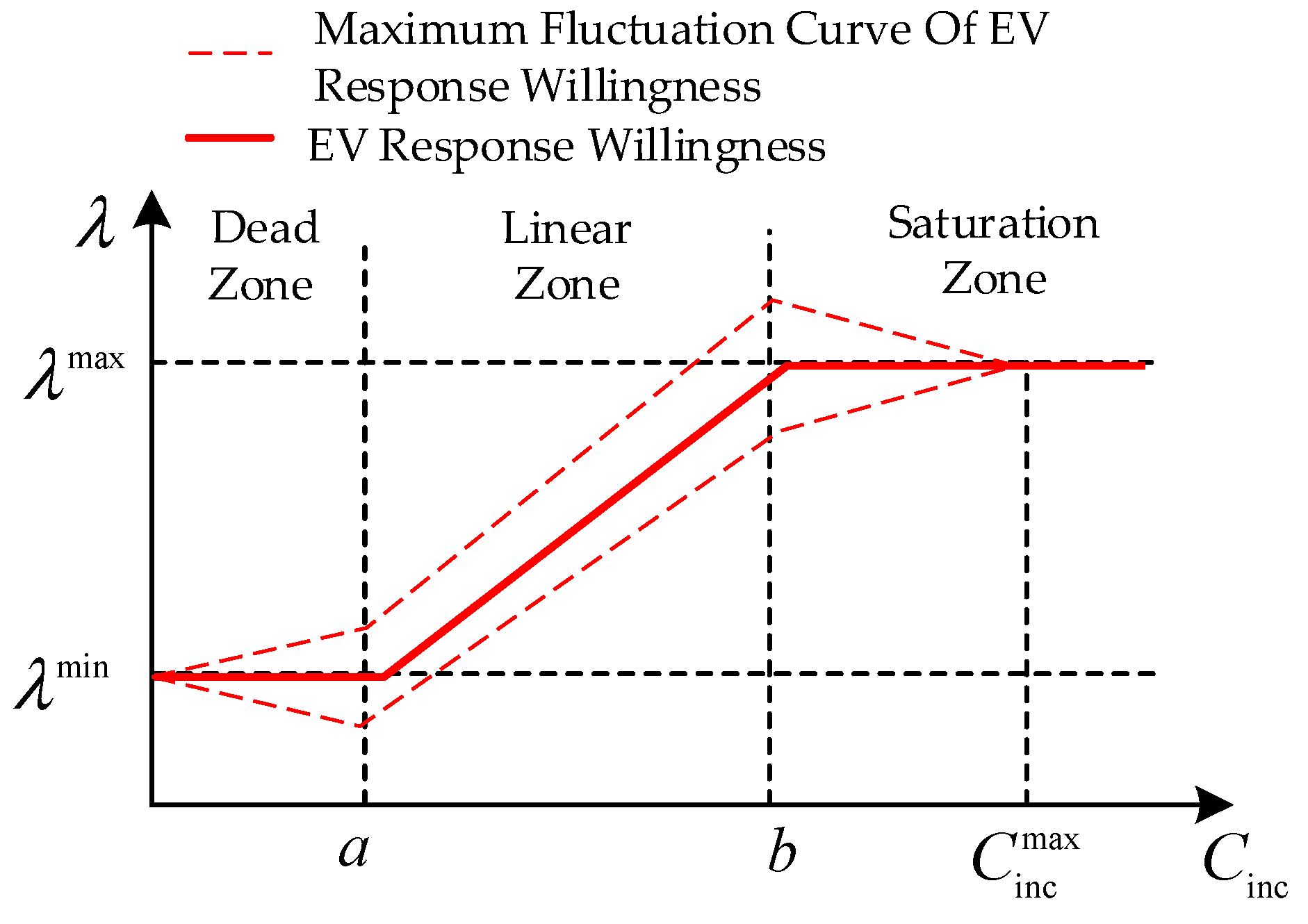
2.1. Uncertainty Model of Electric Vehicles
- (1)
- EV Energy Boundary Model
- (2)
- Uncertainty Model of Electric Vehicle Response
2.2. Energy Uncertainty Model for Renewable Energy Sources
- (1)
- Energy Uncertainty Model of Wind Power Supply
- (2)
- Energy Uncertainty Model of Photovoltaic Power Supply
2.3. Load Uncertainty Model
2.4. Multi-Energy Storage Uncertainty Model
3. Multi-Node Multi-Energy Correlation Measure with Higher-Order Markov Random Field Model (MMCM-HMRF)
3.1. Multi-Energy Correlation Measure Model (MCM)
3.2. MMCM-HMRF Model Based on MRF
4. Multi-Energy Power Grid Partition Model Based on Energy Balance Demand
4.1. Second-Order MRF Model for Equilibrium States of Multi-Energy Regions
4.2. Dynamic Partitioning Solution for Multi-Energy Power Grid Based on Energy Balance Demand
5. Example Analysis
5.1. Simulation Analysis of Multi-Energy Power Grid Partition
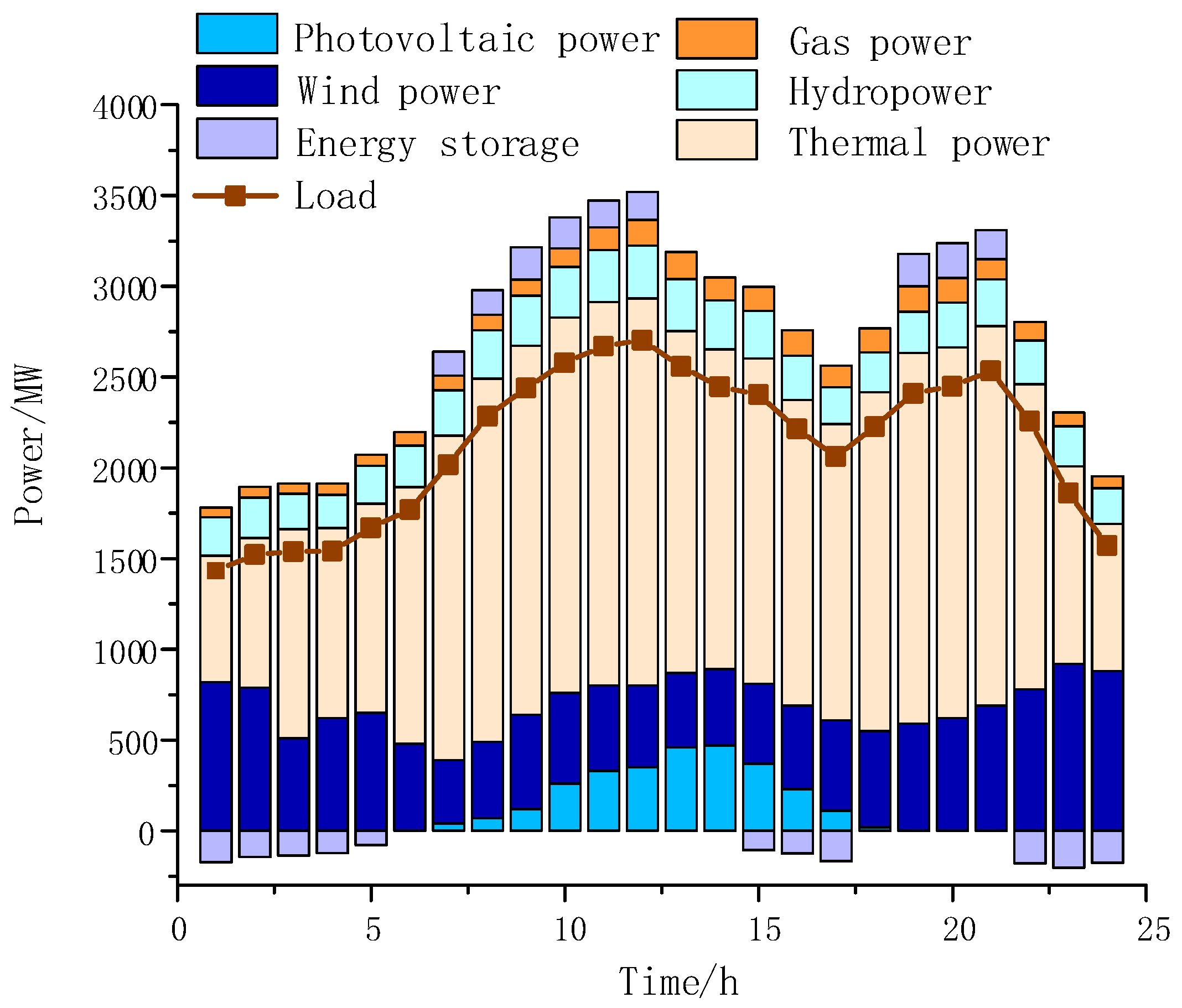
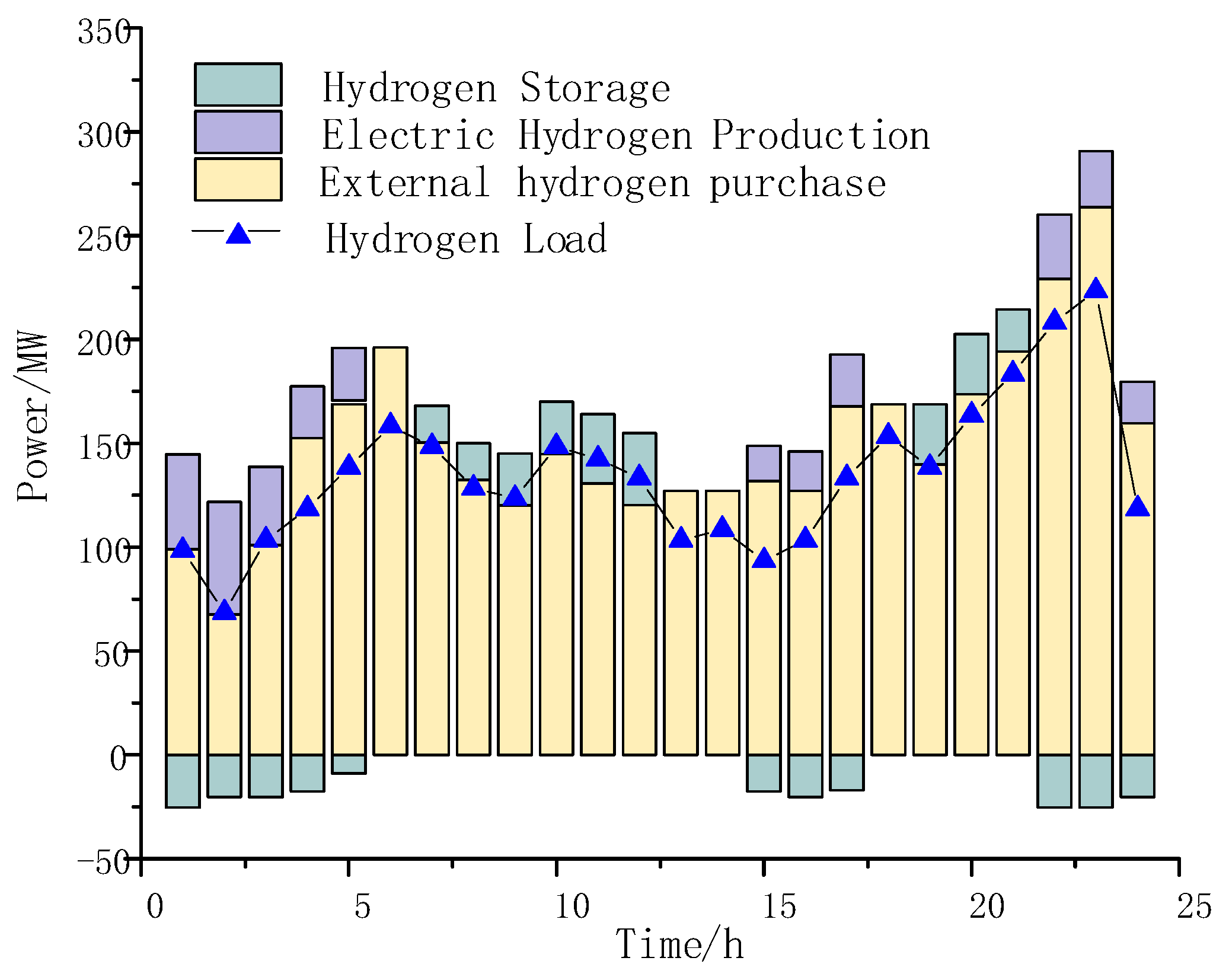
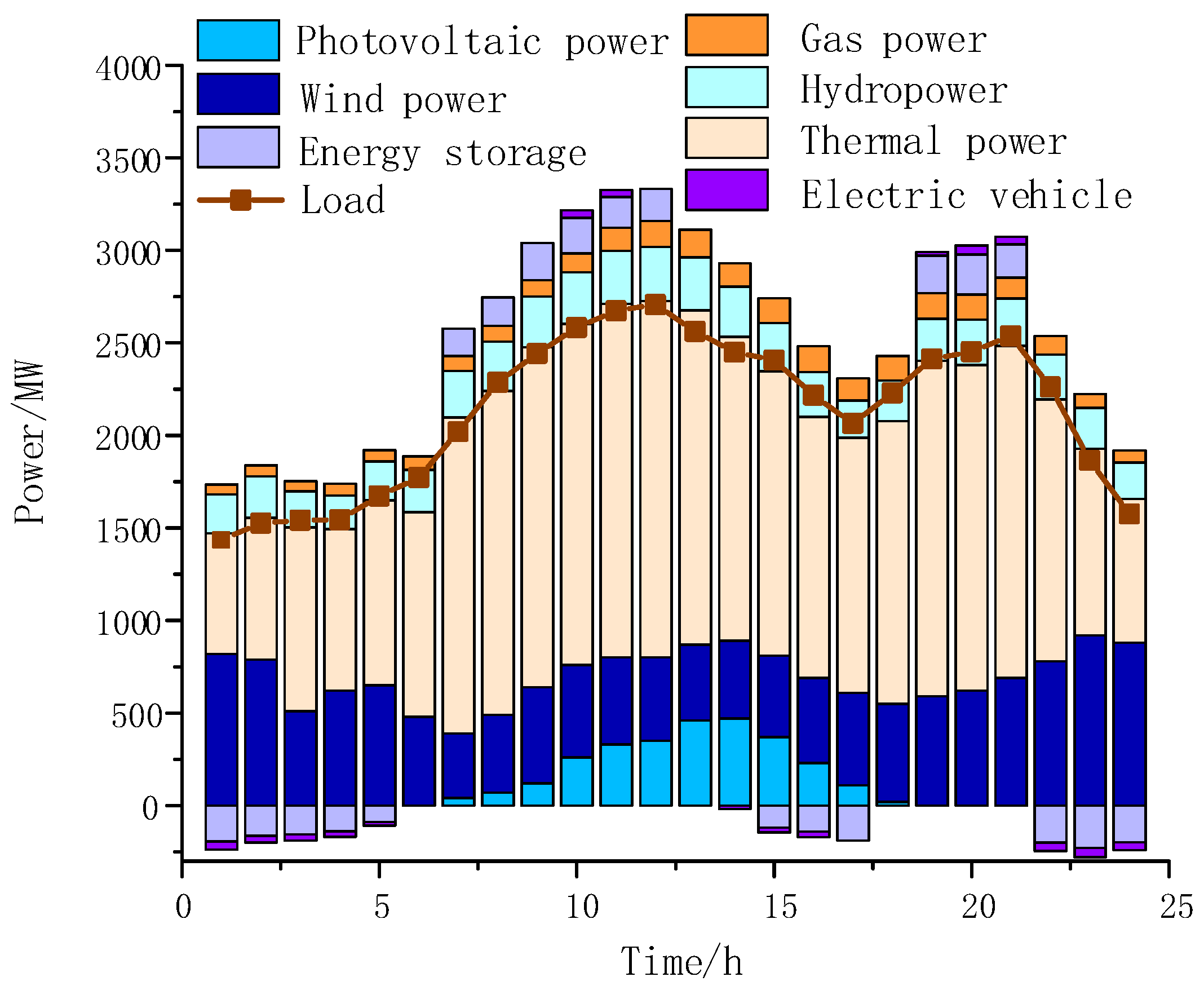
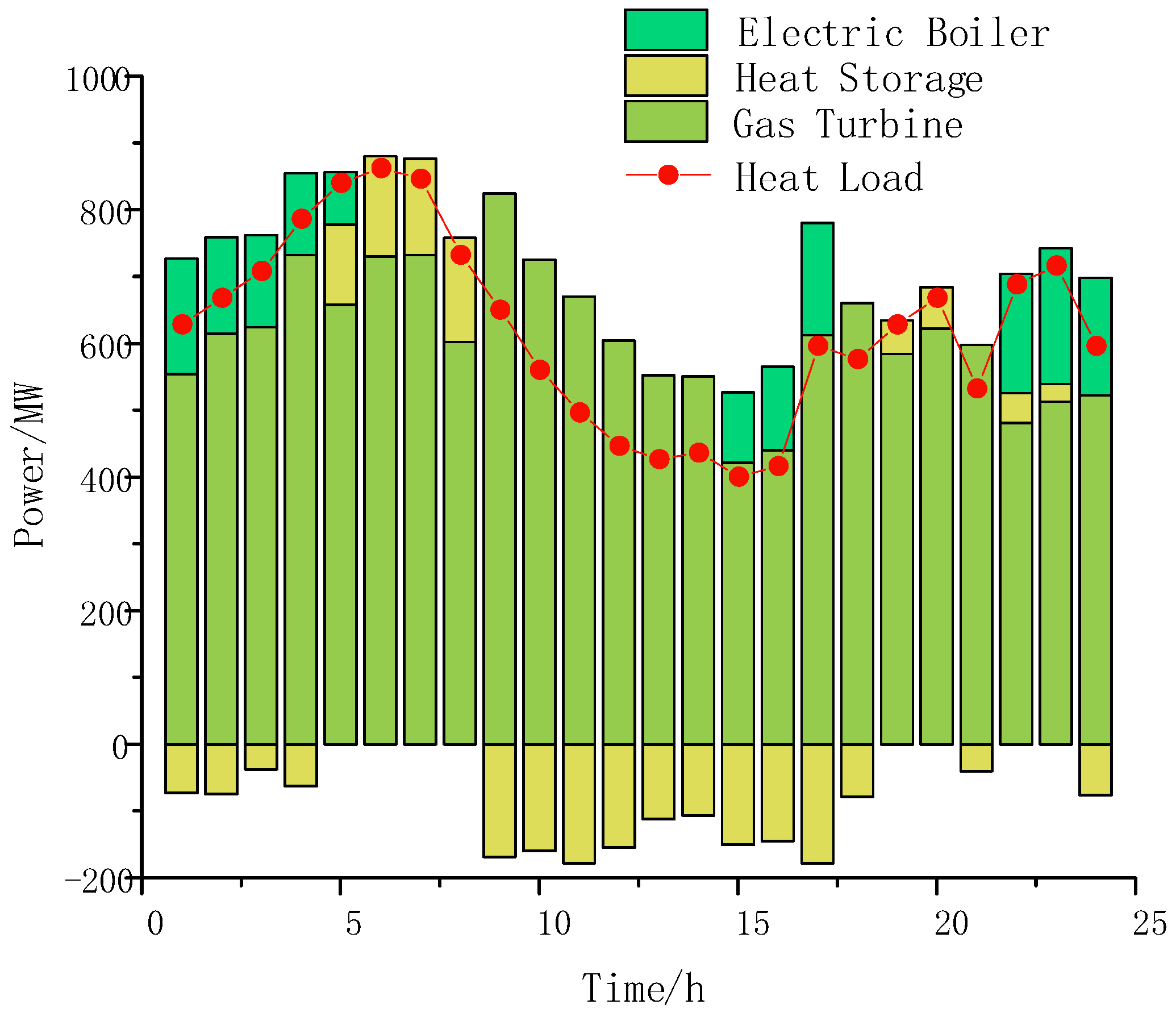
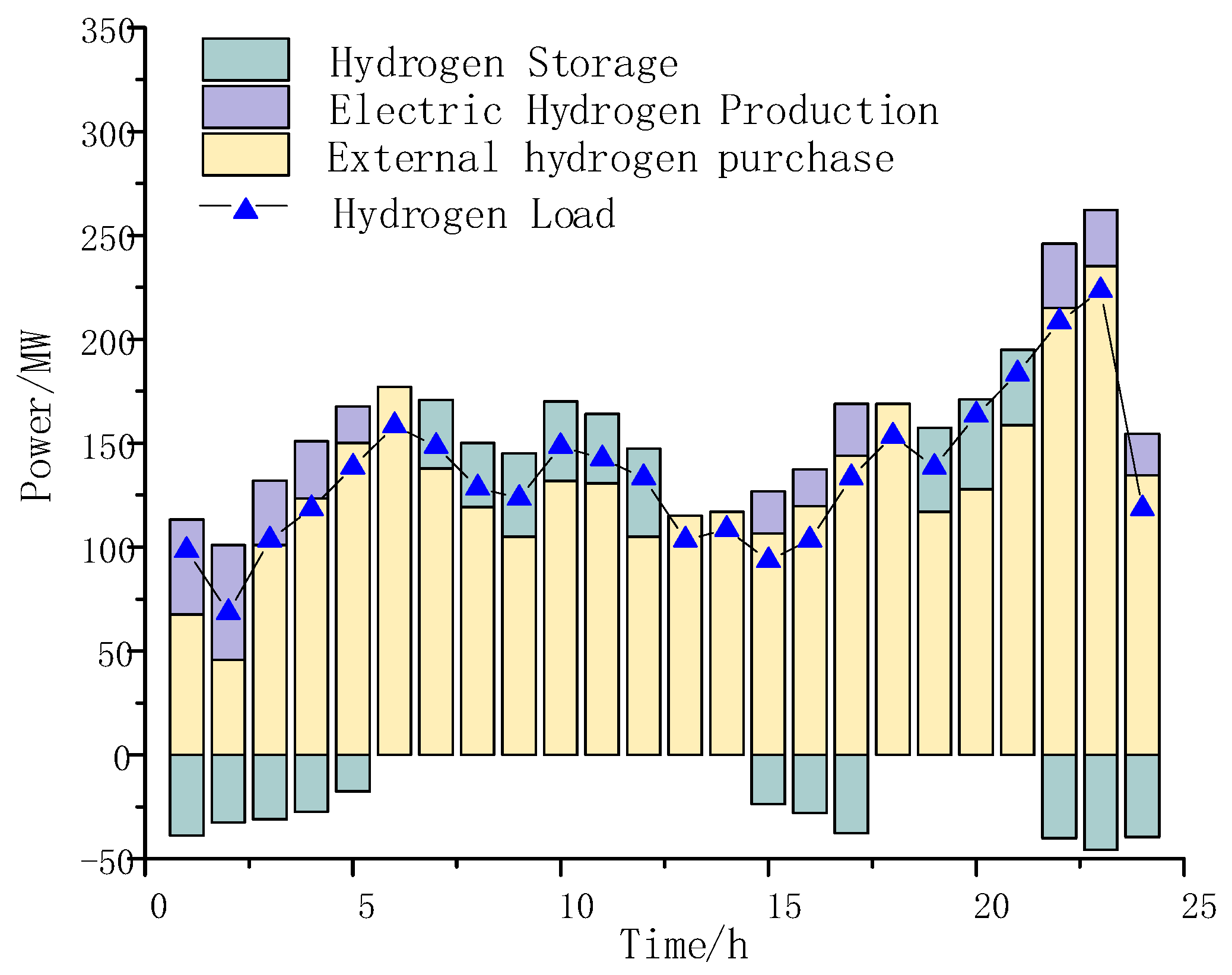
5.2. Energy Balance Analysis of Multi-Energy Power Grid under Partitioned Operation
6. Conclusions
- (1)
- The energy balance zoning method proposed in this article can fully consider the uncertainties of source, load, and storage in the network and quickly and accurately identify local areas of the multi-energy grid where energy imbalance exists. Furthermore, it can optimize the partitioning of multi-energy networks to achieve the peak shaving optimization of different energy forms and maximize energy utilization.
- (2)
- After partitioning the multi-energy power grid based on the energy balance requirements, the complementary coordination ability between multiple types of energy equipment in the multi-energy network can be fully utilized, effectively reducing the startup mode and peak shaving capacity of traditional energy supply units and improving the utilization rate of renewable energy.
- (3)
- After optimizing the demand for multi-energy balance regulation, the system can coordinate and dispatch the load and storage of multiple energy sources in the entire network based on the different types of energy regulation characteristics in different regions, effectively reducing the total peak shaving demand of the entire network and thus achieving the efficient and stable operation of the multi-energy grid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Wang, R.; Ma, D.; Li, M.-J.; Sun, Q.; Zhang, H.; Wang, P. Accurate Current Sharing and Voltage Regulation in Hybrid Wind/Solar Systems: An Adaptive Dynamic Programming Approach. IEEE Trans. Consum. Electron. 2022, 68, 261–272. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Dazhong, M.; Xuguang, H. Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters Under Weak Grids. IEEE Trans. Smart Grid 2020, 11, 2856–2866. [Google Scholar] [CrossRef]
- Cesena, E.A.M.; Mancarella, P. Energy Systems Integration in Smart Districts: Robust Optimisation of Multi-Energy Flows in Integrated Electricity, Heat and Gas Networks. IEEE Trans. Smart Grid 2019, 10, 1122–1131. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Pinjia, Z.; Yonghao, G.; Dehao, Q.; Peng, W. Reduced-Order Transfer Function Model of the Droop-Controlled Inverter via Jordan Continued-Fraction Expansion. IEEE Trans. Energy Convers. 2020, 35, 1585–1595. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, N.; Yang, J.; Wang, Y.; Kang, C. Optimal Configuration Planning of Multi-Energy Systems Considering Distributed Renewable Energy. IEEE Trans. Smart Grid 2019, 10, 1452–1464. [Google Scholar] [CrossRef]
- Yunshou, M.; Jiekang, W.; Ruidong, W.; Zhihong, C.; Ran, Z.; Lingmin, C.; Wenjie, Z. A Collaborative Demand-Controlled Operation Strategy for a Multi-Energy System. IEEE Access 2021, 9, 80571–80581. [Google Scholar] [CrossRef]
- Damavandi, M.Y.; Bahramara, S.; Moghaddam, M.P.; Haghifam, M.-R.; Shafie-Khah, M.; Catalao, J.P.S. Bi-level approach for modeling multi-energy players’ behavior in a multi-energy system. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Bschorer, S.; Kuschke, M.; Strunz, K. Object-oriented modeling for planning and control of multi-energy systems. CSEE J. Power Energy Syst. 2019, 5, 355–364. [Google Scholar]
- Yan, N.; Zhong, Y.; Li, X.; Wang, Y.; Su, L.; Jiang, W.; Zhou, J. Energy Management Method of Electricity Heat Hydrogen Multi-Coupling System for Retired Power Battery Echelon Utilization in Microgrids. IEEE Trans. Appl. Supercond. 2021, 31, 0604605. [Google Scholar] [CrossRef]
- Zhou, X.; Sang, M.; Bao, M.; Wang, S.; Cui, W.; Ye, C.; Ding, Y. Exploiting Integrated Demand Response for Operating Reserve Provision Considering Rebound Effects. IEEE Access 2022, 10, 15151–15162. [Google Scholar] [CrossRef]
- Greening, B.; Braunholtz-Speight, T.; Wood, R.; Freer, M. Batteries and beyond: Multi-vector energy storage as a tool to decarbonise energy services. Front. Energy Res. 2023, 10, 1109997. [Google Scholar] [CrossRef]
- Yang, H.; Li, M.; Jiang, Z.; Zhang, P. Multi-Time Scale Optimal Scheduling of Regional Integrated Energy Systems Considering Integrated Demand Response. IEEE Access 2020, 8, 5080–5090. [Google Scholar] [CrossRef]
- Jin, H.; Teng, Y.; Zhang, T.; Wang, Z.; Deng, B. A locational Marginal Price-Based Partition Optimal Economic Dispatch Model of Multi-Energy Systems. Front. Energy Res. 2021, 9, 694983. [Google Scholar] [CrossRef]
- López, V.; Jove, E.; Gato, F.Z.; Pinto-Santos, F.; Piñón-Pazos, A.J.; Casteleiro-Roca, J.-L.; Quintian, H.; Calvo-Rolle, J.L. Intelligent Model for Power Cells State of Charge Forecasting in EV. Processes 2022, 10, 1406. [Google Scholar] [CrossRef]
- Wang, P.; Xu, J.; Yan, Q.; Lin, H. A two level scheduling optimization model for building microgrids considering demand response and uncertainties of flexible load resources. Electr. Power Constr. 2022, 43, 128–140. [Google Scholar]
- Jawale, S.A.; Singh, S.K.; Singh, P.; Kolhe, M.L. Priority Wise Electric Vehicle Charging for Grid Load Minimization. Processes 2022, 10, 1898. [Google Scholar] [CrossRef]
- Chen, X.; Jia, Y.; Tong, X.; Li, Z. Research on Pedestrian Detection and DeepSort Tracking in Front of Intelligent Vehicle Based on Deep Learning. Sustainability 2022, 14, 9281. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Hu, W.; Li, Y.; Ma, D.; Wang, P. SoC-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems with Constant Power Loads. IEEE Trans. Power Electron. 2021, 36, 7866–7879. [Google Scholar] [CrossRef]
- Cao, Y.; Wang, T.; Kaiwartya, O.; Min, G.; Ahmad, N.; Abdullah, A.H. An EV Charging Management System Concerning Drivers’ Trip Duration and Mobility Uncertainty. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 48, 596–607. [Google Scholar] [CrossRef][Green Version]
- Zhang, X.; Chen, Y.; Wang, Y.; Ding, R.; Zheng, Y.; Wang, Y.; Zha, X.; Cheng, X. Reactive Voltage Partitioning Method for the Power Grid With Comprehensive Consideration of Wind Power Fluctuation and Uncertainty. IEEE Access 2020, 8, 124514–124525. [Google Scholar] [CrossRef]
- Alanazi, M.S. A Modified Teaching—Learning-Based Optimization for Dynamic Economic Load Dispatch Considering Both Wind Power and Load Demand Uncertainties With Operational Constraints. IEEE Access 2021, 9, 101665–101680. [Google Scholar] [CrossRef]
- Descombes, X.; Morris, R.; Zerubia, J.; Berthod, M. Estimation of Markov random field prior parameters using Markov chain Monte Carlo maximum likelihood. IEEE Trans. Image Process. 1999, 8, 954–963. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bahari, M.H.; Dehak, N.; Van Hamme, H.; Burget, L.; Ali, A.M.; Glass, J. Non-Negative Factor Analysis of Gaussian Mixture Model Weight Adaptation for Language and Dialect Recognition. IEEE/ACM Trans. Audio, Speech, Lang. Process. 2014, 22, 1117–1129. [Google Scholar] [CrossRef][Green Version]



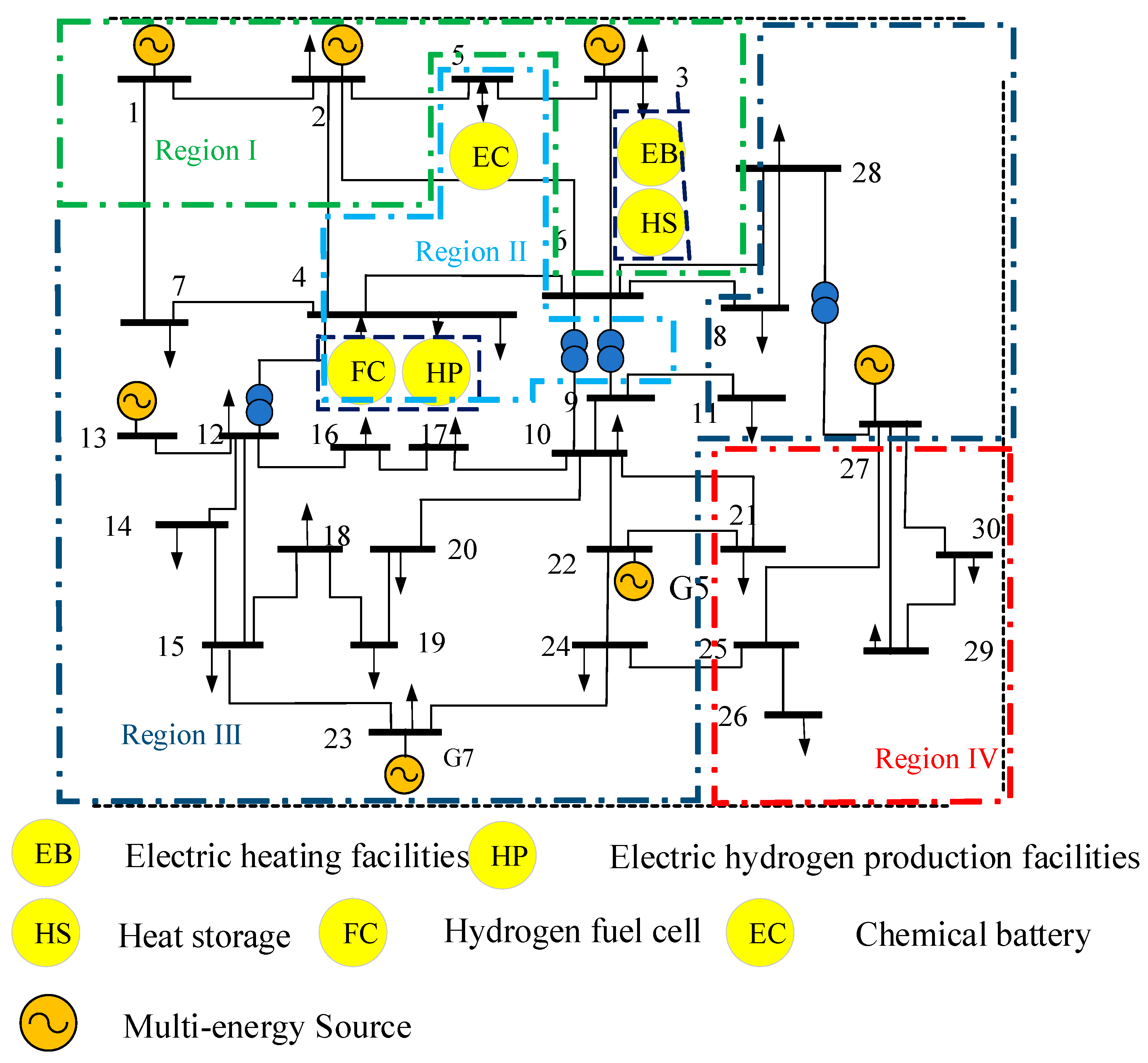
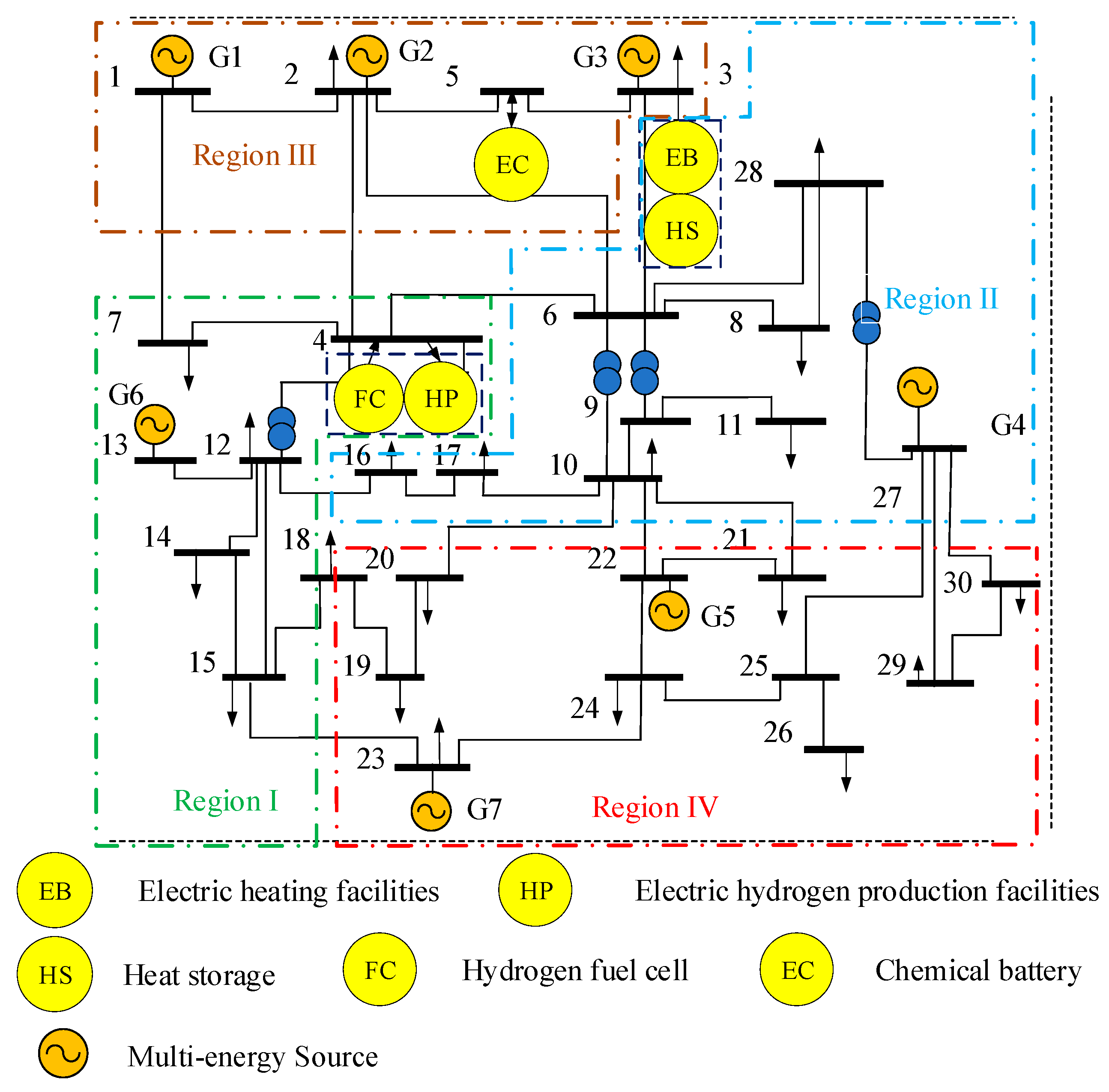

| Node Number | Source Type | Power Capacity (MW) | Energy Storage Type | Energy Storage Capacity (MW) |
|---|---|---|---|---|
| 1 | Wind power | 600 | ||
| 2 | Photovoltaic power | 480 | ||
| 3 | Wind power | 500 | Electric heating and heat storage facilities | 620 |
| 4 | Electric hydrogen production facilities and hydrogen fuel cell | 32 | ||
| 5 | Chemical battery | 100 | ||
| 13,27 | Thermal power | 3650 | ||
| 22 | Gas power | 150 | ||
| 23 | Hydropower | 300 |
| Parameter Name | Data |
|---|---|
| Electric vehicle capacity | 32 kw·h |
| Charging and discharging power | 4 kw |
| Charging and discharging efficiency | 0.9 |
| Power consumption per 100 km | 15 kw·h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, S.; Zhang, K.; Chen, Z.; Ma, Y.; Chen, Z. A Dynamic Partition Model for Multi-Energy Power Grid Energy Balance Considering Electric Vehicle Response Willingness. Processes 2023, 11, 1508. https://doi.org/10.3390/pr11051508
Qiu S, Zhang K, Chen Z, Ma Y, Chen Z. A Dynamic Partition Model for Multi-Energy Power Grid Energy Balance Considering Electric Vehicle Response Willingness. Processes. 2023; 11(5):1508. https://doi.org/10.3390/pr11051508
Chicago/Turabian StyleQiu, Shi, Kun Zhang, Zhuo Chen, Yiling Ma, and Zhe Chen. 2023. "A Dynamic Partition Model for Multi-Energy Power Grid Energy Balance Considering Electric Vehicle Response Willingness" Processes 11, no. 5: 1508. https://doi.org/10.3390/pr11051508
APA StyleQiu, S., Zhang, K., Chen, Z., Ma, Y., & Chen, Z. (2023). A Dynamic Partition Model for Multi-Energy Power Grid Energy Balance Considering Electric Vehicle Response Willingness. Processes, 11(5), 1508. https://doi.org/10.3390/pr11051508








