Optimal Operation of a Benchmark Simulation Model for Sewer Networks Using a Qualitative Distributed Model Predictive Control Algorithm
Abstract
1. Introduction
2. Benchmark Model and Evaluation Criteria
2.1. Benchmark Model Description
- T is the sampling period;
- τi is the time constant of the element i;
- qi(k) is the output flow of the element i;
- Tssout,i is the concentration of suspended solids in the output flow of the element i;
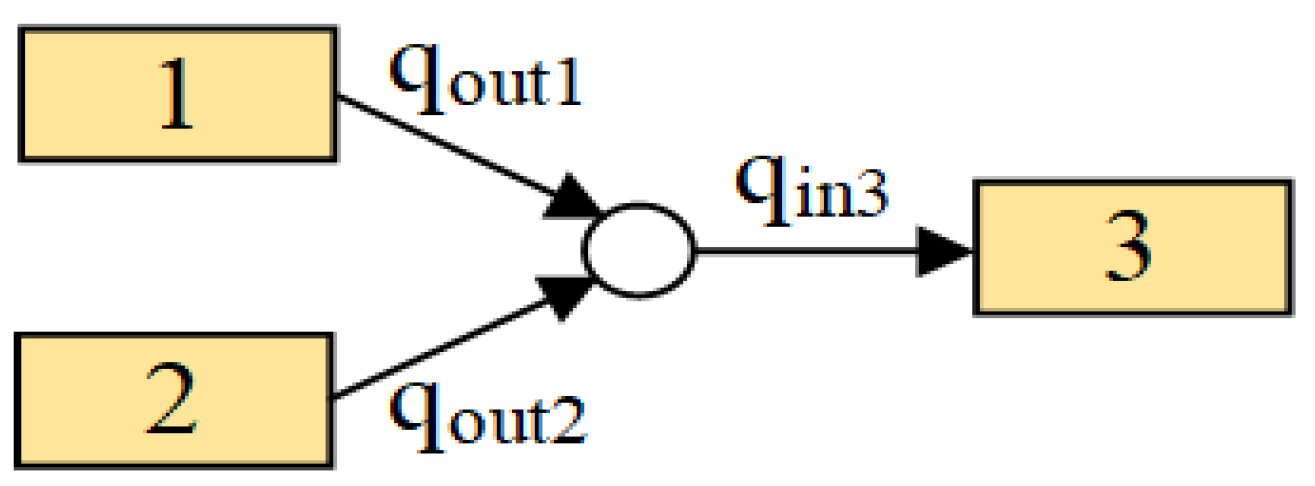
- qu,i(k) is the sum of inflows to the link element i;
- Tssin,i is the concentration of suspended solids in the input flow of the element i;
- ci is the sedimentation coefficient of suspended in the element i (parameter that needs calibration);
- Vmax,i is the maximum capacity of the tank;
- Vi(k) is the filled volume;
- Tssin,i is the concentration of suspended solids in the input flow of the tank i;
- Tssout,i is the concentration of suspended solids in the output and overflow flow of the tank i;
- uin, i(k) is the input flow rate;
- ui(k) is the output flow rate;
- qov,i(k) is the overflow flow rate;
- c0i is the discharge coefficient (experimental parameter depending on the tank i);
- ci is the sedimentation coefficient of suspended in the tank i (parameter that needs calibration);
- Ai is the tank area;
- hmax,i is the tank height;
- hi(k) is the water level;
- ai(k) is the opening of the deposit outlet valve (control variable: ai∈[0, 1]);
2.2. Evaluation Criteria
- Total suspended solids mass (Mssov,i) (kg): this is the total mass of suspended solids at a specific overflow place i. Considering simulation time in days (d) Tsim, if qov,i(t) is the overflow (m3/d) and Tssi(t) is the total suspended solids concentration (g/m3), the total suspended solids mass of pollutant overflowed at the point i is:
- 2.
- Ammonia mass (NHov,i) (kg): this is the total mass of ammonia in wastewater escaping from the sewage at a specific overflow place i. If NHi(t) is the ammonia concentration, the total ammonia mass overflowed at the point i is:
- 3.
- Nitrate mass (NOov,i) (kg): this is the total mass of nitrate in wastewater discharged from a specific overflow place i. If NOi(t) is the nitrate concentration, the total nitrate mass overflowed at the point i is:
- 4.
- Phosphate mass (POov,i) (kg): this is the total mass of phosphate in wastewater escaping from the sewer network at a certain overflow place i. If POi(t) is the phosphate concentration, the total phosphate overflowed at the point i is:
- 5.
- Overflow quality index (OQIi) (kg-pollution units/d): this is an aggregated index representing the total mass of pollutants in wastewater discharged into treated water receivers from a determined overflow place i during a simulation time Tsim. It includes all the pollutants with different weights, like those used in BSM2 for WWTP [22]. In this case, OQIi can be approximated as:
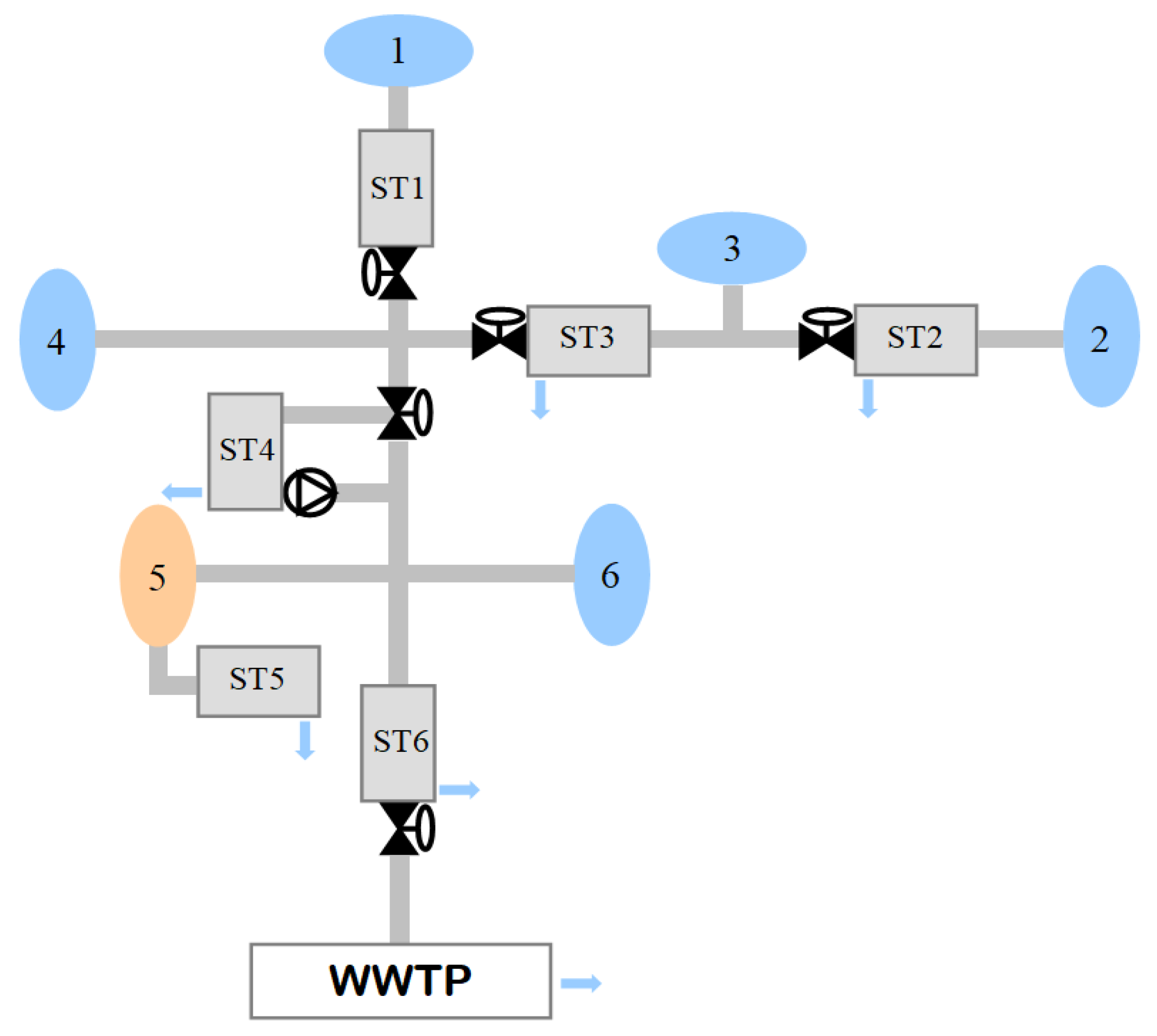
3. Sectorization of the System Model
4. Control Objectives
- Minimization of load overflowed and overflows, and uniform distribution of the stored wastewater and the concentration of total suspended solids:
- 2.
- Maximum usage and minimum overflow at the WWTP influent:
- 3.
- Control efforts minimization:
5. Predictive Control Problem with Online Linearization
5.1. Optimization Problem
5.2. Set-Point Determination
6. DMPC and Fuzzy Negotiation
6.1. Distributed Model Predictive Control (DMPC) with Fuzzy Negotiation
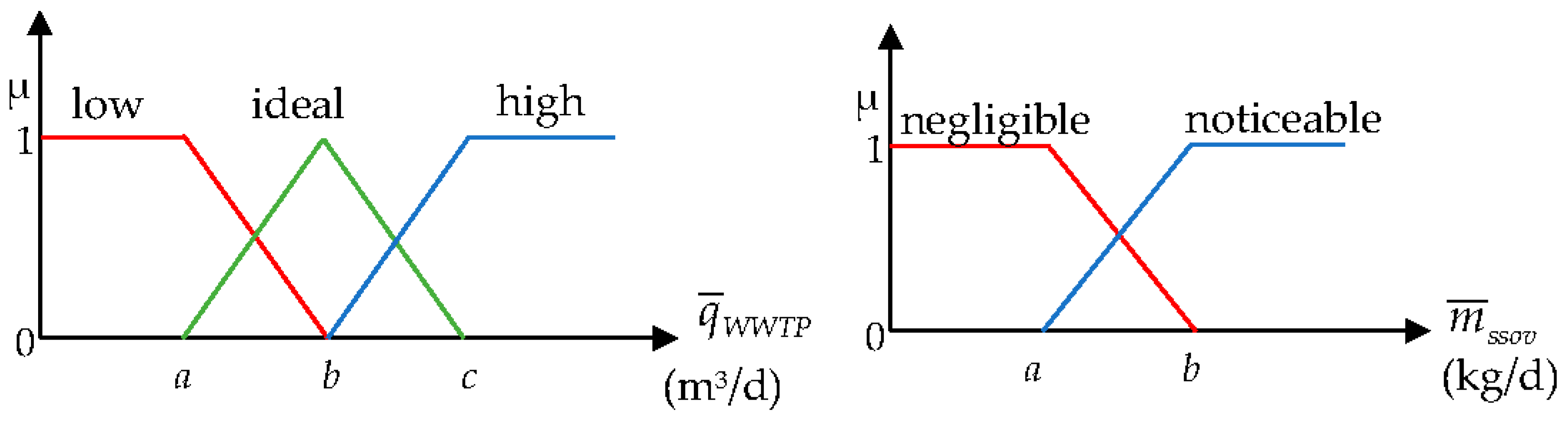
6.2. Fuzzy Negotiation
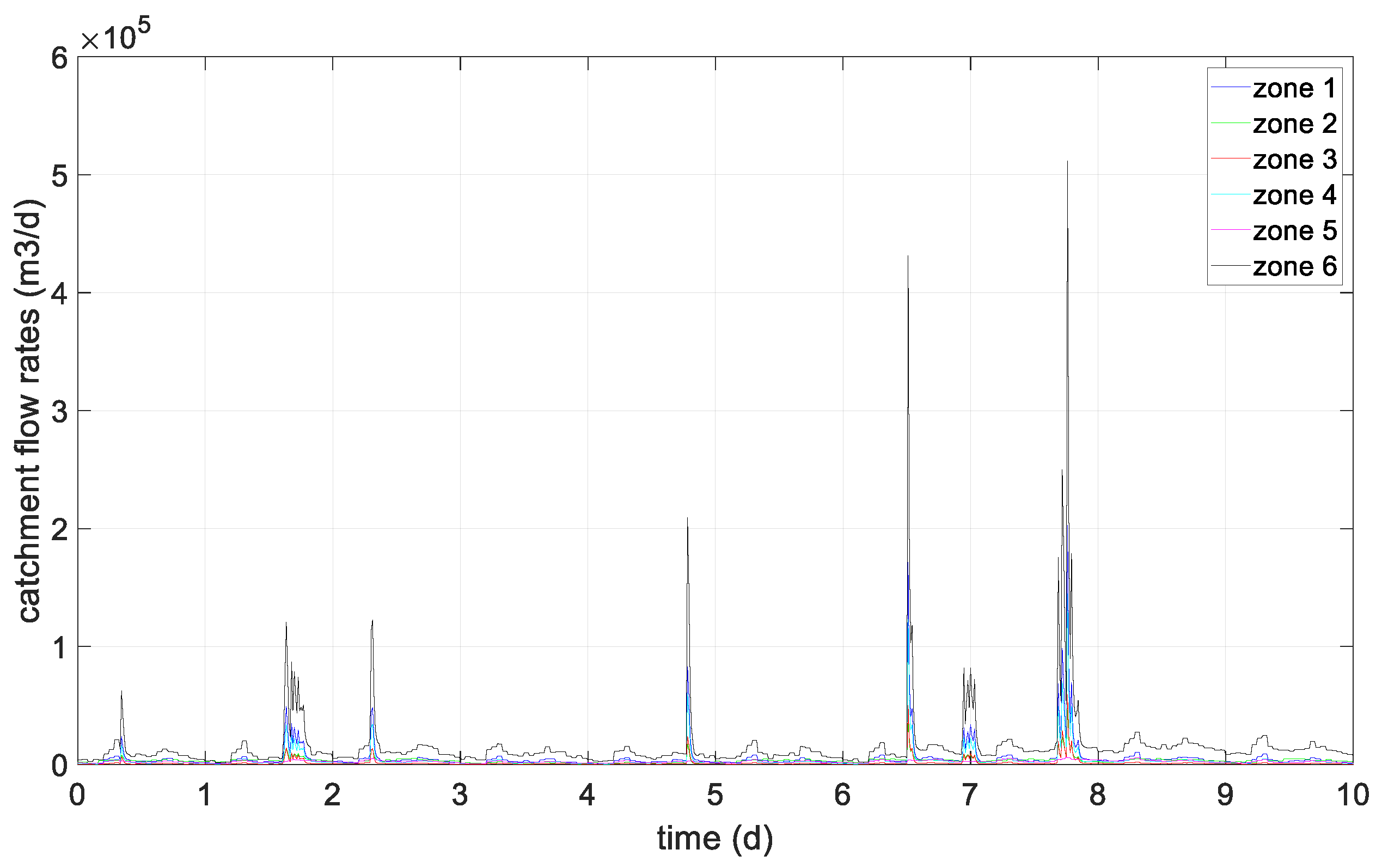
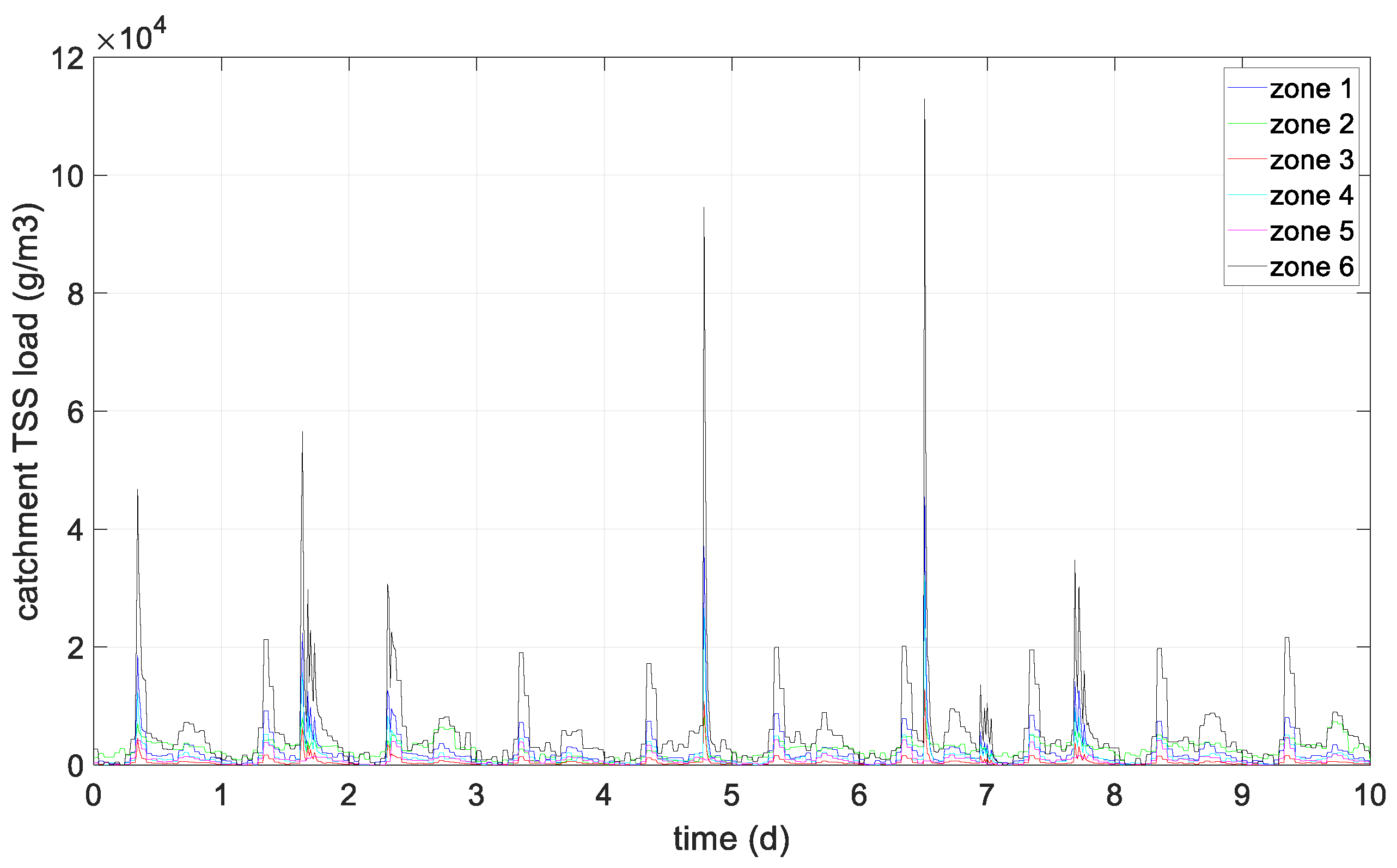
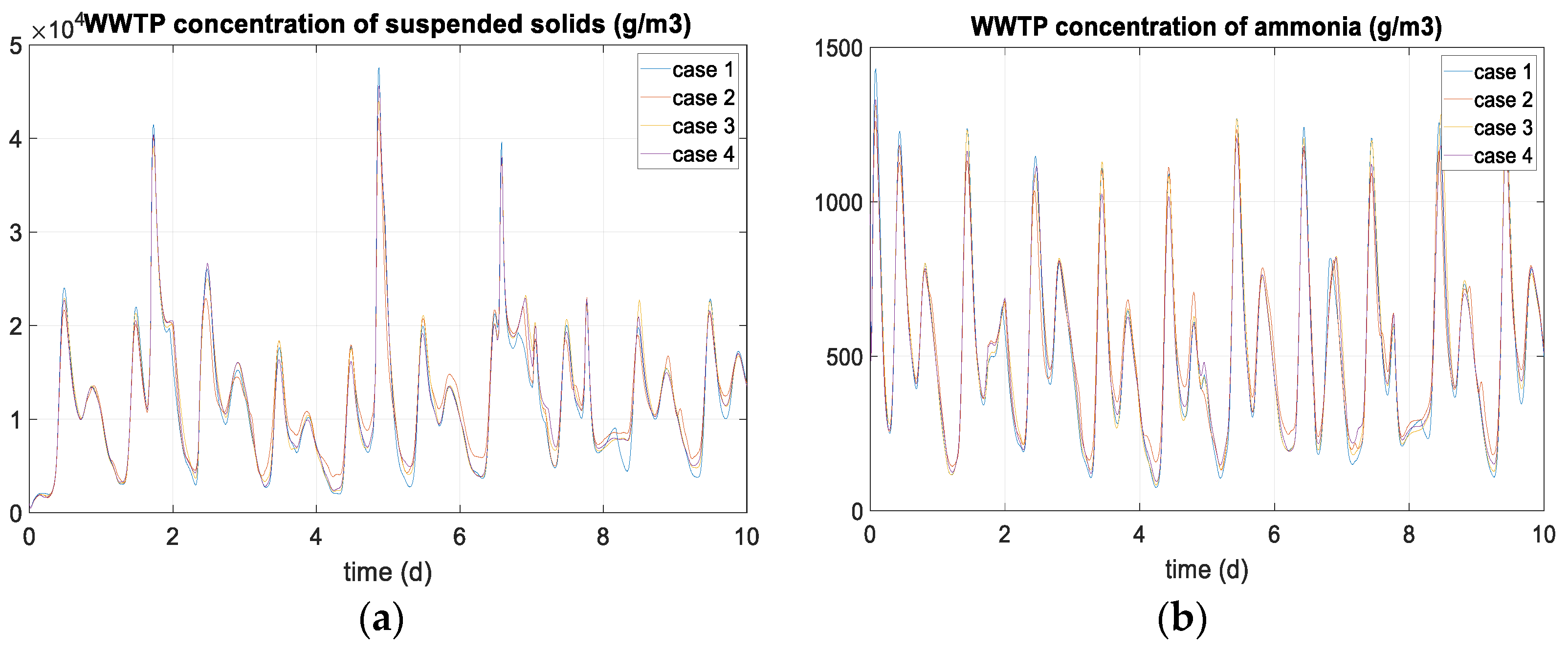
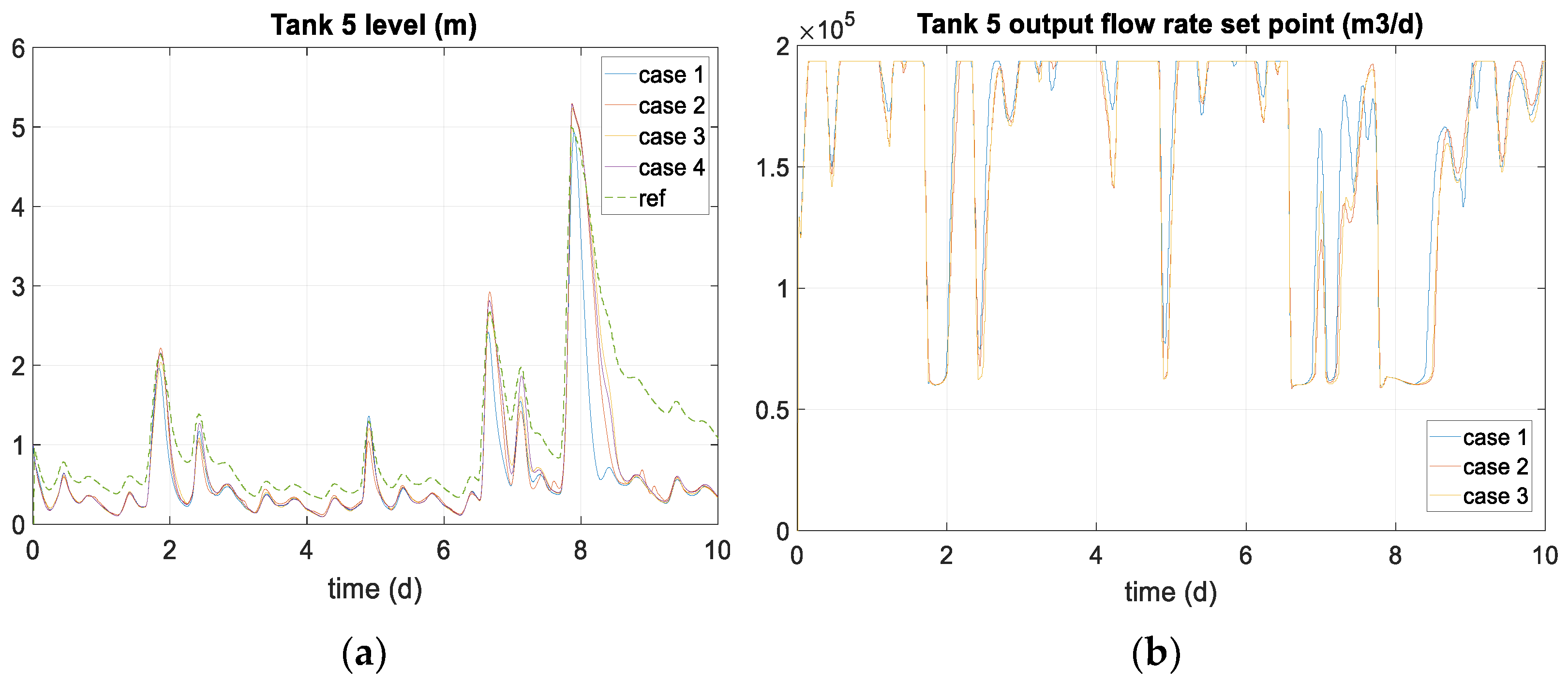
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B

References
- Jamieson, D.G.; Shamir, U.; Martínez, F.; Franchini, M. Conceptual design of a generic, real-time, near-optimal control system for water-distribution networks. J. Hydroinform. 2007, 9, 3–14. [Google Scholar] [CrossRef]
- Fu, G.; Khu, S.T.; Butler, D. Use of surrogate modelling for multiobjective optimisation of urban wastewater systems. Water Sci. Technol. 2009, 60, 1641–1647. [Google Scholar] [CrossRef] [PubMed]
- Cho, J.H.; Sung, K.S.; Ha, S.R. A river water quality management model for optimizing regional wastewater treatment using a genetic algorithm. J. Environ. Manag. 2004, 73, 229–242. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.; Butler, D.; Khu, S.T. Multiple objective optimal control of integrated urban wastewater systems. Environ. Model. Softw. 2008, 23, 225–234. [Google Scholar] [CrossRef]
- Saagi, R.; Flores-Alsina, X.; Fu, G.; Butler, D.; Gernaey, K.V.; Jeppsson, U. Catchment & Sewer Network Simulation Model to Benchmark Control Strategies within Urban Wastewater Systems; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Benedetti, L.; Langeveld, J.G.; Corneau, A.; Corominas, L.; Daigger, G.T.; Martin, C.; Mikkelsen, P.S.; Vezzaro, L.; Weijers, S.; Vanrolleghem, P.A. Modelling and monitoring of integrated urban wastewater systems: Review on status and perspectives. Water Sci. Technol. 2013, 68, 1203–1215. [Google Scholar] [CrossRef]
- García, L.; Barreiro-Gómez, J.; Escobar, E.; Téllez, D.; Quijano, N.; Ocampo-Martínez, C. Modeling and Real-Time Control of Urban Drainage Systems: A review. Adv. Water Resour. 2015, 85, 120–132. [Google Scholar] [CrossRef]
- Beeneken, T.; Erbe, V.; Messmer, A.; Reder, C.; Rohlfing, R.; Scheer, M.; Schuetze, M.; Schumacher, B.; Weilandt, M.; Weyand, M. Real time control (RTC) of urban drainage systems—A discussion of the additional efforts compared to conventionally operated systems. Urban Water J. 2013, 10, 293–299. [Google Scholar] [CrossRef]
- Farina, M.; Scattolini, R. Distributed MPC for Large-Scale Systems; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Li, Z.; Duan, Z. Cooperative Control of Multi-Agent Systems. A Consensus Region Approach; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Klepiszewski, K.; Schmitt, T. Comparison of conventional rule-based flow control with control processes based on fuzzylogic in a combined sewer system. Water Sci. Technol. 2002, 46, 77–84. [Google Scholar] [CrossRef]
- Muschalla, D. Optimization of integrated urban wastewater systems using multi-objective evolution strategies. Urban Water J. 2008, 5, 57–65. [Google Scholar] [CrossRef]
- Barbu, M.; Vilanova, R. Fuzzy Control Applied on a Benchmark Simulation Model for Sewer Networks. In Proceedings of the 20th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 13–15 October 2016. [Google Scholar]
- Regneri, M.; Klepiszewski, K.; Ostrowski, M.; Vanrolleghem, P.A. Fuzzy decision making for multicriteria optimization in integrated wastewater system management. In Proceedings of the 6th International Conference on Sewer Processes and Networks, Surfers Paradise, Australia, 7–10 November 2010; pp. 1–10. [Google Scholar]
- Tagherouit, W.B.; Bennis, S.; Bengassem, J. A fuzzy expert system for prioritizing rehabilitation of sewer networks. Comput. Aided Civ. Infrastruct. Eng. 2011, 26, 146–152. [Google Scholar] [CrossRef]
- Tang, W.; Wang, Z.; Feng, Q.; Wang, M. Application of fuzzy expert control to APMP pulping wastewater treatment process of aerobic. In Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation, Xi’an, China, 4–7 August 2010; pp. 339–344. [Google Scholar] [CrossRef]
- Marinaki, M.; Papageorgiou, M. Linear-quadratic regulators applied to sewer network flow control. In Proceedings of the European Control Conference, Cambridge, UK, 1–4 September 2003; pp. 1–4, ISBN 978-3-9524173-7-9. [Google Scholar]
- Barreiro-Gómez, J.; Obando, G.; Riaño-Briceño, G.; Quijano, N.; Ocampo-Martínez, C. Decentralized control for urban drainage systems via population dynamics: Bogotá case study. In Proceedings of the European Control Conference, Linz, Austria, 15–17 July 2015. [Google Scholar]
- Ramírez-Llanos, E.; Quijano, N. A population dynamics approach for the water distribution problem. Int. J. Control 2010, 83, 1947–1964. [Google Scholar] [CrossRef]
- Sun, C.; Bernat, J.D.; Cembrano, G.; Puig, V.; Meseguer, J. Advanced Integrated Real-Time Control of Combined Urban Drainage Systems using MPC. In Proceedings of the 13th International Conference on Hydroinformatics, Palermo, Italy, 1–6 July 2018. [Google Scholar]
- Xu, M.; Van Overloop, J.; Van de Giesen, N.C. Model Reduction in Model Predictive Control of Combined Water Quantity and Quality in Open Channels. J. Environ. Modell. Software 2013, 42, 72–87. [Google Scholar] [CrossRef]
- Vasiliev, I.; Luca, L.; Vilanova, R.; Caraman, S. Sewer Network Modelling and Control—A literature Review. In Proceedings of the 2022 26th International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 19–21 October 2022; ISBN 978-1-6654-6746-9. [Google Scholar] [CrossRef]
- Schütze, M.; Campisano, A.; Colas, H.; Vanrolleghem, P.; Schilling, W. Real-time control of urban water systems. In Proceedings of the International Conference on Pumps, Electromechanical Devices and Systems Applied to Urban Water Management, Valencia, Spain, 22–25 April 2003; pp. 1–19. [Google Scholar]
- Ocampo-Martínez, C.; Puig, V. Modelling Approaches for Predictive Control of Large-Scale Sewage Systems; Institut de Robòtica I Informàtica Industrial (IRI): Barcelona, Spain, 2009. [Google Scholar]
- Ocampo-Martinez, C.; Puig, V.; Cembrano, G.; Quevedo, J. Application of predictive control strategies to the management of complex networks in the urban water cycle. IEEE Control Syst. Mag. 2013, 33, 15–41. [Google Scholar] [CrossRef]
- Bach, P.M.; Rauch, W.; Mikkelsen, P.S.; McCarthy, D.T.; Deletic, A. A critical review of integrated urban water modelling—Urban drainage and beyond. Environ. Model. Softw. 2014, 54, 88–107. [Google Scholar] [CrossRef]
- Keupers, I.; Willems, P. Development and Testing of a Fast Conceptual River Water Quality Model. Water Res. 2017, 113, 62–71. [Google Scholar] [CrossRef]
- Rauch, W.; Bertrand-Krajewski, J.L.; Krebs, P.; Mark, O.; Schilling, W.; Schütze, M.; Vanrolleghem, P.A. Deterministic modelling of integrated urban drainage systems. Water Sci. Technol. 2002, 45, 81–94. [Google Scholar] [CrossRef]
- Kroll, S.; Fenu, A.; Wambecq, T.; Weemaes, M.; Van Impe, J.; Willems, P. Energy Optimization of the Urban Drainage System by Integrated Real-Time Control during Wet and Dry Weather Conditions. Urban Water J. 2018, 15, 362–370. [Google Scholar] [CrossRef]
- Meneses, E.J.; Gaussens, M.; Jakobsen, C.; Mikkelsen, P.S.; Grum, M.; Vezzaro, L. Coordinating Rule-Based and System-Wide Model Predictive Control Strategies to Reduce Storage Expansion of Combined Urban Drainage Systems: The Case Study of Lundtofte, Denmark. Water 2018, 10, 76. [Google Scholar] [CrossRef]
- Maciejowski, J.M. Predictive Control with Constraints; Pearson Education Limited, Prentice-Hall: London, UK, 2002. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Rawlings, J.; Mayne, D. Model Predictive Control: Theory and Design; Nob Hill Publishing: Madison, WI, USA, 2017. [Google Scholar]
- Cembrano, G.; Quevedo, J.; Salamero, M.; Puig, V.; Figueras, J.; Martí, J. Optimal control of urban drainage systems, a case study. Control Eng. Pract. 2004, 12, 1–9. [Google Scholar] [CrossRef]
- Ocampo-Martínez, C. Model Predictive Control of Wastewater Systems; Springer: London, UK, 2011. [Google Scholar] [CrossRef]
- Giraldo, J.; Leirens, S.; Díaz-Granados, M.; Rodríguez, J. Nonlinear optimization for improving the operation of sewer systems: The Bogotá case study. In Proceedings of the International Congress on Environmental Modelling and Software Modelling for Environments Sake, Ottawa, ON, Canada, 5–8 July 2010; pp. 1–8. [Google Scholar]
- Sun, C.; Joseph-Duran, B.; Maruejouls, T.; Cembrano, G.; Meseguer, J.; Puig, V.; Lítrico, X. Real-Time Control-Oriented Quality Modelling in Combined Urban Drainage Networks. IFAC Pap. 2017, 50, 3941–3946. [Google Scholar] [CrossRef]
- Svensen, J.L.; Niemann, H.H.; Poulsen, N.K. Model Predictive Control of Overflow in Sewer Networks: A comparison of two methods. In Proceedings of the 2019 4th Conference of Control and Fault Tolerant Systems (SysTol), Casablanca, Morocco, 18–20 September 2019; pp. 412–417. [Google Scholar] [CrossRef]
- Barcelli, D. Optimal Decomposition of Barcelona’s Water Distribution Network System for Applying Distributed Model Predictive Control. Master’s Thesis, Universitat Politècnica de Cataluña-IRI-Universitá degli Study di Siena, Barcelona, Spain, 2008. [Google Scholar]
- Real, A.J.D.; Arce, A.; Bordons, C. Combined environmental and economic dispatch of smart grids using distributed model predictive control. Electr. Power Energy Syst. 2014, 54, 65–76. [Google Scholar] [CrossRef]
- Leirens, S.; Zamora, C.; Negenborn, R.R.; De Schutter, B. Coordination in urban water supply networks using distributed model predictive control. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 3957–3962. [Google Scholar] [CrossRef]
- Francisco, M.; Mezquita, Y.; Revollar, S.; Vega, P.; De Paz, J.F. Multi-agent distributed model predictive control with fuzzy negotiation. Expert Syst. Appl. 2019, 129, 68–83. [Google Scholar] [CrossRef]
- Masero, E.; Francisco, M.; Maestre, J.M.; Revollar, S.; Vega, P. Hierarchical distributed model predictive control based on fuzzy negotiation. Expert Syst. Appl. 2021, 176, 114836. [Google Scholar] [CrossRef]
- Ocampo-Martínez, C.; Puig, V.; Grosso, J.; de Oca, S.M. Multi-layer decentralized MPC of large-scale networked systems. In Distributed Model Predictive Control Made Easy; Springer: Berlin/Heidelberg, Germany, 2014; pp. 495–515. [Google Scholar] [CrossRef]
- Maestre, J.M.; Muñoz De La Peña, D.; Camacho, E.F. Distributed model predictive control based on a cooperative game. Optim. Control Appl. Methods 2011, 32, 153–176. [Google Scholar] [CrossRef]
- Cembellín, A.; Francisco, M.; Vega, P. Distributed Model Predictive Control Applied to a Sewer System. Processes 2020, 8, 64. [Google Scholar] [CrossRef]
- Siljak, D.D. Decentralized Control of Complex Systems; Dover Publications, Inc.: Mineola, NY, USA, 1991. [Google Scholar]
- Kroll, S.; Weemaes, M.; Van Impe, J.; Willems, P. A Methodology for the Design of RTC Strategies for Combined Sewer Networks. Water 2018, 10, 1675. [Google Scholar] [CrossRef]
- Marinaki, M. Optimal Real-Time Control of Sewer Networks; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Alex, J.; Schütze, M.; Ogurek, M.; Jumar, U. Systematic Design of Distributed Controllers for Sewer Networks. In Proceedings of the 17th World Congress IFAC, Seoul, Republic of Korea, 6–11 July 2008. [Google Scholar]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained Model Predictive Control: Stability and Optimality; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Maestre, J.M.; Muñoz de la Peña, D.; Camacho, E.F.; Álamo, T. Distributed model predictive control based on agent negotiation. J. Process Control 2011, 21, 685–697. [Google Scholar] [CrossRef]
- Yager, R.; Filev, D. Essentials of Fuzzy: Modeling and Control; Wiley Interscience: New York, NY, USA, 1994. [Google Scholar]
- Zadeh, L.A.; Aliev, R.A. Fuzzy Logic Theory and Applications: Part I and Part II; World Scientific: Hackensack, NJ, USA, 2018. [Google Scholar]
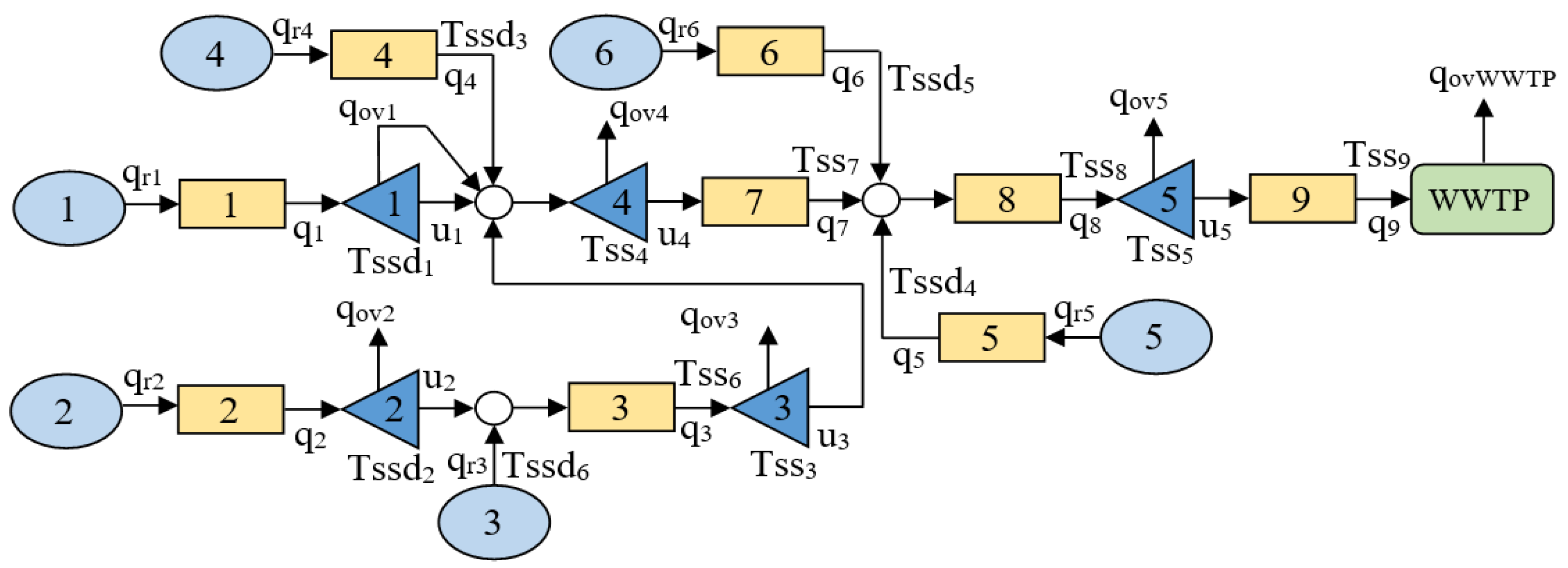
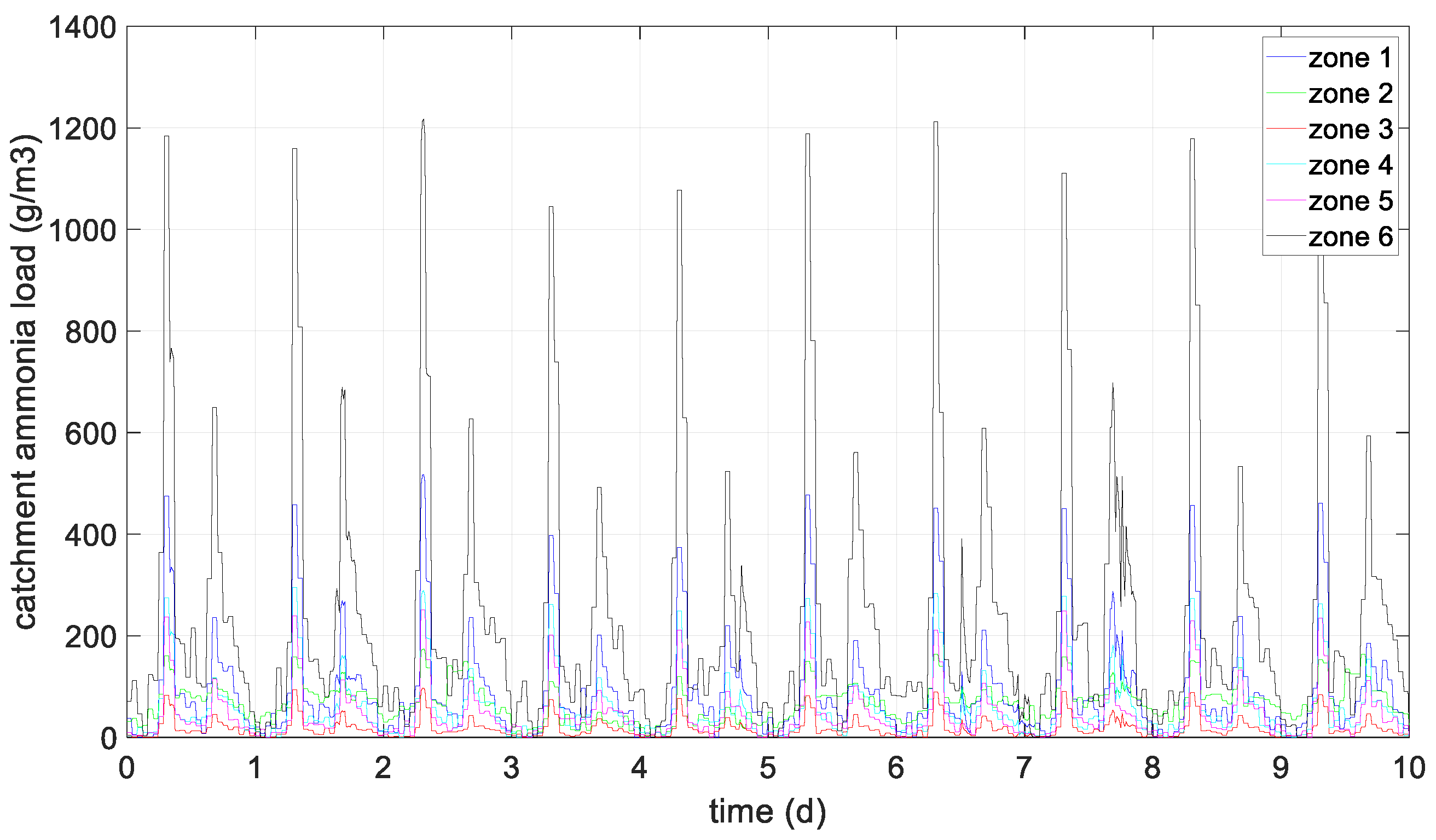
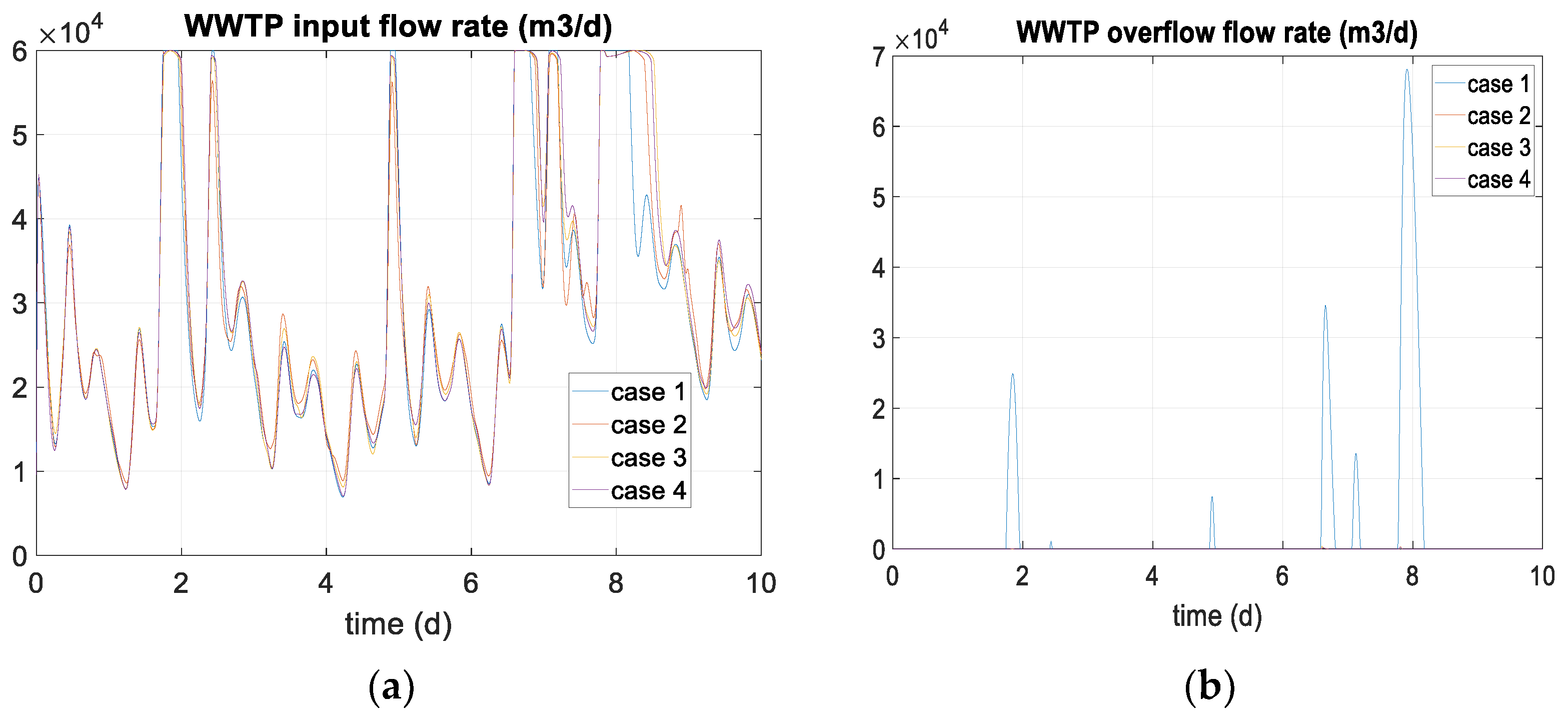

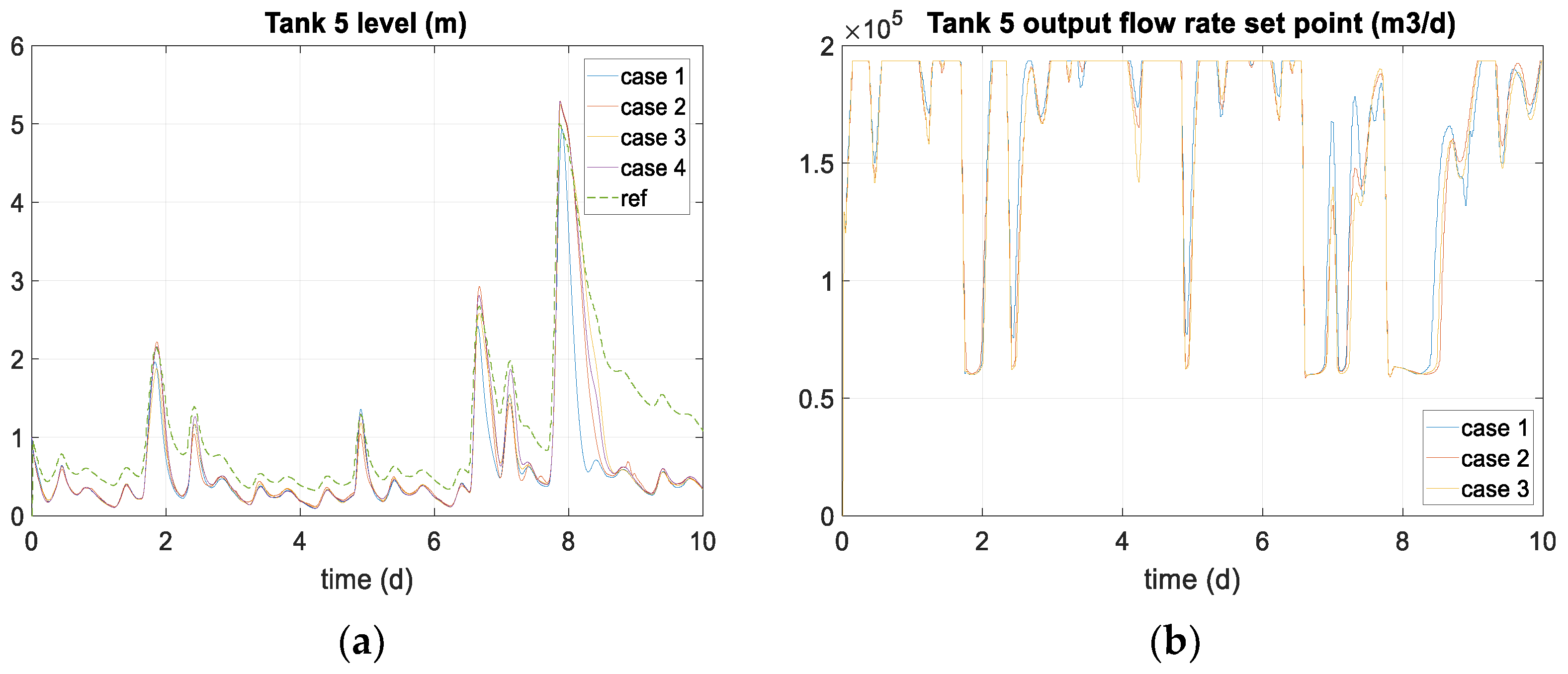
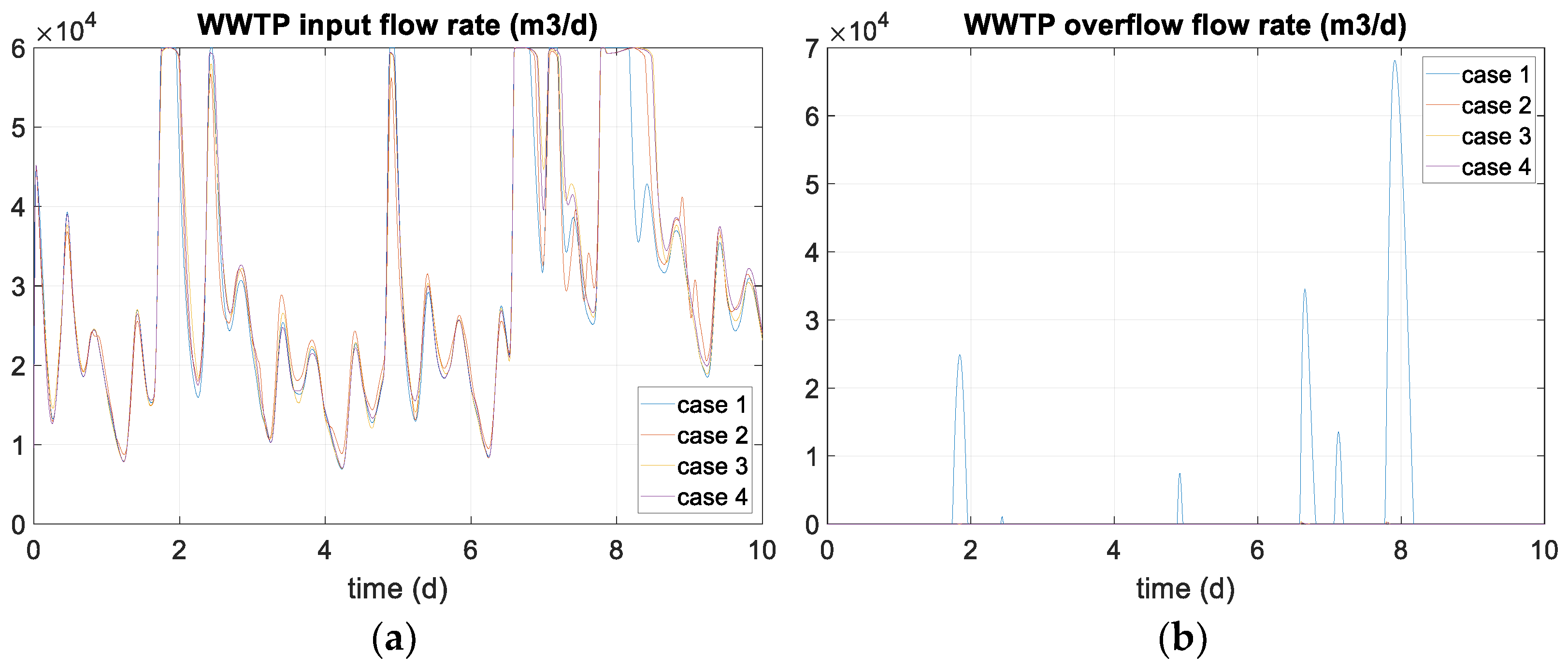
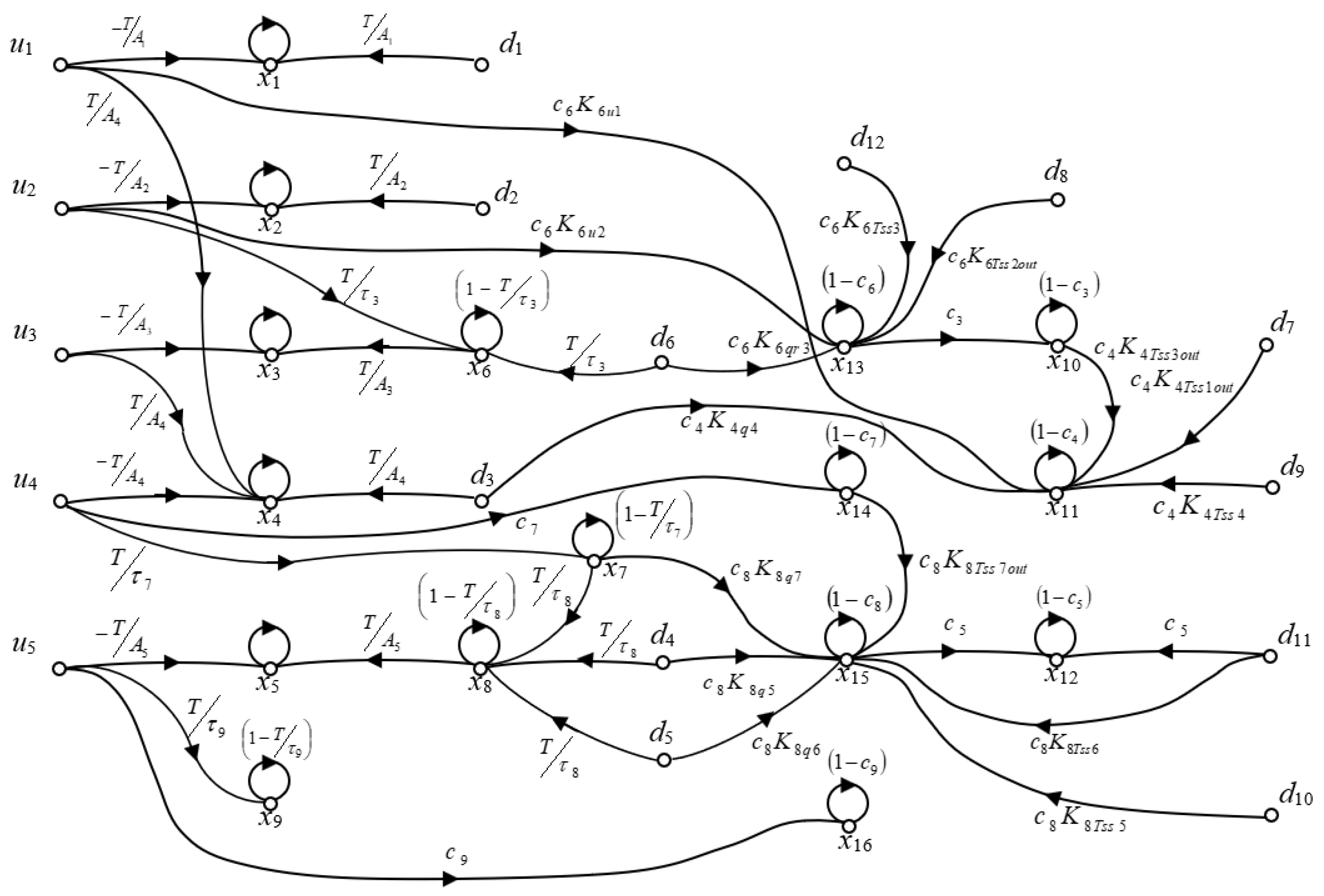
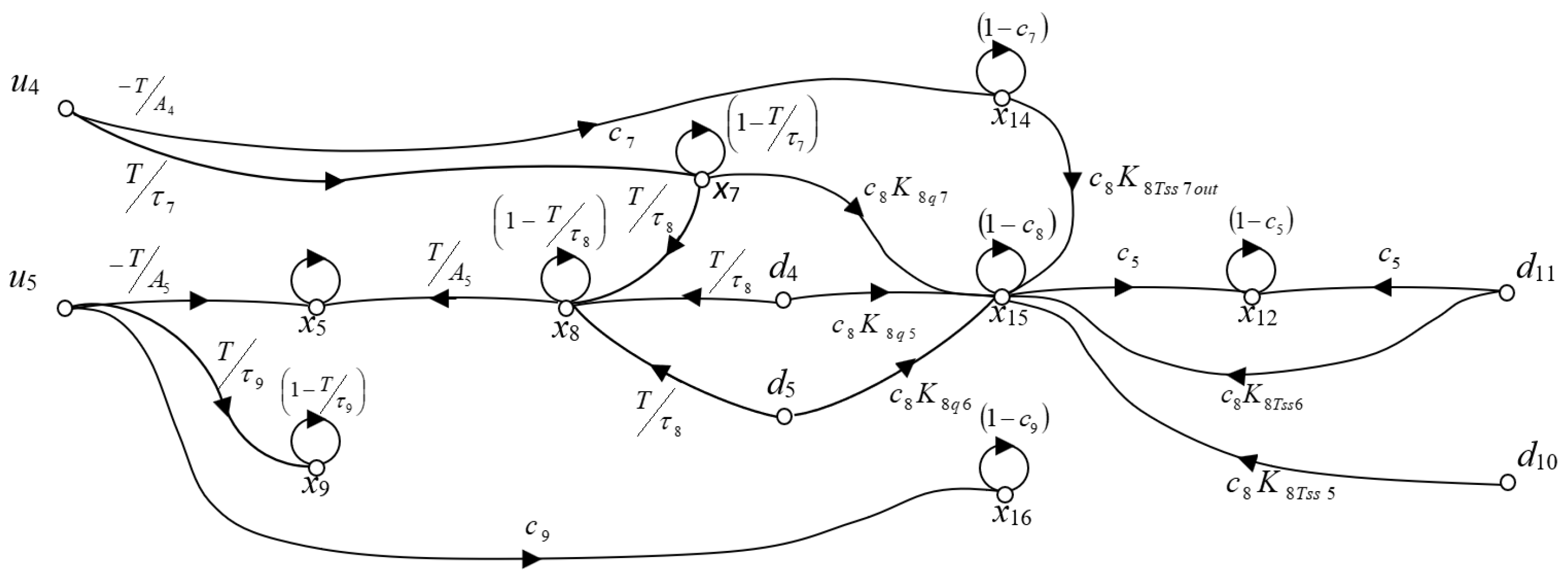
| Space State Model Variables | System Variables | Meaning and Units |
|---|---|---|
| x1, …, x5 | h1, …, h5 | Tank levels (m) |
| x6, x7, x8, x9 | q3, q7, q8, q9 | Pipes 3, 7, 8, and 9 flow rates (m3/d) |
| x10, x11, x12 | Tss3, Tss4, Tss5 | Suspended solids in tanks 3, 4, and 5 (g/m3) |
| x13, x14, x15, x16 | Tss6, Tss7, Tss8, Tss9 | Suspended solids in pipes 3, 7, 8, and 9 (g/m3) |
| u1, …, u5 | u1, …, u5 | Tank output flow rates (m3/d) |
| d1, d2, d3, d4, d5, d6 | q1, q2, q4, q5, q6, qr3 | Catchment flow rates (m3/d) |
| d7, …, d12 | Tssd1, …, Tssd6 | Catchment suspended solids (g/m3) |
| a | b | c | |
|---|---|---|---|
| 56,000 | 58,000 | 60,000 | |
| 1000 | 2000 | - |
| Weights for (19) | Weights for (20), (21) | Weights for (22) |
|---|---|---|
| Parameter | Units | Values |
|---|---|---|
| A1, …, A5 tank areas | m2 | 1188, 252, 348, 852, 2988 |
| c01, …, c05 discharge coefficients | m5/2/d | 1.89, 0.40, 0.55, 1.36, 6.12 (×104) |
| hmax1, …, hmax5 tank heights | m | 5 (for all) |
| hmin1, …, hmin5 minimum levels | m | 0 (for all) |
| qmax1, …, qmax9 maximum flow rates at the pipes outlet | m3/d | 5.99, 1.27, 3.02, 4.29, 4.29, 15.06, 4.29, 23.64, 6 (×104) |
| T sampling time | d | 0.0021 |
| τ1, …, τ9 link elements time constants | d | 0.0313, 0.0104, 0.0104, 0.0208, 0.0208, 0.073, 0.0208, 0.0104, 0.0104 |
| umax1, …, umax5 maximum flow rates at the reservoirs outlet | m3/d | 5.98, 1.27, 1.75, 4.29, 19.34 (×104) |
| c1, …, c9 sedimentation coefficients in tanks and links | - | 0.25 (for all) |
| Data | No Control | DMPC with Cooperative Game | DMPC with Fuzzy Negotiation | Centralized MPC |
|---|---|---|---|---|
| Vov,2 | 184.9266 | 312.9585 | 292.3083 | 202.1544 |
| Vov,3 | 644.9788 | 996.5150 | 795.6183 | 681.0547 |
| Vov,4 | 1.8077 × 103 | 6689.1 | 7968.8 | 3130.0 |
| Vov,5 | 0 | 6577.5 | 4338.3 | 5780.0 |
| Vov,WWTP | 2.6362 × 104 | 18.0810 | 20.3194 | 18.0087 |
| Vov | 28,999 | 14,594 | 13,415 | 9811.2 |
| Mssov,2 | 49.310 | 96.488 | 83.922 | 54.588 |
| Mssov,3 | 128.37 | 274.86 | 192.95 | 139.19 |
| Mssov,4 | 207.37 | 992.50 | 1131.2 | 443.44 |
| Mssov,5 | 0 | 841.16 | 519.96 | 712.53 |
| Mssov,WWTP | 5451.6 | 6.1879 | 7.0636 | 5.9378 |
| Mssov | 5836.6 | 2211.2 | 1935.1 | 1355.7 |
| NHov,2 | 1.2605 | 2.4402 | 2.1236 | 1.3998 |
| NHov,3 | 3.2733 | 7.1891 | 4.9912 | 3.5657 |
| NHov,4 | 6.6447 | 33.5894 | 35.7513 | 14.9230 |
| NHov,5 | 0 | 27.0282 | 16.4251 | 22.6801 |
| NHov,WWTP | 126.8435 | 0.1085 | 0.1033 | 0.1024 |
| NHov | 138.0221 | 70.3554 | 59.3945 | 42.6710 |
| NOov,2 | 0 | 0 | 0 | 0 |
| NOov,3 | 0 | 0 | 0 | 0 |
| NOov,4 | 0.0291 | 0.2452 | 0.4307 | 0.1101 |
| NOov,5 | 0 | 0.0991 | 0.0495 | 0.0772 |
| NOov,WWTP | 0.3251 | 0.0013 | 6.3448 × 10−4 | 6.1315 × 10−4 |
| NOov | 0.3542 | 0.3456 | 0.4808 | 0.1879 |
| POov,2 | 0.1136 | 0.2168 | 0.1916 | 0.1254 |
| POov,3 | 0.3818 | 0.7977 | 0.5628 | 0.4135 |
| POov,4 | 1.2249 | 7.3240 | 6.7831 | 3.1694 |
| POov,5 | 0 | 5.7923 | 3.4800 | 4.8845 |
| POov,WWTP | 26.8422 | 0.0242 | 0.0230 | 0.0227 |
| POov | 28.5626 | 14.1550 | 11.0405 | 8.6155 |
| OQI2 | 23.6549 | 36.6397 | 33.1744 | 25.1296 |
| OQI3 | 45.5329 | 86.6197 | 63.6188 | 48.5771 |
| OQI4 | 71.5591 | 310.2451 | 344.5962 | 143.8839 |
| OQI5 | 10 | 259.9951 | 163.6654 | 221.1111 |
| OQIWWTP | 1483.9 | 11.5668 | 11.7255 | 11.4979 |
| OQI | 1634.6 | 705.0665 | 616.7803 | 450.1995 |
| QWWTP | 28,860 | 30,021 | 30,384 | 30,556 |
| Gu | 48.1006 | 50.0351 | 50.6408 | 50.9265 |
| S | - | 1.7334 × 1011 | 6.9231 × 1010 | 7.6086 × 1010 |
| Data | No Control | DMPC with Cooperative Game | DMPC with Fuzzy Negotiation | Centralized MPC |
|---|---|---|---|---|
| Vov,2 | 184.9266 | 313.2993 | 201.0480 | 203.8316 |
| Vov,3 | 644.9788 | 992.7195 | 672.6625 | 666.7686 |
| Vov,4 | 1.8077 × 103 | 6694.7 | 7765.2 | 3123.6 |
| Vov,5 | 0 | 6682.0 | 4110.8 | 5789.3 |
| Vov,WWTP | 2.6362× 104 | 19.1941 | 24.4878 | 17.9733 |
| Vov | 28,999 | 14,702 | 12,774 | 9801.5 |
| Mssov,2 | 49.310 | 97.191 | 54.191 | 55.108 |
| Mssov,3 | 128.37 | 275.65 | 143.04 | 136.24 |
| Mssov,4 | 207.37 | 993.03 | 1078.7 | 444.60 |
| Mssov,5 | 0 | 857.42 | 478.05 | 713.47 |
| Mssov,WWTP | 5451.6 | 6.5113 | 8.3917 | 5.9371 |
| Mssov | 5836.6 | 2229.8 | 1762.4 | 1355.3 |
| NHov,2 | 1.2605 | 2.4591 | 1.3826 | 1.4142 |
| NHov,3 | 3.2733 | 7.2185 | 3.6652 | 3.4848 |
| NHov,4 | 6.6447 | 33.4184 | 34.3609 | 14.9650 |
| NHov,5 | 0 | 27.4838 | 15.1051 | 22.7104 |
| NHov,WWTP | 126.8435 | 0.1183 | 0.1334 | 0.1016 |
| NHov | 138.0221 | 70.6981 | 59.6472 | 42.6760 |
| NOov,2 | 0 | 0 | 0 | 0 |
| NOov,3 | 0 | 0 | 0 | 0 |
| NOov,4 | 0.0291 | 0.2409 | 0.4353 | 0.1041 |
| NOov,5 | 0 | 0.0998 | 0.0507 | 0.0738 |
| NOov,WWTP | 0.3251 | 0.0013 | 8.8362 × 10−4 | 5.7748 × 10−4 |
| NOov | 0.3542 | 0.3421 | 0.4869 | 0.1784 |
| POov,2 | 0.1136 | 0.2182 | 0.1249 | 0.1265 |
| POov,3 | 0.3818 | 0.8010 | 0.4223 | 0.4045 |
| POov,4 | 1.2249 | 7.2788 | 6.2459 | 3.1790 |
| POov,5 | 0 | 5.8853 | 3.1999 | 4.8879 |
| POov,WWTP | 26.8422 | 0.0263 | 0.0296 | 0.0225 |
| POov | 28.5626 | 14.2096 | 10.0227 | 8.6205 |
| OQI2 | 23.6549 | 36.8371 | 24.9986 | 25.2768 |
| OQI3 | 45.5329 | 86.8660 | 49.6458 | 47.7420 |
| OQI4 | 71.5591 | 309.8305 | 329.8800 | 144.2374 |
| OQI5 | 10 | 264.6245 | 151.2962 | 221.3869 |
| OQIWWTP | 1483.9 | 11.6611 | 12.0823 | 11.4949 |
| OQI | 1634.6 | 709.8192 | 567.9028 | 450.1381 |
| QWWTP | 28,860 | 30,003 | 30,430 | 30,555 |
| Gu | 48.1006 | 50.0050 | 50.7169 | 50.9255 |
| S | - | 1.7073 × 1011 | 6.9069 × 1010 | 7.6321 × 1010 |
| Data | Included TSS Option | DMPC with Cooperative Game | DMPC with Fuzzy Negotiation | Centralized MPC |
|---|---|---|---|---|
| Vov | No | 14,594 | 13,415 | 9811.2 |
| Vov | Yes | 14,702 | 12,774 | 9801.5 |
| Mssov | No | 2211.2 | 1935.1 | 1355.7 |
| Mssov | Yes | 2229.8 | 1762.4 | 1355.3 |
| NHov | No | 70.3554 | 59.3945 | 42.6710 |
| NHov | Yes | 70.6981 | 59.6472 | 42.6760 |
| NOov | No | 0.3456 | 0.4808 | 0.1879 |
| NOov | Yes | 0.3421 | 0.4869 | 0.1784 |
| POov | No | 14.1550 | 11.0405 | 8.6155 |
| POov | Yes | 14.2096 | 10.0227 | 8.6205 |
| OQI | No | 705.0665 | 616.7803 | 450.1995 |
| OQI | Yes | 709.8192 | 567.9028 | 450.1381 |
| QWWTP | No | 30,021 | 30,384 | 30,556 |
| QWWTP | Yes | 30,003 | 30,430 | 30,555 |
| Gu | No | 50.0351 | 50.6408 | 50.9265 |
| Gu | Yes | 50.0050 | 50.7169 | 50.9255 |
| Case | a | b | c | a | b |
|---|---|---|---|---|---|
| DMPC 1 | 56,000 | 58,000 | 60,000 | 1000 Tssm(k) | 2000 Tssm(k) |
| DMPC 2 | 54,000 | 56,000 | 58,000 | 1000 Tssm(k) | 2000 Tssm(k) |
| DMPC 3 | 58,000 | 60,000 | 62,000 | 1000 Tssm(k) | 2000 Tssm(k) |
| DMPC 4 | 56,000 | 58,000 | 60,000 | 0000 Tssm(k) | 1000 Tssm(k) |
| DMPC 5 | 56,000 | 58,000 | 60,000 | 2000 Tssm(k) | 3000 Tssm(k) |
| Data | DMPC1 | DMPC2 | DMPC3 | DMPC4 | DMPC5 |
|---|---|---|---|---|---|
| Vov,2 | 292.3083 | 294.4305 | 310.7161 | 261.1050 | 296.7159 |
| Vov,3 | 795.6183 | 807.0578 | 971.8244 | 687.2200 | 835.2211 |
| Vov,4 | 7968.8 | 7974.8 | 7721.3 | 7905.4 | 7820.3 |
| Vov,5 | 4338.3 | 4341.4 | 4338.3 | 4338.3 | 4343.8 |
| Vov,WWTP | 20.3194 | 20.1841 | 21.2225 | 20.6859 | 20.1757 |
| Vov | 13,415 | 13,438 | 13,982 | 13,189 | 13,316 |
| Mssov,2 | 83.922 | 84.702 | 93.652 | 72.960 | 85.670 |
| Mssov,3 | 192.95 | 196.94 | 259.77 | 155.33 | 206.23 |
| Mssov,4 | 1131.2 | 1133.0 | 1161.4 | 1129.1 | 1102.1 |
| Mssov,5 | 519.96 | 520.58 | 613.08 | 513.98 | 521.12 |
| Mssov,WWTP | 7.0636 | 7.0119 | 6.9094 | 7.2022 | 6.9319 |
| Mssov | 1935.1 | 1942.2 | 2134.8 | 1878.5 | 1922.0 |
| NHov,2 | 2.1236 | 2.1431 | 2.3672 | 1.8504 | 2.1673 |
| NHov,3 | 4.9912 | 5.0960 | 6.7716 | 4.0041 | 5.3391 |
| NHov,4 | 35.7513 | 35.7867 | 39.8640 | 36.1368 | 34.5933 |
| NHov,5 | 16.4251 | 16.4406 | 19.8800 | 16.2649 | 16.4578 |
| NHov,WWTP | 0.1033 | 0.1027 | 0.1165 | 0.1056 | 0.1034 |
| NHov | 59.3945 | 59.5692 | 68.9993 | 58.3617 | 58.6610 |
| NOov,2 | 0 | 0 | 0 | 0 | 0 |
| NOov,3 | 0 | 0 | 0 | 0 | 0 |
| NOov,4 | 0.4307 | 0.4410 | 0.3890 | 0.4154 | 0.4276 |
| NOov,5 | 0.0495 | 0.0505 | 0.0643 | 0.0499 | 0.0500 |
| NOov,WWTP | 6.3448 × 10−4 | 6.3597 × 10−4 | 8.1386 × 10−4 | 6.5225 × 10−4 | 6.2756 × 10−4 |
| NOov | 0.4808 | 0.4921 | 0.4541 | 0.4660 | 0.4782 |
| POov,2 | 0.1916 | 0.1933 | 0.2114 | 0.1675 | 0.1953 |
| POov,3 | 0.5628 | 0.5744 | 0.7573 | 0.4548 | 0.6013 |
| POov,4 | 6.7831 | 6.7948 | 8.5241 | 6.8598 | 6.5964 |
| POov,5 | 3.4800 | 3.4835 | 4.2674 | 3.4520 | 3.4862 |
| POov,WWTP | 0.0230 | 0.0228 | 0.0260 | 0.0235 | 0.0230 |
| POov | 11.0405 | 11.0687 | 13.7862 | 10.9576 | 10.9022 |
| OQI2 | 33.1744 | 33.3891 | 35.8530 | 30.1599 | 33.6553 |
| OQI3 | 63.6188 | 64.7335 | 82.3436 | 53.1236 | 67.3239 |
| OQI4 | 344.5962 | 345.0823 | 363.1114 | 345.3249 | 335.2797 |
| OQI5 | 163.6654 | 163.8365 | 192.7466 | 161.9850 | 163.9967 |
| OQIWWTP | 11.7255 | 11.7134 | 11.7349 | 11.7601 | 11.6996 |
| OQI | 616.7803 | 618.7548 | 685.7893 | 602.3535 | 611.9552 |
| QWWTP | 30,384 | 30,381 | 30,317 | 30,401 | 30,399 |
| Gu | 50.6408 | 50.6354 | 50.5288 | 50.6678 | 50.6643 |
| S | 6.9231 × 1010 | 6.9375 × 1010 | 9.6167 × 1010 | 6.9317 × 1010 | 6.9414 × 1010 |
| Data | DMPC1 | DMPC2 | DMPC3 | DMPC4 | DMPC5 |
|---|---|---|---|---|---|
| Vov,2 | 203.5121 | 204.8541 | 288.4027 | 204.9085 | 205.5031 |
| Vov,3 | 672.5447 | 675.6874 | 722.9298 | 673.0609 | 674.1634 |
| Vov,4 | 7770.5 | 7701.0 | 6205.4 | 7811.8 | 7880.9 |
| Vov,5 | 4109.7 | 4142.8 | 4873.0 | 4108.9 | 4113.2 |
| Vov,WWTP | 24.4633 | 24.5810 | 23.1997 | 24.4242 | 24.3320 |
| Vov | 12,781 | 12,749 | 12,113 | 12,823 | 12,898 |
| Mssov,2 | 54.9411 | 55.2451 | 82.6870 | 55.3666 | 55.5478 |
| Mssov,3 | 142.9723 | 143.8091 | 170.0461 | 143.3309 | 144.106 |
| Mssov,4 | 1079.5 | 1073.9 | 880.6759 | 1083.5 | 1090.4 |
| Mssov,5 | 477.9512 | 482.4708 | 588.7328 | 477.9763 | 478.7065 |
| Mssov,WWTP | 8.3843 | 8.5278 | 7.6018 | 8.3672 | 8.3379 |
| Mssov | 1763.7 | 1763.9 | 1729.7 | 1768.5 | 1777.1 |
| NHov,2 | 1.4013 | 1.4093 | 2.0927 | 1.4119 | 1.4165 |
| NHov,3 | 3.6634 | 3.6850 | 4.3927 | 3.6732 | 3.6952 |
| NHov,4 | 34.3839 | 34.2258 | 28.7100 | 34.5066 | 34.6885 |
| NHov,5 | 15.1017 | 15.2228 | 18.9341 | 15.1034 | 15.1237 |
| NHov,WWTP | 0.1332 | 0.1324 | 0.1287 | 0.1330 | 0.1323 |
| NHov | 54.6835 | 54.6752 | 54.2582 | 54.8281 | 55.0561 |
| NOov,2 | 0 | 0 | 0 | 0 | 0 |
| NOov,3 | 0 | 0 | 0 | 0 | 0 |
| NOov,4 | 0.4302 | 0.4229 | 0.3456 | 0.4393 | 0.4273 |
| NOov,5 | 0.0501 | 0.0502 | 0.0642 | 0.0507 | 0.0487 |
| NOov,WWTP | 8.7218 × 10−4 | 8.4314 × 10−4 | 8.8063 × 10−4 | 8.8474 × 10−4 | 8.4302 × 10−4 |
| NOov | 0.4812 | 0.4739 | 0.4108 | 0.4909 | 0.4768 |
| POov,2 | 0.1267 | 0.1274 | 0.1889 | 0.1276 | 0.1280 |
| POov,3 | 0.4221 | 0.4246 | 0.4967 | 0.4231 | 0.4252 |
| POov,4 | 6.2459 | 6.2178 | 5.7592 | 6.2710 | 6.2872 |
| POov,5 | 3.1989 | 3.2246 | 4.0418 | 3.1996 | 3.2018 |
| POov,WWTP | 0.0296 | 0.0295 | 0.0290 | 0.0296 | 0.0294 |
| POov | 10.0232 | 10.0238 | 10.5156 | 10.0509 | 10.0717 |
| OQI2 | 25.2049 | 25.2895 | 32.8343 | 25.3219 | 25.3717 |
| OQI3 | 49.6267 | 49.8594 | 57.2369 | 49.7280 | 49.9564 |
| OQI4 | 330.1006 | 328.4947 | 273.1868 | 331.2860 | 333.1983 |
| OQI5 | 151.2654 | 152.5351 | 185.0174 | 151.2762 | 151.4811 |
| OQIWWTP | 12.0802 | 12.1066 | 11.9102 | 12.0762 | 12.0682 |
| OQI | 568.2778 | 568.2853 | 560.1855 | 569.6883 | 572.0757 |
| QWWTP | 30,430 | 30,436 | 30,474 | 30,428 | 30,423 |
| Gu | 50.7161 | 50.7267 | 50.7896 | 50.7131 | 50.7055 |
| S | 6.9493 × 1010 | 6.8258 × 1010 | 8.5400 × 1010 | 6.9441 × 1010 | 6.9763 × 1010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cembellín, A.; Francisco, M.; Vega, P. Optimal Operation of a Benchmark Simulation Model for Sewer Networks Using a Qualitative Distributed Model Predictive Control Algorithm. Processes 2023, 11, 1528. https://doi.org/10.3390/pr11051528
Cembellín A, Francisco M, Vega P. Optimal Operation of a Benchmark Simulation Model for Sewer Networks Using a Qualitative Distributed Model Predictive Control Algorithm. Processes. 2023; 11(5):1528. https://doi.org/10.3390/pr11051528
Chicago/Turabian StyleCembellín, Antonio, Mario Francisco, and Pastora Vega. 2023. "Optimal Operation of a Benchmark Simulation Model for Sewer Networks Using a Qualitative Distributed Model Predictive Control Algorithm" Processes 11, no. 5: 1528. https://doi.org/10.3390/pr11051528
APA StyleCembellín, A., Francisco, M., & Vega, P. (2023). Optimal Operation of a Benchmark Simulation Model for Sewer Networks Using a Qualitative Distributed Model Predictive Control Algorithm. Processes, 11(5), 1528. https://doi.org/10.3390/pr11051528








