Research on Landslide Displacement Prediction Based on DES-CGSSA-BP Model

Abstract

A landslide is a type of natural disaster that has the highest frequency, the widest distribution and the heaviest losses worldwide; landslides seriously threaten human life and property and major engineering facilities. Therefore, it is important to improve landslide displacement prediction technology to avoid and mitigate landslide disasters. A landslide displacement prediction method based on a chaotic Gaussian mutation sparrow search algorithm-optimised BP neural network (CG-SSA-BP) is proposed to address the problems of the traditional sparrow search algorithm (SSA)-optimised BP (SSA-BP) neural network; it tends to fall into local optima, and it has slow convergence and a low prediction accuracy for landslide displacement prediction. This paper takes the Baishui River landslide in the Three Gorges reservoir area as the research object, and the double exponential smoothing (DES) method is used to decompose the landslide displacement into a trend term and a periodic term to solve the nonlinear landslide system problem. The results show that the prediction model based on CG-SSA-BP has a better prediction accuracy and better stability compared with the model based on SSA-BP.

1. Introduction

A landslide is a geological phenomenon caused by changes in the natural environment or human activities that alter the equilibrium of a slope. Sudden landslides can cause tremendous loss of life and property [1]. As a result, predicting landslide deformation has become increasingly important, and over the years, researchers have divided landslide prediction models into two categories: physical models and data-driven models. Data-driven models emphasise building relevant mathematical models for prediction based on previously measured data [2]. When there are many factors affecting the landslide stability and the physical mechanism of landslide deformation is complicated, data-driven models offer a better prediction accuracy. With the development of artificial intelligence technology, mathematical models represented by neural network models and support vector machine models have gradually become a research hotspot for data-driven landslide prediction because of their improved accuracy in predicting the behaviour of complex nonlinear systems such as landslide deformation systems under similar complex conditions. Landslides are affected by many nonlinear conditions, such as intrinsic factors, the external environment and human activities, and the monitoring data for landslides show non-linear and non-smooth characteristics; thus, it is necessary to pre-process the monitoring data. The current processing method mainly decomposes the observed displacement into a trend term and a periodic term based on response components, with the trend term being controlled by the geological conditions of the slope itself and the periodic term being controlled by external influencing factors. The decomposition of the displacements generally involves first calculating the trend term and then subtracting the trend term from the total displacement to obtain the fluctuating term. Xing et al. used the double moving average (DMA) method to decompose the cumulative displacement of the Baishui River landslide in the Three Gorges reservoir area into the trend displacement and periodic displacement, and then they used a long short-term memory network to establish a nonlinear mapping relationship between induced factors and the periodic displacement [3]. Feng et al. proposed a landslide displacement prediction method based on double exponential smoothing (DES) and an Elman neural network (The full name of “Simple Recurrent Neural Network” is one of the important theories of nonlinear system identification, which is named after the inventor Jeffury Elman.), and successfully applied it to the prediction of the cumulative displacement of the Baishui River landslide to obtain better results [4].

BP neural network (it is a multilayer feedforward neural network trained according to the error back propagation algorithm, and is one of the most widely used neural network models), as one of the classic machine learning algorithms, has been widely used in landslide displacement prediction [5,6]. BP neural networks is a feed-forward network that can be used in multiple scenarios, and its performance is affected by the network environment. The optimisation of thresholds, weights and biases is expected to result in better-quality predictions [7]. However, BP neural networks also have problems such as easy to fall into local convergence and paralysis. Therefore, the combination of intelligent optimisation algorithm and BP neural network applied to landslide displacement prediction research has been further developed. For example, Chen et al. combined genetic algorithm (GA) with BP neural network, using a combination of genetic algorithm and simulated annealing algorithm to optimise the weights and biases of the neural network, and the improved model improved the accuracy of landslide deformation prediction, which has some practical value [8]. Zhu et al. combined particle swarm optimisation (PSO) with BP neural network to determine the initial weights and thresholds in BP neural network, and applied it to large area landslide risk assessment with certain effect [9]. Song et al. used a combined model of sparrowsearch algorithm (SSA) and BP neural network to achieve fast and accurate prediction of landslide dams stability, which is an effective means to predict the stability of landslide dams [10].

The sparrow search algorithm (SSA) is a swarm intelligence optimisation algorithm proposed by Xue et al. that is based on the behaviour of sparrows that are foraging and escaping predators; it was first proposed in 2020 and has the advantages of strong local search capabilities and fast convergence [11]. Liu et al. proposed landslide displacement prediction forecasting based on the evoked factor response (the relationship between dynamic changes in landslide influencing factors and changes in landslide displacement) and a BP neural network; this method basically reflects the overall trend of landslide cumulative displacement and has some engineering significance [12]. Ma et al. proposed a new multivariate displacement prediction method using the sparrow search algorithm (SSA), which was combined with the kernel extreme learning machine (KELM) algorithm, for the prediction of the displacement variation of landslides and compared it with the traditional support vector machine (SVM); they obtained good displacement prediction results [13]. Yang et al. established a landslide monitoring and early warning model based on SSA-LSTM, and the hyperparameters of the LSTM neural network (long short-term memory) were optimised using the SSA; the prediction capabilities of the optimised SSA-LSTM model were significantly improved, and the results are significant for landslide hazard early warning systems [14].

BP models based on the sparrow search algorithm have been used for practical engineering optimisation problems such as fault diagnosis and wind power prediction [15,16], but they have not been utilised for landslide displacement prediction. In this paper, we propose an optimised BP neural network based on the chaos Gaussian mutant sparrow search algorithm (CG-SSA) for landslide displacement prediction. It is based on the traditional BP neural network model, which has a low accuracy, and the original sparrow search algorithm (SSA) with reduced population diversity; it is easy for this algorithm to fall into local optimal solutions as it approaches the global optimum. First, the cumulative landslide displacement is decomposed into a trend term and a periodic term using double exponential smoothing (DES), where the periodic term displacement is initialised using a chaotic tent sequence to make the initial individuals as uniformly distributed as possible, while Gaussian mutation and chaotic perturbation are introduced to strengthen the local search ability and improve the search accuracy; this helps the SSA overcome its disadvantages of poor convergence speed and weak global search capabilities, so that its optimised BP neural network is more accurate in predicting landslide displacement. Finally, the trend term and the periodic term are summed to obtain the final prediction. The prediction results were compared with those of a BP model and an SSA-BP model, and three indicators, the root mean square error, mean absolute percentage error and correlation coefficient, were used to evaluate the accuracy of the landslide prediction model. The prediction model proposed in this paper is validated by taking the actual measured data from the Baishui River landslide in the Three Gorges reservoir area as an example to prove the feasibility and superiority of the proposed model.

2. The Forecast Model of Landslide Displacement

2.1. Double Exponential Smoothing (DES)

The double exponential smoothing method is an effective model that continuously corrects forecasts based on the latest data [17]. The method obtains a weighted average of the measured displacements in chronological order, where the weight of the most recent observation is higher than that of the previous observation. According to the type of smoothing that is implemented, it can be divided into primary exponential smoothing, secondary exponential smoothing, etc. For a time series fluctuating within a certain range, primary exponential smoothing is generally used, as shown in Equation (2); for a time series with a trend, the double exponential smoothing method provides better forecasting results, as shown in Equation (3). The cumulative landslide displacement is a typical time series with a trend; thus, this paper uses the double exponential smoothing (DES) method to predict the trend displacement of landslides. The prediction process is as follows:

$$t_1=c_1$$

(1)

$$t_{i-1}=\alpha c_{i-2}+(1-\alpha )t_{i-2}$$

(2)

$$\begin{array}{l}{t}_i=\alpha c_{i-1}+(1-\alpha )t_{i-1}\\ =\alpha c_{i-1}+(1-\alpha )(\alpha c_{i-2}+(1-\alpha )t_{i-2})\\ =\alpha c_{i-1}+\alpha (1-\alpha )c_{i-2}+{(1-\alpha )}^2{t}_{i-2}\end{array}$$

(3)

where $t_i$ denotes the trend displacement at moment $i$, $c_{i-1}$ denotes the cumulative displacement at moment $i-1$ and $\alpha$ denotes the exponential decay degree and takes a value between 0 and 1. On the basis of obtaining the predicted trend displacement, this trend displacement is subtracted from the cumulative displacement to obtain the periodic displacement:

$$p_i=c_i-t_i,$$

(4)

where $p_i$ denotes the periodic displacement at time $i$.

2.2. Sparrow Search Algorithm (SSA)

The SSA is a novel swarm intelligence optimisation algorithm, mainly inspired by sparrow foraging and anti-predation behaviours, with strong global optimisation-seeking capabilities, no dependence on gradient information, good parallelism and a fast convergence speed [18].

(1)

In the sparrow search algorithm, discoverers generally account for 10% to 20% of the population, and the positions of these sparrows are updated as follows:

$$x_{id}^{t+1}=\{\begin{array}{c}{x}_{id}^{t}exp\left(-\frac{i}{a^T}\right),R_2<S_T\\ x_{id}^t+QL,R_2\ge S_T\end{array},$$

(5)

where $t$ is the number of current iterations, $T$ is a constant indicating the maximum number of iterations, $x_{id}$ is the position information of the $i$-th sparrow in the $d$-dimension, $a\in (0,1]$ is a random number, $R_2\in (0,1)$ and $S_T\left[0.5,1\right]$ are the warning value and safety value, respectively, $Q$ is a random number obeying the standard normal distribution and $L$ is a matrix of size 1 by $d$, where all the entries are 1.

(2)

For joiners, the position is updated according to the following equation:

$$x_{id}^{t+1}=\{\begin{array}{l}Q\cdot exp(\frac{X_{worst}^t-x_{id}^t}{i^2}),i>\frac{n}{2}\\ X_{best}^{t+1}+\left|X_{id}^t-X_{best}^{t+1}\right|A^{+}\cdot L,i<\frac{n}{2}\end{array},$$

(6)

where $X_{best}$ is the best position currently occupied by the discoverer, $X_{worst}$ is the current global worst position and $A$ is a $1\times d$-dimensional matrix in which each element is randomly assigned a value of 1 or −1. When $i>\frac{n}{2}$, this indicates that the $i$-th participant with a lower fitness value is not obtaining food and is in a very hungry state and that it needs to go to other places to forage for food.

(3)

Assuming that sparrows that are aware of danger account for 10–20% of the total number of sparrows and that the initial positions of these sparrows are randomly generated in the population, the mathematical expression is:

$$X_{id}^{t+1}=\{\begin{array}{l}{X}_{best}^t+\beta \left|X_{id}^t-X_{best}^t\right|,f_i\ne f_g\\ X_{id}^t+K(\frac{\left|X_{id}^t-X_{worst}^t\right|}{(f_i-f_w)+\epsilon }),f_i=f_g\end{array},$$

(7)

where $X_{best}$ is the current global optimum position, $\beta$ is the step control parameter, which is a normally distributed random number with a mean of 0 and a variance of 1, $k$ belongs to a random number between 1 and −1, $f_i$ is the current fitness value of the individual sparrow, $f_g$ and $f_w$ are the current global optimum and worst fitness values, respectively, and $\epsilon$ is a very small constant to avoid having a zero in the denominator.

2.3. Tent Chaos and Gaussian Mutation Sparrow Search Algorithm (CG-SSA)

2.3.1. Chaotic Tent Sequence

Chaos, as a nonlinear phenomenon that is prevalent in nature, has been applied to optimisation search problems by many researchers because of the randomness, ergodicity and regularity of chaotic variables, which can not only effectively maintain the diversity of populations but also allow the algorithm to jump out of local optima and improve the global search capability [19]. The common logistic mapping represents a typical chaotic system. It can be seen from Figure 1 that the probability that it will take values in the two ranges of [0, 0.05] and [0.95, 1] is high, so the algorithm’s seeking speed is affected by the inhomogeneity of logistic traversal, and the efficiency of the algorithm will be reduced. Shan-Liang et al. showed that the traversal uniformity and convergence speed of the tent mapping are better than those of the logistic mapping, and they proved that the tent mapping can be used as a chaotic sequence to generate optimisation algorithms using rigorous mathematical reasoning [20]. The tent mapping expression is:

$$z_{i+1}=\{\begin{array}{cc}2z_i& 0\le z\le \frac{1}{2}\\ 2(1-z_i)& \frac{1}{2}<z\le 1\end{array}.$$

(8)

The tent mapping is expressed by a Bernoulli shift transformation as

$$z_{i+1}=(2z_i)\mathrm{mod}1,$$

(9)

The analysis reveals that there are small cycles in the chaotic tent sequence and that there are unstable cycle points. In order to keep the algorithm from falling into small or unstable periodic points without destroying the three main properties of chaotic variables, Zhang et al. introduced random variables $rand(0,1)\times \frac{1}{N_T}$ into the original tent mapping expression, and the improved expression is:

$$\{\begin{array}{cc}2z_i+rand(0,1)·\frac{1}{N_T}& 0\le z\le \frac{1}{2}\\ 2(1-z_i)z+rand(0,1)·\frac{1}{N_T}& \frac{1}{2}<z\le 1\end{array}.$$

(10)

The expression after the Bernoulli transformation is:

$${\mathrm{z}}_{i+1}=(2z_i)\mathrm{mod}1+rand(0,1)·\frac{1}{N_T},$$

(11)

where $N_T$ is the number of particles within the chaotic sequence and $rand(0,1)$ is a random number in the range [0, 1].

According to the properties of tent mapping, the steps for generating chaotic sequences in the feasible domain are as follows:

(1)

Randomly generate an initial value $z_0$ within (0, 1) that is denoted $i=0$.

(2)

Iterate using Equation (11) to produce a sequence of $Z$, with $i$ self-increasing by 1.

(3)

If the maximum number of iterations is reached, the program runs and stops, saving the resulting $Z$-sequence.

As shown in Figure 1, the common logistic chaotic mapping is less efficient in finding the best solution; on the contrary, the improved tent mapping takes more uniform values, so the algorithm can improve the quality of the initial solution and enhance the global search capabilities of the algorithm.

2.3.2. Tent Chaotic Perturbation

Chaotic perturbation is introduced to keep the algorithm from falling into local optima and to improve the global search capabilities and the accuracy of finding the optimum. The chaotic perturbation process is described as follows [21]:

(1)

Apply Equation (11) to generate the chaotic variable $Z_d$.

(2)

Carry chaotic variables into the solution space of the problem to be solved:

$$X_{new}^d=d_{\min }+(d_{\max }-d_{\min })Z_d,$$

(12)

where $d_{\min }$ and $d_{\max }$ are the minimum and maximum values of the $d$-dimensional variable $X_{new}^d$, respectively.

(3)

Perform the chaotic perturbation of individuals according to Equation (13):

$$X_{new}^{\prime }=(X^{\prime }+X_{new})/2,$$

(13)

where $X^{\prime }$ is the individual to be chaotically perturbed, $X_{new}$ is the amount of chaotic perturbation generated and $X_{new}^{\prime }$ is the individual after chaotic perturbation.

2.3.3. Gaussian Mutation

The Gaussian mutation is derived from the Gaussian distribution; specifically, when the variance operation is performed, the original parameter value is replaced by a random number that fits a normal distribution with a mean $\mu$ and a variance ${\sigma }^2$ [22]. The mutation formula is:

$$mutation(x)=x(1+N(0,1)),$$

(14)

where $x$ is the original parameter value, $N(0,1)$ denotes a normally distributed random number with an expectation of 0 and a standard deviation of 1 and $mutation(x)$ is the value after Gaussian variation.

Due to the properties of the normal distribution, it is known that Gaussian variation is focused on a local area near the original individual. The Gaussian distribution has strong local search capabilities, which can help the algorithm to find global minima with high efficiency and accuracy for optimisation problems with a large number of local minima; it also improves the robustness of the algorithm in this paper [23,24].

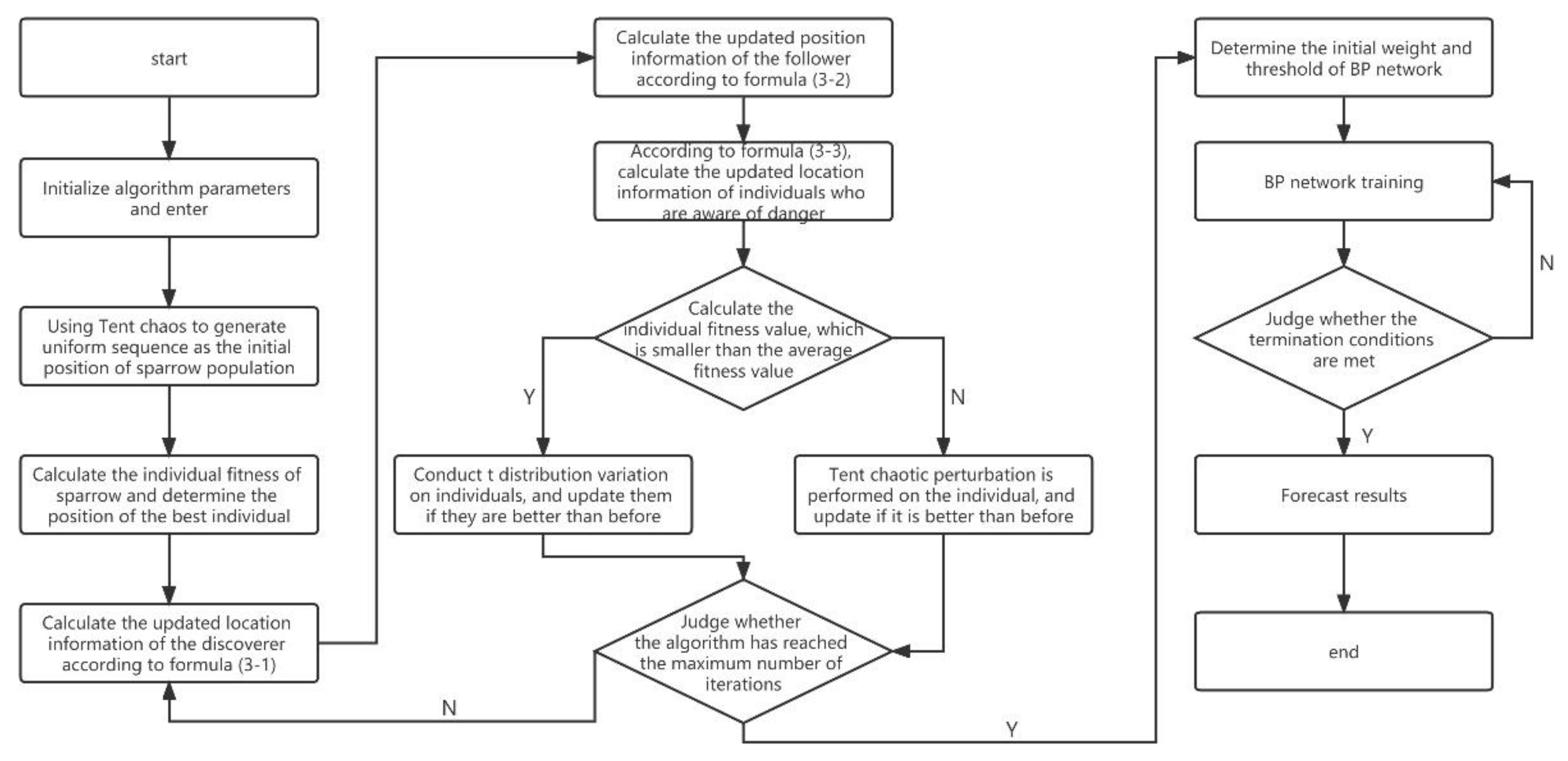
2.4. Optimised BP Neural Network Model Using CGSSA

In view of the disadvantages of the BP neural network optimised using the original SSA, such as slow convergence, the tendency to fall into local optima and poor stability, this paper uses the CGSSA to optimise the BP neural network. The basic idea of the model is to introduce tent chaos search and Gaussian variation to improve the SSA to improve the search performance of the algorithm by keeping it from falling into local optima; then, the CGSSA is used to optimise the initial weights of the BP neural network, as well as the thresholds, several times to form a CG-SSA-BP neural network. The flow chart for optimising the BP neural network based on chaotic tent search and a Gaussian variant of the sparrow search algorithm is shown in Figure 2, and the specific implementation steps are as follows:

(1)

Initialise the parameters of the sparrow search algorithm. These include the sparrow population size $N$, the number of discoverers $p_{Num}$, the number of sparrows for reconnaissance warning $s_{Num}$, the dimensionality of the objective function $D$, the upper and lower bounds of the initial values $lb$ and $ub$, and the maximum number of iterations $T$.

(2)

Initialise the sparrow population using the chaotic tent sequence described in Section 2.3.1, generate $N$ $D$-dimensional vectors $Z_i$ and each component is transferred to the value range of the space variable of the original problem through the carrier of formula (12).

(3)

Calculate the fitness value $f_i$ of each sparrow and find the current optimal fitness value $f_g$ and the worst fitness value $f_w$ and the corresponding positions.

(4)

Some of the sparrows with better fitness values are chosen as discoverers, and the remaining sparrows are chosen as followers; the positions of discoverers and followers are updated according to Equations (5) and (6).

(5)

Randomly select some sparrows $s_{Num}$ in the sparrow population as vigilantes and update their positions according to Equation (7).

(6)

After one iteration, recalculate the fitness value $f_i$ for each sparrow and the average fitness value $f_{avg}$ for the sparrow population.

➀

When $f_i<f_{avg}$, this indicates the phenomenon of ‘aggregation’, and Gaussian variation is performed according to Equation (14).

➁

When $f_i\ge f_{avg}$, this indicates a ‘divergence’ trend, and the individuals are perturbed with tent chaos, as described in Section 2.3.2. If the perturbed individuals have a better performance, the perturbed individuals are used to replace the pre-turbulent individuals; otherwise, the original individuals remain unchanged.

(7)

Based on the current state of the sparrow population, update the optimal position $X_{best}$ and its fitness $f_g$ and the worst position $X_{worst}$ and its fitness $f_w$ experienced by the entire population.

(8)

The judgment algorithm runs if the maximum number of iterations is reached: the loop ends and the location information of the sparrow with the best global fitness value is output. Otherwise, the algorithm returns to step (4).

(9)

Determine the initial weights of the BP neural network, as well as the threshold values, build the BP neural network model for training and output the prediction results.

2.5. Model Accuracy Evaluation

Three metrics are used to evaluate the model accuracy, namely the root mean square error ($RMSE$), mean absolute error ($MAE$) and mean absolute relative error ($MAPE$). The lower the value of each of these metrics, the better the prediction results. The formulas for each accuracy evaluation index follow:

(1)

Root mean square error:

$$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{(\stackrel{\wedge }{d_i}-d_i)}^2}}.$$

(15)

(2)

Mean absolute error:

$$MAE=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|d_i-\stackrel{\wedge }{d_i}\right|}.$$

(16)

(3)

The absolute value of the average relative error:

$$MAPE=\frac{1}{N}{\displaystyle \sum _{i=1}^N\left|\frac{d_i-\stackrel{\wedge }{d_i}}{d_i}\right|},$$

(17)

where $N$ is the number of predicted values, $d_i$ is the true value and $\stackrel{\wedge }{d_i}$ is the predicted value.

3. Study Area Overview and Application Analysis

3.1. Study Area

The Baishui landslide is a typical mound landslide in the Three Gorges reservoir area, located on the south bank of the Yangtze River, 56 km from the Three Gorges Dam site; it is near the village of Baishui and the town of Shazhenxi. The geographical coordinates are (31°01′34″, 110°32′09″). The location of the Baishui River landslide is shown in Figure 3. The landslide body is in the Yangtze River wide valley section; it has a monoclinic cascade slope, which is high in the south and low in the north, with step-like spreading to the Yangtze River. The elevation of its back edge is 410 m, with the rock and soil division as the boundary; the front edge is against the Yangtze River, and the east and west sides of the bedrock ridge also act as boundaries. The overall slope is about 30°. Its north-south length is 600 m, and its east-west width is 700 m. The average thickness of the slide is about 30 m, and the volume is 1260 × 104 m³. It is an accumulation-layer landslide, and the slope body is a downward slope.

Since June 2003, many monitoring points have been arranged to professionally monitor the Baishui River landslide. Since site ZG118 has more complete monitoring data, this point is used in this paper to verify the validity of the proposed model. The cumulative displacement, reservoir level and rainfall data observed at this monitoring site from January 2007 to December 2012 are shown in Figure 4. The cumulative displacement moves faster at the beginning of the rainy season from May to September each year and after the reservoir level drops from June to July each year; the rapid movement period ends before the end of the rainy season. It can be seen that the changes in the reservoir water level and rainfall have a very strong influence on the changes in the landslide cumulative displacement, indicating that the rainfall and reservoir water level are the main factors that control landslide deformation and damage in the Baishui River.

3.2. Research Methodology

3.2.1. Cumulative Displacement Decomposition

The cumulative landslide displacement is divided into a trend term and a periodic term using the double exponential smoothing method described in Section 2.1. After several experiments, it was found that the decay degree index $a=0.4$ can be decomposed to obtain better trend and periodic displacements. The trend displacement can be expressed as follows:

$$t_1=c_1,$$

(18)

$$t_i=0.4c_{i-1}+0.6t_{i-1},$$

(19)

$$t_{i+1}=0.4c_i+0.24c_{i-1}+0.36t_{i-1}.$$

(20)

In this paper, the DES algorithm is used to decompose the landslide cumulative displacement into a trend term and a periodic term; then, the periodic displacement is calculated according to Equation (4). The decomposition results of the time series are shown in Figure 5. It can be seen that the trend term can better reflect the trend of the landslide cumulative displacement, while the random fluctuation of the periodic term is larger; this is the focus of landslide displacement prediction research.

3.2.2. Periodic Displacement Model Prediction

The monitoring data for the reservoir level, rainfall, and displacement from December 2006 to December 2012 at the monitoring point ZG118 for the Baishui River landslide were selected as the dataset for periodic term displacement prediction. The rainfall and displacement values are the cumulative values of each month, and the water level value is the average value of each month. The data from January 2007 to December 2011 were used as the training data set, and the data from January 2012 to December 2012 were used as the validation data set to test the prediction accuracy of the model. Additionally, in order to verify the prediction accuracy of the model, the root mean square error (RMSE), mean absolute error (MAE), and mean absolute relative error (MAPE) were selected to evaluate the prediction effectiveness of the model.

To improve the prediction accuracy of the model, the periodic displacement influencing factors mentioned in the literature [26] were selected as the model input. They include the maximum rainfall of the current month, cumulative rainfall of the current month, cumulative rainfall over two months, reservoir level of the current month, change in the reservoir level in the current month, change in the reservoir level over two months, change in the cumulative displacement in the current month, change in the cumulative displacement over two months and change in the cumulative displacement over three months. Due to the different data types, all monitoring data were normalised to [0, 1] in order to eliminate the influence of the magnitudes of different types of data:

$$y=\frac{(x_i-x_{i\min })}{(x_{i\max }-x_{i\min })},$$

(21)

where $x_{i\mathrm{m}\mathrm{a}\mathrm{x}}$ is the maximum value of variable $i$, $x_{i\mathrm{m}\mathrm{i}\mathrm{n}}$ is the minimum value of variable $i$, $x_i$ is the original value and $y$ is the normalised value.

After normalising the data to be input into the CG-SSA-BP model, the SSA-BP model and BP model were also trained on the same data set to verify the proposed model’s effectiveness, and the actual and predicted values were analysed and compared.

In the BP neural network, the number of neurons in the input layer is 9; the number of neurons in the hidden layer was set to 9 after 100 experiments. The output layer provides the predicted value of the actual landslide displacement after 100 iterations with a learning rate of 0.01.

The parameters of the SSA-BP neural network prediction model and CG-SSA-BP neural network prediction model had the following values: the sparrow population size was 10, the maximum number of iterations was 100, discoverers made up 20% of the population and the maximum safety threshold was 0.8.

Based on the parameters of each model, the prediction results of the periodic displacement of the CG-SSA-BP model are given in Figure 6. From the figure, it can be seen that the prediction trend of the CG-SSA-BP model is closest to the actual values; it provides better prediction results than the other two models.

3.2.3. Cumulative Displacement Prediction

The trend displacement and the periodic displacement are added to obtain the final landslide cumulative displacement. The prediction results are shown in Figure 7. It can be seen that the predicted curve follows the real curve and is very close to the real values, which indicates that the prediction method proposed in this paper is effective. The root mean square error (RMSE), mean absolute error (MAE) and mean absolute percentage error (MAPE) for the three models are given in

Table 1. Comparison of cumulative-level prediction accuracy of three models.

Model	RMSE	MAE	MAPE
CG-SSA-BP	5.604	3.947	0.0017
SSA-BP	6.583	4.681	0.0020
BP	7.744	6.632	0.0029

. It is worth noting that the models with lower RMSE, MAE and MAPE values have a better predictive performance. The RMSE, MAE and MAPE of the CG-SSA-BP model were 5.604 mm, 3.947 mm and 0.17%, respectively; the MAPE was reduced by 13% and 20%, and the RMSE was reduced by 1 mm and 2 mm, respectively, compared with the SSA-BP and BP models. The three indicators are lower for the CG-SSA-BP model than for the SSA-BP and BP models. This shows that the stability of the CG-SSA-BP model proposed in this paper is better, and it has a higher accuracy when it comes to the displacement prediction of mounded landslides.

The cumulative displacement prediction results of the three models shown in Figure 7 are given in

Table 2. Prediction results of CG-SSA-BP model (mm).

Date	True Value	Predicted Value	Error
01-2012	2209.6	2204.3	−5.28
02-2012	2201.8	2201.6	−0.21
03-2012	2211.6	2206.4	−5.24
04-2012	2215.8	2214.1	−1.68
05-2012	2207.7	2210.6	2.95
06-2012	2245.1	2238.2	−6.9
07-2012	2303.9	2301.9	−1.98
08-2012	2314.1	2328.5	14.41
09-2012	2331.7	2332.7	1
10-2012	2332.8	2332.6	−0.19
11-2012	2325.6	2325.1	−0.51
12-2012	2328.4	2321.4	−7.03

,

Table 3. Prediction results of SSA-BP model (mm).

Date	True Value	Predicted Value	Error
01-2012	2209.6	2213.45	3.85
02-2012	2201.8	2206.48	4.68
03-2012	2211.6	2213.36	1.76
04-2012	2215.8	2216.67	0.87
05-2012	2207.7	2211.62	3.92
06-2012	2245.1	2245.28	0.18
07-2012	2303.9	2300.89	−3.01
08-2012	2314.1	2329.67	15.57
09-2012	2331.7	2329.18	−2.52
10-2012	2332.8	2335.58	2.78
11-2012	2325.6	2339.28	13.68
12-2012	2328.4	2331.75	3.35

and

Table 4. Prediction results of BP model (mm).

Date	True Value	Predicted Value	Error
01-2012	2209.6	2217.29	7.69
02-2012	2201.8	2208.69	6.89
03-2012	2211.6	2214.52	2.92
04-2012	2215.8	2212.01	−3.79
05-2012	2207.7	2204.61	−3.09
06-2012	2245.1	2238.27	−6.83
07-2012	2303.9	2313.15	9.25
08-2012	2314.1	2323.32	9.22
09-2012	2331.7	2344.92	13.22
10-2012	2332.8	2319.33	−13.47
11-2012	2325.6	2324.97	−0.63
12-2012	2328.4	2330.99	2.59

. From the prediction results, it can also be seen that the chaotic tent mapping and Gaussian variational sparrow search algorithm-optimised BP neural network, sparrow search algorithm-optimised BP neural network and traditional BP neural network can effectively predict landslide displacement deformation, while the predicted values of the CG-SSA-BP model proposed in this paper are closer to the real landslide displacement values.

4. Conclusions

This article proposed a landslide displacement prediction method based on chaos Gaussian mutation sparrow search algorithm (CG-SSA) to address the low prediction accuracy of traditional BP neural network models, while the original sparrow search algorithm (SSA) reduces population diversity, converges slowly, and is prone to falling into local optima when approaching global optima, and it has been successfully applied to the high-precision prediction of displacement and deformation of the Baishui River landslide, a typical accumulation layer landslide in the Three Gorges Reservoir Area of China, and has achieved good results. It can be used as a reference model for similar landslide monitoring and warning.

Meanwhile, based on the research of this paper, the landslide displacement prediction model based on chaotic Gaussian mutation sparrow search algorithm (CG-SSA) optimised BP neural network has the following advantages and main conclusions compared with the traditional BP prediction model:

• In terms of decomposition methods, the traditional moving average method has been abandoned and a more suitable trend-based time series prediction method, the double exponential smoothing method (DES), has been adopted. Through this method, the landslide displacement is decomposed into trend and periodic terms, solving the nonlinear problem of the landslide system.
• The Chaotic Gaussian mutation sparrow search algorithm (CG-SSA) improves the quality of initial solutions and enhances the global search ability of the algorithm by improving the population initialisation of the Tent chaotic sequence. Second, the Gaussian mutation method is introduced to enhance local search ability and improve search accuracy. At the same time, based on the search for stagnant solutions, a Tent chaotic sequence is generated. This chaotic sequence is used to perturb some individuals trapped in local optima, prompting the algorithm to continue searching beyond the limit, thereby optimizing the structure of the BP neural network and significantly improving the network prediction performance.
• From the RMSE, MAE and MAPE indicators of the three models, it can be seen that CGSSA-BP and SSA-BP models have higher prediction accuracy than the BP neural network before the improvement. In particular, the CGSSA-BP model has the best displacement prediction performance, which is closest to the real displacement value, has good applicability and robustness and is more suitable for high-precision prediction of long-term displacement of landslides.

In this paper, a Tent chaotic mapping and Gaussian mutation sparrow search algorithm optimised BP neural network prediction model mainly for landslide time-series monitoring displacement is constructed, but the factors affecting landslide high-precision prediction in practice are extremely complicated. With the continuous development of deep learning algorithm research, a comprehensive high-precision prediction model of landslide disaster combining landslide multi-source monitoring data, advanced deep learning algorithm, multiple environmental influencing factors outside the landslide and the geological conditions of the landslide itself will be the next key research direction of this paper.