Control for a Class of Unstable High-Order Systems with Time Delay Based on Observer–Predictor Approach
Abstract
:1. Introduction
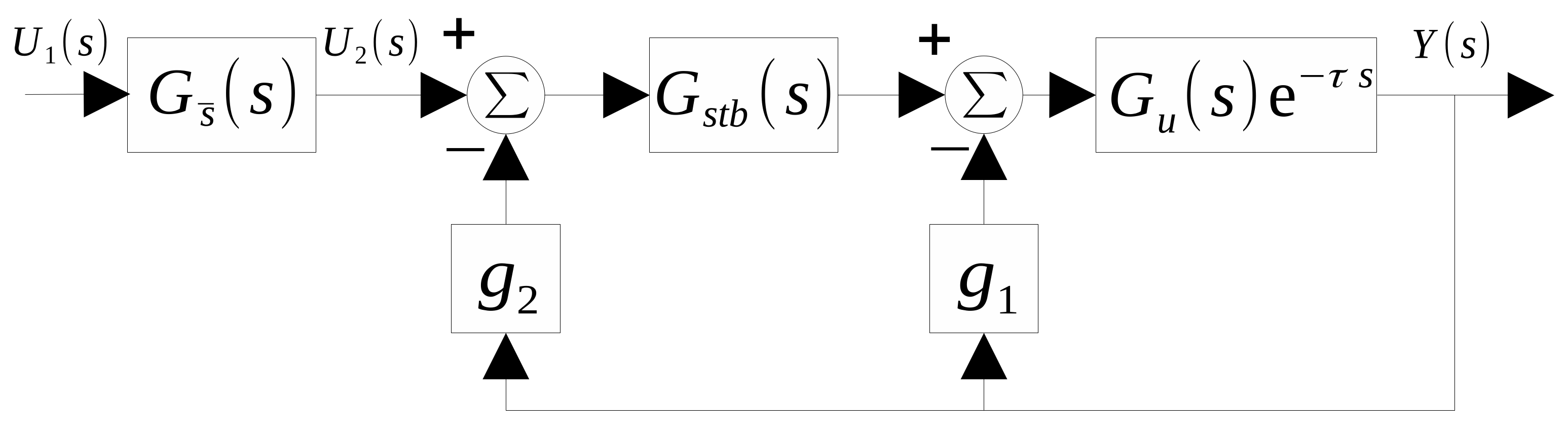
2. The Class of Systems
3. Preliminary Results
4. Main Results
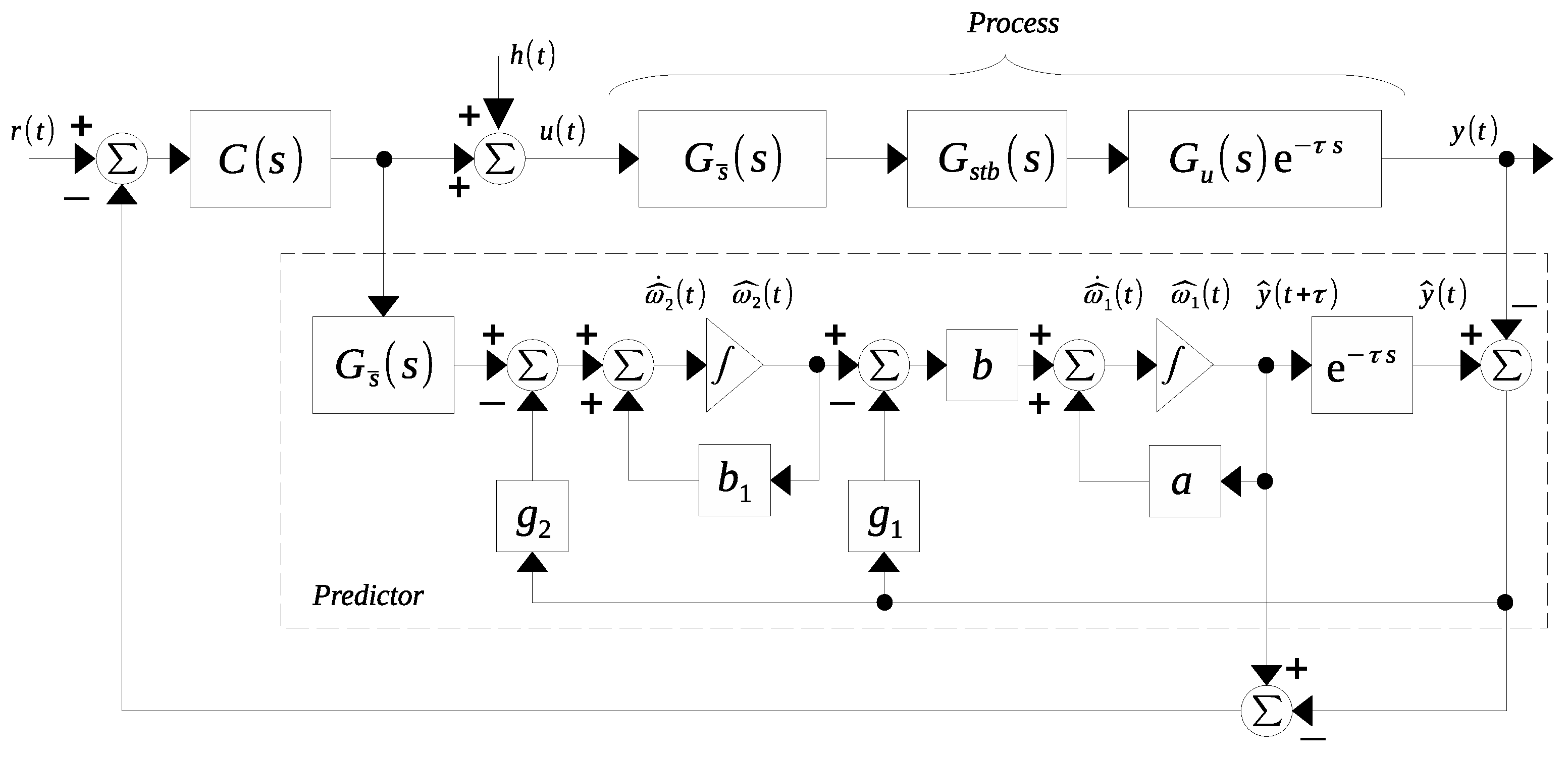
4.1. Estimation Strategy
- (i)
- unstable delayed second order ().
- (ii)
- unstable delayed higher order ( with ).
4.2. Controller Design
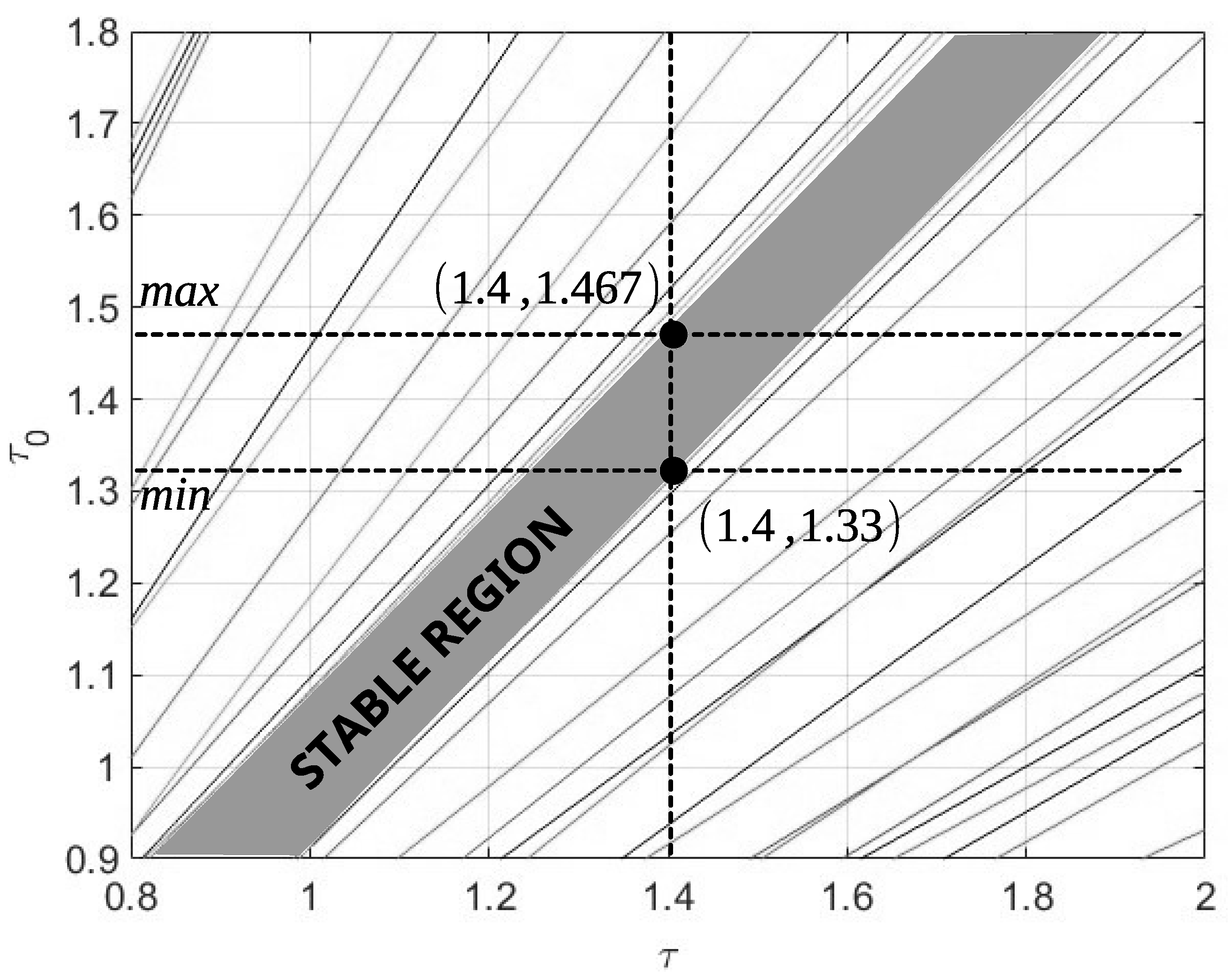
4.3. Improved Stability Conditions
5. Disturbance Rejection and Tracking Reference
5.1. Tracking Reference
5.2. Disturbance Rejection
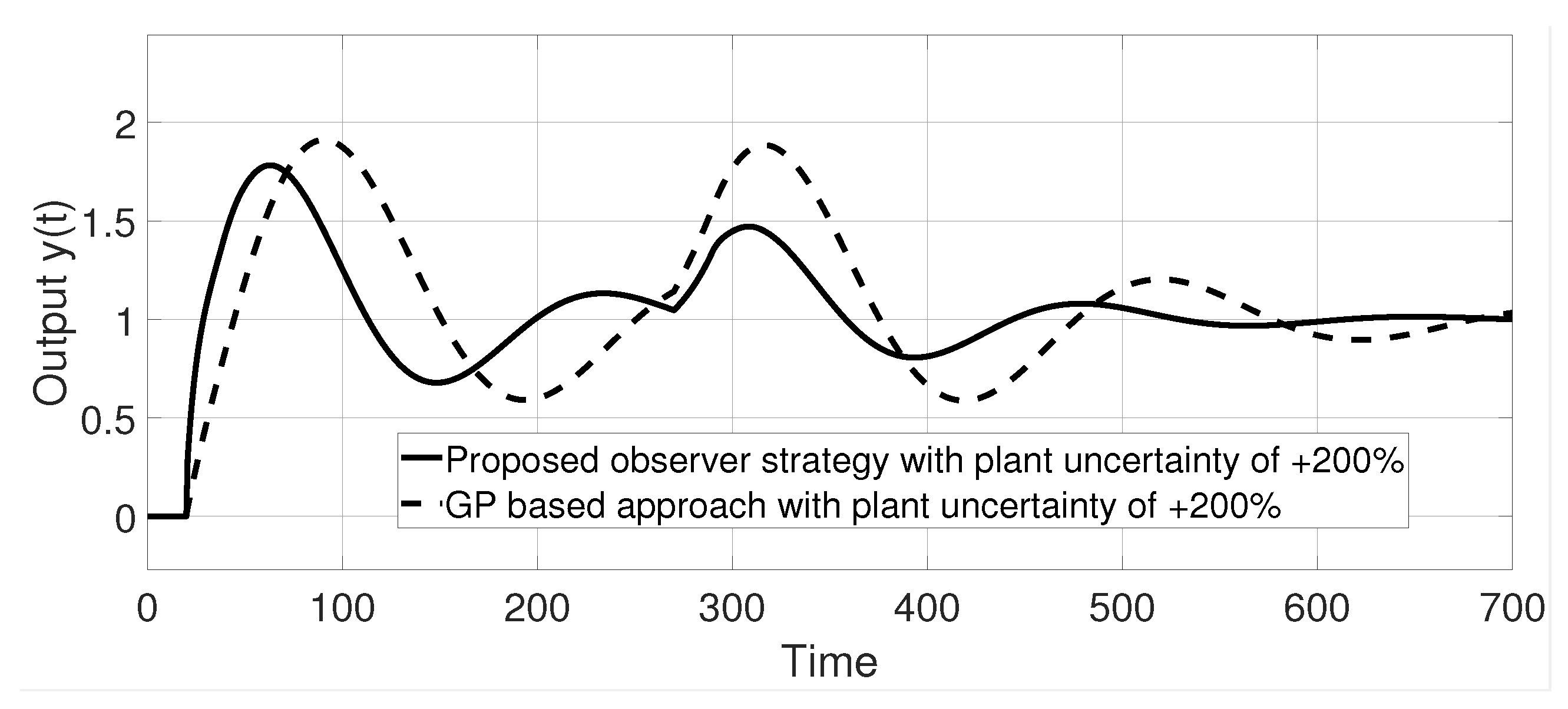
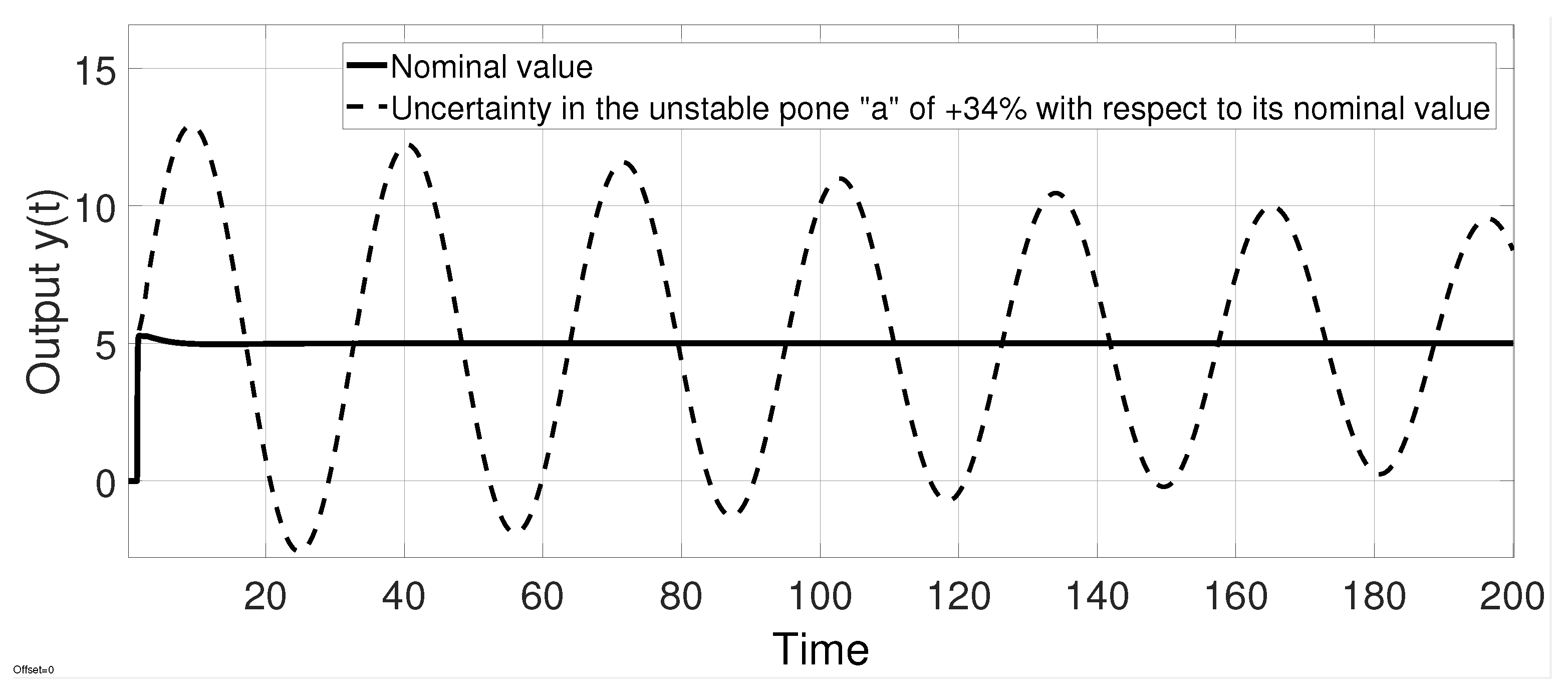
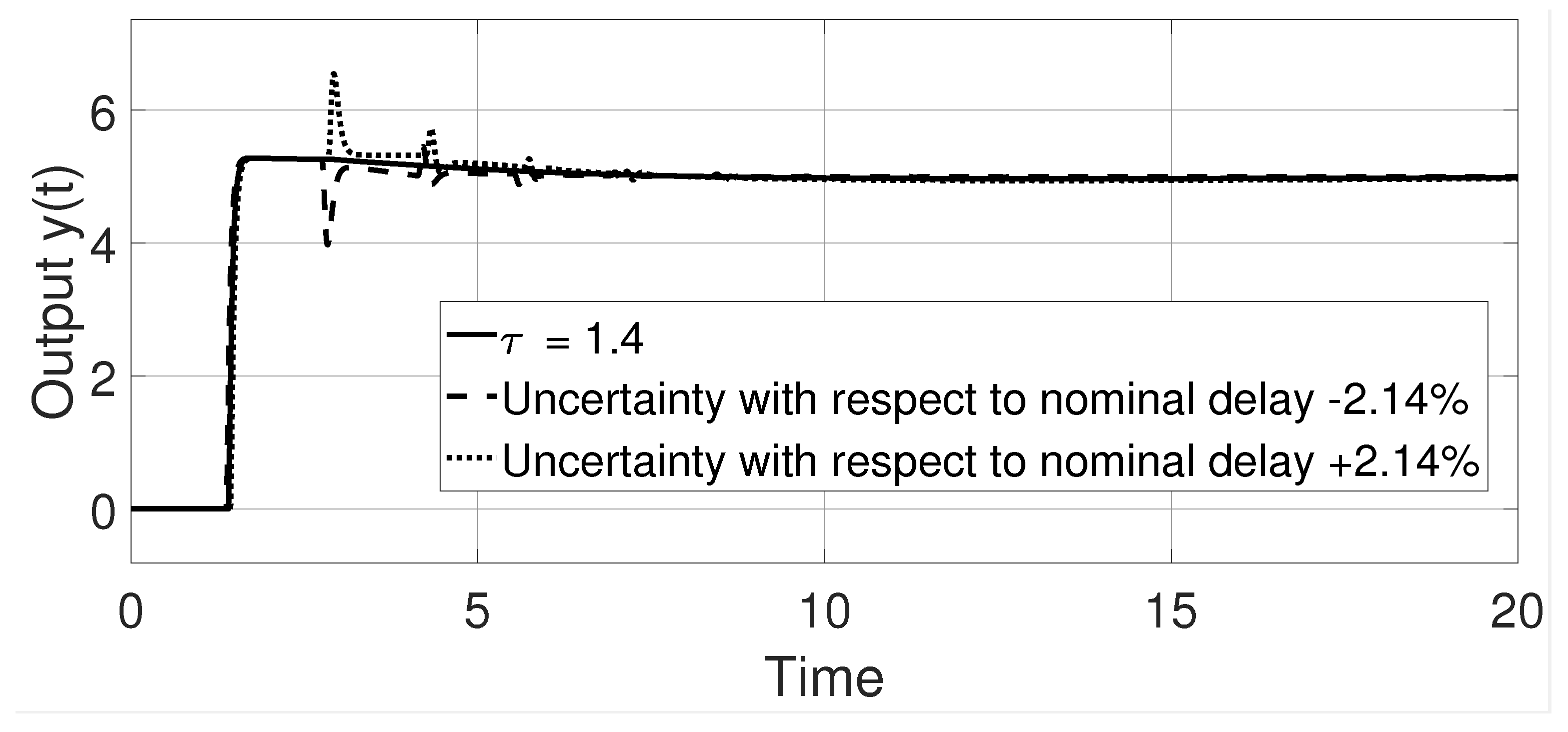
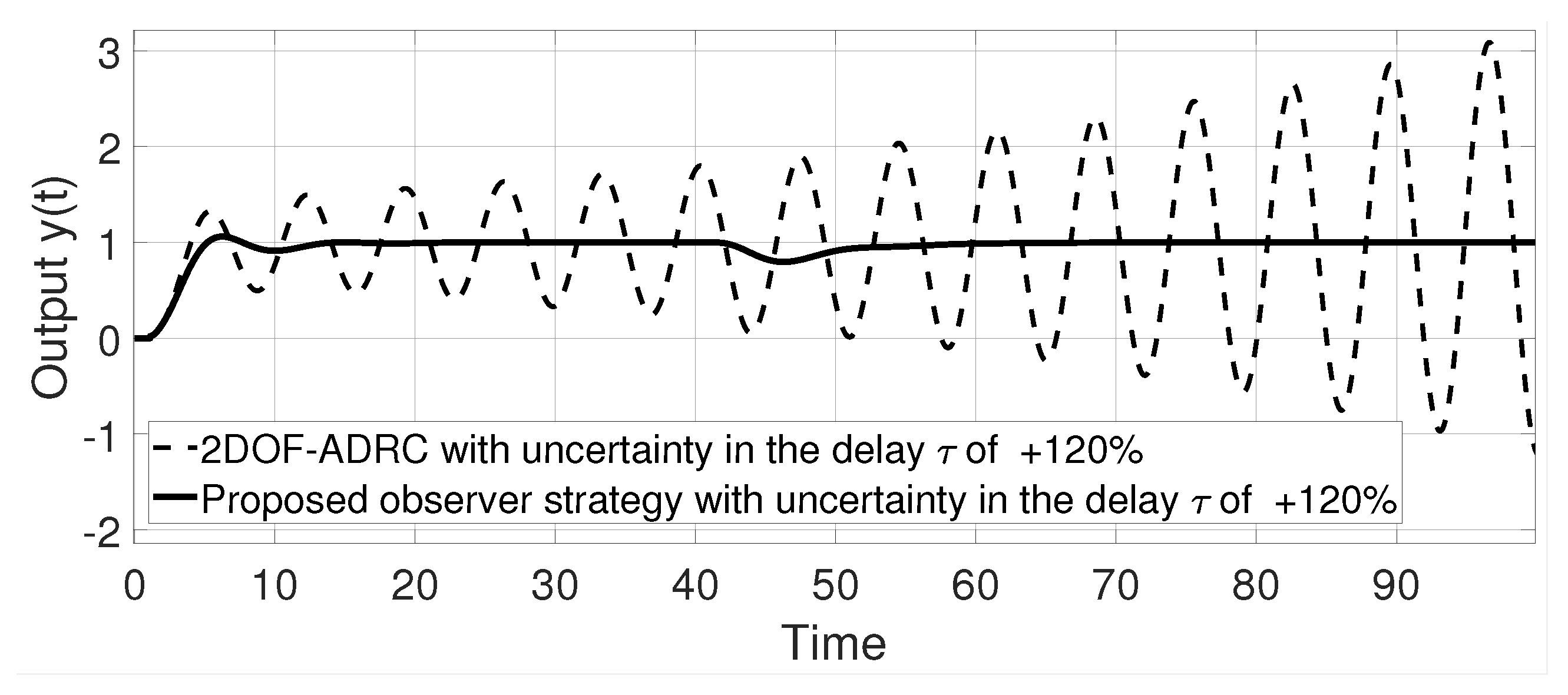
6. Robustness with Respect to Uncertainty in the Time Delay
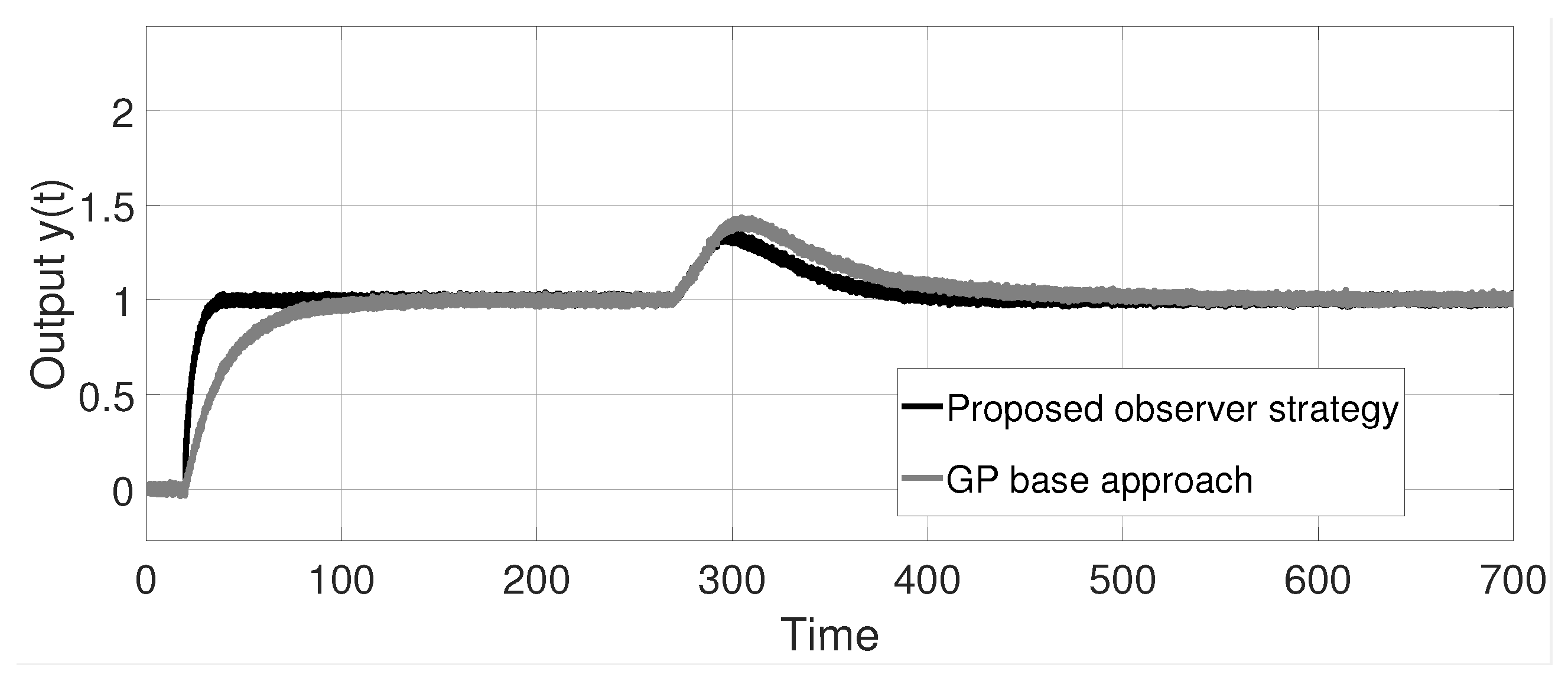
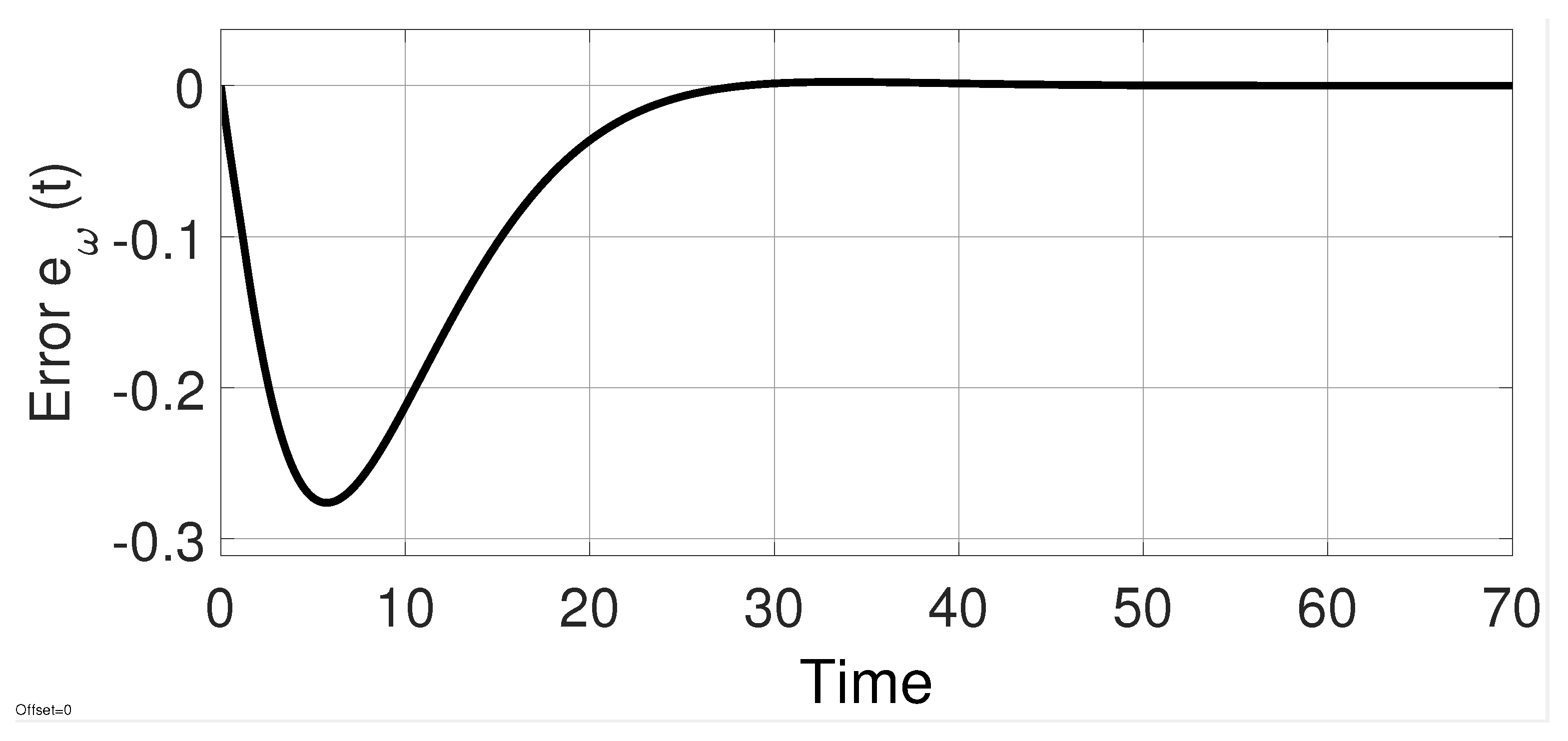
7. Simulation Results
7.1. Example 1
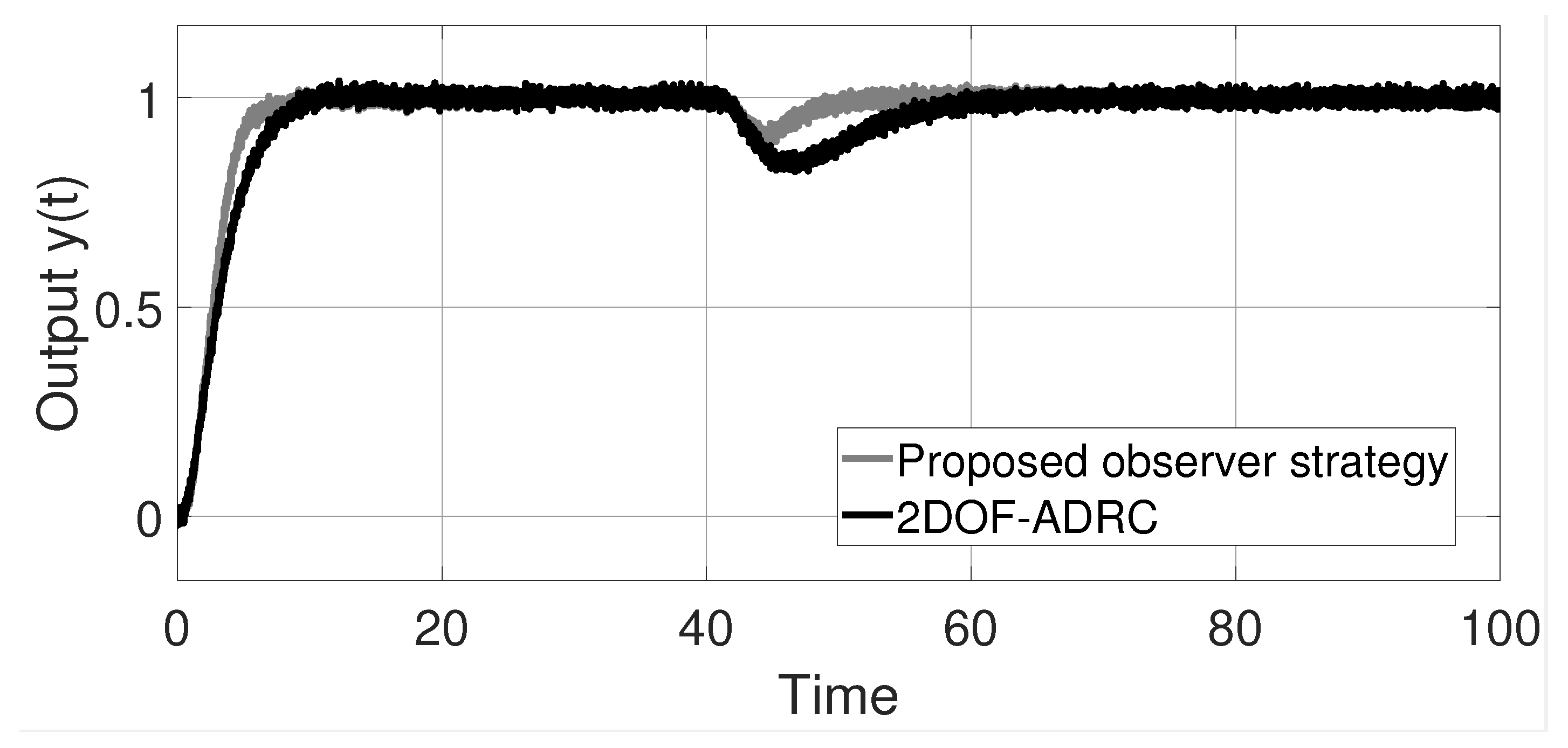
7.2. Example 2
7.3. Example 3
7.4. Practical Contributions
- When theoretical results (such as those provided in the present manuscript) are taken in order to implement real-practical experiments, it is very important to know quickly if the theoretical proposed control strategy can be used for solving the stability problem or not. In this way, providing necessary and sufficient conditions for the existence of the stabilizing control strategy allows one to obtain this information immediately by making simple computations of the stated conditions. This facilitates the task of the control design for the engineers, in contrast with control strategies that are developed under heuristic methods or just present necessary or sufficient conditions.
- In general, the time-delays phenomenon due to measurement of variables, material transportation, or teleoperation complicates the design of control strategies, however in the particular case when the size of time-delay is greater than the dominant dynamic of the system, the control design has an additional degree of complexity. This is because, under this situation, the time delay has greater adverse effects than the behavior of the controlled system when the delay time is small. As an example of this problem, there are many proposed control strategies [11,24] that are well performed for a “small” time delay, but these control strategies cannot be used for controlling systems with large delay terms. This problem is illustrated and partially solved in the new version of the work; see Example 3 (Figure 15). Therefore, in this work, it is possible to control systems with greater delay size with respect to previously reported works ([11,24]). For example, in [17], the maximum size of the delay is for a second order delayed system, in the present work, this bound is , i.e., the double of the previous delay size. This practical advantage allows the controlling of a greater variety of systems, ensuring closed-loop stability.
- In practice, a control strategy that provides stability with respect to the uncertainties of the model is desired. These problems arise mainly from model mismatching. In this way, analytical robustness with respect to time delay is developed in Section 6. Additionally, the proposed control strategy has been evaluated via simulations on face-to-model mismatching of the process, obtaining positive results such as the preservation of closed-loop stability under the adverse mentioned condition.
- Many industrial solutions (such as chemical engineering applications) require the regulation problem, which consists in keeping a variable at a desired value even in the presence of disturbances. In this way, the capability of a control system for tracking desired step-references and disturbance rejection is essential for solving the regulation problem. Thus, the results provided in Section 5 are related to this issue and illustrated in numerical simulations.
- The control action and the output measurable variable performances are qualitative and quantitatively evaluated using a numerical simulation; the control action can be seen as the spent energy of the control stage to achieve the stabilization of the process, which is a very important issue from a practical viewpoint.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Lemma 4
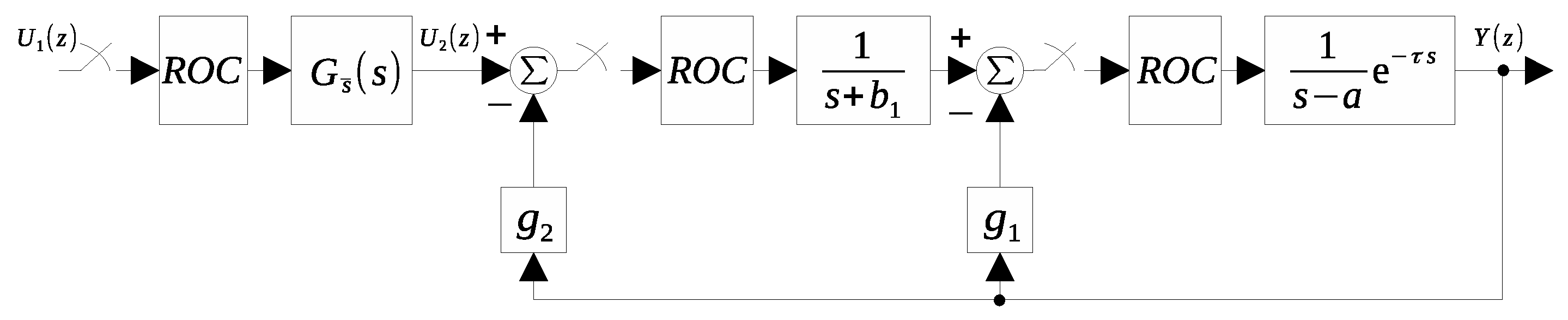

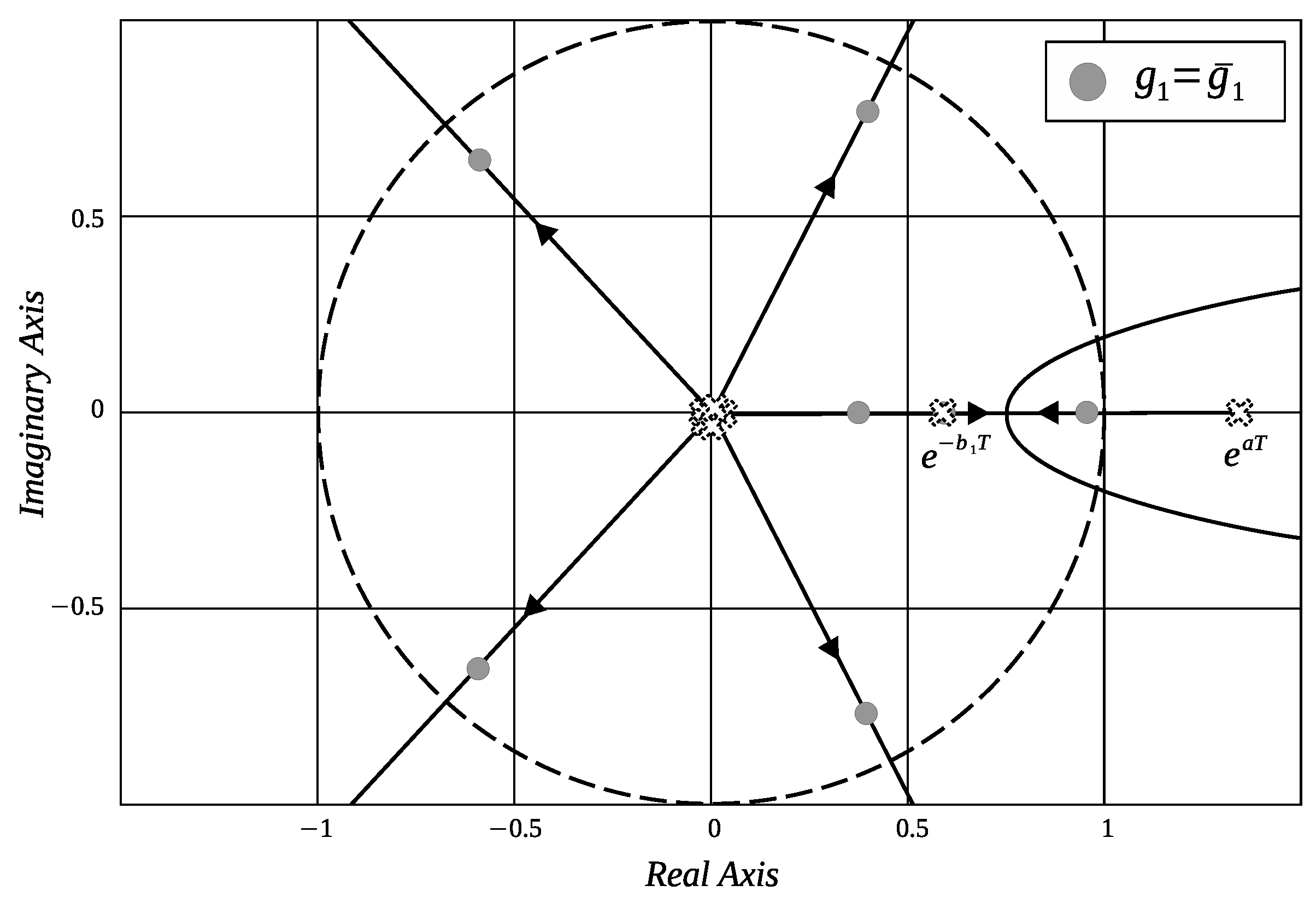
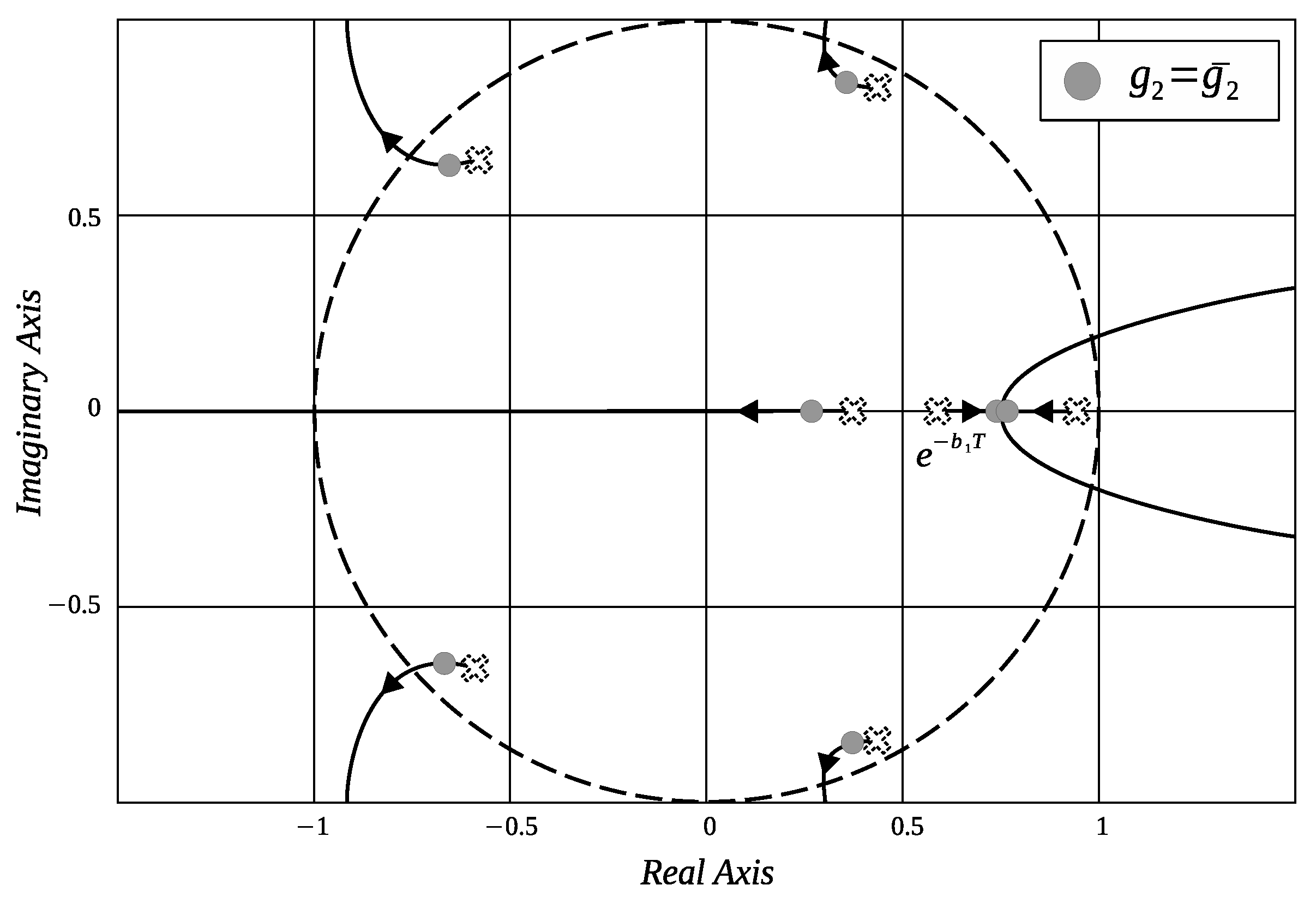
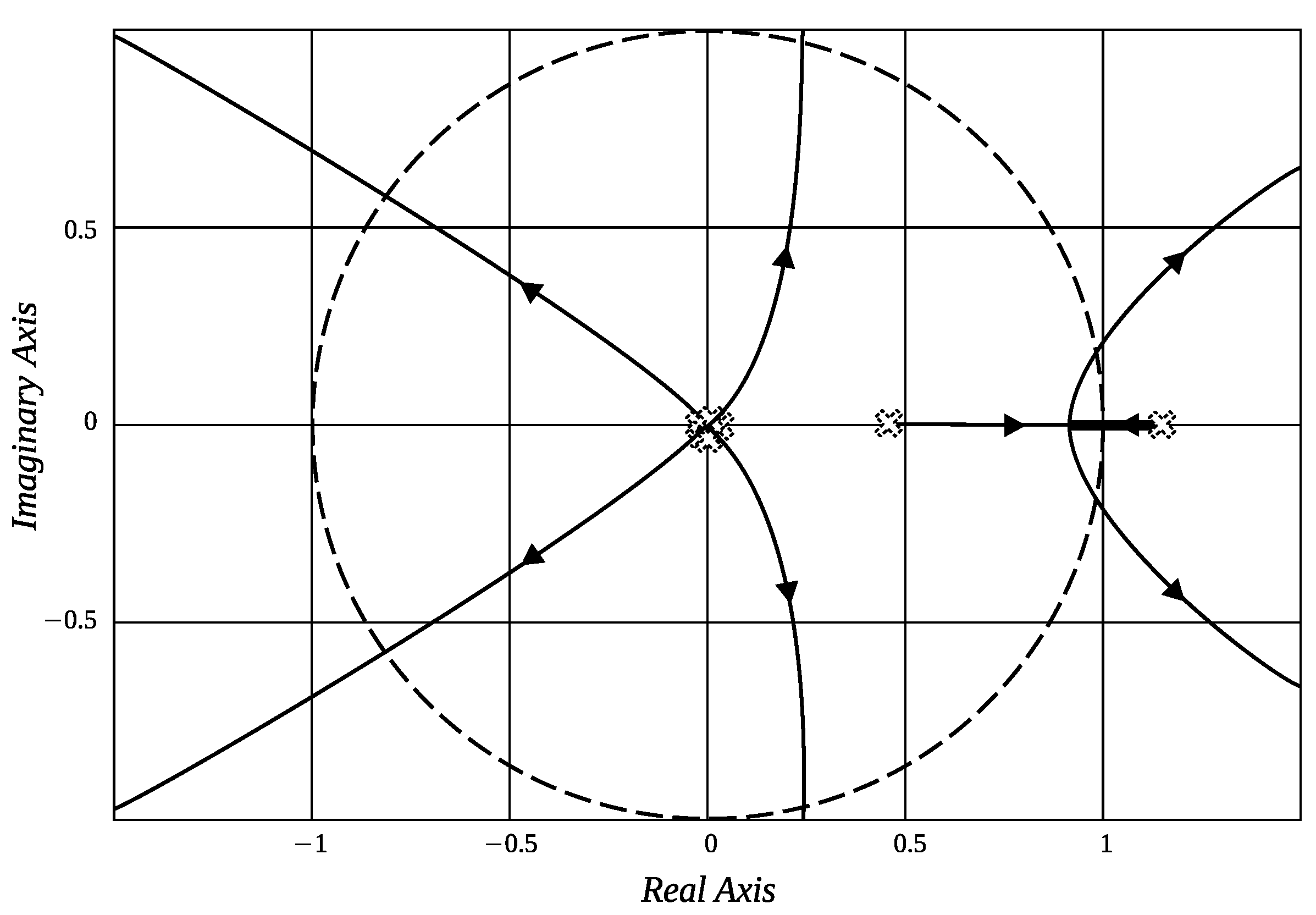
Appendix B. Proof of Corollary 1
References
- Liu, T.; Zhang, W.; Gu, D. Analytical design of two-degree-of-freedom control scheme for open-loop unstable processes with time delay. J. Process. Control 2005, 15, 559–572. [Google Scholar] [CrossRef]
- Hernández, R.R.L. Análisis del Método MFSP (Múltiple Frames into Single Packet) para Contrarrestar Los Retardos en Los Sistemas Satelitales en Transmisión de Voip. 2009. Available online: https://bibdigital.epn.edu.ec/handle/15000/1908 (accessed on 16 April 2023).
- Romero-Galván, G. Análisis de Estabilidad Robusta para Sistemas Dinámicos con Retardo; Universidad Autónoma de Nuevo León: San Nicolás de los Garza, Mexico, 1997. [Google Scholar]
- Niculescu, S.I. Delay Effect on Stability: A Robust Control Approach; Springer: Cham, Switzerland, 2001. [Google Scholar]
- Delgado, D.C.; Rivera, J.L. Performance Study of Distributed Power Control Algorithms under Time-Delays and Measurement Uncertainty. IEEE Lat. Am. Trans. 2013, 11, 690–697. [Google Scholar] [CrossRef]
- Ailon, A.; Gil, M.I. Stability analysis of a rigid robot with output-based controller and time delay. Syst. Control Lett. 2000, 40, 31–35. [Google Scholar] [CrossRef]
- Gouaisbaut, F.; Peaucelle, D. Stability of Time-Delay Systems with Non-Small Delay. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006. [Google Scholar]
- Lizárraga Lizárraga, M.A. Approximation of Systems with Delay. Master’s Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, Baja, CA, USA, 2018; p. 68. [Google Scholar]
- Marquez-Rubio, J.F.; Pimentel-Medina, V.M.; Del Muro-Cuéllar, B.; Novella-Rodrıguez, D. Obtención de los parámetros de un observador de estados propuesto para sistemas con retardo. In Proceedings of the Congreso Nacional de Control Automático (AMCA), Puebla, Mexico, 23–25 October 2019. [Google Scholar]
- Silvia, G.J.; Bhattacharyya, S.P. PID Controller for Time-Delay Systems; Birkhuser: Boston, MA, USA, 2005. [Google Scholar]
- Lee, S.C.; Wang, Q.-G.; Xiang, C. Stabilization of all-pole unstable delay processes by simple controllers. J. Process. Control 2010, 20, 235–239. [Google Scholar] [CrossRef]
- So, G.-B. Design of Linear PID Controller for Pure Integrating Systems with Time Delay Using Direct Synthesis Method. Processes 2022, 10, 831. [Google Scholar] [CrossRef]
- Wu, Z.; Li, D.; Xue, Y. A New PID Controller Design with Constraints on Relative Delay Margin for First-Order Plus Dead-Time Systems. Processes 2019, 7, 713. [Google Scholar] [CrossRef]
- del-Muro-Cuéllar, B.; Márquez-Rubio, J.F.; Velasco-Villa, M.; de Jesús Álvarez-Ramírez, J. On the control of unstable first order linear systems with large time lag: Observer based approach. Eur. J. Control 2012, 18, 439–451. [Google Scholar] [CrossRef]
- Barragan-Bonilla, L.A.; Márquez-Rubio, J.F.; Del Muro Cuéllar, B.; Vázquez-Guerra, R.J.; Martínez, C. Observer-based control for high order delayed systems with an unstable pole and a pole at the origin. Asian J. Control 2023, 25, 1759–1774. [Google Scholar] [CrossRef]
- Smith, J.M. Close Control of Loops with Dead Time. Chem. Eng. Prog. 1957, 53, 217–219. [Google Scholar]
- Normey-Rico, J.E.; Camacho, E.F. Simple Robust Dead-Time Compensator for First-Order plus Dead-Time Unstable Processes. Ind. Eng. Chem. Res. 2008, 47, 4784–4790. [Google Scholar] [CrossRef]
- Rao, A.S.; Chidambaram, M. Enhanced Smith Predictor for Unstable Processes with Time Delay. Ind. Eng. Chem. Res. 2005, 44, 8291–8299. [Google Scholar] [CrossRef]
- Fu, C.; Tan, W. Control of unstable processes with time delays via ADRC. ISA Trans. 2017, 71, 530–541. [Google Scholar] [CrossRef]
- Xie, L.; Shieh, L.-S.; Tsai, J.; Guo, S.-M.; Dunn, A. Digital Redesign of Analog Smith Predictor for Systems with Long Input Time Delays. J. Frankl. Inst. 2017, 354, 5797–5812. [Google Scholar] [CrossRef]
- İçmez, Y.; Can, M.S. Smith Predictor Controller Design Using the Direct Synthesis Method for Unstable Second-Order and Time-Delay Systems. Processes 2023, 11, 941. [Google Scholar] [CrossRef]
- Albertos, P.; García, P. Robust control design for long time-delay systems. J. Process Control 2009, 19, 1640–1648. [Google Scholar] [CrossRef]
- Rico, N.; Elias, J.; Fernández Camacho, E. Unified approach for robust dead-time compensator design. J. Process. Control 2009, 19, 38–47. [Google Scholar] [CrossRef]
- Cruz-Díaz, C.; del-Muro-Cuéllar, B.; Duchén-Sánchez, G.; Márquez-Rubio, J.; Velasco-Villa, M. Observer-Based PID Control Strategy for the Stabilization of Delayed High Order Systems with up to Three Unstable Poles. Mathematics 2022, 10, 1399. [Google Scholar] [CrossRef]
- Wang, Q.-G.; Cheng, X.; Lu, X. Stabilization of second-order unstable delay processes by pid controllers. IFAC Proc. Vol. 2006, 39, 19–24. [Google Scholar] [CrossRef]
- Seer, Q.H.; Nandong, J. Stabilization and PID tuning algorithms for second-order unstable processes with time-delays. ISA Trans. 2017, 67, 233–245. [Google Scholar] [CrossRef]
- Xiang, C.; Wang, Q.; Lu, X.F.; Nguyen, L.; Lee, T.R. Stabilization of second-order unstable delay processes by simple controllers. J. Process. Control 2007, 17, 675–682. [Google Scholar] [CrossRef]
- Márquez-Rubio, J.; del-Muro-Cuéllar, B.; Villa, M.; Ramírez, J. An improved sufficient condition for stabilisation of unstable first-order processes by observer-state feedback. Int. J. Control 2015, 88, 403–412. [Google Scholar] [CrossRef]
- Sanz, R.; García, P.; Albertos, P. A generalized smith predictor for unstable time-delay SISO systems. ISA Trans. 2017, 72, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Gu, K.; Niculescu, S.; Chen, J. On stability crossing curves for general systems with two delays. J. Math. Anal. Appl. 2005, 311, 231–253. [Google Scholar] [CrossRef]
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design, and Tuning; ISA—The Instrumentation, Systems and Automation Society: Pittsburgh, PA, USA, 1995. [Google Scholar]






| Nominal Case | Robust Análisis (+200% Plant Uncertainties) | |||||||
|---|---|---|---|---|---|---|---|---|
| System | . | |||||||
| Control Action | ||||||||
| Tuning methods | ISE | ITSE | IAE | ITAE | ISE | ITSE | IAE | ITAE |
| Proposed strategy | 217 | 1.087 × | 408.1 | 1.584 × | 3067 | 4.156 × | 874.1 | 3.13 × |
| GP-based approach | 265.5 | 1.116 × | 394 | 1.6 × | 1279 | 4.515 × | 874.8 | 3.17 × |
| Output | ||||||||
| Tuning methods | ISE | ITSE | IAE | ITAE | ISE | ITSE | IAE | ITAE |
| Proposed strategy | 717. 7 | 2.585 × | 695.7 | 2.51 × | 814.9 | 2.65 × | 726.1 | 2.51 × |
| GP based approach | 725. 5 | 2.69 × | 693. 7 | 2.56 × | 918.7 | 2.90 × | 744.2 | 2.56 × |
| Nominal Case | Robust Análisis (Uncertainty in the Delay of +100%) | |||||||
|---|---|---|---|---|---|---|---|---|
| System | ||||||||
| Control Action | ||||||||
| Tuning methods | ISE | ITSE | IAE | ITAE | ISE | ITSE | IAE | ITAE |
| Proposed strategy | 255.1 | 1800 | 68.95 | 2818 | 262.4 | 1835 | 72. 07 | 2824 |
| 2DOF-ADRC | 89.41 | 1866 | 73.97 | 2882 | 191. 8 | 3022 | 93. 55 | 3072 |
| Output | ||||||||
| Tuning methods | ISE | ITSE | IAE | ITAE | ISE | ITSE | IAE | ITAE |
| Proposed strategy | 92.46 | 4843 | 94.99 | 4916 | 92. 67 | 4840 | 94. 99 | 4914 |
| 2DOF-ADRC | 95.32 | 4951 | 96.61 | 4974 | 96. 25 | 4960 | 96. 6 | 4973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Márquez-Rubio, J.F.; Del Muro-Cuéllar, B.; Barragan-Bonilla, L.A.; Vazquez-Guerra, R.J.; Urquiza-Castro, A. Control for a Class of Unstable High-Order Systems with Time Delay Based on Observer–Predictor Approach. Processes 2023, 11, 1613. https://doi.org/10.3390/pr11061613
Márquez-Rubio JF, Del Muro-Cuéllar B, Barragan-Bonilla LA, Vazquez-Guerra RJ, Urquiza-Castro A. Control for a Class of Unstable High-Order Systems with Time Delay Based on Observer–Predictor Approach. Processes. 2023; 11(6):1613. https://doi.org/10.3390/pr11061613
Chicago/Turabian StyleMárquez-Rubio, Juan Francisco, Basilio Del Muro-Cuéllar, Luis Alberto Barragan-Bonilla, Rocio Jasmin Vazquez-Guerra, and Alejandro Urquiza-Castro. 2023. "Control for a Class of Unstable High-Order Systems with Time Delay Based on Observer–Predictor Approach" Processes 11, no. 6: 1613. https://doi.org/10.3390/pr11061613
APA StyleMárquez-Rubio, J. F., Del Muro-Cuéllar, B., Barragan-Bonilla, L. A., Vazquez-Guerra, R. J., & Urquiza-Castro, A. (2023). Control for a Class of Unstable High-Order Systems with Time Delay Based on Observer–Predictor Approach. Processes, 11(6), 1613. https://doi.org/10.3390/pr11061613






