Mixing Transport Mechanism of Three-Phase Particle Flow Based on CFD-DEM Coupling
Abstract
:1. Introduction
2. Mathematical Model and Solution Method
2.1. Flow Field Control Equations
2.2. Discrete Element Method
2.3. An Interphase Coupling Solution Method for Fluid and Particle
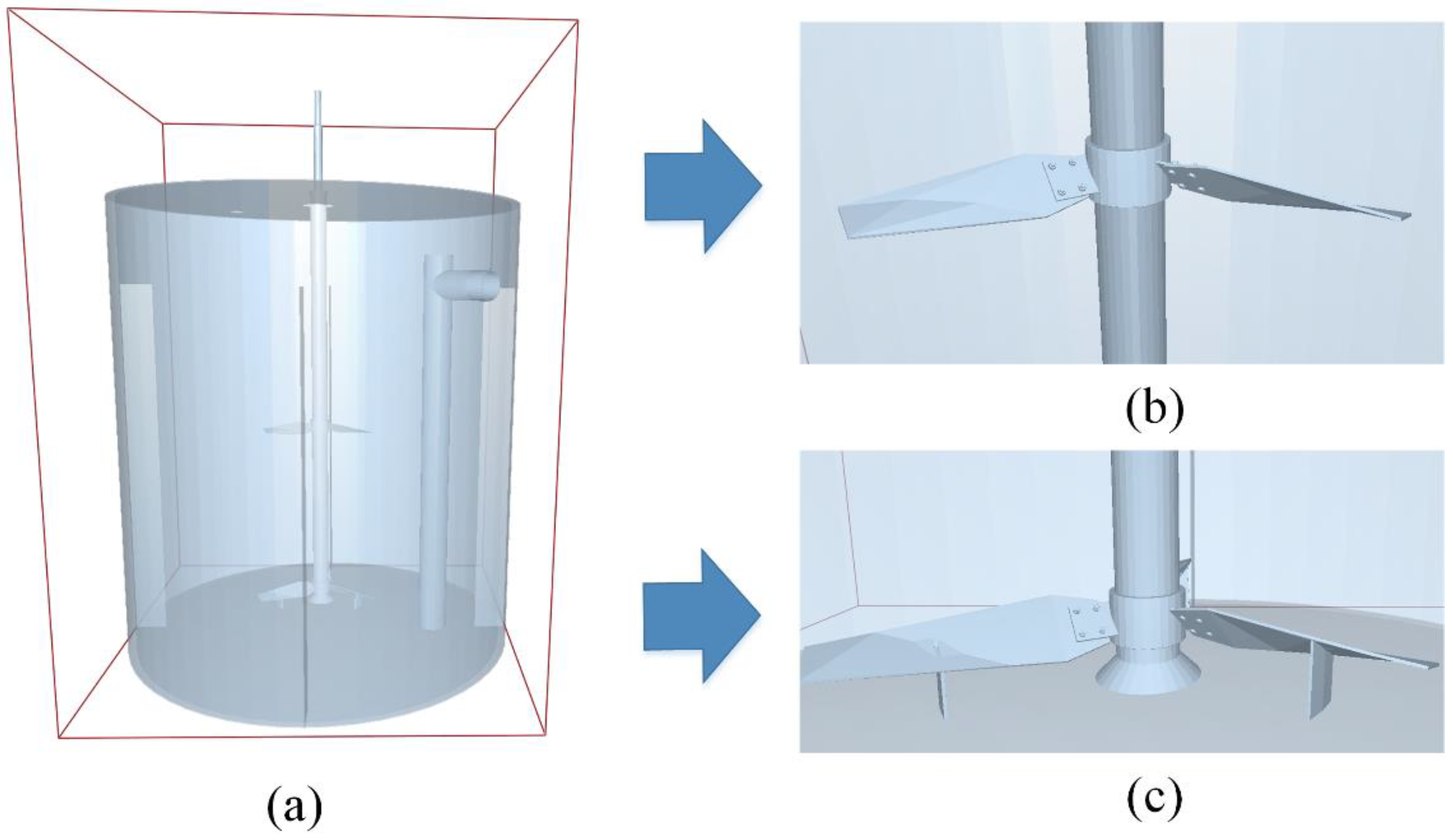
3. Model Implementation and Boundary Conditions
3.1. Physical and Numerical Models
3.2. Boundary Conditions and Initial Conditions
4. Numerical Results and Discussion
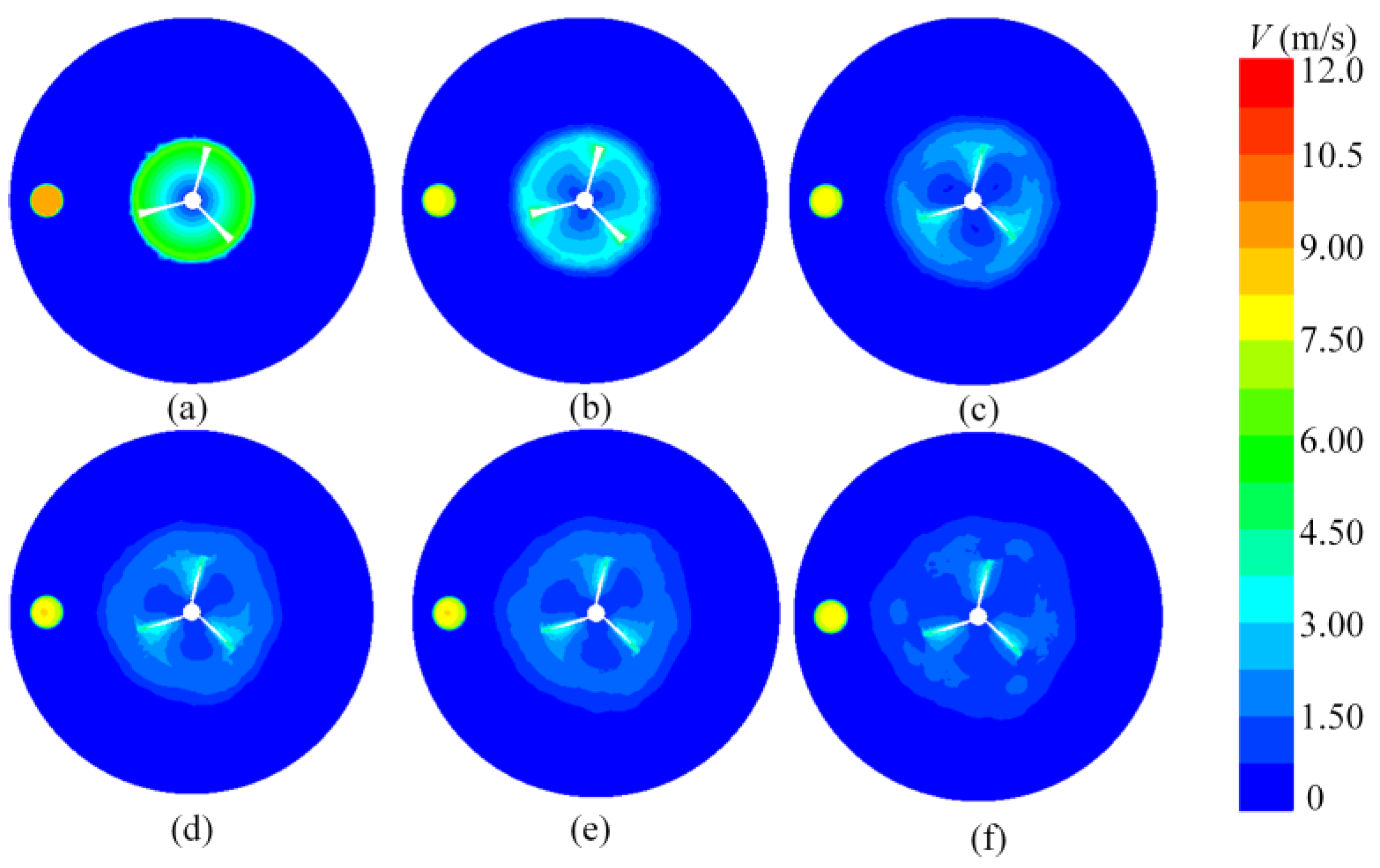
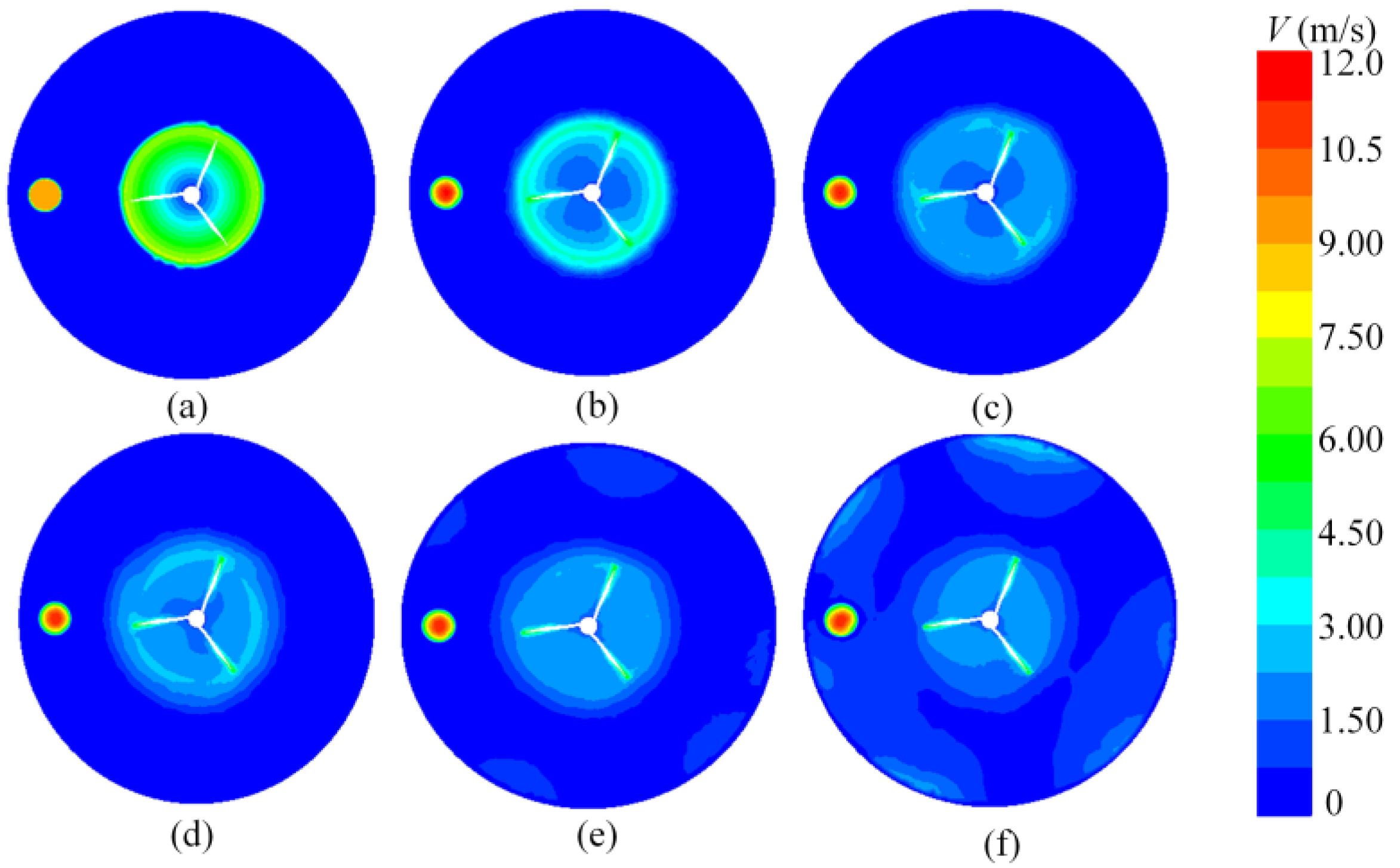
4.1. Gas–Liquid–Solid Three-Phase Flow Mixing Process
4.2. Bearing Power Calculation
4.3. Evolution Law of Particle Flows
5. Conclusions
- (1)
- A three-phase particle flow dynamic model is built based on the coupled CFD-DEM method. An interphase coupling solution method is utilized to solve the interaction effects of the fluid and particle. The particle flow mixing transfer mechanism is revealed via the evolution laws of relevant physical characteristics (such as velocity, pressure, particle vector, etc.);
- (2)
- The flow field near the blade has a high-velocity gradient change due to the influence of stirring speed, the stirring blade’s size, and structure. A low stirring speed area near the wall occurs and may lead to the deposition of particles. The effect of impeller rotation, the velocity disturbance in the bottom center area, increases. Under aeration, the flow velocity at the bottom diffuses around and forms a local upward flow trend near the wall surface. The speed inside the pipeline is also enormous, so the particle physics near the pipe mouth can quickly be sucked away;
- (3)
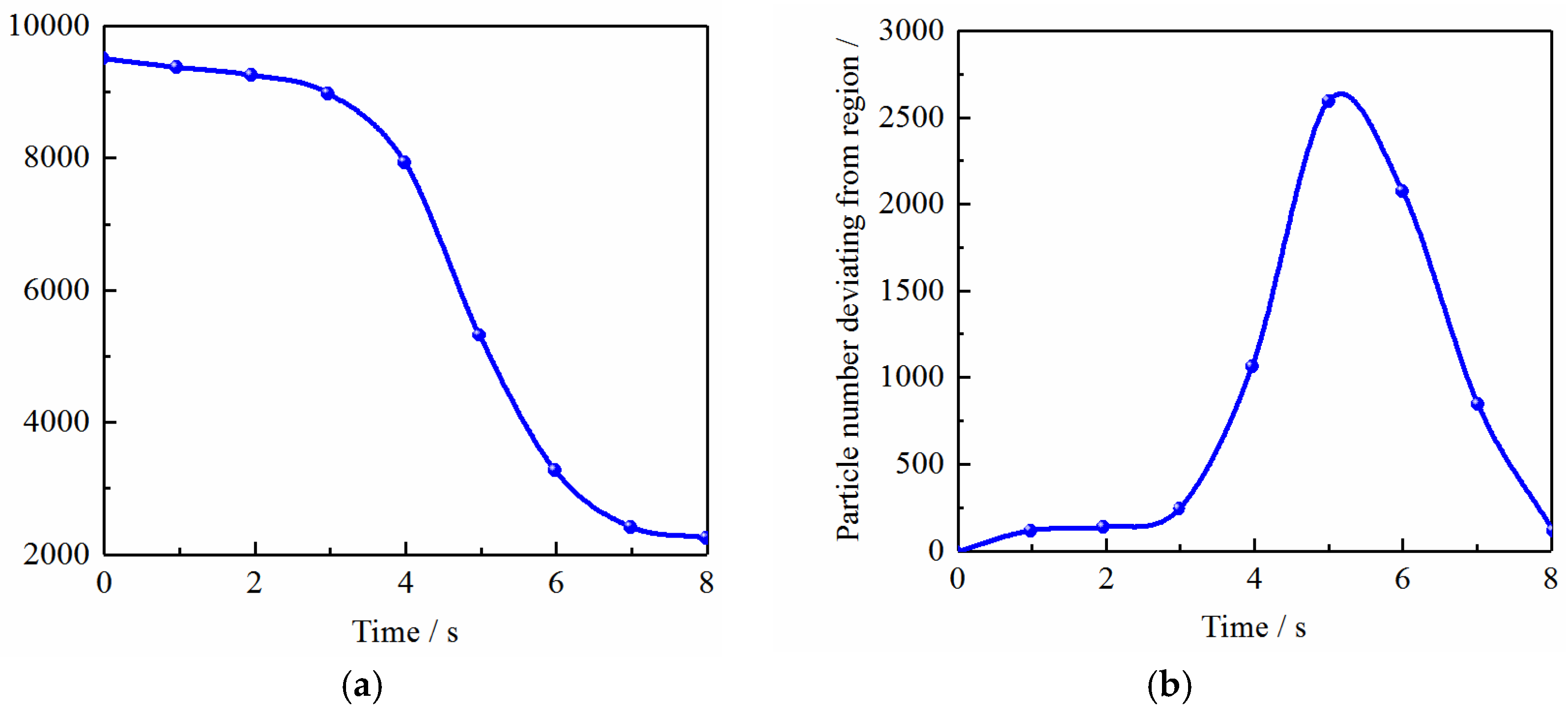
- As the particle material settles and accumulates to a certain extent, the particle movement is blocked, and the stirring speed of the particle material near the blade is reduced. The flow field disturbed by the lower impeller will also suspend many materials, and the material at the bottom will be suspended for 2 s. The mixing effect of the particle material will be reduced near the wall. It can provide a valuable reference for particle flow transport and pattern identification and support technical support for homogenate mixing, chemical extraction, and pharmacy process regulation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, L.; Qi, H.; Yin, Z.; Li, D.; Zhu, Z.; Tangwarodomnukun, V.; Tan, D. Investigation on the multiphase sink vortex Ekman pumping effects by CFD-DEM coupling method. Powder Technol. 2020, 360, 462–480. [Google Scholar] [CrossRef]
- Yuan, W.L.; Zhang, S.J.; Su, C.G. Flow analysis on carbonaceous deposition of heavy oil droplets and catalyst particles for coking formation process. Energy 2022, 252, 124025. [Google Scholar] [CrossRef]
- Jin, X.; Liu, B.; Liao, S.; Cheng, C.; Zhang, Y.; Zhao, Z.; Lu, J. Wasserstein metric-based two-stage distributionally robust optimization model for optimal daily peak shaving dispatch of cascade hydroplants under renewable energy uncertainties. Energy 2022, 260, 125107. [Google Scholar] [CrossRef]
- Li, L.; Tan, D.; Yin, Z.; Wang, T.; Fan, X.; Wang, R. Investigation on the multiphase vortex and its fluid-solid vibration characters for sustainability production. Renew. Energy 2021, 175, 887–909. [Google Scholar] [CrossRef]
- Wang, J.; Gao, S.; Tang, Z.; Tan, D.; Cao, B.; Fan, J. A context-aware recommendation system for improving manufacturing process modeling. J. Intell. Manuf. 2021, 34, 1347–1368. [Google Scholar] [CrossRef]
- Tan, D.; Li, L.; Yin, Z.; Li, D.; Zhu, Y.; Zheng, S. Ekman boundary layer mass transfer mechanism of free sink vortex. Int. J. Heat Mass Transfer. 2020, 150, 119250. [Google Scholar] [CrossRef]
- Li, L.; Tan, Y.; Xu, W.; Ni, Y.; Yang, J.; Tan, D. Fluid-induced transport dynamics and vibration patterns of multiphase vortex in the critical transition states. Int. J. Mech. Sci. 2023, 252, 108376. [Google Scholar] [CrossRef]
- Li, L.; Gu, Z.; Xu, W.; Tan, Y.; Fan, X.; Tan, D. Mixing mass transfer mechanism and dynamic control of gas-liquid-solid multiphase flow based on VOF-DEM coupling. Energy 2023, 272, 127015. [Google Scholar] [CrossRef]
- Li, L.; Li, Q.H.; Ni, Y.S.; Wang, C.Y.; Tan, Y.F.; Tan, D.P. Critical penetrating vibration evolution behaviors of the gas-liquid coupled vortex flow. Energy, 2023; in press. [Google Scholar]
- Li, L.; Wan, Y.; Lu, J.; Fang, H.; Yin, Z.; Wang, T.; Wang, R.; Fan, X.; Zhao, L.; Tan, D. Lattice Boltzmann Method for Fluid-Thermal Systems: Status, Hotspots, Trends and Outlook. IEEE Access 2020, 8, 27649–27675. [Google Scholar] [CrossRef]
- Xu, W.; Tan, Y.; Li, M.; Sun, J.; Xie, D.; Liu, Z. Effects of surface vortex on the drawdown and dispersion of floating particles in stirred tanks. Particuology 2020, 49, 159–168. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, B.; Lin, M.; Gao, Z.; Yang, J. Influence of impeller diameter on overall gas dispersion properties in a sparged multi-impeller stirred tank. Chin. J. Chem. Eng. 2015, 23, 890–896. [Google Scholar] [CrossRef]
- Gu, D.; Liu, Z.; Xie, Z.; Li, J.; Tao, C.; Wang, Y. Numerical simulation of solid-liquid suspension in a stirred tank with a dual punched rigid-flexible impeller. Adv. Powder Technol. 2017, 28, 2723–2734. [Google Scholar] [CrossRef]
- Blais, B.; Bertrand, F. CFD-DEM investigation of viscous solid-liquid mixing: Impact of particle properties and mixer characteristics. Chem. Eng. Res. Des. 2017, 118, 270–285. [Google Scholar] [CrossRef]
- Kou, B.; Hou, Y.; Fu, W.; Yang, N.; Liu, J.; Xie, G. Simulation of Multi-Phase Flow in Autoclaves Using a Coupled CFD-DPM Approach. Processes 2023, 11, 890. [Google Scholar] [CrossRef]
- Brazhenko, V.; Qiu, Y.; Mochalin, I.; Zhu, G.; Cai, J.-C.; Wang, D. Study of hydraulic oil filtration process from solid admixtures using rotating perforated cylinder. J. Taiwan Inst. Chem. Eng. 2022, 141, 104578. [Google Scholar] [CrossRef]
- Li, L.; Tan, D.; Wang, T.; Yin, Z.; Fan, X.; Wang, R. Multiphase coupling mechanism of free surface vortex and the vibration-based sensing method. Energy 2021, 216, 119136. [Google Scholar] [CrossRef]
- Tan, D.-P.; Li, L.; Zhu, Y.-L.; Zheng, S.; Yin, Z.-C.; Li, D.-F. Critical penetration condition and Ekman suction-extraction mechanism of a sink vortex. J. Zhejiang Univ. Sci. A 2019, 20, 61–72. [Google Scholar] [CrossRef]
- Li, L.; Lu, B.; Xu, W.-X.; Gu, Z.-H.; Yang, Y.-S.; Tan, D.-P. Mechanism of multiphase coupling transport evolution of free sink vortex. Acta Phys. Sin. 2023, 72, 034702. [Google Scholar] [CrossRef]
- Tan, D.-P.; Ni, Y.-S.; Zhang, L.-B. Two-phase sink vortex suction mechanism and penetration dynamic characteristics in ladle teeming process. J. Iron Steel Res. Int. 2017, 24, 669–677. [Google Scholar] [CrossRef]
- Zheng, S.; Yu, Y.; Qiu, M.; Wang, L.; Tan, D. A modal analysis of vibration response of a cracked fluid-filled cylindrical shell. Appl. Math. Model. 2021, 91, 934–958. [Google Scholar] [CrossRef]
- Yin, Z.C.; Ni, Y.S.; Li, L.; Wang, T.; Wu, J.F.; Li, Z.; Tan, D.P. Numerical modelling and experimental investigation of a two-phase sink vortex and its fluid-solid vibration characteristics. J. Zhejiang Univ. Sci. A, 2022; in press. [Google Scholar]
- Li, S.; Chen, R.; Wang, H.; Liao, Q.; Zhu, X.; Wang, Z.; He, X. Numerical investigation of the moving liquid column coalescing with a droplet in triangular microchannels using CLSVOF method. Sci. Bull. 2015, 60, 1911–1926. [Google Scholar] [CrossRef]
- Tan, D.P.; Tao, Y.; Zhao, J. Free sink vortex Ekman suction-extraction evolution mechanism. Acta Phys. Sin. 2016, 65, 054701. [Google Scholar]
- Zhang, B.; Li, B.; Fu, S.; Mao, Z.; Ding, W. Vortex-Induced Vibration (VIV) hydrokinetic energy harvesting based on nonlinear damping. Renew. Energy 2022, 195, 1050–1063. [Google Scholar] [CrossRef]
- Park, I.S.; Sohn, C.H. Experimental and numerical study on air cores for cylindrical tank draining. Int. Commun. Heat Mass Transf. 2011, 38, 1044–1049. [Google Scholar] [CrossRef]
- Fan, X.; Guo, K.; Wang, Y. Toward a high performance and strong resilience wind energy harvester assembly utilizing flow-induced vibration: Role of hysteresis. Energy 2022, 251, 123921. [Google Scholar] [CrossRef]
- Zeng, Y.; Shi, W.; Michailides, C.; Ren, Z.; Li, X. Turbulence model effects on the hydrodynamic response of an oscillating water column (OWC) with use of a computational fluid dynamics model. Energy 2022, 261, 124926. [Google Scholar] [CrossRef]
- Stroh, A.; Daikeler, A.; Nikku, M.; May, J.; Alobaid, F.; von Bohnstein, M.; Ströhle, J.; Epple, B. Coarse grain 3D CFD-DEM simulation and validation with capacitance probe measurements in a circulating fluidized bed. Chem. Eng. Sci. 2019, 196, 37–53. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Yin, Y.; Zhang, Y.; Li, L.; Tan, D. Analytical approach for nonlinear vibration response of the thin cylindrical shell with a straight crack. Nonlinear Dyn. 2023, 111, 10957–10980. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, Y. CFD-DEM simulation of fluidized bed with an immersed tube using a coarse-grain model. Chem. Eng. Sci. 2020, 231, 116290. [Google Scholar] [CrossRef]
- Kang, Q.; He, D.; Zhao, N.; Feng, X.; Wang, J. Hydrodynamics in unbaffled liquid-solid stirred tanks with free surface studied by DEM-VOF method. Chem. Eng. J. 2020, 386, 122846. [Google Scholar] [CrossRef]
- Zheng, M.; Han, D.; Peng, T.; Wang, J.; Gao, S.; He, W.; Li, S.; Zhou, T. Numerical investigation on flow induced vibration performance of flow-around structures with different angles of attack. Energy 2021, 244, 122607. [Google Scholar] [CrossRef]
- Singh, N.K.; Premachandran, B. A coupled level set and volume of fluid method on unstructured grids for the direct numerical simulations of two-phase flows including phase change. Int. J. Heat Mass Transf. 2018, 122, 182–203. [Google Scholar] [CrossRef]
- Tan, D.-P.; Li, L.; Zhu, Y.-L.; Zheng, S.; Ruan, H.-J.; Jiang, X.-Y. An Embedded Cloud Database Service Method for Distributed Industry Monitoring. IEEE Trans. Ind. Inform. 2017, 14, 2881–2893. [Google Scholar] [CrossRef]
- He, X.; Xu, H.; Li, W.; Sheng, D. An improved VOF-DEM model for soil-water interaction with particle size scaling. Comput. Geotech. 2020, 128, 103818. [Google Scholar] [CrossRef]
- Li, L.; Yang, Y.-S.; Xu, W.-X.; Lu, B.; Gu, Z.-H.; Yang, J.-G.; Tan, D.-P. Advances in the Multiphase Vortex-Induced Vibration Detection Method and Its Vital Technology for Sustainable Industrial Production. Appl. Sci. 2022, 12, 8538. [Google Scholar] [CrossRef]
- Son, J.H.; Sohn, C.H.; Park, I.S. Numerical study of 3-D air core phenomenon during liquid draining. J. Mech. Sci. Technol. 2015, 29, 4247–4257. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Wu, J.; Li, L.; Tan, D. Machinability evolution of gas–liquid-solid three-phase rotary abrasive flow finishing. Int. J. Adv. Manuf. Technol. 2023, 1–20. [Google Scholar] [CrossRef]
- Zheng, G.; Shi, J.; Li, L.; Li, Q.; Gu, Z.; Xu, W.; Lu, B.; Wang, C. Fluid-Solid Coupling-Based Vibration Generation Mechanism of the Multiphase Vortex. Processes 2023, 11, 568. [Google Scholar] [CrossRef]
- Song, Y.; Pan, Z.; Yu, T.; Zhou, S.; Li, Y.; Jin, W.; Gao, Z.; Ma, Y. Nanoindentation characterization on competing propagation between the transgranular and intergranular cracking of 316H steel under creep-fatigue loading. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 2258–2271. [Google Scholar] [CrossRef]
- Zheng, G.; Gu, Z.; Xu, W.; Lu, B.; Li, Q.; Tan, Y.; Wang, C.; Li, L. Gravitational Surface Vortex Formation and Suppression Control: A Review from Hydrodynamic Characteristics. Processes 2023, 11, 42. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Xu, W.; Xie, Y.; Li, L.; Tan, D. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ. Sci. A 2023, 1–20. [Google Scholar] [CrossRef]
- Li, L.; Xu, W.; Tan, Y.; Yang, Y.; Yang, J.; Tan, D. Fluid-induced vibration evolution mechanism of multiphase free sink vortex and the multi-source vibration sensing method. Mech. Syst. Signal Process. 2023, 189, 110058. [Google Scholar] [CrossRef]
- Wu, L.; Gong, M.; Wang, J. Development of a DEM–VOF Model for the Turbulent Free-Surface Flows with Particles and Its Application to Stirred Mixing System. Ind. Eng. Chem. Res. 2018, 57, 1714–1725. [Google Scholar] [CrossRef]





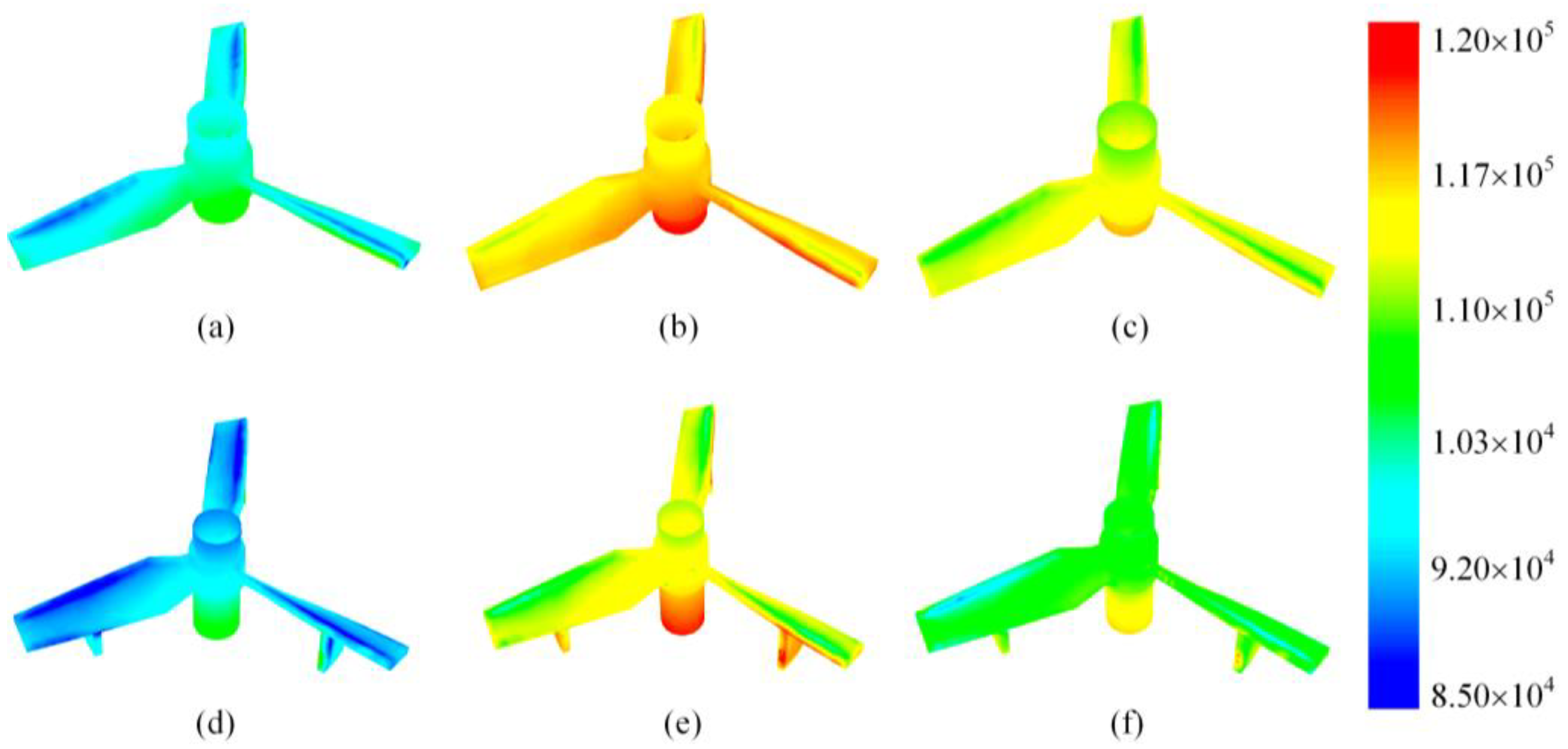
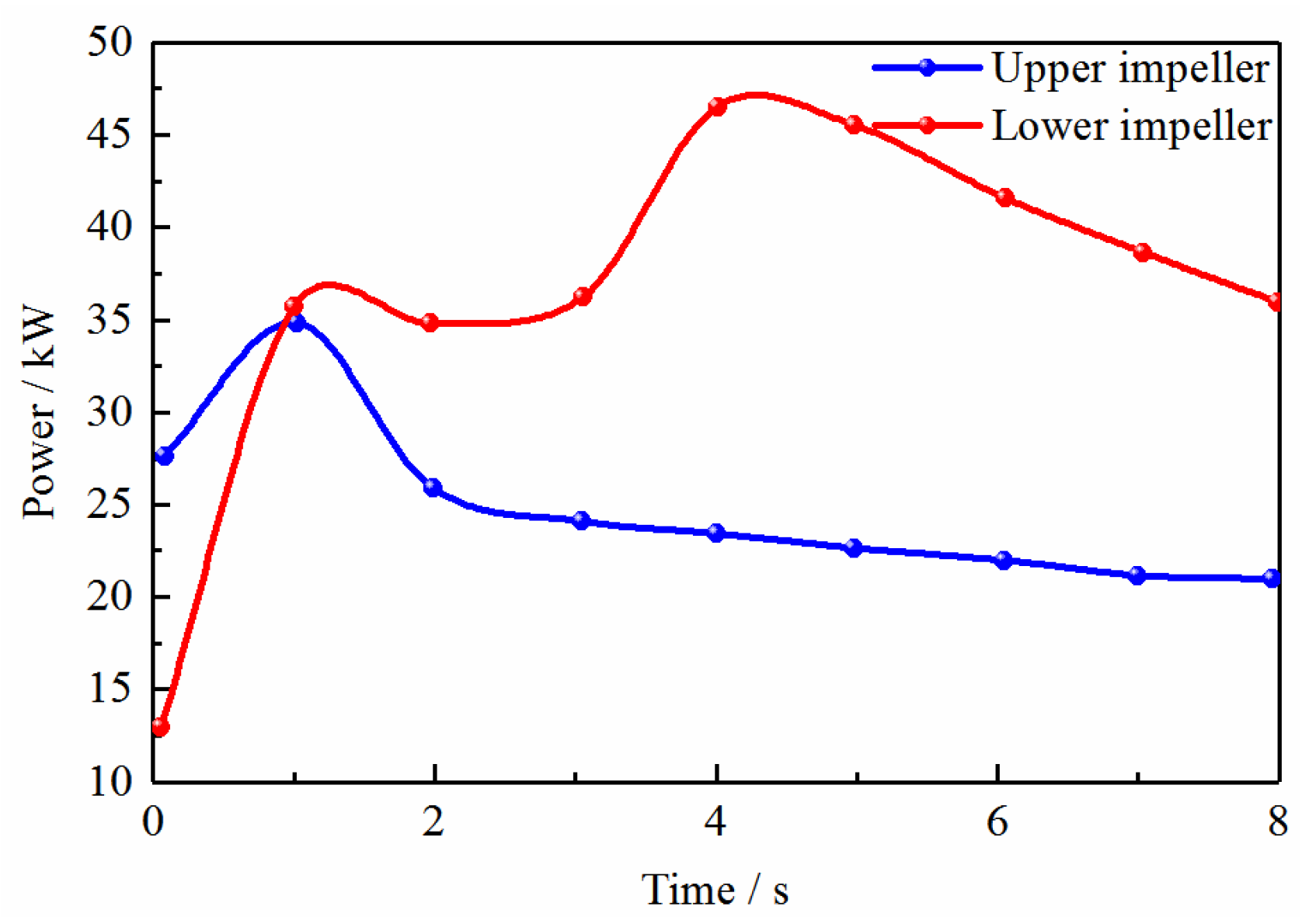


| Impeller | Time | Pressure Loading (N·m) | Viscous Force Action (N·m) | Total Moment (N·m) |
|---|---|---|---|---|
| 1 s | 12,653.136 | 79.339 | 12,732.475 | |
| 2 s | 9424.393 | 85.636 | 9510.029 | |
| 3 s | 8755.418 | 84.049 | 8839.467 | |
| 4 s | 8447.325 | 83.166 | 8530.491 | |
| Upper | 5 s | 8241.532 | 84.754 | 8326.287 |
| 6 s | 7947.013 | 88.372 | 8035.385 | |
| 7 s | 7729.401 | 92.781 | 7822.182 | |
| 8 s | 7658.066 | 96.378 | 7754.444 | |
| 1 s | 12,998.457 | 251.779 | 13,250.237 | |
| 2 s | 9069.175 | 261.869 | 9331.044 | |
| 3 s | 13,124.848 | 262.515 | 13,387.363 | |
| Lower | 4 s | 16,885.797 | 220.347 | 17,106.144 |
| 5 s | 16,595.645 | 217.653 | 16,813.298 | |
| 6 s | 15,205.691 | 229.587 | 15,435.278 | |
| 7 s | 13,960.441 | 242.001 | 14,202.442 | |
| 8 s | 13,170.671 | 259.899 | 13,430.572 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, M.; Chen, J.; Zhao, L.; Zheng, G. Mixing Transport Mechanism of Three-Phase Particle Flow Based on CFD-DEM Coupling. Processes 2023, 11, 1619. https://doi.org/10.3390/pr11061619
Ge M, Chen J, Zhao L, Zheng G. Mixing Transport Mechanism of Three-Phase Particle Flow Based on CFD-DEM Coupling. Processes. 2023; 11(6):1619. https://doi.org/10.3390/pr11061619
Chicago/Turabian StyleGe, Man, Juntong Chen, Longyun Zhao, and Gaoan Zheng. 2023. "Mixing Transport Mechanism of Three-Phase Particle Flow Based on CFD-DEM Coupling" Processes 11, no. 6: 1619. https://doi.org/10.3390/pr11061619
APA StyleGe, M., Chen, J., Zhao, L., & Zheng, G. (2023). Mixing Transport Mechanism of Three-Phase Particle Flow Based on CFD-DEM Coupling. Processes, 11(6), 1619. https://doi.org/10.3390/pr11061619





