Artificial Neural Network Model for Temperature Prediction and Regulation during Molten Steel Transportation Process
Abstract
:1. Introduction
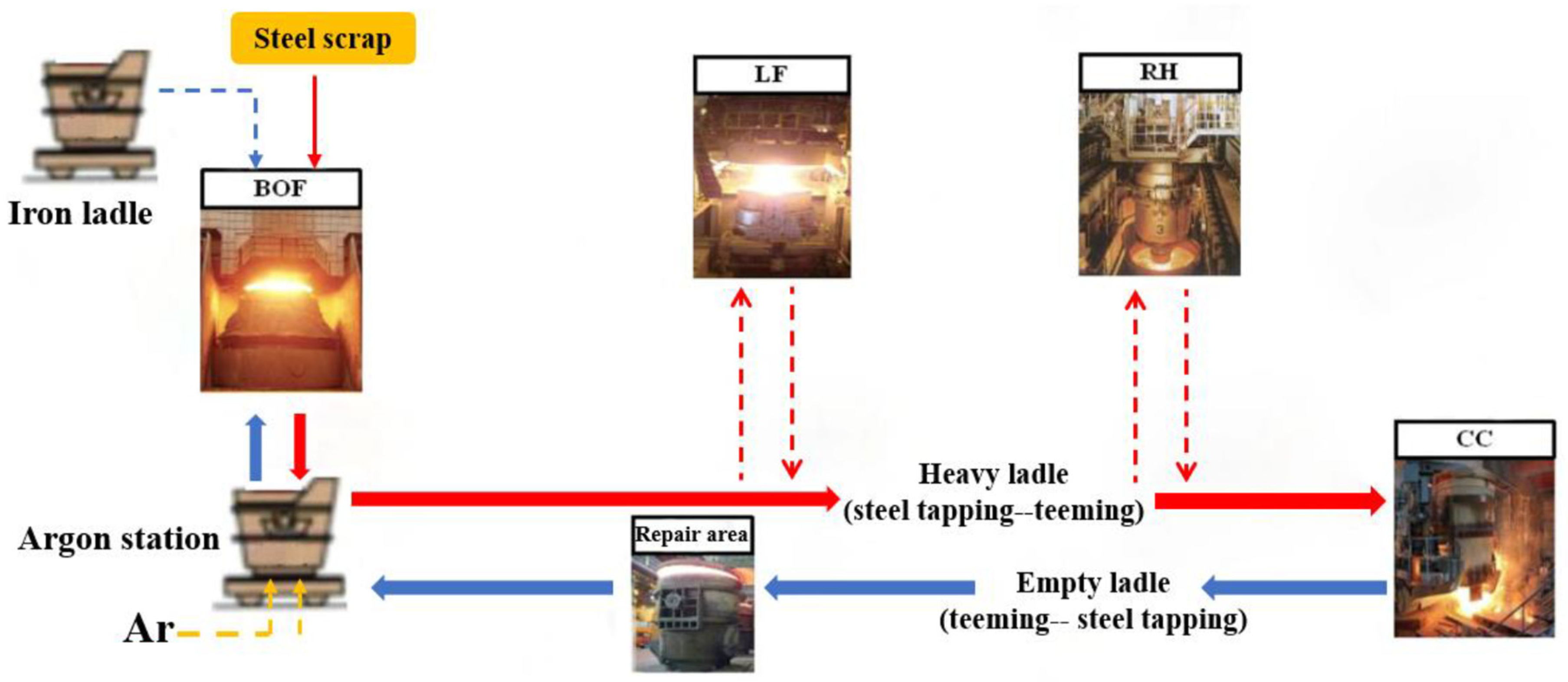
2. Materials and Methods
2.1. Factors Affecting the Temperature of Steel
2.1.1. Mechanism Analysis of BOF
2.1.2. Mechanism Analysis of LF
2.1.3. Mechanism Analysis of RH
2.2. Data Preprocessing
2.2.1. Data Outlier Elimination
2.2.2. Data Normalization
2.3. Algorithm Description
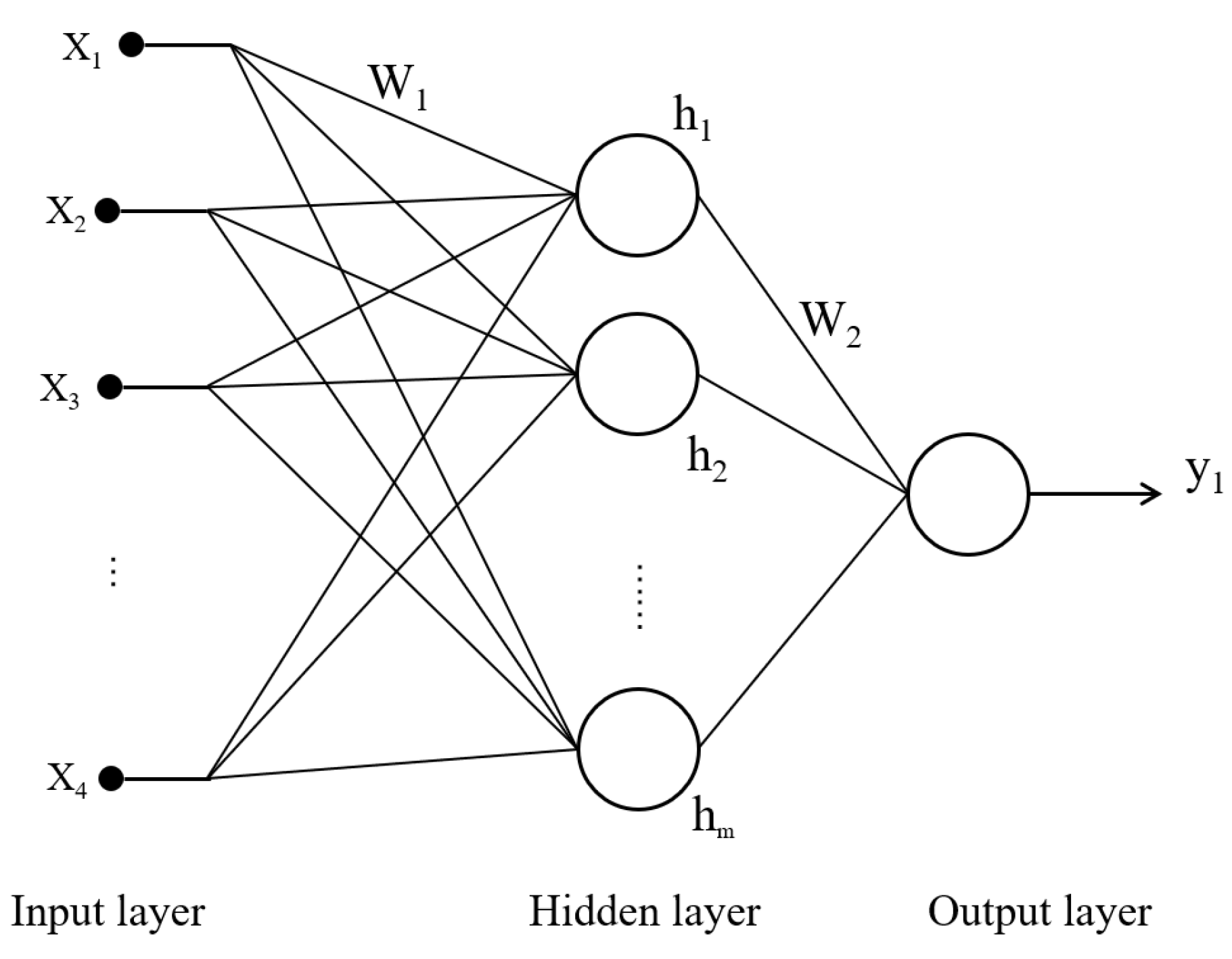
2.3.1. BP Neural Network
2.3.2. Optimization of Network Algorithms
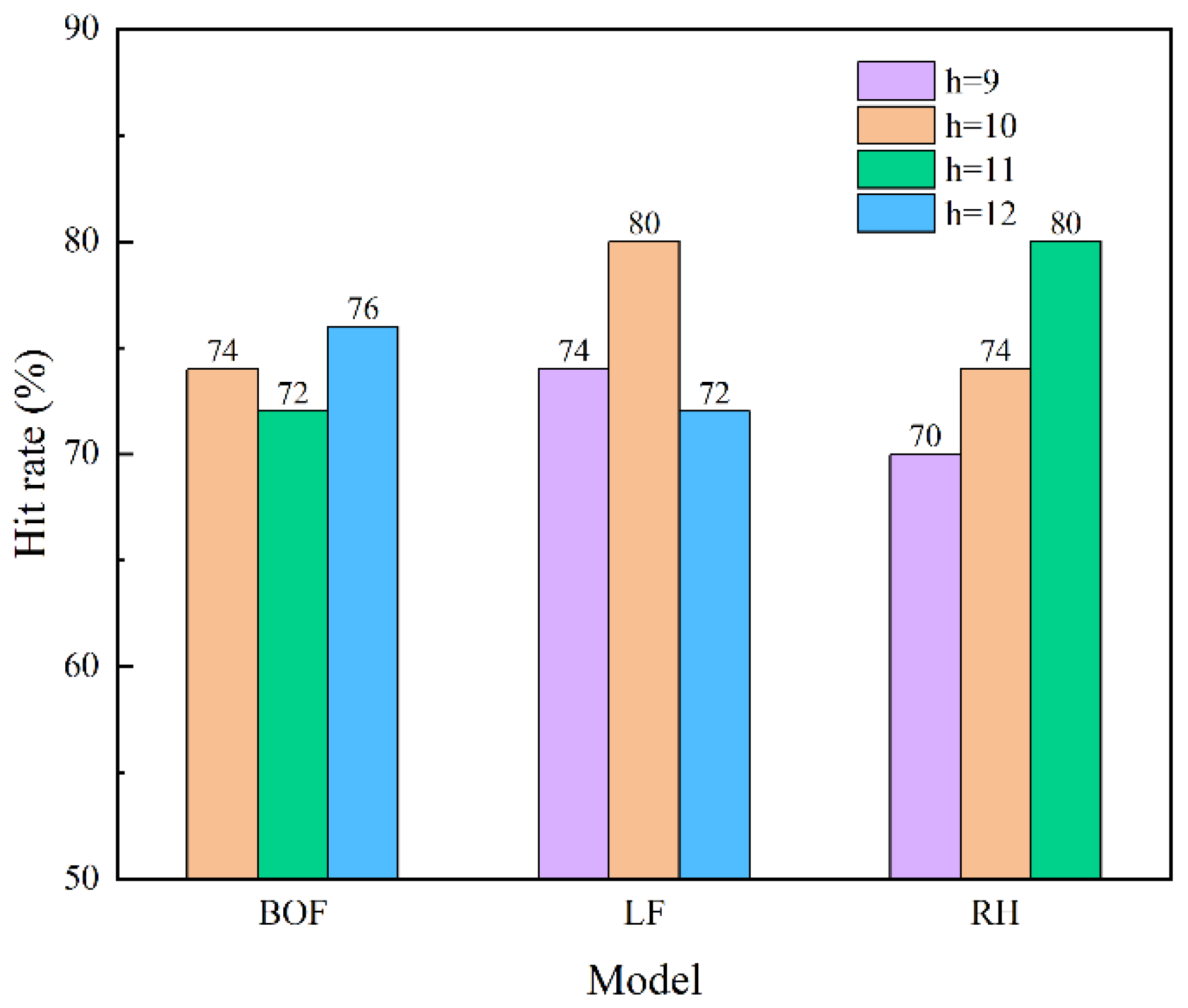
2.3.3. Selection of Hidden Layer Node Number
3. Results
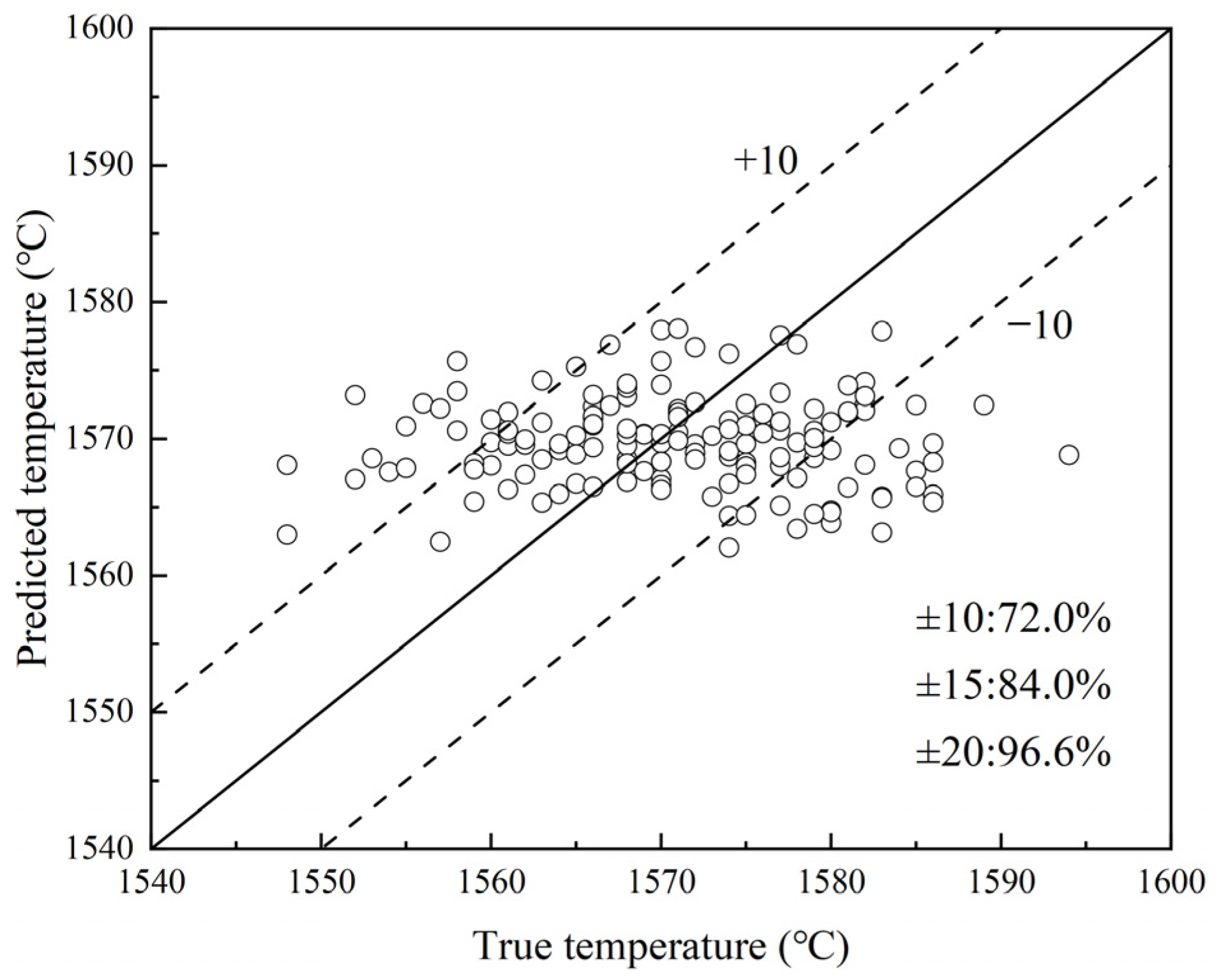
3.1. Sample Prediction
3.2. The Influence of Important Influencing Factors on the Temperature of Steel
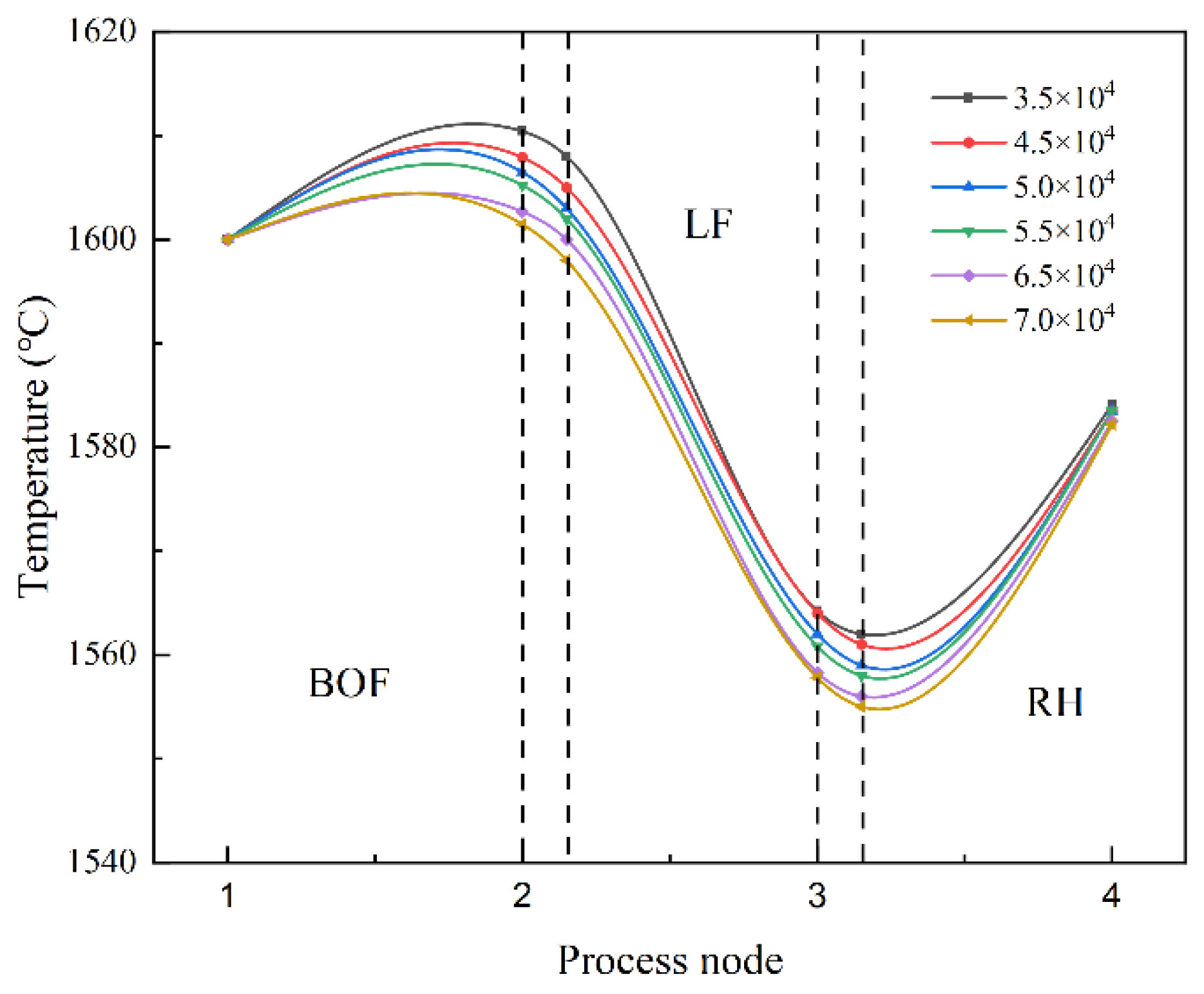
3.2.1. Effect of Scrap Input on Steel Temperature
3.2.2. Effect of Electric Energy Consumption on Steel Temperature
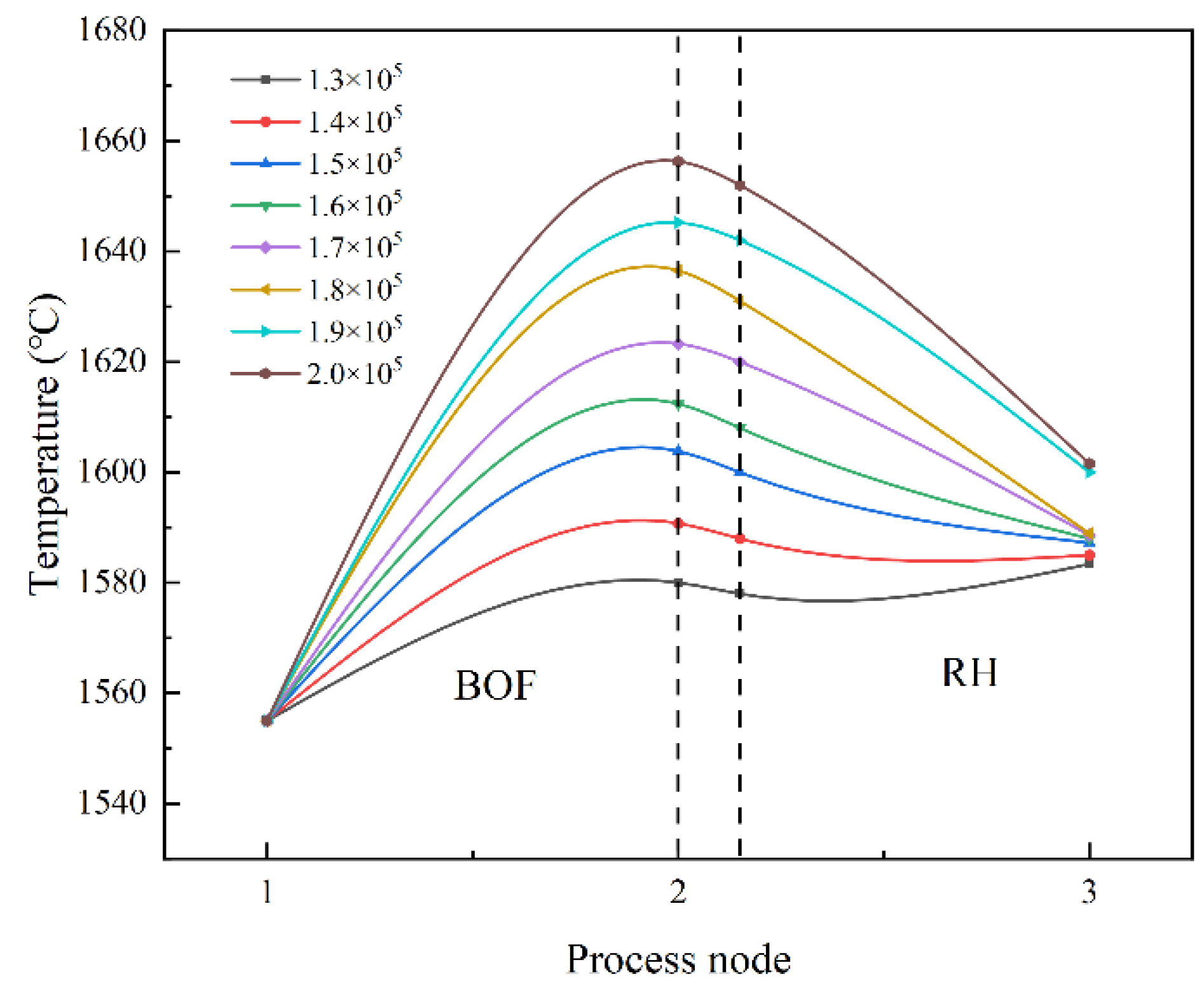
3.2.3. Effect of the Amount of Molten Iron Added on the Temperature of Steel
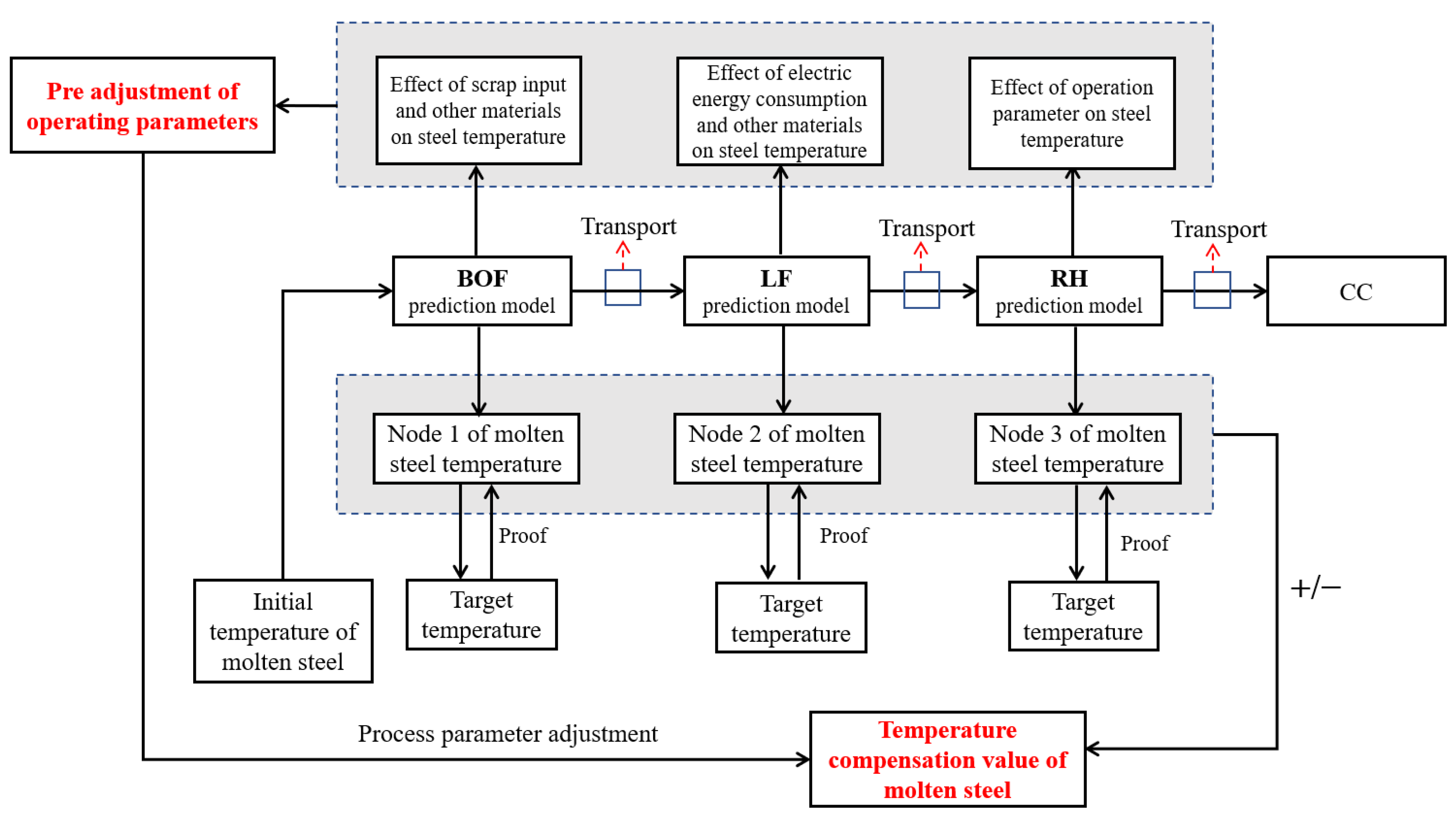
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, G.Q.; Li, J.N.; Xu, D.; Zheng, B. Energy balance between multiple supersonic jets and molten bath in BOF steelmaking. Ironmak. Steelmak. 2022, 49, 726–736. [Google Scholar] [CrossRef]
- Zhou, K.X.; Lin, W.H.; Sun, J.K.; Zhang, J.S.; Zhang, D.Z.; Feng, X.M.; Liu, Q. Prediction model of end-point phosphorus content for BOF based on monotone-constrained BP neural network. J. Iron. Steel Res. Int. 2022, 29, 751–760. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Q.; Liu, H.T.; Wei, S.Z. A review of end-point carbon prediction for BOF steelmaking process. High Temp. Mater. Process. 2020, 39, 653–662. [Google Scholar] [CrossRef]
- Guo, J.; Cheng, S.S.; Guo, H.J. Thermodynamics and Industrial Trial on Increasing the Carbon Content at the BOF Endpoint to Produce Ultra-Low Carbon IF Steel by BOF-RH-CSP Process. High Temp. Mater. Process. 2019, 38, 822–826. [Google Scholar] [CrossRef]
- Yuan, F.; Xu, A.J.; Gu, M.Q. Development of an improved CBR model for predicting steel temperature in ladle furnace refining. Int. J. Miner. Metall. Mater. 2021, 28, 1321–1331. [Google Scholar] [CrossRef]
- Shi, C.Y.; Guo, S.Y.; Wang, B.S.; Yin, X.X.; Sun, P.; Wang, Y.K.; Zhang, L.; Ma, Z.C. The Forcast of Slag Addition during the Ladle Furnace (LF) Refining Process Based on LWOA-TSVR. Metalurgija 2023, 62, 197–200. Available online: https://hrcak.srce.hr/290050 (accessed on 3 April 2023).
- Feng, K.; Xu, A.J.; Wu, P.F.; He, D.F.; Wang, H.B. Case-based reasoning model based on attribute weights optimized by genetic algorithm for predicting end temperature of molten steel in RH. J. Iron. Steel Res. Int. 2019, 26, 585–592. [Google Scholar] [CrossRef]
- Zhu, G.S.; Deng, X.X.; Ji, C.X. Effect of vacuum degree on inclusion removal in ultra-low carbon steel during RH refining process. Iron. Steel. 2022, 57, 99–105. [Google Scholar] [CrossRef]
- Bi, C.B.; Zhang, Y.Z.; Shi, S.Y.; Guo, Y.X.; Huang, J. Prediction on temperature of hot metal on ironmaking and steelmaking interface based on GA-BP. J. Mater. Metall. 2021, 20, 17–22. [Google Scholar] [CrossRef]
- Machado, E.; Pinto, T.; Guedes, V.; Morais, H. Electrical Load Demand Forecasting Using Feed-Forward Neural Networks. Energies 2021, 14, 7644. [Google Scholar] [CrossRef]
- Hancock, J.T.; TKhoshgoftaar, M. Survey on categorical data for neural networks. J. Big Data 2020, 7, 993–1022. [Google Scholar] [CrossRef]
- Mohammadazadeh, A.; Sabzalian, M.H.; Castillo, O.; Rathinasamy, S.; El-Sousy, F.F.M.; Mobayen, S. Neural Networks and Learning Algorithms in MATLAB; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Duarte, I.C.; Almeida, G.M.; Cardoso, M. Heat-loss cycle prediction in steelmaking plants through artificial neural network. J. Oper. Res. Soc. 2022, 73, 326–337. [Google Scholar] [CrossRef]
- Wang, L.; Ji, X.M.; Liu, J. Application of artificial intelligence in intelligent manufacturing in steel industry. Iron. Steel. 2021, 56, 1–8. [Google Scholar] [CrossRef]
- Zhang, X.Q. Application of Artificial Neural Networks in Iron and Steel Materials Research. Metal. Mater. Metall. Eng. 2012, 40, 59–63. [Google Scholar] [CrossRef]
- Sabzalian, M.H.; Kharajinezhadian, F.; Tajally, A.; Reihanisaransari, R.; Hamzah, A.A.; Bokov, D. New bidirectional recurrent neural network optimized by improved Ebola search optimization algorithm for lung cancer diagnosis. Biomed. Signal Process. Control. 2023, 84, 104965. [Google Scholar] [CrossRef]
- Altikat, S. Prediction of CO2 emission from greenhouse to atmosphere with artificial neural networks and deep learning neural networks. Int. J. Environ. Sci. Technol. 2021, 18, 3169–3178. [Google Scholar] [CrossRef]
- Ofrikhter, I.V.; Ponomaryov, A.B.; Zakharov, A.V.; Shenkman, R.I. Estimation of soil properties by an artificial neural network. Mag. Civ. Eng. 2022, 110, 11011. [Google Scholar] [CrossRef]
- Akiyama, K.; Kang, I.; Kanno, T.; Uchida, N. Prediction of Residual Mg Contents in Ladle and Product after Graphite Spheroidizing Treatment by Using Artificial Neural Network: Technical Article. Mater. Trans. 2021, 62, 461–467. [Google Scholar] [CrossRef]
- Wang, X.J.; You, M.S.; Mao, Z.Z.; Yuan, P. Tree-Structure Ensemble General Regression Neural Networks applied to predict the molten steel temperature in Ladle Furnace. Adv. Eng. Inf. 2016, 30, 368–375. [Google Scholar] [CrossRef]
- He, F.; He, D.F.; Xu, A.J.; Wang, H.B.; Tian, N.Y. Hybrid Model of Molten Steel Temperature Prediction Based on Ladle Heat Status and Artificial Neural Network. J. Iron. Steel Res. Int. 2014, 21, 181–190. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, S.S.; Liu, P.B. Prediction model of BOF end-point P and O contents based on PCA–GA–BP neural network. High Temp. Mater. Process. 2022, 41, 505. [Google Scholar] [CrossRef]
- Smith, J.L. Advances in neural networks and potential for their application to steel metallurgy. Mater. Sci. Technol. 2020, 36, 1805–1819. [Google Scholar] [CrossRef]
- Simion, C.P.; Verde, C.A.; Mironescu, A.A.; Anghel, F.G. Digitalization in Energy Production, Distribution, and Consumption: A Systematic Literature Review. Energies 2023, 16, 1960. [Google Scholar] [CrossRef]
- Zeng, G.Q.; Wang, J.T.; Zhang, L.; Xie, X.Y.; Wang, X.F.; Chen, G.B. Multi-Domain Modeling and Analysis of Marine Steam Power System Based on Digital Twin. J. Mar. Sci. Eng. 2023, 11, 429. [Google Scholar] [CrossRef]
- Wang, M.; Gao, C.; Ai, X.G.; Zhai, B.P.; Li, S.L. Whale Optimization End-point Control Model for 260 tons BOF Steelmaking. ISIJ Int. 2022, 62, 1684–1693. [Google Scholar] [CrossRef]
- Huang, H.G.; Liu, Y.G.; Huang, H.L.; Chen, G.; Wang, X.D. Prediction and control for head warpage of hot-rolled slab based on machine vision detection and BP neural network. Chin. Metall. 2022, 32, 85–89, 96. [Google Scholar] [CrossRef]
- Wen, H.; Zhu, S.X.; Han, F.; Zhu, Z.M.; Yu, H. Composition optimization and production practice of large angle steel for iron tower based on BP neural network. J. Iron. Steel Res. Int. 2022, 34, 95–100. [Google Scholar] [CrossRef]
- Choi, B.; Lee, S.; You, D. Prediction of molten steel flow in a tundish with water model data using a generative neural network with different clip sizes. J. Mech. Sci. Technol. 2022, 36, 749–759. [Google Scholar] [CrossRef]
- Xuan, M.T.; Li, J.J.; Wang, N.; Chen, M. Endpoint prediction of basic oxygen furnace steelmaking based on FOA-GRNN model. J. Mater. Metall. 2019, 18, 31–36, 57. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.C.; Kim, J.T. Migration from the traditional to the smart factory in the die-casting industry: Novel process data acquisition and fault detection based on artificial neural network. J. Mater. Process. Technol. 2021, 290, 116972. [Google Scholar] [CrossRef]
- Chi, C.; Janiga, G.; Thevenin, D. On-the-fly artificial neural network for chemical kinetics in direct numerical simulations of premixed combustion. Combust. Flame. 2021, 226, 467–477. [Google Scholar] [CrossRef]
- Cui, X.N.; Wang, Q.C.; Dai, J.P.; Xue, Y.J.; Duan, Y. Intelligent crack detection based on attention mechanism in convolution neural network. Adv. Struct. Eng. 2021, 24, 1859–1868. [Google Scholar] [CrossRef]
- Gao, M. Basic Research on Scrap Melting Processes in Steelmaking Processes. Ph.D. Thesis, University of Science and Technology Beijing, Beijing, China, 2021. [Google Scholar] [CrossRef]
- Wu, Y. Research on Temperature Prediction and Control Model for RH Vacuum Refining. Master’s Thesis, Wuhan University of Science and Technology, Wuhan, China, 2014. [Google Scholar] [CrossRef]
- Maria, T.G.; Stefano, C.; Sudip, C.; Vincenza, C. Application of Artificial Neural Networks for Modelling and Control of Flux Decline in Cross-Flow Whey Ultrafiltration. Processes 2023, 11, 1287. [Google Scholar] [CrossRef]
- Yagan, Y.E.; Vardar, K. Artificial neural networks controllers for three-phase neutral point clamped inverters. Eng. Sci. Technol. an Int. J. 2023, 41, 101390. [Google Scholar] [CrossRef]






| Element | Reaction Formula | Reaction Heat (KJ/kg) |
|---|---|---|
| C | 10,950 | |
| C | 34,520 | |
| Si | 28,314 | |
| P | 18,923 | |
| Mn | 7020 | |
| Fe | 5020 | |
| Fe | 6670 | |
| SiO2 | 2070 | |
| P2O5 | 5020 |
| Element | Reaction Formula | Reaction Heat (KJ/kg) |
|---|---|---|
| Decarbonization | −22.202 | |
| −282.544 | ||
| Aluminum oxide reaction | 10.71 | |
| −1205.12 |
| Working Condition | Parameter | Minimum | Maximum |
|---|---|---|---|
| BOF | Scrap input (kg) | 24,650 | 71,100 |
| Iron water quantity (kg) | 123,300 | 204,700 | |
| Blowing duration (s) | 533 | 1377 | |
| Oxygen consumption (Nm3) | 29 | 12,375 | |
| Initial steel temperature (°C) | 1112 | 1798 | |
| Melt bath level (cm) | 845 | 970 | |
| Argon-blowing duration (s) | 845 | 2285 | |
| LF | Electrical energy consumption (KWH) | 1088 | 38,963 |
| Total heating time (min) | 2 | 85 | |
| Argon blowing duration (min) | 33 | 198 | |
| Argon-blowing consumption (Nm3) | 1 | 98 | |
| Initial steel temperature (°C) | 936 | 1756 | |
| Alloy addition (kg) | 184 | 8593 | |
| RH | Initial steel temperature (°C) | 1536 | 1648 |
| Total amount of top-blown oxygen (Nm3) | 8 | 599 | |
| Initial amount of steel (kg) | 198,649 | 264,279 | |
| Minimum vacuum (Pa) | 50 | 826 | |
| Refining duration (s) | 1571 | 9190 | |
| Alloy addition amount (kg) | 182 | 8698 |
| Working Condition | Parameter | Value | Preprocessing Data |
|---|---|---|---|
| BOF | Scrap input (kg) | 50,000 | 0.546 |
| Iron water quantity (kg) | 150,600 | 0.335 | |
| Blowing duration (s) | 701 | 0.199 | |
| Oxygen consumption (Nm3) | 8638 | 0.697 | |
| Initial steel temperature (°C) | 1624 | 0.746 | |
| Melt bath level (cm) | 880 | 0.280 | |
| Argon-blowing duration (s) | 1499 | 0.454 | |
| LF | Electrical energy consumption (KWH) | 9356 | 0.218 |
| Total heating time (min) | 21 | 0.229 | |
| Argon-blowing duration (min) | 93 | 0.364 | |
| Argon-blowing consumption (Nm3) | 6 | 0.052 | |
| Initial steel temperature (°C) | 1588 | 0.795 | |
| Alloy addition (kg) | 2717 | 0.301 | |
| RH | Initial steel temperature (°C) | 1594 | 0.518 |
| Total amount of top-blown oxygen (Nm3) | 149 | 0.239 | |
| Initial amount of steel (kg) | 236,160 | 0.572 | |
| Minimum vacuum (Pa) | 83 | 0.043 | |
| Refining duration (s) | 6603 | 0.660 | |
| Alloy addition amount (kg) | 2555 | 0.279 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, L.; Su, F.; Kang, Z.; Zhu, H. Artificial Neural Network Model for Temperature Prediction and Regulation during Molten Steel Transportation Process. Processes 2023, 11, 1629. https://doi.org/10.3390/pr11061629
Fang L, Su F, Kang Z, Zhu H. Artificial Neural Network Model for Temperature Prediction and Regulation during Molten Steel Transportation Process. Processes. 2023; 11(6):1629. https://doi.org/10.3390/pr11061629
Chicago/Turabian StyleFang, Linfang, Fuyong Su, Zhen Kang, and Haojun Zhu. 2023. "Artificial Neural Network Model for Temperature Prediction and Regulation during Molten Steel Transportation Process" Processes 11, no. 6: 1629. https://doi.org/10.3390/pr11061629
APA StyleFang, L., Su, F., Kang, Z., & Zhu, H. (2023). Artificial Neural Network Model for Temperature Prediction and Regulation during Molten Steel Transportation Process. Processes, 11(6), 1629. https://doi.org/10.3390/pr11061629






