Development of an MCTS Model for Hydrogen Production Optimisation

Abstract

Hydrogen has the potential to revolutionize the energy industry due to its clean-burning and versatile properties. It is the most abundant element in the universe and can be produced through a variety of methods, including electrolysis. The widespread adoption of hydrogen faces various challenges, including the high cost of production; thus, it is important to optimise the production processes. This research focuses on development of models for hydrogen production optimisation based on various external factors and parameters. Models based on electricity prices are developed and compared between different market situations. To run hydrogen production more effectively, it is required to use renewable energy sources for the production process. Adding the solar power component to the economic evaluation model outcome is more positive. The Monte Carlo tree search (MCTS) algorithm is adapted to effectively control the electrolysis process. MCTS schedule optimization was performed for a 24 h time horizon applying two time-resolution settings—1 h and 15 min. The results demonstrate the potential of the MCTS algorithm for finding good schedules for water electrolyser devices by taking into account variable environmental factors. Whereas the MCTS with a 15 min resolution ensures mathematically better results, it requires more computational power to solve the decision tree.

1. Introduction

The unstoppable growth of the population and the world economy, together with shifting from rural to urban living has led to a significant increase in energy demand [1,2]. Utilisation of fossil fuels as the main source of energy caused an increase in the carbon dioxide (CO₂) in the atmosphere, which is the main cause of global warming [3]. It would be beneficial for future energy sustainability, resilience and global security to decarbonise the energy supply by using renewable energy sources [4]. One of the options is to use hydrogen (H₂). H₂ has received a great deal of attention as an energy carrier from both scientists and policymakers [5]. Hydrogen energy is a clean and low-carbon energy, and its combustion product is water that has no carbon emissions [6]. It is predicted that H₂ will play a significant role in shifting the global energy system towards a sustainable energy system by 2050 [7]. In 2019, the entire worldwide hydrogen production was around 500 billion m³ per year [8]. Hydrogen can be produced from different resources, including fossil fuels and renewable energy (RE) resources [9]; however, only the type produced using renewable energy is considered as “green” hydrogen [10]. Additionally, nuclear power could bring a significant contribution to hydrogen supplies in the future [11]). Nowadays, 96% of H₂ is produced from non-renewables and the remaining 4 % by water electrolysis [12]. Thus, RE resources will play a significant role in the transition process towards a clean and sustainable energy system worldwide [13]. Unfortunately, renewable energy (such as solar or wind) is intermittent and can be random [14], so it is not possible to fully account for it while the hydrogen production process is ongoing. In addition, it should be mentioned that renewable energy characteristics can significantly influence electrolyser performance [15]. To increase the economic efficiency of the hydrogen production process, it is required to control the process based on various parameters, including the availability of renewable sources, actual electricity prices, demand for hydrogen, etc. In the long term, a hydrogen-based economy could contribute towards reducing carbon dioxide emissions and local environmental pollution, securing energy independence and achieving a sustainable energy supply [16].

Two primary methods are used to produce H₂: steam methane reforming of natural gas and electrolysis of water. Within this study, the latter method is considered, which contributes to green and sustainable energy production policy. Electrolysis is an electrochemical reaction that splits water into H₂ and O₂ with electricity input and it is considered the most developed and commercial technology for hydrogen production [17].

There are different hydrogen production systems available for the electrolysis of water; the most common are alkaline (AEL) and polymer electrolyte membrane (PEMEL) systems. Alkaline electrolysers have good durability and maturity but have a low partial load range and low current density [18]. Compared with AEL systems, polymer PEMEL enables flexible operation, requires less than 1 min for start-up and seconds to ramp up from an idle state to the maximum rated power [19]. A fast response to dynamic power supplies allows PEMEL to provide services in the control reserves market and to take advantage of dynamic electricity prices as it is one of the important issues in hydrogen production.

The aim of this study was to develop different models based on electricity prices and the Monte Carlo tree search (MCTS) algorithm to effectively control the electrolysis process by changing the operation modes of the electrolyser (switching on/off).

The MCTS was selected as it provides capabilities to solve decision trees with high branching factors. Additionally, the MCTS is not dependent upon the starting position (root) of the decision tree and can be used ad hoc when it is needed. The authors found a new opportunity for this algorithm application, which is usually limited to gaming environments.

In regard to electricity price modelling, various methods of electricity pricing such as critical peak pricing (CPP), time-of-use pricing (TUP), real-time pricing (RTP) and so forth have been presented. RTP is reportedly one of the best methods [20].

Optimal control strategies can significantly boost the efficiency of hydrogen electrolysers [21]. Control strategies for hydrogen-producing systems that use solar energy are important and required because several parameters (e.g., the number of electrolyser on/off cycles, system component power levels) affect the performance of the whole system [22,23]. Regarding the control strategies, [23] proposed a novel model that aims to schedule the production of hydrogen by an alkaline water electrolysis system and using renewable energy. The developed model was a mixed-integer linear program that incorporates several variables describing operational states and transitions, as well as taking into account the hydrogen flow. A scheduling approach using a combination of solar power and power from the grid was also proposed by [24], where various aspects within the alkaline water electrolysis system were considered, such as electricity price, costs related to the operation of the electrolyser, the solar radiation profile, etc. The control of the scheduling was based on solving optimisation formulas that include the aforementioned aspects. In a study by [25], a segmented fuzzy control method was proposed for scheduling the alkaline electrolyser by using a wind power system. The implementation of fluctuating and highly intermittent renewable energy for the electrolyser operation is challenging, as each component of a hydrogen energy system needs to be optimised to increase the operation time and system efficiency [26].

It is important to note that the field of electrolysis process control is dynamic and that new methods and technologies can emerge in the future. Some of the methods used for the control of electrolysis processes are:

• Advanced Process Control (APC): APC techniques involve using sophisticated algorithms and models to optimise the performance of electrolysis processes [27]. These methods take into account various process parameters and use real-time data to adjust operating conditions and optimise energy efficiency.
• Model Predictive Control (MPC): MPC is an advanced control strategy that uses mathematical models of the process to predict its behaviour and optimise control actions [28]. By considering process constraints and objectives, MPC can determine the optimal setpoints for various process variables, such as temperature, current density and electrolyte flow rate.
• Machine Learning and Artificial Intelligence (AI): Machine learning and AI techniques have gained significant attention in process control applications. These methods involve developing models and algorithms that can learn from data and make predictions or control decisions. By utilizing historical data and real-time measurements, machine learning algorithms can optimise the electrolysis process and improve its performance [29].

2. Materials and Methods

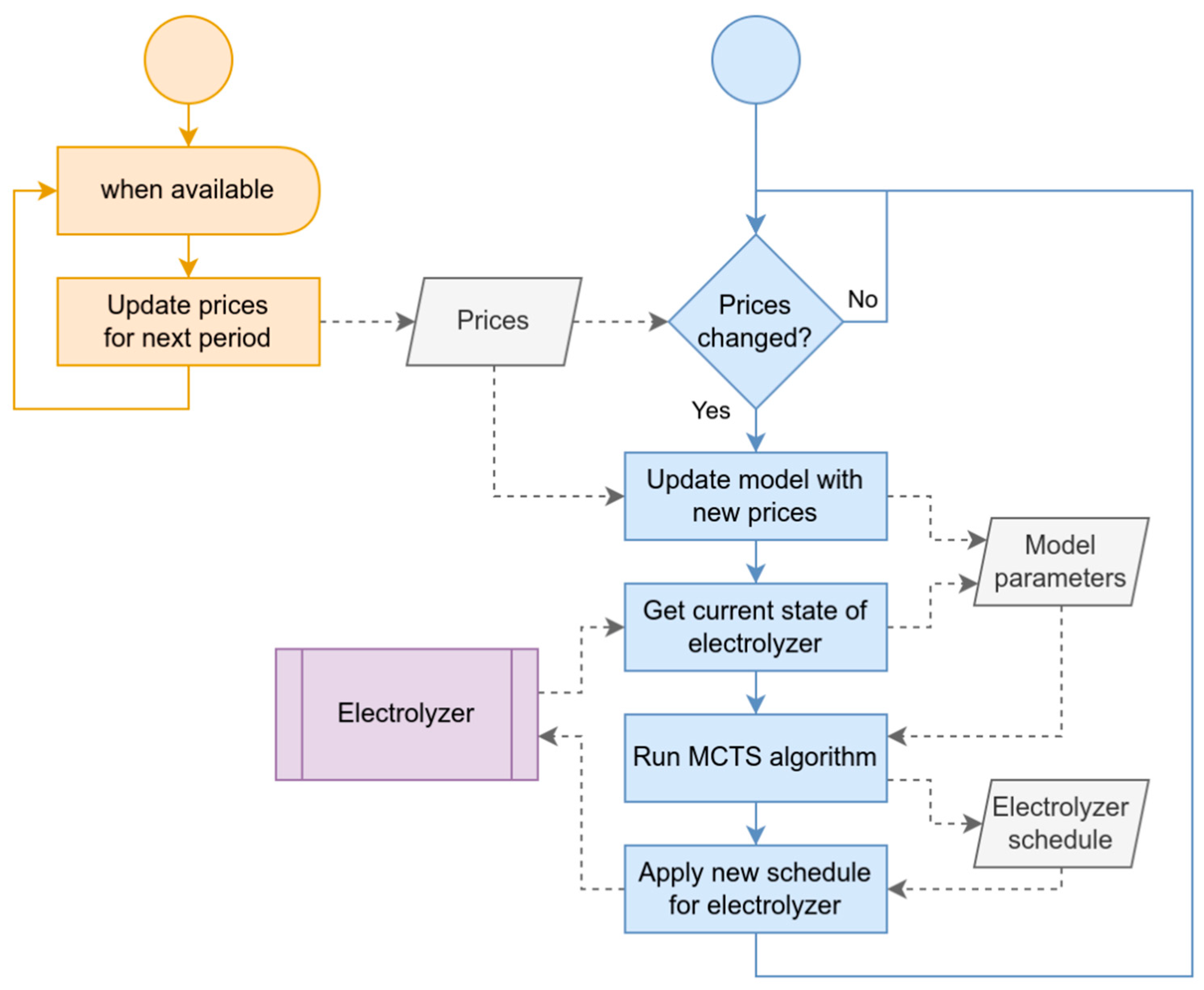
2.1. Electricity-Price-Based Electrolyser Control

In the first stage, simple models based on electricity prices are developed to showcase different scenarios for hydrogen production in various markets. For the comparison, four countries are selected: Latvia, Germany, Spain and Romania, as these countries are partners in the ERA-NET project “New technology to produce hydrogen from Renewable Energy Sources based on AI with optimized costs for environmental applications” (HydroG(re)EnergY-Env).

From the available technoeconomic analysis, it was found that the cost of electricity constitutes up to 40–57% of the levelised cost of hydrogen. However, this cost can be reduced by considering different geographical locations and smart operation strategies. Additionally, the carbon footprint of the electricity source must be considered to ensure that the hydrogen produced has a minimal emission of CO₂.

For this study, electricity prices are taken from the “Nord Pool” market (https://www.nordpoolgroup.com/ (accessed on 8 February 2023) but data are acquired from the EU Transparency platform ENTSO-E (https://newtransparency.entsoe.eu/ (accessed on 8 February 2023) using the provided application programming interface (API).

For calculation purposes, a small hydrogen production facility is considered with a power consumption of 58 kWh (which could produce approx. 1 kg of H₂). For this approach (electricity-price-based electrolyser control), only H₂ prices are considered: 6.25 EUR/kg.

For model demonstration purposes, the time frame for the calculations is taken as one week, but if required it can be changed and adapted based on calculation and analysis needs.

To increase the profit of the production, it is advisable to switch off the technological process when the market electricity price is high and costs for the production exceeds the potential income from the hydrogen. A threshold of 150 EUR/MWh was selected, which corresponds to the daily income for H₂ production—at this threshold H₂ production becomes profitable (24 kg of H₂ per day with a H₂ price of 6.25 EUR/kg).

2.2. Electrolyser Schedule Optimisation Using the MCTS Algorithm

At the next stage, the aforementioned approach was extended with additional input parameters and variables and the Monte Carlo tree search (MCTS) algorithm was adopted to optimise the electrolyser operation schedule.

By the definition, the MCTS is a heuristic best-first search algorithm that combines Monte Carlo simulation with searching combinatorial spaces represented by decision trees. In such trees, nodes denote states and edges denote transitions (actions) from one state to another [30]. The MCTS iteratively explores the space by repeating random samples according to Monte Carlo simulation technique [31] and gradually biassing the exploration toward the most promising regions of the decision tree [32].

Each iteration of the MCTS algorithm usually involves four phases: selection, expansion, simulation and backpropagation [33]. Although intermediate states do not need to be evaluated, the MCTS is very good at shrinking large-sized problems by only taking the reward from the terminal state at the end of the simulation process, then balancing the exploitation and exploration [34].

The MCTS has been widely used in planning problems and video and board games such as Go, Poker, Settlers of Catan, Civilization, Sokoban, etc. [35,36,37,38,39,40].

In the authors case, a flow chart for the execution of the MCTS for the problem solution is depicted in Figure 1:

The execution of the MCTS algorithm involves updating of the prices for electricity, hydrogen and oxygen in the expenses model when available. The current state of the electrolyser is taken into account as one of the model parameters. The MCTS algorithm resolves the decision tree defined by the model and produces a schedule that can be applied for changing the operational modes of the electrolyser.

Several MCTS algorithm varieties have been developed over the years for specific-use cases. In particular, single-player MCTS was proposed by [41]. The main differences between SP-MCTS and MCTS are the range of values for the problem states—for two-player environments the reward value alternates depending on which of the players makes the decision (the best move for a player is the worst move for his opponent). Additionally, SP-MCTS has no uncertainty about the opponent’s action, as there are no opponents.

2.3. Optimisation Problem Setup

An algorithm adaptation based on the ideas from the SP-MCTS was used for finding the optimal control strategy of a H₂-producing electrolyser considering variable external parameters. The authors used a simplified model for the H₂ production process via electrolysis and only critical parts of it were considered for the demonstration of the MCTS approach. The possible states and corresponding parameters of the modelled electrolyser are depicted in Figure 2.

A distinctive feature of electrolysers is the characteristic process inertia—H₂ production does not start immediately upon powering up the electrolyser, nor stop immediately after powering it down—electrolysers go through specific “StartUp” and “Shutdown” sequences that can take up to 1 h (used in authors model). The time for these sequences can vary for different electrolysers, as it is dependent on the required electrolyte temperature for maximum efficiency as well as on the membrane types used. Moreover, due to internal component degradation (mostly membrane), electrolysers have a limited number of “On/Off” cycles before maintenance is needed. The distinct state sequences were introduced into the model with the associated energy consumption profiles. The fixed costs associated with the Start/Shutdown state cycles represent the maintenance costs due to internal component degradation.

Upon reaching the production state, the electrolyser load can be varied within a limited range. The product output (H₂ and O₂) changes according to the applied electrical power. Discrete low/medium/high production states are used within the model. The assumptions are made based on small-scale electrolysers available on the market (e.g., https://pureenergycentre.com/hydrogen-products-pure-energy-centre/hydrogen-electrolyser/ (accessed on 8 February 2023), taking an hourly H₂ production of 1 kg and an energy consumption of ~60 kWh.

The model variables (see

Table 1. List of nomenclature.

Symbol	Property	Units
RH2	H2 production rate	kg/h
RO2	O2 production rate	kg/h
C	Fixed costs	EUR
E	Electrical energy	kWh
T	Timespan	s
PH2	Price of H2	EUR
PO2	Price of O2	EUR
PE	Price of electricity per kWh	EUR
F	Profit	EUR
QH2	Quantity of H2 produced	kg
QO2	Quantity of O2 produced	kg

) and parameters (see

Table 2. Summary of the electrolyser states and their parameters.

Electrolyser State	Electrical Energy E, kWh	Fixed Costs C, EUR	RH2, kg/h	RO2, kg/h	Remarks
Start	2.0	3.00	-	-	Flat maintenance costs represent membrane degradation over time
Purge	5.0	-	-	-	Electrolyser purging (water pumping) before starting production
Heating	15.0	-	-	-	Energy consumption for reaching optimal electrolyte temperature
BuildUp	20.0	-	-	-	Pressure build-up phase with no product output
Shutdown	2.0	3.00	-	-	Flat maintenance costs represent membrane degradation over time
Low production	20.0	-	0.2	1.6	H2 production on low energy profile
Mid production	40.0	-	0.6	4.8	H2 production on medium energy profile
High production	60.0	-	1.0	8.0	H2 production on high energy profile

) of the modelled electrolyser are summarised in below. The selected parameters are not taken from any source and are assumed by the authors based on the descriptions of small-scale electrolysers available on market and used for demonstration purposes only.

Electrolysers are not used as stand-alone devices but rather as a part of a larger infrastructure that provides access to all needed supplies (electricity and water), storage and other facilities. Within the model, such infrastructure components are considered as external parameters and are modelled in the form of costs of supplies and the value of output products. The following components are included in the model:

• An array of photovoltaic solar (PV) cells with a maximum capacity of 100 kW of energy. This represents a source of renewable energy with available excess power that varies over the day.
• The relative solar irradiation is modelled for a 12 h long light day, which roughly corresponds to the spring or fall equinoxes. Depending on the actual day of the year and the latitude the solar declination angle will change further, affecting the solar irradiation captured by the PV cells.
• The power grid connection represents a source of energy with virtually unlimited capacity but with prices changing every hour. Real “Nord Pool” spot market prices for 8 February 2023 were used for modelling (see Figure 3). The model assumes that all available renewable energy is used first and that only the remaining demand is covered by the power grid.
• Output products (H₂ and O₂) are considered as income for the production process and modelled as sold for a fixed price. The H₂ price can vary based on various factors and production methods [42]. The oxygen generated by electrolysis can be used for some medical and niche applications [43], so can also provide additional income. The prices considered for the model were: P_H2 for 5.00 EUR/kg and P_O2 for 0.10 EUR/kg.

The objective function (OF) is defined as (1) and aims to maximize revenue from H₂ and O₂ production for a 24 h schedule by taking into account varying energy prices and available renewable energy sources.

$$OF=\sum _{t=1}^T\left\{Q_t^{H_2}·P^{H_2}+Q_t^{O_2}·P^{O_2}-max\left(E_t-E_t^{PV},0\right)·P_t^E-C_t\right\}$$

(1)

where:

• T is the timespan;
• Q_t is the quantity of products produced;
• P is the price of products;
• E_t is the energy consumed by the electrolyser;
• $E_t^{PV}$ is the energy provided by the PV cells;
• $P_t^E$ is the grid energy price;
• C_t is the fixed maintenance cost (component degradation).

2.4. MCTS Adaptation for Electrolyser Schedule Optimisation

The MCTS algorithm finds the best solution by exploring the most promising branches of decision space. For the electrolyser schedule optimisation, the tree nodes represent possible electrolyser states and each tree level corresponds to a discrete time step. The MCTS algorithm starts from the root of the decision tree and selects child nodes based on their value. The root of the tree corresponds to the current state of the system, which in the case of electrolyser was selected as the off state at midnight.

Upon reaching a leaf node (unexplored branch of the decision tree), the MCTS algorithm expands the tree by adding possible transitions to the next states. The next one of the newly added states is selected and simulated: uniform random actions are applied to the electrolyser until it reaches the end of the timespan. At the end of the simulation stage, the objective function value OF is calculated.

Finally, the obtained OF value is back propagated to all previously selected nodes of the decision tree via updating their value. This gives an estimate of how valuable the previously selected branch of the decision tree is, and the MCTS algorithm balances between exploring new branches and exploiting the most promising branches that are already known. The MCTS workflow is depicted in Figure 4.

The MCTS algorithm usually evaluates nodes using the value of upper confidence bound 1 applied to trees (UCT), which also ensures balancing between exploration and exploitation strategies. However, the UCT was originally designed for zero-sum two-player games and specifically considers binary results of the simulation—either a win or a loss—which keeps the average value for the node in the range of [0; 1].

For the electrolyser, the OF values represent the costs and revenues of production and are not bound to specific ranges. To overcome this peculiarity, the authors applied sigmoid scaling on the average OF value prior to the UCT calculation. The parameters of the sigmoid (see Equations (2) and (3) and Figure 5) are experimentally selected to fit the range [−250; 150] from the electrolyser model (the parameters of the model have been biased towards expenses, thus most common OF values are negative).

$$\mathrm{f}\left(v\right)=\frac{v-\left(v_{min}+\frac{v_{max}-v_{min}}{2}\right)}{10\left(v_{max}-v_{min}\right)}$$

(2)

where:

• v is the raw value of the objective function OF
• v_min is the lower range bound (−250)
• v_max is the upper range bound (150)

$$\mathsf{\sigma }\left(v\right)=\frac{1}{1+e^{-f\left(v\right)}}$$

(3)

The final UCT formula used in the MCTS algorithm is (4).

$$\mathrm{U}\mathrm{C}\mathrm{T}=\mathsf{\sigma }\left(\frac{v}{n}\right)+\mathrm{c}\sqrt{\frac{\ln N}{n}}$$

(4)

where:

• v is the total value of the node;
• n is the total number of simulations from the node;
• N is the total number of simulations from the node’s parent;
• c is the exploration parameter; a value of 1.5 is used by the authors.

3. Results

3.1. The Economic Results of Electricity-Price-Based Electrolyser Control

Figure 6 demonstrates the possible scenario of hydrogen production operation for one week (in four countries), taking into account the costs for electricity and the potential income from the H₂. The specification of the electrolyser should be considered as there could be some limitations to the number of on/off switching cycles. Modern electrolysers did not require much time to start production at the maximal rate and almost instantly start up.

The production costs and income calculations results are as follows:

• 24 × 6.25 = EUR 150 (income per day when using a ~60 kWh electrolyser that produces ~1 kg of H₂ per h) as a threshold (shown in Figure 6);
• The overall income per week = 150 × 7 = EUR 1050;
• The overall costs for H₂ production for the selected countries are: LV—EUR 1160.71; RO—EUR 1468.17; DE—EUR 1439.10; ES—EUR 1256.10.

It can be concluded that hydrogen production only using the grid power is not economically feasible in all the selected countries for the selected week (4–10 February 2023), as the costs for electricity are higher than the potential income.

With the dynamic market price for electricity, the operating modes for hydrogen production can be changed and production can potentially be stopped during hours when the electricity price is higher than the defined threshold. In Figure 7, the below electricity price for one specific date is demonstrated and it can be concluded that hydrogen production can be stopped from 8 to 10 and from 14 to 18, thus minimising the overall production costs. Obviously, the amount of hydrogen produced will also be decreased. In this case, hydrogen production will be for 16 h out of 24 h and costs will be EUR 80.67, but the income from H₂ = EUR 100. Therefore, it is profitable in this case, with a profit of EUR 19.33.

Calculating the income and costs for one week (but excluding hours with high electricity prices) leads to the following results: H₂ production hours: 120 h; total energy used: 6960 kWh; costs: EUR 665.30; income: EUR 780; profit: EUR 114.70.

To run hydrogen production more effectively, it is required to use renewable energy sources for the production process. Adding the solar power component to the economic evaluation model outcome is more positive. A solar system of 100 kW is taken as a reference for calculations.

Figure demonstrates the usage of grid and solar power within a one-day timeframe. The bars in Figure 8 represent the electricity market price.

The calculations for the Latvian market prices for the one-week scenario presented are as follows: costs = EUR 718.95; however, without solar power it was EUR 1160.71, so the costs are decreased by 441.76 (38%). The usage of solar power would decrease the operational costs of hydrogen production, but investments in the solar system also should be taken into consideration in real projects.

3.2. MCTS Results

MCTS schedule optimisation was performed for a 24 h time horizon. The schedule started at midnight with the electrolyser switched off. Two time-resolution settings were used in the experiments—1 h and 15 min. The first implies a 24-level deep decision tree; the latter has a depth of 96 levels. Figure 9 and Figure 10 show the best solutions found by the MCTS algorithm alongside a few manually created schedules for comparison. The summaries for each schedule include the total energy consumed E, hydrogen produced Q_H2, oxygen produced Q_O2 and profit F.

The results demonstrate the potential of the MCTS algorithm to find good schedules for water electrolyser devices by considering variable environmental factors. Although the MCTS with a 15 min resolution ensures mathematically better results (the estimated profit is EUR 47.24 vs. EUR 47.37), it requires more computational power to solve the decision tree. The electrolyser state model has an average branching factor of 3, thus the number of possible states to evaluate is around 3²⁴ and 3⁹⁶ for the 1 h and 15 min resolutions, respectively.

An additional advantage of the MCTS is that it is able to search for solutions from any state of the electrolyser and thus can be used ad hoc. Figure 11 shows the best schedules found by the MCTS algorithm considering the initial state of the electrolyser. Such a feature allows the use of the MCTS in a reactive manner when external factors change in order to adapt to the actual situation. Another useful feature of the MCTS is partial results. MCTS, at its core, investigates a decision tree and gradually builds confidence in the most promising branches. After a number of iterations, even if the time horizon is not yet reached by the algorithm, the latest branching option has already converged to a solution and can thus be used for decision making.

4. Discussion

The described hydrogen production scheduling problem can be also solved by other approaches and methods. For instance, reinforcement learning (RL) can be applied. RL is a branch of machine learning that incorporates human-level control [44]. As a branch of machine learning, RL is gaining popularity beyond the machine learning community because of its broader applicability. As reinforcement learning does not require a previous data set for training and the agent can learn instantly, it has a strong appeal for real-time applications, for example for UAV task scheduling [45], for building-energy management [46] and for robot manipulations [47]; it can also be applied in intelligent healthcare applications [48], etc. The general model for RL consists of the agent, environment, actions, states and rewards. The purpose of RL is for the agent to maximise the reward by continuously taking actions in response to an environment. The next action can be defined based on the rewards and exploration–exploitation strategies [49].

Both RL and MCTS share some important similarities in their approach to decision-making problems, but they also have some key differences in their algorithms and applications. Both of these approaches involve learning from experience and involve exploration and the use of value functions. Additionally, RL and MCTS can be combined with deep learning. Deep RL combines reinforcement learning with deep neural networks to handle high-dimensional state spaces. Deep MCTS combines MCTS with neural networks to improve the search process.

Another platform that can be used for such a problem is Google’s OR-Tools (Operations Research) (https://developers.google.com/optimization (accessed on 20 March 2023). OR-Tools is an open-source software suite for optimisation that is tuned for tackling the world’s toughest problems in vehicle routing, flows, integer and linear programming and constraint programming.

The achieved modelling results cannot be truly validated and directly compared with other experiments in the literature, as a similar setup is not found in sources and industrial experiments. However, the main outcome of this study is the proof-of-concept validation of the MCTS algorithm and its potential application for the control of the electrolysis process. In the future, we plan to extend the model with additional parameters and to apply this method for controlling the real electrolysis process in an experimental plant.

5. Conclusions

Hydrogen can be produced from a variety of sources, including fossil fuels, renewable energy sources and water. Cost reductions in renewable energy sources such as solar, wind and electrolysers will increase hydrogen production competitiveness over time.

Due to its unique properties and potential applications, hydrogen is the subject of active research and development in many fields.

Simple models based on electricity prices can be used to demonstrate different scenarios for hydrogen production in various markets. It is found that to gain economic benefits, the usage of solar or other renewable energy power is mandatory.

The study of this algorithm, which is based on SP-MCTS ideas, is used to define the optimal control strategy for the electrolyser in terms of the production of H2.

One of the advantages of MCTS is that it is able to search for problem solutions when the electrolyser is in any state and can thus be used ad hoc.