Research on the Gas-Liquid Two-Phase Distribution Behavior and Influencing Factors of Swirling Flow in Horizontal Pipe
Abstract
:1. Introduction
2. Research Methods
2.1. Experimental Methods and Image Processing
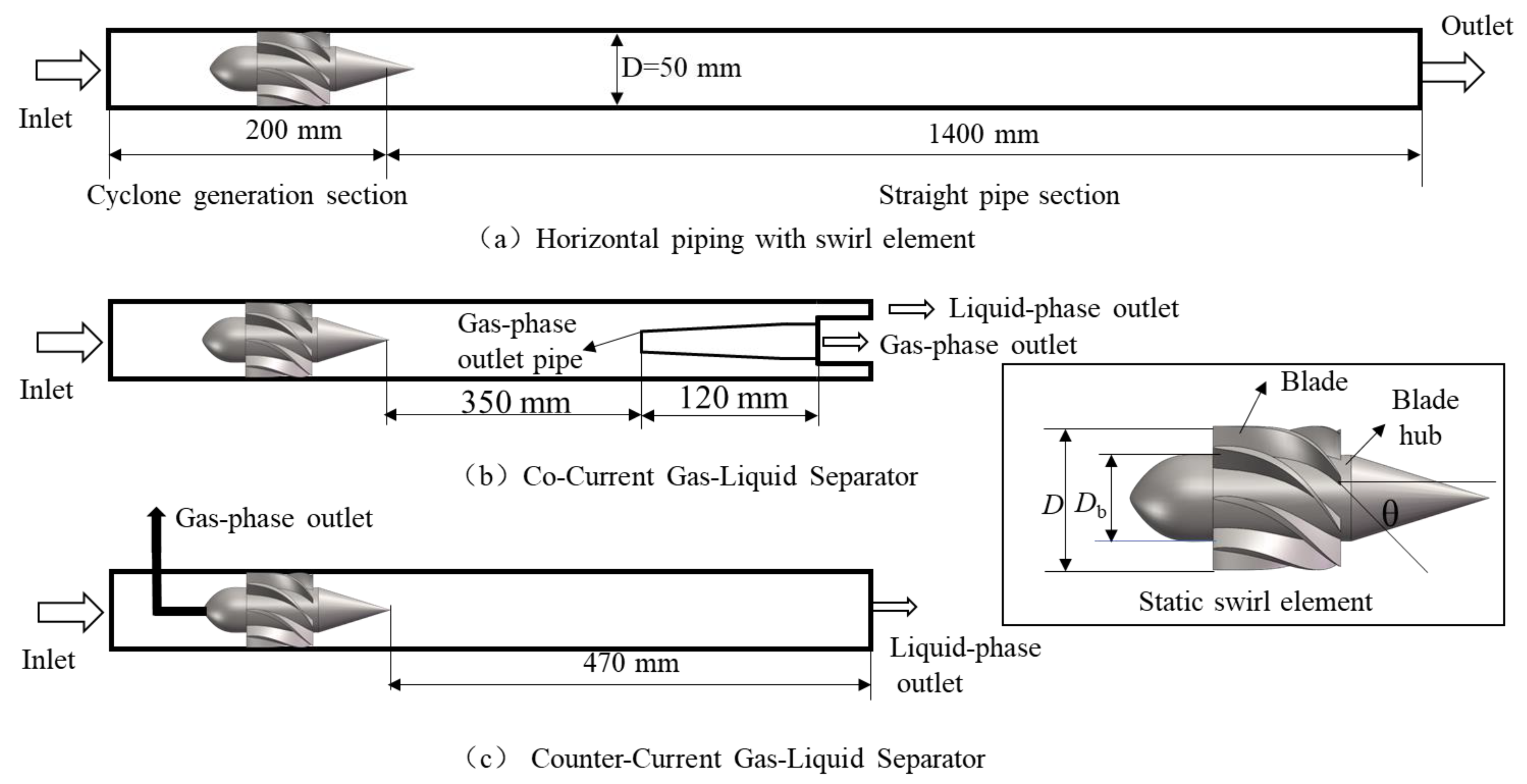
2.1.1. Research Object
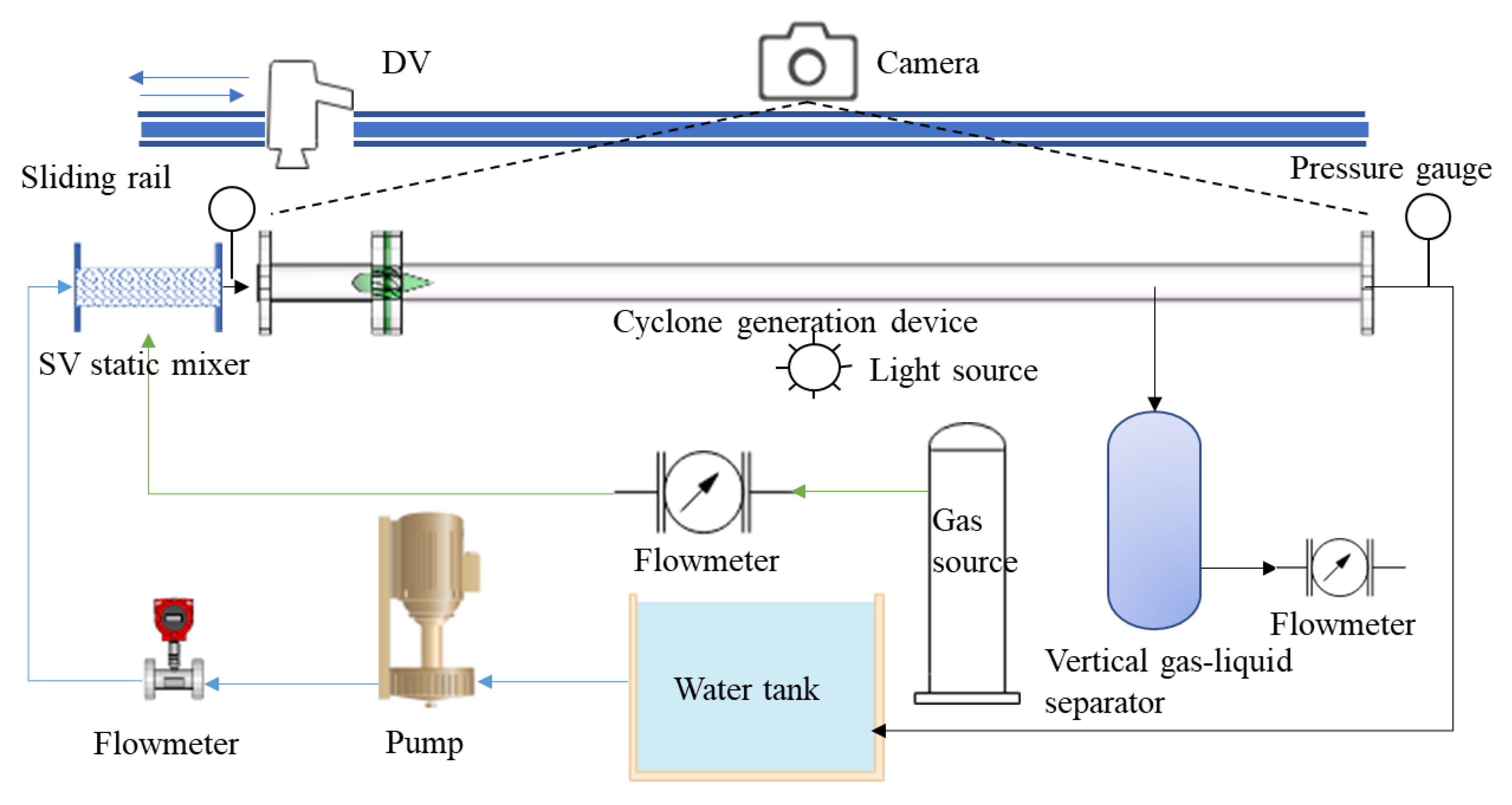
2.1.2. Visualization Experiment System
2.1.3. Image Processing Process
2.2. Numerical Simulation Methods and Model Validation
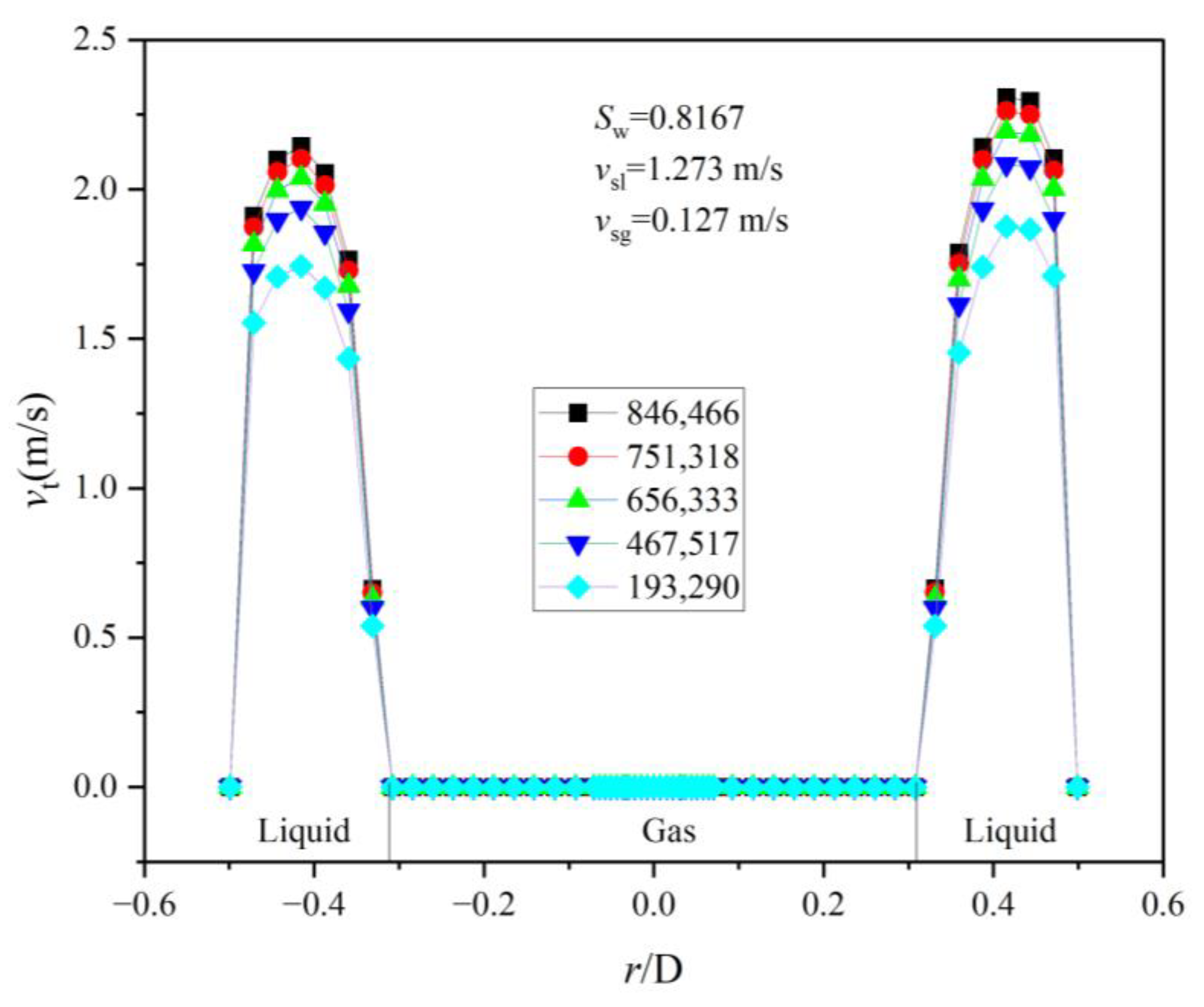
2.2.1. Grid Generation and Validation
2.2.2. Model Settings
2.2.3. Model Validation
3. Results and Discussion
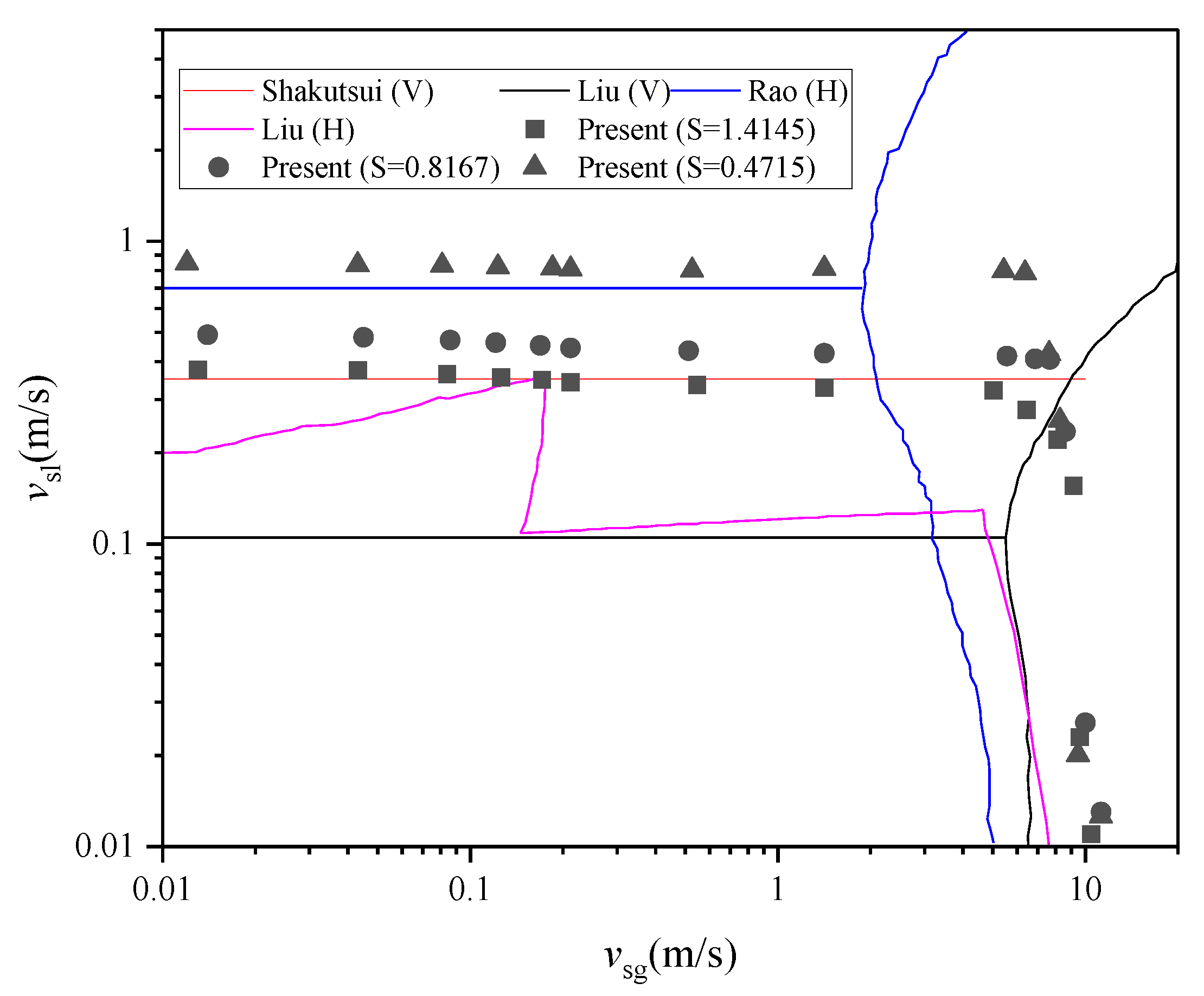
3.1. Formation Conditions of Swirling Flow
3.2. Rotational Field Decay and Its Effect on Rotational Flow
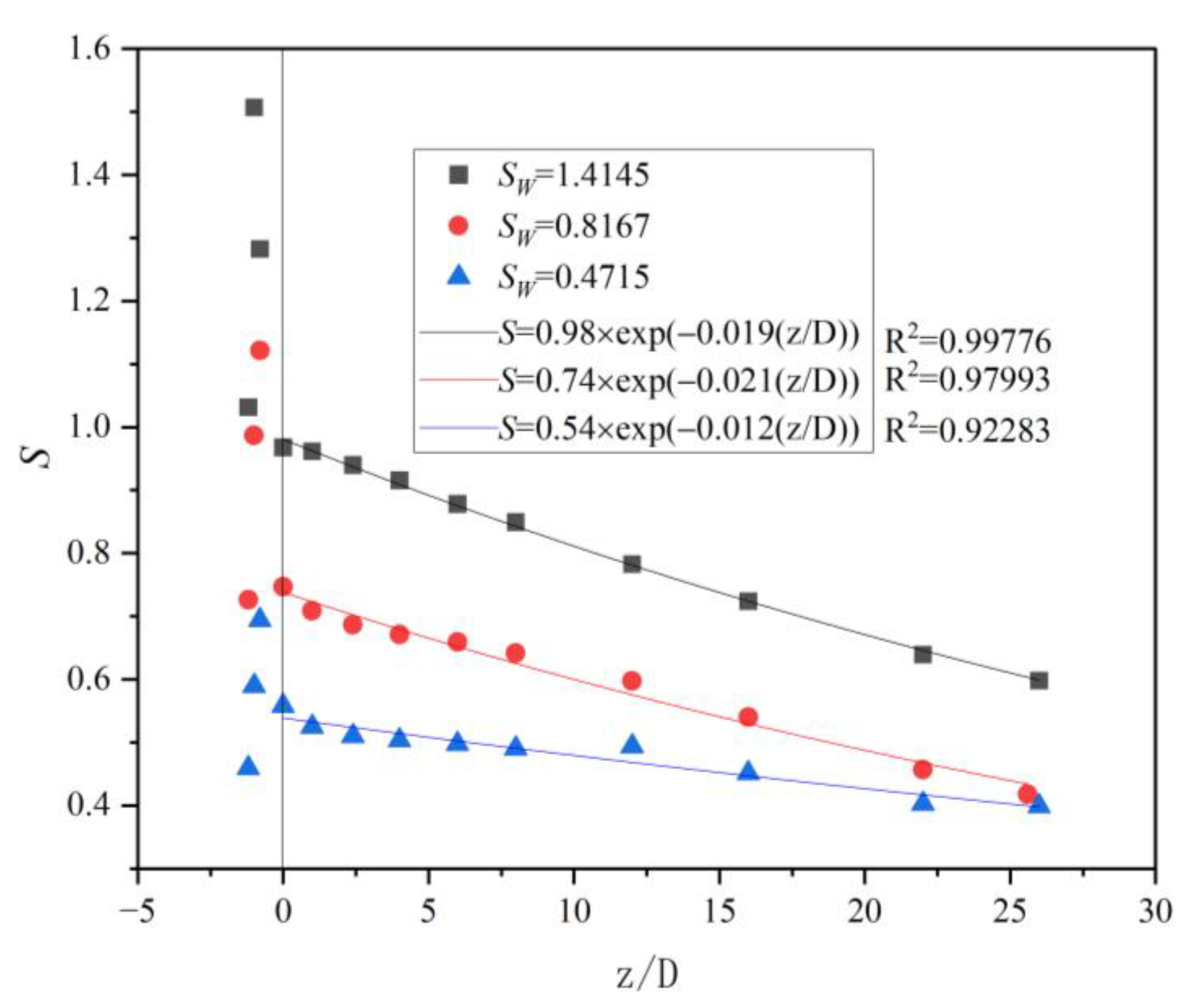
3.2.1. Decay Law of the Rotational Flow Field
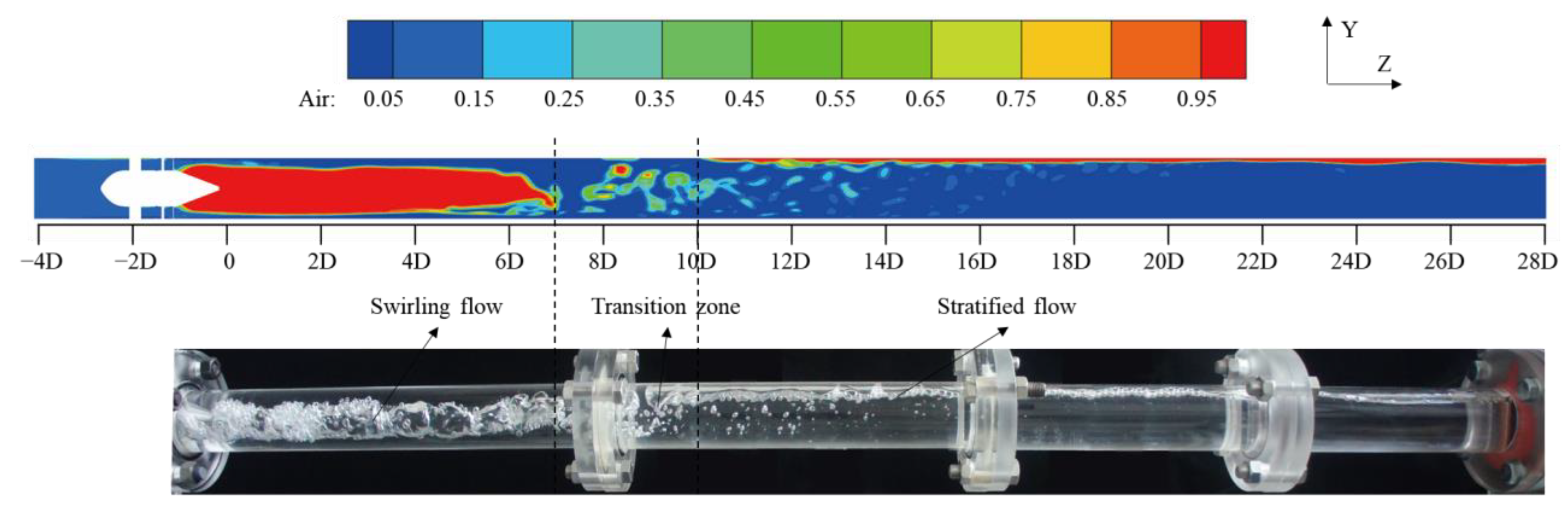
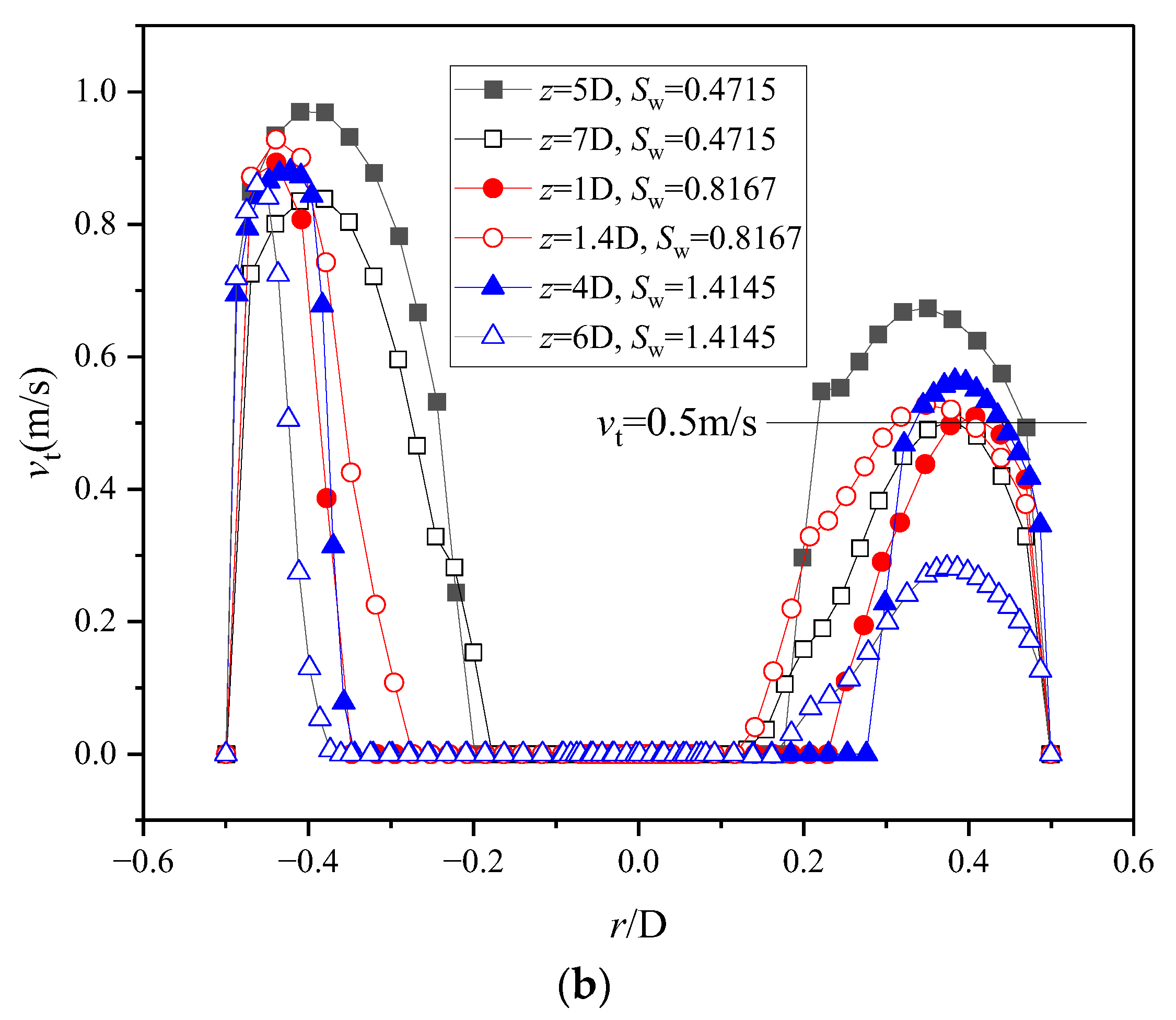
3.2.2. Effect of Cyclonic Field Decay on Flow Pattern Transformation
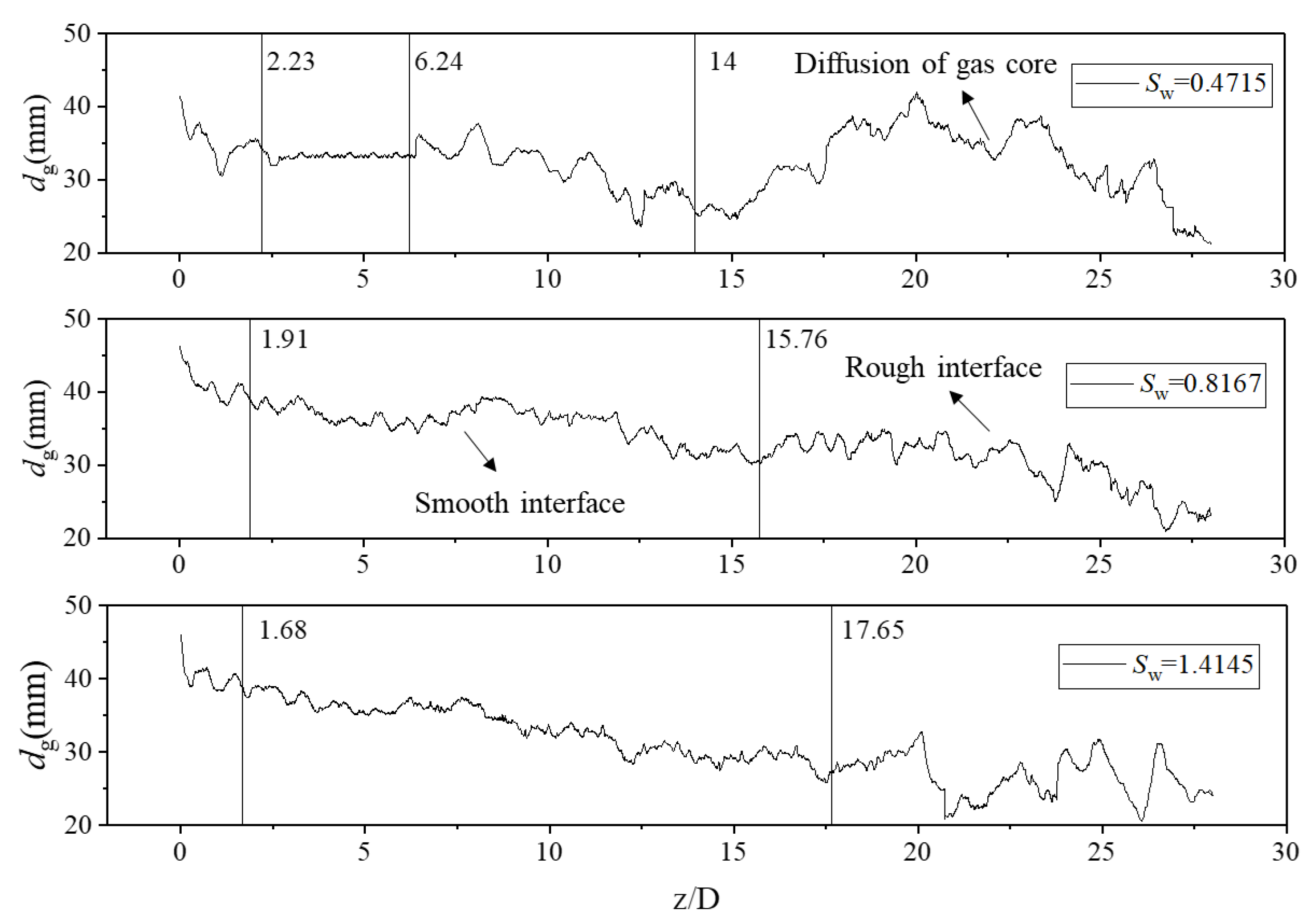
3.2.3. Effect of Cyclonic Field Decay on the Gas-Liquid Interface
3.3. Effect of Separation Method on the Gas-Liquid Morphology of Swirling Flow
3.3.1. Gas-Liquid Morphology in Co-Current Gas-Liquid Separator
- (1)
- Effect of flow split on gas-liquid morphology
- (2)
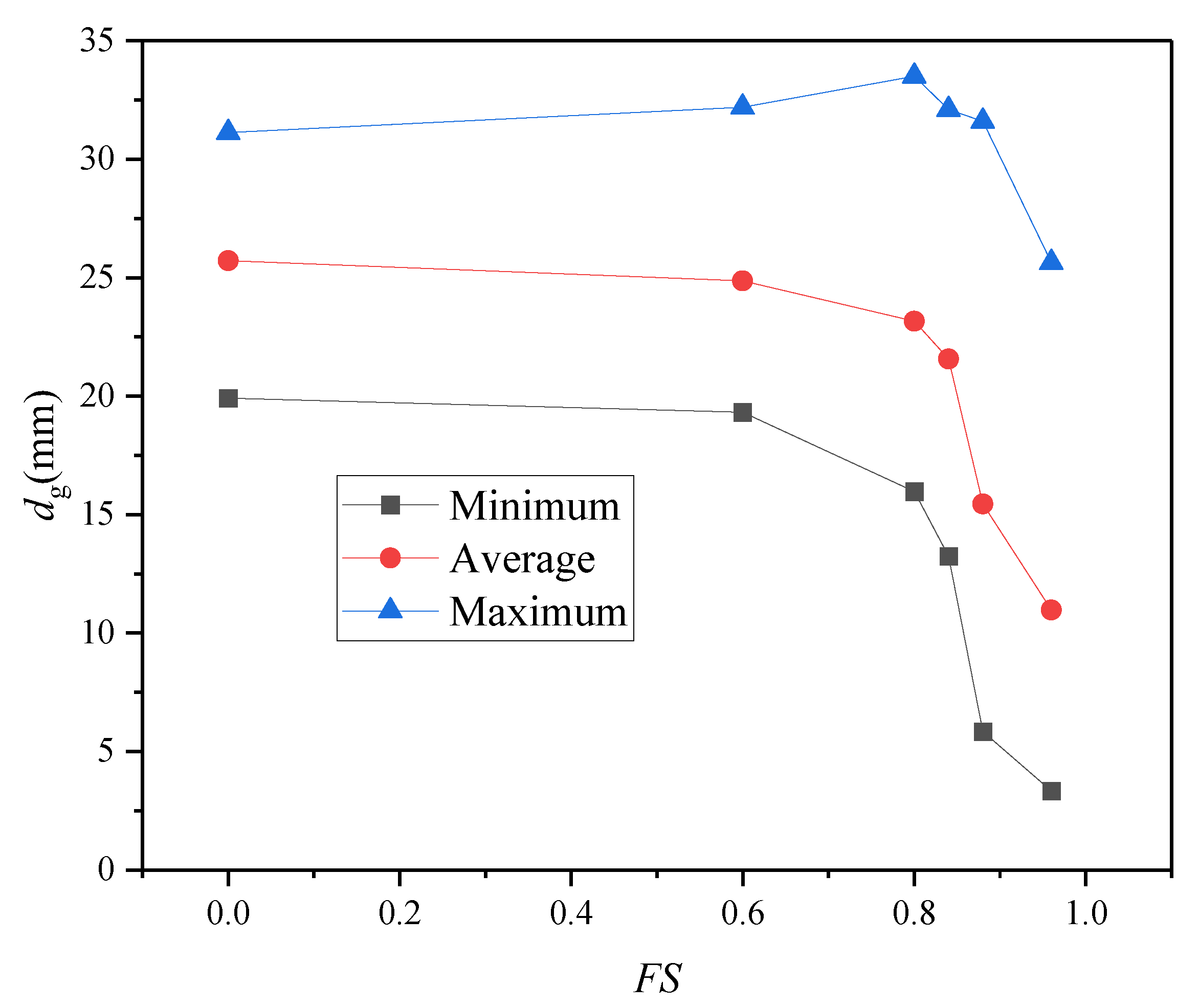
- Effect of FS on gas core diameter
3.3.2. Gas-Liquid Morphology in the Counter Gas-Liquid Separator
- (1)
- Effect of flow split on gas-liquid morphology
- (2)
- Effect of FS on gas core diameter
4. Conclusions
- (1)
- Experimental methods are used to obtain the critical condition for the formation of swirling flow in horizontal pipe. The formation of rotational flow is determined by the inlet superficial liquid velocity and influenced by the geometric swirl number when the inlet superficial gas velocity is less than 10 m/s. However, for superficial gas velocities greater than 10 m/s, the inlet superficial liquid velocity hardly affects the formation of rotational flow.
- (2)
- The effects of the decay of swirl number and tangential velocity on the gas-liquid flow pattern and interface morphology in the horizontal pipe are investigated. The decay of tangential velocity in the flow field is the key to transforming the rotational flow into a stratified flow when the rotational intensity is small. The decay of the flow field mainly affects the gas-liquid interface at higher rotational intensities.
- (3)
- In both co-current and counter gas-liquid separators, there exists a critical FS value that will cause vortex core breakdown at the center of the rotational flow field. The location of the vortex core breakdown is related to the low-pressure region in the cyclonic field. The diameter of the central gas core remains essentially the same when the FS < 0.6. When the FS > 0.6, the diameter of the gas core gradually reduces with the increment of the FS. The variation of gas core diameter is mainly related to the pressure distribution and vortex core breakdown of the cyclonic field in the separation section.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sines, J.N.; Straiton, B.J.; Zuccarelli, C.E.; Marashdeh, Q.M.; Teixeira, F.L.; Fan, L.-S.; Motil, B.J. Study of Gas-Water Flow Inside of a Horizontal Passive Cyclonic Gas-Liquid Phase Separator System Using Displacement-Current Phase Tomography. Gravit. Space Res. 2018, 6, 28–43. [Google Scholar] [CrossRef]
- Yin, J.; Qian, Y.; Zhang, T.; Wang, D. Measurement on the Flow Structure of a Gas-Liquid Separator Applied in TMSR. Ann. Nucl. Energy 2019, 126, 20–32. [Google Scholar] [CrossRef]
- Liu, S.; Yang, L.-L.; Zhang, D.; Xu, J.-Y. Separation Characteristics of the Gas and Liquid Phases in a Vane-Type Swirling Flow Field. Int. J. Multiph. Flow 2018, 107, 131–145. [Google Scholar] [CrossRef] [Green Version]
- Høydal, J.; Kristiansen, O.; Eikrem, G.O.; Fjalestad, K. Method and System for Fluid Separation with an Integrated Control System. US20150290560A1, 28 February 2018. Available online: https://patents.google.com/patent/US20150290560A1/en (accessed on 30 June 2023).
- Krishna, V.; Sripriya, R.; Kumar, V.; Chakraborty, S.; Meikap, B.C. Identification and Prediction of Air Core Diameter in a Hydrocyclone by a Novel Online Sensor Based on Digital Signal Processing Technique. Chem. Eng. Process. Process Intensif. 2010, 49, 165–176. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M.; Dirkzwager, M. A Fluid Mechanics Model for an Axial Cyclone Separator. Ind. Eng. Chem. Res. 1995, 34, 3399–3404. [Google Scholar] [CrossRef]
- Wang, S.L.; Rao, Y.C.; Wu, Y.X.; Zhou, S.D.; Sun, L. Experimental Study on Gas-Liquid Spiral Flow Generated by Twist Tape. Chin. J. Hydrodyn. Ser. A 2013, 28, 105–110. [Google Scholar]
- Liu, W.; Bai, B. Transition from Bubble Flow to Slug Flow along the Streamwise Direction in a Gas–Liquid Swirling Flow. Chem. Eng. Sci. 2019, 202, 392–402. [Google Scholar] [CrossRef]
- Liu, L.; Bai, B. Flow Regime Identification of Swirling Gas-Liquid Flow with Image Processing Technique and Neural Networks. Chem. Eng. Sci. 2019, 199, 588–601. [Google Scholar] [CrossRef]
- Liu, S.; Liu, L.; Zhang, J.; Gu, H. Experimental Study on Flow Patterns of Decaying Swirling Gas-Liquid Flow in a Horizontal Pipe. In Volume 3: Student Paper Competition—Thermal-Hydraulics: Verification and Validation, Proceedings of the 2020 International Conference on Nuclear Engineering Collocated with the ASME 2020 Power Conference, Virtual, Online, 4–5 August 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020. [Google Scholar]
- Wang, G.; Yan, C.; Fan, G.; Wang, J.; Xu, J.; Zeng, X.; Liu, A. Experimental Study on a Swirl-Vane Separator for Gas–Liquid Separation. Chem. Eng. Res. Des. 2019, 151, 108–119. [Google Scholar] [CrossRef]
- Hoffmann, A.C.; de Jonge, R.; Arends, H.; Hanrats, C. Evidence of the ‘Natural Vortex Length’ and Its Effect on the Separation Efficiency of Gas Cyclones. Filtr. Sep. 1995, 32, 799–804. [Google Scholar] [CrossRef]
- Qian, F.; Zhang, M. Study of the Natural Vortex Length of a Cyclone with Response Surface Methodology. Comput. Chem. Eng. 2005, 29, 2155–2162. [Google Scholar] [CrossRef]
- Concha, F.; Barrientos, A.; Montero, J.; Sampaio, R. Air Core and Roping in Hydrocyclones. Int. J. Min. Process. 1996, 44–45, 743–749. [Google Scholar] [CrossRef]
- Davidson, M.R. An Adaptive Method of Predicting the Air Core Diameter for Numerical Models of Hydrocyclone Flow. Int. J. Min. Process. 1995, 43, 167–177. [Google Scholar] [CrossRef]
- Steffens, P.R.; Whiten, W.J.; Appleby, S.; Hitchins, J. Prediction of Air Core Diameters for Hydrocyclones. Int. J. Min. Process. 1993, 39, 61–74. [Google Scholar] [CrossRef]
- Neesse, T.; Dueck, J. Air Core Formation in the Hydrocyclone. Min. Eng. 2007, 20, 349–354. [Google Scholar] [CrossRef]
- Yin, J.; Qian, Y.; Ma, Y.; Wang, D. Experimental Study on the Bubble Trajectory in an Axial Gas-Liquid Separator Applied for Tritium Removal for Molten Salt Reactors. Nucl. Eng. Des. 2017, 320, 133–140. [Google Scholar] [CrossRef]
- Stevenson, P.; Sederman, A.J.; Mantle, M.D.; Li, X.; Gladden, L.F. Measurement of Bubble Size Distribution in a Gas–Liquid Foam Using Pulsed-Field Gradient Nuclear Magnetic Resonance. J. Colloid Interface Sci. 2010, 352, 114–120. [Google Scholar] [CrossRef] [PubMed]
- Ansys Fluent 2020 R1-Theory Guide. Available online: https://forum.ansys.com/forums/topic/ansys-fluent-2020-r1-theory-guide-user-guide-full-pdf/ (accessed on 30 June 2023).
- Chen, G.; Wang, Q.; He, S. Assessment of an Eulerian Multi-Fluid VOF Model for Simulation of Multiphase Flow in an Industrial Ruhrstahl-Heraeus Degasser. Metall. Res. Technol. 2019, 116, 617. [Google Scholar] [CrossRef]
- Zahedi, P.; Zhang, J.; Arabnejad, H.; McLaury, B.S.; Shirazi, S.A. CFD Simulation of Multiphase Flows and Erosion Predictions under Annular Flow and Low Liquid Loading Conditions. Wear 2017, 376–377, 1260–1270. [Google Scholar] [CrossRef]
- Parsi, M.; Agrawal, M.; Srinivasan, V.; Vieira, R.E.; Torres, C.F.; McLaury, B.S.; Shirazi, S.A.; Schleicher, E.; Hampel, U. Assessment of a Hybrid CFD Model for Simulation of Complex Vertical Upward Gas-Liquid Churn Flow. Chem. Eng. Res. Des. 2016, 105, 71–84. [Google Scholar] [CrossRef]
- Akhlaghi, M.; Mohammadi, V.; Nouri, N.M.; Taherkhani, M.; Karimi, M. Multi-Fluid VoF Model Assessment to Simulate the Horizontal Air–Water Intermittent Flow. Chem. Eng. Res. Des. 2019, 152, 48–59. [Google Scholar] [CrossRef]
- Tianxing, Z.; Khezzar, L.; AlShehhi, M.; Xia, Y.; Hardalupas, Y. Experimental Investigation of Air–Water Turbulent Swirling Flow of Relevance to Phase Separation Equipment. Int. J. Multiph. Flow 2019, 121, 103110. [Google Scholar] [CrossRef]
- Shakutsui, H.; Hayashi, K.; Suzuki, T. Flow Patterns of Gas-Liquid Two-Phase Swirling Flow in a Vertical Pipe. Jpn. J. Multiph. Flow 2010, 24, 305–312. [Google Scholar] [CrossRef]
- Rao, Y.; Liu, Z.; Wang, S.; Li, L. Numerical Simulation on the Flow Pattern of a Gas–Liquid Two-Phase Swirl Flow. ACS Omega 2022, 7, 2679–2689. [Google Scholar] [CrossRef] [PubMed]
- Sheen, H.J.; Chen, W.J.; Jeng, S.Y.; Huang, T.L. Correlation of Swirl Number for a Radial-Type Swirl Generator. Exp. Fluid Sci. 1996, 12, 444–451. [Google Scholar] [CrossRef]
- Li, H.; Tomita, Y. Characteristics of Swirling Flow in a Circular Pipe. J. Fluids Eng. 1994, 116, 370–373. [Google Scholar] [CrossRef]
- Kitoh, O. Experimental Study of Turbulent Swirling Flow in a Straight Pipe. J. Fluid Mech. 1991, 225, 445–479. [Google Scholar] [CrossRef]
- Steenbergen, W.; Voskamp, J. The Rate of Decay of Swirl in Turbulent Pipe Flow. Flow Meas. Instrum. 1998, 9, 67–78. [Google Scholar] [CrossRef]
- Murphy, S.; Delfos, R.; Pourquié, M.J.B.M.; Olujić, Ž.; Jansens, P.J.; Nieuwstadt, F.T.M. Prediction of Strongly Swirling Flow within an Axial Hydrocyclone Using Two Commercial CFD Codes. Chem. Eng. Sci. 2007, 62, 1619–1635. [Google Scholar] [CrossRef]
- Reader-Harris, M.J. The Decay of Swirl in a Pipe. Int. J. Heat Fluid Flow 1994, 15, 212–217. [Google Scholar] [CrossRef]
- Lucca-Negro, O.; O’Doherty, T. Vortex Breakdown: A Review. Prog. Energy Combust. Sci. 2001, 27, 431–481. [Google Scholar] [CrossRef]
- Jochmann, P.; Sinigersky, A.; Hehle, M.; Schäfer, O.; Koch, R.; Bauer, H.-J. Numerical Simulation of a Precessing Vortex Breakdown. Int. J. Heat Fluid Flow 2006, 27, 192–203. [Google Scholar] [CrossRef]
- Syred, N. A Review of Oscillation Mechanisms and the Role of the Precessing Vortex Core (PVC) in Swirl Combustion Systems. Prog. Energy Combust. Sci. 2006, 32, 93–161. [Google Scholar]
- Gomez, E.L. Dispersed Two-Phase Swirling Flow Characterization for Predicting Gas Carry-under in Gas-Liquid Cylindrical Cyclone Compact Separators. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2001. [Google Scholar]












| Research Subjects | Inlet Superficial Liquid Velocity (m/s) | Inlet Superficial Gas Velocity (m/s) | Geometric Swirl Number | Flow Split | Experiment | CFD |
|---|---|---|---|---|---|---|
| cyclonic flow pipe | 0.142, 0.283, 0.325, 0.375, 1.415, 1.839 | 0.042 | 1.4145 | 0 | √ | × |
| 0.375 | 0.127, 0.212 | 1.4145 | 0 | √ | × | |
| 1.839 | 0.042, 0.127, 0.212 | 1.4145 | 0 | √ | × | |
| 1.13 | 0.21 | 0.4715, 0.8167, 1.4145 | 0 | √ | √ | |
| 0.318 | 0.032 | 1.4145 | 0 | √ | √ | |
| 0.4 | 0.04 | 0.8167 | 0 | √ | √ | |
| 0.6 | 0.06 | 0.4715 | 0 | √ | √ | |
| co-current gas-liquid separators | 1.13 | 0.21 | 1.4145 | 0, 0.2, 0.6, 0.8, 0.84, 0.88, 0.92, 0.96 | √ | × |
| 0.5, 0.9, 1.0 | × | √ | ||||
| counter gas-liquid separators | 1.13 | 0.21 | 1.4145 | 0, 0.6, 0.8, 0.84, 0.88, 0.96 | √ | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Chen, J.; Wang, Q.; Kong, L.; Shang, C.; Wang, C.; Ding, G.; Ji, Y.; Lei, J. Research on the Gas-Liquid Two-Phase Distribution Behavior and Influencing Factors of Swirling Flow in Horizontal Pipe. Processes 2023, 11, 2057. https://doi.org/10.3390/pr11072057
Zhang M, Chen J, Wang Q, Kong L, Shang C, Wang C, Ding G, Ji Y, Lei J. Research on the Gas-Liquid Two-Phase Distribution Behavior and Influencing Factors of Swirling Flow in Horizontal Pipe. Processes. 2023; 11(7):2057. https://doi.org/10.3390/pr11072057
Chicago/Turabian StyleZhang, Ming, Jiaqing Chen, Qiangqiang Wang, Lingzhen Kong, Chao Shang, Chunsheng Wang, Guodong Ding, Yipeng Ji, and Junyong Lei. 2023. "Research on the Gas-Liquid Two-Phase Distribution Behavior and Influencing Factors of Swirling Flow in Horizontal Pipe" Processes 11, no. 7: 2057. https://doi.org/10.3390/pr11072057
APA StyleZhang, M., Chen, J., Wang, Q., Kong, L., Shang, C., Wang, C., Ding, G., Ji, Y., & Lei, J. (2023). Research on the Gas-Liquid Two-Phase Distribution Behavior and Influencing Factors of Swirling Flow in Horizontal Pipe. Processes, 11(7), 2057. https://doi.org/10.3390/pr11072057





