Abstract
As technology advances, electronic circuits are more vulnerable to errors. Soft errors are one among them that causes the degradation of a circuit’s reliability. In many applications, protecting critical modules is of main concern. One such module is Fast Fourier Transform (FFT). Real FFT (RFFT) is a memory-based FFT architecture. RFFT architecture can be optimized by its processing element through employing several types of adder and multipliers and an optimized memory usage. It has been seen that various blocks operate simultaneously in many applications. For the protection of parallel FFTs using conventional Error Correction Codes (ECCs), algorithmic-based fault tolerance (ABFT) techniques like Parseval checks and its combination are seen. In this brief, the protection schemes are applied to the single RAM-based parallel RFFTs and dual RAM-based parallel RFFTs. This work is implemented on platforms such as field programmable gate arrays (FPGAs) using Verilog HDL and on application-specific integrated circuit (ASIC) using a cadence encounter digital IC implementation tool. The synthesis results, including LUTs, slices registers, LUT–Flip-Flop pairs, and the frequency of two types of protected parallel RFFTs, are analyzed, along with the existing FFTs. The two proposed architectures with the combined protection scheme Parity-SOS-ECC present an 88% and 33% reduction in area overhead when compared to the existing parallel RFFTs. The performance metrics like area, power, delay, and power delay product (PDP) in an ASIC of 45 nm and 90 nm technology are evaluated, and the proposed single RAM-based parallel RFFTs architecture presents a 62.93% and 57.56% improvement of PDP in 45 nm technology and a 67.20% and 60.31% improvement of PDP in 90 nm technology compared to the dual RAM-based parallel RFFTs and the existing architecture, respectively.
1. Introduction
Due to the shrinkage of device dimensions in terms of length, width, and oxide thickness, as well as diminishing operating supply voltages, tolerating soft errors has become a major design technology problem that is challenging the reliability of VLSI system implementation. In turn, scaling reduces the area consumption and improves the throughput of the system, thereby reducing the cost of the overall system [1]. In recent years, the communication and signal processing circuits have become exceedingly complex to meet various features. An increase in area complexity can be handled efficiently by using technologies like CMOS through scaling the device, in order to incorporate a greater number of transistors within a smaller area. But this technology scaling makes the CMOS device highly error-prone [2]. Soft errors are one of the types of errors that temporarily upset the actual circuit operation. The prevention of soft errors can be performed either by employing specific manufacturing processes like Silicon on Insulator (SOI) or can be mitigated by adding additional hardware to the original circuitry for its protection [3].
Algorithm-based fault tolerance (ABFT) uses redundant computations within the algorithms to detect and correct errors caused by permanent or transient failures in the hardware, concurrently with normal operation, as it is an error detection, location, and correction scheme. Time redundancy and space redundancy are some of the means of classifying fault-tolerant schemes. For adding fault tolerance, time redundancy is a popular technique, in which the same computation is performed on the same processor at two (or more) different but close enough time periods, and then the results are compared, whereas in space redundancy, each computation is performed at more than one location in space (on different processors) and the results are compared. Generally, these computations are performed at the same time. Hardware and software fault tolerance are another two dimensions in the classification of fault-tolerant techniques.
All the above specified fault-tolerant techniques contain the below stages and these stages of fault tolerance are applicable to all the four classes of fault-tolerant schemes.
The stages are:
- error detection;
- fault location;
- reconfiguration;
- recovery and continued service.
The below scheme in Figure 1 outlines the operations in an ABFT system.

Figure 1.
Operations in ABFT algorithm.
To detect and correct errors caused by permanent or transient failures in the hardware, an ABFT uses redundant computations within the algorithm. It is clear from above that this approach is not a general mechanism as other approaches (e.g., the triple modular redundancy). On the contrary, it differs from algorithm to algorithm. However, when the modified algorithm is actually executed on a multiprocessor architecture, the overheads are required to be minimal in comparison to TMR. When compared to the original algorithm, the modified algorithm could take more time to operate on the encoded data. Checks are performed on the processing elements (PEs) to test the correctness of the output data in some of the existing fault-tolerant schemes. Checks are always performed on the data elements produced by the PEs in an ABFT scheme. To make this possible, the faulty PEs must not mask the error during the error detection or error correction phase [4].
An algorithm-based fault tolerance (ABFT) is one of the alternatives to make parallel operating modules fault-tolerant; it utilizes the circuit’s algorithmic properties for error identification and rectification. The area overhead is much smaller compared to the conventional protection schemes [5].
Under this, various schemes of protection came into existence, the conventional scheme includes the N-modular redundancy (NMR), in which the unprotected block is replicated N times and a voting mechanism is conducted between all the blocks for the error identification and correction [6]. One of the familiar schemes is the triple modular redundancy (TMR), where the original block is triplicated. But the added redundancy can increase the overhead in terms of area and power consumption. An energy-efficient soft error tolerance approach for digital signal processor (DSP) systems named algorithmic soft error tolerance (ASET) techniques are proposed, which provide an area and power overhead two times less to that of TMR [7].
The Fast Fourier Transform (FFT) block is the main module in various communication systems and signal processing circuits like digital filtering, digital image processing, etc. The protection of FFT networks is observed in [8,9,10]. Although countless FFT architectures are available, the pipelined and memory-based FFTs are commonly used [11,12].
Memory-based architectures, unlike pipelined architectures, generally use only one butterfly unit. Thus, their advantage is to save the hardware cost. Because a single butterfly processing element can complete only one butterfly operation per clock cycle, it implies a loss in overall processing speed. We can compensate this disadvantage by using the high radix or split radix algorithms. Furthermore, we can increase the system clock rate to achieve the required speed.
A type of FFT architecture that processes real signals, i.e., RFFT, is proposed, as most of the signals in the environment are real. This RFFT finds its applications in the biomedical field like optical coherence tomography (OCT), electrocardiography (ECG), electroencephalography (EEG), etc. [13,14,15].
In this work, the security of parallel memory-based RFFTs is considered. In particular, it is assumed that there can only be a single error on the method at any given point in time, and a novel combined fault-tolerant scheme is proposed and used in memory-based RFFT processors to decrease the failure recovery time.
In this brief, our major contributions are:
- We research the issues and challenges related to soft errors in digital systems.
- We propose a solution that can detect and correct the errors.
- We design and implement two memory-based Real Fast Fourier Transform (RFFT) architectures that achieve the proposed goals.
- Experimental results show that the proposed single RAM-based and dual RAM-based fault-tolerant parallel RFFT architectures are fault-tolerant, along with less hardware utilization in both FPGA and ASIC platforms.
- The successful implementation of RFFT architectures with a reduced hardware utilization.
This work is organized into seven sections, of which, Section 2 describes a brief literature survey on the various RFFT designs and protection schemes for parallel FFTs. Section 3 presents the problem statement and solution to it. Section 4 illustrates a brief study about different RFFT architecture methodologies. In Section 5, various protection schemes for parallel FFTs are studied. In Section 6, an experimental result of protected parallel RFFTs of different architectures is seen. Section 7 covers the conclusion of this work.
2. Literature Survey
Zhen Gao et al., in [16], proposed schemes for the protection of parallel CORDIC--based FFTs. The three schemes in it includes the traditional Error Correction Code (ECC) scheme, Parseval checks (Parity-SOS), and a new technique which is a combination of both, i.e., Parity-SOS-ECC. The resources requirement is less for the new technique in comparison to the previous two techniques.
Zhen Guo Ma et al., in [17], proposed a new memory-based Real Fast Fourier Transform (RFFT) architecture with a novel strategy of stage partitioning in radix-2 DIF RFFT algorithm to achieve a smaller data path area and a lower number of computation cycles using one or more processing elements. This work provides the best hardware utilization and less area time (AT) to that of the pipelined architecture.
Yu Xie et al., in [18], proposed a fault-tolerant method for a parallel pipelined structure in order to protect a single FFT. The proposed parallel pipelined architecture incorporates a modified reduced precision redundancy algorithm with ECCs, which can provide a better protection of FFTs with a moderate area overhead. To evaluate hardware utilization and validity, the architectures were implemented on an FPGA platform.
Xin Liang et al., in [19], presented a novel online ABFT scheme to detect and correct the soft errors in the FFT architectures. Whenever an error occurred, the proposed ABFT scheme needed to repeat a part of the computation. Based on the evaluation results, it improves the efficiency of the architectures twofold via a comparison with the existing schemes.
Ricardo Gonzalez-Toral et al., in [20], proposed three concurrent error detection schemes for the implementation of FFT architectures, particularly in static RAM-based FPGAs. To analyze the performance of the proposed architectures in detecting the errors occurring at the output stage, they forcefully injected the upsets in the FPGA configuration bits. Experimental results show that the architectures occupy a smaller area and are also less susceptible to single-event upsets.
Chuang-An Mao et al., in [21], designed an FFT architecture with automated fault injection by combining C++ and ICAP applications and the proposed architecture implemented on FPGA Xilinx Kintex 7 board to evaluate the design parameters.
Xin Wei et al., in [22], proposed a novel single-event upsets scheme with a dynamic partial reconfiguration technique for the protection of an FFT processor to reduce the failure recovery time. In this, authors used soft error mitigation (SEM) intellectual property IP cores to perform the SEU detection and correction of soft errors occurring in the configurable RAM and examined the trade-off between the consumption of hardware resources and fault tolerance; also, the architecture was implemented on Xilinx Kintex 7 FPGA platform.
T. Rajasekhar et al., in [23], presented the LC-CSLA-RFFT architecture to reduce the hardware complexity of an RFFT by employing a low-cost carry-select adder instead of a normal adder in its processing element. This work improved performance parameters such as the frequency of operation to that of a conventional RFFT when implemented on FPGA, as well as area, power, delay, APP, and ADP when implemented on ASIC.
Rajasekhar Turaka et al., in [24], illustrated a DRAM-VM-CLA methodology of an RFFT architecture, which uses the DRAM instead of two separate memories of a conventional RFFT for holding intermediate results, and an output of RFFT to improve the area constraint, as well as a Vedic multiplier and carry-look-ahead adder in butterfly unit for better operation. The results are evident for a reduction in area and an increase in frequency when implemented on FPGA.
Amit kumar et al. [25] proposed several variable-length FFT architectures, which support four radix types implemented on Virtex-5 FPGA board. All the modules were designed with very-high-speed hardware description language (VHDL) and analyzed the hardware performance in terms of DSP slices, blocked RAMs, and frequency with the help of Chipscope Pro Analyzer in Xilinx ISE software (https://www.xilinx.com).
From the above survey, it is understood that many researchers are carrying out investigations on different FFT architectures to understand the impact of power and area against the performance of the processors. Moreover, there is little research available related to the protection of memory-based FFT architectures.
With the above facts in mind, the present investigation was carried out and we developed a problem statement; the solutions are presented in Section 3.
3. Problem Statement
- For applications like OCT, OFDM, etc., high-speed and fault-tolerant FFTs are used, in which all of the FFTs operate in parallel to process different data at a time.
- In the FFT architecture, the processing element (PE) plays a major role. The efficient design of its components decides the entire architectural efficiency (in terms of area, power, and delay), which depends on choosing proper adder and multiplier architectures.
- Soft error occurrence may affect the FFT operation for an iteration time, which leads to the corruption of the processed data of that particular iteration.
- Therefore, protected parallel FFTs with less redundancy is needed.
Solution: In this work, to achieve the highly protective and reduced amount of overhead parallel FFTs, there is a requirement of incorporating fault-tolerant methodology through schemes, such as error correction codes (ECCs), Parseval check, and a fusion of ECCs and Parseval check to the different types of RFFT architectures mentioned in Section 3. In this paper, two memory-based parallel architectures single RAM-based RFFT and a dual RAM-based RFFT are proposed. The former uses only a single memory block and the latter uses two memory blocks for the complete computations of butterfly operations involved in the 32-point RFFT architecture. Both proposed architectures avoid the memory conflict, which is the major constraint in the implementation of memory-based or in-place RFFT architectures. The single RAM-based RFFT bank provides protection with high speed and less area than that of dual RAM-based RFFTs when implemented on FPGA, and vice versa in ASIC.
4. RFFT Architectures
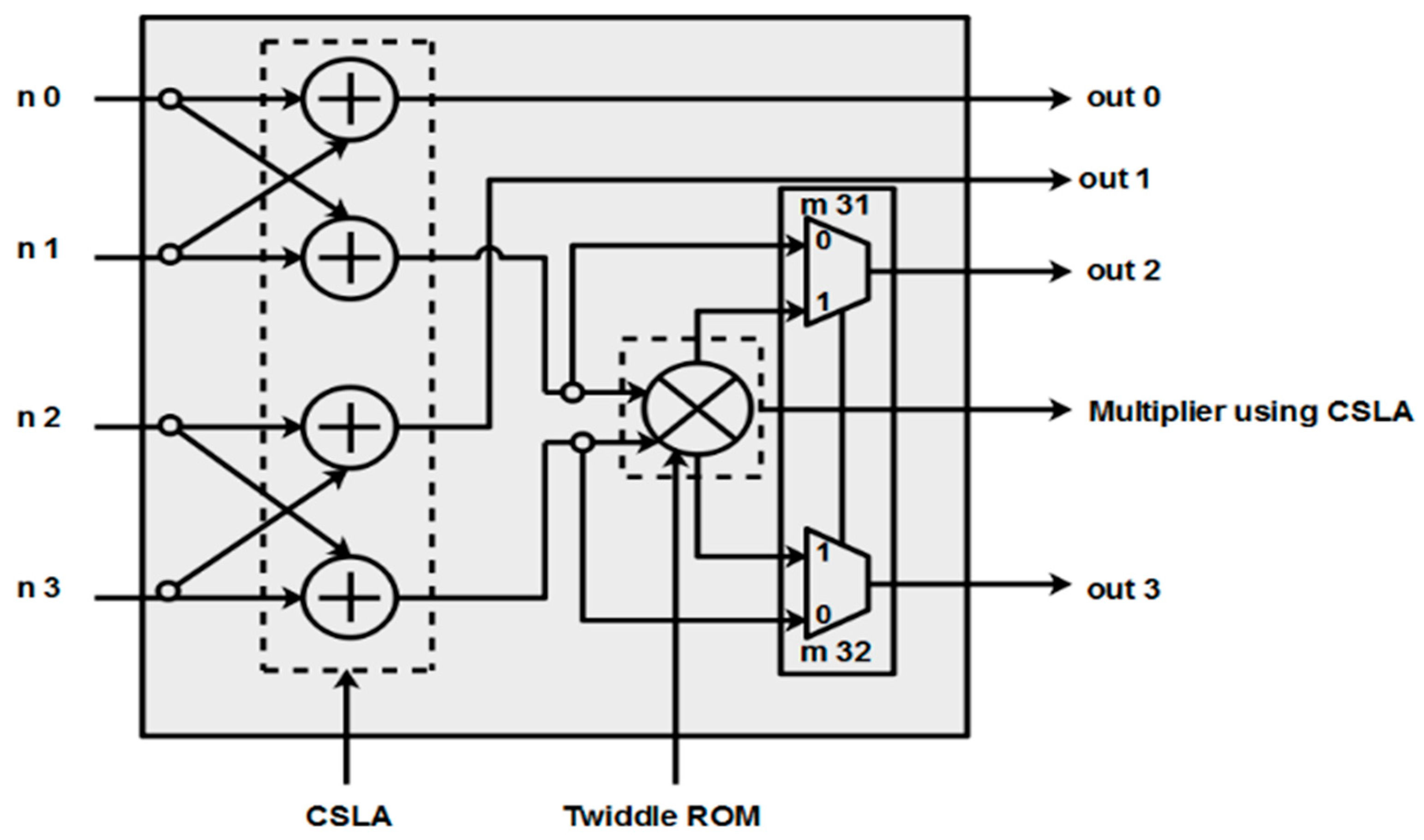
An RFFT architecture is used in applications where the processing of the signals in an environment is needed, as discussed in Section 1. A previous pipelined RFFT architecture exists, which provides hardware optimization at the cost of less speed. However, A novel memory-based RFFT architecture was later introduced, which improves the speed of operation along with the feature to overcome the challenge of high hardware utilization by employing a new stage partition strategy. In this strategy, the last two stages do not have any multiplier units, and the case of multiplication with ‘W0’ twiddle factor is also avoided, as its value is ‘1’. The new stage partition representation for a 32-point input of radix-2-based DIF FFT is shown in Figure 2 [16]. This work included the processing of input using one or two processing elements that require a smaller number of complex adders and complex multipliers and memory to that of conventional RFFTs. The hardware utilization can be further improved in dual RAM-based CSLA methodology and single RAM-based VM-CLA methodology of RFFT architectures.

Figure 2.
A 32-point DIF RFFT butterfly.
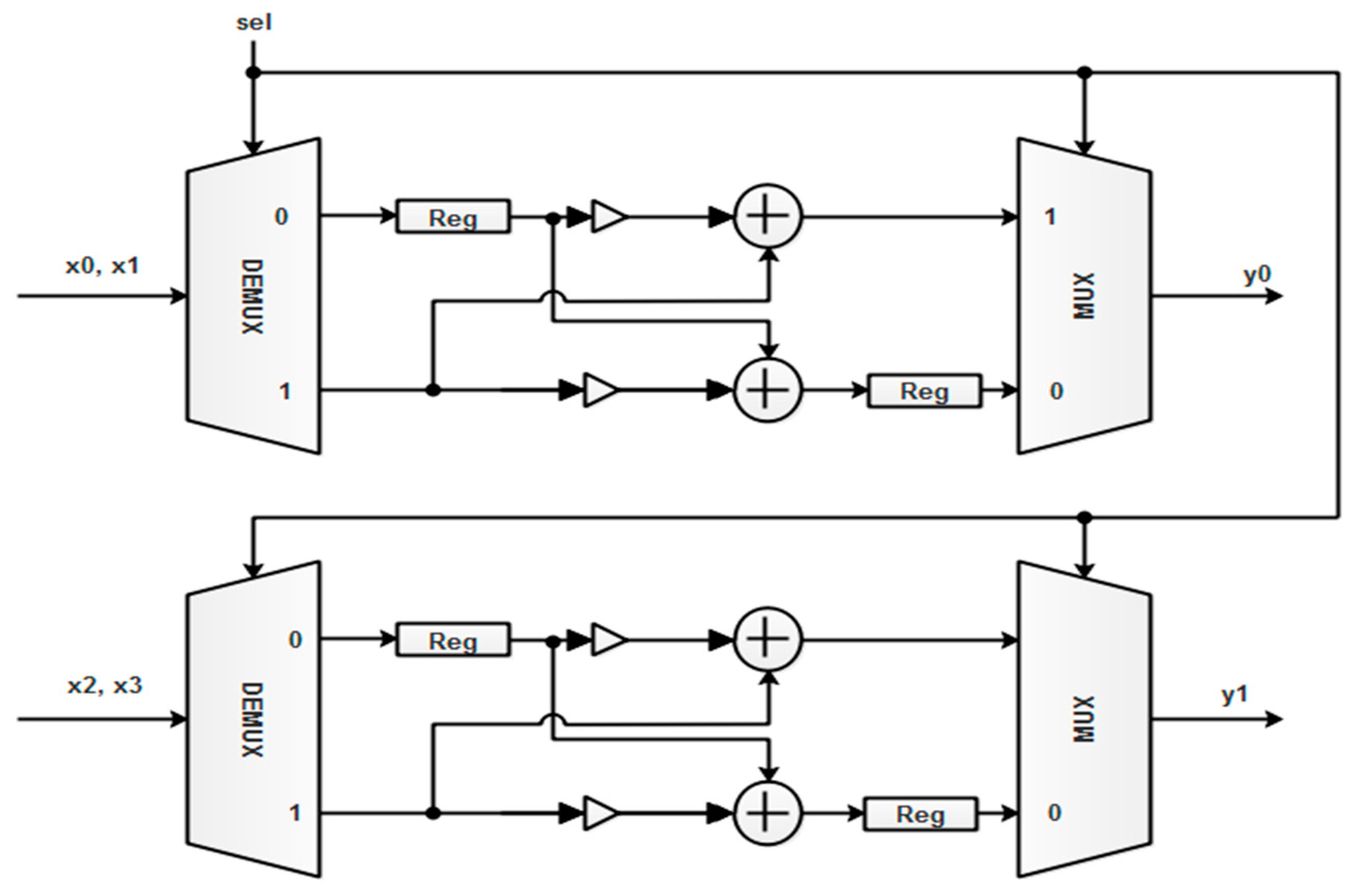
4.1. Dual RAM-Based RFFT Architecture
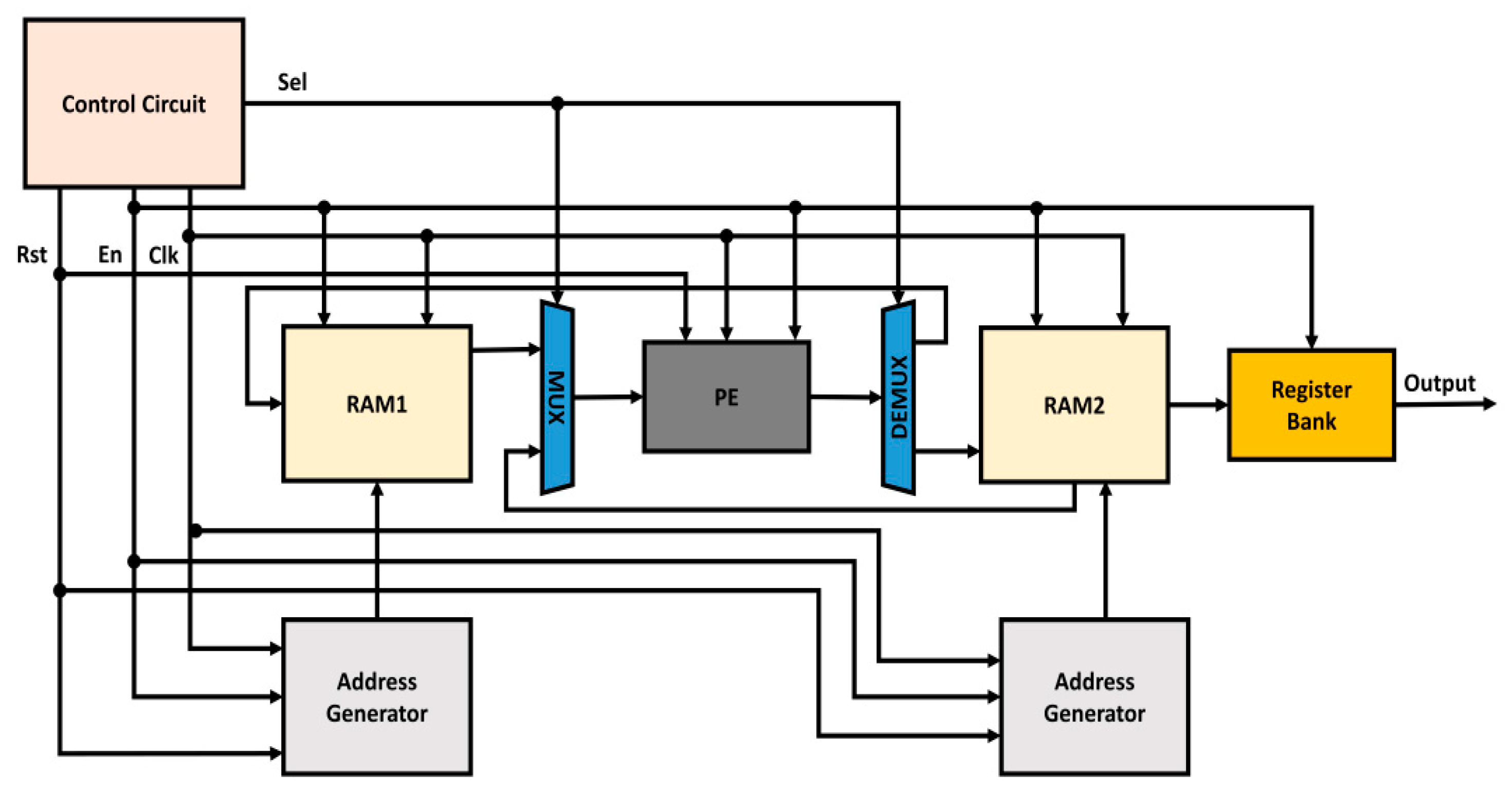
The basic blocks in this type of RFFT architecture [17] is depicted in Figure 3. The operation of each block can be summarized as below:
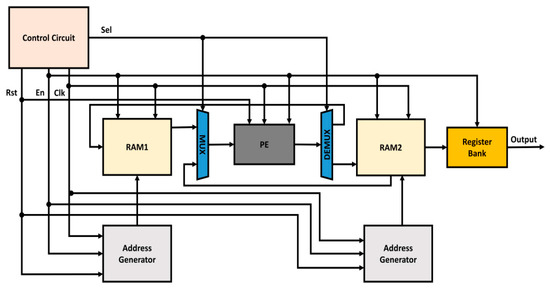
Figure 3.
Block diagram of dual RAM-based RFFT architecture.
- Control unit: For coordinating each and every block in the architecture.
- RAM0: To hold input data.
- RAM1: To hold intermediate data and output results.
- Address generators: To provide addresses to RAM0 and RAM1.
- Processing element: To perform butterfly operation.
- Multiplexer: To select which data to process among input and intermediate data.
- Demultiplexer: Distributes the processed data to RAM units.
- Register bank: Stores the final output.
The main components that the butterfly unit of FFT comprises are adders, multipliers, and multiplexers. The representation of a processing element with the carry-select adder as an adder architecture improves the FFT operation more than when using normal adders. ROM unit is to store the twiddle factor values generated using MATLAB R2022a.
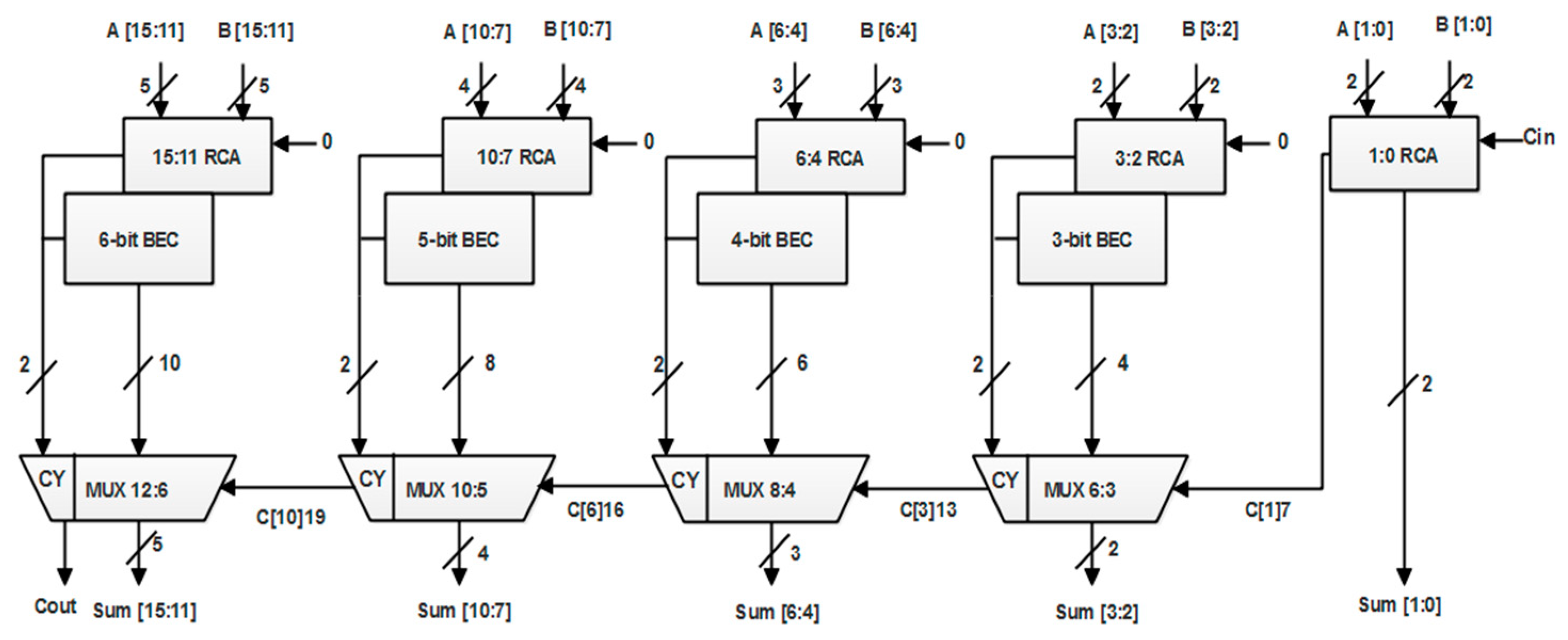
The block representation of PE with CSLA is depicted in Figure 4. Generally, the carry-select adder (CSLA) consists of ripple-carry adders and selection circuit such as multiplexer. Here, the carry-select adder is implemented with ripple-carry adders, binary-to-excess-1 code (BEC) circuits and multiplexers. The output carry and sum from the ‘k’ bit ripple-carry adder with input carry as bit ‘0’ fed to the ‘k + 1’ bit BEC results in an output that is the same as the output when we use the ripple-carry adder instead. The 16-bit CSLA implemented with BEC is shown in Figure 5. The number of logic gates required to implement BEC is less compared with the ripple-carry adder. Therefore, the use of BEC instead of normal ripple-carry adders result in a low design cost.
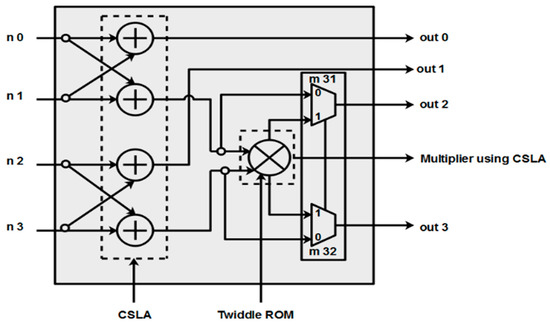
Figure 4.
Processing element with CSLA.
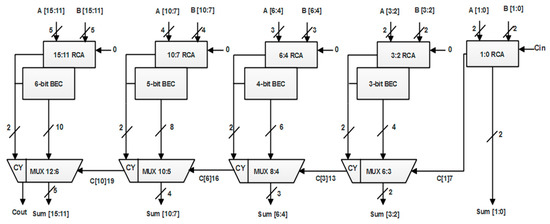
Figure 5.
16-bit CSLA implementation with BECs.
4.2. Single RAM-Based RFFT Architecture
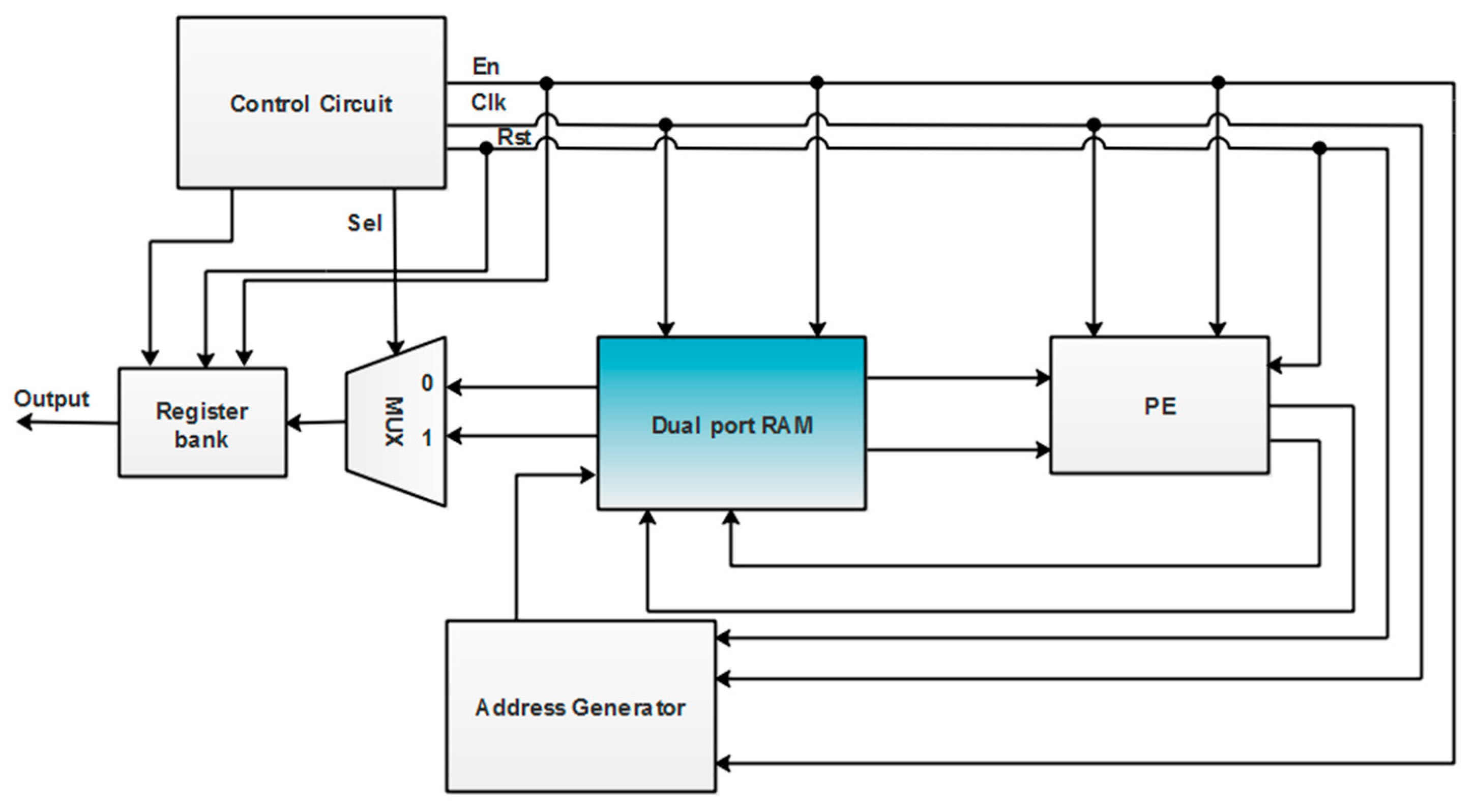
In this type of RFFT architecture [18], a single dedicated memory named ‘Dual-Port RAM’ (DPRAM) is considered here. It can handle the reading and writing of input, intermediate, and output data, to and from the PE. Moreover, aside from the adders, multipliers inside the processing element are also implemented with a Vedic multiplier (VM) and a carry-look-ahead adder (CLA) for a better FFT operation. The block diagram of this type of RFFT architecture is shown in Figure 6.
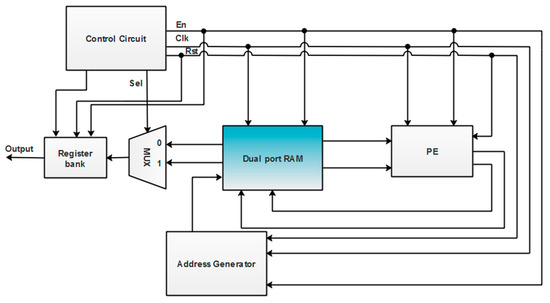
Figure 6.
Block diagram of single dual port RAM-based RFFT architecture.
The block diagram of a PE with the considered carry-look-ahead adder (CLA) and its result multiplied with the twiddle factors stored in twiddle ROM using Vedic multipliers and CLAs are depicted in Figure 7.
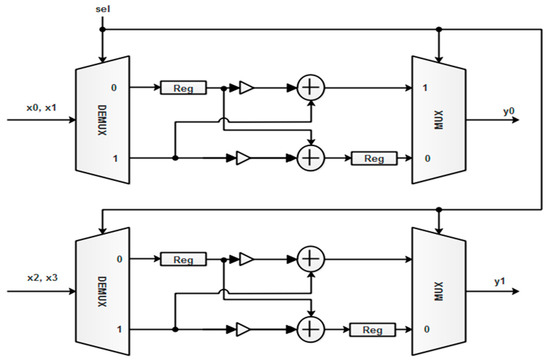
Figure 7.
Processing element with CLA.
5. Proposed Memory-Based Protection Techniques for Parallel RFFTs
5.1. Using Error Correction Codes (ECCs)
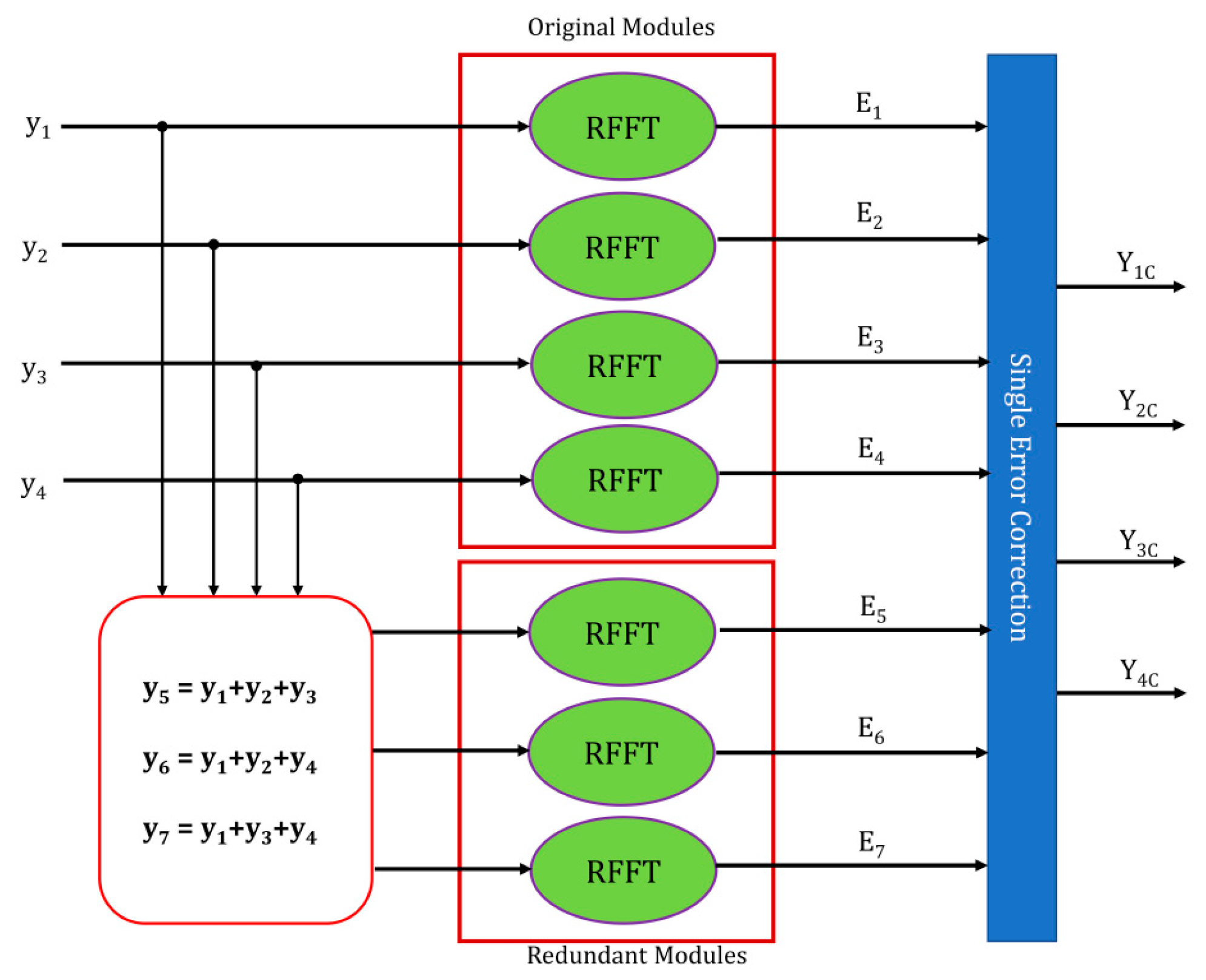
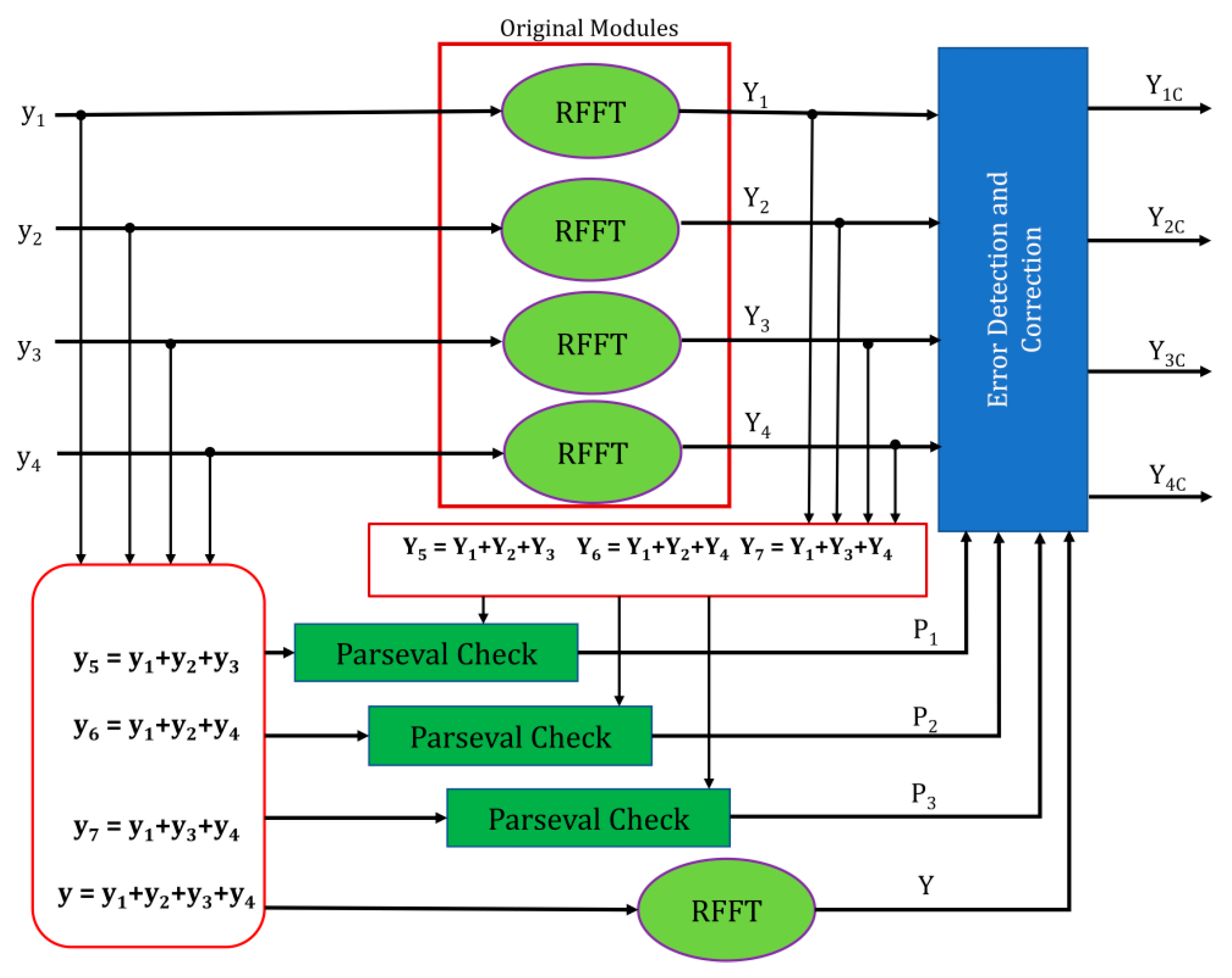
The protection of digital filters based on error correction codes (ECCs) is detailed in [14]. This work is considered as one of the main references for the protection of parallel RFFTs in our work. The protection of four parallel RFFTs using ECCs is presented in Figure 8. One of the ECCs, i.e., Hamming code, is utilized here for single-fault identification and rectification. For the protection of four actual RFFT modules, three additional RFFT blocks are added. The error identification and rectification using those three additional modules is explained with the help of necessary equations as follows.
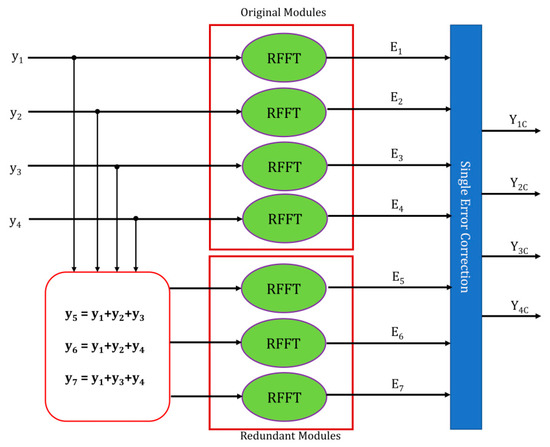
Figure 8.
Protection using error correction codes.
The actual RFFTs are fed with four inputs y1, y2, y3, and y4, having the four outputs E1, E2, E3, and E4, respectively. Each of the additional (Parity) blocks is fed with different linear combinations of actual inputs, according to the Hamming code concept, i.e.:
y5 = y1 + y2 + y3
y6 = y1 + y2 + y4
y7 = y1 + y3 + y4
As DFT obeys the linearity principle, the corresponding transformation results are:
E5 = E1 + E2 + E3
E6 = E1 + E2 + E4
E7 = E1 + E3 + E4
Each of these transformed results of additional blocks is treated as a check equation, i.e., b1, b2, and b3, to identify the fault presence. Once the fault is identified, its location is denoted by the combination of check equations tabulated in Table 1.

Table 1.
Error positions corresponding to check bits combination.
After that, the fault can be rectified by the correction equations. For instance, if the fault is identified at block Y2, then it can be corrected by the equation:
Y2c = E6 − E1 − E4
Similar correction equations are constructed for the remaining blocks, if they are at fault. Protection by this scheme requires ‘1 + log2k’ number of RFFT replicas. The hardware used increases when the power requirement is increased.
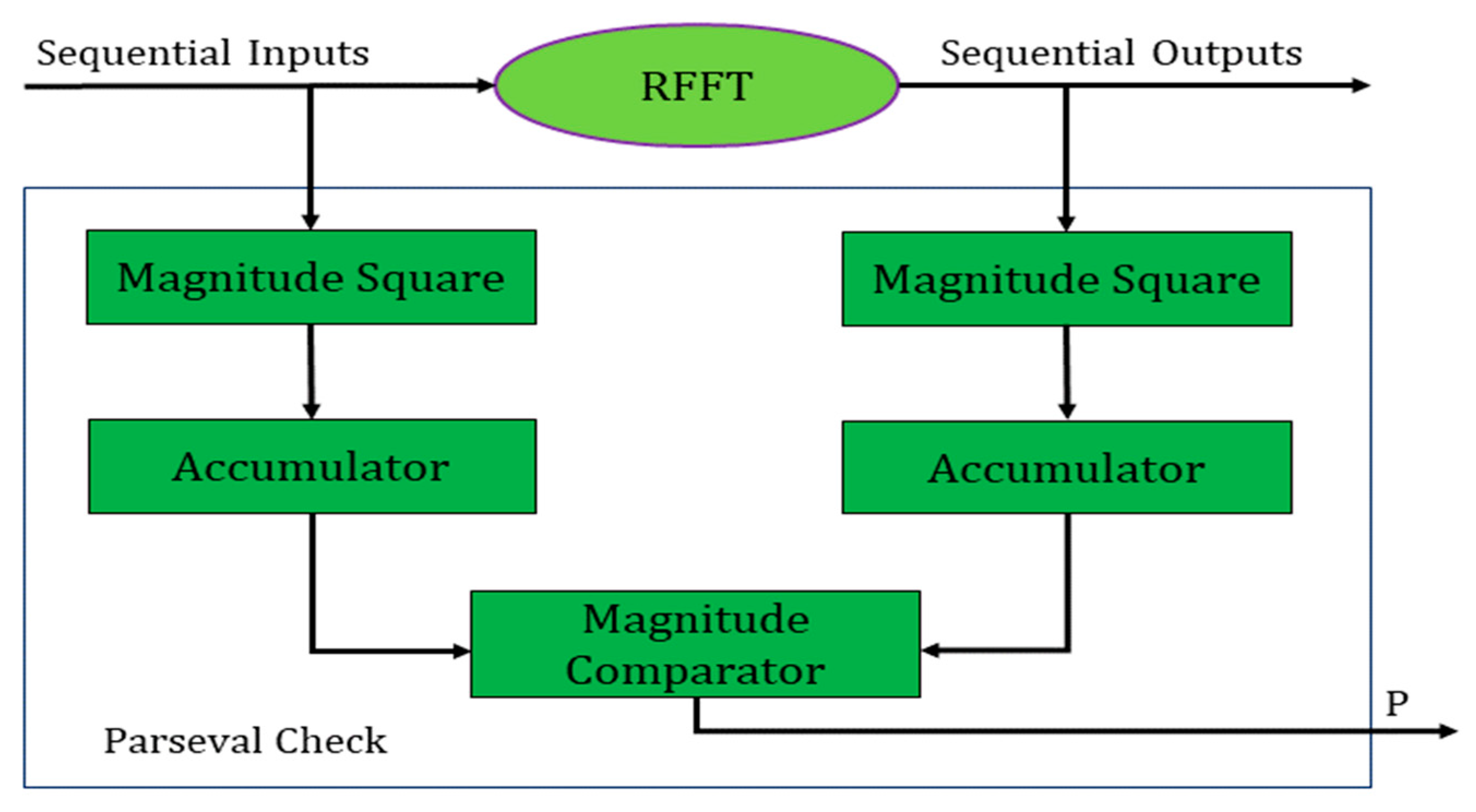
5.2. Using Parity Sum of Squares (SOSs)
The proposed Parity sum-of-squares (SOSs) technique relies on the Parseval theorem, which formulates that the sum of squares of inputs fed to a system is equal to the sum of squares of individual outputs with some multiplication factor. The SOS block for an FFT is shown in Figure 9.
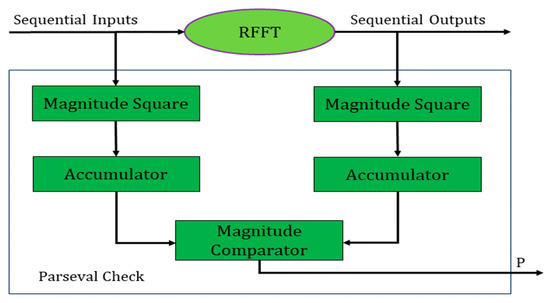
Figure 9.
Parseval (SOS) check for an FFT.
The protection of four RFFT blocks using SOS checks is depicted in Figure 10. In this scheme, each RFFT block is appended with an SOS block. These SOS blocks can only identify the fault by generating check bits (P1, P2, P3, P4). For fault correction, the extra RFFT (Parity) block is to be employed, having the input as a combination of actual inputs (y1, y2, y3, y4).
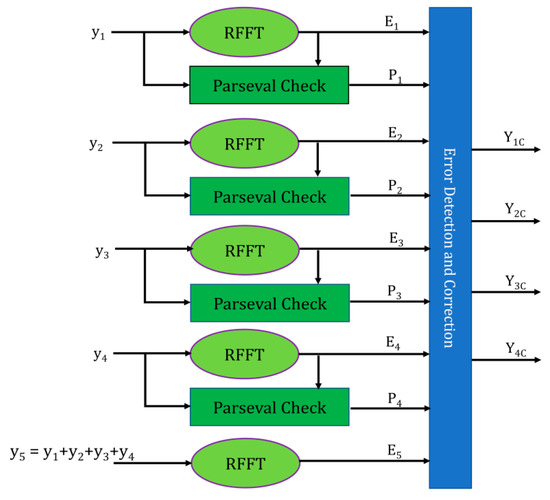
Figure 10.
Protection using Parity-SOS (Parseval check).
The error correction can be performed by the unaffected outputs. For instance, if the second RFFT is affected by the fault, P2 will be set and correction can be performed using Equation (8):
Y2c = Y − P1 − P3 − P4
It is observed that the hardware required to implement Parseval check is a lower amount to that of implementing FFT. By reducing the FFT number to one for protection, it is evident that the resource consumption is less in this scheme.
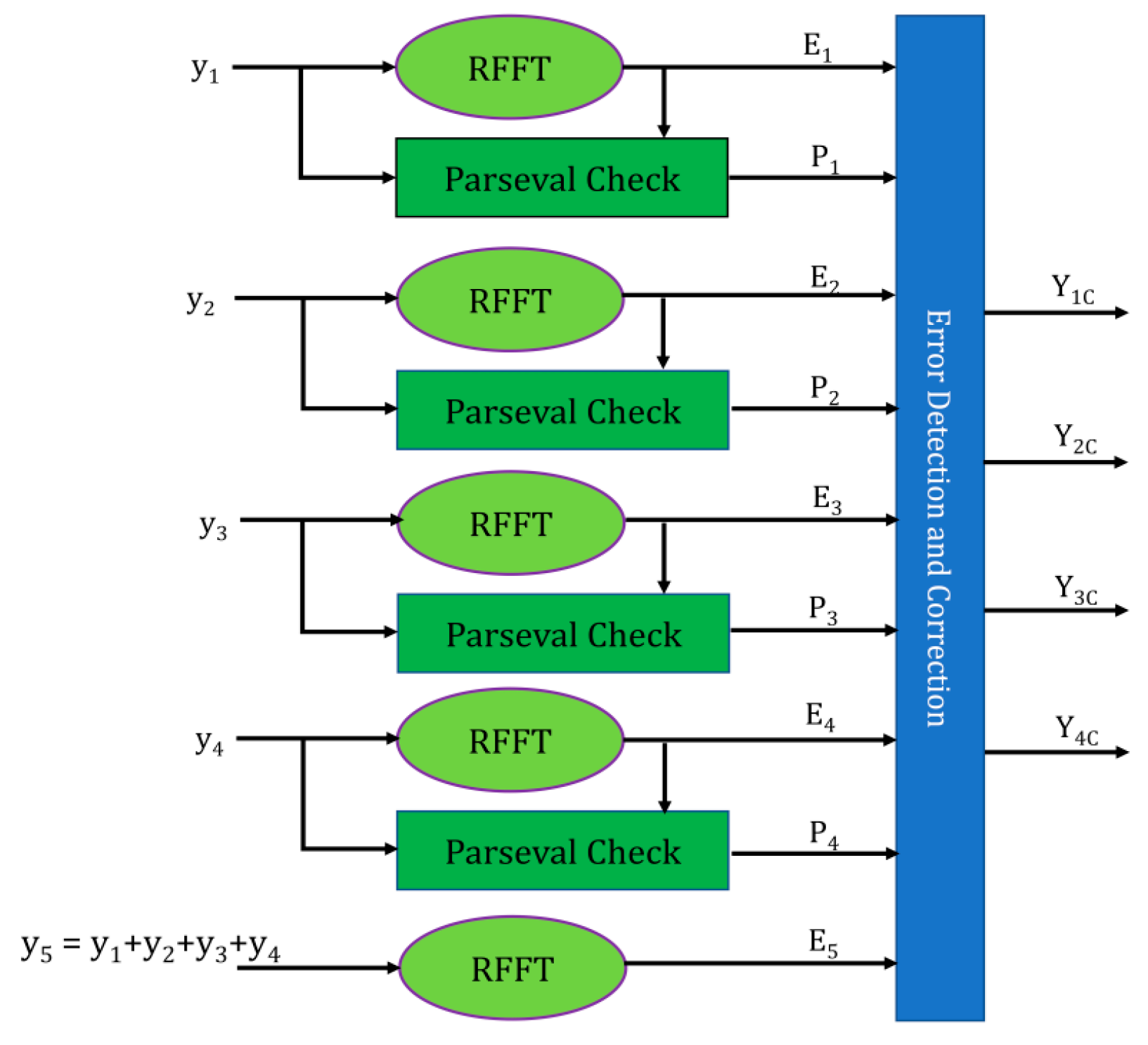
5.3. Using Parity-SOS-ECC
In this scheme, two previously refereed schemes are combined for providing better protection along with a reduced overhead in terms of area. In this scheme, the ECC is performed on SOS blocks rather than on RFFTs; in the first scheme, it is used for error recognition, and the correction of these errors can be performed by the redundant RFFT, similarly to the second scheme. This scheme’s block diagram is presented in Figure 11, where y1, y2, y3, and y4 are the four inputs to the parallel RFFTs, and the corresponding transformations are Y1, Y2, Y3, and Y4, respectively.
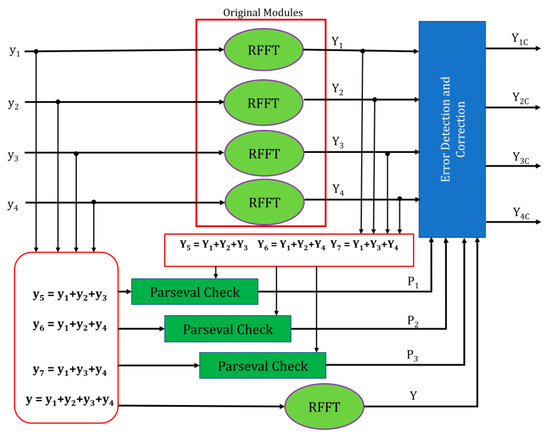
Figure 11.
Protection using Parity-SOS-ECC.
The linear combination of inputs (y5, y6, y7) based on the Hamming code, fed to the Parseval check blocks that identifies the error. Parity RFFT is fed with the sum of all actual inputs and Y is its output. The Y1, Y2, Y3, and Y4 are the correct transformed inputs. The number of SOS blocks is reduced to “1 + log2k” in this scheme instead of ‘k’ (where ‘k’ denotes the number of original RFFTs) in Parity-SOS. Therefore, the protection overhead is further reduced.
6. Experimental Results and Discussion
The three protection techniques, i.e., ECC, Parity-SOS, and the combination of the previous two techniques (Parity-SOS-ECC), are implemented for the parallel single RAM-based RFFTs and parallel dual RAM-based RFFTs. Here, four parallel RFFTs are considered. Each RFFT is implemented in radix-2 decimation-in-frequency (DIF) fed with an input of 32-bit length. These are implemented on Artex-7 FPGA devices using Verilog HDL in Xilinx Vivado 2022.1. The area in terms of slice registers, slice LUTs, LUT–Flip-Flop pairs, frequency, and delay are analyzed. Table 2 presents the FPGA resource usage of the protected parallel RFFTs. The hardware resource utilization single RAM-based RFFTs is better in terms of slice registers, slice LUTs, and LUT–Flip-Flop pairs; and the frequency of operation also improved by 22.76% and 63.84% when compared to the dual RAM-based RFFTs and Radix-2 Burst I/O [25], respectively, for the combined Parity-SOS-ECC technique.

Table 2.
Resource utilization of protected parallel RFFTs on Artix-7 FPGA.
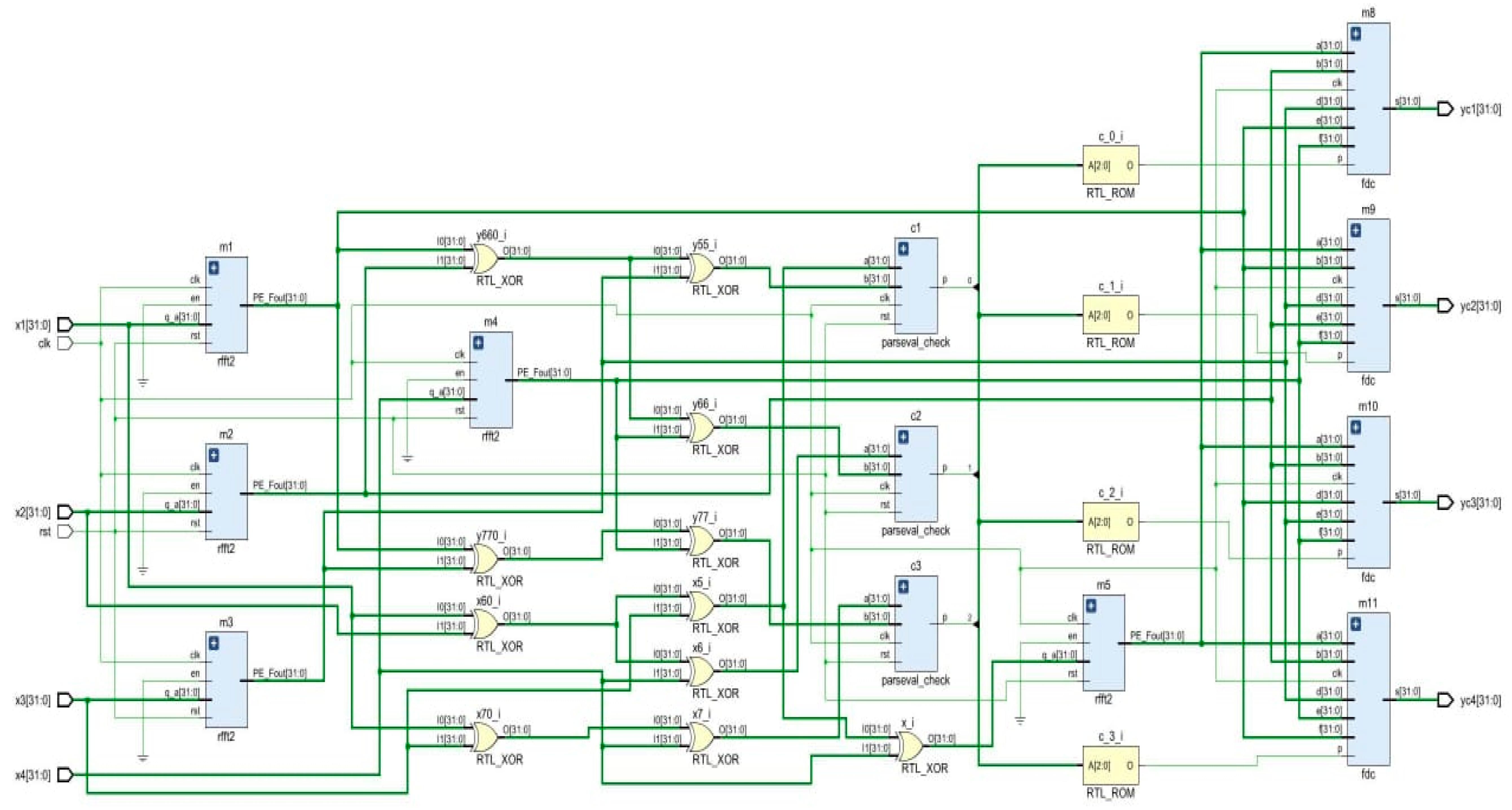
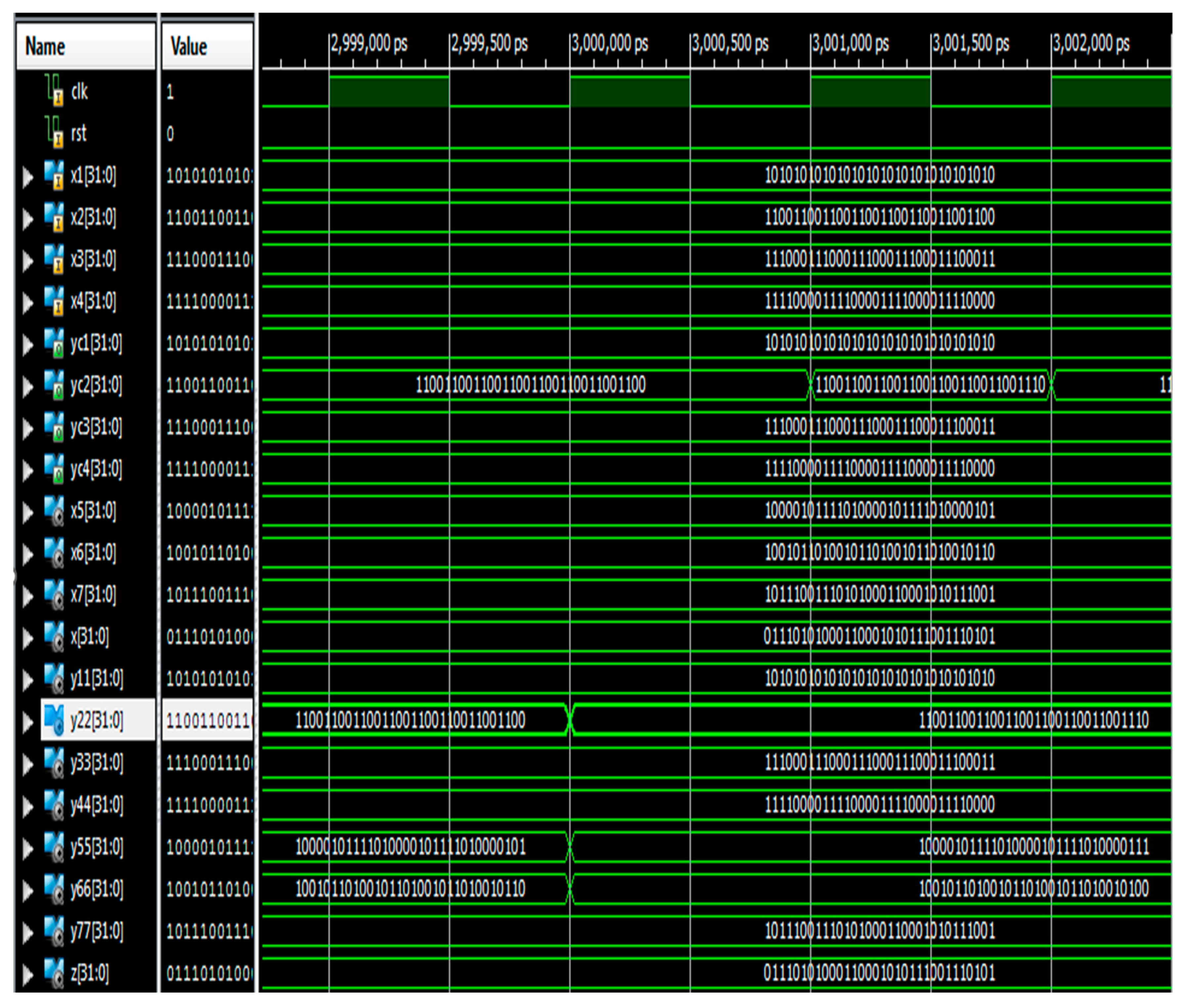
RTL schematic and simulation results for the fault identification of parallel RFFTs using Parity-SOS-ECC are depicted in Figure 12 and Figure 13, respectively, in the form of a screenshot taken from the Xilinx Vivado 2022.1 window.
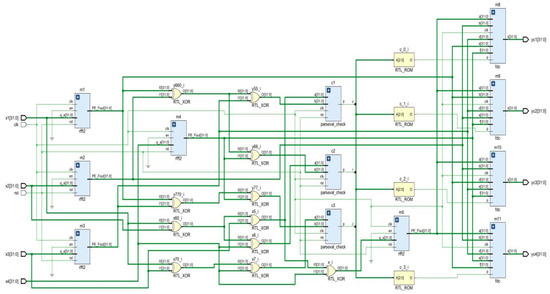
Figure 12.
RTL schematic of fault-tolerant parallel RFFTs using Parity-SOS-ECC.
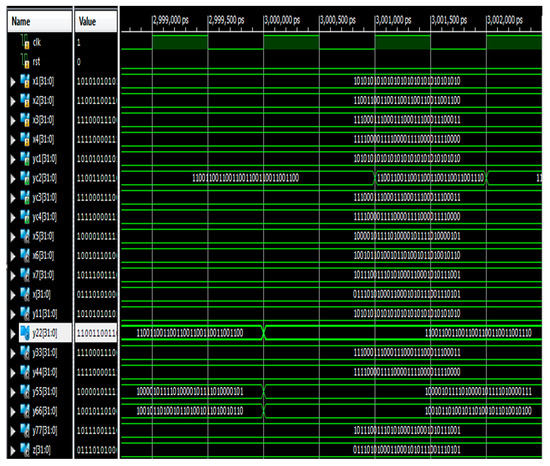
Figure 13.
Simulation results of fault-tolerant parallel RFFTs using Parity-SOS-ECC.
In Figure 13, X1, X2, X3, and X4 indicate the inputs and yc1, yc2, yc3, and yc4 indicate the outputs, respectively.
For example, if the second RFFT is affected by the fault at the second bit position, i.e., 1100 1100 1100 1100 1100 1100 1100 1110 (the actual value is 1100 1100 1100 1100 1100 1100 1100 1100), P2 will be set and correction can be performed by Equation (8), which is shown in Figure 13.
The proposed fault-tolerant architectures are implemented on ASIC using cadence 45 nm and 90 nm technology. Through this, the metrics such as area, power, delay, and power delay product are analyzed and tabulated in Table 3.

Table 3.
Resource usage for the protected parallel RFFTs implemented on ASIC.
From Table 3, single RAM-based parallel RFFTs consume less power with better power delay product when compared to the remaining two parallel RFFTs. The comparison of ASIC results for the single RAM-based fault-tolerant parallel RFFTs, with respect to dual RAM-based parallel RFFTs and Radix-2 Burst I/O [25], in terms of percentage reduction in power and power delay product (PDP) in both 45 nm and 90 nm technology are tabulated in Table 4. This is because a single dedicated memory is used and it can handle not only the reading and writing of input, but also intermediate and output data, to and from the PE. And the adders and multipliers inside the PE are implemented with VMs and CLAs for a better FFT operation.

Table 4.
Percentage reduction in power and PDP in single RAM-based protected parallel RFFTs.
From this table, it is evident that, for 45 nm technology, 62.08% and 57.90% of power is reduced in single RAM-based parallel RFFTs, and 60.51% and 57.70% for 90 nm technology, respectively, compared to Radix-2 Burst I/O and dual RAM-based parallel RFFTs using Parity-SOS-ECC technique.
7. Conclusions
In this work, the parallel FFT blocks are protected using three types of techniques. In the entire work, it is assumed that there is an occurrence of fault on a single block at a time. For the considered two types of RFFT architectures, their parallel modules protection is seen against the single fault. The Parity-SOS and Parity-SOS-ECC schemes consume a smaller number of slice LUTs and LUT–Flip-Flop pairs with improved frequencies to that of the ECC technique for the two-fault-tolerant parallel RFFTs. The two proposed architectures with the combined protection scheme present an 88% and 33% reduction in area overhead and an enhanced the frequency of operation when compared to the existing parallel pipelined RFFT architectures. In ASIC implementation, the single RAM-based RFFTs utilize less area and delay than ECC with less PDP on both 45 nm and 90 nm. The proposed single RAM-based RFFTs fault-tolerant RFFT architecture presents a 62.93% and 57.56% improvement of PDP in 45 nm technology and 67.20% and 60.31% improvement of PDP in 90 nm technology compared to the dual RAM-based fault-tolerant parallel RFFT and the existed architectures, respectively. On the other hand, for fault-tolerant single memory-based RFFTs, the power and PDP both are improved in the two technologies. On comparing the three types of fault-tolerant parallel RFFTs, the FPGA results convey that single RAM-based FFTs are better with a smaller area overhead and a high fault tolerance, whereas in ASIC, single RAM-based RFFTs are better with a smaller chip area and power-delay product along with same fault tolerance. Furthermore, we can improve the fault coverage of the proposed architectures for higher lengths for two or more numbers of soft errors with better performance metrics in both FPGA and ASIC.
Author Contributions
Conceptualization: R.T. and J.C.B.; methodology development: R.T., J.C.B. and B.A.; software implementation: M.K. and B.A.; validation process: A.K., M.K. and R.T.; formal data analysis: J.C.B., B.A. and M.K.C.; investigation conducted by M.K.; resource allocation: B.A.; data curation: R.T.; initial draft preparation: A.K.; manuscript review and editing: R.T., M.K.C. and M.K.; visualization of results: J.C.B.; project supervision: M.K.; project administration handled by A.K. and R.T.; funding acquisition managed by B.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R440) Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baumann, R. Soft errors in advanced computer systems. IEEE Des. Test Comput. 2005, 22, 258–266. [Google Scholar] [CrossRef]
- International Technology Roadmap for Semiconductors. 2008. Available online: http://www.itrs.net/Links/2008ITRS/Home2008.html (accessed on 14 August 2008).
- Ko, Y. Characterizing System-Level Masking Effects against Soft Errors. Electronics 2021, 10, 2286. [Google Scholar] [CrossRef]
- Vijay, M.; Mittal, R. Algorithm-based fault tolerance: A review. Microprocess. Microsyst. 1997, 21, 151–161. [Google Scholar] [CrossRef]
- Reddy, L.N.; Banerjee, P. Algorithm-based fault detection for signal processing applications. IEEE Trans. Comput. 1990, 39, 1304–1308. [Google Scholar] [CrossRef]
- Koren, I.; Su, S. Reliability Analysis of N-Modular Redundancy Systems with Intermittent and Permanent Faults. IEEE Trans. Comput. 1979, C-28, 514–520. [Google Scholar] [CrossRef]
- Shim, B.; Shanbhag, N.R. Energy-efficient soft error-tolerant digital signal processing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2006, 14, 336–348. [Google Scholar] [CrossRef]
- Jou, J.Y.; Abraham, J.A. Fault-tolerant FFT networks. IEEE Trans. Comput. 1988, 37, 548–561. [Google Scholar] [CrossRef]
- Wang, S.-J.; Jha, N.K. Algorithm-based fault tolerance for FFT networks. IEEE Trans. Comput. 1994, 43, 849–854. [Google Scholar] [CrossRef]
- Saravanan, M.; Parthasarathy, E. Impact of Pocket Layer on Linearity and Analog/RF Performance of InAs-GaSb Vertical Tunnel Field-Effect Transistor. J. Electron. Mater. 2023, 52, 2772–2779. [Google Scholar] [CrossRef]
- Saravanan, M.; Parthasarathy, E. A Review of III-V Tunnel Field Effect Transistors for Future Ultra Low Power Digital/Analog Applications. Microelectron. J. 2021, 114, 105102. [Google Scholar] [CrossRef]
- Joshi, S.M. FFT Architectures: A Review. Int. J. Comput. Appl. 2015, 116, 33–36. [Google Scholar]
- Tang, S.-N.; Jan, F.-C.; Cheng, H.-W.; Lin, C.-K.; Wu, G.-Z. Multimode Memory-Based FFT Processor for Wireless Display FD-OCT Medical Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 3394–3406. [Google Scholar] [CrossRef]
- Stüber, G.L.; Barry, J.R.; McLaughlin, S.W.; Li, Y.; Ingram, M.A.; Pratt, T.G. Broadband MIMO-OFDM wireless communications. Proc. IEEE 2004, 92, 271–294. [Google Scholar] [CrossRef]
- Ayinala, M.; Brown, M.; Parhi, K.K. Pipelined parallel FFT architectures via folding transformation. IEEE Trans. VLSI Syst. 2012, 20, 1068–1081. [Google Scholar] [CrossRef]
- Gao, Z.; Reviriego, P.; Pan, W.; Xu, Z.; Zhao, M.; Wang, J.; Maestro, J.A. Fault tolerant parallel filters based on error correction codes. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2015, 23, 384–387. [Google Scholar] [CrossRef]
- Gao, Z.; Reviriego, P.; Xu, Z.; Su, X.; Zhao, M.; Wang, J.; Maestro, J.A. Fault Tolerant Parallel FFTs Using Error Correction Codes and Parseval Checks. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 769–773. [Google Scholar] [CrossRef]
- Xie, Y.; Yang, C.; Mao, C.-A.; Chen, H.; Xie, Y.-Z. A novel low-overhead fault tolerant parallel-pipelined FFT design. In Proceedings of the 2017 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT), Cambridge, UK, 23–25 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Liang, X.; Chen, J.; Tao, D.; Li, S.; Wu, P.; Li, H.; Ouyang, K.; Liu, Y.; Song, F.; Chen, Z. Correcting soft errors online in fast fourier transform. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (SC ‘17), Denver, CO, USA, 12–17 November 2017; Association for Computing Machinery: New York, NY, USA, 2017. Article 30. pp. 1–12. [Google Scholar] [CrossRef]
- González-Toral, R.; Reviriego, P.; Maestro, J.A.; Gao, Z. A Scheme to Design Concurrent Error Detection Techniques for the Fast Fourier Transform Implemented in SRAM-Based FPGAs. IEEE Trans. Comput. 2018, 67, 1039–1045. [Google Scholar] [CrossRef]
- Mao, C.-A.; Xie, Y.; Xie, Y.; Chen, H.; Shi, H. An Automated Fault Injection Platform for Fault Tolerant FFT Implemented in SRAM-Based FPGA. In Proceedings of the 2018 31st IEEE International System-on-Chip Conference (SOCC), Arlington, VA, USA, 4–7 September 2018; pp. 192–196. [Google Scholar] [CrossRef]
- Wei, X.; Xie, Y.Z.; Xie, Y.; Chen, H. Dynamic partial reconfiguration scheme for fault-tolerant FFT processor based on FPGA. Inst. Eng. Technol. J. 2019, 2019, 7424–7427. [Google Scholar] [CrossRef]
- Rajasekhar, T.; Ram, M.S.S. Low area high-speed LC-CSLA-FFT architecture for radix-2 decimation in frequency algorithm. J. Adv. Res. Dyn. Control Syst. 2018, 10, 811–826. [Google Scholar]
- Rajasekhar, T.; Ram, M.S.S. Low power VLSI implementation of real fast Fourier transform with DRAM-VM-CLA. Microprocess. Microsyst. 2019, 69, 92–100. [Google Scholar]
- Kumar, A.; Kumar, A.; Devrari, A. Hardware Chip Performance Analysis of Different FFT Architecture. Int. J. Electron. 2020, 108, 1124–1140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).