Optimal Discrete Element Parameters for Black Soil Based on Multi-Objective Total Evaluation Normalized-Response Surface Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Definition of the Intrinsic Characteristics of Black Soil
- (1)
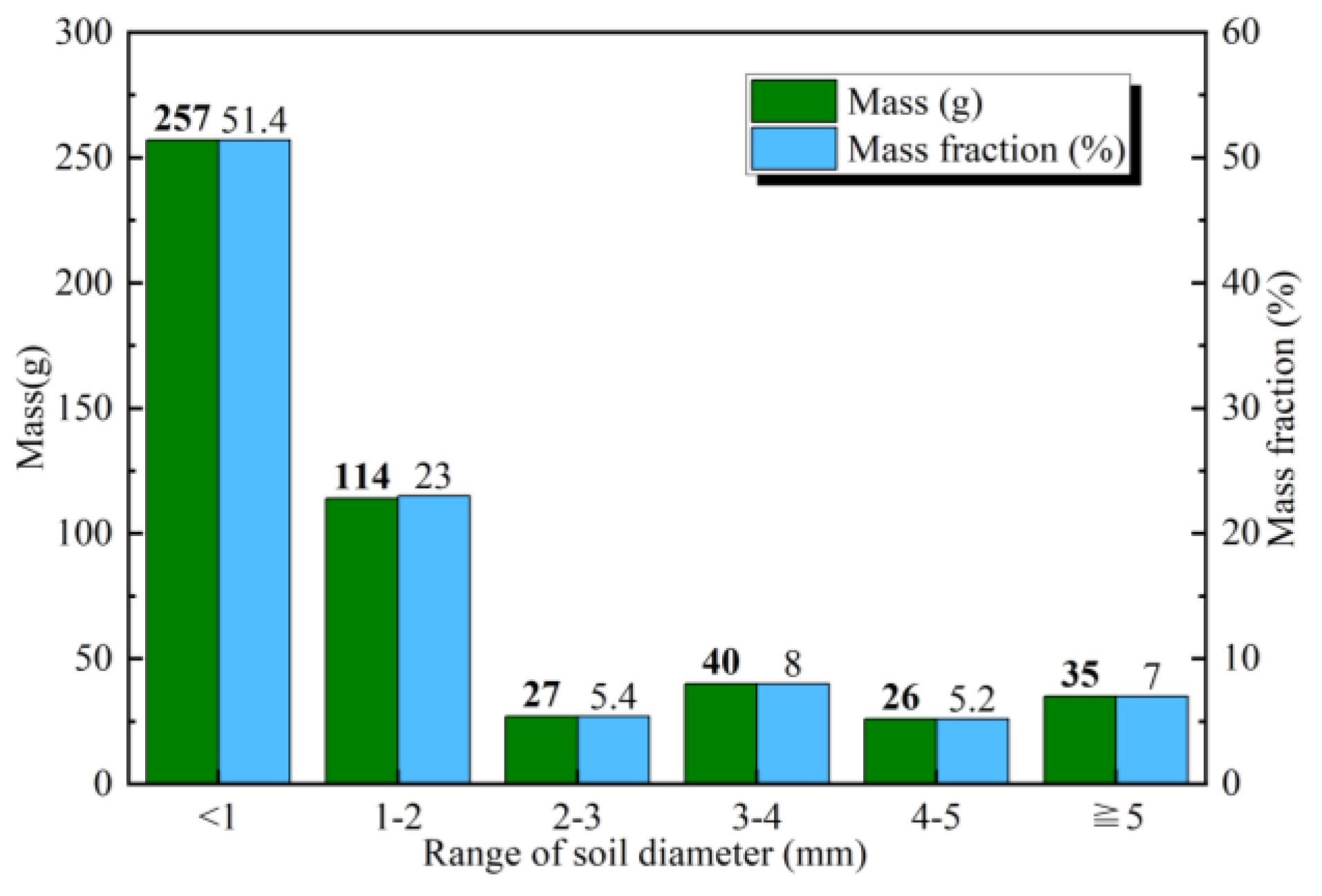
- Size distribution of black soil
- (2)
- Black soil density, Poisson’s ratio, and shear modulus
- (3)
- Black soil stacking angle
2.2. Black Soil Simulation Contact Model
2.3. Black Soil Discrete Element Parameters
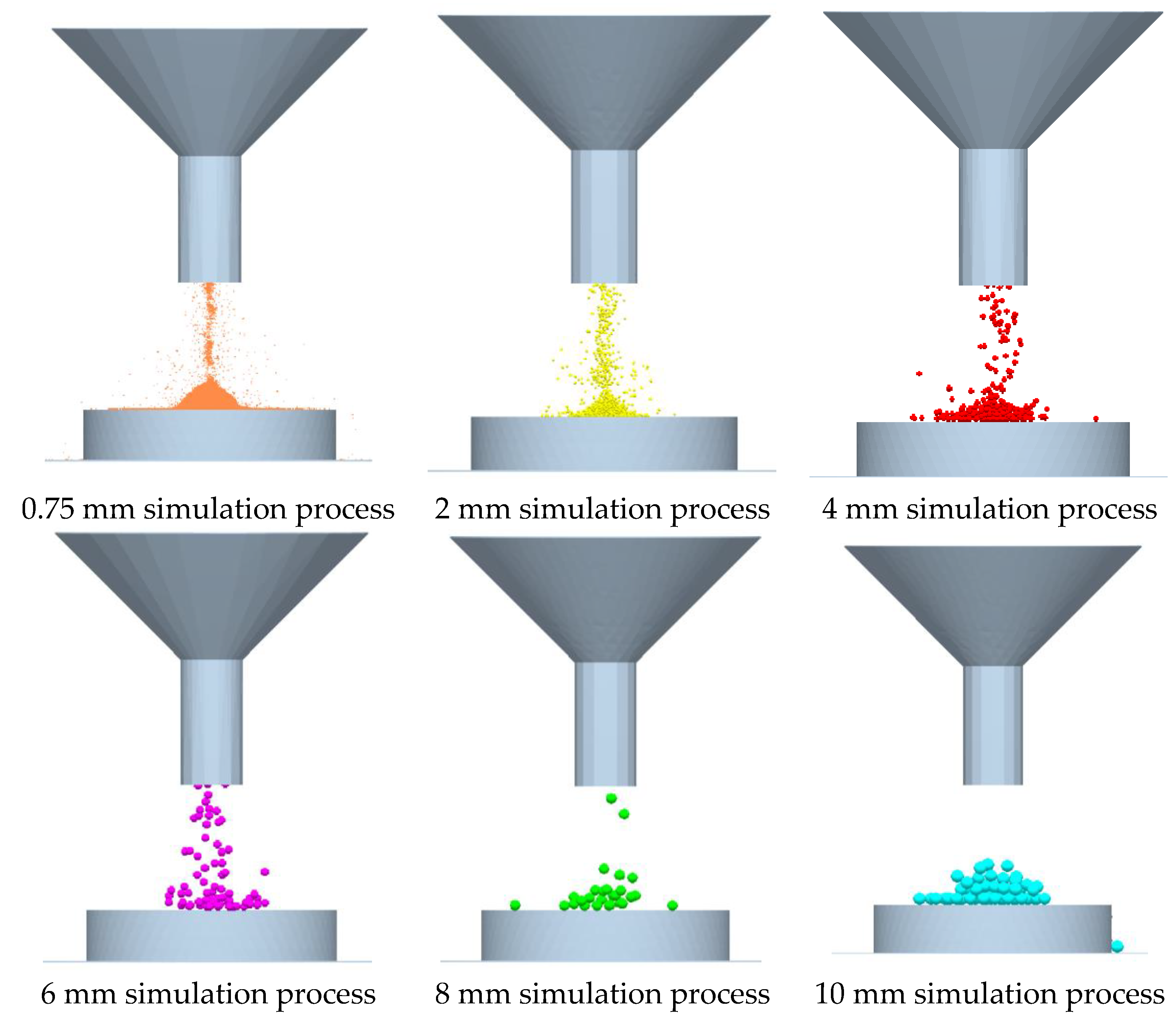
2.4. Black Soil Discrete Element Model
2.5. The Calibration Method of the Simulation Parameter
3. Results and Discussion
3.1. Plackett–Burman Test
3.2. The Steepest Climb Test
3.3. Box–Behnken-Test Response Surface Methodology to Optimize the Optimal Contact Parameters for Different Particle Sizes
3.3.1. Regression Model Interaction Effect
3.3.2. Regression Model Interaction Effect Analysis
3.3.3. Determination and Validation of Optimal Parameter Combinations
4. Conclusions
- (1)
- The Plackett–Burman experiments with different particle sizes showed that the variables affecting the accumulation angle of black soil particles were the black soil–black soil static friction coefficient, black soil–black soil rolling friction coefficient, and black soil–stainless steel rolling friction coefficient.
- (2)
- The optimum parameters for the black earth contact parameters were 1.045 for the black soil–black soil static friction coefficient, 0.464 for the black soil–black soil rolling friction coefficient, and 0.215 for the black soil–stainless steel rolling friction coefficient.
- (3)
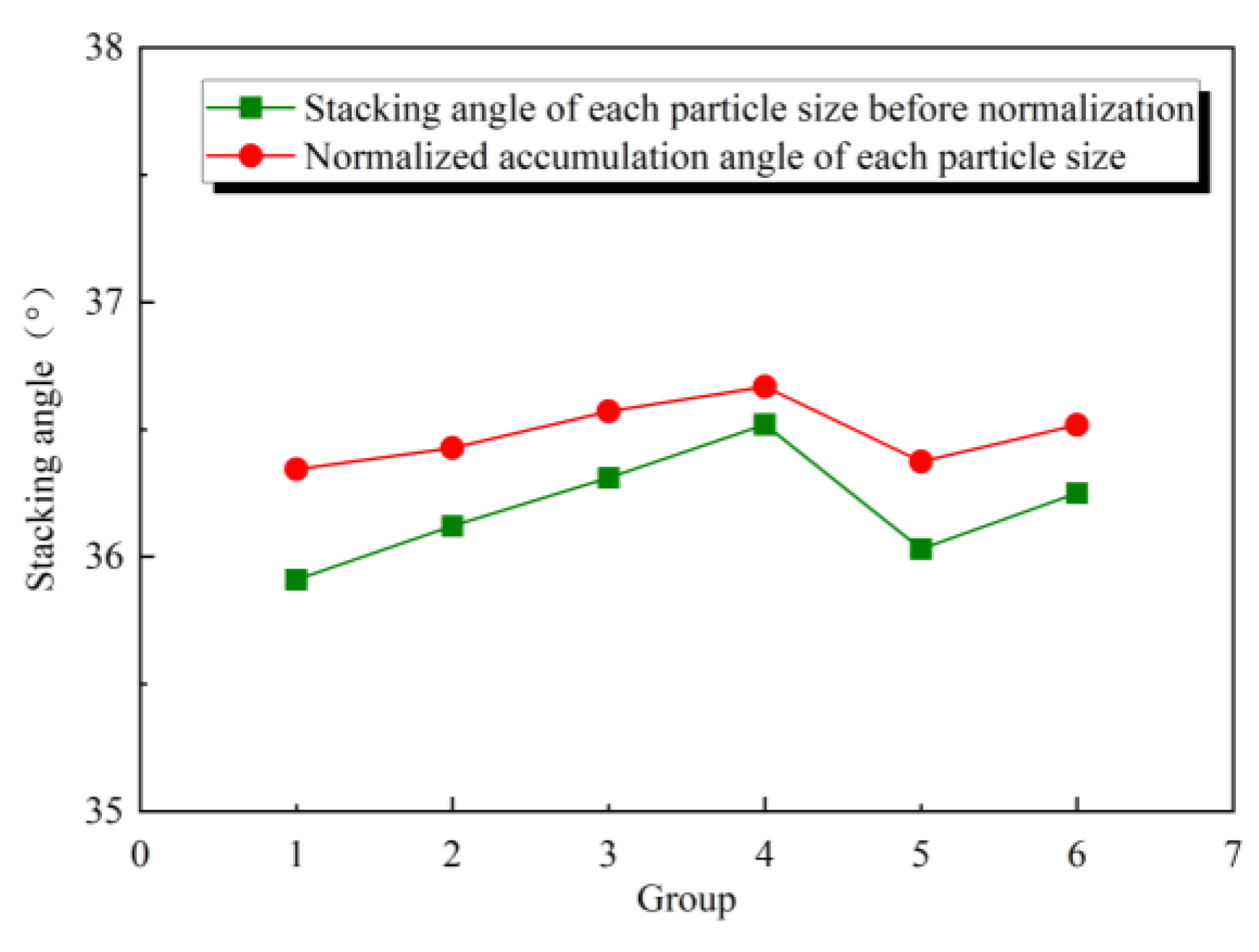
- The errors of the simulation test and physical experiment before and after normalization for each particle size of 0.75 mm, 2 mm, 4 mm, 6 mm, 8 mm, and 10 mm of black soil were 2.92%, 2.35%, 1.84%, 1.27, 2.6%, and 2%, and 2.03%, 1.65%, 1%, 0.7%, 1.89%, and 1.24%, respectively. The errors of the simulation and physics experiments before and after normalization were reduced by 0.89%, 0.7%, 0.84%, 0.57%, 0.71%, and 0.76% for each particle size of black soil, with an average error reduction of 0.745%.
- (4)
- The 6 mm particle size is most suitable for the best discrete element contact parameter after normalization. The simulation results did not differ significantly from the physical measurements. Thus, it can give a guide value to the design and improvement of related agricultural equipment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ucgul, M.; Fielke, J.M.; Saunders, C. 3D DEM tillage simulation: Validation of a hysteretic spring (plastic) contact model for a sweep tool operating in a cohesionless soil. Soil Till Res. 2014, 144, 220–227. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Lenaerts, B.; Aertsen, T.; Tijskens, E.; De Ketelaere, B.; Ramon, H.; De Baerdemaeker, J.; Saeys, W. Simulation of grain-straw separation by Discrete Element Modeling with bendable straw particles. Comput. Electron. Agric. 2014, 101, 24–33. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Chen, J. Modeling of soil-claw interaction using the discrete element method (DEM). Soil Till Res. 2016, 158, 177–185. [Google Scholar] [CrossRef]
- Binelo, M.O.; de Lima, R.F.; Khatchatourian, O.A.; Stransky, J. Modelling of the drag force of agricultural seeds applied to the discrete element method. Biosyst. Eng. 2019, 178, 168–175. [Google Scholar] [CrossRef]
- Qi, L.; Chen, Y.; Sadek, M. Simulations of soil flow properties using the discrete element method (DEM). Comput. Electron. Agric. 2019, 157, 254–260. [Google Scholar] [CrossRef]
- Zhu, J.Z.; Zou, M.; Liu, Y.S.; Gao, K.; Su, B.; Qi, Y.C. Measurement and calibration of DEM parameters of lunar soil simulant. Acta Astronaut. 2022, 191, 169–177. [Google Scholar] [CrossRef]
- Bu, H.R.; Yu, S.Y.; Dong, W.C.; Wang, Y.Q.; Zhang, L.X.; Xia, Y.Q. Calibration and Testing of Discrete Element Simulation Parameters for Urea Particles. Processes 2022, 10, 511. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, H.P.; Xu, L.Y.; Song, S.Y.; Zhang, C.; Yu, Q.X. Parameter calibration of coconut bran substrate simulation model based on discrete element and response surface methodology. Powder Technol. 2022, 395, 183–194. [Google Scholar] [CrossRef]
- Guo, Y.X.; Deng, Z.H.; Guo, S.Y.; Li, Y.J.; Mao, S.; Zhang, T.; Yang, Q.; Chen, Y.; Wang, Y.J.; Li, Q.; et al. Optimization of Ethanol-Based Extraction Process for Duliang Formula by Central Composite Design and Response Surface Methodology. Nat. Prod. Commun. 2022, 17. [Google Scholar] [CrossRef]
- Li, Y.; Ye, M.; Zhang, Y.; Sun, Y.D.; Hao, C.F. Optimization of Particle Distribution for Asphalt Mixtures in Screw Conveyer of Paver Based on Discrete Element Method and Response Surface Methodology. Adv. Theor. Simu. 2023. [Google Scholar] [CrossRef]
- Shi, G.K.; Li, J.B.; Ding, L.P.; Zhang, Z.Y.; Ding, H.Z.; Li, N.; Kan, Z. Calibration and Tests for the Discrete Element Simulation Parameters of Fallen Jujube Fruit. Agriculture 2022, 12, 38. [Google Scholar] [CrossRef]
- Hu, Y.Z.; Chan, E.L.; Tsuji, T.; Tanaka, T.; Washino, K. Geometric similarity on interparticle force evaluation for scaled-up DEM particles. Powder Technol. 2022, 404, 117483. [Google Scholar] [CrossRef]
- Lommen, S.; Schott, D.; Lodewijks, G. DEM speedup: Stiffness effects on behavior of bulk material. Particuology 2014, 12, 107–112. [Google Scholar] [CrossRef]
- Hu, M.J.; Xia, J.F.; Zhou, Y.; Luo, C.M.; Zhou, M.K.; Liu, Z.Y. Measurement and Calibration of the Discrete Element Parameters of Coated Delinted Cotton Seeds. Agriculture 2022, 12, 286. [Google Scholar] [CrossRef]
- Chen, S.; Liu, W.W.; Li, S.Q. A fast adhesive discrete element method for random packings of fine particles. Chem. Eng. Sci. 2019, 193, 336–345. [Google Scholar] [CrossRef]
- Roessler, T.; Katterfeld, A. Scaling of the angle of repose test and its influence on the calibration of DEM parameters using upscaled particles. Powder Technol. 2018, 330, 58–66. [Google Scholar] [CrossRef]
- Sakai, M.; Takahashi, H.; Pain, C.C.; Latham, J.P.; Xiang, J.S. Study on a large-scale discrete element model for fine particles in a fluidized bed. Adv. Powder Technol. 2012, 23, 673–681. [Google Scholar] [CrossRef]
- Dai, Z.W.; Wu, M.L.; Fang, Z.C.; Qu, Y.B. Calibration and Verification Test of Lily Bulb Simulation Parameters Based on Discrete Element Method. Appl. Sci. 2021, 11, 749. [Google Scholar] [CrossRef]
- Ma, G.G.; Sun, Z.J.; Ma, H.; Li, P.C. Calibration of Contact Parameters for Moist Bulk of Shotcrete Based on EDEM. Adv. Mater. Sci. Eng. 2022, 2022, 6072303. [Google Scholar] [CrossRef]
- Xia, R.; Li, B.; Wang, X.W.; Li, T.J.; Yang, Z.J. Measurement and calibration of the discrete element parameters of wet bulk coal. Measurement 2019, 142, 84–95. [Google Scholar] [CrossRef]
- GB/T 16913.2-1997; Methods of Test for Dust Properties—Part 2: Determination of Effective Density. Standards Press China: Beijing, China, 1997.
- Tian, X.; Cong, X.; Qi, J.; Guo, H.; Li, M.; Fan, X. Parameter Calibration of Discrete Element Model for Corn Straw-Soil Mixture in Black Soil Areas. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2021, 52, 100–108+242. [Google Scholar] [CrossRef]
- GB/T 16913.5-1997; Methods of Test for Dust Properties—Part 5: Determination of Angle of Repose. Standards Press China: Beijing, China, 1997.
- Zhao, X.F.; Zheng, P.F.; He, L.; Tao, M. Cutting edge preparation using the discrete element software EDEM. J. Braz. Soc. Mech. Sci. 2020, 42, 163. [Google Scholar] [CrossRef]
- Wang, N.; Yang, S.Q.; Zhao, T.T.; Cao, B.; Wang, C.W. Amending Research on the Expression of the Contact Force of the Spindle Barrel Finishing Based on EDEM Simulation. Chin. J. Mech. Eng. 2020, 33, 83. [Google Scholar] [CrossRef]
- Sun, J.; Liu, Q.; Yang, F.; Liu, Z.; Wang, Z. Calibration of Discrete Element Simulation Parameters of Sloping Soil on Loess Plateau and Its Interaction with Rotary Tillage Components. Trans. Chin. Soc. Agric. Mach. 2022, 53, 63–73. [Google Scholar] [CrossRef]
- Weinhart, T.; Hartkamp, R.; Thornton, A.R.; Luding, S. Coarse-grained local and objective continuum description of three-dimensional granular flows down an inclined surface. Phys. Fluids 2013, 25, 7147–7151. [Google Scholar] [CrossRef]
- Li, Y.; Li, F.; Xu, X.; Shen, C.; Meng, K.; Chen, J.; Chang, D. Parameter calibration of wheat flour for discrete element method simulation based on particle scaling. Trans. Chin. Soc. Agric. Mach. 2019, 35, 320–327. [Google Scholar] [CrossRef]
- Yuan, Q.; Xu, L.; Xing, J.; Duan, Z.; Ma, S.; Yu, C.; Chen, C. Parameter calibration of discrete element model of organic fertilizer particles for mechanical fertilization. Trans. Chin. Soc. Agric. Mach. 2018, 34, 21–27. [Google Scholar] [CrossRef]





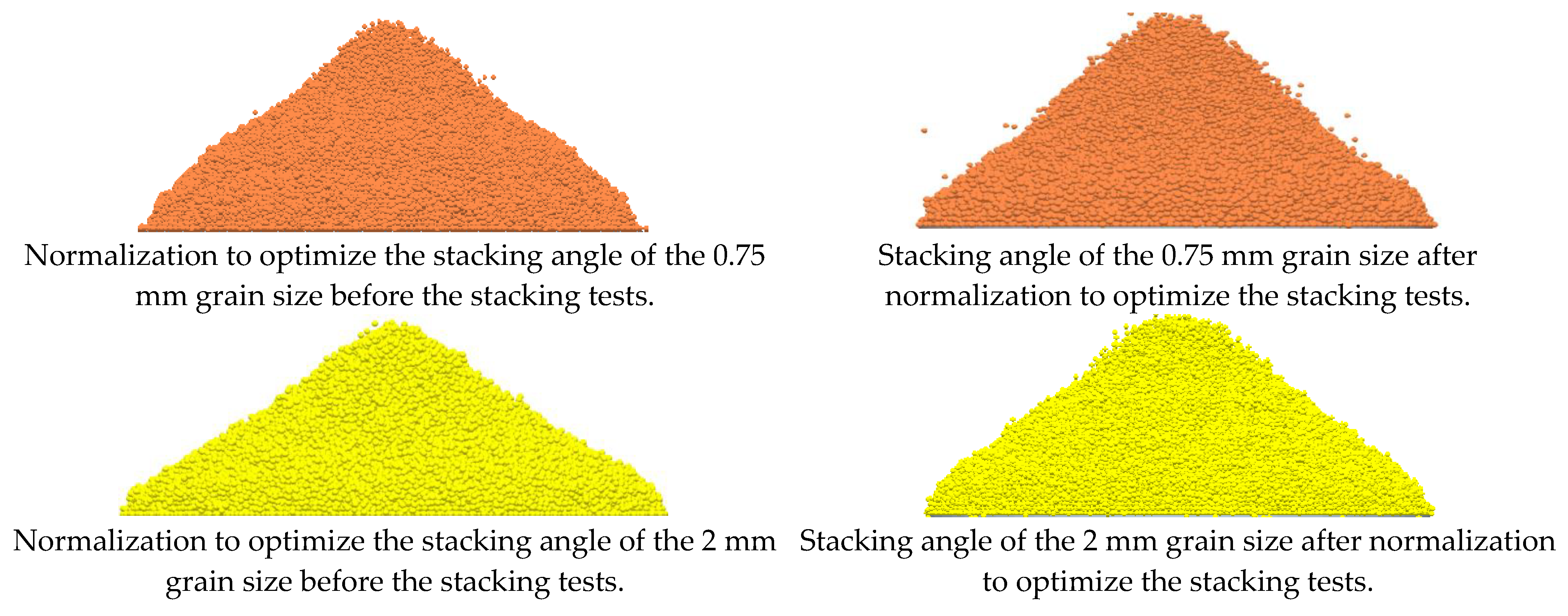
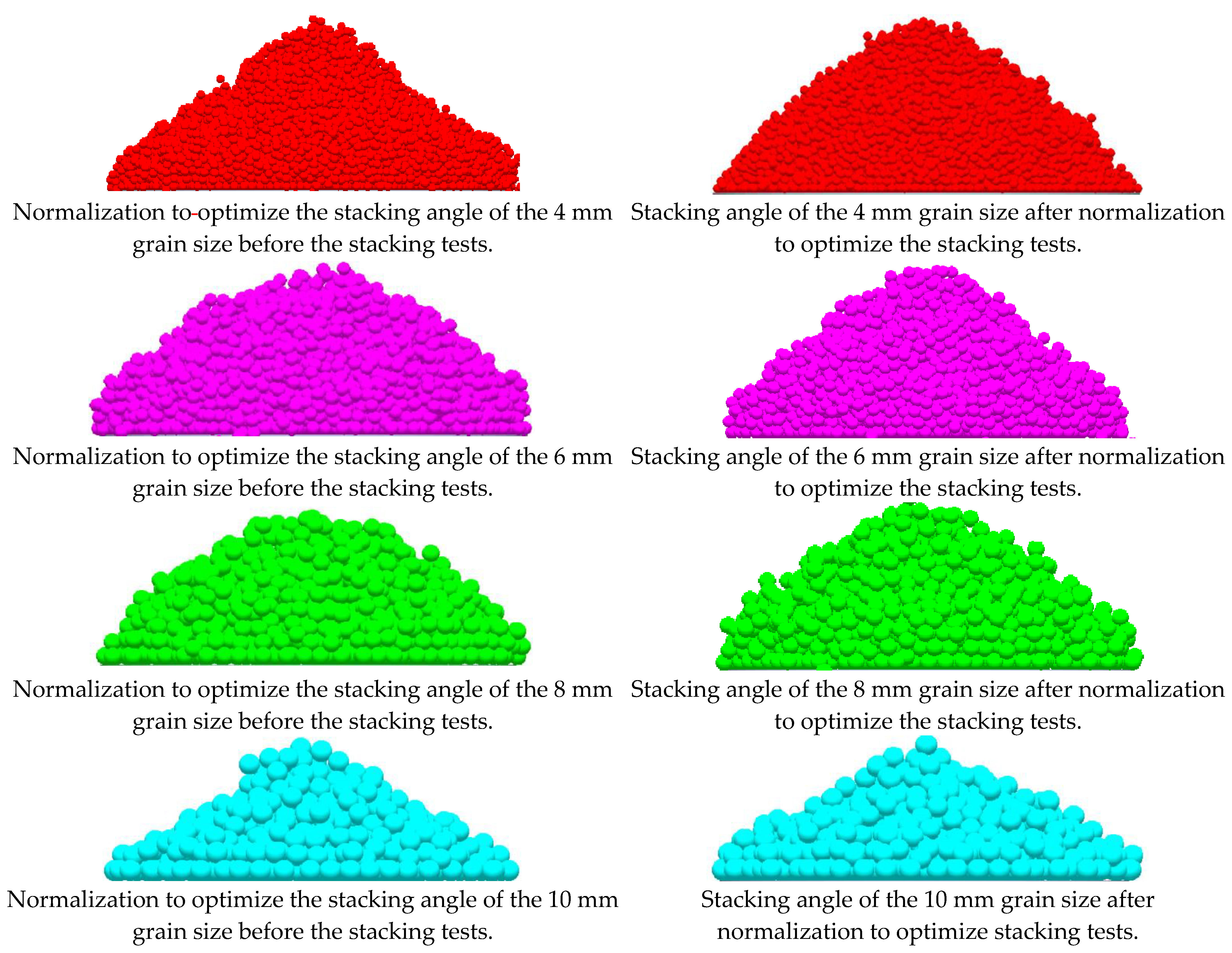

| Parameter | Value |
|---|---|
| Density of black soil (kg/m3) | 2000 |
| Poisson’s ratio of black soil | 0.46 |
| Shear modulus of black soil/Pa | 1 × 106 |
| Density of stainless steel/(kg/m3) | 7800 |
| Poisson’s ratio of stainless steel | 0.3 |
| Shear modulus of stainless steel/Pa | 7 × 1010 |
| Black soil–black soil restitution coefficient | 0.2–0.6 |
| Black soil–black soil static friction coefficient | 0.2–1.16 |
| Black soil–black soil rolling friction coefficient | 0.01–0.7 |
| Black soil–stainless steel restitution coefficient | 0.2–0.5 |
| Black soil–stainless steel coefficient of static friction | 0.4–0.8 |
| Black soil–stainless steel coefficient of rolling friction | 0.05–0.25 |
| Symbol | Parameter | Low Level (−1) | High Level (+1) |
|---|---|---|---|
| A | Black soil–black soil restitution coefficient | 0.2 | 0.4 |
| B | Black soil–black soil static friction coefficient | 0.2 | 0.4 |
| C | Black soil–black soil rolling friction coefficient | 0.05 | 0.1 |
| D | Black soil–stainless steel restitution coefficient | 0.2 | 0.4 |
| E | Black soil–stainless steel coefficient of static friction | 0.4 | 0.8 |
| F | Black soil–stainless steel coefficient of rolling friction | 0.05 | 0.1 |
| V1 | Virtual parameter | −1 | 1 |
| V2 | Virtual parameter | −1 | 1 |
| V3 | Virtual parameter | −1 | 1 |
| V4 | Virtual parameter | −1 | 1 |
| V5 | Virtual parameter | −1 | 1 |
| Number | A | B | C | D | E | F | V1 | V2 | V3 | V4 | V5 | 0.75 mm Angle | 2 mm Angle | 4 mm Angle | 6 mm Angle | 8 mm Angle | 10 mm Angle |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | 21.38 | 26.9 | 27.71 | 27.47 | 24.03 | 22.39 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20.6 | 24.72 | 25.81 | 25.64 | 23.88 | 22.51 |
| 3 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 17.11 | 21.56 | 22.31 | 20.95 | 20.89 | 19.68 |
| 4 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 21.85 | 25.1 | 27.14 | 27.1 | 24.47 | 23.57 |
| 5 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 19.09 | 22.38 | 24.03 | 24.23 | 22.56 | 21.39 |
| 6 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | 20.35 | 22.18 | 23.03 | 22.78 | 21.8 | 20.75 |
| 7 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 21.4 | 23.49 | 24.52 | 25.3 | 23.35 | 22.27 |
| 8 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | 22.92 | 24.16 | 25.99 | 26.2 | 25.64 | 24.52 |
| 9 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | −1 | 17.1 | 20.52 | 21.8 | 21.31 | 20.41 | 20.2 |
| 10 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 20.4 | 24.35 | 25.41 | 26.12 | 24.23 | 22.28 |
| 11 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 21.5 | 25.8 | 25.99 | 26.79 | 25.33 | 23.16 |
| 12 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 18.1 | 23.58 | 24.23 | 23.75 | 22.35 | 21.06 |
| 13 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | 19.1 | 24.12 | 24.52 | 24.7 | 23.99 | 22.24 |
| Parameters | 0.75 mm Contribution/ Significance | 2 mm Contribution/ Significance | 4 mm Contribution/Significance | 6 mm Contribution/ Significance | 8 mm Contribution/ Significance | 10 mm Contribution/ Significance |
|---|---|---|---|---|---|---|
| A | 1.1807% (6) | 0.33% (6) | 0.99% (4) | 2.85% (4) | 1.83% (5) | 0.28% (6) |
| B | 29.52% (1) | 54.77% (1) | 58.64% (1) | 51.31% (1) | 45.72% (1) | 2.31% (3) |
| C | 25.62% (2) | 14.90% (3) | 27.52% (2) | 25.72% (2) | 21.89% (2) | 14.05% (2) |
| D | 8.45% (5) | 0.21% (5) | 0.27% (5) | 0.30% (5) | 2.43% (4) | 1.08% (4) |
| E | 12.28% (4) | 4.61% (4) | 0.18% (6) | 0.13% (6) | 0.15% (6) | 0.58% (5) |
| F | 12.99% (3) | 20.38% (2) | 7.16% (3) | 14.4% (3) | 11.03% (3) | 42.13% (1) |
| Serial Number | Black Soil–Black Soil Static Friction Coefficient | Black Soil–Black Soil Rolling Friction Coefficient | Black Soil–Stainless Steel Coefficient of Rolling Friction | 0.75 mm Repose Angle θ/(°) | 2 mm Repose Angle θ/(°) | 4 mm Repose Angle θ/(°) | 6 mm Repose Angle θ/(°) | 8 mm Repose Angle θ/(°) | 10 mm Repose Angle θ/(°) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 0.01 | 0.05 | 14.86 | 15.2 | 15.6 | 15.3 | 16.6 | 15.64 |
| 2 | 0.55 | 0.13 | 0.13 | 26.5 | 29.28 | 31.49 | 28.37 | 27.82 | 27.47 |
| 3 | 0.9 | 0.25 | 0.21 | 33.05 | 36.03 | 36.11 | 35.75 | 34.12 | 33.42 |
| 4 | 1.25 | 0.37 | 0.29 | 36.7 | 37.63 | 37.69 | 37.4 | 37.23 | 36.63 |
| 5 | 1.6 | 0.49 | 0.37 | 38.69 | 39.5 | 39.83 | 39.01 | 38.92 | 38.75 |
| Serial Number | B | C | F | 0.75 mm Repose Angle θ/(°) | 2 mm Repose Angle θ/(°) | 4 mm Repose Angle θ/(°) | 6 mm Repose Angle θ/(°) | 8 mm Repose Angle θ/(°) | 10 mm Repose Angle θ/(°) | OD Value |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 36.35 | 37.45 | 37.69 | 37.58 | 37.23 | 36.45 | 0.47 |
| 2 | 1 | 0 | 1 | 37.47 | 38.56 | 40.25 | 39.98 | 37.85 | 37.65 | 0.89 |
| 3 | 1 | −1 | 0 | 36.15 | 38.1 | 39.55 | 38.93 | 36.67 | 36.22 | 0.6 |
| 4 | 0 | −1 | 1 | 35.9 | 37.64 | 39.08 | 38.12 | 36.61 | 36.01 | 0.51 |
| 5 | 1 | 0 | −1 | 37.33 | 38.16 | 39.96 | 39.81 | 37.85 | 37.43 | 0.83 |
| 6 | −1 | 0 | 1 | 35.5 | 36.96 | 38.11 | 37.91 | 36.23 | 35.75 | 0.38 |
| 7 | −1 | 0 | −1 | 34.12 | 35.61 | 37.51 | 37.01 | 35.48 | 34.52 | 0.06 |
| 8 | 0 | 1 | 1 | 37.85 | 38.85 | 39.93 | 39.55 | 38.1 | 38.05 | 0.92 |
| 9 | 0 | 0 | 0 | 36.75 | 37.96 | 38.19 | 37.98 | 37.63 | 36.85 | 0.512 |
| 10 | 0 | −1 | −1 | 35.8 | 36.51 | 38.23 | 38.13 | 36.88 | 36.01 | 0.43 |
| 11 | 0 | 0 | 0 | 36.88 | 38.15 | 38.44 | 38.18 | 37.83 | 36.96 | 0.54 |
| 12 | 1 | 1 | 0 | 38.09 | 38.85 | 40.33 | 40.13 | 38.62 | 38.11 | 1 |
| 13 | 0 | 1 | −1 | 36.52 | 37.8 | 39.9 | 38.62 | 37.55 | 36.87 | 0.69 |
| 14 | −1 | −1 | 0 | 34.02 | 35.55 | 36.72 | 36.13 | 35.31 | 34.35 | 0 |
| 15 | −1 | 1 | 0 | 34.86 | 36.95 | 38.055 | 37.35 | 36.13 | 35.26 | 0.28 |
| Source of Variation | Mean Square | Freedom | Quadratic Sum | F Value | p Value |
|---|---|---|---|---|---|
| Model | 1.22 | 9 | 0.1355 | 204.79 | <0.0001 |
| B | 0.8450 | 1 | 0.8450 | 1277.34 | <0.0001 |
| C | 0.2278 | 1 | 0.2278 | 344.37 | <0.0001 |
| F | 0.0595 | 1 | 0.0595 | 89.96 | 0.0002 |
| BC | 0.0036 | 1 | 0.0036 | 5.44 | 0.0670 |
| CF | 0.0169 | 1 | 0.0169 | 25.55 | 0.0039 |
| B2 | 0.0056 | 1 | 0.0056 | 8.50 | 0.0332 |
| F2 | 0.0168 | 1 | 0.0168 | 25.37 | 0.0040 |
| Residual | 0.0033 | 1 | 0.0033 | 5.05 | 0.0745 |
| Lack of fit | 0.0370 | 1 | 0.0370 | 55.91 | 0.0007 |
| Pure error | 0.0033 | 5 | 0.0007 | ||
| Sum | 0.0008 | 3 | 0.0003 | 0.2215 | 0.8754 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhu, T.; Wang, Y.; Ma, F.; Zhao, C.; Li, X. Optimal Discrete Element Parameters for Black Soil Based on Multi-Objective Total Evaluation Normalized-Response Surface Method. Processes 2023, 11, 2422. https://doi.org/10.3390/pr11082422
Wang Z, Zhu T, Wang Y, Ma F, Zhao C, Li X. Optimal Discrete Element Parameters for Black Soil Based on Multi-Objective Total Evaluation Normalized-Response Surface Method. Processes. 2023; 11(8):2422. https://doi.org/10.3390/pr11082422
Chicago/Turabian StyleWang, Zhipeng, Tong Zhu, Youzhao Wang, Feng Ma, Chaoyue Zhao, and Xu Li. 2023. "Optimal Discrete Element Parameters for Black Soil Based on Multi-Objective Total Evaluation Normalized-Response Surface Method" Processes 11, no. 8: 2422. https://doi.org/10.3390/pr11082422
APA StyleWang, Z., Zhu, T., Wang, Y., Ma, F., Zhao, C., & Li, X. (2023). Optimal Discrete Element Parameters for Black Soil Based on Multi-Objective Total Evaluation Normalized-Response Surface Method. Processes, 11(8), 2422. https://doi.org/10.3390/pr11082422






