Optimizing Photovoltaic Power Production in Partial Shading Conditions Using Dandelion Optimizer (DO)-Based MPPT Method
Abstract
:1. Introduction
2. Modeling of PV Cells and Analysis of Partial Shading Conditions
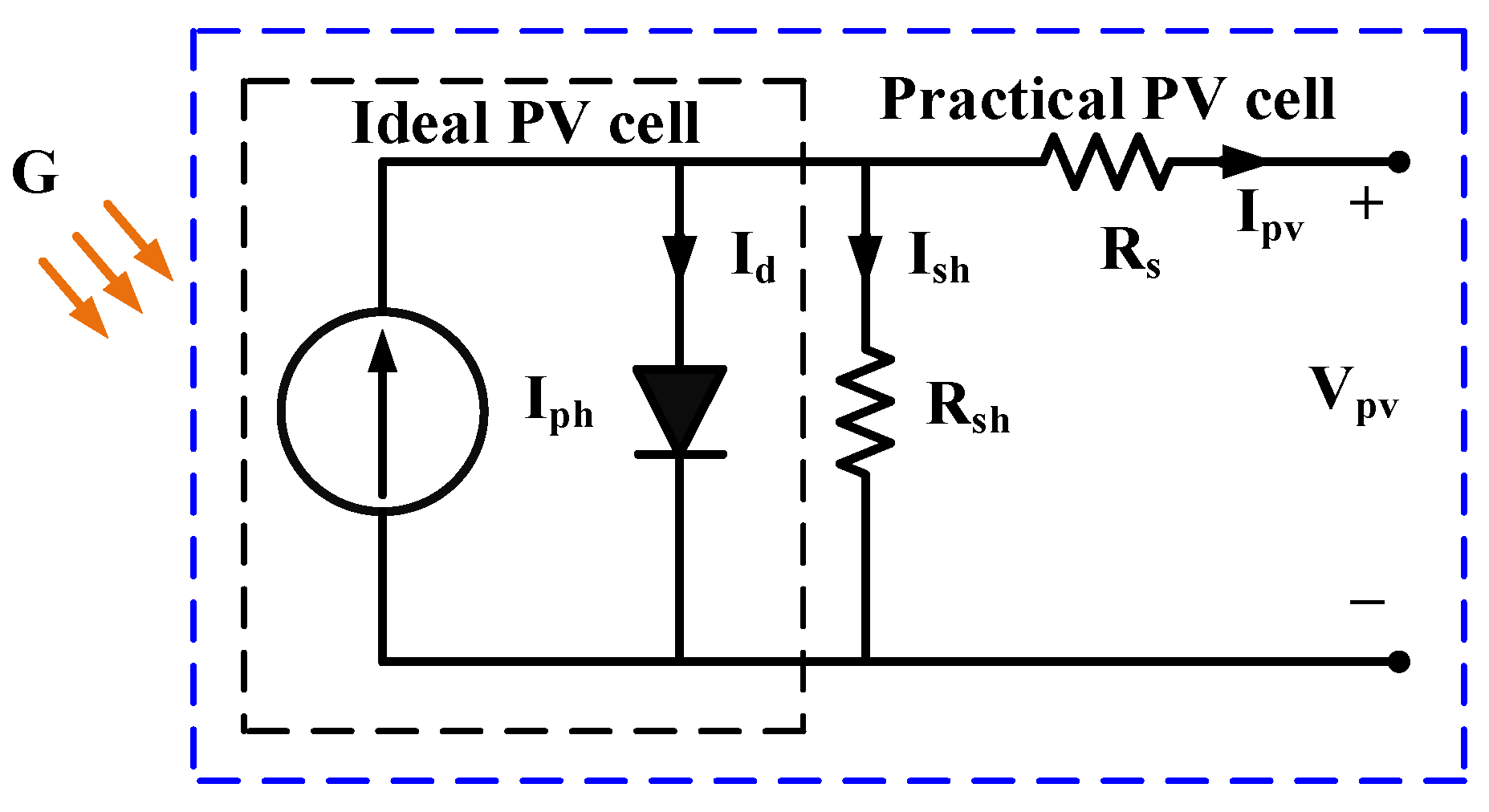
2.1. Single Diode Model of PV Cell
- : PV output current, .
- : photocurrent of PV cell, .
- : reverse PV cell saturation current, .
- : PV output voltage, .
- : number of parallel PV cells.
- : number of PV cells in series.
- : electron charge, .
- : p-n junction diode ideality factor, .
- : Boltzmann’s constant, .
- : absolute operating temperature, .
- : short-circuit current at .
- : temperature coefficient of short-circuit current, .
- : the temperature at standard test conditions, .
- : PV cell irradiance, .
- : standard irradiance for testing purposes, .
- : reverse saturation current of the diode, .
- : band-gap energy of the semiconductor material utilized in the PV cell, .
2.2. Partial Shading Phenomenon
3. Dandelion Optimizer-Based MPPT Technique
3.1. Dandelion Optimization (DO) Algorithm
3.1.1. Rising Stage
- : position of a dandelion seed in the tth iteration.
- : position of a dandelion seed in the (t+1)th iteration.
- : step size parameter.
- : lift coefficient in the horizontal direction.
- : lift coefficient in the vertical direction.
- : lognormal distribution.
- : random starting position of the dandelion seed.
3.1.2. Declining Stage
- : Brownian motion derived from the normal distribution.
- : average position of the seeds during the tth iteration.
- is computed using Equation (15).
3.1.3. Land Stage
- : optimal position of the dandelion seed in the tth iteration.
- linearly increasing function that ranges from 0 to 2.
- : Levy flight function.
- is calculated using Equation (17).
3.2. Execution of DO Algorithm for MPPT
- Duty Ratio Initialization and Restrictions: The duty ratios in the DO algorithm represent the control signals transmitted to the converter, akin to dandelion seeds in the natural analogy. To begin the optimization process, the duty ratios must be initialized within a certain search space, which is limited by the maximum value and the minimum value . The reason for these restrictions is to confine the optimization to a safe and feasible range of duty ratios that do not cause instability or exceed the operational limits of the converter. This ensures that the algorithm starts with reasonable values for power conversion, avoiding any unsafe or impractical configurations.
- Iterative Optimization Process: The DO algorithm proceeds with an iterative optimization process, consisting of three stages: rising, descending, and landing. During the rising stage, the duty ratios undergo random trajectories, allowing for a broad exploration of the search space to identify potential optimal points. In the descending stage, the Brownian motion trajectory is employed to refine the optimization process, focusing on promising regions in the search space. Finally, the landing stage utilizes a linear increasing function with Levy flight to fine-tune the duty ratios, aiming to converge towards the GMPP.
- Obtaining the Optimum Duty Ratio: Through the iterative process, the DO algorithm continuously updates the positions of the duty ratios until it reaches a point of convergence, where the optimum duty ratio representing the GMPP is identified. This duty ratio is then sent to the converter, adjusting the power conversion to operate at the optimal power output of the PV system.
4. Simulation Results and Analysis
4.1. Simulation Study under Partial Shading Conditions
- (1)
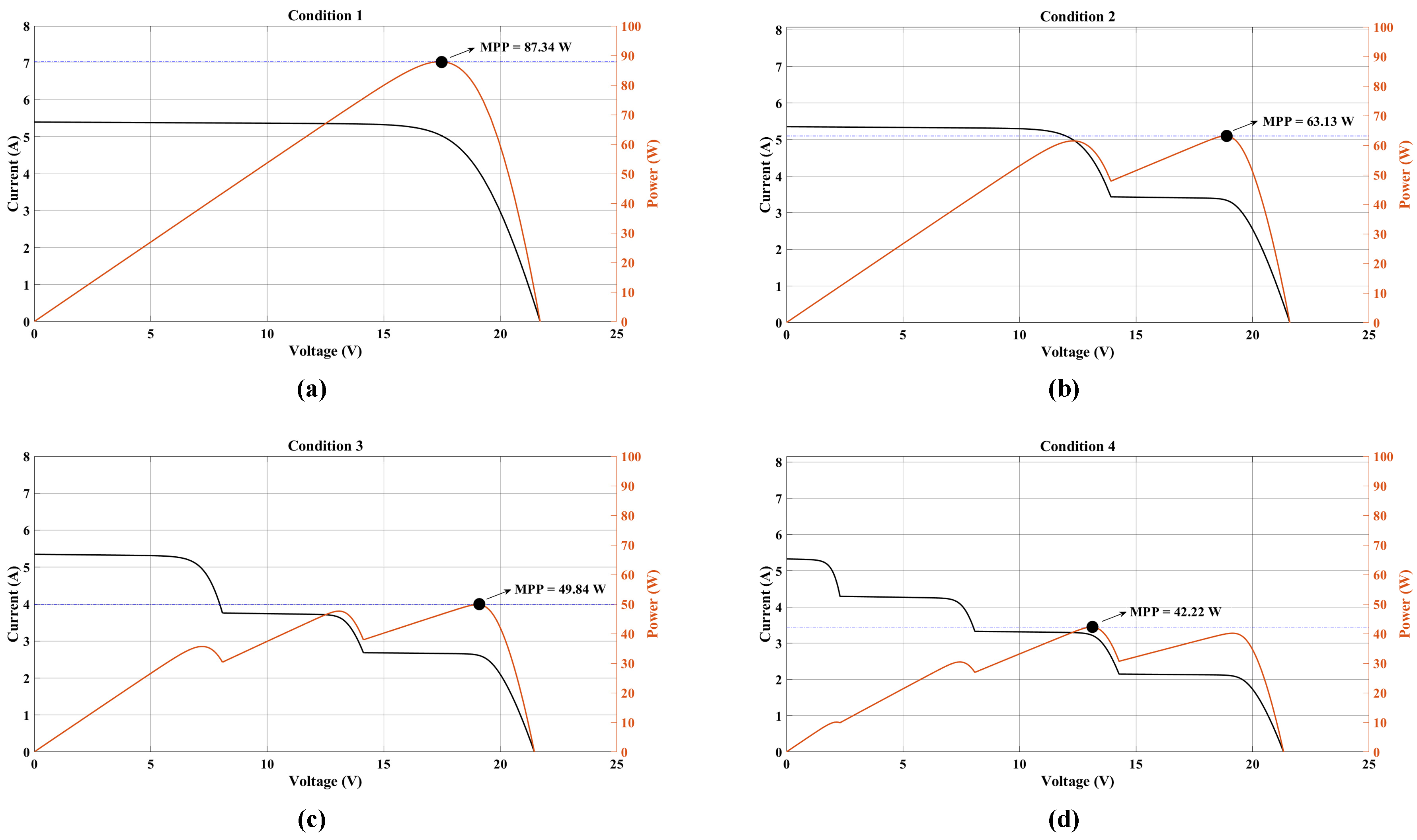
- Pattern 1: In the first pattern, the simulation represents a scenario without any shading. In this configuration, all PV panels (G1, G2, G3, G4) receive an equal irradiation level of 1000 W/m2, resulting in the generation of equal currents. As a result, the P-V curve displays a single peak with the maximum power, referred to as GMPP, as shown in Figure 8a.
- (2)
- Pattern 2: In this pattern, the simulation represents a light shade condition. In this configuration, modules G1, G2, and G3 receive an irradiance of 1000 W/m2, while module G4 receives only 500 W/m2 due to partial shading. Consequently, the current caused by the PV string and the shaded module are equal. However, the maximum current due to the unshaded PV panels can be bypassed through the bypass diodes across each panel. This disparity in currents results in the generation of two distinct peaks in the P-V curves, as illustrated in Figure 8b.
- (3)
- Pattern 3: In this pattern, the simulation depicts a scenario where modules G1 and G2 obtain an irradiance of 1000 W/m2, while modules G3 and G4 receive 700 W/m2 and 400 W/m2, respectively, due to partial shading. Consequently, the current produced by the PV string aligns with that of the shaded modules (G3 and G4). This results in the generation of three distinct peaks in the P-V curves, owing to the variation in currents, as illustrated in Figure 8c.
- (4)
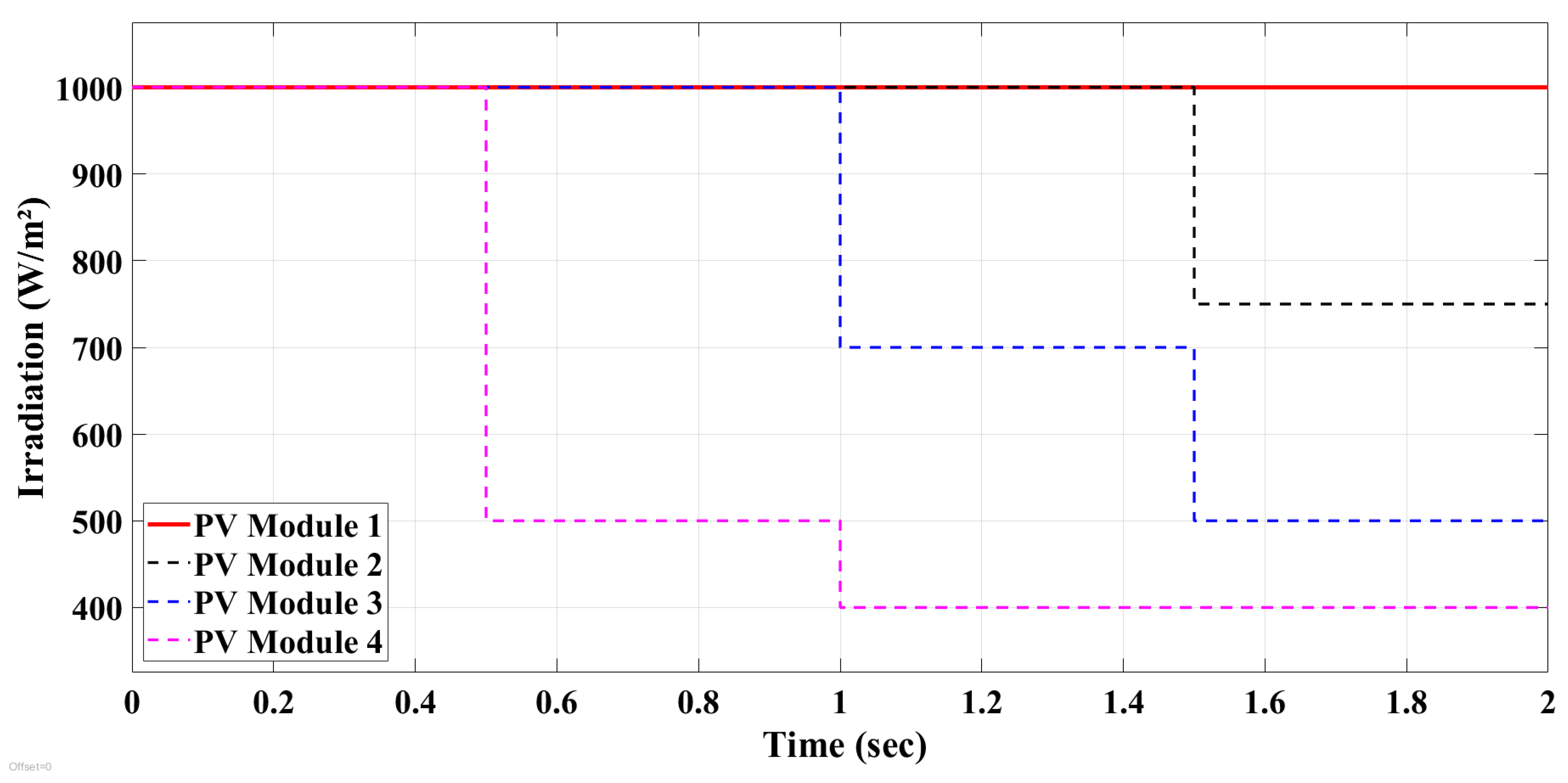
- Pattern 4: This pattern represents a strong shade condition, where PV modules G1, G2, G3, and G4 obtain irradiance levels of 1000 W/m2, 750 W/m2, 500 W/m2, and 400 W/m2, respectively. Each module experiences a different degree of shading, leading to the development of distinct currents. Consequently, the P-V curves exhibit multiple peaks, as depicted in Figure 8d. Among these peaks, only one corresponds to the GMPP, while the others are identified as LMPPs.
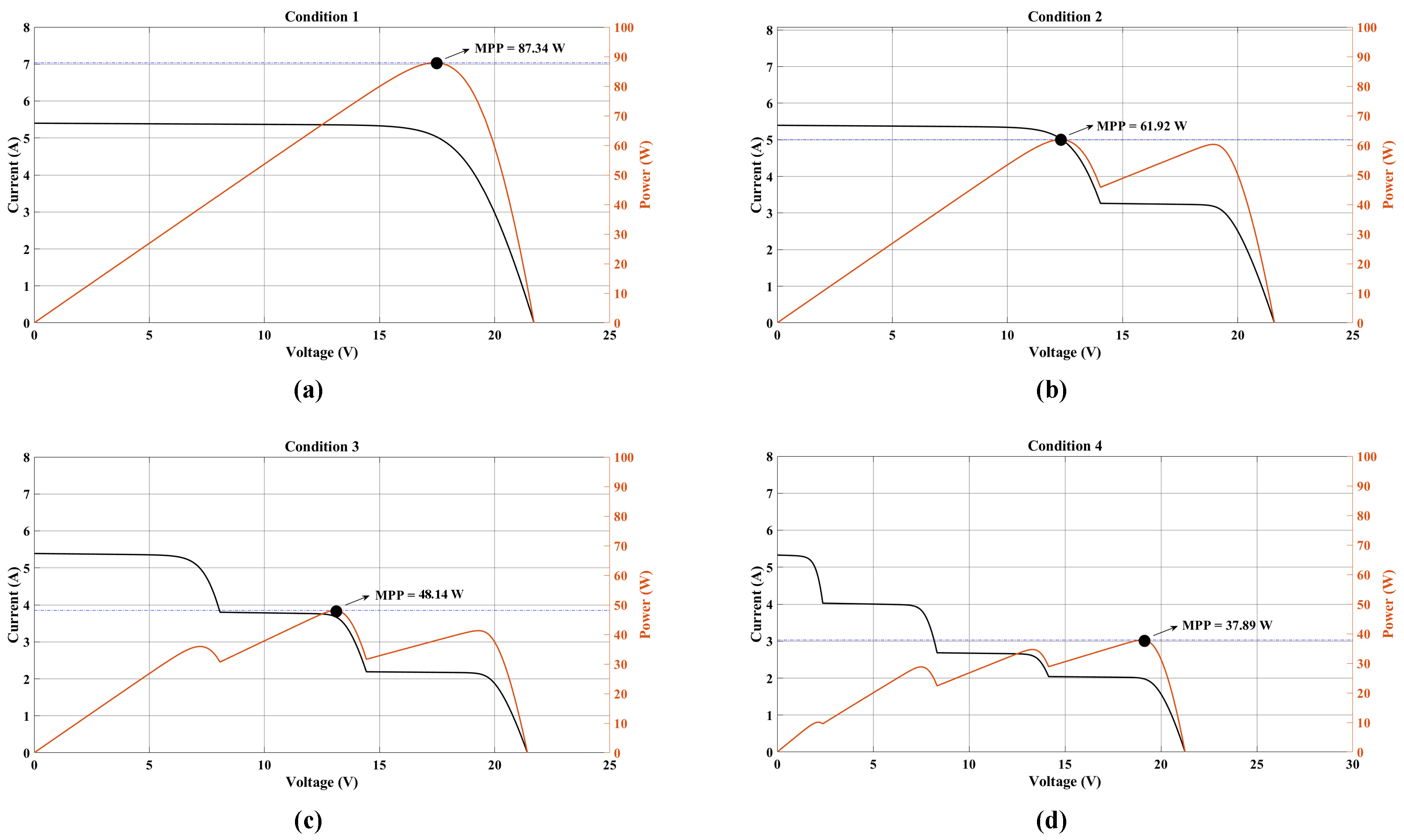
4.1.1. Shading Condition 1
4.1.2. Shading Condition 2
4.1.3. Shading Condition 3
4.1.4. Shading Condition 4
4.2. Simulation Study under Varying Irradiation
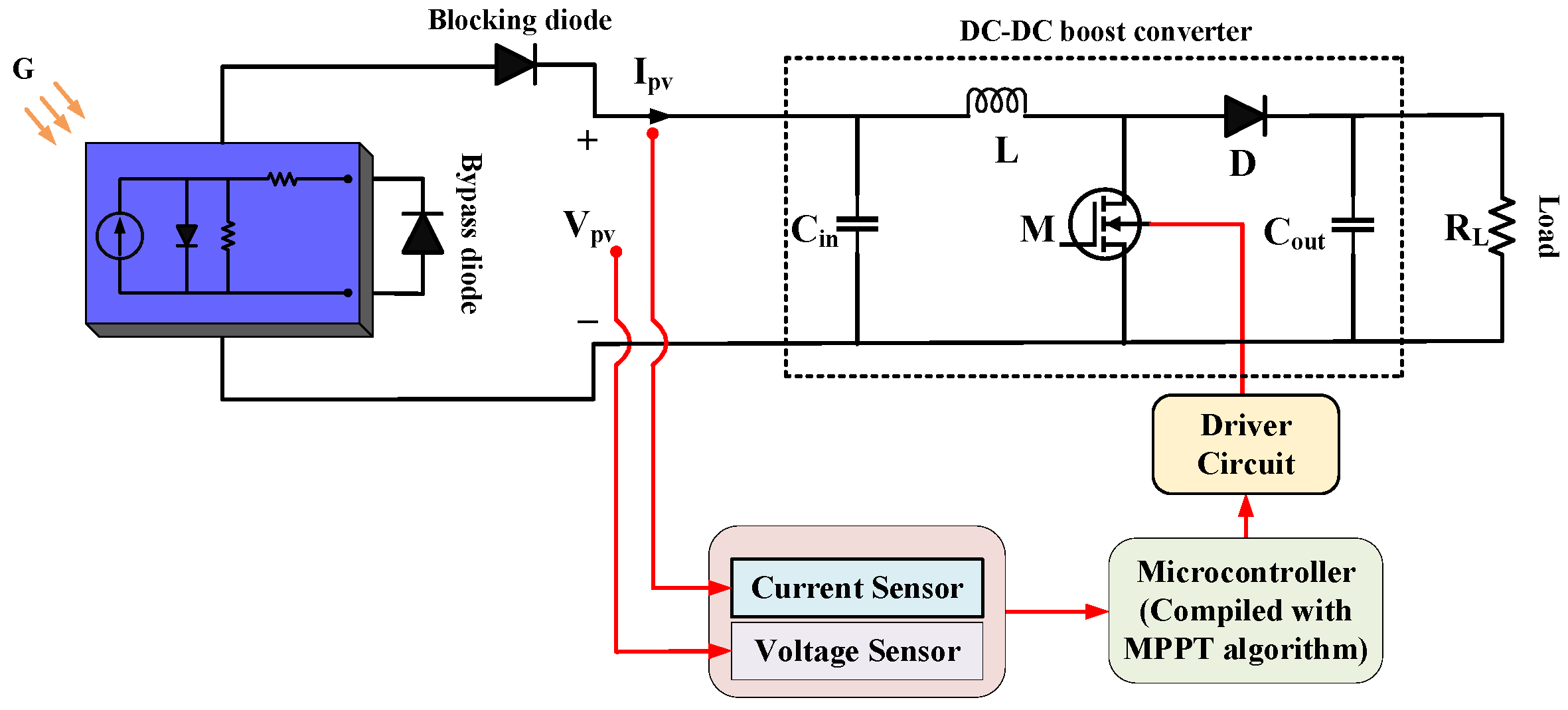
5. Hardware-in-the-Loop (HIL) Implementation
5.1. Static Shading Conditions
- (1)
- In scenario 1, there is no shading, and all photovoltaic (PV) panels—G1, G2, G3, and G4—receive an equal irradiation level of 1000 W/m2. This uniform irradiation leads to the generation of equal currents. The corresponding P-V curve demonstrates a solitary peak, referred to as the GMPP, as shown in Figure 15a.
- (2)
- In scenario 2, a light shading condition is present, where only the G4 module receives an irradiance of 600 W/m2, while the remaining modules—G1, G2, and G3—receive an irradiance of 1000 W/m2. The presence of bypass diodes enables the bypassing of the maximum current generated by the unshaded PV panels. As a result, the P-V curves have two separate peaks. This behavior is depicted in Figure 15b.
- (3)
- In the third scenario, the PV modules experience different levels of irradiance: G1 and G2 receive 1000 W/m2, G3 receives 700 W/m2, and G4 receives 500 W/m2. Consequently, the shaded modules G3 and G4 generate lower currents than the unshaded modules. This difference in currents, assisted by the bypass diode, causes the P-V curves to exhibit three separate peaks. Figure 15c visually represents these peaks.
- (4)
- Scenario 4 is characterized by a significant shading effect, where each PV panel experiences a different level of shading. This circumstance causes several peaks to appear on the P-V curves. Specifically, the G1, G2, G3, and G4 modules receive irradiance levels of 1000 W/m2, 700 W/m2, 600 W/m2, and 400 W/m2, respectively. In this scenario, only one peak corresponds to the GMPP, while the other peaks are regarded as LMPPs. The behavior of the P-V curve under this scenario is illustrated in Figure 15d.
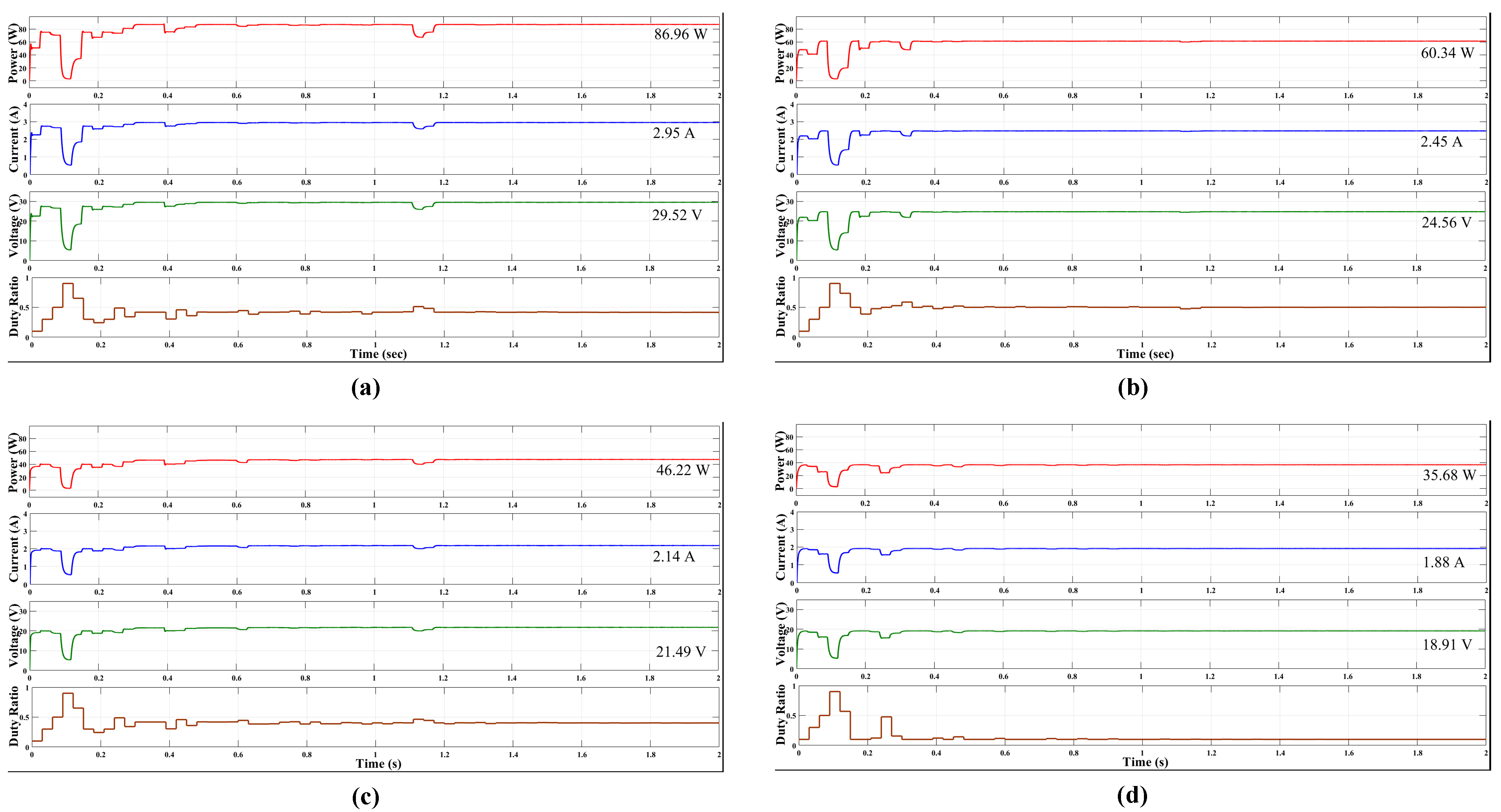
5.1.1. Shading Condition 1
5.1.2. Shading Condition 2
5.1.3. Shading Condition 3
5.1.4. Shading Condition 4
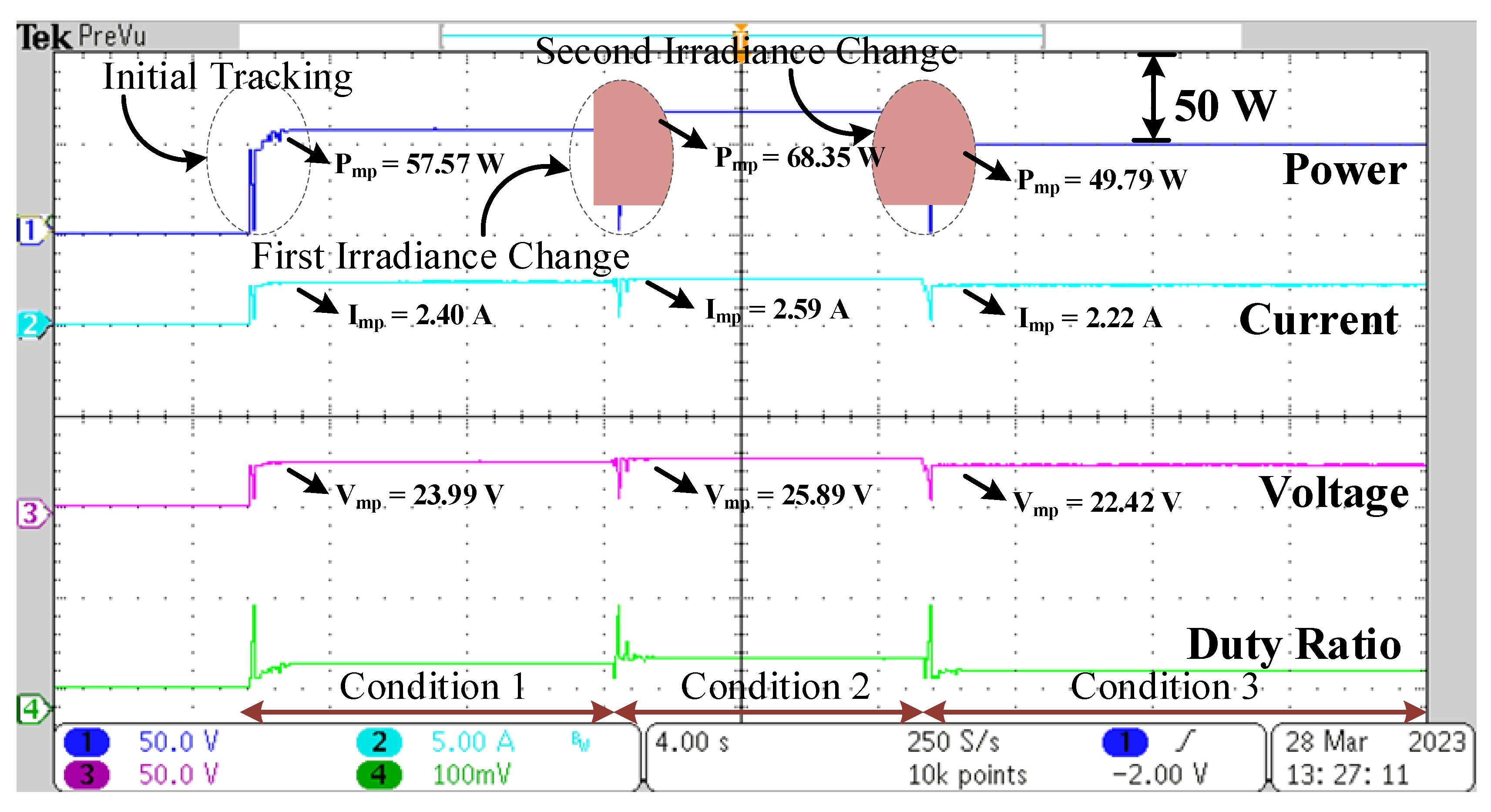
5.2. Dynamic Changes in Shading Pattern
6. Discussion
- Three-Stage Process: DO models the dandelion seed flight dynamics as a three-stage process: rise, descent, and landing. Each stage is designed to serve a specific purpose in the optimization process, making the algorithm more effective in capturing the GMPP.
- Incorporation of Random Trajectories: In the rising stage, DO incorporates random trajectories. By doing so, the algorithm can easily adjust to different weather conditions, which is particularly beneficial in real-world PV systems that experience varying environmental factors. This adaptability allows DO to efficiently explore the search space and avoid becoming trapped in local optima.
- Utilization of Brownian Motion and Levy Flight: In the descending stage, DO employs Brownian motion trajectory, which adds a level of randomness to the movement, helping to further explore the search space. Additionally, in the landing stage, DO uses a linear increasing function with Levy flight. Levy flight is known for its ability to perform long-range jumps, facilitating a more thorough exploration of the search space.
- Harmonious Exploration and Exploitation: The trajectory patterns exhibited by DO, combining random trajectories, Brownian motion, and Levy flight, enable the algorithm to achieve a harmonious balance between exploration (discovering new areas in the search space) and exploitation (focusing on promising regions). This balance is essential in effectively locating the GMPP, as it prevents premature convergence and ensures that the algorithm explores potential optimal solutions.
- Precision in GMPP Localization: By incorporating these trajectory patterns and balancing exploration and exploitation, DO enhances the precision in locating the GMPP. The algorithm can quickly and accurately track the optimal power output, leading to improved MPPT performance and higher energy harvesting efficiency in PV systems.
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Belhachat, F.; Larbes, C. Comprehensive review on global maximum power point tracking techniques for PV systems subjected to partial shading conditions. Sol. Energy 2019, 183, 476–500. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, T.; Wang, J.; Shu, H.; Yu, T.; Zhang, X.; Yao, W.; Sun, L. Comprehensive overview of maximum power point tracking algorithms of PV systems under partial shading condition. J. Clean. Prod. 2020, 268, 121983. [Google Scholar] [CrossRef]
- Yang, B.; Zhong, L.; Zhang, X.; Shu, H.; Yu, T.; Li, H.; Jiang, L.; Sun, L. Novel bio-inspired memetic salp swarm algorithm and application to MPPT for PV systems considering partial shading condition. J. Clean. Prod. 2019, 215, 1203–1222. [Google Scholar] [CrossRef]
- Rehman, H.; Sajid, I.; Sarwar, A.; Tariq, M.; Bakhsh, F.I.; Ahmad, S.; Mahmoud, H.A.; Aziz, A. Driving training-based optimization (DTBO) for global maximum power point tracking for a photovoltaic system under partial shading condition. IET Renew. Power Gener. 2023, 17, 2542–2562. [Google Scholar] [CrossRef]
- Zafar, M.H.; Khan, N.M.; Mirza, A.F.; Mansoor, M. Bio-inspired optimization algorithms based maximum power point tracking technique for photovoltaic systems under partial shading and complex partial shading conditions. J. Clean. Prod. 2021, 309, 127279. [Google Scholar] [CrossRef]
- Sajid, I.; Sarwar, A.; Tariq, M.; Bakhsh, F.I.; Hussan, R.; Ahmad, S.; Mohamed, A.S.N.; Ahmad, A. Runge Kutta optimization-based selective harmonic elimination in an H-bridge multilevel inverter. IET Power Electron. 2023. [Google Scholar] [CrossRef]
- Sajid, I.; Iqbal, D.; Alam, M.S.; Rafat, Y.; Al Ammar, E.; Alrajhi, H. Feasibility Analysis of Open Vehicle Grid Integration Platform (OVGIP) for Indian Scenario. In Proceedings of the 2022 2nd International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies, ICAECT, Bhilai, India, 21–22 April 2022. [Google Scholar] [CrossRef]
- Seyedmahmoudian, M.; Soon, T.K.; Horan, B.; Ghandhari, A.; Mekhilef, S.; Stojcevski, A. New ARMO-based MPPT Technique to Minimize Tracking Time and Fluctuation at Output of PV Systems under Rapidly Changing Shading Conditions. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Awan, M.M.A.; Asghar, A.B.; Javed, M.Y.; Conka, Z. Ordering Technique for the Maximum Power Point Tracking of an Islanded Solar Photovoltaic System. Sustainability 2023, 15, 3332. [Google Scholar] [CrossRef]
- Yousri, D.; Babu, T.S.; Allam, D.; Ramachandaramurthy, V.K.; Etiba, M.B. A Novel Chaotic Flower Pollination Algorithm for Global Maximum Power Point Tracking for Photovoltaic System Under Partial Shading Conditions. IEEE Access 2019, 7, 121432–121445. [Google Scholar] [CrossRef]
- Pervez, I.; Pervez, A.; Tariq, M.; Sarwar, A.; Chakrabortty, R.K.; Ryan, M.J. Rapid and Robust Adaptive Jaya (Ajaya) Based Maximum Power Point Tracking of a PV-Based Generation System. IEEE Access 2021, 9, 48679–48703. [Google Scholar] [CrossRef]
- Abdel-Salam, M.; El-Mohandes, M.-T.; Goda, M. An improved perturb-and-observe based MPPT method for PV systems under varying irradiation levels. Sol. Energy 2018, 171, 547–561. [Google Scholar] [CrossRef]
- Fatemi, S.M.; Shadlu, M.S.; Talebkhah, A. Comparison of Three-Point P&O and Hill Climbing Methods for Maximum Power Point Tracking in PV Systems. In Proceedings of the 2019 10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 12–14 February 2019; pp. 764–768. [Google Scholar] [CrossRef]
- Safari, A.; Mekhilef, S. Simulation and Hardware Implementation of Incremental Conductance MPPT With Direct Control Method Using Cuk Converter. IEEE Trans. Ind. Electron. 2010, 58, 1154–1161. [Google Scholar] [CrossRef]
- Sher, H.A.; Murtaza, A.F.; Noman, A.; Addoweesh, K.E.; Al-Haddad, K.; Chiaberge, M. A New Sensorless Hybrid MPPT Algorithm Based on Fractional Short-Circuit Current Measurement and P&O MPPT. IEEE Trans. Sustain. Energy 2015, 6, 1426–1434. [Google Scholar] [CrossRef]
- Baimel, D.; Tapuchi, S.; Levron, Y.; Belikov, J. Improved Fractional Open Circuit Voltage MPPT Methods for PV Systems. Electronics 2019, 8, 321. [Google Scholar] [CrossRef]
- Debnath, A.; Olowu, T.O.; Parvez, I.; Dastgir, M.G.; Sarwat, A. A Novel Module Independent Straight Line-Based Fast Maximum Power Point Tracking Algorithm for Photovoltaic Systems. Energies 2020, 13, 3233. [Google Scholar] [CrossRef]
- Algarín, C.R.; Giraldo, J.T.; Álvarez, O.R. Fuzzy Logic Based MPPT Controller for a PV System. Energies 2017, 10, 2036. [Google Scholar] [CrossRef]
- Jyothy, L.P.; Sindhu, M.R. An Artificial Neural Network based MPPT Algorithm for Solar PV System. In Proceedings of the 2018 4th International Conference on Electrical Energy Systems (ICEES), Chennai, India, 7–9 February 2018; pp. 375–380. [Google Scholar] [CrossRef]
- Li, X.; Wen, H.; Hu, Y.; Jiang, L. A novel beta parameter based fuzzy-logic controller for photovoltaic MPPT application. Renew. Energy 2019, 130, 416–427. [Google Scholar] [CrossRef]
- Hai, T.; Zhou, J.; Muranaka, K. An efficient fuzzy-logic based MPPT controller for grid-connected PV systems by farmland fertility optimization algorithm. Optik 2022, 267, 169636. [Google Scholar] [CrossRef]
- Hayder, W.; Ogliari, E.; Dolara, A.; Abid, A.; Ben Hamed, M.; Sbita, L. Improved PSO: A Comparative Study in MPPT Algorithm for PV System Control under Partial Shading Conditions. Energies 2020, 13, 2035. [Google Scholar] [CrossRef]
- Alshareef, M.; Lin, Z.; Ma, M.; Cao, W. Accelerated Particle Swarm Optimization for Photovoltaic Maximum Power Point Tracking under Partial Shading Conditions. Energies 2019, 12, 623. [Google Scholar] [CrossRef]
- Mosaad, M.I.; El-Raouf, M.O.A.; Al-Ahmar, M.A.; Banakher, F.A. Maximum Power Point Tracking of PV system Based Cuckoo Search Algorithm; review and comparison. Energy Procedia 2019, 162, 117–126. [Google Scholar] [CrossRef]
- Cuong-Le, T.; Minh, H.-L.; Khatir, S.; Wahab, M.A.; Tran, M.T.; Mirjalili, S. A novel version of Cuckoo search algorithm for solving optimization problems. Expert Syst. Appl. 2021, 186, 115669. [Google Scholar] [CrossRef]
- Gonzalez-Castano, C.; Restrepo, C.; Kouro, S.; Rodriguez, J. MPPT Algorithm Based on Artificial Bee Colony for PV System. IEEE Access 2021, 9, 43121–43133. [Google Scholar] [CrossRef]
- Boutasseta, N.; Bouakkaz, M.S.; Fergani, N.; Attoui, I.; Bouraiou, A.; Neçaibia, A. Experimental Evaluation of Moth-Flame Optimization Based GMPPT Algorithm for Photovoltaic Systems Subject to Various Operating Conditions. Appl. Sol. Energy 2022, 58, 1–14. [Google Scholar] [CrossRef]
- Guo, K.; Cui, L.; Mao, M.; Zhou, L.; Zhang, Q. An Improved Gray Wolf Optimizer MPPT Algorithm for PV System with BFBIC Converter Under Partial Shading. IEEE Access 2020, 8, 103476–103490. [Google Scholar] [CrossRef]
- Mansoor, M.; Mirza, A.F.; Ling, Q.; Javed, M.Y. Novel Grass Hopper optimization based MPPT of PV systems for complex partial shading conditions. Sol. Energy 2020, 198, 499–518. [Google Scholar] [CrossRef]
- Kaya, C.B.; Kaya, E.; Gökkuş, G. Training Neuro-Fuzzy by Using Meta-Heuristic Algorithms for MPPT. Comput. Syst. Sci. Eng. 2022, 45, 69–84. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Oliva, D.; Cuevas, E.; Pajares, G. Parameter identification of solar cells using artificial bee colony optimization. Energy 2014, 72, 93–102. [Google Scholar] [CrossRef]
- Ghani, F.; Rosengarten, G.; Duke, M.; Carson, J. The numerical calculation of single-diode solar-cell modelling parameters. Renew. Energy 2014, 72, 105–112. [Google Scholar] [CrossRef]
- Bastidas-Rodriguez, J.; Petrone, G.; Ramos-Paja, C.; Spagnuolo, G. A genetic algorithm for identifying the single diode model parameters of a photovoltaic panel. Math. Comput. Simul. 2017, 131, 38–54. [Google Scholar] [CrossRef]








| Parameters | Values |
|---|---|
| Number of PV modules in series | 4 |
| 72 | |
| 87.348 W | |
| 5.02 A | |
| 17.4 V | |
| Short-circuit current | 5.34 A |
| Open-circuit voltage | 21.7 V |
| 0.075%/°C | |
| −0.37501%/°C | |
| 5.3624 A | |
| 3.052 × 10−10 A | |
| 0.12439 | |
| 79.3172 Ω | |
| 0.081018 Ω |
| Components | Values |
|---|---|
| 21.837 W | |
| 10 Ω |
| Parameters | PSO | CS | DO |
|---|---|---|---|
| 4 | 4 | 4 | |
| 10 | 10 | 10 | |
| 1.2 | |||
| 1.6 | |||
| 0.4 | |||
| 0.8 | |||
| 1.5 | 1.5 | ||
| 0.01 |
| Shading Condition | Insolation (W/m2) | Method | Imp (A) | Vmp (V) | Pmp (W) | Rated Power (W) | Eff. (%) | Settling Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | G3 | G4 | ||||||||
| 1 | 1000 | 1000 | 1000 | 1000 | DO | 2.94 | 29.59 | 87.26 | 87.34 | 99.90 | 0.25 |
| CS | 2.95 | 29.52 | 86.96 | 99.56 | 1.17 | ||||||
| PSO | 2.94 | 29.41 | 86.47 | 99.00 | 1.48 | ||||||
| 2 | 1000 | 1000 | 1000 | 500 | DO | 2.48 | 24.84 | 61.71 | 61.92 | 99.66 | 0.25 |
| CS | 2.45 | 24.56 | 60.34 | 97.44 | 0.34 | ||||||
| PSO | 2.44 | 24.44 | 59.71 | 96.43 | 1.38 | ||||||
| 3 | 1000 | 1000 | 700 | 400 | DO | 2.18 | 21.84 | 47.68 | 48.14 | 99.04 | 0.25 |
| CS | 2.14 | 21.49 | 46.22 | 96.01 | 1.17 | ||||||
| PSO | 2.12 | 21.23 | 46.02 | 95.59 | 1.32 | ||||||
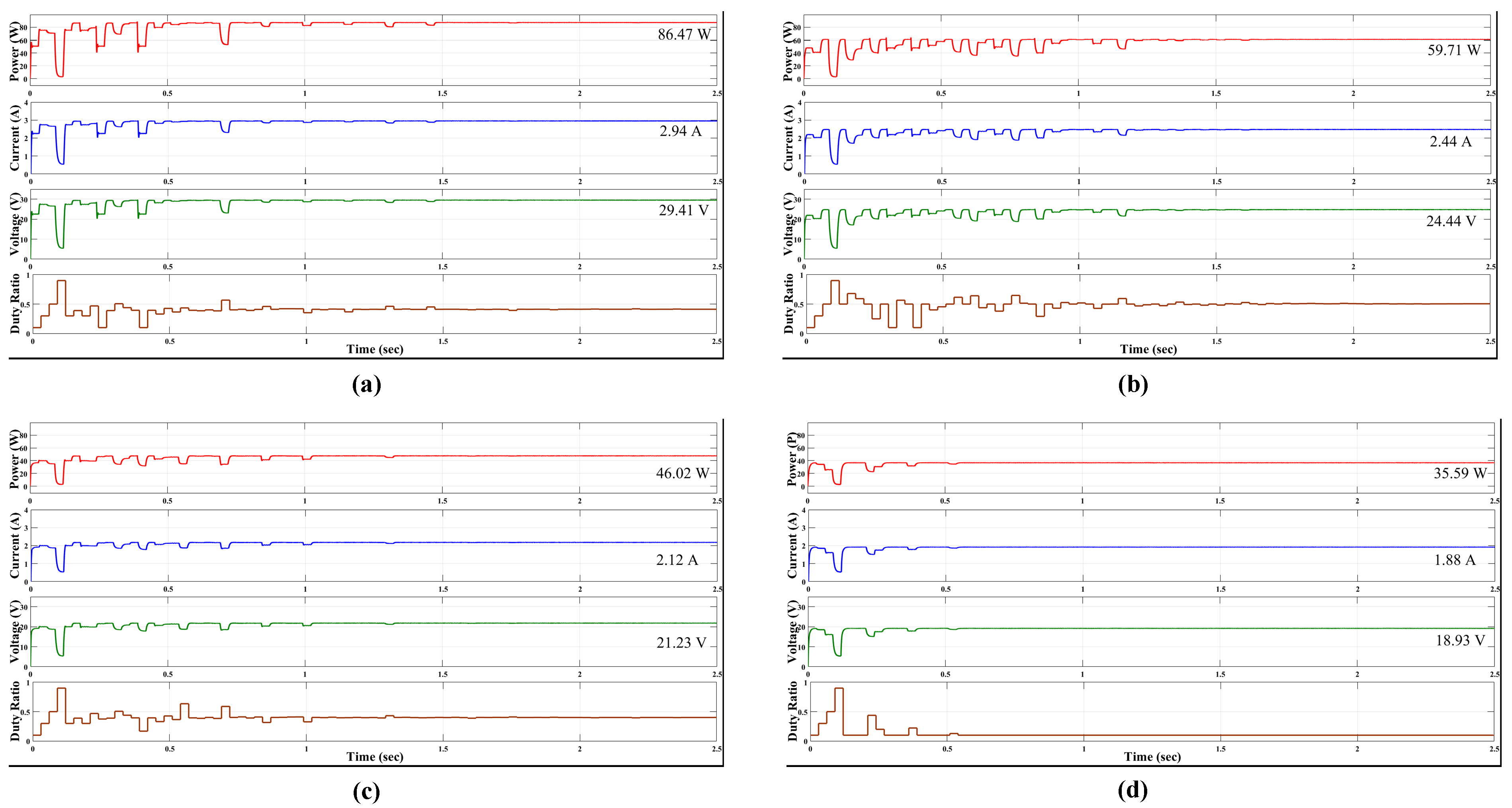
| 4 | 1000 | 750 | 500 | 400 | DO | 1.91 | 19.20 | 36.85 | 37.89 | 97.25 | 0.10 |
| CS | 1.88 | 18.91 | 35.68 | 94.16 | 0.48 | ||||||
| PSO | 1.88 | 18.93 | 35.59 | 93.92 | 0.54 | ||||||
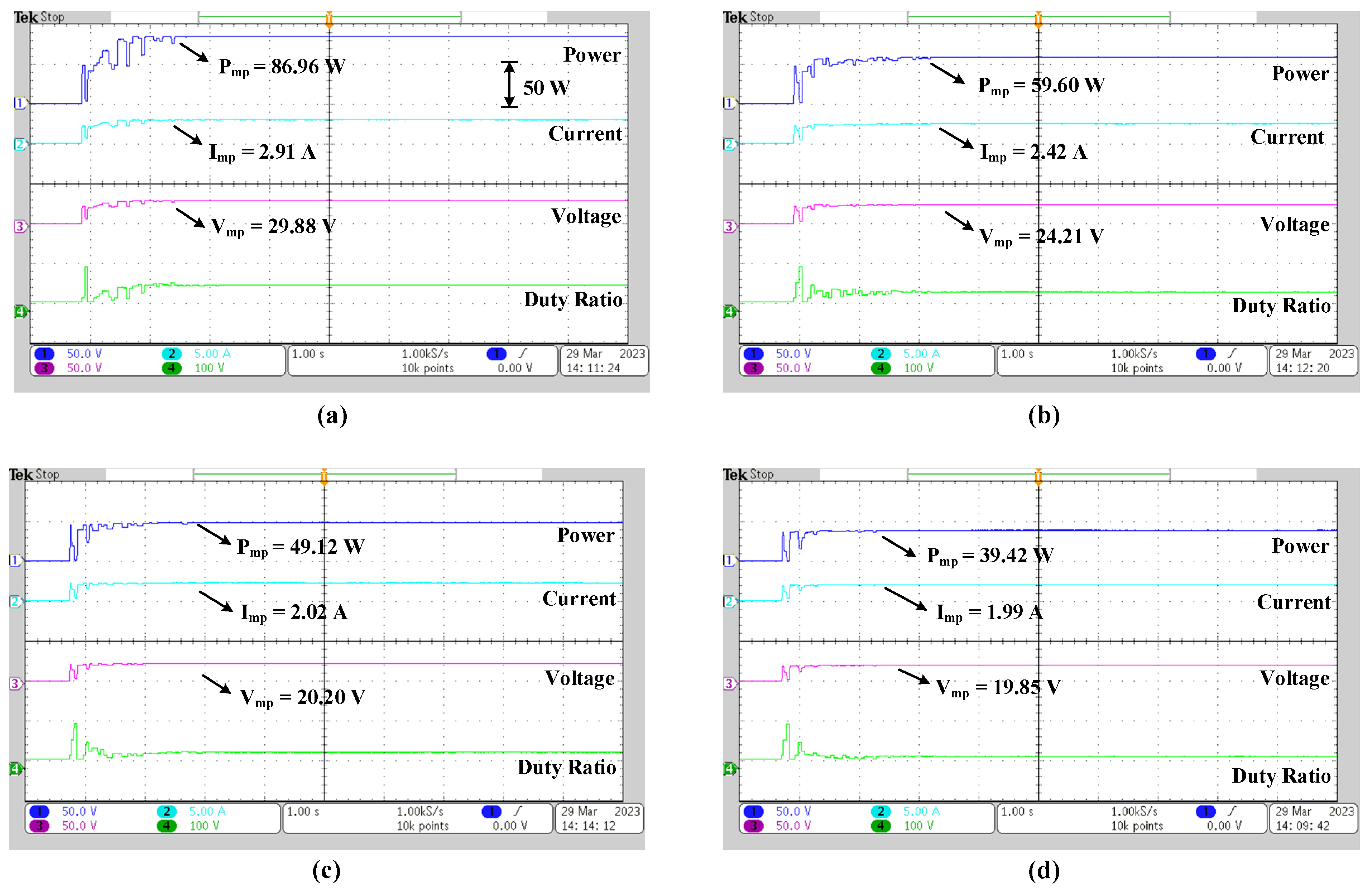
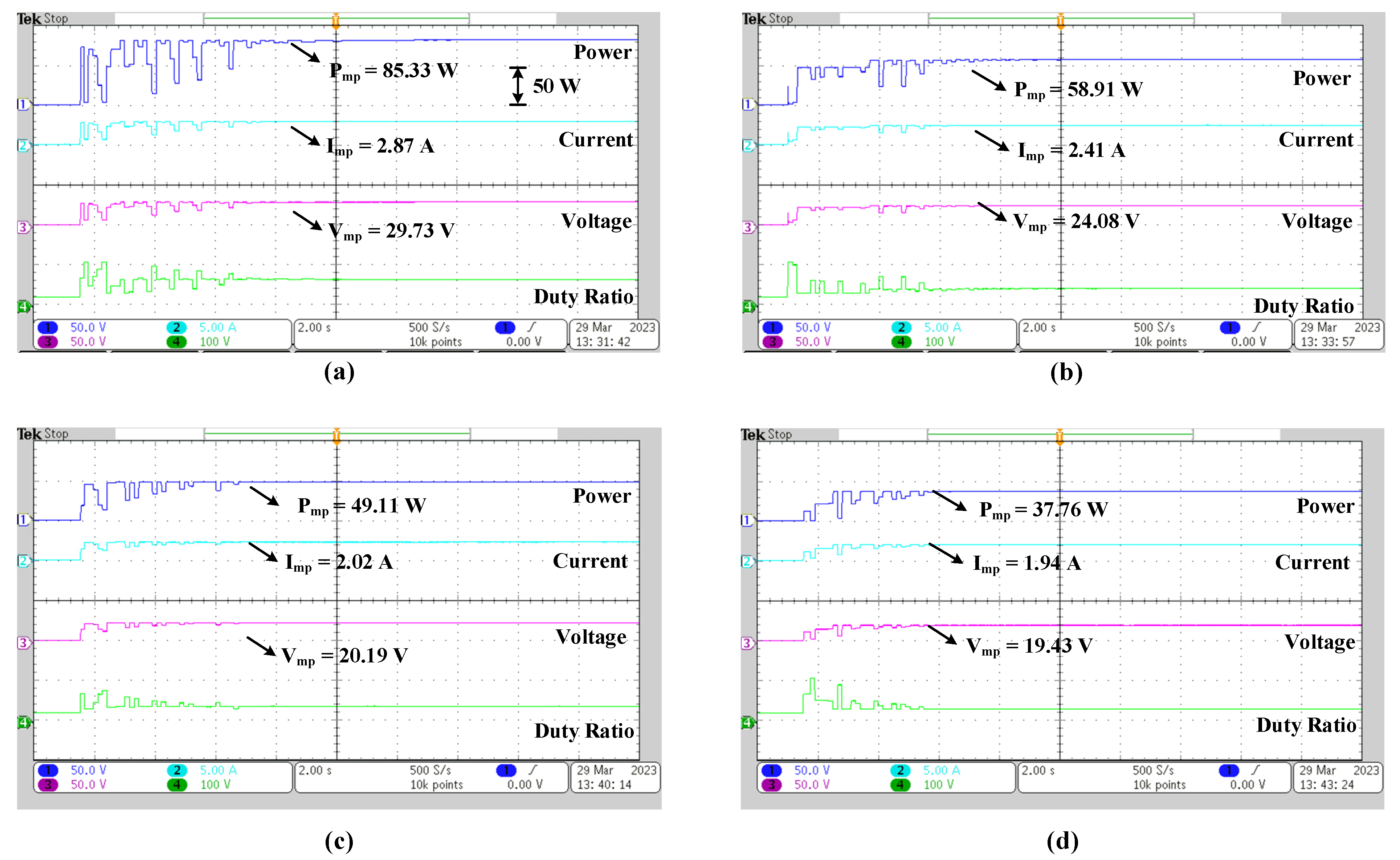
| Shading Condition | Insolation (W/m2) | Method | Imp (A) | Vmp (V) | Pmp (W) | Rated Power (W) | Eff. (%) | Settling Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | G3 | G4 | ||||||||
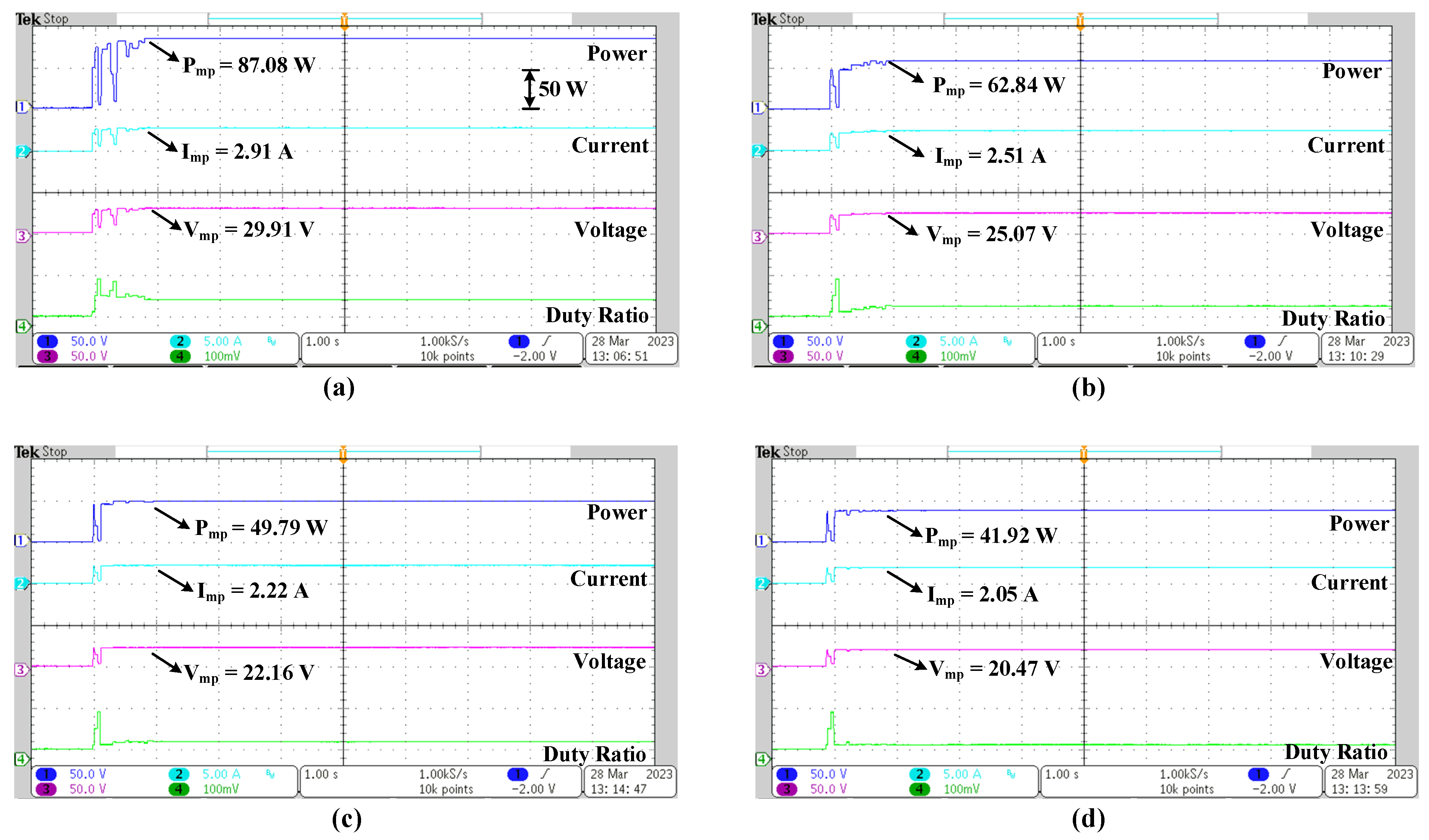
| 1 | 1000 | 1000 | 1000 | 1000 | DO | 2.91 | 29.91 | 87.08 | 87.34 | 99.70 | 0.8 |
| CS | 2.91 | 29.88 | 86.96 | 99.56 | 1.6 | ||||||
| PSO | 2.87 | 29.73 | 85.33 | 97.69 | 6.8 | ||||||
| 2 | 1000 | 1000 | 1000 | 600 | DO | 2.51 | 25.07 | 62.84 | 63.13 | 99.54 | 0.8 |
| CS | 2.42 | 24.21 | 59.60 | 94.40 | 2.4 | ||||||
| PSO | 2.41 | 24.08 | 58.91 | 93.31 | 5.0 | ||||||
| 3 | 1000 | 1000 | 700 | 500 | DO | 2.22 | 22.16 | 49.79 | 49.84 | 99.89 | 1.0 |
| CS | 2.02 | 20.20 | 49.12 | 98.55 | 2.0 | ||||||
| PSO | 2.02 | 20.19 | 49.11 | 98.53 | 4.8 | ||||||
| 4 | 1000 | 700 | 600 | 400 | DO | 2.05 | 20.47 | 41.92 | 42.22 | 99.28 | 1.0 |
| CS | 1.99 | 19.85 | 39.42 | 93.36 | 2.6 | ||||||
| PSO | 1.94 | 19.43 | 37.76 | 89.43 | 4.0 | ||||||
| Irradiance Condition | Insolation (W/m2) | Imp (A) | Vmp (V) | Pmp (W) | Rated Power (W) | Eff. (%) | Settling Time (s) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | G3 | G4 | |||||||
| 1 | 1000 | 1000 | 700 | 600 | 2.40 | 23.99 | 57.57 | 87.34 | 98.22 | 1.0 |
| 2 | 1000 | 1000 | 700 | 1000 | 2.59 | 25.89 | 68.35 | 63.13 | 98.84 | 1.6 |
| 3 | 1000 | 500 | 700 | 1000 | 2.22 | 22.42 | 49.79 | 49.84 | 99.89 | 1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajid, I.; Gautam, A.; Sarwar, A.; Tariq, M.; Liu, H.-D.; Ahmad, S.; Lin, C.-H.; Sayed, A.E. Optimizing Photovoltaic Power Production in Partial Shading Conditions Using Dandelion Optimizer (DO)-Based MPPT Method. Processes 2023, 11, 2493. https://doi.org/10.3390/pr11082493
Sajid I, Gautam A, Sarwar A, Tariq M, Liu H-D, Ahmad S, Lin C-H, Sayed AE. Optimizing Photovoltaic Power Production in Partial Shading Conditions Using Dandelion Optimizer (DO)-Based MPPT Method. Processes. 2023; 11(8):2493. https://doi.org/10.3390/pr11082493
Chicago/Turabian StyleSajid, Injila, Ayushi Gautam, Adil Sarwar, Mohd Tariq, Hwa-Dong Liu, Shafiq Ahmad, Chang-Hua Lin, and Abdelaty Edrees Sayed. 2023. "Optimizing Photovoltaic Power Production in Partial Shading Conditions Using Dandelion Optimizer (DO)-Based MPPT Method" Processes 11, no. 8: 2493. https://doi.org/10.3390/pr11082493






