Self-Assembly in Curved Space: Ordering, Defect and Entropy
Abstract
:1. Introduction
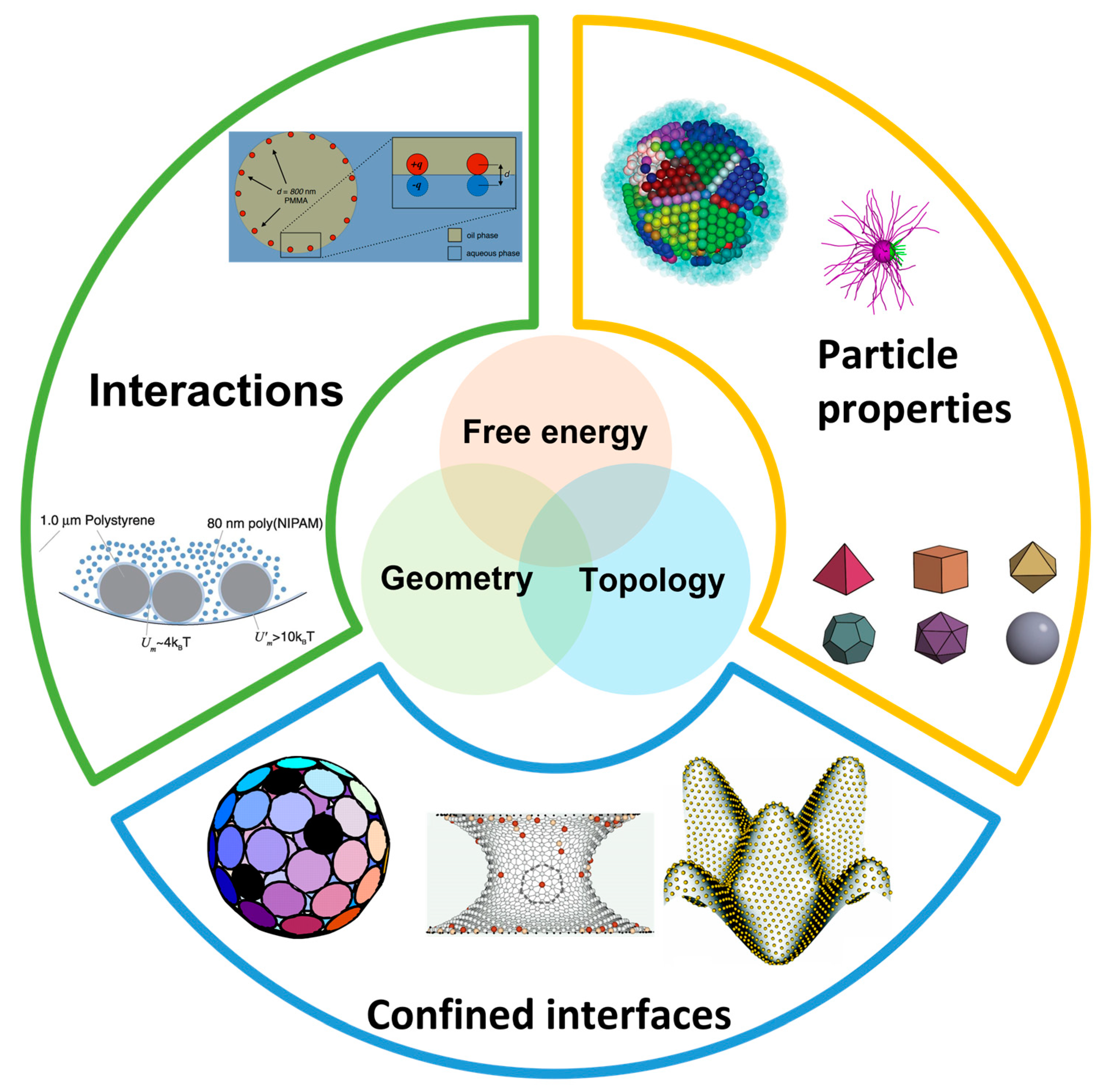
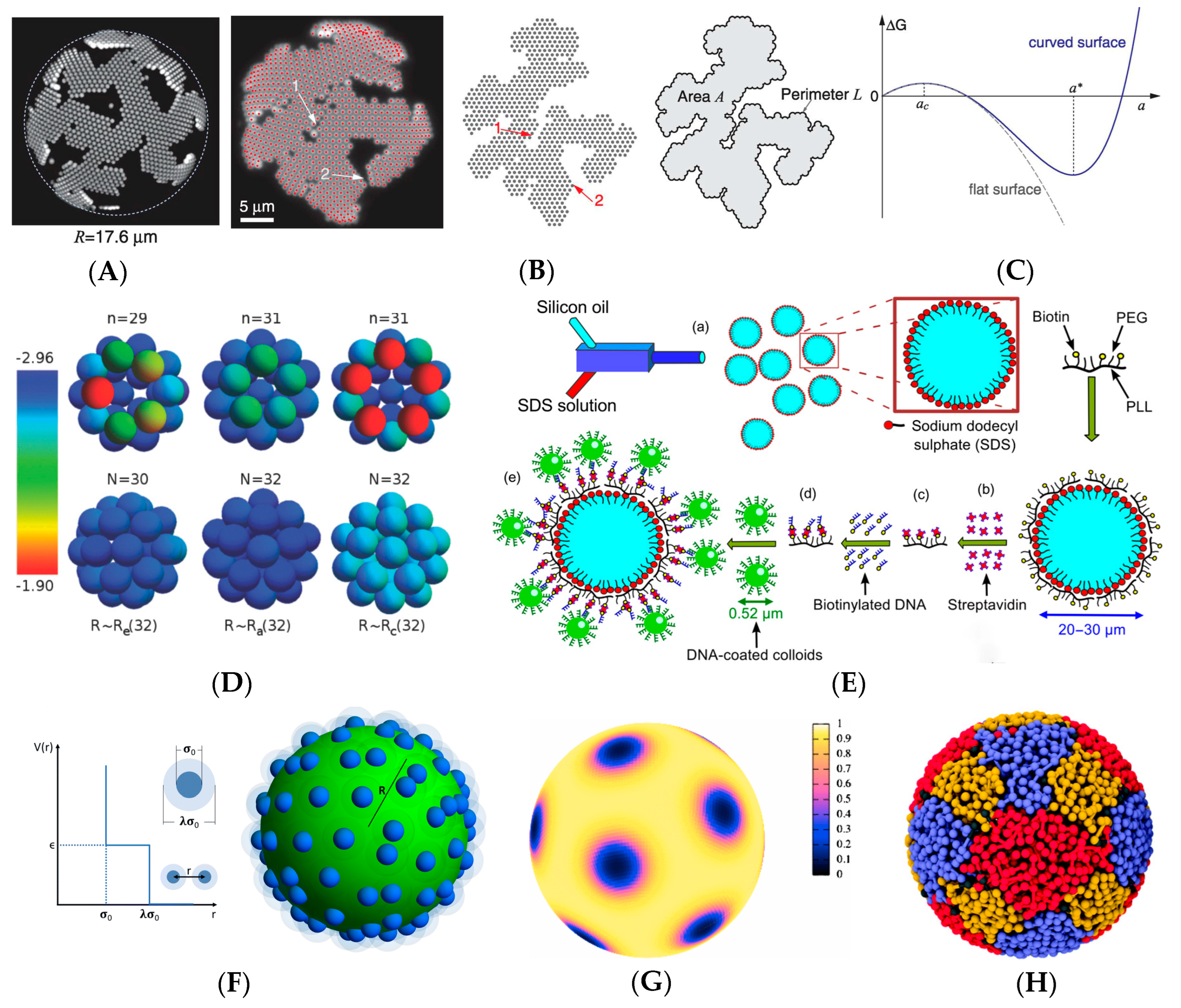
2. Colloids in Curved Space
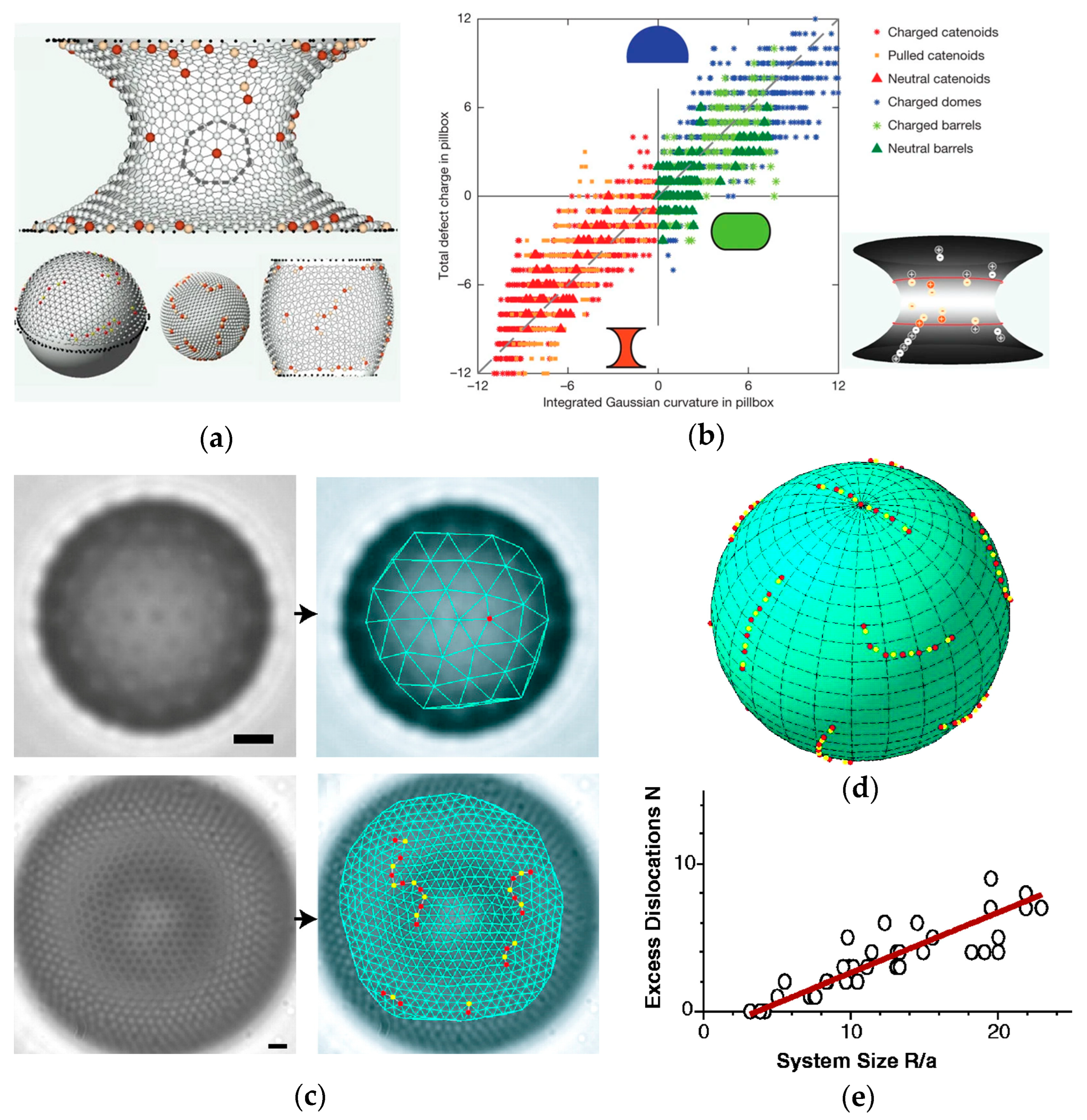
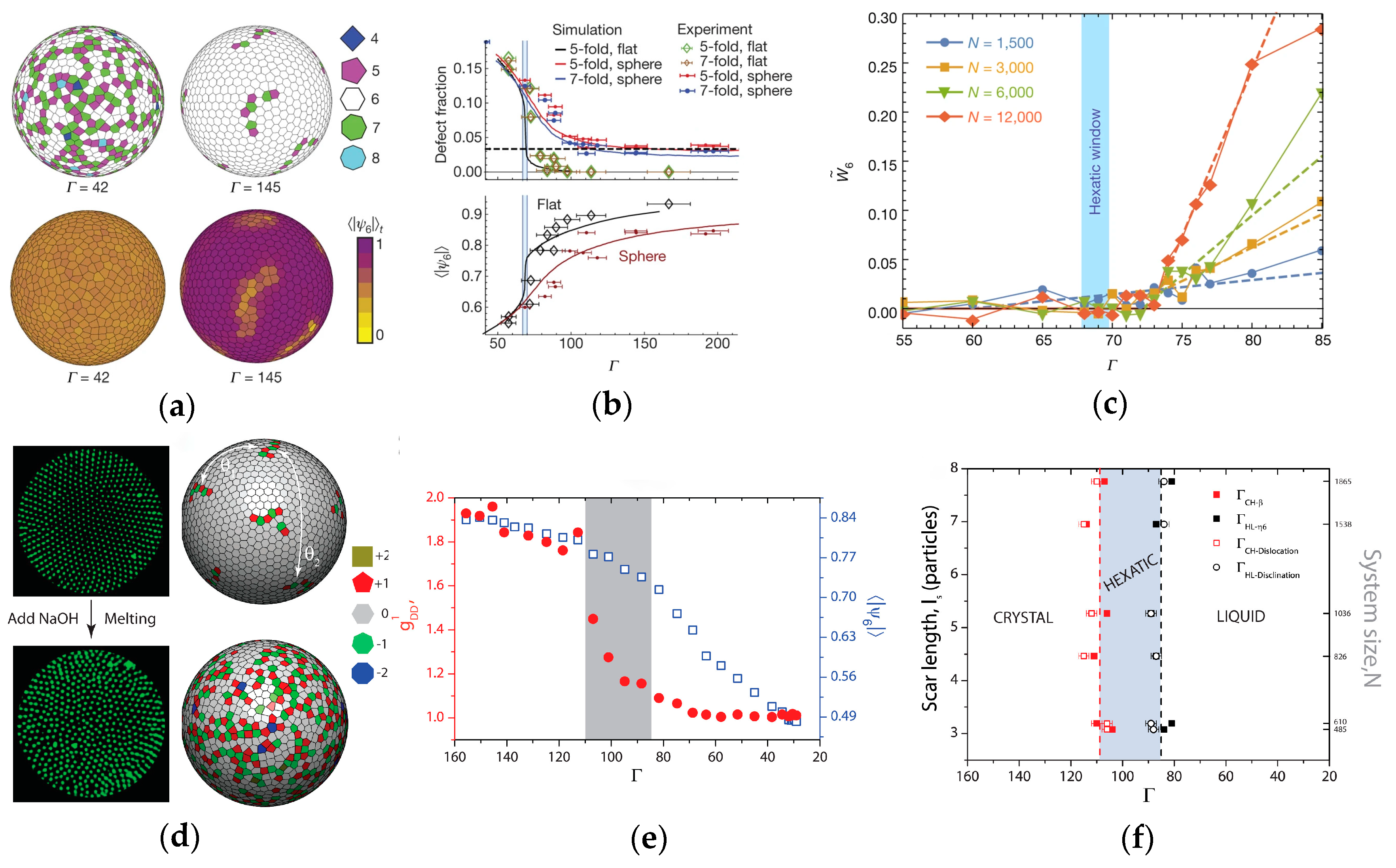
3. Factors Controlling Self-Assembly in Curved Spaces
4. Practical Applications and Control Strategies
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Whitesides, G.M.; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- Boles, M.A.; Engel, M.; Talapin, D.V. Self-assembly of colloidal nanocrystals: From intricate structures to functional materials. Chem. Rev. 2016, 116, 11220–11289. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N. Colloidal matter: Packing, geometry, and entropy. Science 2015, 349, 1253751. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Xu, Z.; Yang, Y.; Dai, X.; Yan, L.-T. Hierarchical crystals formed from DNA-functionalized Janus nanoparticles. ACS Nano 2018, 12, 9467–9475. [Google Scholar] [CrossRef] [PubMed]
- Choi, B.; Yu, J.; Paley, D.W.; Trinh, M.T.; Paley, M.V.; Karch, J.M.; Crowther, A.C.; Lee, C.-H.; Lalancette, R.A.; Zhu, X. Van der waals solids from self-assembled nanoscale building blocks. Nano Lett. 2016, 16, 1445–1449. [Google Scholar] [CrossRef] [PubMed]
- Willerich, I.; Gröhn, F. Molecular structure encodes nanoscale assemblies: Understanding driving forces in electrostatic self-assembly. J. Am. Chem. Soc. 2011, 133, 20341–20356. [Google Scholar] [CrossRef]
- Sánchez-Iglesias, A.; Grzelczak, M.; Altantzis, T.; Goris, B.; Perez-Juste, J.; Bals, S.; Van Tendeloo, G.; Donaldson, S.H., Jr.; Chmelka, B.F.; Israelachvili, J.N. Hydrophobic interactions modulate self-assembly of nanoparticles. ACS Nano 2012, 6, 11059–11065. [Google Scholar] [CrossRef]
- Min, Y.; Akbulut, M.; Kristiansen, K.; Golan, Y.; Israelachvili, J. The role of interparticle and external forces in nanoparticle assembly. Nat. Mater. 2008, 7, 527–538. [Google Scholar] [CrossRef]
- Zandi, R.; Reguera, D.; Bruinsma, R.F.; Gelbart, W.M.; Rudnick, J. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. USA 2004, 101, 15556–15560. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, G.; Gao, L.; Xu, D.; Wan, H.; Dai, X.; Zhang, X.; Tao, L.; Yan, L.-T. Configurational Entropy-Enabled Thermostability of Cell Membranes in Extremophiles: From Molecular Mechanism to Bioinspired Design. Nano Lett. 2023, 23, 1109–1118. [Google Scholar] [CrossRef]
- Eggeling, C.; Ringemann, C.; Medda, R.; Schwarzmann, G.; Sandhoff, K.; Polyakova, S.; Belov, V.N.; Hein, B.; Von Middendorff, C.; Schönle, A. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature 2009, 457, 1159–1162. [Google Scholar] [CrossRef] [PubMed]
- Bausch, A.R.; Bowick, M.J.; Cacciuto, A.; Dinsmore, A.D.; Hsu, M.F.; Nelson, D.R.; Nikolaides, M.G.; Travesset, A.; Weitz, D.A. Grain Boundary Scars and Spherical Crystallography. Science 2003, 299, 1716–1718. [Google Scholar] [CrossRef] [PubMed]
- Irvine, W.T.; Vitelli, V.; Chaikin, P.M. Pleats in crystals on curved surfaces. Nature 2010, 468, 947–951. [Google Scholar] [CrossRef] [PubMed]
- Guerra, R.E.; Kelleher, C.P.; Hollingsworth, A.D.; Chaikin, P.M. Freezing on a sphere. Nature 2018, 554, 346–350. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Sood, A.; Ganapathy, R. Observation of two-step melting on a sphere. Proc. Natl. Acad. Sci. USA 2022, 119, e2206470119. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, P.; Bowick, M.J.; Meinke, J.H.; Nelson, D.R.; Bausch, A.R. Direct visualization of dislocation dynamics in grain-boundary scars. Nat. Mater. 2005, 4, 407–411. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Dai, X.; Gao, L.; Xu, D.; Wan, H.; Wang, Y.; Yan, L.-T. The entropy-controlled strategy in self-assembling systems. Chem. Soc. Rev. 2023, 52, 6806–6837. [Google Scholar] [CrossRef]
- McGorty, R.; Fung, J.; Kaz, D.; Manoharan, V.N. Colloidal self-assembly at an interface. Mater. Today 2010, 13, 34–42. [Google Scholar] [CrossRef]
- Stratford, K.; Adhikari, R.; Pagonabarraga, I.; Desplat, J.-C.; Cates, M.E. Colloidal jamming at interfaces: A route to fluid-bicontinuous gels. Science 2005, 309, 2198–2201. [Google Scholar] [CrossRef]
- Herzig, E.M.; White, K.; Schofield, A.B.; Poon, W.C.; Clegg, P.S. Bicontinuous emulsions stabilized solely by colloidal particles. Nat. Mater. 2007, 6, 966–971. [Google Scholar] [CrossRef]
- Chai, Y.; Lukito, A.; Jiang, Y.; Ashby, P.D.; Russell, T.P. Fine-tuning nanoparticle packing at water–oil interfaces using ionic strength. Nano Lett. 2017, 17, 6453–6457. [Google Scholar] [CrossRef] [PubMed]
- Caciagli, A.; Singh, R.; Joshi, D.; Adhikari, R.; Eiser, E. Controlled optofluidic crystallization of colloids tethered at interfaces. Phys. Rev. Lett. 2020, 125, 068001. [Google Scholar] [CrossRef] [PubMed]
- Glotzer, S.C.; Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 2007, 6, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Akcora, P.; Liu, H.; Kumar, S.K.; Moll, J.; Li, Y.; Benicewicz, B.C.; Schadler, L.S.; Acehan, D.; Panagiotopoulos, A.Z.; Pryamitsyn, V. Anisotropic self-assembly of spherical polymer-grafted nanoparticles. Nat. Mater. 2009, 8, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Lattuada, M.; Hatton, T.A. Synthesis, properties and applications of Janus nanoparticles. Nano Today 2011, 6, 286–308. [Google Scholar] [CrossRef]
- Wang, D.; Hermes, M.; Kotni, R.; Wu, Y.; Tasios, N.; Liu, Y.; de Nijs, B.; van der Wee, E.B.; Murray, C.B.; Dijkstra, M.; et al. Interplay between spherical confinement and particle shape on the self-assembly of rounded cubes. Nat. Commun. 2018, 9, 2228. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, J.; Ge, B.; Deng, K.; Wu, X.; Xiao, T.; Jiang, T.; Quan, Z.; Cao, Y.C.; Wang, Z. Understanding Fe3O4 nanocube assembly with reconstruction of a consistent superlattice phase diagram. J. Am. Chem. Soc. 2019, 141, 3198–3206. [Google Scholar] [CrossRef]
- Henzie, J.; Andrews, S.C.; Ling, X.Y.; Li, Z.; Yang, P. Oriented assembly of polyhedral plasmonic nanoparticle clusters. Proc. Natl. Acad. Sci. USA 2013, 110, 6640–6645. [Google Scholar] [CrossRef]
- Croissant, J.G.; Fatieiev, Y.; Khashab, N.M. Degradability and clearance of silicon, organosilica, silsesquioxane, silica mixed oxide, and mesoporous silica nanoparticles. Adv. Mater. 2017, 29, 1604634. [Google Scholar] [CrossRef]
- Meng, G.; Paulose, J.; Nelson, D.R.; Manoharan, V.N. Elastic Instability of a Crystal Growing on a Curved Surface. Science 2014, 343, 634–637. [Google Scholar] [CrossRef]
- de Nijs, B.; Dussi, S.; Smallenburg, F.; Meeldijk, J.D.; Groenendijk, D.J.; Filion, L.; Imhof, A.; van Blaaderen, A.; Dijkstra, M. Entropy-driven formation of large icosahedral colloidal clusters by spherical confinement. Nat. Mater. 2015, 14, 56–60. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Wang, Y.; Gao, L.; Xu, Z.; Zhang, X.; Dai, X.; Dai, L.; Hou, C.; Yan, L.-T. Entropy-driven self-assembly of tethered Janus nanoparticles on a sphere. Fundam. Res. 2021, 1, 641–648. [Google Scholar] [CrossRef]
- Teich, E.G.; Van Anders, G.; Klotsa, D.; Dshemuchadse, J.; Glotzer, S.C. Clusters of polyhedra in spherical confinement. Proc. Natl. Acad. Sci. USA 2016, 113, E669–E678. [Google Scholar] [CrossRef] [PubMed]
- García, N.A.; Register, R.A.; Vega, D.A.; Gómez, L.R. Crystallization dynamics on curved surfaces. Phys. Rev. E 2013, 88, 012306. [Google Scholar] [CrossRef] [PubMed]
- Murayama, M.; Howe, J.; Hidaka, H.; Takaki, S. Atomic-level observation of disclination dipoles in mechanically milled, nanocrystalline Fe. Science 2002, 295, 2433–2435. [Google Scholar] [CrossRef] [PubMed]
- Irvine, W.T.; Vitelli, V. Geometric background charge: Dislocations on capillary bridges. Soft Matter 2012, 8, 10123–10129. [Google Scholar] [CrossRef]
- Kusumaatmaja, H.; Wales, D.J. Defect motifs for constant mean curvature surfaces. Phys. Rev. Lett. 2013, 110, 165502. [Google Scholar] [CrossRef]
- Einert, T.; Lipowsky, P.; Schilling, J.; Bowick, M.J.; Bausch, A.R. Grain Boundary Scars on Spherical Crystals. Langmuir 2005, 21, 12076–12079. [Google Scholar] [CrossRef]
- Bowick, M.J.; Nelson, D.R.; Travesset, A. Interacting topological defects on frozen topographies. Phys. Rev. B 2000, 62, 8738. [Google Scholar] [CrossRef]
- Torquato, S.; Truskett, T.M.; Debenedetti, P.G. Is random close packing of spheres well defined? Phys. Rev. Lett. 2000, 84, 2064. [Google Scholar] [CrossRef]
- Hales, T.C. Sphere packings, I. In The Kepler Conjecture: The Hales-Ferguson Proof; Springer Science & Business Media: Berlin, Germany, 2011; pp. 379–431. [Google Scholar]
- Hales, T.C. Sphere packings, II. Discret. Comput. Geom. 1997, 18, 135–149. [Google Scholar] [CrossRef]
- Pusey, P.N.; Van Megen, W. Phase behaviour of concentrated suspensions of nearly hard colloidal spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Zhu, G.; Gao, L.; Xu, Z.; Dai, X.; Zhang, X.; Yan, L.-T. Entropy-Driven Unconventional Crystallization of Spherical Colloidal Nanocrystals Confined in Wide Cylinders. Nano Lett. 2021, 21, 8439–8446. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Mbah, C.F.; Przybilla, T.; Apeleo Zubiri, B.; Spiecker, E.; Engel, M.; Vogel, N. Magic number colloidal clusters as minimum free energy structures. Nat. Commun. 2018, 9, 5259. [Google Scholar] [CrossRef] [PubMed]
- Echt, O.; Sattler, K.; Recknagel, E. Magic numbers for sphere packings: Experimental verification in free xenon clusters. Phys. Rev. Lett. 1981, 47, 1121. [Google Scholar] [CrossRef]
- Martin, T.P. Shells of atoms. Phys. Rep. 1996, 273, 199–241. [Google Scholar] [CrossRef]
- Mughal, A.; Chan, H.; Weaire, D.; Hutzler, S. Dense packings of spheres in cylinders: Simulations. Phys. Rev. E 2012, 85, 051305. [Google Scholar] [CrossRef]
- Mughal, A.; Chan, H.K.; Weaire, D. Phyllotactic description of hard sphere packing in cylindrical channels. Phys. Rev. Lett. 2011, 106, 115704. [Google Scholar] [CrossRef]
- Pickett, G.T.; Gross, M.; Okuyama, H. Spontaneous chirality in simple systems. Phys. Rev. Lett. 2000, 85, 3652. [Google Scholar] [CrossRef]
- Fu, L.; Steinhardt, W.; Zhao, H.; Socolar, J.E.; Charbonneau, P. Hard sphere packings within cylinders. Soft Matter 2016, 12, 2505–2514. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181. [Google Scholar] [CrossRef]
- Nelson, D.R.; Halperin, B. Dislocation-mediated melting in two dimensions. Phys. Rev. B 1979, 19, 2457. [Google Scholar] [CrossRef]
- Young, A. Melting and the vector Coulomb gas in two dimensions. Phys. Rev. B 1979, 19, 1855. [Google Scholar] [CrossRef]
- Zahn, K.; Lenke, R.; Maret, G. Two-stage melting of paramagnetic colloidal crystals in two dimensions. Phys. Rev. Lett. 1999, 82, 2721. [Google Scholar] [CrossRef]
- Irvine, W.T.M.; Bowick, M.J.; Chaikin, P.M. Fractionalization of interstitials in curved colloidal crystals. Nat. Mater. 2012, 11, 948–951. [Google Scholar] [CrossRef]
- Bowick, M.J.; Nelson, D.R.; Shin, H. Interstitial fractionalization and spherical crystallography. Phys. Chem. Chem. Phys. 2007, 9, 6304–6312. [Google Scholar] [CrossRef]
- Chen, Y.; Yao, Z.; Tang, S.; Tong, H.; Yanagishima, T.; Tanaka, H.; Tan, P. Morphology selection kinetics of crystallization in a sphere. Nat. Phys. 2021, 17, 121–127. [Google Scholar] [CrossRef]
- Wang, J.; Mbah, C.F.; Przybilla, T.; Englisch, S.; Spiecker, E.; Engel, M.; Vogel, N. Free energy landscape of colloidal clusters in spherical confinement. ACS Nano 2019, 13, 9005–9015. [Google Scholar] [CrossRef]
- Altschuler, E.L.; Williams, T.J.; Ratner, E.R.; Tipton, R.; Stong, R.; Dowla, F.; Wooten, F. Possible global minimum lattice configurations for Thomson’s problem of charges on a sphere. Phys. Rev. Lett. 1997, 78, 2681. [Google Scholar] [CrossRef]
- Wales, D.J.; Ulker, S. Structure and dynamics of spherical crystals characterized for the Thomson problem. Phys. Rev. B 2006, 74, 212101. [Google Scholar] [CrossRef]
- Pérez-Garrido, A.; Moore, M. Symmetric patterns of dislocations in Thomson’s problem. Phys. Rev. B 1999, 60, 15628. [Google Scholar] [CrossRef]
- Miller, W.L.; Cacciuto, A. Two-dimensional packing of soft particles and the soft generalized Thomson problem. Soft Matter 2011, 7, 7552–7559. [Google Scholar] [CrossRef]
- Bowick, M.; Cacciuto, A.; Nelson, D.R.; Travesset, A. Crystalline order on a sphere and the generalized Thomson problem. Phys. Rev. Lett. 2002, 89, 185502. [Google Scholar] [CrossRef] [PubMed]
- Bowick, M.J.; Giomi, L. Two-dimensional matter: Order, curvature and defects. Adv. Phys. 2009, 58, 449–563. [Google Scholar] [CrossRef]
- Pieranski, P. Two-dimensional interfacial colloidal crystals. Phys. Rev. Lett. 1980, 45, 569. [Google Scholar] [CrossRef]
- Gasser, U.; Eisenmann, C.; Maret, G.; Keim, P. Melting of crystals in two dimensions. ChemPhysChem 2010, 11, 963–970. [Google Scholar] [CrossRef] [PubMed]
- Luque, A.; Reguera, D.; Morozov, A.; Rudnick, J.; Bruinsma, R. Physics of shell assembly: Line tension, hole implosion, and closure catastrophe. J. Chem. Phys. 2012, 136, 184507. [Google Scholar] [CrossRef]
- Vest, J.-P.; Tarjus, G.; Viot, P. Glassy dynamics of dense particle assemblies on a spherical substrate. J. Chem. Phys. 2018, 148, 164501. [Google Scholar] [CrossRef]
- Asakura, S.; Oosawa, F. On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys. 1954, 22, 1255–1256. [Google Scholar] [CrossRef]
- Grason, G.M. Perspective: Geometrically frustrated assemblies. J. Chem. Phys. 2016, 145, 110901. [Google Scholar] [CrossRef]
- Joshi, D.; Bargteil, D.; Caciagli, A.; Burelbach, J.; Xing, Z.; Nunes, A.S.; Pinto, D.E.; Araújo, N.A.; Brujic, J.; Eiser, E. Kinetic control of the coverage of oil droplets by DNA-functionalized colloids. Sci. Adv. 2016, 2, e1600881. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Figueroa, S.E.; Gallegos-Lozano, A.; Mendoza, C.I. Packing core-corona particles on a spherical surface. Soft Matter 2022, 18, 6812–6824. [Google Scholar] [CrossRef] [PubMed]
- Chantawansri, T.L.; Bosse, A.W.; Hexemer, A.; Ceniceros, H.D.; Garcia-Cervera, C.J.; Kramer, E.J.; Fredrickson, G.H. Self-consistent field theory simulations of block copolymer assembly on a sphere. Phys. Rev. E 2007, 75, 031802. [Google Scholar] [CrossRef] [PubMed]
- Hain, T.M.; Schröder-Turk, G.E.; Kirkensgaard, J.J. Patchy particles by self-assembly of star copolymers on a spherical substrate: Thomson solutions in a geometric problem with a color constraint. Soft Matter 2019, 15, 9394–9404. [Google Scholar] [CrossRef] [PubMed]
- Jiménez-Millán, S.; García-Alcántara, C.; Ramírez-Hernández, A.; Sambriski, E.; Hernández, S. Self-Aassembly of core-corona colloids under cylindrical confinement: A Monte Carlo study. J. Mol. Liq. 2021, 335, 116219. [Google Scholar] [CrossRef]
- Kramer, E.J. Melted by mistakes. Nature 2005, 437, 824–825. [Google Scholar] [CrossRef] [PubMed]
- Tobochnik, J.; Chapin, P.M. Monte Carlo simulation of hard spheres near random closest packing using spherical boundary conditions. J. Chem. Phys. 1988, 88, 5824–5830. [Google Scholar] [CrossRef]
- Giarritta, S.P.; Ferrario, M.; Giaquinta, P. Statistical geometry of hard particles on a sphere. Phys. A 1992, 187, 456–474. [Google Scholar] [CrossRef]
- Binks, B.P.; Clint, J.H. Solid wettability from surface energy components: Relevance to Pickering emulsions. Langmuir 2002, 18, 1270–1273. [Google Scholar] [CrossRef]
- Dinsmore, A.; Hsu, M.F.; Nikolaides, M.; Marquez, M.; Bausch, A.; Weitz, D. Colloidosomes: Selectively permeable capsules composed of colloidal particles. Science 2002, 298, 1006–1009. [Google Scholar] [CrossRef]
- Kralchevsky, P.A.; Nagayama, K. Capillary interactions between particles bound to interfaces, liquid films and biomembranes. Adv. Colloid Interface Sci. 2000, 85, 145–192. [Google Scholar] [CrossRef] [PubMed]
- Travesset, A. Binary nanoparticle superlattices of soft-particle systems. Proc. Natl. Acad. Sci. USA 2015, 112, 9563–9567. [Google Scholar] [CrossRef] [PubMed]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Predictive self-assembly of polyhedra into complex structures. Science 2012, 337, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.Y.; Ross, B.M.; Hong, S.; Lee, L.P. Bioinspired nanocorals with decoupled cellular targeting and sensing functionality. Small 2010, 6, 503–507. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Glotzer, S.C. Self-assembly of patchy particles. Nano Lett. 2004, 4, 1407–1413. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, A.; Misra, B. Grafting: A versatile means to modify polymers: Techniques, factors and applications. Prog. Polym. Sci. 2004, 29, 767–814. [Google Scholar] [CrossRef]
- Frederick, K.K.; Marlow, M.S.; Valentine, K.G.; Wand, A.J. Conformational entropy in molecular recognition by proteins. Nature 2007, 448, 325–329. [Google Scholar] [CrossRef]
- Thaner, R.V.; Kim, Y.; Li, T.I.; Macfarlane, R.J.; Nguyen, S.T.; Olvera de la Cruz, M.; Mirkin, C.A. Entropy-driven crystallization behavior in DNA-mediated nanoparticle assembly. Nano Lett. 2015, 15, 5545–5551. [Google Scholar] [CrossRef]
- Rogers, W.B.; Shih, W.M.; Manoharan, V.N. Using DNA to program the self-assembly of colloidal nanoparticles and microparticles. Nat. Rev. Mater. 2016, 1, 16008. [Google Scholar] [CrossRef]
- Huang, Z.; Lu, C.; Dong, B.; Xu, G.; Ji, C.; Zhao, K.; Yan, L.-T. Chain stiffness regulates entropy-templated perfect mixing at single-nanoparticle level. Nanoscale 2016, 8, 1024–1032. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, R.; Xu, G.; Huang, Z.; Yan, L.-T. Entropy-mediated mechanical response of the interfacial nanoparticle patterning. Nano Lett. 2014, 14, 6910–6916. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Mondal, A.; Reddy, C.M. Harnessing molecular rotations in plastic crystals: A holistic view for crystal engineering of adaptive soft materials. Chem. Soc. Rev. 2020, 49, 8878–8896. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- van Anders, G.; Klotsa, D.; Ahmed, N.K.; Engel, M.; Glotzer, S.C. Understanding shape entropy through local dense packing. Proc. Natl. Acad. Sci. USA 2014, 111, E4812–E4821. [Google Scholar] [CrossRef] [PubMed]
- Haji-Akbari, A.; Engel, M.; Keys, A.S.; Zheng, X.; Petschek, R.G.; Palffy-Muhoray, P.; Glotzer, S.C. Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra. Nature 2009, 462, 773–777. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Glotzer, S.C. Entropically engineered formation of fivefold and icosahedral twinned clusters of colloidal shapes. Nat. Commun. 2022, 13, 7362. [Google Scholar] [CrossRef] [PubMed]
- Cersonsky, R.K.; van Anders, G.; Dodd, P.M.; Glotzer, S.C. Relevance of packing to colloidal self-assembly. Proc. Natl. Acad. Sci. USA 2018, 115, 1439–1444. [Google Scholar] [CrossRef]
- van Anders, G.; Ahmed, N.K.; Smith, R.; Engel, M.; Glotzer, S.C. Entropically Patchy Particles: Engineering Valence through Shape Entropy. ACS Nano 2014, 8, 931–940. [Google Scholar] [CrossRef]
- Smallenburg, F.; Löwen, H. Close packing of rods on spherical surfaces. J. Chem. Phys. 2016, 144, 164903. [Google Scholar] [CrossRef]
- de Folter, J.W.J.; Hutter, E.M.; Castillo, S.I.R.; Klop, K.E.; Philipse, A.P.; Kegel, W.K. Particle Shape Anisotropy in Pickering Emulsions: Cubes and Peanuts. Langmuir 2014, 30, 955–964. [Google Scholar] [CrossRef]
- Giomi, L.; Bowick, M. Crystalline order on Riemannian manifolds with variable Gaussian curvature and boundary. Phys. Rev. B 2007, 76, 054106. [Google Scholar] [CrossRef]
- Gómez, L.R.; García, N.A.; Vitelli, V.; Lorenzana, J.; Vega, D.A. Phase nucleation in curved space. Nat. Commun. 2015, 6, 6856. [Google Scholar] [CrossRef] [PubMed]
- Garcia, N.A.; Pezzutti, A.D.; Register, R.A.; Vega, D.A.; Gómez, L.R. Defect formation and coarsening in hexagonal 2D curved crystals. Soft Matter 2015, 11, 898–907. [Google Scholar] [CrossRef] [PubMed]
- Burke, C.J.; Mbanga, B.L.; Wei, Z.; Spicer, P.T.; Atherton, T.J. The role of curvature anisotropy in the ordering of spheres on an ellipsoid. Soft Matter 2015, 11, 5872–5882. [Google Scholar] [CrossRef]
- Sausset, F.; Tarjus, G.; Nelson, D.R. Structure and dynamics of topological defects in a glassy liquid on a negatively curved manifold. Phys. Rev. E 2010, 81, 031504. [Google Scholar] [CrossRef] [PubMed]
- Hexemer, A.; Vitelli, V.; Kramer, E.J.; Fredrickson, G.H. Monte Carlo study of crystalline order and defects on weakly curved surfaces. Phys. Rev. E 2007, 76, 051604. [Google Scholar] [CrossRef] [PubMed]
- Marzec, C.J.; Day, L.A. Pattern formation in icosahedral virus capsids: The papova viruses and Nudaurelia capensis beta virus. Biophys. J. 1993, 65, 2559–2577. [Google Scholar] [CrossRef]
- Caspar, D.L.; Klug, A. Physical principles in the construction of regular viruses. Cold Spring Harbor Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef]
- Ganser, B.K.; Li, S.; Klishko, V.Y.; Finch, J.T.; Sundquist, W.I. Assembly and analysis of conical models for the HIV-1 core. Science 1999, 283, 80–83. [Google Scholar] [CrossRef]
- Schneider, S.; Gompper, G. Shapes of crystalline domains on spherical fluid vesicles. Europhys. Lett. 2005, 70, 136. [Google Scholar] [CrossRef]
- Rossier-Miranda, F.; Schroën, C.; Boom, R. Colloidosomes: Versatile microcapsules in perspective. Colloids Surf. A 2009, 343, 43–49. [Google Scholar] [CrossRef]
- Thompson, K.L.; Williams, M.; Armes, S.P. Colloidosomes: Synthesis, properties and applications. J. Colloid Interface Sci. 2015, 447, 217–228. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N.; Elsesser, M.T.; Pine, D.J. Dense packing and symmetry in small clusters of microspheres. Science 2003, 301, 483–487. [Google Scholar] [CrossRef] [PubMed]
- Meng, G.; Arkus, N.; Brenner, M.P.; Manoharan, V.N. The free-energy landscape of clusters of attractive hard spheres. Science 2010, 327, 560–563. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N.; Pine, D.J. Building materials by packing spheres. MRS Bull. 2004, 29, 91–95. [Google Scholar] [CrossRef]
- Manoharan, V.N. Colloidal spheres confined by liquid droplets: Geometry, physics, and physical chemistry. Solid State Commun. 2006, 139, 557–561. [Google Scholar] [CrossRef]
- Soni, V.; Gómez, L.R.; Irvine, W.T. Emergent geometry of inhomogeneous planar crystals. Phys. Rev. X 2018, 8, 011039. [Google Scholar] [CrossRef]
- Yao, Z.; De La Cruz, M.O. Topological defects in flat geometry: The role of density inhomogeneity. Phys. Rev. Lett. 2013, 111, 115503. [Google Scholar] [CrossRef]
- Jiménez, F.L.; Stoop, N.; Lagrange, R.; Dunkel, J.; Reis, P.M. Curvature-controlled defect localization in elastic surface crystals. Phys. Rev. Lett. 2016, 116, 104301. [Google Scholar] [CrossRef]
- Brojan, M.; Terwagne, D.; Lagrange, R.; Reis, P.M. Wrinkling crystallography on spherical surfaces. Proc. Natl. Acad. Sci. USA 2015, 112, 14–19. [Google Scholar] [CrossRef]
- Breid, D.; Crosby, A.J. Curvature-controlled wrinkle morphologies. Soft Matter 2013, 9, 3624–3630. [Google Scholar] [CrossRef]
- Bruss, I.R.; Grason, G.M. Non-Euclidean geometry of twisted filament bundle packing. Proc. Natl. Acad. Sci. USA 2012, 109, 10781–10786. [Google Scholar] [CrossRef] [PubMed]
- Grason, G.M. Defects in crystalline packings of twisted filament bundles. I. Continuum theory of disclinations. Phys. Rev. E 2012, 85, 031603. [Google Scholar] [CrossRef] [PubMed]
- Hall, D.M.; Bruss, I.R.; Barone, J.R.; Grason, G.M. Morphology selection via geometric frustration in chiral filament bundles. Nat. Mater. 2016, 15, 727–732. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wan, H.; Gao, L.; Wu, Y.; Yan, L.-T. Self-Assembly in Curved Space: Ordering, Defect and Entropy. Processes 2024, 12, 119. https://doi.org/10.3390/pr12010119
Wang Y, Wan H, Gao L, Wu Y, Yan L-T. Self-Assembly in Curved Space: Ordering, Defect and Entropy. Processes. 2024; 12(1):119. https://doi.org/10.3390/pr12010119
Chicago/Turabian StyleWang, Yuming, Haixiao Wan, Lijuan Gao, Yibo Wu, and Li-Tang Yan. 2024. "Self-Assembly in Curved Space: Ordering, Defect and Entropy" Processes 12, no. 1: 119. https://doi.org/10.3390/pr12010119




